2. 中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国人民解放军91053部队,北京 100070
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. No.91053 Unit of PLA, Beijing 100070, China
一直以来,近岸海域水上水下地形测量是海洋工程领域的一项重要内容,对于海运安全、港口领航、维护国家主权、沿海城市及岛礁的海洋开发、规划决策等都具有重要意义[1]。近岸海域周围具有环境复杂、缺乏先验信息和海况恶劣等特点,而无人水面艇作为一种小型智能无人平台,具备自主感知环境信息、路径规划、自主航行的能力,可通过人工预置或自主信息采集处理的方式完成环境感知、目标识别与探测、自主规划等多种任务。近年来,相关研究人员针对不同的任务需求进行水运航道、水库、岛屿等水域的水上水下地形测量。但在测量过程中,多以人工设定测量路径的方式为主[2-5],在测量区域较大或较为复杂的情况下,需耗费巨大人力、物力和财力,且布设测量路径带有人为主观性,影响最终测量效果。
操文芷[6]使用电子海图与雷达图像叠加匹配方式,在此基础上进行无人水面艇路径规划,可有效进行障碍物规避以及局部路径规划动任务。刘强等[7]采用船载多传感器一体化测量技术对海岛礁、港口地区与水中构筑物、湖泊、库区进行测量,完成了对测量区域的水上水下一体化点云无缝拼接。苗润龙等[8]使用基于重复海湾和遗漏海湾的搜索行为设计方法完成了海洋自主航行器多海湾区域完全遍历路径规划试验,规划结果在遍历性、重复率方面优于其他遍历方法。上海大学 “精海3号”无人艇水面船在金塘大桥附近按设定的规划航线进行测绘工作,因人为规划航线只能扫测航线所覆盖部分的区域,钟雨轩等[9]提出一种考虑主动方向的动态栅格法与启发式搜索算法的无人水面艇岛礁海域完全遍历路径规划方法,并通过了仿真验证。
由现研究现状分析知,在进行水上水下一体化测量时均将海图作为已知输入,若在未知地形复杂的近岸海域进行测量工作时,无法进行测量相关的路径规划工作,同时易出现搁浅、刮底事故,不能保障研究人员及设备安全。因此,设计一种能够适应近岸复杂的水上水下环境,准确感知周围态势信息并合理规划测量路径的方法是解决以上问题的关键。现阶段,采用具有自主定位、导航、感知及控制功能的无人水面艇,携带相关测量设备,无疑是解决上述问题、并可以更快、更经济和更安全地完成近岸水上水下地形测量任务的一种理想手段。本文以USV为研究平台,搭载导航雷达、深度计、POS MV、多波束测深仪及激光扫描仪和其他必要设备,面向近岸地形测量任务需求,基于离线电子海图,实现测量路径在线规划,以完全覆盖预设待测量海域,最终获取未知环境的水上水下地形地貌。首先,基于感知、测量设备信息,实现在线地图构建工作[10],本文的在线地图信息输入来自于雷达感知及深度计信息,其中,雷达感知数据提供无人水面艇所在环境周围态势信息,由深度计提供无人水面艇实时深度信息,通过POS MV获取USV实时位姿,融合信息输入,实时构建测量地图。在此基础上,采用基于神经元激励方法下的完全遍历路径规划设计,结合A星算法路径搜寻优势防止路径规划锁死,为USV提供安全有效的规划路径,提高USV测量工作的安全性、合理性、有效性。同时,考虑实时水深对测量设备扫测的影响,自主调节测量路径的梳型间距,以达到要求的扫描重叠率,实现完全覆盖预定测量区域[11]。
1 地图构建方法设计首先,存在一个基本问题,即如何使用地图描述测量区域环境,目前已存在多种地图表示方法,主要分为栅格地图、特征地图和拓扑地图3类[12]。本文采用栅格地图方式,使用占据概率的栅格地图将测量区域分成若干相同边长的栅格,将每个栅格分配概率值以表示被障碍物占据的可能性大小。无人艇搭载导航雷达和深度计设备,实时更新栅格地图,根据路径规划方法生成符合海底地形测量要求的实时梳型路径[13-14],能应对复杂环境下各类问题,在实时性和安全性方面具有较强优势[15]。
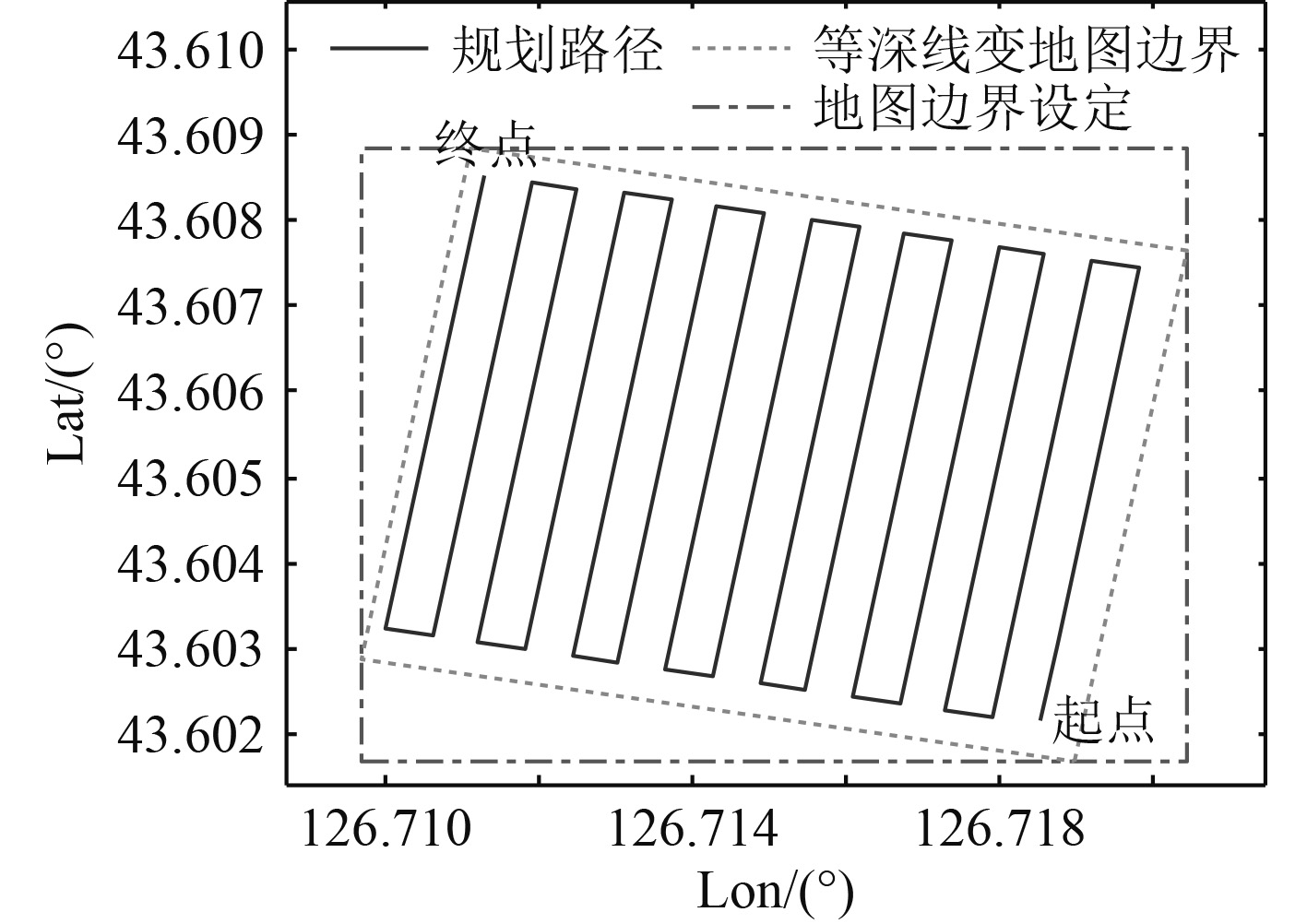
|
图 3 初始全局完全遍历路径规划结果 Fig. 3 Initial global complete traversal path planning result |
在线地图构建过程如图1所示。其中,基准地图是指由初始离线地图和实时的雷达感知信息以及水深等信息所构建的实时地图,地图北向为等深线[16]由深至浅方向;测量地图是由基准地图作为输入,根据水深情况以及海底地形测量标准需求更新栅格大小,该地图直接用于测量路径规划算法输入。
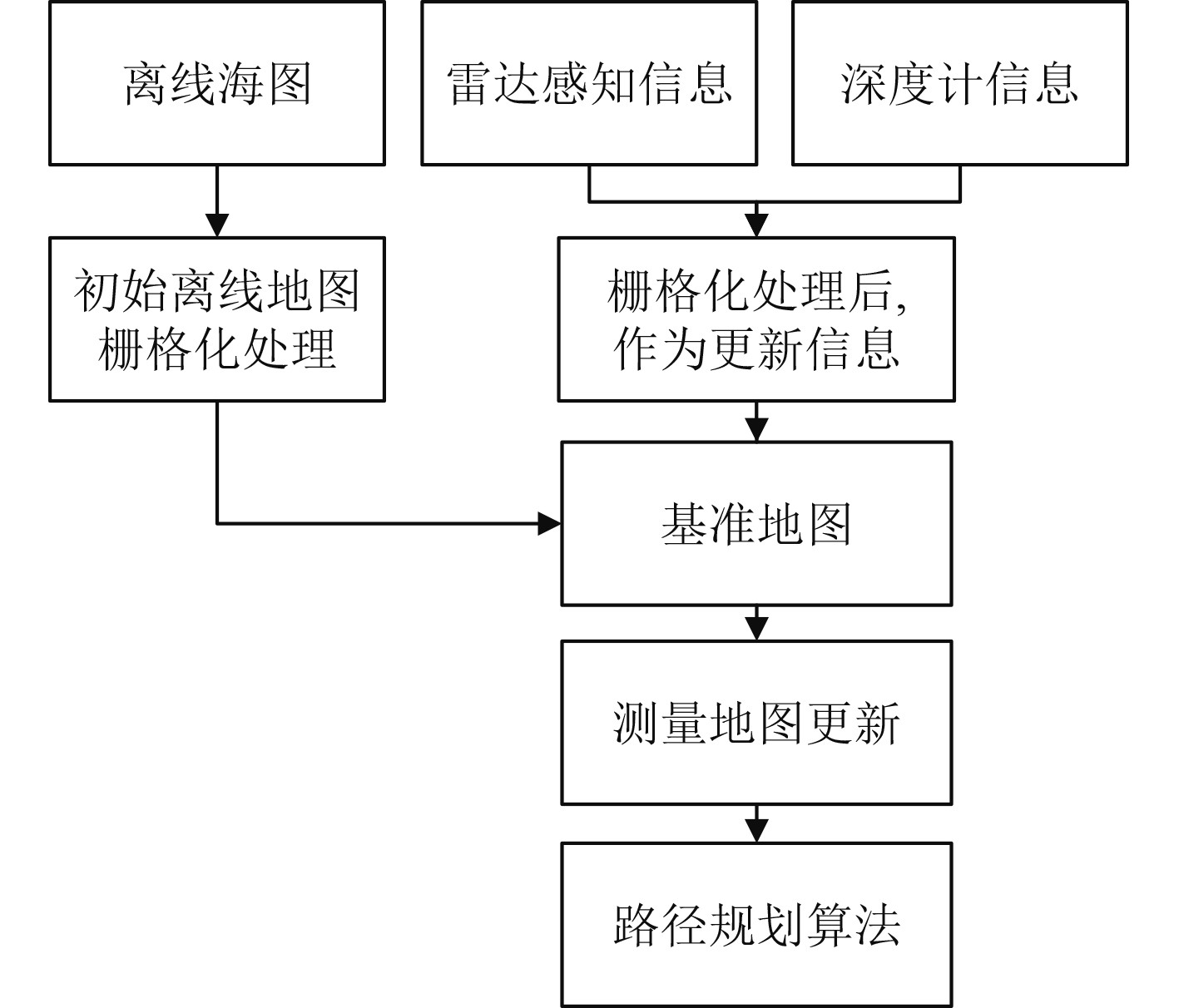
|
图 1 在线地图构建流程图 Fig. 1 Flow chart of online map construction |
地图构建采用一种基于贝叶斯估计方式的占据栅格建图方法。占据栅格地图把测量范围分解成若干二元随机变量填充的栅格,分为占据或空闲2种状态。每一个栅格具有独立性,估计环境地图需要对每个独立的栅格进行估计,更新地图时,通过传感器观测结果计算获得[17]。
初始离线地图/基准地图采用一系列二值随机变量表示,该二值数据表示该位置是否被占据,即是否存在障碍物[18],而待更新地图处理方法是对二值随机变量进行后验估计。现已知USV位姿信息
| $ m{\text{ = }}\left\{ {{m_{ij}}} \right\},i \in \left( {0,M} \right],j \in \left( {0,N} \right] 。$ | (1) |
其中,
| $ p\left( {m|{z_{1:k}},{x_{1:k}}} \right) = \prod\nolimits_j^N {\prod\nolimits_i^M {p\left( {{m_{ij}}|{z_{1:k}},{x_{1:k}}} \right)} }。$ | (2) |
地图中每个栅格单元的占据概率由静态二值贝叶斯滤波方法获得,该方法依靠传感器的测量信息来估计环境地图中一个固定的二值数,该二值数分别表示此次更新为占据或空闲,且假设地图在此期间的状态不改变。该方法中,占据概率用后验概率的对数几率表示,以保证0和1附近数值的稳定性。
则在时刻
| $ {p_{k,ij}}{\text{ = log}}\frac{{p\left( {{m_{ij}}|{z_{1:k}},{x_{1:k}}} \right)}}{{1 - p\left( {{m_{ij}}|{z_{1:k}},{x_{1:k}}} \right)}} 。$ | (3) |
因此,可得后验概率为:
| $ p\left({m}_{ij}|{z}_{1:k},{x}_{1:k}\right)\text=1\text-\frac{1}{1\text+{2}^{{p}_{k\text{,}ij}}} 。$ | (4) |
证明式(3)。
对于后验概率,由贝叶斯准则有:
| $ p\left( {{m_{ij}}|{z_{1:k}},{x_{1:k}}} \right) = \frac{{p\left( {{z_k}|{m_{ij}},{x_{1:k}},{z_{1:k - 1}}} \right) \cdot p\left( {{m_{ij}}|{x_{1:k}},{z_{1:k - 1}}} \right)}}{{p\left( {{z_k}|{x_{1:k}},{z_{1:k - 1}}} \right)}}。$ | (5) |
对于
| $ p\left( {{z_k}|{m_{ij}},{x_{1:k}},{z_{1:k - 1}}} \right) = p\left( {{z_k}|{m_{ij}},{x_k}} \right) ,$ | (6) |
| $ p\left( {{z_k}|{x_{1:k}},{z_{1:k - 1}}} \right) = p\left( {{z_k}|{x_k}} \right) 。$ | (7) |
再对
| $ p\left( {{z_k}|{m_{ij}},{x_k}} \right){\text{ = }}\frac{{p\left( {{m_{ij}}|{z_k},{x_k}} \right) \cdot p\left( {{z_k}|{x_k}} \right)}}{{p\left( {{m_{ij}}|{x_k}} \right)}}。$ | (8) |
在
| $\begin{aligned}[b] & p\left( {{m_{ij}}|{z_{1:k}},{x_{1:k}}} \right) =\\ & \frac{{p\left( {{m_{ij}}|{z_k},{x_k}} \right) \cdot p\left( {{z_{1:k}}|{x_{1:k}}} \right) \cdot p\left( {{m_{ij}}|{x_{1:k - 1}},{z_{1:k - 1}}} \right)}}{{p\left( {{m_{ij}}} \right) \cdot p\left( {{z_k}|{x_k}} \right)}}= \\ & \frac{{p\left( {{m_{ij}}|{z_k},{x_k}} \right) \cdot p\left( {{m_{ij}}|{x_{1:k - 1}},{z_{1:k - 1}}} \right)}}{{p\left( {{m_{ij}}} \right)}} 。\end{aligned} $ | (9) |
其中,分布
对于
| $ \begin{aligned}[b] & p\left( {\overline {{m_{ij}}} |{z_{1:k}},{x_{1:k}}} \right)= \\ & \frac{{p\left( {\overline {{m_{ij}}} |{z_k},{x_k}} \right) \cdot p\left( {{z_{1:k}}|{x_{1:k}}} \right) \cdot p\left( {\overline {{m_{ij}}} |{x_{1:k - 1}},{z_{1:k - 1}}} \right)}}{{p\left( {\overline {{m_{ij}}} } \right) \cdot p\left( {{z_k}|{x_k}} \right)}}= \\ & \frac{{\left[ {1 - p\left( {{m_{ij}}|{z_k},{x_k}} \right)} \right] \cdot \left[ {1 - p\left( {{m_{ij}}|{x_{1:k - 1}},{z_{1:k - 1}}} \right)} \right]}}{{1 - p\left( {{m_{ij}}} \right)}}。\end{aligned} $ | (10) |
则式(9)除以式(10),并取对数,可得:
| $ \begin{split} {p_{k,ij}} =& \log \left( {\frac{{p\left( {{m_{ij}}|{z_{1:k}},{x_{1:k}}} \right)}}{{p\left( {\overline {{m_{ij}}} |{z_{1:k}},{x_{1:k}}} \right)}}} \right) = \log \frac{{p\left( {{m_{ij}}|{z_k},{x_k}} \right)}}{{1 - p\left( {{m_{ij}}|{z_k},{x_k}} \right)}} - \\ &\log \frac{{p\left( {{m_{ij}}} \right)}}{{1 - p\left( {{m_{ij}}} \right)}} + {p_{k - 1,ij}} 。\end{split} $ | (11) |
其中,
| $ {p_{0,ij}} = \log \frac{{p\left( {{m_{ij}}} \right)}}{{1 - p\left( {{m_{ij}}} \right)}} 。$ | (12) |
则有:
| $ {p_{k,ij}} = \log \frac{{p\left( {{m_{ij}}|{z_k},{x_k}} \right)}}{{1 - p\left( {{m_{ij}}|{z_k},{x_k}} \right)}} - {p_{0,ij}} + {p_{k - 1,ij}}。$ | (13) |
式中,
将式(13)更新方式为迭代更新,则有:
| $ {p_k} = \log \frac{{p\left( {m|{z_k},{x_k}} \right)}}{{1 - p\left( {m|{z_k},{x_k}} \right)}} + {p_{k - 1}} 。$ | (14) |
对于环境中未被探索区域中栅格,设初始化值
由于无人艇在不同位姿
| $ p\left( {{m_{ij}}|{z_k},{x_k}} \right) = f\left( {{x_k},{d_R},{\kappa _{ij}},{p_{{S_{ij}}}}} \right) 。$ | (15) |
其中,
初始离线地图栅格化边长或输入雷达感知信息和深度计信息所构成的栅格边长设为
| $ S = \frac{1}{2}\sum\limits_{i = 1}^n {\left( {{x_i}{y_{i + 1}} - {x_{i + 1}}{y_i}} \right)} 。$ | (16) |
式中,
通过以上方法得到基准地图每个栅格的面积大小。由此可得面积覆盖比率,等效为面积覆盖概率,有
| $ {p_{{S_{ij}}}} = \frac{1}{{{L^2}}}\sum\limits_{k = 1}^K {{S_k}}。$ | (17) |
式中:
将式(15)结果代入式(3)获得在时刻
测量地图的设定需按照海底地形测量及多波束扫描重复率相关要求进行设计。首先,确定测量地图栅格边长
| $ \begin{split} {L_{sd}} =& ceil\left( {{{\varGamma \cdot \left( {1 + \eta } \right)} \mathord{\left/ {\vphantom {{\Gamma \cdot \left( {1 + \eta } \right)} {\frac{{\Gamma \cdot \left( {1 + \eta } \right)}}{{2 \cdot {d_{wat}} \cdot \tan \left( {{\raise0.7ex\hbox{$\Omega $} \mathord{\left/ {\vphantom {\Omega 2}}\right.} \lower0.7ex\hbox{$2$}}} \right)}} + 1}}} \right. } {\frac{{\varGamma \cdot \left( {1 + \eta } \right)}}{{2 \cdot {d_{wat}} \cdot \tan \left( {{\raise0.7ex\hbox{$\varOmega $} \mathord{\left/ {\vphantom {\Omega 2}}\right.} \lower0.7ex\hbox{$2$}}} \right)}} + 1}}} \right) =\\ & ceil\left( {\frac{{\varGamma \cdot \left( {1 + \eta } \right) \cdot 2 \cdot {d_{wat}} \cdot \tan \left( {{\raise0.7ex\hbox{$\varOmega $} \mathord{\left/ {\vphantom {\Omega 2}}\right.} \lower0.7ex\hbox{$2$}}} \right)}}{{\varGamma \cdot \left( {1 + \eta } \right) + 2 \cdot {d_{wat}} \cdot \tan \left( {{\raise0.7ex\hbox{$\varOmega $} \mathord{\left/ {\vphantom {\Omega 2}}\right.} \lower0.7ex\hbox{$2$}}} \right)}}} \right),L < {L_{sd}} < {L_{s{d_{\max }}}},\end{split} $ | (18) |
| $ {L_{s{d_{\max }}}} = floor\left( {2 \cdot {d_l} \cdot \sin \left( {{\raise0.7ex\hbox{$\varOmega $} \mathord{\left/ {\vphantom {\Omega 2}}\right.} \lower0.7ex\hbox{$2$}}} \right)} \right)。$ | (19) |
式中:
然后,将基准地图信息按照上述使用面积法求取概率,并依据式(17)求出在时刻
在
| $ \left\{ \begin{gathered} Q = \lambda + c\tau ,c\tau \ll \lambda,\\ \lambda = \frac{1}{x} 。\end{gathered} \right. $ | (20) |
式中:
| $ \begin{split} & \tau = 1 - \frac{{4\left| \delta \right|}}{{3{\text{π}} }} \cdot \frac{{{d_m}}}{{\sqrt 2 }}, \\ & \delta \in - \frac{{3{\text{π}} }}{4}:\frac{{\text{π}} }{4}:\frac{{3{\text{π}} }}{4}, \\ & {d_m} \in \left[ {1,\sqrt 2 } \right] 。\end{split} $ | (21) |
式中:
将式(21)代入式(20),分别选择当前栅格周围的7个栅格(不计上一周期所在栅格,尽量避免USV原地掉头)作为下一移动目标,在其中选择活性值最大的作为移动目标。
在实际海底地形测量过程中,无人艇所在区域环境复杂,由于海底地形测量要求以及无人艇操纵性限制,在路径规划过程中可能出现锁死现象,因此加入A*算法[20]作为疏导策略,寻找距离当前位置最近的非障碍物栅格位置。同时,对A*所规划路径进行平滑处理,使得无人艇最快速度到达指定栅格位置。
此外,在出现危险状况时,如突然进入测量区域的非合作船舶、水深变浅等,伴随测量地图的变化,进行路径重规划工作,为防止再次将已完成测量的区域作为规划区域,在进行测量路径重规划时,将历史形式区域神经元活性值置-1,以保证测量工作的高效性。
在Matlab仿真平台下,设定测量地图
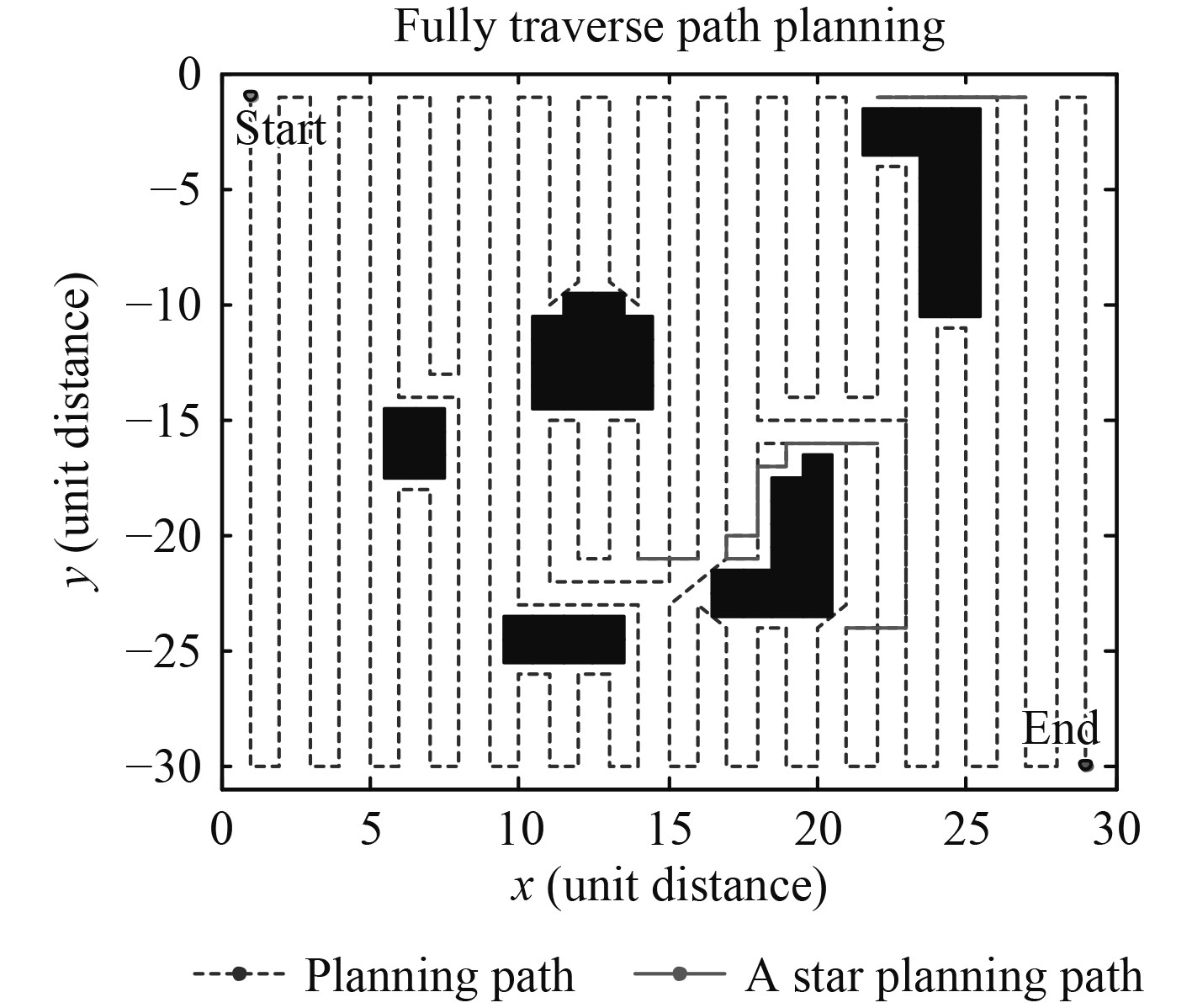
|
图 2 完全遍历路径规划仿真结果 Fig. 2 Simulation results of complete traversal path planning |
可知,该路径规划方法可在复杂环境中较好地规划出符合海底地形测量标准的梳型路径,对所测区域进行全覆盖遍历,且有效避免了规划过程中出现规划锁死现象,以最快方式到达符合要求的下一规划位置,继续完成路径规划任务。这种方法在实际的复杂环境中具有较好的环境适应性和安全性,尤其可较好地应对未知海域岛岸环境。
3 实航验证情况基于水上水下一体化无人测量任务需求,以中科院沈阳自动化研究所研制的“问海”号无人水面测量艇作为试验平台,对本文提出的在线地图构建方法和完全遍历路径规划方法在松花湖某区域进行实航验证。
设定测量区域为700 m×800 m近岸水域,多波束扫描重复率设置值
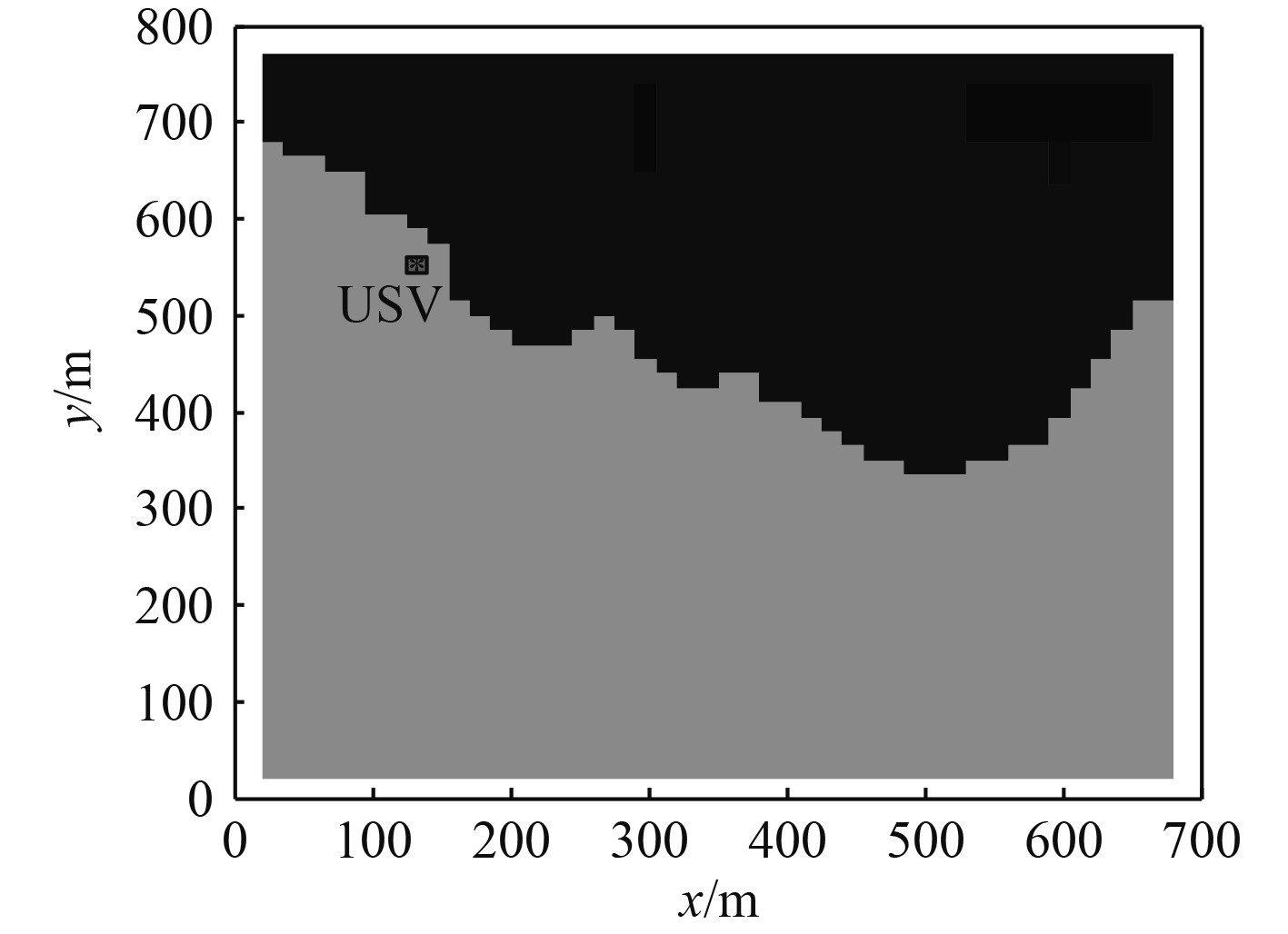
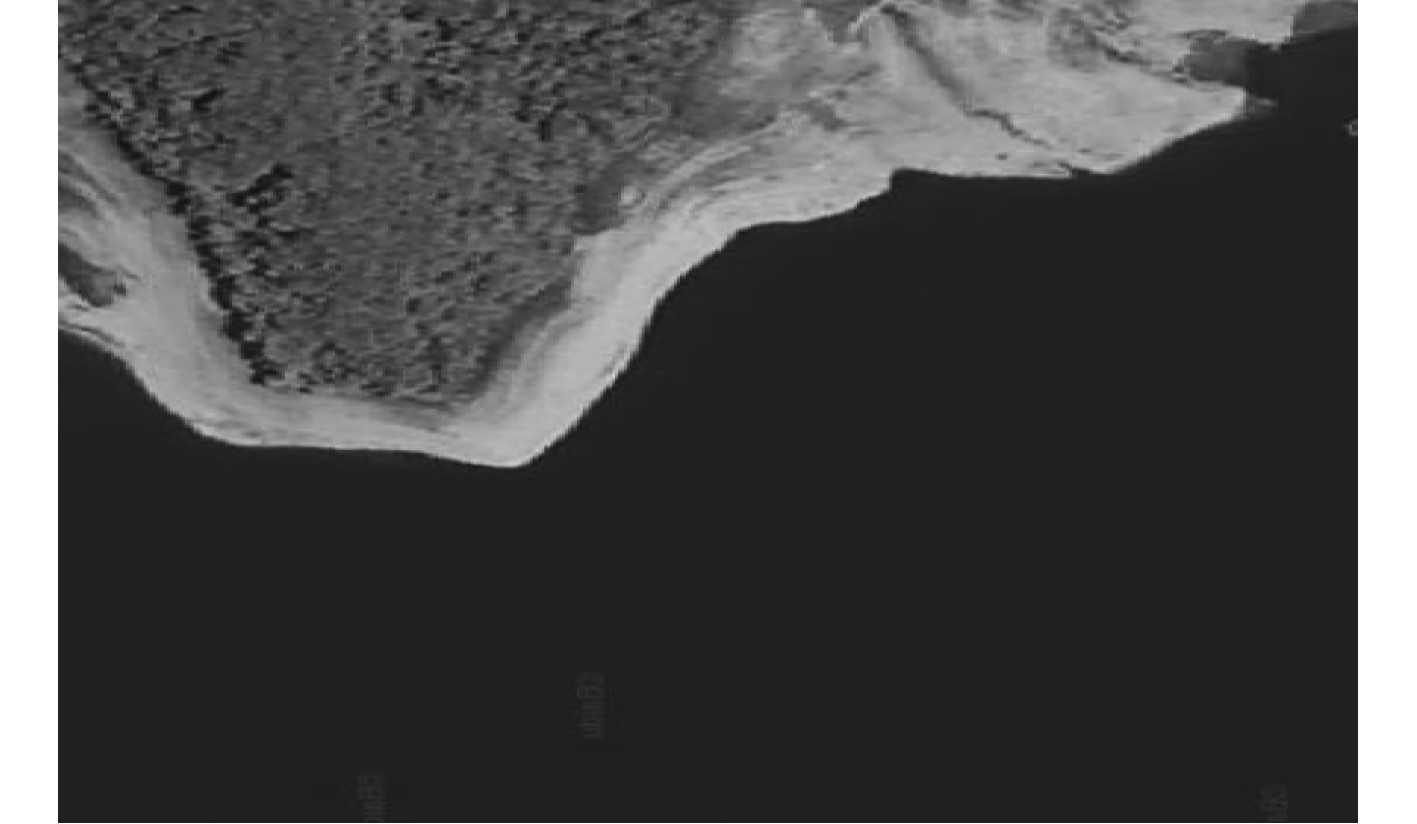
由试验结果分析可知,在设定测量区域后,问海号USV可实时感知周围环境。经过实时的雷达感知信息栅格化处理以及占据概率计算形成数据更新源,实时改变基准地图,最终构建测量地图,经过与实际的测量区域卫星图比对,地图构建精度满足测量路径规划要求。基准地图的实时更新驱动路径规划方法的重规划功能,如图5和图7所示。此时USV在图中所示的起点位置附近,按照路径规划方法设计,其能够在此种环境中进行任意的梳型路径规划,且可保证避免规划过程中的锁死情况。通过图8和图10可知,基于完全遍历路径规划方法,可实现待测区域的测量路径全覆盖。图11为一体化成图效果,完成了水上水下的无缝拼接。然后对测量质量进行评估,多波束测深仪测量内均方差不大于0.03 m,可形成1∶500数字高程地图。该结果满足测量精度和测量效率的要求,即本文提出的在线地图构建方法以及完全遍历路径规划方法设计合理可行,测量结果满足海洋工程地形测量规范要求。

|
图 4 初次基准地图构建结果 Fig. 4 Initial baseline map construction results |

|
图 5 初次路径重规划结果 Fig. 5 Result of the initial path replanning |

|
图 6 二次雷达感知信息处理结果 Fig. 6 Results of secondary radar sensing information processing |
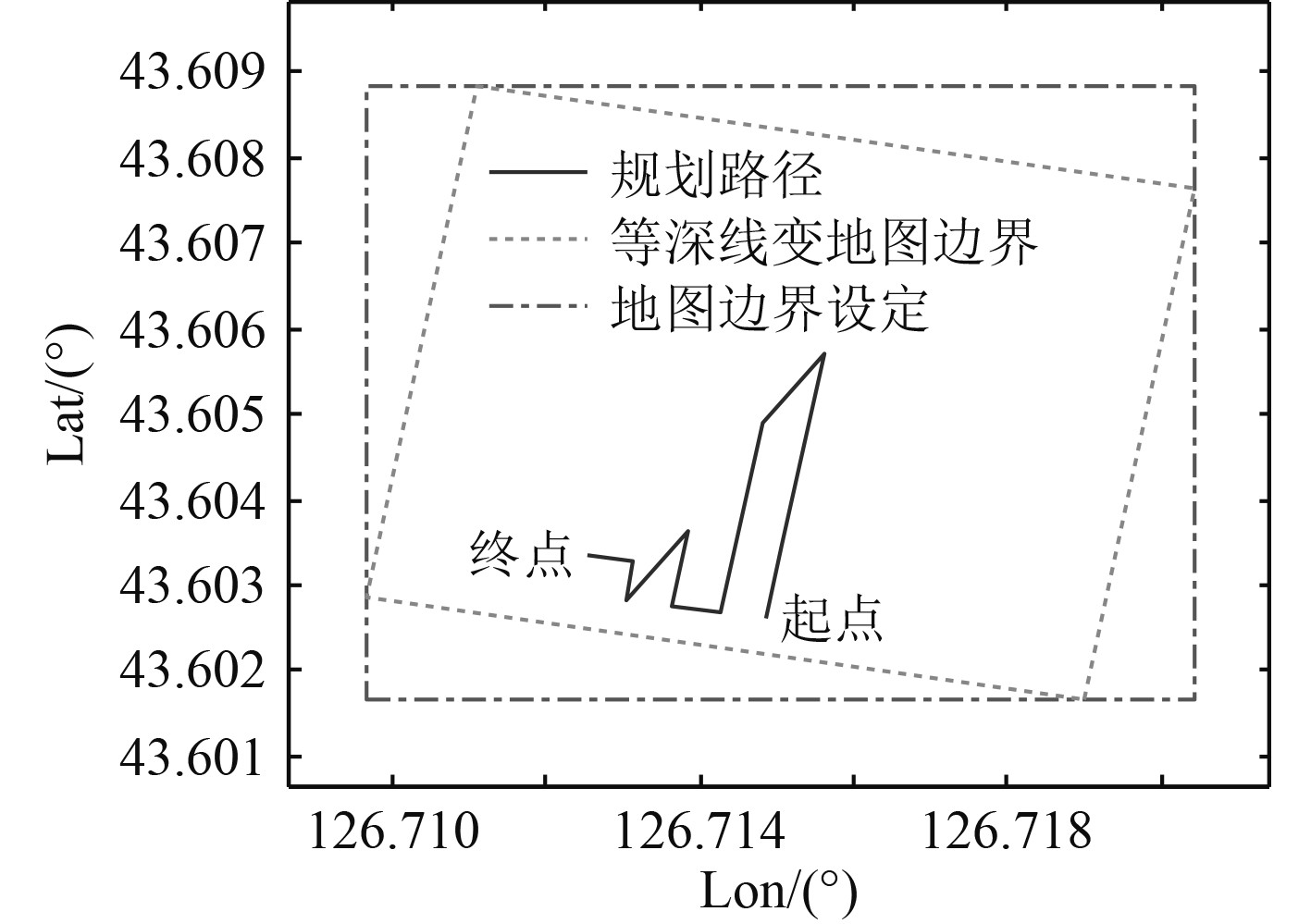
|
图 7 二次路径重规划结果 Fig. 7 Result of the secondary path replanning |
|
图 8 测量地图构建结果 Fig. 8 Mapping and updating map construction results |
|
图 9 测量区域卫星图截图 Fig. 9 Screenshot of satellite image of measurement area |

|
图 10 USV航行路径结果 Fig. 10 USV navigation path result |

|
图 11 水上水下一体化无人测量结果效果图 Fig. 11 Above and underwater integrated unmanned measurement result rendering |
针对近岸水域周边的地形测量需求,本文提出基于贝叶斯估计的在线地图构建方法和完全遍历路径规划方法,给出了一种解决方案,并利用无人水面测量艇进行了实航验证,测量结果满足海洋工程地形测量规范要求。通过试验结果,分析可得出结论如下:
1)USV搭载导航雷达、深度计、多波束测深仪及激光测距仪等设备,使用基于贝叶斯估计的在线地图构建方法,该基准地图与实际环境相比平均误差不大于15 m,可保证无人艇航行安全;
2)基于在线地图构建结果,通过完全遍历路径规划方法得到符合近岸水域地形测量要求的规划路径。USV依据规划路径内容执行,实现了对预定水域水上水下地形测量的全覆盖,可使多波束点云数据进行无缝拼接,测量结果满足海洋工程地形测量规范标准,即表明了设计方案的可行性。
按本文方法设计,USV在搭载指定设备后,可自主完成近岸水域地形的测量工作。
| [1] |
金久才, 张杰, 等. 自动表面船用于岛礁水深测绘[J]. 海洋技术, 2010, 29(2): 5-8. |
| [2] |
赵培, 王之顺, 叶瑞峰, 等. 无人测量船在水库水下地形测量中的应用[J]. 经纬天地, 2018(01): 68-71. DOI:10.3969/j.issn.1673-7563.2018.01.022 |
| [3] |
赵春明, 叶作安, 谢志茹, 等. 水上水下一体化测量技术探讨[J]. 中国水运, 2016, 16(9): 288-290. ZHAO Chunming, YE Zuoan, XIE Zhiru, et al. Discussion on integrated measurement technology of water and underwater[J]. China Water Transport, 2016, 16(9): 288-290. |
| [4] |
范彦斌, 张晓飞, 孙祝友, 等. 连云港赣榆港区水下地形地貌研究[J]. 地质学刊, 2017, 41(4): 652-654. DOI:10.3969/j.issn.1674-3636.2017.04.019 |
| [5] |
张倩, 梅赛, 石波, 等. 船载水上水下一体化测量技术及应用——以舟山册子岛为例[J]. 海洋地质前沿, 2019, 35(9): 70-75. DOI:10.16028/j.1009-2722.2019.09011 |
| [6] |
操文芷. 基于电子海图和航海雷达的无人水面艇路径规划研究[D]. 大连: 大连海事大学, 2017.
|
| [7] |
刘强, 翟国君, 卢秀山. 船载传感器一体化测量技术与应用[J]. 测绘通报, 2019(10): 127-132. |
| [8] |
苗润龙, 庞硕, 姜大鹏, 等. 海洋自主航行器多海湾区域完全遍历路径规划[J]. 测绘学报, 2019, 48(2): 256-264. DOI:10.11947/j.AGCS.2019.20180385 |
| [9] |
钟雨轩, 葛磊, 张鑫, 等. 无人水面艇岛礁海域完全遍历路径规划[J]. 上海大学学报, 2017, 23(1): 18-26. |
| [10] |
危双丰, 庞帆, 刘振彬, 等. 基于激光雷达的同时定位与地图构建方法综述[J]. 计算机应用研究, 2020, 37(2): 327-332. DOI:10.19734/j.issn.1001-3695.2018.09.0674 |
| [11] |
于鹏. 浅海水下地形雷达成像理论研究与应用[D]. 上海: 华东师范大学, 2017.
|
| [12] |
殷波. 移动机器人同时定位与地图创建方法研究[D]. 青岛: 中国海洋大学, 2006.
|
| [13] |
SHIN Y S, LEE Y J, CHOI H T, et al. Bundle adjustment from sonar images and SLAM application for seafloor mapping [C] //OCEANS 2015 - MTS/IEEE Conf. Exhib, Washington, DC, USA: IEEE, 2015: 1–6.
|
| [14] |
JIE L, MICHAEL K, RYAN M. E, et al. Pose-graph SLAM using forward-looking sonar [C] //Robotics and Automation Letters IEEE, vol. 3, no. 3, USA: IEEE, 2018: 2330–2337.
|
| [15] |
柴进柱. 水深测量作业中的测线布设与实施策略研究[J]. 海洋测绘, 2013, 33(3): 44-46. DOI:10.3969/j.issn.1671-3044.2013.03.011 |
| [16] |
李靖涵. 海底地貌自动制图综合算法研究[D]. 郑州: 战略支援部队信息工程大学, 2018.
|
| [17] |
夏天. 基于激光2D-SLAM的地图构建算法研究[D]. 杭州: 杭州电子科技大学, 2020.
|
| [18] |
魏杨. 基于激光雷达的即时定位与制图技术[D]. 哈尔滨: 哈尔滨工业大学, 2017.
|
| [19] |
王仲民, 井平安, 朱博. 基于神经元激励的移动机器人遍历路径规划[J]. 控制工程, 2017, 24(2): 284–286.
|
| [20] |
郭强. 基于改进的A星算法和B样条函数的仿生机器鱼路径规划研究[D]. 天津: 天津大学, 2011.
|
 2023, Vol. 45
2023, Vol. 45

