0 引　言

由于空间狭小，当前对导弹发射试验筒内部管道的监测主要还是依赖人工目测，由于管道深度大、光线暗，造成人工检测困难，给管道的维护和保养带来难度。为更加客观掌握管道内部状态^[1]，保证设备运行的可靠性，需要对试验筒内部的管道状态进行全面的检查和勘验。

国外从20世纪40年代开始研究，90年代初得到迅猛的发展，并研制了许多实验样机。韩国延世大学^[2]研制了履带式管道机器人PAROYS-II，适用于400~700 mm的管道，可通过弯管和锥形管。日本立命馆大学^[3-4]研发了一种支撑轮式管道内机器人，该机器人采用一种不完全驱动的平行四边形驱动机构，在遇到管内障碍时，履带可从普通形状转变为平行四边形形状，提高了机器人的拖缆能力。韩国成均馆大学^[5]研发了MRINSPECT系列管道机器人，其中MRINSPECT VII为最新的一代，该机器人基于多轴差速齿轮机构，通过机械调节主动车轮的速度而无需任何控制工作，以适应如直管或弯管等管道环境。国内对管道机器人的研究始于20世纪60年代，邓宗全等^[6]研制了一种六独立轮式管内检测牵引机器人，唐德威等^[7]研制了一种三轴差动式管道机器人，该机器人在水平直管、弯管及障碍管道的通过性较好，适用于直径为310 mm左右的管道，三轴差动式管道机器人整体只有一个电机，电机通过三轴差速机构实现全驱动。冯敬之^[8]1996 年研制出轮式驱动排水管道自动清淤机器人。

国内外针对狭窄空间的管道机器人研究较少，缺乏简单有效的结构设计，针对该问题，本文设计一种能够可用于狭小间隙内的轮式自适应变径管道机器人装置，使得管道机器人可在65~90 mm的管内自主行走，实现了对狭小变径管道的适应性。同时，对管道机器人驱动装置运行机理和力学特性、牵引能力以及弯管通过性进行分析。此外，配套的便携式手持视频显控平台可实时展现回传的视频画面，使工作人员对空调管内的状态进行实时诊断并对管道机器人进行反馈操作^[9]。

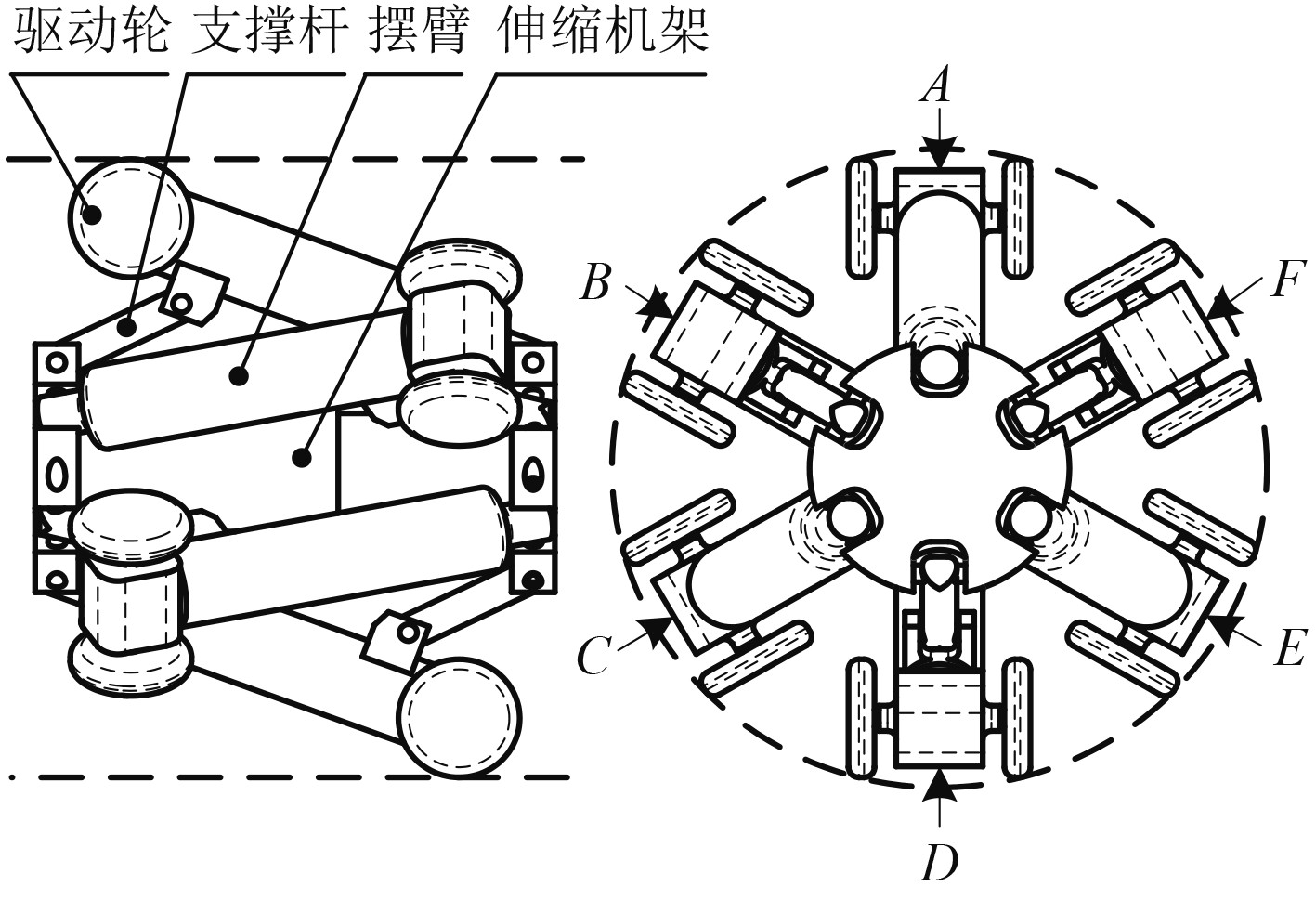
1 管道机器人运动特性分析 1.1 管道机器人工作原理

本文所设计的管道机器人可适应65~90 mm范围变化的管道。机器人主要由伸缩机架、摆臂、支撑杆和驱动轮组成，如图1所示。6个驱动轮按前向、后向2组相向布置，每组驱动轮在圆周方向上均匀分布。驱动电机选用微型直流行星减速电机，具有效率高、速度稳定、调速范围广等特点，在行星齿轮内孔配置有滚针轴承，可有效提高负载能力与寿命。管道内行进时，6组驱动电机分别通过齿轮传动机构带动驱动轮转动，使6组动力机构协同工作，依靠驱动轮与管壁间的摩擦力使管道机器人按照期望速度移动^[10]。

机器人在管道内行走时，拉伸弹簧处于变形状态，为驱动轮和管壁间提供正压力，驱动轮依靠这个压力产生的摩擦力实现爬升运动以及机体支撑^[11]。当行走装置行进至管径收缩部位，因为驱动轮紧贴管壁运动，会使摆臂向管径中心方向收缩，使伸缩机架伸长，以适应管径变化。当通过管径收缩部位后，在拉伸弹簧作用下，伸缩机架缩短，摆臂向管壁方向扩展，保证驱动轮与管壁之间时刻压紧。通过伸缩机架实现行走装置半径方向上的调整，提高了行走装置的通用性^[12]。

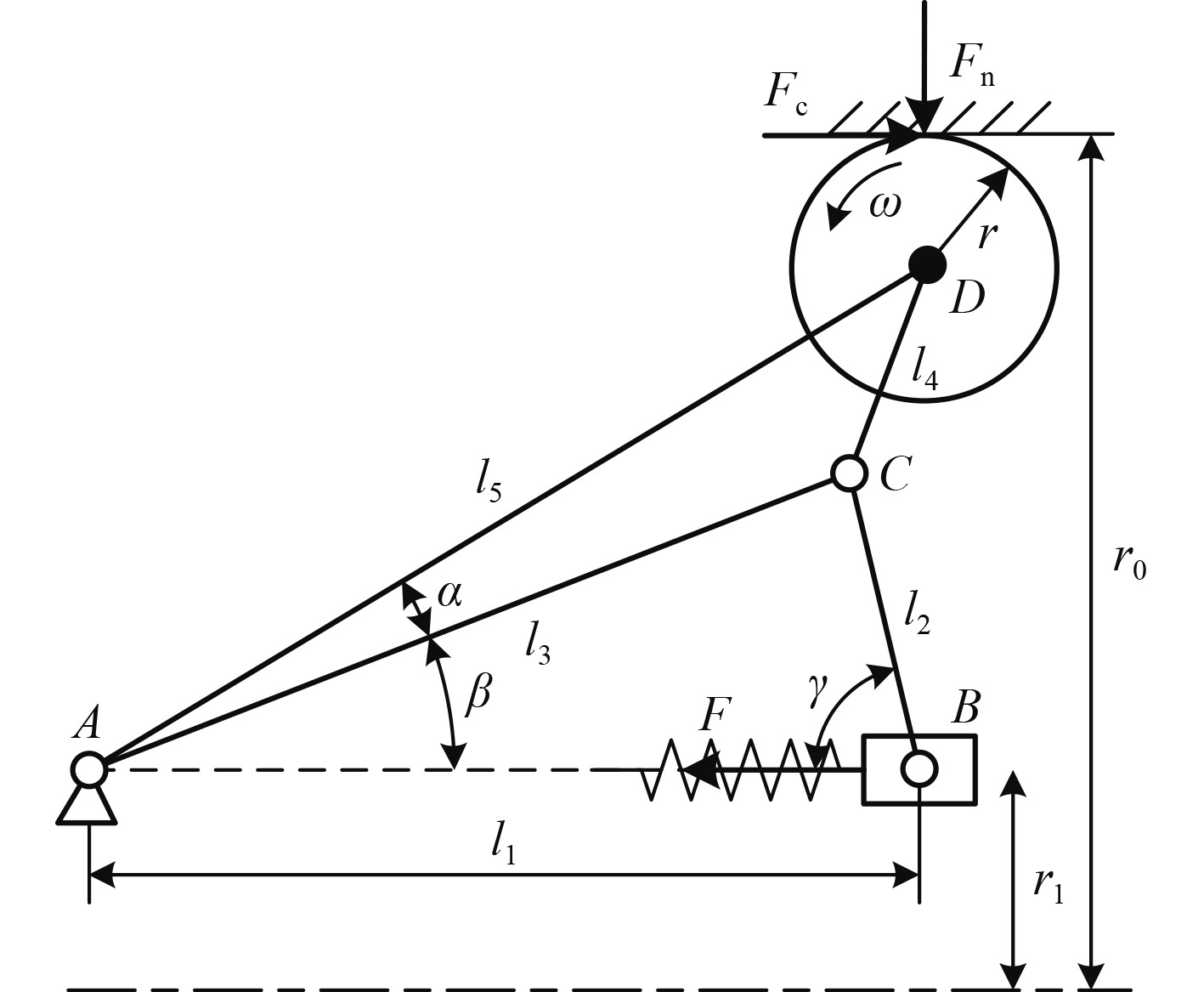
1.2 行走机构力学特性分析

对机器人在管道中行走时的受力情况进行分析，为便于分析，将每一组驱动轮简化为中间对称面上的当量驱动轮。以单个驱动轮为分析对象，受力情况如图2所示。

驱动轮在伸缩机架内部弹簧力的作用下，压紧在管道内壁上。机器人在内径为 $ r_{0} $ 的管道内行走时，机器人本体的固定参考铰接点A与移动铰接点B间的距离 $ l_{1} $ 为：

$ {l_1} = {l_3}\cos \beta + {l_2}\cos \gamma 。$

(1)

式中： $ {l_2} $ 为铰接点B与铰接点C间距离，m； $ I_{3} $ 为铰接点A与铰接点C间距离，m； $ \beta $ 为摆臂与伸缩机架间夹角， $ \beta = \arcsin \dfrac{{{r_0} - {r_1} - r}}{{{l_5}}} - \alpha $ ，rad； $ {r_1} $ 为铰接点A与铰接点B的偏心距，m； $ \alpha $ 为摆臂内部夹角， $ \alpha = {\text{arccos}}\dfrac{{l_3^2 + l_5^2 - l_4^2}}{{2{l_3}{l_5}}} $ ，rad； $ \gamma $ 为支撑杆与伸缩机架间夹角， $ \gamma = {\text{arcsin}}\dfrac{{{l_3}\sin \beta }}{{{l_2}}} $ ，rad。

伸缩机架内调整弹簧的伸长量 $ \Delta x $ 为：

$ \Delta x = {l_{\text{1}}} - {x_{\text{0}}}，$

(2)

式中： $ {x_{\text{0}}} $ 为调整弹簧的初始长度，m。

对于弹簧被拉伸时，支撑圆盘所收到的轴向拉力F可以表示为：

$ F = k\Delta x ，$

(3)

铰点C受到支撑圆盘的作用力为：

$ {F_{{B}}} = \frac{F}{{3\cos \gamma }}，$

(4)

分析以铰点A的受力情况，建立其力矩矩平衡方程为：

$ {F_{{B}}} = \frac{F}{{3\cos \gamma }}，$

(5)

管道内壁对驱动轮的正压力可表示为：

$ {F_n} = \frac{{{F_B}{l_{\text{1}}}{\sin}\gamma - {F_c}({r_{\text{0}}} - {r_{\text{1}}}{)}}}{{{l_5}\cos \left( {\alpha + \beta } \right)}}。$

(6)

式中： $ {F_{\text{c}}} $ 为驱动轮与管道内壁间摩擦力，N； $ {l_5} $ 为铰接点A与铰接点D间距离，m； $ {r_1} $ 为管道内壁半径，m； $ r $ 为驱动轮半径，m。

当驱动轮与管壁之间为纯滚动而不发生相对位移时，纵向驱动力 $ {F_{{c}}} $ 与管壁的法向支反力 $ {F_{{n}}} $ 满足关系式为：

$ {F_{{c}}} \leqslant {\mu _\varphi }{F_{\text{n}}} ，$

(7)

式中， $ {\mu _\varphi } $ 为橡胶驱动轮的附着系数。

根据式（6）与式（7），得到驱动轮与管壁不产生相对滑动时，管壁的极限法向支反力 $ {F_{{n}}} $ 为：

$ {F_{{n}}} = \frac{{{F_{\text{B}}}{l_{\text{1}}}{\text{sin}}\gamma }}{{{l_5}\cos \left( {\alpha + \beta } \right) + {\mu _\varphi }{(}{r_0} - {r_{\text{1}}}{)}}} ，$

(8)

再由式（7）与式（8）可推出驱动轮的最大驱动力表示为：

$ {F_{{c}}} = \frac{{{\mu _\varphi }{F_{\text{B}}}{l_{\text{1}}}{\text{sin}}\gamma }}{{{l_5}\cos \left( {\alpha + \beta } \right) + {\mu _\varphi }{(}{r_0} - {r_{\text{1}}}{)}}}。$

(9)

根据上述分析结果，绘制机器人的长度（铰接点A与铰接点B间距离）、单个驱动轮的最大牵引力与管道直径间的关系曲线，如图3所示。分析结果表明，随管道直径逐渐增大，机器人的长度逐渐减小，而单个驱动轮的最大牵引力先逐渐增大，后快速增大。

2 行走性能分析 2.1 过弯管时行走姿态分析

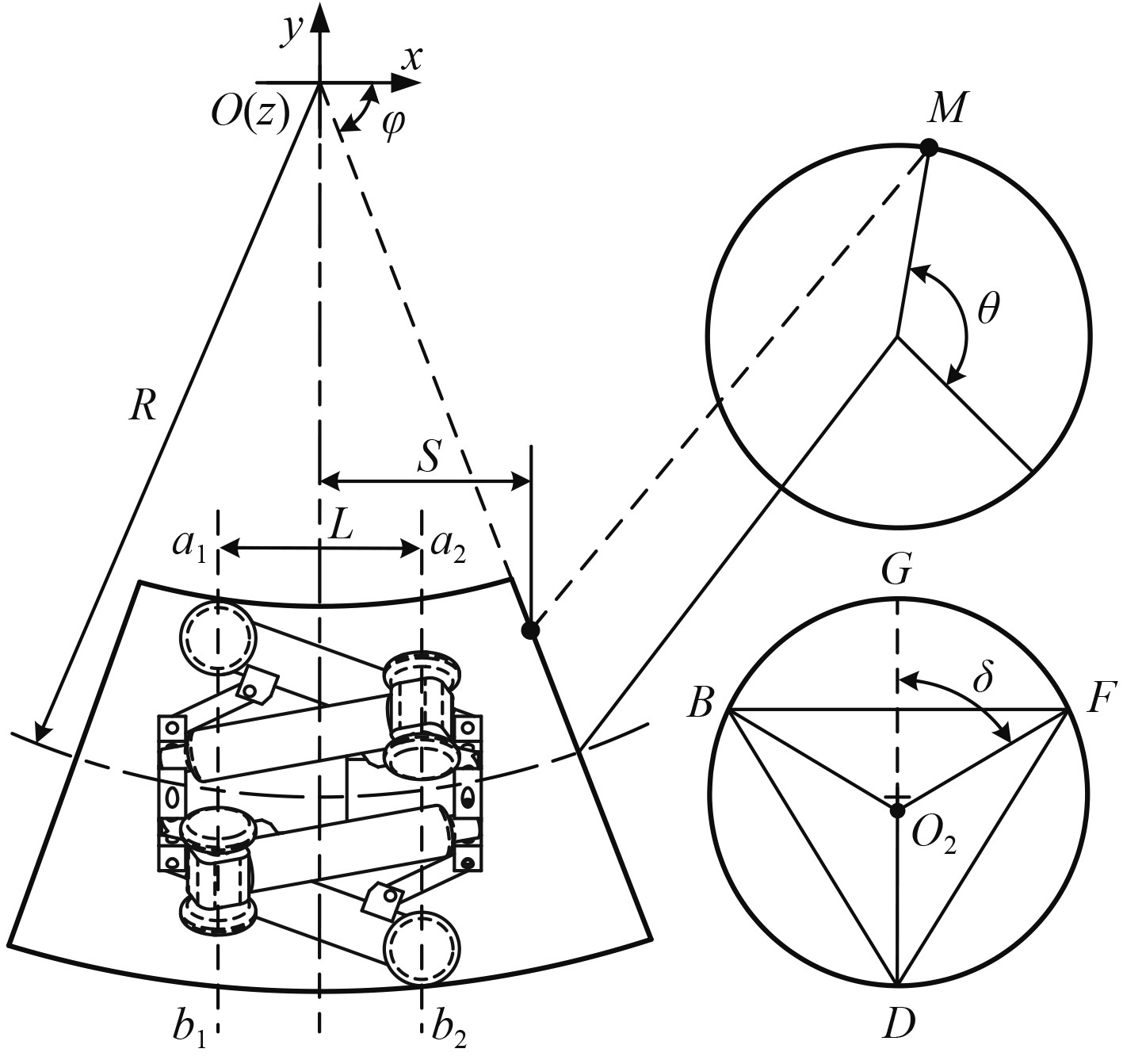
弯管是管道机器人在管道内行走时经常遇到的一种工况，也是考量管道机器人行走性能指标的一个重要参考^[13]。忽略管道机器人零部件的加工误差与装配误差因素，假设管道机器人在直管内行走时，前、后2组驱动轮与管道内壁均匀接触，各接触点的接触状态与接触力均相同。而在弯管内行走时，如图4所示，各接触点处弯管内壁曲率不同，导致接触状态均不相同。以a₁b₁与a₂b₂分别表示前、后2组驱动轮与管道内壁接触点形成的理论截面。

管道内壁任一轮壁接触点M的运动轨迹可表示为：

$ \left\{ \begin{gathered} M\left( {\varphi ,\theta } \right) = \left[ {S,S\tan \varphi ,{r_0}\sin \theta } \right]，\\ S = \left( {R + {r_0}\cos \theta } \right)\cos \varphi。\\ \end{gathered} \right. $

(10)

式中： $ R $ 为管道弯曲半径，m； $ S $ 为接触点M到弯管中心面的距离，m。

得到管道内壁的旋转曲面方程为：

$ {\left( {\sqrt {{x^2} + {y^2}} - R} \right)^{\text{2}}}+ {z^{\text{2}}} = r_0^2，$

(11)

由右侧3个驱动支腿B、D、F与管道内壁接触点确定的非圆截面a₂b₂方程为：

$ {\left( {\sqrt {\frac{{{L^2}}}{4} + {y^2}} - R} \right)^{\text{2}}} + {z^{\text{2}}} = r_0^2 ，$

(12)

截面a₂b₂处3个驱动支腿与管道内壁接触点组成等边三角形△BDF，存在：

$ \overline {BD} = \overline {BF} = \overline {DF}，$

(13)

顶部接触点的位移顶点为：

$ G = \left( {\frac{L}{2}, - \sqrt {{{\left( {R - {r_0}} \right)}^2} - \frac{{{L^2}}}{4}} ,0} \right)，$

(14)

$ {O_2} = \left( {\frac{L}{2},\frac{{{y_{{B}}} + {y_{{D}}} + {y_{{F}}}}}{3},\frac{{{z_{{B}}} + {z_{{D}}} + {z_{{F}}}}}{3}} \right) ，$

(15)

接触点F的姿态角δ为：

$ \delta = \arccos \frac{{{{\overline {{O_2}F} }^2} + {{\overline {{O_2}G} }^2} - {{\overline {FG} }^2}}}{{2\overline {{O_2}F} \overline {{O_2}G} }}。$

(16)

2.2 管内运动分析

管道机器人的牵引力由管道内壁与驱动轮间的摩擦力提供。最大牵引力取决于驱动轮与内壁间的正压力与摩擦系数。以整个机器人主体为研究对象，将各个驱动轮所产生的纵向驱动力求和，可得管道机器人能达到的最大总牵引力为：

$ F = {F_{\text{c}}} \times 6，$

(17)

对管道机器人在直管中的运动过程进行分析，机器人沿直管上升时运动方程为：

$ m a=6\left(\frac{T_{0} \eta i}{r}-\mu_{d} F_{2}\right)-m g \sin \vartheta。$

(18)

式中： $ m $ 为管道机器人质量，kg； $ a $ 为管道机器人加速度，m/s²； $ {T_{\text{O}}} $ 为电机驱动力矩，Nm； $ \eta $ 为传动机构效率； $ i $ 为传动机构减速比； $ {\mu _{\text{d}}} $ 为驱动轮与管壁间滚动摩擦系数； $ \vartheta $ 为管道倾角，rad。

机器人沿直管下降时的运动方程为：

$ m a=\sigma\left(\frac{T_{0} n f}{r_{d}}-\mu_{d} F_{d}\right)+m g \sin \vartheta 。$

(19)

2.3 越障能力分析

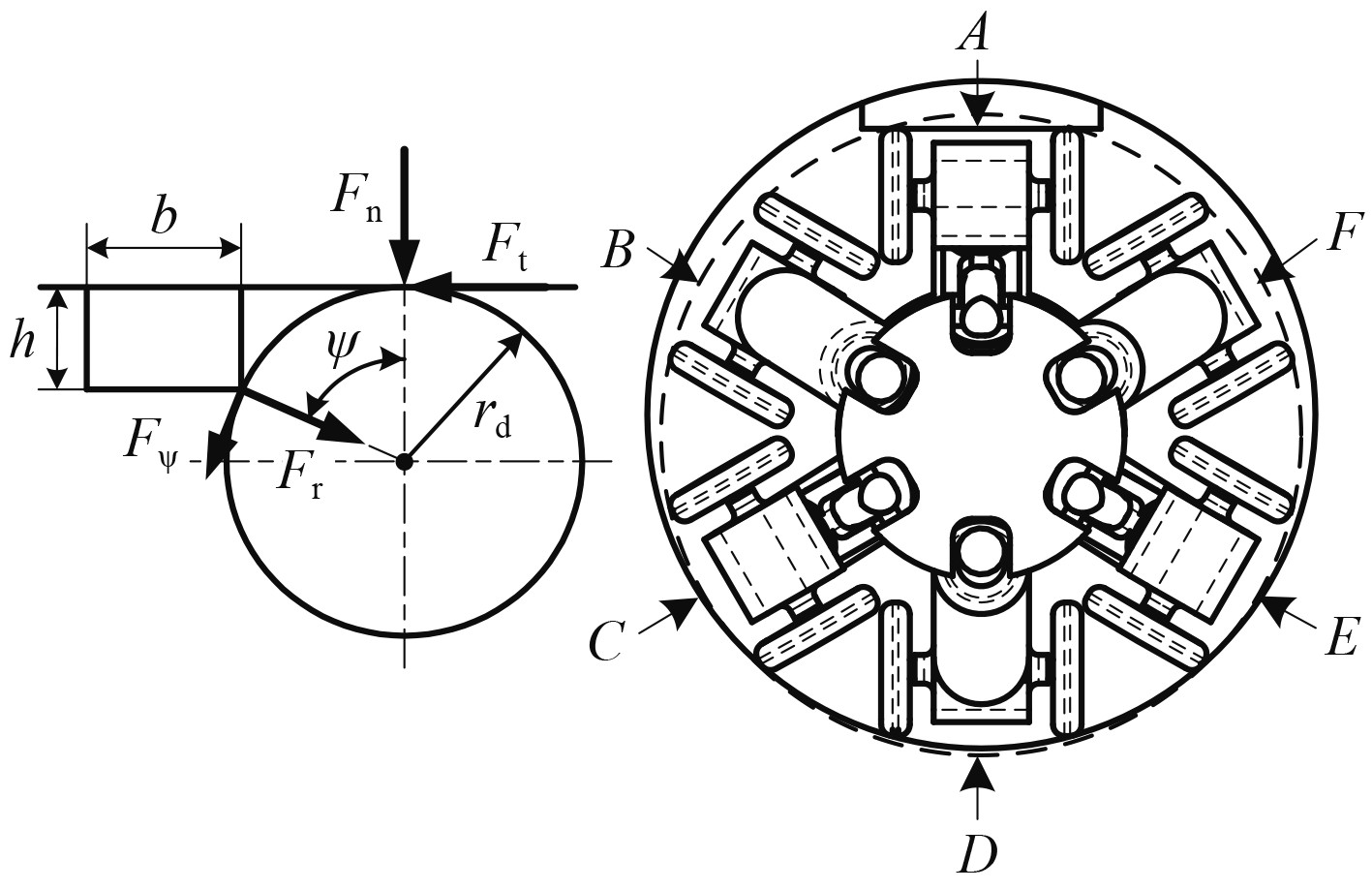
轮式变径管道机器人利用六轮独立驱动方式与伸缩机架适应管道适应管径变化，是保持足够牵引力与可靠接触的前提，对机器人在管道内的越障能力尤为重要。图5为机器人过凸起障碍时的力学分析模型。驱动轮越障瞬间，且轮与障碍间无相对滑动时，应有：

$ \begin{array}{l} F_{\mathrm{c}} l_{1} \sin \gamma-F_{\psi} l_{s} \sin (\alpha+\beta+\psi)- \\ F_{{r}} l_{5} \cos (\alpha+\beta+\psi)=0。\end{array} $

(20)

式中： $ \psi $ 为越障角， $ \psi {\text{ = }}\arccos \dfrac{{{r_{{d}}} - h}}{h} $ ，rad； $ {F_{{r}}} $ 为障碍接触点处支反力，N； $ {F_\psi } $ 为障碍接触点驱动力，N。

$ F_{p} \leqslant \varphi F_{{r}} ，$

(21)

机器人越障时的总牵引力 $ {F_0} $ 为：

$ F_{b}=\frac{3 T_{0} \eta I}{r_{d}}-2 \mu_{d} F_{t}-\mu_{d} F_{\tau}+\left(2 \mu_{\psi}-\sin \vartheta\right) m g。$

(22)

3 控制系统设计 3.1 管道机器人控制系统原理

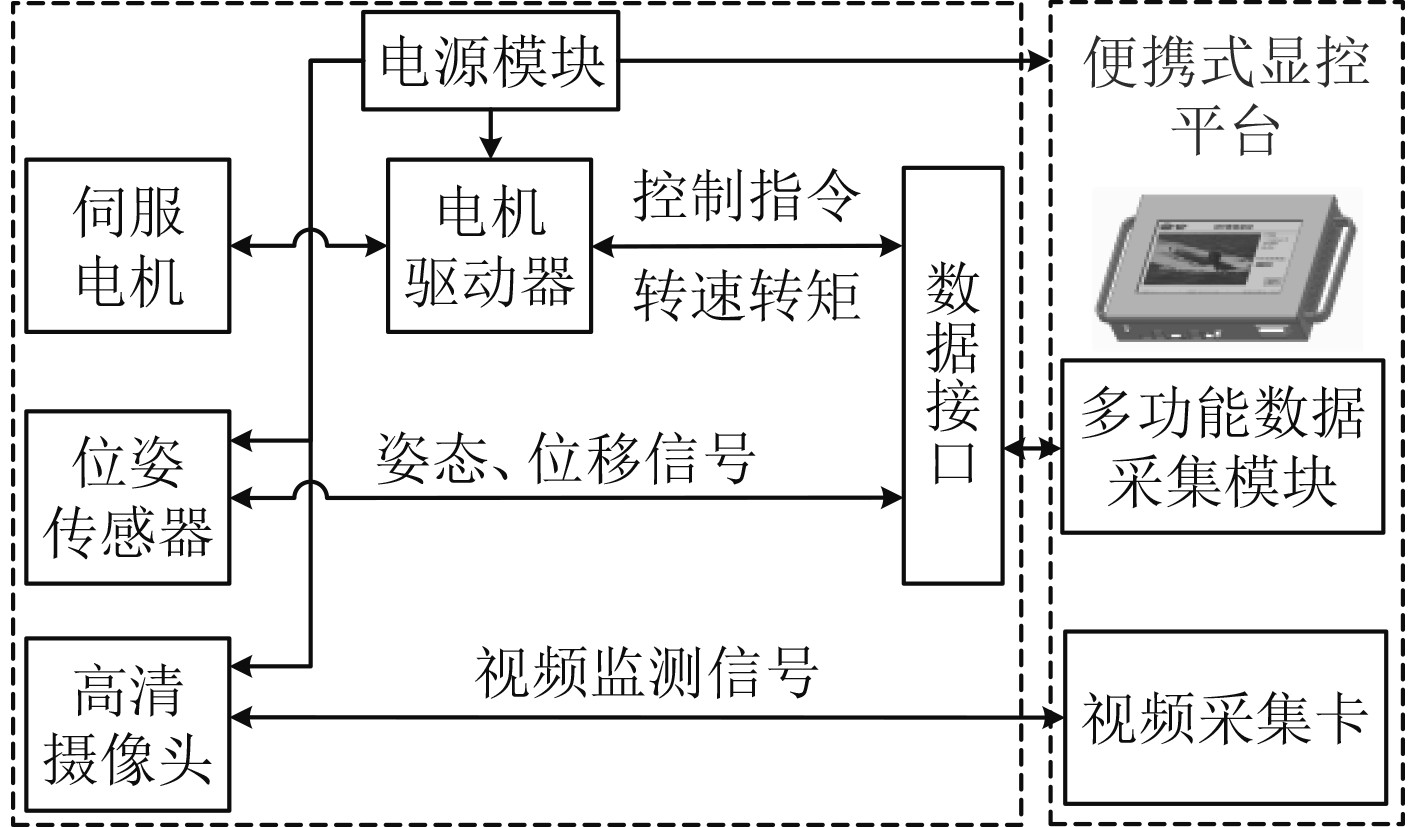
管道机器人控制系统工作原理如图6所示。便携式显控平台通过多功能数据采集卡发出行走装置行走指令^[14]，行走装置电机驱动器接收到控制指令后控制伺服电机转动，使行走装置在60～90 mm管径内自主行走。行走装置上安装有位姿传感器及高清红外摄像机，实时检测行走状态与管内状态，并将采集得到的传感信息与视频状态信息实时回传至便携式可移动显控平台工控主板，经多功能数据采集卡与视频采集卡转码处理后显示在高清液晶显示屏上。

3.2 控制系统硬件组成

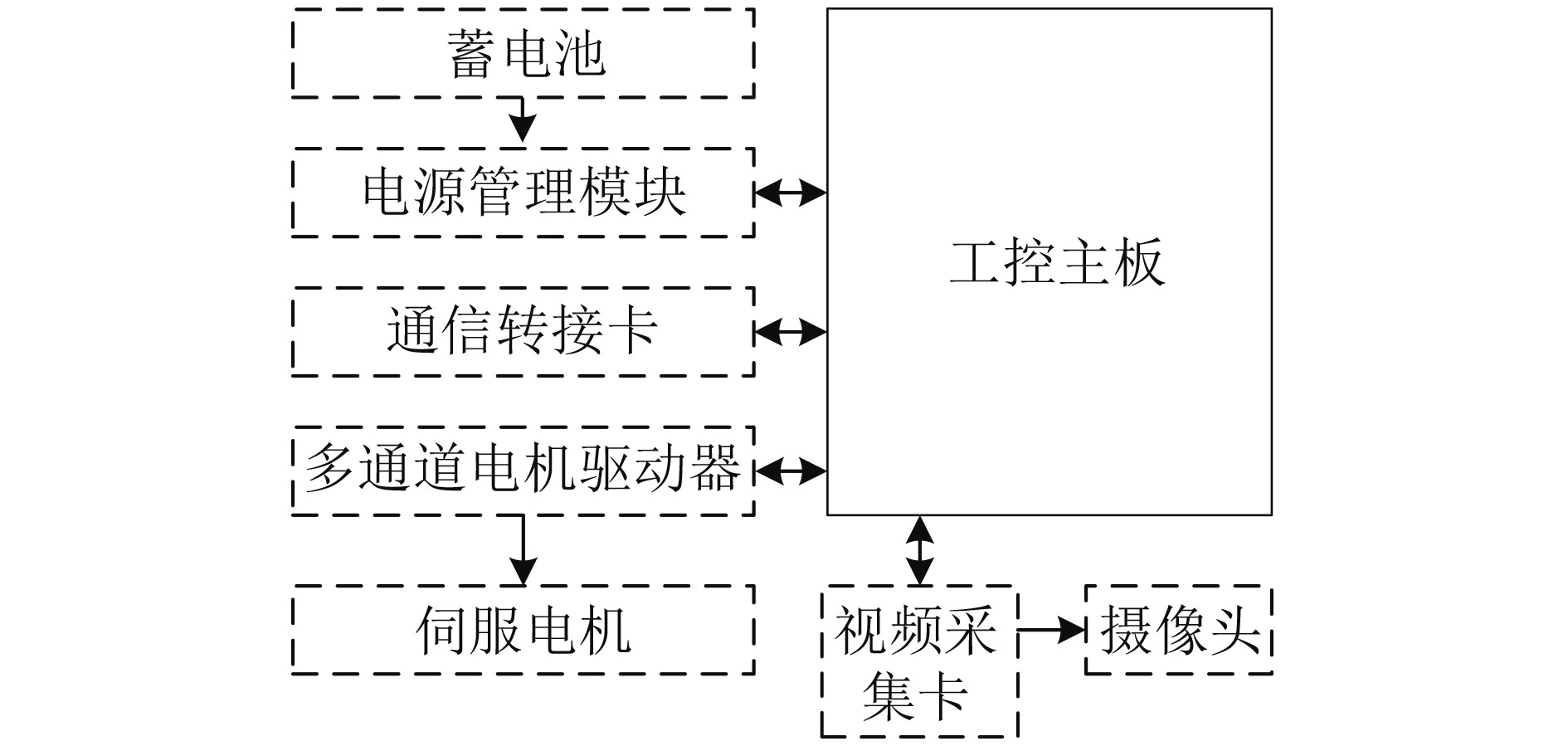
根据设计要求，手持式显控平台的主要功能是装载管道机器人系统的上位机系统，实时显示并储存行走装置回传的视频数据、发送出行走装置的控制指令。此外，还需实现电源管理模块的充放电功能。工控主板模块的外设接口有以太网接口、USB接口、视频AV端子接口、COM接口、充放电接口等。硬件接口连接方式设计如图7所示。上位机操作主界面主要由5个部分所组成：标题栏、工具栏、操作区、视频窗口和状态栏。

4 试验验证 4.1 管道行走试验

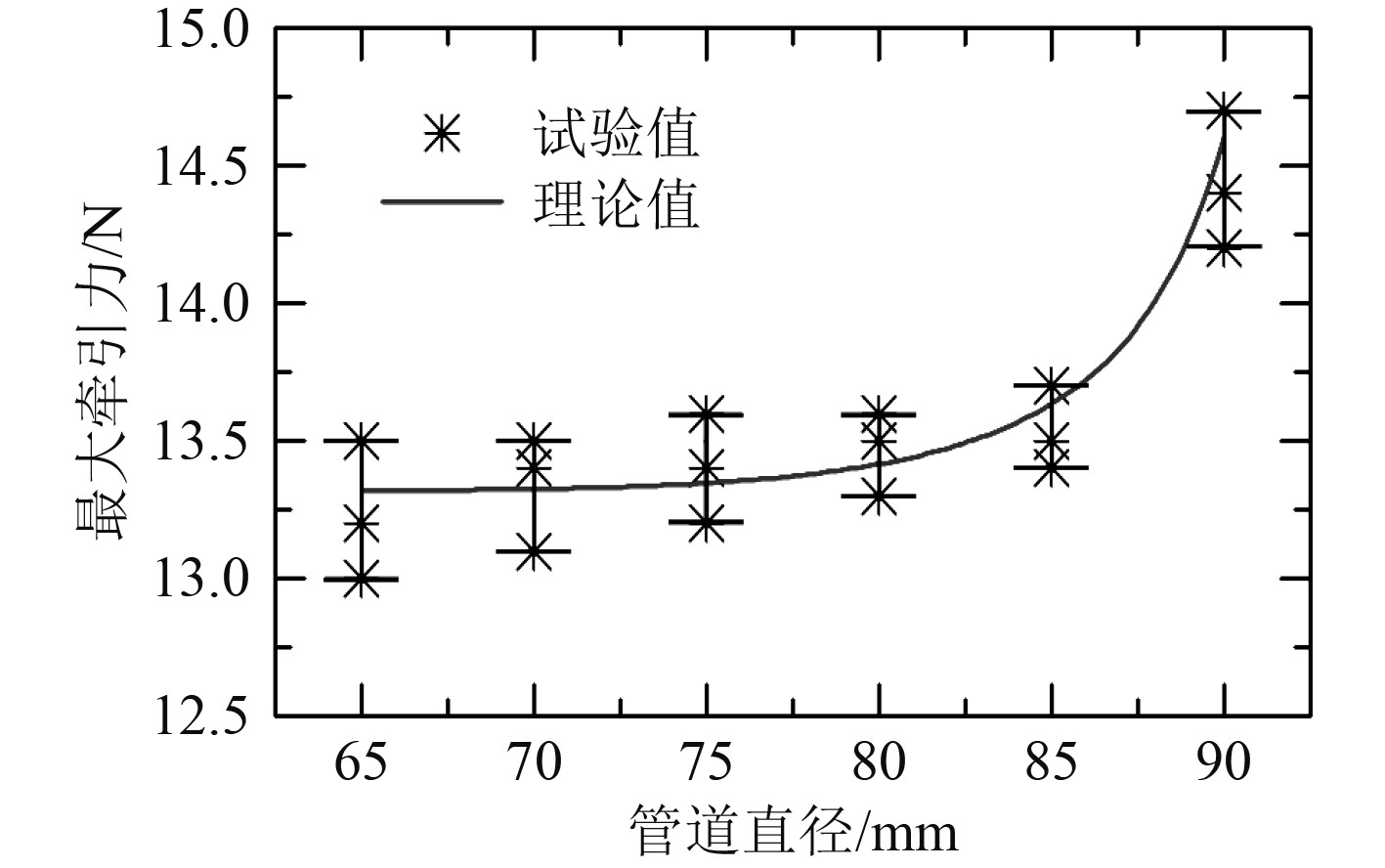
在直径变化范围为60～200 mm的垂直管道内开展管道机器人在变径管道中的行走试验，测试管道机器人在不同直径管道内的移动速度与最大牵引力，试验结果如图8所示。

试验结果表明，管道机器人能够在不同管径的管道中保持支撑腿与管道内壁之间良好的接触状态。在直径为60 mm管道内行走时，移动速度为2.64 m/min，最大牵引力为37.3 N；随管道直径增大，机器人的移动速度逐渐增大，最大牵引力逐渐减小。

4.2 管道裂纹识别试验

分别采用YOLO v3、YOLO-辅助、YOLO-GIoU、YOLO-AUX 这4种算法对样本容量为600的管道内壁损伤数据集开展识别试验，识别结果如表1所示。结果表明，优化后的YOLO v3-AUX算法的准确率提高了4.8%，漏检率和错检率分别降低了2.8%和2.9%，提升了检测的鲁棒性。

5 结　语

1）管道机器人采用直流无刷电机与行星减速器的驱动，结构紧凑，对称分散布置，有效减小了机器人本体尺寸，同时可快速进行前进与后退的转换。

2）采用六轮独立驱动与主动式伸缩机架形式，改善了在直管与弯管内的附着与驱动性能，在保证一定的牵引能力和过弯能力的前提下，有效提升管道机器人对管径变化与弯管的适应能力，扩展了管道机器人的应用场景。

3）在设计管道机器人控制系统的前提下，进行了垂直管道行走试验，测试了机器人在不同管径中的最大速度与最大牵引力。分别采用4种识别算法对管壁损伤情况进行了检测，结果表明优化后的YOLO v3-AUX网络算法的检测准确率较高。