近年来,随着能效指数EEDI、EEXI的持续推进,节能减排技术在船舶设计领域得到广泛应用。但是对于大多数内河船,相关约束不如海船严格,在运营的大部分内河船性能指标老旧,已经很难适应国内外航运界节能减排的需求,缺乏持续竞争力。因此,亟需开发性能优秀、具有良好经济性的新一代内河船型。
我国长江水域吃水较浅,内河船螺旋桨直径受限制,采用双尾鳍船型可有效增大船身效率并改善操纵性[1]。Kim 等[2]应用CFD 方法对某一集装箱船在不同尾鳍倾斜角和间距下的水动力性能进行研究,通过分析尾部流场的变化,发现尾鳍间距对阻力性能的影响相比于尾鳍倾斜角更大。张大有等[3]通过分析一系列典型长江双尾鳍客船的尾轴间距特征,得出当尾轴间距与船宽之比在 0.50~0.55范围内时,由两轴之间引起的伴流不均匀问题得到改善。张琪等[4]应用参数化建模软件CAESES结合NSGA-Ⅱ优化算法对某双尾鳍集装箱船进行尾部线型优化,以阻力及伴流均匀度为优化目标进行寻优,优化后的船型不仅降低了阻力, 伴流均匀度也得到明显改善。Keumjae等[5]应用Friendship对一型LNG船进行全参数化建模,研究了两轴间距、尾鳍倾斜角等参数的影响,通过优化降低模型收到功率约3%。
本文应用Friendship-Framework参数化设计平台,以某LPG船为参考船,对其尾部型线进行全参数化建模,并通过粘势耦合计算方法对不同参数组合下的型线方案进行阻力和自航计算,根据数值计算结果结合专家经验得到最终优化线型。
1 Friendship参数化建模 1.1 特征参数在对尾部线型的全参数化建模过程中,特征参数的选取尤为关键。对于多参数寻优设计而言,减少设计参数可以显著提升寻优的效率,且可以降低参数之间的相关性,有利于找到最优的结果。
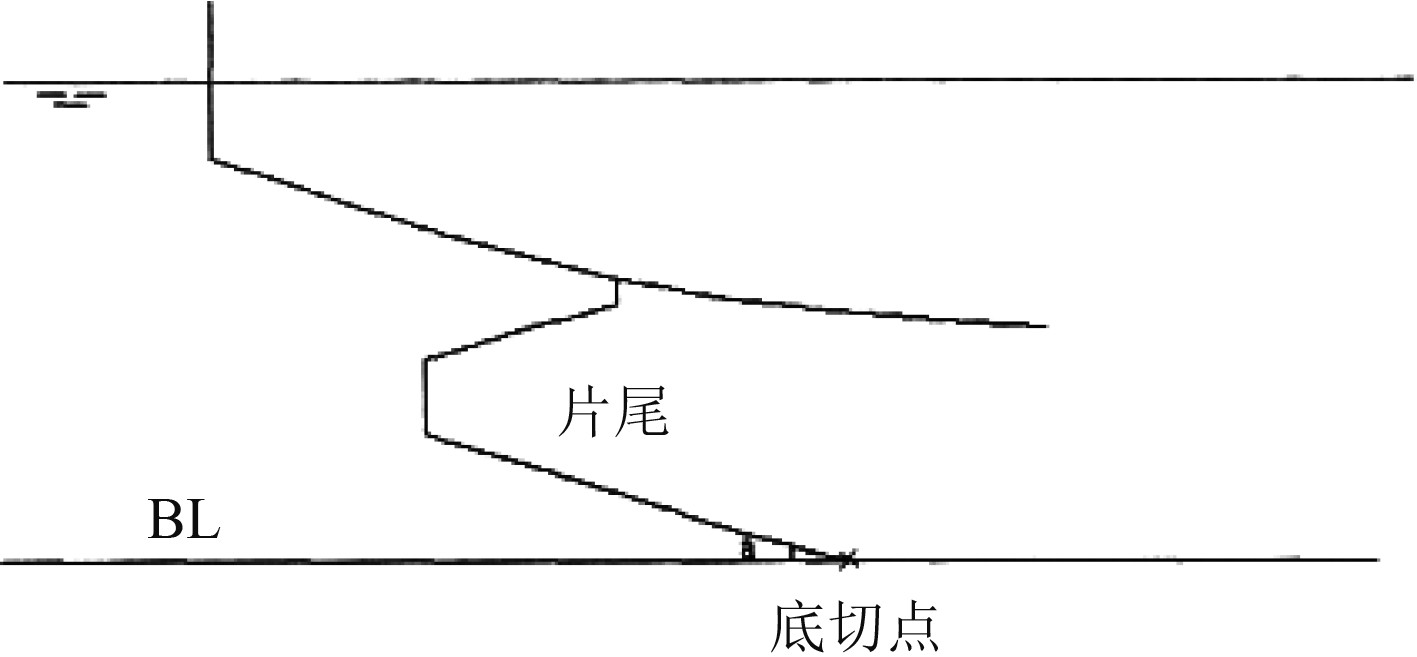
根据文献[6],尾鳍的中剖线与底部基线相切处的夹角α(见图1)对于尾部粘压阻力和桨前来流都有较大影响,建议取在13°以内,本文取为12°。
|
图 1 尾鳍的中剖线与底部基线夹角示意图 Fig. 1 Angle between the skeg center line and base line |
另一方面,合理地缩减参数的变化范围也可提升整个优化流程的效率。参考文献[3]的研究,尾轴间距与船宽之比的变化范围取为0.5~0.55。
除上述提到的设计参数外,其余设计特征参数主要如表1所示。
|
|
表 1 设计特征参数表 Tab.1 Table of the design characteristic parameters |
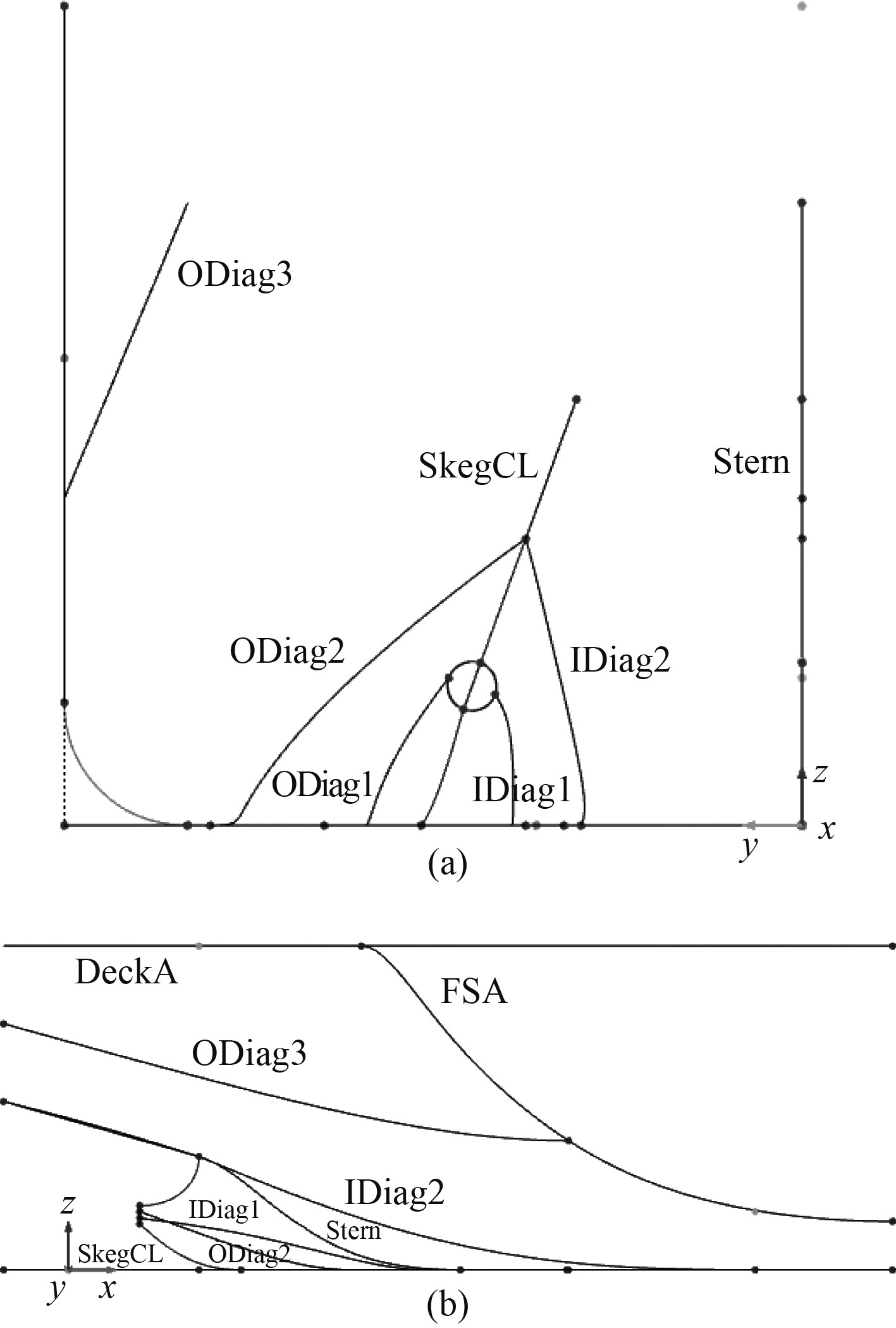
纵向特征曲线主要包括纵向位置曲线、纵向微分曲线和纵向积分曲线3类。纵向位置曲线包括常规的平底线、平边线、甲板边线、中纵剖线、艉鳍中剖线等,而要实现对曲面精确的参数化控制,还需要在横剖线曲率变化较大的地方增加斜线,如图2所示。纵向积分曲线主要为横剖面面积曲线,一般用于控制较大范围的曲面,不适用于局部特征参数的变换,因此本次建模未采用该特征曲线;纵向微分曲线主要控制各位置曲线的角度分布以及丰满度分布,这些曲线以曲面光顺为主要目的,通过合理地关联相关特征参数可在保证曲面光顺的同时扩大特征参数的搜索范围。
|
图 2 纵向特征曲线 Fig. 2 Longitudinal characteristic curves |
建立参数化曲面时,首先需要将构成每个曲面所用到的纵向特征曲线以特定的关系组合成横剖面曲线,并应用Fridendship的Curve Engine功能定义一个“模板”来实现该横剖面曲线在纵向的连续分布。该“模板”曲线通过Feature[7]定义,用参数化形式规定了不同纵向特征曲线之间的过渡方式。对于任意给定的横坐标,Curve Engine可根据给定的参数和纵向特征曲线生成光顺的横剖面曲线。然后,应用Fridendship的Meta Surface功能生成基于Curve Engine曲线表达的参数化曲面。由于船体曲面较为复杂,需根据不同的位置,定义不同的曲线模板(即Curve Engine),从而船体曲面通常由几个光顺连接的曲面构成。本次优化主要考虑尾部线型特征影响,首部保持不变,最终生成的船体尾部全参数化曲面如图3所示。

|
图 3 尾部全参数化曲面 Fig. 3 The full parametric surface of stern |
采用基于粘势耦合方法的CFD软件进行优化计算,该软件可与Friendship平台协同作业,软件采用自动网格划分和分区计算模式(见图4)。在区域1内根据自由表面边界的线性或非线性条件进行势流理论计算,在区域2内对船体前部2/3表面的边界层进行求解计算得到摩擦阻力,在区域3内采用k-ε湍流模型和壁面函数对船体尾部及船后流域进行粘性求解计算。该CFD软件具有极高的计算效率,在大批量方案优化计算中具有显著优势。

|
图 4 船体周围流场划分 Fig. 4 The flow field around the ship |
应用Fridendship软件集成的Sobol方法进行设计参数寻优,以总阻力和螺旋桨收到功率最小为目标进行优化计算。优化的基本流程为:首先应用Sobol方法生成一批设计方案,对其进行阻力性能计算;以总阻力系数、平均伴流分数值、排水量作为监测量,剔除各监测量超过平均值较大的方案;对剩下的方案进行自航计算,最后以收到功率最小为目标确定最优方案及其对应的设计特征参数。由于自航计算需消耗较多计算资源,该流程能最大程度地提升计算效率,从而缩短整个优化流程的周期。
2.3 优化分析应用Sobol方法生成100个设计方案并进行计算分析,经阻力计算初步筛选得到45个方案,然后对其进行螺旋桨外旋状态下的自航计算,各方案计算的模型收到功率与原型比较的分布情况如图5所示(正值表示收到功率相比原型增加)。可知,最优方案的模型收到功率相比原型下降约5.8%(图中圆圈标注),优化效果显著。

|
图 5 各方案模型收到功率与原型对比分布 Fig. 5 Distribution of delivered power of different designs compared with the original line in model scale |
设计特征参数的变化情况如表2所示。可知,相比于初始线型,最优方案的尾鳍倾斜角由90°变为74.3°,通过在桨前流场产生预旋进而提升推进效率;两轴间距为0.516,与原型基本相当;斜剖线ODiag2与ODiag3之间的曲面在靠近船尾部分变瘦,靠近船首部分变胖;中纵剖线相比原型略微变瘦,反曲点抬高;其余特征参数变化不大。
|
|
表 2 设计特征参数变化情况 Tab.2 Variation situation of design characteristic parameters |
最终得到的优化方案与原型的尾部横剖线对比如图6所示。图中浅色为初始线型,深色为优化线型。设计吃水下的静水力对比情况见表3。由表3可知,最终优化线型与原型静水力差异不大,方型系数CB略小于原型。

|
图 6 尾部横剖线对比 Fig. 6 Comparison of the transverse line of aftbody |
|
|
表 3 线型静水力对比 Tab.3 Comparison of the hydrostatic performance |
选取优化得到的最佳方案,通过全粘流数值计算CFD软件进行模型尺度下半船的阻力数值仿真计算。计算域取船前1.5倍船长,船后2.5倍船长。同时,在水面和开尔文波处进行加密,壁面y+值控制在60左右,生成的网格如图7所示,网格量约为120万。采用SST

|
图 7 阻力计算网格 Fig. 7 Mesh of the resistance calculation |
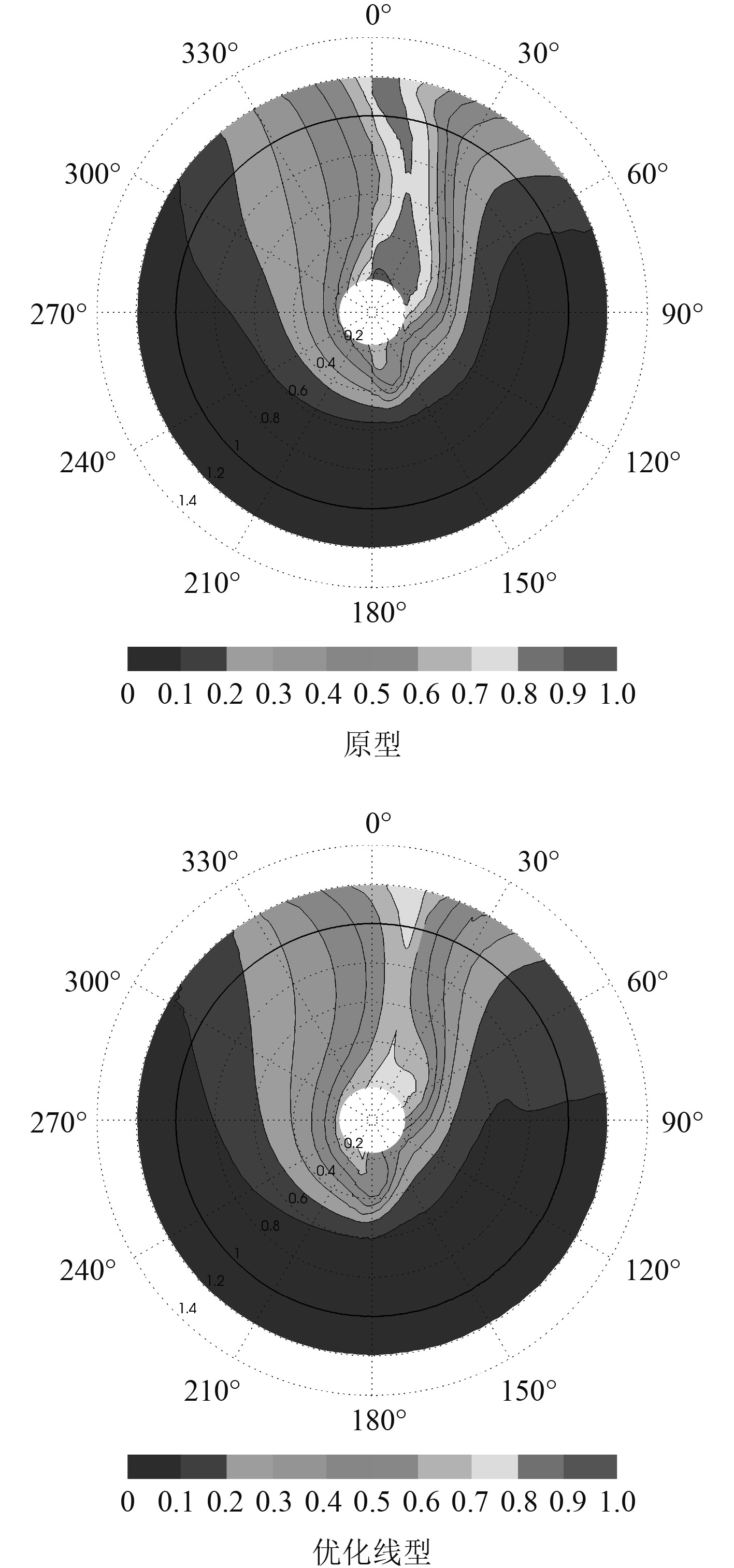
根据阻力仿真的结果,对原型和优化线型的尾部表面压力分布和桨盘面处轴向伴流分布进行对比分析,结果如图8和图9所示。

|
图 8 尾部压力分布对比 Fig. 8 Comparison of the pressure distribution of aftbody |
|
图 9 桨盘面轴向伴流分布对比 Fig. 9 Comparison of the axial wake distribution at propeller disk |
由图8和图9可知,优化线型的尾部压力分布相比原型负压区和正压区均有增大,阻力性能基本相当。而对于桨盘面处的轴向伴流分布优化线型比原型有明显改善,在桨盘面0°~15°方向对称轴附近的高伴流区域相比原型有所减小,且在1~1.2倍半径上方区域的伴流分布也得到明显改善,整体伴流分布更趋均匀。模型总阻力和伴流分数计算值的比较见表4。
|
|
表 4 全粘流阻力计算结果比较 Tab.4 Comparison of the full viscous resistance calculation results |
基于以上优化方案,开展设计吃水模型试验验证,试验模型示意图如图10所示。

|
图 10 试验模型示意图 Fig. 10 Figure of the experiment model |
在设计吃水、优化的目标航速下,试验结果与CFD评估结果对比如表5所示。
|
|
表 5 试验值与CFD评估值比较 Tab.5 Comparison of the experiment and CFD value |
可知,CFD计算得到的剩余阻力系数与试验值吻合较好,计算模型状态下推进效率为0.76,试验预估实船推进效率为0.72。表明经过尾部线型优化,相比于常规内河船其推进效率得到大幅提升,是一款水动力性能优秀的内河船双尾鳍线型。
5 结 语本文以Friendship的参数化建模功能为基础,通过建立双尾鳍的尾部全参数化模型,结合Sobol优化算法和粘势耦合CFD计算软件,对某LPG船的阻力和自航性能优化设计进行研究。同时,应用全粘流CFD软件对优化结果进行了不同角度的数值计算验证。最后通过水池模型试验验证了数值优化效果,结论如下:
1)基于参数化建模的优化设计方法有效且可靠,能极大缩短线型优化的设计周期;
2)设计吃水、设计航速时优化线型CFD计算得到的模型收到功率相比原型下降5.8%,其中阻力下降0.97%,推进效率增加4.83%;
3)优化线型经模型试验验证,具有较高的推进效率,表明该设计流程具有较高工程应用价值,为内河船双尾鳍线型优化提供思路。
| [1] |
许娜. 双尾鳍船型线设计方法研究[D]. 大连: 大连理工大学, 2009.
|
| [2] |
KIM H K, KIM H T, VAN S H. Numerical analysis of flow characteristic of a twin-skeg container ship with variation of stern hull shape[J]. Journal of the Society of Naval Architects of Korea, 2007(6): 551-563. |
| [3] |
张大有, 朱涛, 李绍波. 双尾鳍船型研究及发展分析[J]. 船舶工程, 2006(6): 58-62. DOI:10.3969/j.issn.1000-6982.2006.06.001 |
| [4] |
张琪, 姜栋, 张明. 双尾鳍船型的参数化建模及线型优化[J]. 船舶, 2021(4): 24-30. DOI:10.19423/j.cnki.31-1561/u.2021.04.024 |
| [5] |
KEUNJAE K, FABIAN T, NICOLAS B. Hydrodynamic optimization of twin-skeg LNG ships by CFD and model testing[J]. Int. J. Nav. Archit. Ocean Eng., 2014(6): 392-405. |
| [6] |
李世漠. 双尾节能船型[J]. 中国造船, 1988(1): 69-75. |
| [7] |
张萍. 船型参数化设计[D]. 无锡: 江南大学, 2009.
|
 2023, Vol. 45
2023, Vol. 45

