2. 广州海工船舶设备有限公司,广东 广州 511495
2. Guangzhou Haigong Ship Equipment Co., Ltd., Guangzhou 511495, China
无轴轮缘推进器(Rim-Driven thruster,RDT)是将传统的导管螺旋桨与驱动电机集成在一起的新型推进器,它由驱动电机、导管、螺旋桨、水润滑轴承组成。采用RDT的船舶相比于采用传统船用螺旋桨的船舶有诸多优点,如机舱空间利用率高、震动噪声低等优点 [1]。
1940年,德国的Kort[2]提出了RDT的理论模型,此后Pierro [3]、Taylor 等也相继建立了RDT的理论模型,以上模型都集中在设备概念方面,而RDT性能问题并没有解决。随着现代电机技术的进步,设计制造RDT成为了可能。2005年,美国海军发布的Tango Bravo计划中,RDT技术被作为未来潜艇发展的关键技术。随着RDT研究的深入[4],荷兰的 Vander Velden Marine System公司在2006年研制出了7叶无轮毂驱动推进器,功率可达295 kW,并且已被安装到实船上;挪威Brunvoll公司已开发出了功率900 kW的RDT。RDT在国内的研究起步比较晚[5],但取得了许多研究成果[6]。
RDT物理样机取得技术突破的同时,各国学者对RDT做了许多水动力性能方面的研究。Michael等[7]运用欧拉求解器,通过涡格方法对一种RDT的水动力性能进行过成功的预报。Aleksande[8]运用 OpenFOAM进行仿真计算,证明了在低进速系数工况下,k-ω SST湍流模型更适合用来对RDT模型进行仿真计算。杨蕾等[1] 以Ka4-70+19A导管螺旋桨为基础,构造了叶梢厚,叶根薄的反厚度规律的RDT桨叶,通过CFD软件对其进行了水动力计算,为RDT的反厚度螺旋桨设计提供参考。兰加芬等[6]将RDT和对转螺旋桨进行了有机融合,基于Flunte软件 对对转RDT进行水动力性能的计算,分析了叶数、桨距及转速与其性能之间的关系,并提出相应的优化途径。
本文基于STAR-CCM+软件,采用Realizablek k-ε模型对RDT水动力性能进行计算,并将计算结果分别与RDT模型的实验结果和常规导管桨敞水性能CFD值进行对比分析。
1 数值计算理论 1.1 控制方程 1.1.1 质量守恒方程流体微团在流动过程中需要满足质量守恒。质量守恒定律是指在流体系统中的流体在流动过程中质量保持不变即流过流体微团表面的质量通量等于流体微团质量的变化率。质量守恒定律的微分表达形式为:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho u)}}{{\partial x}} + \frac{{\partial (\rho v)}}{{\partial y}} + \frac{{\partial (\rho w)}}{{\partial z}} = 0。$ | (1) |
式中:ρ为流体的密度;u、v、w为流体在笛卡尔坐标系中i、j、k三个方向的速度。本文所讨论的流动为定常流动,因此式(1)可写为:
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0 。$ | (2) |
流体的动量守恒方程来源于牛顿第二定律,是流体流动过程必须满足的定律,在流体力学中通常用N-S方程来描述动量守恒方程,如下式:
| $ \frac{{{\rm{d}}V}}{{{\rm{d}}t}} = F - \frac{1}{\rho }{\rm{gradp}} + \frac{1}{\rho }{\rm{div}}(2\mu S) - \frac{2}{3}{\rm{grad}}(\mu {\rm{div}}V) 。$ | (3) |
式中:V为流体速度,F为流体所受体力,μ为流体粘度系数,P为流体压力,S为应变率张量。
1.1.3 湍流模型的选择RDT 旋转时Re较高,所以其场周围流动属湍流,且以RDT旋转域和其表面的流场表现最为突出。场中各变量与t及空间坐标关系密切,使得湍流方程组直接求解难度较大,工程上一般采用由雷诺时均方程出发的模拟方法。
本文采用RANS法模拟湍流,软件中RDT湍流模型选用Realizablek k-ε模型来求解。
2 建立模型 2.1 无轴轮缘推进器桨叶模型的建立RDT桨叶主参数如表1所示。
|
|
表 1 RDT桨叶主参数 Tab.1 Main parameters of RDT propeller blades |
参考上交版《船舶原理》中KA桨的二维型值点,首先应用坐标变换公式得到桨叶三维坐标,再将桨的厚度值沿径向逆向变换成RDT桨型值坐标。桨叶相对坐标用O1-X1Y1Z1表示,相应绝对坐标用O-XYZ表示;Φ为螺距角,θ为纵倾角,r为桨叶叶切面所在圆柱的半径,M为2个坐标系相对距离,坐标变换公式如下式:
| $ \begin{split} & X = {Z_1}\sin \phi + {X_1}\cos \phi + M\sin \phi - {{r}}\tan \theta,\\ & {Y}={r}\mathrm{cos}\left(\frac{{Z}_{1}\mathrm{cos}\varphi +{X}_{1}\mathrm{sin}\varphi +M\mathrm{cos}\varphi }{r}\right),\\ & {Z}={r\sin}\left(\frac{{Z}_{1}\mathrm{cos}\varphi +{X}_{1}\mathrm{sin}\varphi +M\mathrm{cos}\varphi }{{r}}\right)。\end{split} $ | (4) |
将RDT的桨叶的各r处叶切面值代入式(4),应用Excel软件并据坐标转化关系得到叶背及叶面上的三维值点。将三维点的坐标导入CATIA中,由各半径处导入的点连接成线,再经扫掠生成光顺的叶面,最后周向排列便可得到其余的桨叶,在CATIA中建立的RDT模型如图1所示

|
图 1 螺旋桨模型图 Fig. 1 Propeller model |
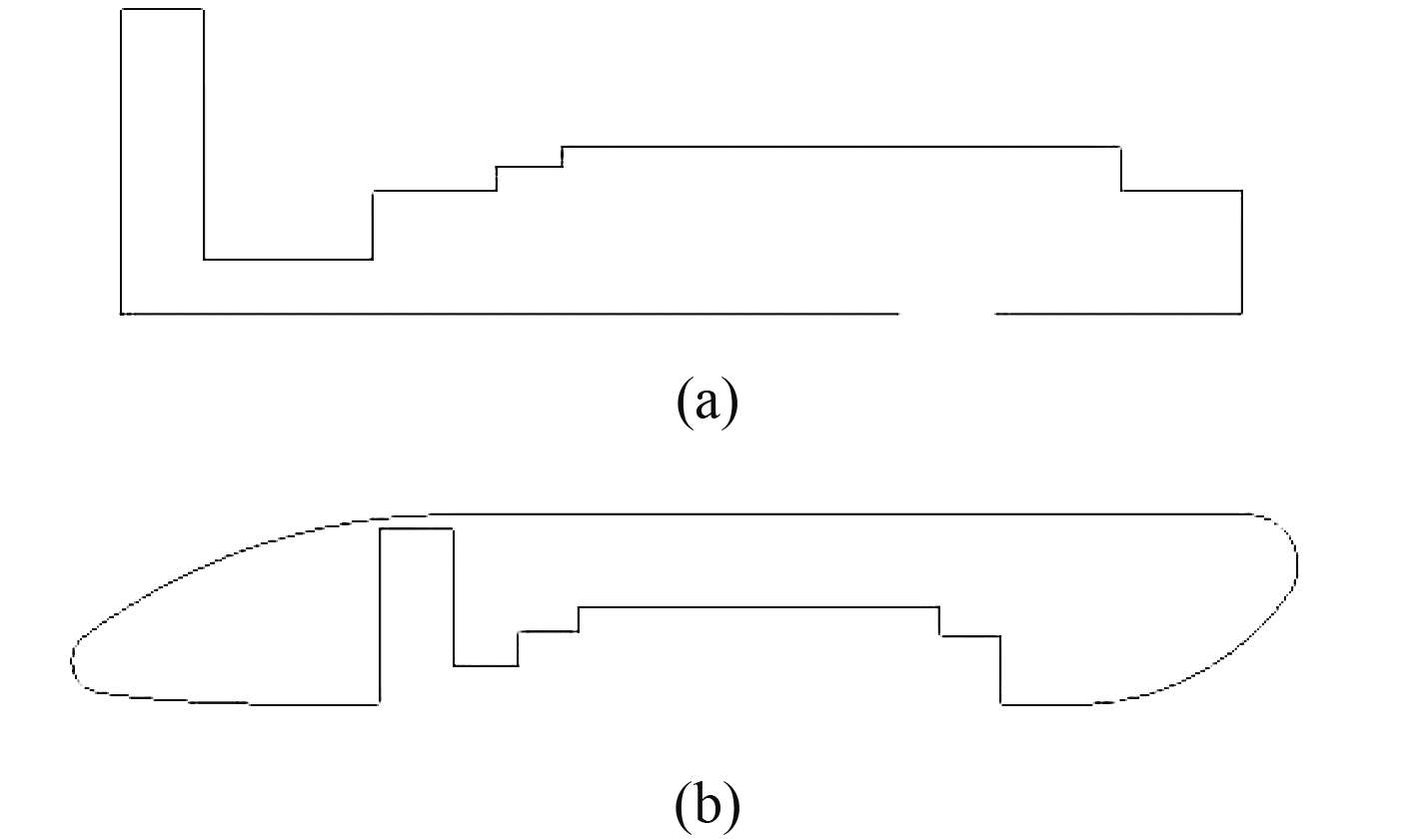
无轴轮缘推进器转子及导管壳体的二维图如图2所示。由于形状是一个回转体,因此可绘制出二维剖面线后导入到三维CATIA建模软件中,然后将剖面线绕Y轴旋转生成导管模型,最后将桨叶、转子、导管壳体组装成无轴轮缘推进器模型。桨叶叶梢与转环间固定连接,桨盘面轴向位置位于 1/3 的导管弦长处,RDT 的三维模型如图3所示。
|
图 2 转子及导管壳体二维图 Fig. 2 2D Drawing of rotor and guide tube shell |

|
图 3 RDT 三维模型 Fig. 3 Three dimensional solid diagram of RDT propeller |
将上述RDT模型导入STAR−CCM+中,进行域网格划分。RDT由于存在旋转运动,所以计算域外、内分别设置静止和旋转域。旋转域将贴近导管壳内壁一部分作为壁面,域内含桨及转子;静止域由入口、出口、远场和导管壳体外壁部分所组成,如图4所示。考虑到域大小对计算精度的影响,最终确定域半径为3D的圆柱体,入口距桨盘距离6D,出口距桨盘8D,其中D为RDT桨叶直径。

|
图 4 计算域划分示意图 Fig. 4 Schematic diagram of computing domain division |
此次计算应用STAR−CCM+网格划分功能,选用切割体进行网格划分。为保证RDT敞水性能的计算结果精确度,需细化桨面网格尺寸。具体有桨叶导边、随边以及导管前、后缘设置线加密,桨叶及导管壁面控制加密网格,RDT周围以及旋转域用体控制进行加密,以更好捕捉流动状况,其他区域依据前面体控制网格大小进行适当处理,保证网格连续性和计算精度。
3.2 设置边界条件对RDT域边界条件设定如下:静止域入口设为速度入口,自由压力出口设在出口处。RDT桨叶、转子和导管表面设为壁面。域外侧面用滑移壁面与来流相对静止,还需设来流速度方向。旋转域绕Y轴旋转,旋向为左旋,转速为RDT转速。Interface设在静止域和旋转域相互接触的界面上,静止域和旋转域之间通过Interface传递信息。湍流模型选定Realizablek k-ε模型并结合壁面函数来进行非定常水动力计算及分析[10-12]。
3.3 水动力性能计算结果 3.3.1 计算结果表达为方便比较分析,将仿真计算得到的推力、扭矩均以无量纲形式表达,定义如下:
进速系数
| $ J = \frac{{{V_A}}}{{ND}} ,$ | (5) |
螺旋桨推力系数
| $ {K_{TP}} = \frac{{{T_P}}}{{\rho {N^2}{D^4}}} ,$ | (6) |
环转子推力系数
| $ {K_{TR}} = \frac{{{T_R}}}{{\rho {N^2}{D^4}}} ,$ | (7) |
带环螺旋桨推力系数
| $ {K_{TPR}} = \frac{{{T_{PR}}}}{{\rho {N^2}{D^4}}},$ | (8) |
导管推力系数
| $ {K_{TD}} = \frac{{{T_D}}}{{\rho {N^2}{D^4}}} ,$ | (9) |
推进器总推力系数
| $ {K_{TT}} = \frac{{{T_{PR}} + {T_D}}}{{\rho {N^2}{D^4}}} = {K_{TPR}} + {K_{TD}} ,$ | (10) |
螺旋桨转矩系数
| $ {K_{QP}} = \frac{{{Q_P}}}{{\rho {N^2}{D^5}}},$ | (11) |
环转子转矩系数:
| $ {K_{QR}} = \frac{{{Q_R}}}{{\rho {N^2}{D^5}}} ,$ | (12) |
推进器总转矩系数
| $ {K_Q} = \frac{{{Q_P} + {Q_R}}}{{\rho {N^2}{D^5}}} = {K_{QP}} + {K_{QR}}。$ | (13) |
式中:VA为代表进速;N为螺旋桨转速;D为螺旋桨直径;TP为螺旋桨推力;TR为环转子推力;TPR为带环螺旋桨推力;TD为导管推力;QP为螺旋桨转矩;QR为环转子转矩。
3.3.2 计算结果无轴轮缘推进器转速设为700 r/min,通过改变流速控制计算进速系数J的变化,计算J在0.2~1.0时的敞水性能。相关的计算结果及图如表2和图5~图7所示。
|
|
表 2 RDT水动力性能数值计算结果 Tab.2 Numerical calculation results of RDT hydrodynamic performance |
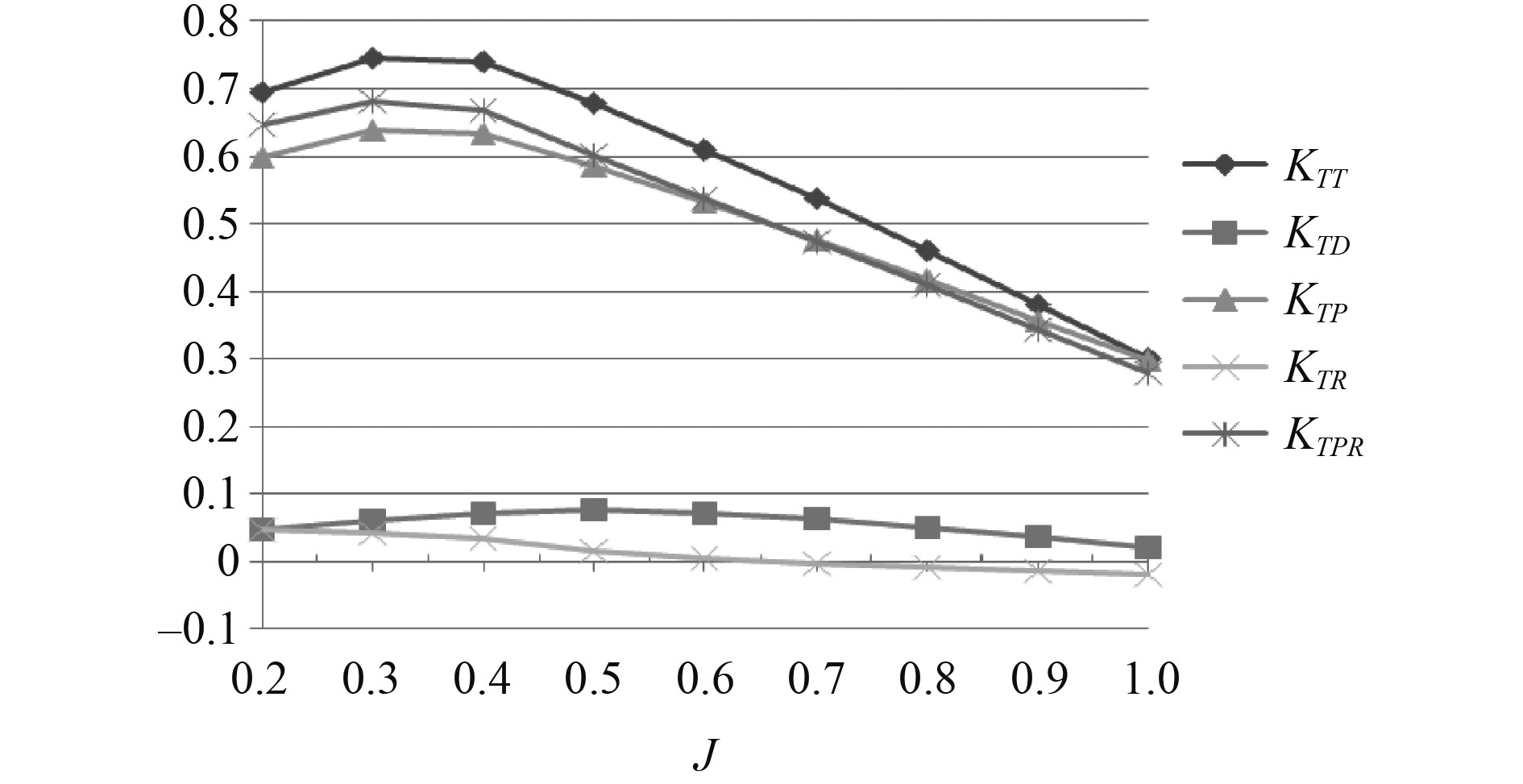
|
图 5 RDT 推力系数结果图 Fig. 5 RDT thrust coefficient results |

|
图 6 RDT 扭矩系数结果图 Fig. 6 RDT torque coefficient result |
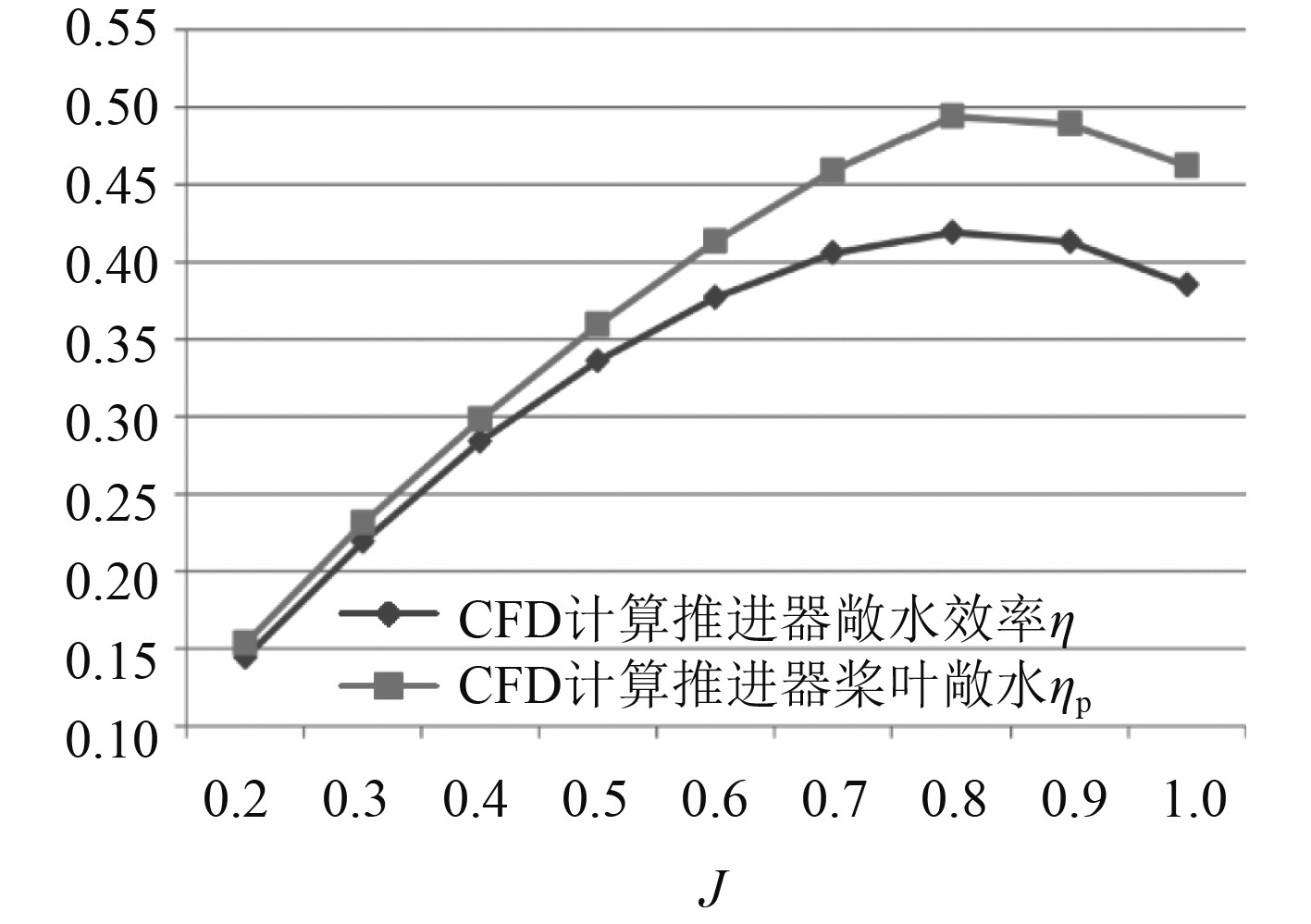
|
图 7 RDT 敞水效率计算结果图 Fig. 7 Calculation results of RDT open water efficiency |
可以看出,RDT推进器在低进速时其推力效果并不显著,并且低进速时其转矩会出现随进速系数增大而增大的现象,进而会在某一进速下达到最大。这可能是由于本身桨叶设计或者模型建立出现的误差导致。随进速系数增大,推力系数和转矩系数走向趋于正常。在推力系数中,桨叶推力仍是推力的主要来源,而转子的推力在总推力中约占14%~20%左右,且随着进速的提升,转子的推力在J=0.8后反而不利于推进。对于转矩而言,转子的转矩随进速的增加,其转矩值也越来越大。但转子转矩值涨幅较小。所以敞水效率较裸桨效率略有较低,但整体推力变大。整体而言,RDT推进器具有较好的推进效果。
3.4 无轴轮缘推进器模型实验对比 3.4.1 模型实验准备应用变频器动力仪测量RDT的推力和扭矩,推进器型号为GRM45,额定电频率140 Hz,额定电压214.8 V,额定电流94 A,极对数:8(8对16极),精度为±1.0%。采用应变式单分量天平测量RDT推力,其精度为±5.0%;记录仪采用多路应变测量计算机数据采集系统,数据采集动态精度为±4.0%。推进器模型包括一个5叶环转子螺旋桨、导管(包含定子),定、转子外包裹材料为环氧树脂,导管为铁质,模型尺寸与计算模型相同。
3.4.2 实验结果及分析对测得的实验数据进行无量纲化处理,最终得到轮缘推进器的部分试验数据如表3所示。经过对实验结果进行换算及处理并结合设计和制造经验,可得在设计航速下的推力系数及转矩系数以及推进效率如表4所示。将处理换算后的值和CFD值进行对比,如表5所示。
|
|
表 3 RDT 推进器实验部分数据 Tab.3 Experimental data of RDT propeller |
|
|
表 4 设计航速下RDT 推进器敞水性能 Tab.4 Open water performance of RDT propeller at design speed |
|
|
表 5 CFD 与实验敞水性能对比 Tab.5 Comparison of CFD and experimental open water performance |
由上述数据及对比结果可知,在设计航速下,RDT推进器敞水性能CFD值与实验值仍有一定的误差,但控制在在10%以内。该误差与桨叶模型、网格质量、湍流模型的选取和数值离散的方式可能都有一定的关系。总体来看,本文计算方法预报RDT敞水性能有一定准确性。
3.5 无轴轮缘推进器与常规导管桨性能对比分析将RDT与常规导管桨敞水性能的CFD值进行对比,分析无轴推进器较常规导管桨的性能优劣。用于分析的常规导管桨借鉴文献[10]。其敞水特性的CFD值如表6所示。
|
|
表 6 导管桨总推力系数KTT CFD值与实验值比较 Tab.6 Comparison of total thrust coefficient KTT value of propeller with experimental value |
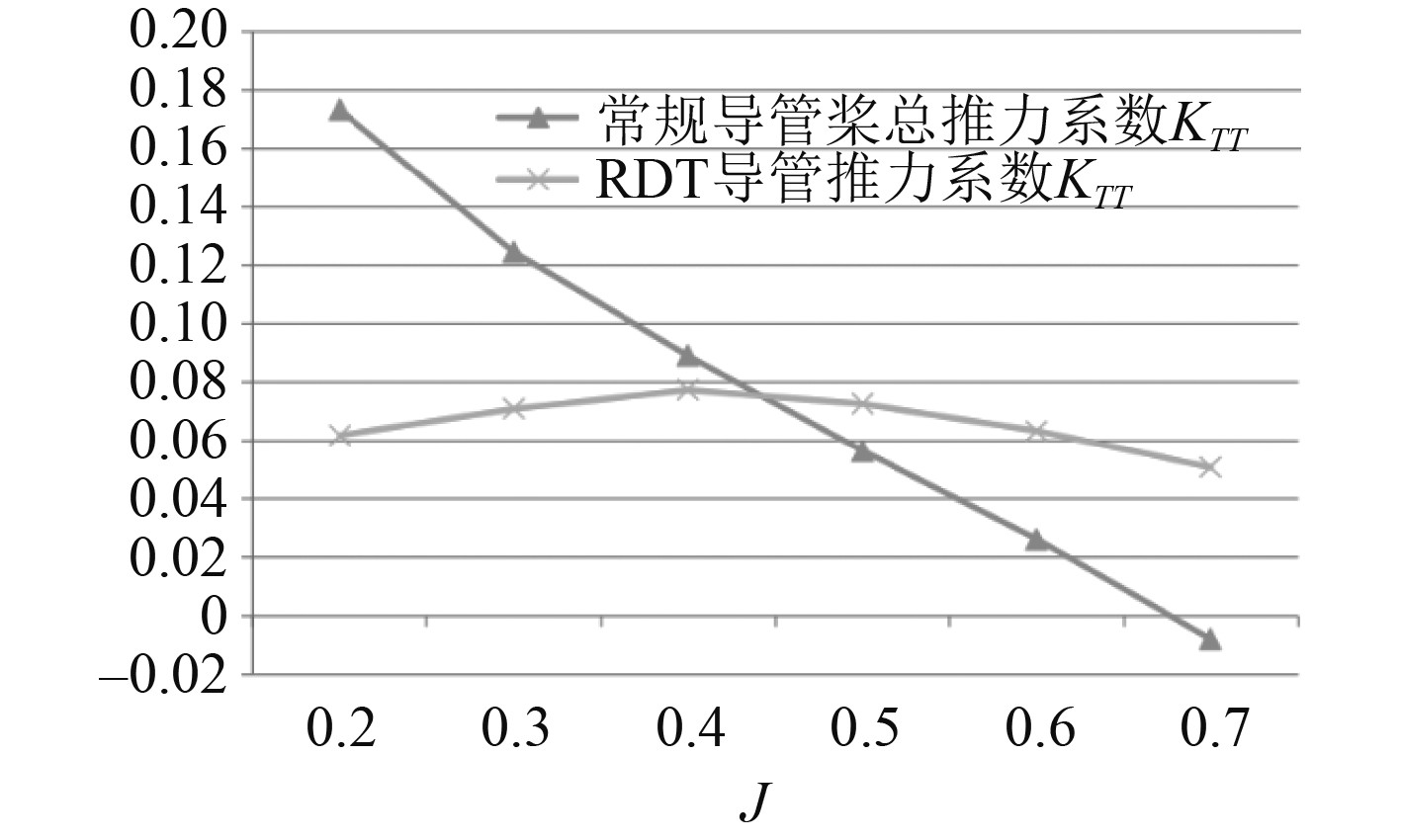
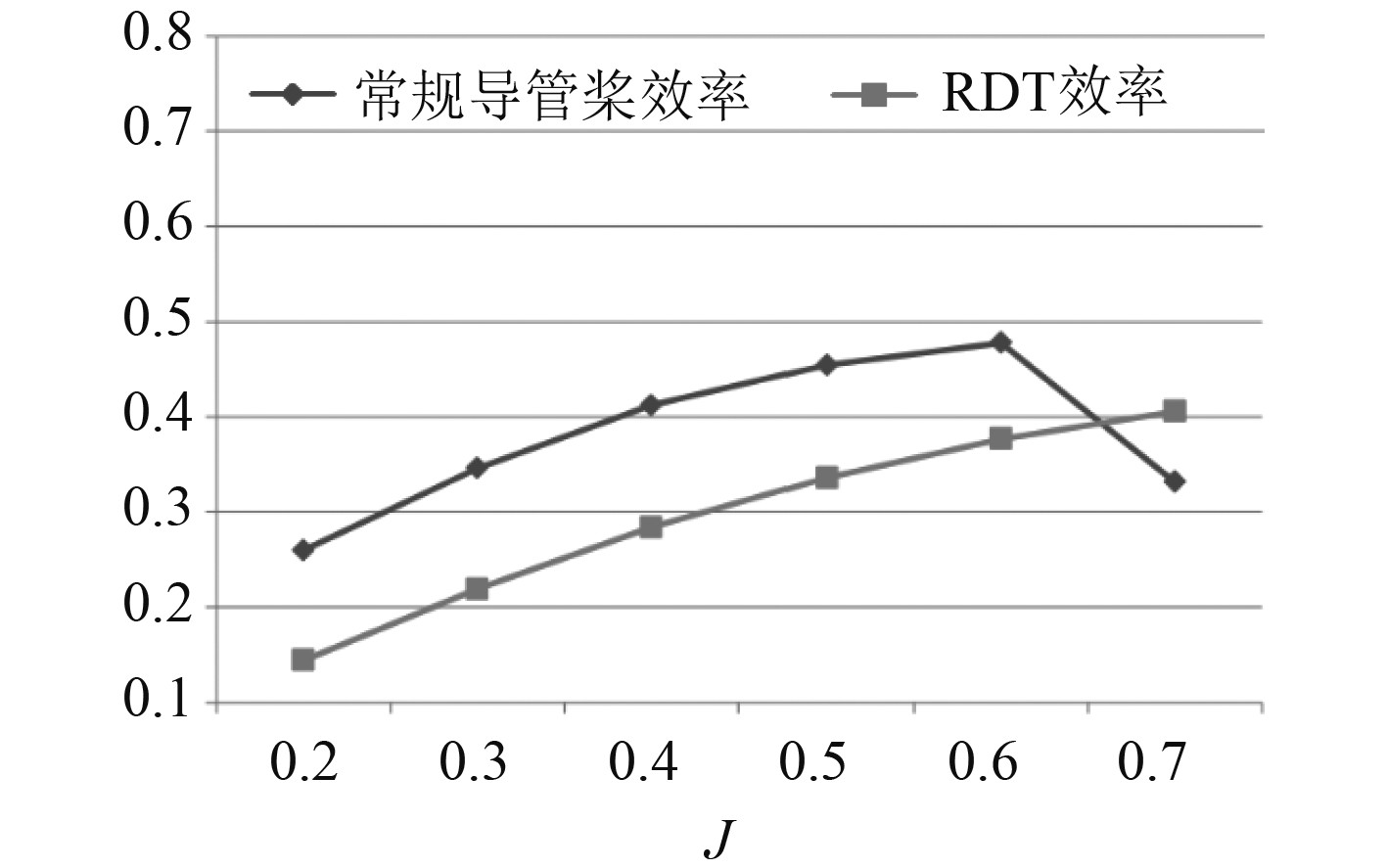
结合上述常规导管桨敞水计算值和RDT敞水值,对2种桨的敞水特性值(KTT 、KTD 、10KQ 和 ɳ)分别进行比较,如图8~图11所示。可以得出:1)RDT的推力较常规导管桨大,但由于环转子的存在使得RDT的转矩较大,从而使得RDT的敞水效率较常规导管桨要小;2)中低进速时常规导管桨导管推力较RDT导管对总推力影响较大,而随着进速继续增加常规导管桨导管推力对推力的影响较RDT越来越小;3)对两者的敞水效率而言,常规导管桨敞水效率在中低进速时其敞水效率要略高于RDT,而随着进速系数继续增加RDT的敞水效率会逐渐超过常规导管桨。
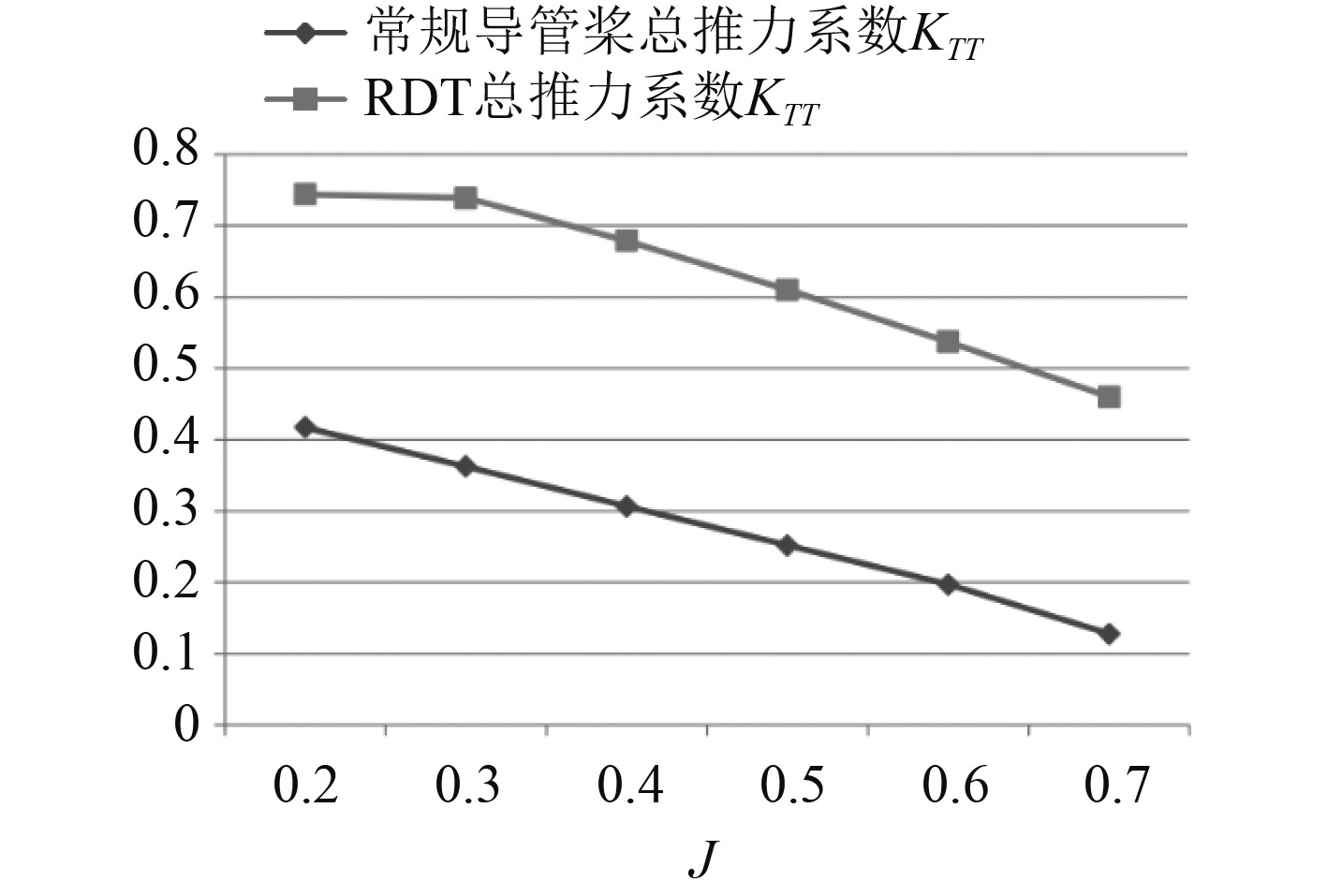
|
图 8 常规导管桨与 RDT 总推力系数 KTT比较 Fig. 8 Comparison of total thrust coefficient KTT between conventional guide propeller and RDT |
|
图 9 常规导管桨与 RDT 导管推力系数 KTD 比较 Fig. 9 Comparison of thrust coefficient KTD between conventional duct propeller and RDT duct |

|
图 10 常规导管桨与 RDT 总转矩系数 10KQ比较 Fig. 10 Comparison of total torque coefficient 10KQ betweenconventional guide propeller and RDT |
|
图 11 常规导管桨与RDT敞水效率ɳ比较 Fig. 11 Comparison of open water efficiency ɳ betweenconventional guide propeller and RDT |
本文提出RDT几何模型的建立方法,并在此基础上讨论了计算域的生成、网格划分的技术要点和边界条件的设定。计算了RDT的敞水推力系数、转矩系数及推进效率,并分析了推力系数与转矩系数随进速系数变化的规律。通过对RDT进行模型实验,将实验值与CFD值进行对比分析,可以看出在设计航速下RDT敞水性能的CFD值与RDT敞水性能的实验值存在差值,差值在10%以内,说明通过仿真计算的方法预报RDT敞水性能具有一定准确性。通过将RDT敞水性能的CFD值与常规导管桨敞水性能的CFD值比较可知,随着进速系数不断增加RDT的敞水效率会逐渐超过常规导管桨的敞水效率,为船舶推进器的选型提供了一定参考。
| [1] |
杨蕾, 周军伟, 闫文辉, 等. 轮缘推进器反厚度规律桨叶的翼型对比分析[J]. 中国造船, 2022, 63(1): 113-125. YANG Lei, ZHOU Junwei, YAN Wenhui, et al. Comparative analysis of anti-thickness regular propellers of rim-driven thruster[J]. shipbuilding of China, 2022, 63(1): 113-125. DOI:10.3969/j.issn.1000-4882.2022.01.010 |
| [2] |
KORT L. Elektrisch angertriebene schiffsschraube. DE 688114[P]. 1940.
|
| [3] |
PIERRO J. Gearless drive method and means. US 3708251[P]. 1973.
|
| [4] |
谈微中, 严新平, 刘正林, 等. 无轴轮缘推进系统的研究现状与展望[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(3): 601-605. TAN Wei-zhong, YAN Xin-ping, LIU Zheng-lin, et al. Technology development and prospect of shaftless rim-driven propulsion system[J]. Journal of Wuhan University of Technology(Transportation Science& Engineering), 2015, 39(3): 601-605. |
| [5] |
胡举喜, 吴均云, 陈文聘. 无轴轮缘推进器综述[J]. 数字海洋与水下攻防, 2020, 3(3): 185-191. HU Juxi, WU Junyun, CHEN Wenpin. Research of shaftless rim-driven propeller[J]. Digital Ocean & Underwater Warfare, 2020, 3(3): 185-191. DOI:10.19838/j.issn.2096-5753.2020.03.002 |
| [6] |
兰加芬. 对转无轴轮缘推进器水动力性能分析及优化研究[D]. 武汉: 武汉理工大学, 2019.
|
| [7] |
MICHAEL T, JESSUP S, SCHERER O. AHFID propulsor performance prediction[R]. NSWCCD Technical Report No. NSWCCD-50-TR-2002/003.2002
|
| [8] |
DUBAS A J, BRESSLOFF N W, SHARKH S M. Numerical modelling of rotor–stator interaction in rim driven thrusters[J]. Ocean Engineering. 2015, 106: 281–288.
|
| [9] |
刘报, 严新平, 欧阳武. 无轴轮缘推进器的间隙流动功耗与散热[J]. 船舶工程, 2017, 39(12): 32-17. LIU Bao, YAN Xinping, OUYANG Wu. Power consumption and heart dissipation of gap flow in shaftless rim-driven thruster[J]. Ship Engineering, 2017, 39(12): 32-17. DOI:10.13788/j.cnki.cbgc.2017.12.032 |
| [10] |
邱鹏. 轮缘推进器水动力性能数值研究[D]. 武汉: 武汉理工大学, 2017.
|
| [11] |
SONG Bao-wei, WANG You-jiang, TIAN Wen-long. Open water performance comparison between hub-type and hubless rim driven thrusters based on CFD method[J]. Ocean Engineering, 2015, 103: 55-63. DOI:10.1016/j.oceaneng.2015.04.074 |
| [12] |
STEFANO GAGGERO, CESARE M. RIZZO, GIORGIO T, et al. EFD and CFD design and analysis of a propeller in decelerating duct[J]. International Journal of Rotating Machinery, 2012, 106: 281-288. |
 2023, Vol. 45
2023, Vol. 45
