2. 上海市船舶工程重点实验室,上海 200011
2. Shanghai Key Laboratory on Ship Engineering, Shanghai 200011, China
在大型船舶遭遇的事故中,碰撞以及搁浅是主要占比之一,在发生碰撞和搁浅事故时通常伴有破舱浸水,破损稳性不满足要求的船舶存在发生倾覆危险,严重危害船上人员生命安全。国际海事组织(IMO)因此颁布了海上生命安全规范(SOLAS)、安全返港(SRtP)规范、人员撤离规范等强制性法规以保障船上人员的生命安全。为切实保障大型船舶在破损情况下具有足够存活能力,有必要开展船舶的概率破损研究和时域数值模拟研究,证明船舶的破损稳性满足要求。特别是大型船舶的破损稳性时域数值模拟,虽然研究难度较大,但却具有很高的研究价值。
大型船舶在发生碰撞或搁浅事故时通常伴有破舱浸水,若破损稳性不满足要求则存在发生倾覆的危险,将严重危害到船上人员的生命安全。现有的破损稳性计算一般采用准静态方法,如常用的重量增加法和浮力损失法。采用准静态方法可得到船舶发生破损后的最终平衡状态,进而得到该状态下的GZ曲线用于规范校核。但准静态方法存在两方面的局限,一是无法还原船舶发生破损后海水在各舱室间的流动和漫延过程,也无法获悉不同时间点对应的船舶姿态变化情况,因而无法用于发生破损后的应对决策和人员疏散撤离模拟;二是准静态方法无法纳入波浪、风等环境载荷对于破损后船舶的运动影响,在环境载荷作用下,船舶的运动特性发生改变,除舱室进水引起的姿态变化外还将受到波频运动的影响,同时舱室内部的流动情况也将变得更为复杂,从而增大船舶发生倾覆的风险。综上,有必要对大型船舶破损稳性的时域模拟技术加以研究。
破损船舶在波浪中运动包含船体、海况和舱室进水过程3个要素。船舶破损稳性问题取决于这些要素及其相互作用的模拟。在分析整个船舶破损稳性问题过程中,需解决以下3个关键问题[1]:
1)波浪和风等环境激励下,破损船舶的运动响应时域预报;
2)船舱内部积水在舱室间的流动及其与船体相互作用的特性模拟;
3)进舱水流通过破损口流入/流出过程的模拟。
通过对上述问题的模拟,并将其准确、有效地结合起来,就能建立起破损船舶在波浪中的时域运动数值计算程序,由此预报船舶的破损稳性。
国外船舶破损稳性理论研究所用的数值方法几乎都是建立在非线性时域模拟基础之上[2]。Vassalos等[3]和Zaraphonitis等[4]基于势流理论计算入射波浪引起的水动力载荷,基于脉冲响应函数将频域水动力系数转换到时域中,基于修正后的伯努利公式模拟破口处的进流和出流,利用半经验公式处理流体粘性且忽略积水在舱室内部的晃荡影响。这一经典方法非常实用且能够满足工程应用的精度要求,至今仍得到广泛采用。为更好地模拟舱室内部流体的物理特性,Santos等[5]利用浅水波方程模拟了舱内积水流动的非线性特性。
国内与时域破损稳性相关的研究相对较少,钱昆等[6]利用改进的切片法研究了破损船舶受到的波浪载荷。李佳和马宁[7]基于简化的伯努利方程研究了规则波中二维舱室的进水过程。郭显杰和黄衍顺[8]基于二维切片法和准静态方法研究了破损船体的运动响应。
除势流方法外,CFD方法在破损稳性中的应用也日益广泛,特别是在高精度的局部流动模拟方面[9-11]。然而,受制于计算能力的限制,目前还难以满足工程应用需求。
1 时域破损稳性数值建模及预报方法 1.1 破损船舶的动力学模型进行破损船舶的动力学模型建模时,将破损后进出船体的海水视作具有质量的独立刚体,则由船舶和进/出水自由质量组成的多刚体质量系统的六自由度运动数学模型可表示为:
| $\begin{aligned} & \left\{ { M + {{M_w}\left( t \right)} + {{A_\infty }} } \right\} {\ddot Q} + \left\{ { {{{\dot M}_w}\left( t \right)} + {{B_v}}} \right\} {\dot Q} + \\ & \int_0^t {\left\{ { {K\left( {t - \tau } \right)} {\dot Q\left( \tau \right)} } \right\}{\text{d}}\tau } = {{F_{wave}}} + {{F_{drift}}} + {{F_{wind}}} + \\ & {{F_{current}}} + {{F_{restoring}}} + {{F_{gravity}}} + {{F_{WOD}}} 。\end{aligned} $ | (1) |
式中:M为广义质量矩阵;Mw为广义进水质量矩阵;A∞为广义附加质量矩阵;Bv为非线性阻尼系数矩阵;积分表征辐射阻尼的卷积;F为广义力向量,从左至右依次为一阶波浪力、二阶波浪力、风作用力、流作用力、恢复力、重力和进水产生的动力效应。各受力的详细推导及计算方法可参考文献[12]。
1.2 破舱进水与舱室之间的相互作用船体在破损之后,破舱进水会首先作用于船体,而船体的舱室边界也会限制破舱进水的运动,进而影响或者激励破舱进水的运动,因此对于船体与破舱进水而言,两者是一个相互耦合、相互作用的,无法将2个单独割裂开进行研究。参考以往的文献,对于以上问题,采用“质点轨迹法”[13]进行研究可以相对更好模拟破舱进水与船体之间的作用。根据“质点轨迹法”,将破舱进水假定其作用点都集中在破舱进水的质心,这样可以用一个质点来表征破舱进水,将破舱进水在运动时所有楔形体形心相连所形成的线即是这个质点的运动轨迹。这样质点运动与船体运动之间将会形成相位差[2]。
根据Zaraphonitis等[4]的研究,船舶破损之后,海水虽然进入船体舱室内,但破舱进水不一定会加剧船舶的运动,相反在某些情况下,与减摇水舱原理类似,可能会减小其运动性能。通过一些实验也显示,当船体破损并大量进水时,水在舱室内的晃荡现象比预期中的小很多,水与船体运动之间没有显著相位差,船体的运动性能反而得到了缓解,舱室内液体晃荡现象只有当破舱进水量较小时才会变得较为显著,但由于破舱进水此时过小,对于船体而言,其作用也可忽略不计。综上,采用“质点轨迹法”进行舱内进水与船体的相互作用模拟是具有合理性的。
1.3 破口进流/出流数学模型影响破口处进流与出流的因素很多,包括内外液面差、船体运动、波浪参数等。采用Jasionowski提出的简化模型[12]。该模型的理论基础建立在小孔出流问题之上,通过伯努利积分得到破口处的水流速度:
| $ v = \sqrt {2g\left| {{h_{out}} - {h_{in}}} \right|} ,$ | (2) |
破损口处的流量可由在破口处进行积分得到,积分范围为破口对应的面积:
| $ Q\left( t \right) = {K_{dam}} \cdot {\text{sign}}\left( {{h_{out}} - {h_{in}}} \right) \cdot \sqrt {2g\left| {{h_{out}} - {h_{in}}} \right|} \cdot {S_{dam}}。$ | (3) |
式中:hin为破损舱的内水压头高度;hout为破损舱的外水压头高度;g为重力加速度;Sdam为破损口的面积;Kdam为进流/出流系数,一般由试验确定。其中Kdam这个系数会受到诸多参数的影响,如破舱进水在舱室内的晃荡,船体破损之后的运动,波浪的入射作用,破损口的形状,大小,相对位置等,经过Jasionowski模型发现,考虑到进出流的相互影响,Kdam可选取为0.7为宜[2]。
2 CAE软件及目标船 2.1 时域破损仿真软件Proteus船舶时域破损仿真CAE软件是目前国际上最前沿的时域破损仿真工具之一,能够实现各类船舶在风、浪、流联合作用下,发生多舱破损情况下的时域六自由度运动仿真预报,具有以下特点:
1)船体运动预报所需的水动力系数采用切片法高效计算获得;
2)通过数据库方式生成破损船体在不同浮态下对应的水动力系数;
3)采用脉冲响应函数法建立六自由度的船舶时域运动模型;
4)运动模型中的FK力和恢复力采用瞬时湿表面积分方式获得;
5)基于FMPS(Free-Mass-on-Potential-Surface)模型模拟舱内进水运动;
6)基于Bernoulli方程模拟破口处的进水/出水;
7)采用四阶Runge-Kutta-Feldberg方法求解时域运动。
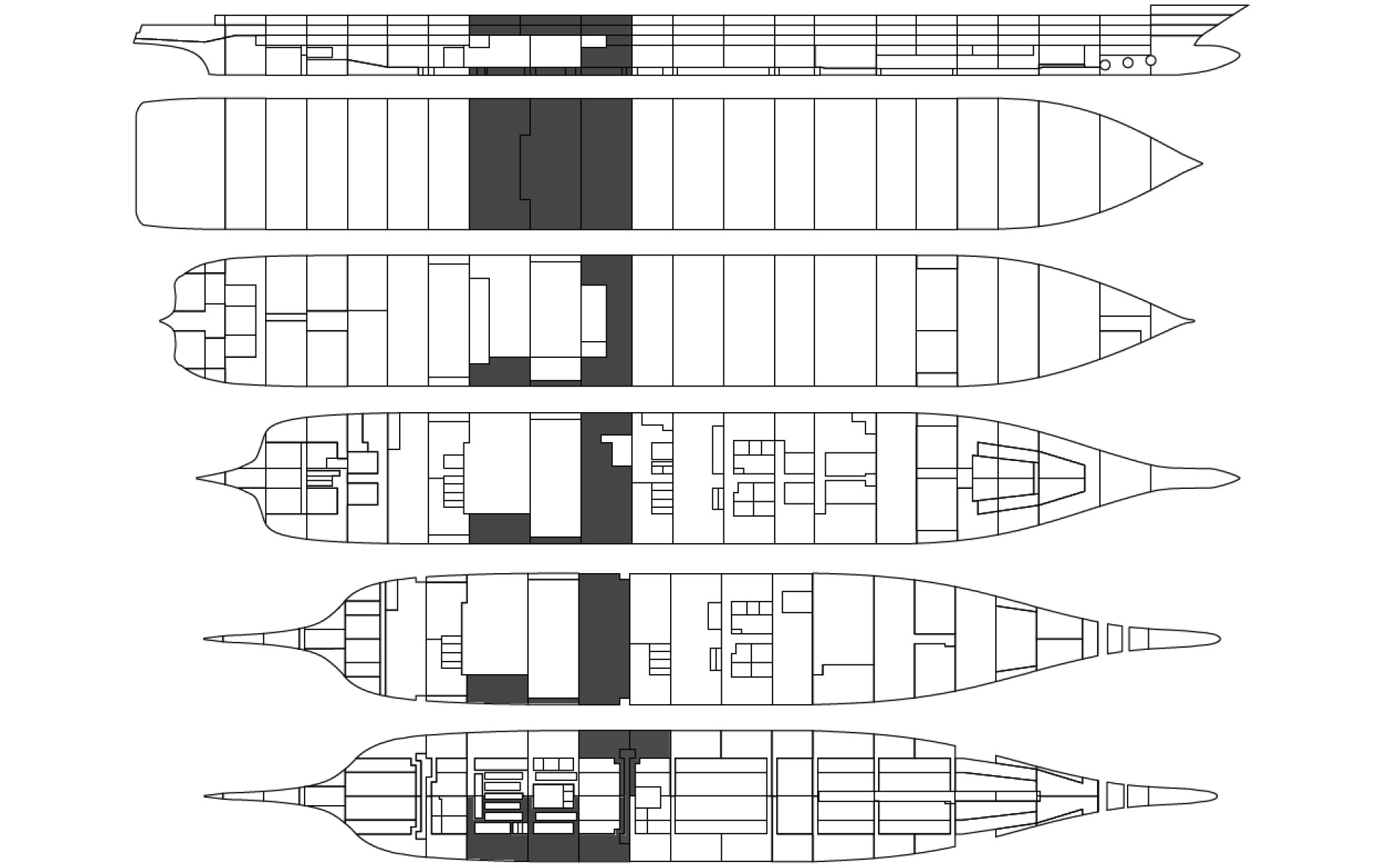
2.2 目标船信息本文以1艘大型船舶为研究对象,其垂线间长为287.1 m,型宽为37.2 m,吃水为8.25 m,排水量为67 022.4 t,初稳性高为1.75 m。在开展时域破损仿真之前,依据SOLAS概率破损稳性规范校核要求,利用NAPA软件对船体进行破损稳性计算分析,并从破损稳性校核结果报告中挑选一个典型的危险破损工况专门用于时域破损仿真研究。该工况的破损舱室信息如图1所示,共涉及13个舱室。根据破损舱室分布信息,建立相关舱段以二维切片形式表达的几何模型,如图2所示,其中的实心方块代表联结各舱室的开口。
|
图 1 危险破损工况 Fig. 1 Critical damage load case |

|
图 2 仿真相关舱段几何模型 Fig. 2 Geometry model of relevant cargo hold of simulation |
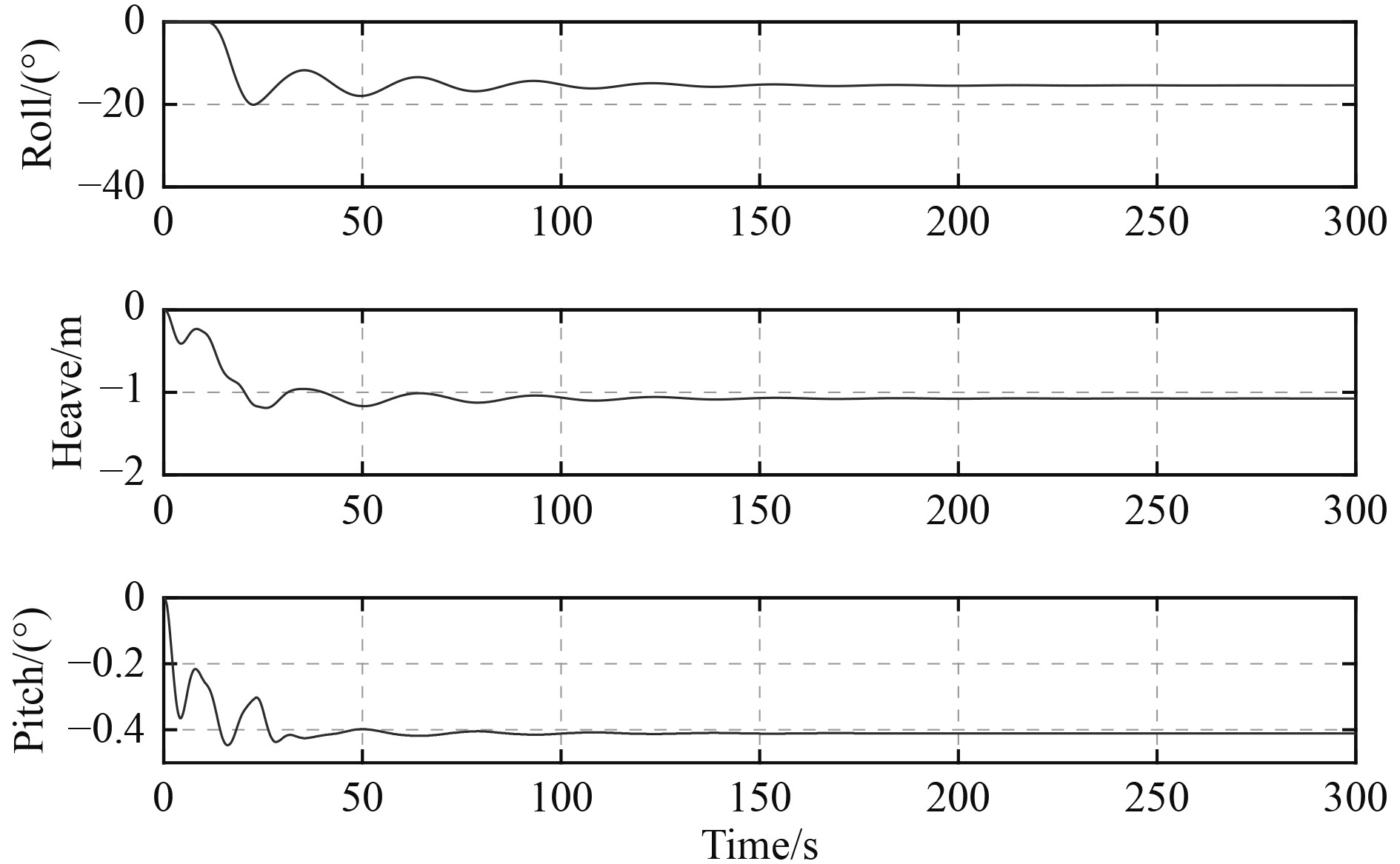
首先,开展船体在静水中的计算仿真,考虑全部舱室均发生破损的最危险情况,计算稳定时的船舶状态如图3所示。该工况对应的船体运动时历曲线如图4所示,船舶发生破损后首先会向一侧发生大幅横倾,最大值达到20°;之后经过约150 s达到稳定状态,最终的稳定横倾角为15.4°。
|
图 3 静水时域破损仿真(船舶达到稳定状态) Fig. 3 Still water time domain damage simulation (stable state) |
|
图 4 静水时域破损仿真(船舶运动时历曲线) Fig. 4 Still water time domain damage simulation (ship motion duration curve) |
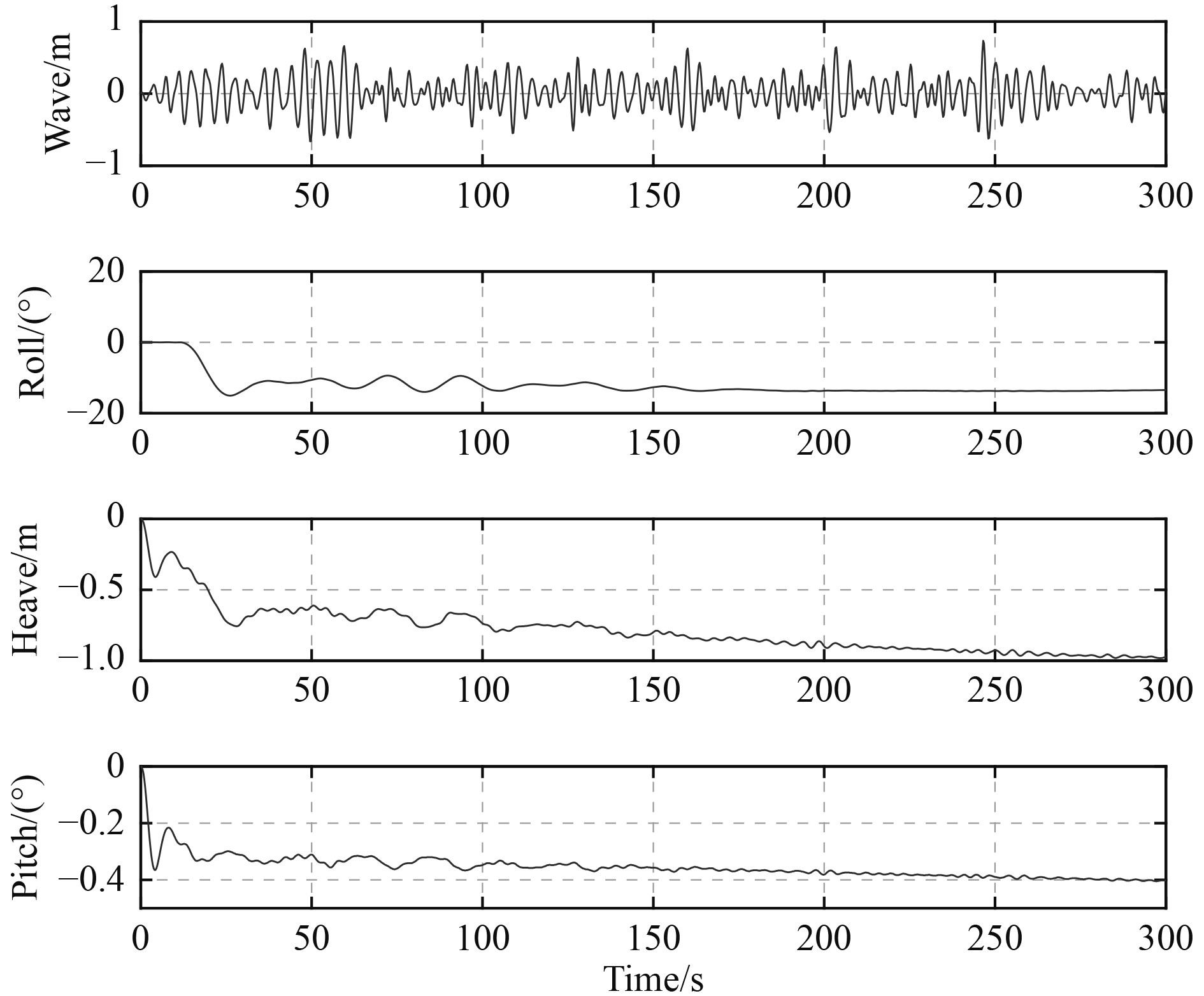
虽然在静水中该危险工况尚不足以使船舶发生倾覆,但实际船舶在海上运营过程中还将遭遇风浪等环境载荷的作用,因此有必要对环境载荷的影响开展计算研究。因此,对多种破损及规则波、不规则波组合下的目标船破损情况进行时域仿真。有义波高2 m不规则波工况的仿真结果如图5所示。从仿真的结果看,全部仿真工况下船舶均未发生倾覆,波浪的作用主要是使船体产生波频的摇荡,并使舱室间的进出水变得更为频繁。
|
图 5 有义波高2 m不规则波中时域破损仿真(船舶运动时历曲线) Fig. 5 Time domain damage simulation for irregular wave of 2 m Hs (ship motion duration curve) |
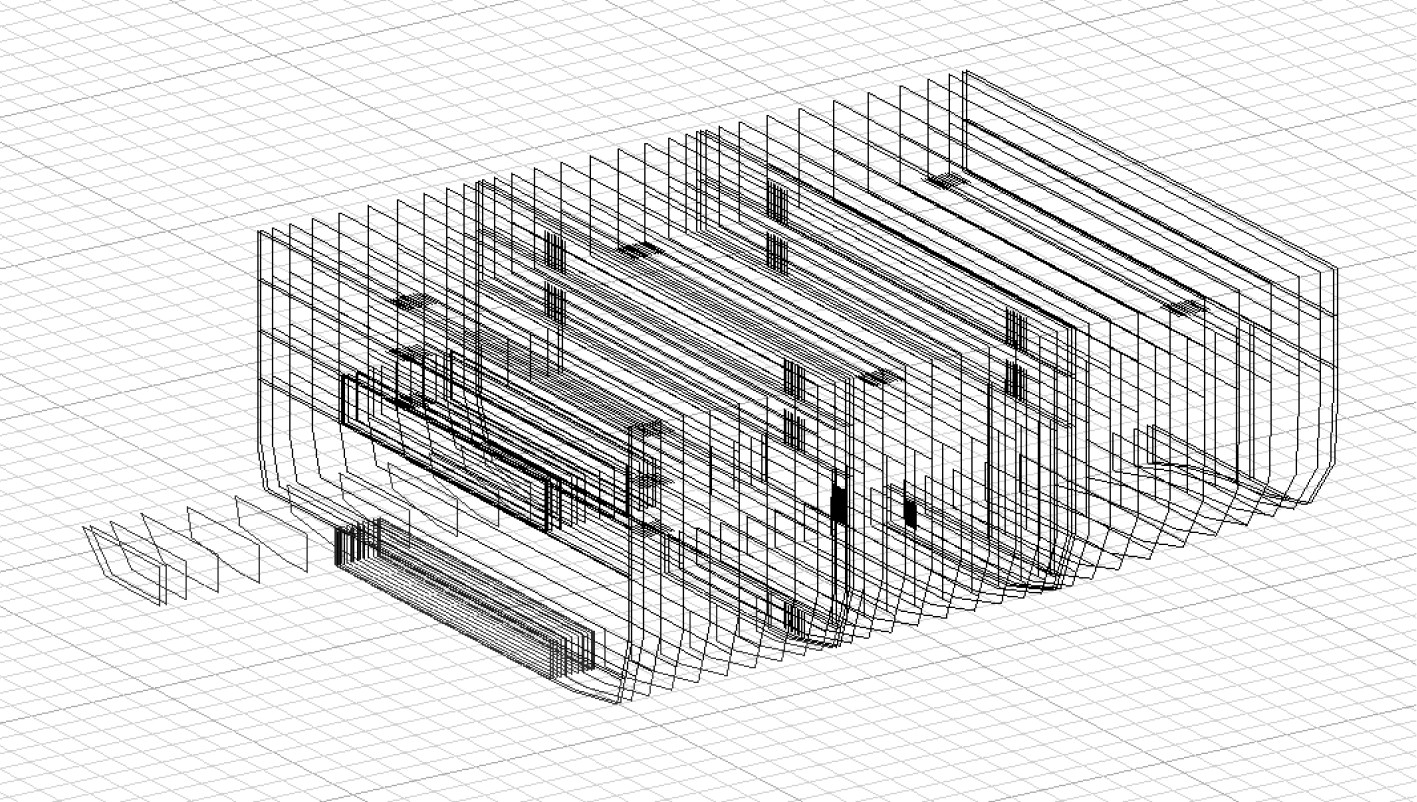
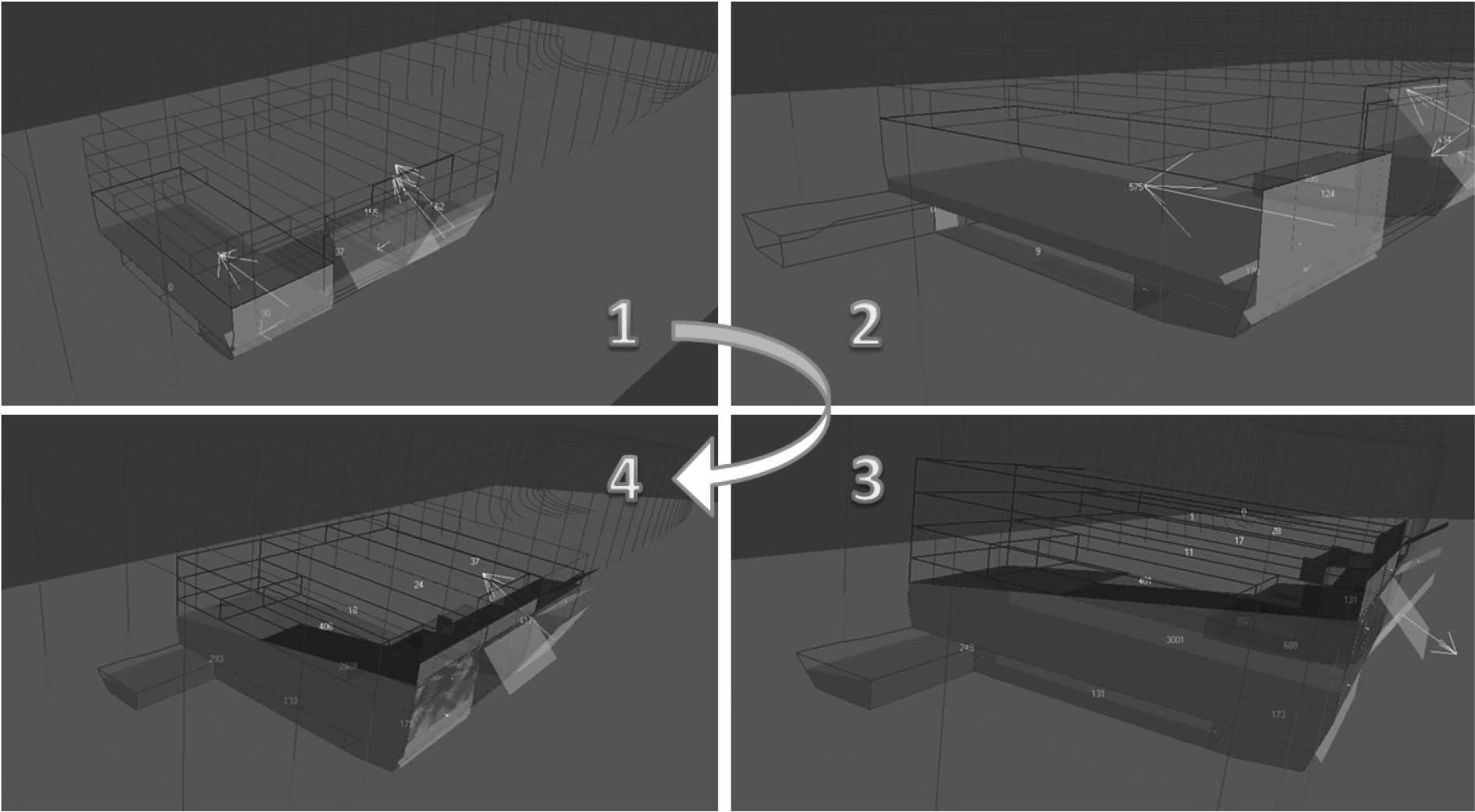
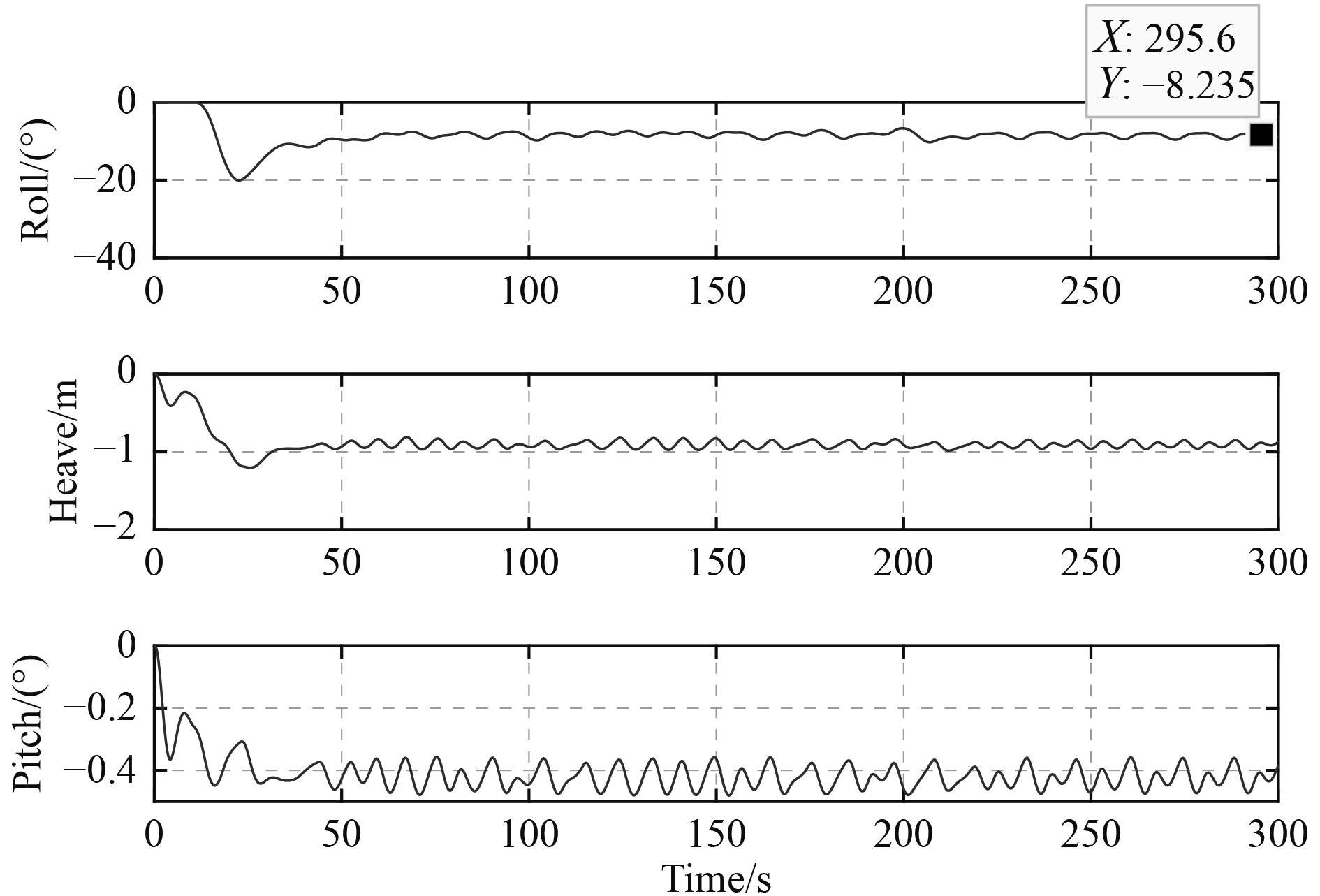
通过研究舱室布置情况,提出采用横贯进水通道的舱室布置方式,以减少船舶发生破损后的横倾角。船底所采用的横贯进水通道如图6中的高亮部分所示。当船舶的舷侧发生破损进水后,可利用该通道使海水从破损侧舱室流到对称一侧的舱室中,从而减少船体发生破损后的横倾角。采用横贯进水后的静水中仿真结果如图7所示,分别截取破损发生、海水流入横贯通道、海水流入破口对面一侧舱室,以及最终达到稳定的过程。采用横贯进水通道设计后,稳定状态的横倾角为8.2°(见图8),较之前未采用横贯进水通道有明显减小。
|
图 6 横贯进水舱室设置 Fig. 6 Cross-flooding tank arrangement |
|
图 7 横贯进水过程 Fig. 7 Cross-flooding procedure |
|
图 8 设置横贯进水舱室后的船舶破损运动时历 Fig. 8 Time domain damage simulation with cross-flooding tank |
利用时域破损仿真CAE软件对1艘大型船舶开展研究,结果表明通过时域模拟不但能够还原船舶发生破损后海水在各舱室间的流动和漫延过程,还能获悉不同时间点对应的船舶姿态变化情况,进而可服务于船舶发生破损后的应对决策和人员疏散撤离模拟;在船舶大型化的趋势下,舱室的布置日趋复杂,通过时域模拟可纳入波浪、风等环境载荷对于破损后船舶的运动影响,更加真实地反映船舶是否存在发生倾覆的风险,为后续船舶舱室的布置及优化提供技术手段。
通过破损稳性方面的研究,可以对舱室的开口布置和通道设计进行优化,通过设置横贯进水舱室等手段,增加船舶在发生破损后的存活能力,并且提升紧急情况下人员撤离的效率和安全性。对于后续大型船舶的总布置及舱室设计具有参考价值。
| [1] |
夏利清, 范佘明. 船舶在波浪中破损稳性数值计算方法综述[C]//船舶水动力学学术会议, 中国武汉, 2004.
|
| [2] |
马丽君, 冯其, 张楠. 国外船舶破损稳性理论分析[J]//中国舰船研究, 2012, 7(2): 9–13
|
| [3] |
VASSALOS D, TURAN O. A realistic approach to assessing the damage survivability of passenger ships[J]. Transactions of the Society of Naval Architects and Marine Engineers, 1994, 102: 367–394
|
| [4] |
ZARAPHONITIS G, PAPANIKOLAOU A, SPANOS D. On a 3D mathematical model of the damage stability of ships in waves[C]//Proceedings of the 6th International Conference on Stability of Ships and Ocean Vehicles, Varna, 1997.
|
| [5] |
SANTOS T, SOARES G. Study of damaged ship motions taking into account floodwater dynamics[J]. Journal of Marine Science and Technology, 2008, 13(3): 291–307.
|
| [6] |
QIAN K, WANG D. Calculation of wave load encountered by damaged ships[C]// Proceedings of the 7th International Conference on Stability of Ships and Ocean Vehicles, Australia, 2000.
|
| [7] |
李佳, 马宁. 船舶破舱状态浮态的时域计算分析, 中国航海, 2009, 32(1): 49–53.
|
| [8] |
郭显杰. 规则斜浪中破损船舶进水后的运动响应研究[D]. 天津: 天津大学, 2007.
|
| [9] |
NABAVI Y, CALISAL S, AKINTURK A, et al. A computational investigation of the three dimensional geometric parameters’s effects on the discharge rate of a ship opening[C]//Proceedings of the 9th International Conference on Stability of Ships and Ocean Vehicles, Rio de Janeiro, 2006.
|
| [10] |
SKAAR D, VASSALOS D, JASIONOWSKI A. The use of a meshless CFD method in modeling progressive flooding and damaged stability of ships[C]//Proceedings of the 9th International Conference on Stability of Ships and Ocean Vehicles, Rio de Janeiro, 2006.
|
| [11] |
GAO Z, VASSALOS D. The dynamics of the floodwater and damaged ship in wave[J]. Journal of Hydrodynamics, 2015, 27(5): 689–695.
|
| [12] |
JASIONOWSKI A. An integrated approach to damage ship survivability assessment. PhD thesis[D].Glasgow: University of Strathclyde, 2001.
|
| [13] |
MURASHIGE S, KOMURO M, AIHARA K. Nonlinear roll motion and bifurcation of a Ro-Ro ship with flooded water in regular beam waves[C]//Proceedings of Third International Workshop on Theoretical Advances in Ship Stability and Practical Impact, Crete, Greece, 1997.
|
 2023, Vol. 45
2023, Vol. 45

