在1987年Lakes成功制备出泊松比为−0.17的聚氨酯材料后,近些年随着科学技术的发展进步,越来越多的拉胀结构和负泊松比材料被发现并制作出来,这些结构在航空航天等领域发挥了重要的作用[1-2]。拉胀结构在受拉时会横向膨胀,受压时横向收缩,所以又被称为负泊松比结构[3]。由于拉胀结构特殊的变形模式,使得这种结构具有特殊的力学性能[4]。AWerson[5]分析了手型多胞结构轴向压缩力学模型,得出棱数为4和6的手型结构具有负泊松比的性质。郭春霞等[6]对正弦负泊松比多孔蜂窝梁进行了面内三点弯曲实验,并与传统方孔蜂窝梁进行对比分析,实验结果表面负泊松比结构相较于传统正泊松比结构具有更好的吸能效果。张振华等[7]对金字塔点阵单胞结构在压缩载荷下的力学性能进行研究,得出了结构泊松比合影边之间的规律。新型结构和材料在越来越多的领域发挥着自己独特的作用,朱伟杰等[8]通过仿真计算的方式分析了水下微穿孔板声超材料应用于新型声导流罩独特优势。赵昌方等[9]对复合材料负泊松比结构的拉压力学性能进行了仿真研究,验证了其负泊松比特性。刘宇等[10]对负泊松比基元蜂窝结构的吸能效果进行仿真研究,得出负泊松比结构在同等质量条件下吸能量相比于传统结构更高的结论。
本文选取三维反手性负泊松比单胞结构作为研究对象。通过万能试验机压缩并通过摄影记录、利用游标卡尺量取侧向位移的方式来获取结构的泊松比,得到结构在压缩载荷下的泊松比变化规律,并结合数值仿真研究反手性负泊松比结构的变形破坏模式和静压载荷下的应力分布情况,为三维反手性负泊松比结构的力学性能研究提供参考。
1 实验研究 1.1 模型设计采用三维反手性负泊松比结构中的单体胞元,如图1所示。

|
图 1 结构示意图 Fig. 1 Schematic diagram of structure |
该胞元由3层板和2层各16根方杆组成。其中3层板结构相同,由4个正方形薄板和4根方杆组成,如图2所示。由于四向反手性负泊松比结构是周期型结构,所以上下2层板的厚度为中间板厚度的一半。上层板可以通过下层板平移得到,中层板可以通过下层板绕结构上下两层板质心连线旋转90°之后平移并复制后得到。结构中每4个相邻的方杆可以通过其中1根方杆绕与其相连的2个正方形薄板的质心连线环形阵列得到,把4个相邻的方杆视为1个方杆组,1层内与已经得到的方杆组相邻的的2个方杆组可以通过镜像的方式得到,最后1个方杆组可以通过第1个方杆组平移得到。第2层方杆可以通过将第1层16根方杆绕结构上下2层板质心连线整体旋转90°之后平移得到。该结构尺寸主要参数为:正方形薄板边长A=14 mm,正方形薄板之间的距离L=7 mm,直杆宽度d=3 mm,板厚T=3 mm,方杆高度H=10 mm,方杆端部正方形边长a=4 mm,斜杆与XY平面夹角α=45°。

|
图 2 单胞结构图 Fig. 2 Diagram of single-cell structure |
本文所采用的三维反手性负泊松比结构为立体镂空结构,结构构造较为复杂,传统工艺难以加工,故采用FDM增材制造技术,选用聚碳酸酯(PC)作为打印材料,使用Raise3D Pro2型号的3D打印机制作该模型,模型如图1和图2所示[11]。聚碳酸酯材料的力学性能指标见表1。
|
|
表 1 材料PC的性能参数 Tab.1 Performance parameters of polycarbonate |
使用MTS万能试验机对试样进行压缩,实验开始前布置实验背景为黑色背景,与白色图像形成反差色,便于后续分析处理。将试验机通过数据传输线与电脑相连接,在电脑客户端控制上下夹具与模型上下面板接触,并施加小于50 N的初始力,此时将应力值和位移值清零。
实验过程中,将万能试验机的加载模式设置为方向竖直向下大小为1 mm/min等量加载状态,符合静态压缩的实验要求。每当试验机输出模型轴向位移增加0.1 mm时暂停实验,使用游标卡尺测量模型中间板X方向尺寸并使用相机遥控拍照记录,数据记录结束后开始试验继续加载。如此循环直至模型发生破坏,实验结束。根据游标卡尺测量数据得到模型的宏观横向位移。模型的纵向位移和力可以由实验系统直接导出。
泊松比定义公式的物理意义为,当模型受到轴向载荷时,物体的横向应变和轴向应变值之比的相反数即为物体的泊松比。根据以上数据便可得到模型的宏观泊松比。
| $ \nu = - \frac{{{\varepsilon _x}}}{{{\varepsilon _y}}}。$ | (1) |
在压缩过程中,第1层斜杆在与杆件成一定角度的力和力矩的作用下发生弯曲和扭转变形,带动上中2层板结构中的正方形薄板旋转,使连接正方形薄板的水平杆件产生弯曲变形,继而使结构产生横向收缩变形,呈现负泊松比效应。随着万能试验机施加的轴向位移的增大,结构轴向的压缩变形进一步增大,如图3所示。

|
图 3 单胞结构压缩实验图 Fig. 3 Picture of single-cell structure compression test |
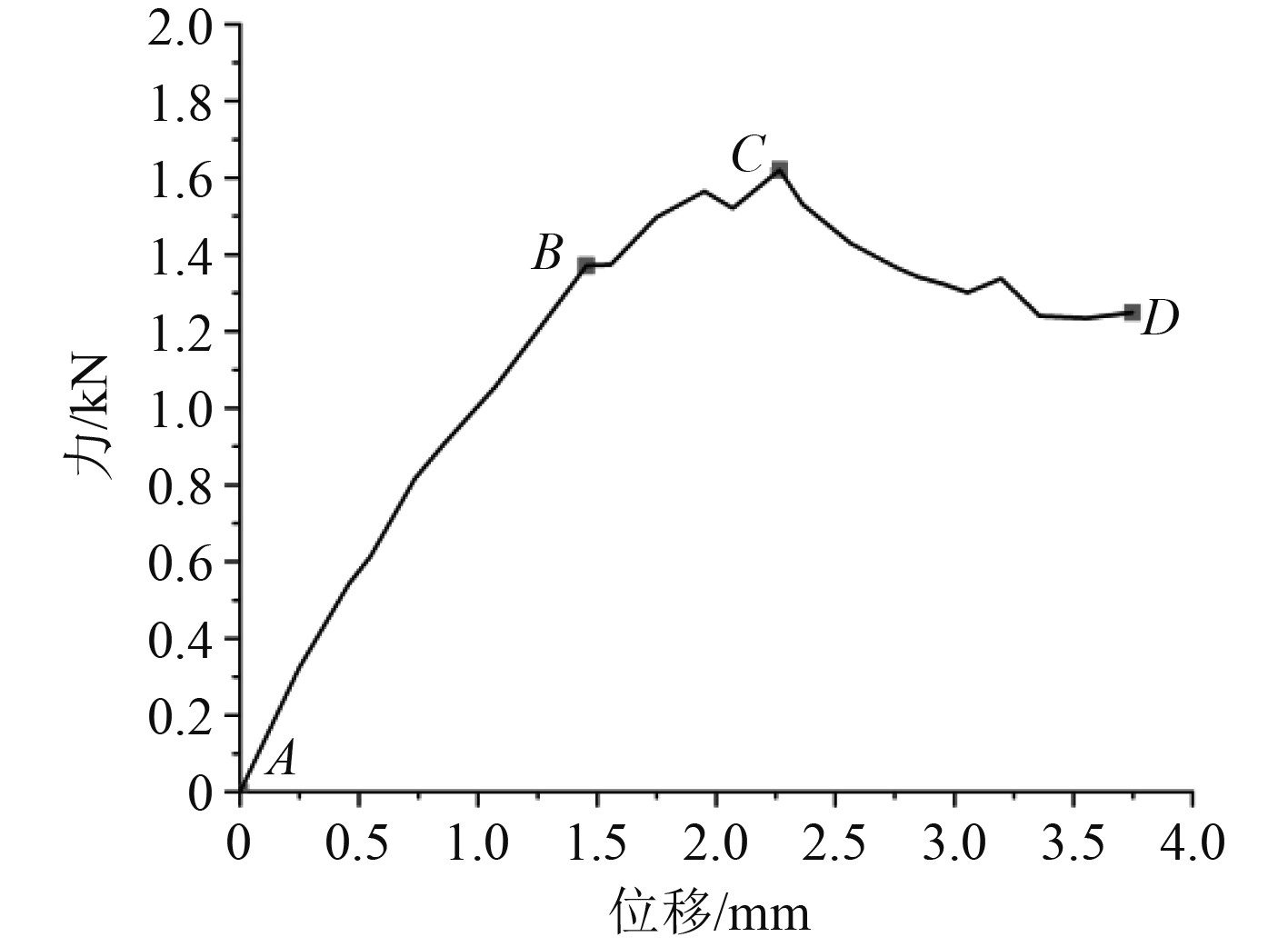
|
图 4 宏观力—位移曲线 Fig. 4 Macro force-displacementcurve |
由于实验操作采用等位移加压法,所以实验得到的模型宏观力位移曲线存在许多均匀分布的锯齿状结构。从图4可以看出,模型在静态压缩中的变形可以分为3个阶段:弹性阶段、塑性阶段和破坏阶段。
弹性阶段(AB段):当0≤S<1.45 mm时,处于这个阶段下的模型各部分产生了不同程度上的弹性变形,模型展现出的弹性模量大小为95.77 MPa。
塑性阶段(BC段):当1.45 mm≤S<2.26 mm时,模型部分区域产生塑性变形,力位移曲线斜率变小,力的增大速度明显减小。采用“最远法”确定屈服点B的位置[11-12],即B点在曲线AC上,且满足AB和BC线段之和最大的点即为模型屈服点。当模型压缩位移为1.45 mm时,支反力大小为1.37 kN,屈服强度为5.36 MPa。当模型压缩位移为2.26 mm时,模型最大承载力为1.62 kN,强度极限为6.3 MPa。
破坏阶段(CD段):当S≥2.26 mm时,部分模型逐渐发生破坏,力位移曲线呈现出阶梯式下跌。当S=3.74 mm时,中层板连接杆件发生破坏,结构彻底失去承载能力,此时,模型被完全破坏,破坏强度为4.88 MPa。
2 仿真分析 2.1 有限元建模采用Abaqus/ CAE软件对结构进行实体建模,并对实验过程进行仿真计算。使用体单元对结构进行划分网格,采用C3D4四节点线性四面体单元进行网格化分。部件实例布种设置近似全局尺寸为2 mm,共产生节点26894个,单元105802个。材料属性设置如下:密度1.19E−9 kg/mm³,杨氏模量2.048E9 Pa,泊松比0.3。赋予结构截面设置为:实体,均质。为和真实实验条件保持一致,在结构上方设置刚性薄板模拟万能试验机上部压头,并赋予薄板下表面和结构上表面相互作用为有限滑移的表面与表面接触,接触面摩擦公式定义为粗糙。为结构底部面板添加固定边界条件,施加大小为0.016 mm/s方向沿Z轴负向的位移于薄板上,分析步类型选择静力通用,分析步时长设置为1 000 s。仿真模型如图5所示。

|
图 5 单胞结构仿真模型 Fig. 5 Single cell structure simulation model |
在仿真输出数据库中提取上面板支反力和位移数据,绘制力位移曲线并和实验得到的结构力位移曲线进行对比。结果显示,在结构变形的弹性阶段由仿真方法和试验方法在同一位移刻度下的支反力相差不大,以位移为−1.0 mm时的支反力为例,仿真计算得出力位移曲线并进行线性内插得到位移为−0.1 mm时作用在薄板上的支反力大小为159.3 N,实验数据中对应位移为−0.1 mm时的支反力为170.6 N,两者误差为6.3%,2种计算方法之间的误差随着位移的增大而不断增大,这是由于实验采用等量增压方式而仿真采取连续加压方式造成的。以薄板位移1.29 mm时为例,结构的位移仿真计算图如图6所示。可看出,与图3所示的压缩实验结构变形模式相一致,2层斜杆呈弯扭变形,使得中间面板上的方盘旋转从而带动直杆产生歪曲变形,由于方盘和斜杆的相互作用使得结构在水平方向上内缩,同时结构在薄板的压力作用下在竖直方向上收缩,产生负泊松比效应。从力位移曲线趋势和弹性阶段的误差来看,数值仿真结果和实验结果较为吻合,这说明仿真结果比较准确且有效(见图7)。

|
图 6 位移U=1.29 mm时的位移云图 Fig. 6 Displacement nephogram of displacement U =1.29 mm |
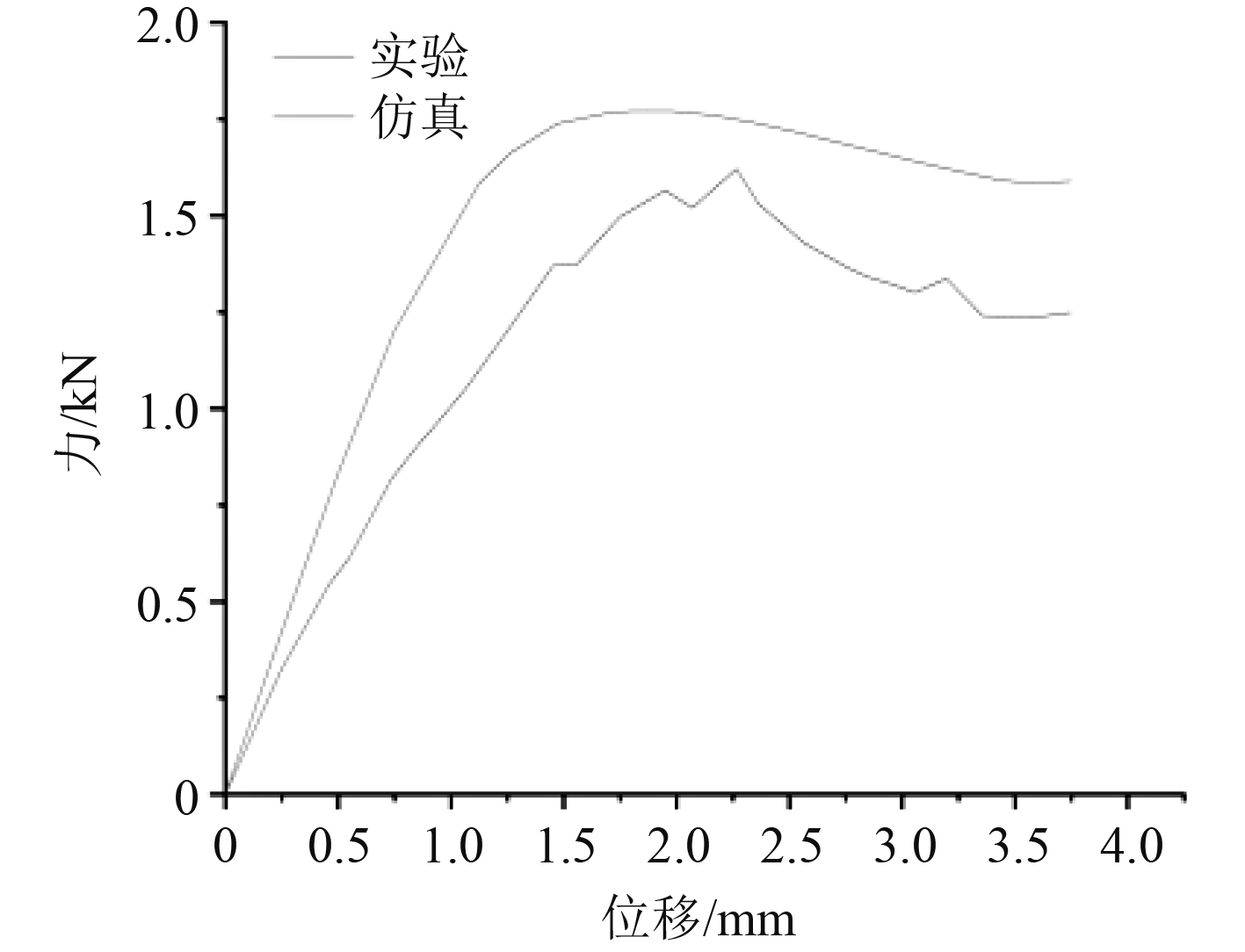
|
图 7 实验与仿真结果 Fig. 7 Experimental and simulated results |
在Abaaqus仿真软件中提取出三维反手性负泊松比结构在压缩过程中变形图并提取结构横向位移值。在横向位移范围0~3.74 mm中n种工况下通过仿真计算方法得出来的结构泊松比数值可以根据结构的纵向位移和横向位移计算出纵向应变和横向应变通过式(1)得到,结果见表2。
|
|
表 2 泊松比计算结果 Tab.2 Results of Poisson's ratio calculation |
可以得出,该四向反手性结构具有负泊松比性质,在纵向位移为0~3.74 mm过程中,结构的泊松比数值在压缩过程中于−0.5上下变化,上下浮动不超过±0.05,且变化速度较为缓和。
3.2 变形模式分析根据数值仿真与压缩实验宏观应力—应变曲线的对应关系,可得图8所示结果。图8(a)单胞结构位移变形最大值为0.276 mm,出现在上面板边角处;中层板连接杆中段的应变出现最大值7.98×10−3,其它部位的应变较小;应力最大值为22.18 MPa,出现在斜杆上与面板相接触的部分。图8(b)单胞结构位移变形最大值为2.057 mm,出现在上面板边角处;中层板连接杆中段的应变出现最大值0.285,其他部位的应变较小;应力最大值为35.80 MPa,出现在斜杆中间部分。图8(c)单胞结构位移变形最大值为3.492 mm,出现在上面板边角处;中层板连接杆中段的应变出现最大值1.132,其他部位的应变较小;应力最大值为39.25 MPa,出现在斜杆上与面板相接触的部分。

|
图 8 仿真压缩过程应变、应力、位移云图 Fig. 8 Strain,stress nephograms and displacement for simulated compression |
综上,斜杆的位移、应力往往是最大的,中层板连接连接杆中段的变形最明显,且中层板连接杆的断裂是制约结构承载能力的主要原因。这说明随着压缩载荷的增加,单胞结构更容易在斜杆和连接杆处首先发生破坏。
图9为单胞结构在压缩试验过程中的最终破坏形式和结构破坏时的应力云图。可以看出,在实验过程中,中层板和中层杆的连接处发生断裂而导致结构产生破坏从而丧失承载能力,但在仿真计算中,而是由于中层板连接杆中段发生了严重的塑性收缩导致了单胞结构的破坏。这种现象的出现和FEM增材制造技术为分层打印和打印精度不高从而导致了一定的结构缺陷有关。以上结果表明,在压缩过程中中层板连接杆在x−y方向的弯矩和压力的同时作用下率先发生破坏,从而导致结构丧失承载能力。

|
图 9 杆件破坏示意图 Fig. 9 Schematic diagram of rod failure |
采用FEM增材制造的方式,使用Raise3D Pro2 3D打印机制作了四向反手性负泊松比结构单胞模型,使用万能试验机对模型进行压缩实验,运用数值仿真方法研究单胞结构的力学性能,得到了反手性单胞结构在压缩过程中的泊松比数值变化规律,分析了反手性单胞结构的变形模式和破坏模式,得出结论如下:
1) 该型反手性单胞结构在静态压缩实验过程中呈现出明显的负泊松比效应,泊松比数值在−0.5左右变化,且变化幅度不超过0.05。
2) 通过仿真建模的方式重现了该单胞结构的静态压缩实验过程,并通过力-位移曲线验证了仿真建模的正确性。根据仿真计算的结果,单胞结构在静态压缩过程中发生弹塑性变形,变形过程可以分为弹性变形阶段、屈服变形阶段和破坏阶段,其中屈服强度为5.36 MPa,强度极限为6.33 MPa,破坏强度为4.88 MPa。
3) 在轴向压缩载荷作用下,随着载荷的增大,轴向位移不断增大,该单胞结构各部分变形量也在逐渐增大。在变性过程中,位移、应变的最大值出现在中间板连接杆中部,而应力最大值出现在斜杆与面板的连接处,最终中间板连接杆在压缩载荷和弯曲力的作用下首先发生断裂破坏从而导致结构丧失承载能力。由于分层打印和原材料缺陷,该单胞结构在实验过程中中间板连接杆首先发生破坏的位置不是仿真结果显示的杆件中间处而是板件与杆件的连接处。
| [1] |
LAKES R. Foam structures with a negative Poisson’s ratio[J]. Science, 1987, 235: 1038-1040. DOI:10.1126/science.235.4792.1038 |
| [2] |
高玉魁. 负泊松比超材料和结构[J]. 材料工程, 2021, 49(5): 38-47. |
| [3] |
任鑫, 张相玉, 谢亿民. 负泊松比材料和结构的研究进展[J]. 力学学报, 2019(3): 656-687. |
| [4] |
QIAO J X , CHEN C . The impact resistance of uniform and functionally giaded auxetic double arrowhead honeycombs[J]. International Jounral of Impact Engineering, 2015, 83:47−58.
|
| [5] |
BACIGALUPO A , GAMBAROTTA L . Multiscale modeling of periodic chiral cellular materials[C]// 2014.
|
| [6] |
黄秀峰, 张振华. 聚脲涂覆三维负泊松比点阵结构的静态力学性能研究[J]. 中国科学: 物理学、力学、天文学, 2021, 51(5): 112-130. |
| [7] |
郭春霞, 赵冬, 孙永涛, 等. 正弦负泊松比多孔蜂窝梁平面内三点弯吸能性能实验研究[J]. 应用力学学报, 2020, 37(6): 2404-2409. DOI:10.11776/cjam.37.06.B175 |
| [8] |
朱伟杰, 崔汉国, 何世平. 水下微穿孔板声超材料的几何结构优化[J]. 舰船电子工程, 2020, 40(3): 139-143. DOI:10.3969/j.issn.1672-9730.2020.03.034 |
| [9] |
赵昌方, 朱宏伟, 仲健林, 任杰, 马威. 复合材料负泊松比结构力学性能数值研究——拉压力学性能[J]. 江苏师范大学学报(自然科学版), 2020, 38(4): 61-64. |
| [10] |
刘宇, 郝琪, 田钰楠, 等. 负泊松比基元蜂窝结构研究[J]. 机械科学与技术, 2021, 40(10): 1629-1635. DOI:10.13433/j.cnki.1003-8728.20200237 |
| [11] |
张旭苑. 3D打印在结构设计中的应用[J]. 机械工程与自动化, 2021(5): 222-223+226. DOI:10.3969/j.issn.1672-6413.2021.05.085 |
| [12] |
冯鹏, 强翰霖, 叶列平. 材料、构件、结构的“屈服点”定义与讨论[J]. 工程力学, 2017, 34(3): 36-46. FENG Peng, QIANG Han-lin, YE Lie-ping. Discussion and definition on yield points of materials, members and structures[J]. Engineering Mechanics, 2017, 34(3): 36-46. DOI:10.6052/j.issn.1000-4750.2016.03.0192 |
| [13] |
殷晓三. 无明显屈服特征构件屈服点的确定与评价[J]. 地震工程与工程振动, 2019, 39(3): 143-150. YIN Xiao-san. Evaluation and determination methods on yield point of structural components without obvious yield feature[J]. Earthquake Engineering and Engineering Dynamics, 2019, 39(3): 143-150. DOI:10.13197/j.eeev.2019.03.143.yinxs.014 |
 2023, Vol. 45
2023, Vol. 45
