2. 浙江清华长三角研究院,浙江嘉兴 314006;
3. 清华大学 能源与动力工程系,北京 100084
2. Yangtze Delta Region Institute of Tsinghua University Zhejiang, Jiaxing 314006, China;
3. Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China
在设计过程中,对船舶航行阻力的计算必不可少,如何快速准确的估算出船舶航行阻力是船舶行业一直以来重点关注的问题[1]。目前,关于船舶阻力的估算方法有船模试验法、近似值估算法以及数值模拟法[2]。随着现代船舶用途以及船型等的改变,很多近似值估算法已经不能满足实际工程的计算需要。而对船舶进行水池试验虽然精确度较高,但是成本高且耗费周期长。随着计算流体力学以及计算机仿真技术的不断发展,采用数值模拟方法来计算船舶阻力逐渐成为主流。
目前关于船舶数值模拟的软件有两类:一种是采用势流理论、发展较为成熟的专业软件,如Shipflow;另一类是采用粘性理论的商用数值计算软件,如Ansys-Fluent、STAR-CCM+等。势流理论对于以前比较简单的船舶型线的阻力计算具有计算快、精度高的特点。但是,由于现在船舶的型线不断发展改变,采用势流理论计算船舶阻力的准确性有待提高。因此,目前更多学者开始采用基于粘性理论的商用软件STAR CCM+[3-6]。虽然商用软件均具备给出误差较小的计算结果的能力,但是在数值模拟过程中,由于计算的复杂度,精确度很大程度上取决于计算策略。例如,同样是对DTMB45船模计算,刘飞[7]的计算区域距船首前为1.5倍船长,船尾后为2.5倍船长,自由液面上下部分均为2倍船长,对船舶的波形区域进行加密并选取标准k-Epsilon湍流模型,最后计算结果的误差在3.31%以内;而尹辉[5]选取的计算区域距船首前约1倍船长,距船尾后约3倍船长,整个计算域的上部为一倍船长,下部为2倍船长,采用K-Omega湍流模型,傅汝德数为0.2~0.35时,计算结果的误差在2.65%以下,但是在弗汝德数为0.05时误差则达到16%。罗良[8]采用了Star−CCM+对KCS船舶进行数值模拟,计算区域在船长方向为4倍船长,SST K-Omega湍流模型,仿真误差在2%以内。倪崇本等[9]采用K-Espilon湍流模型对KCS进行数值计算,计算误差达到6.5%。
对于船舶数值模拟来说,目前常用的湍流模型有RANS模型中的SST K-Omega湍流模型、标准K-Epsilon湍流模型、标准K-Omega湍流模型、可实现的K-Espilon湍流模型4种,总的来说,这些湍流模型预测船舶总阻力较为可靠[10-15]。
由此可知,不同的计算策略对于船舶阻力性能的精确度有着不同程度的影响[16]。但是目前对于数值模拟中计算区域大小、网格密度以及湍流模型对于数值模拟的总阻力、摩擦阻力和耗费时长的研究还存在不足,因此本文对船舶数值模拟过程中的这些影响因素进行对比分析,提出一种满足实际工程需求的数值模拟方法。
1 数值计算 1.1 数值计算模型本文以某30 000 t的散货船为例进行数值建模,船舶的设计参数如表1所示,为了减少计算量,数值计算模型与实际船体比例尺采用29.3∶1。由于船舶在静水中的直线航行是对称的,为了减少计算量又不影响计算精度,仅对一半的船舶进行仿真计算。将船尾轴中心线和船舶设计吃水线的交点设置为坐标原点,船尾指向船首方向为
|
|
表 1 某30 000 t船舶参数 Tab.1 Parameters of 30 000 t ship |
数值计算模型基于RANS湍流模型,使用商业CFD软件包STAR-CCM+开发,流场中采用的控制方程为不可压缩流体的连续性方程和动量方程。
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0,$ | (1) |
动量方程:
| $ \frac{{\partial (\rho \overline {{u_i}} )}}{{\partial t}} + \frac{{\partial (\rho \overline {{u_i}} \overline {{u_j}} )}}{{\partial {x_j}}} = - \frac{{\partial \bar p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \rho \overline {{{\dot u}_i}{{\dot u}_i}} } \right) + \rho {f_i} 。$ | (2) |
式中:
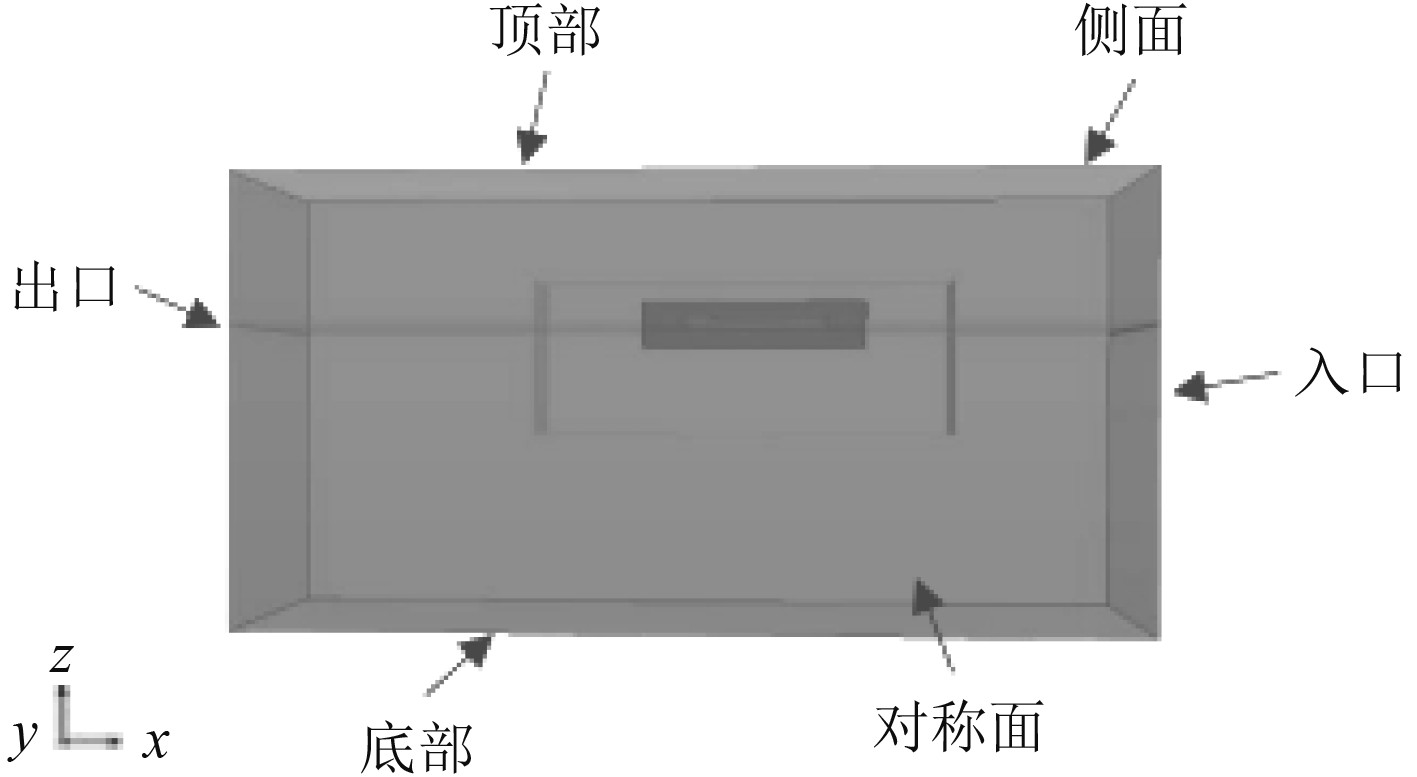
本文对计算流场的边界条件设置如图1所示。将对称面设置为对称边界条件,顶部设置为压力出口边界,其他面均设为速度入口边界,船体表面设置为无滑移的壁面。对计算区域进口、出口、以及侧面设置进行Wave Forcing消波,Wave Forcing可以在指定的距离内,迫使离散化N-S方程的解趋向于另一种解,相比于阻尼消波,这种方法既可以消除区域边界上的波浪反射,又可以设置较小的计算区域从而减少网格数量,节省计算时长。
|
图 1 数值计算区域划分 Fig. 1 Division of numerical calculation area |
通过创建自动网格,选择面网格、切割体网格以及棱柱层网格。为了提高计算精确度、捕捉船舶航行中波浪的变化,采用切割体网格单元生成器,对自由液面处
采用VOF(Volume of Fluid)法来模拟船舶航行中自由液面,VOF方法在网格单元内设置流体体积分数的值
| $ {\alpha _i} = \frac{{{V_i}}}{V} 。$ | (3) |
式中:
在数值仿真过程中,一个网格单元体中不同的流体的体积分数值的和为1。在船舶航行的过程中,自由液面处的流体包含水和空气,因此,在数值计算过程中,在自由液面处设置值为0.5来捕捉自由液面,如图2所示,水的体积分数用于反映计算单元的状态。值为0.5表示计算单元中填充了50%的水和50%的空气,代表自由表面。值0和1表示计算单元分别充满空气和水。

|
图 2 船体水的体积分数 Fig. 2 Volume fraction of water on the hull |
首先以航速19 kn,试验阻力值924 600 N为例,对30 000 t散货船模型尺度下的静水阻力进行数值模拟。采用了计算区域尺寸从4倍船长到8倍船长的5种尺寸进行数值模拟,计算区域内宽度约为2倍船长,自由液面以下约为2倍船长,自由液面以上约1倍船长。其中,网格基础尺寸均为0.14 m,采用SST K-Omega湍流模型。计算时间步长为0.03,计算时间为90 s,每个时间步长迭代次数为5,在整个数值模拟过程迭代1.5万次。
采用三因次换算法[2]将数值模拟总阻力换算为实船阻力,并与实船试验值进行对比。为了减少换算误差,摩擦阻力采用的模型阻力值,计算结果如表2所示。其他条件不变时,随着计算区域的增加,网格数量也增加,计算时长也不断增加,误差先减小后增大,在6倍船长时误差达到最小值1.39%。但是计算区域大小对于船舶摩擦阻力的影响基本不变。因此,在对船舶进行数值计算过程中,推荐采用6倍计算区域。
|
|
表 2 计算区域对数值计算结果的影响 Tab.2 Influence of calculation area on numerical results |
在数值模拟过程中,分别取误差最大的4倍船长和误差最小的6倍船长计算区域,船速为19 kn,其他条件不变,通过改变网格的基础尺寸的基础设置,以此来改变网格密度。探究网格密度对于数值模拟的精确度的影响。
由表3可知,在基础尺寸是0.12和0.14时,6倍船长的误差均小于4倍船长。基础尺寸为0.12的4倍船长误差和基础尺寸为0.14的6倍船长相差不大,因此减少基础尺寸,适当的增加计算区域,可以在保证计算精度的情况下,减少计算时长。计算区域6倍船长,基础尺寸为0.12时,误差最小,达到−0.62%,但是基础尺寸为0.16时的误差达到1.39%,也可以满足实际工程,且整体耗时也较短。
|
|
表 3 网格密度对数值计算结果的影响 Tab.3 Influence of grid density on numerical results |
为探究不同湍流模型对船舶数值计算精度及耗时的影响,在航速19 kn,计算区域为6倍船长,网格大小为157.6万的情况下,分别采用SST K-Omega、可实现的K-Espilon湍流和标准K-Omega等3种模型,进行数值计算和时间估算,结果如表4所示。
|
|
表 4 湍流模型对数值计算结果的影响 Tab.4 Influence of turbulence model on numerical results |
可知,SST K-Omega在船舶数值模拟过程中,对船舶的数值计算的精确度较高,误差仅有1.39%,而且耗时最短,这是由于SST K-Omega是标准的K-Omega和标准K-Epsilon湍流模型结合优化后的结果。不同的湍流模型对于摩擦阻力的影响较大,可实现的K-Espilon湍流和SST K-Omega对于摩擦阻力的数值计算较为接近,这是由于这2个模型相对于标准的标准K-Omega模型增加了额外的计算项。因此,本文推荐采用SST K-Omega湍流模型来进行船舶总阻力的数值计算。
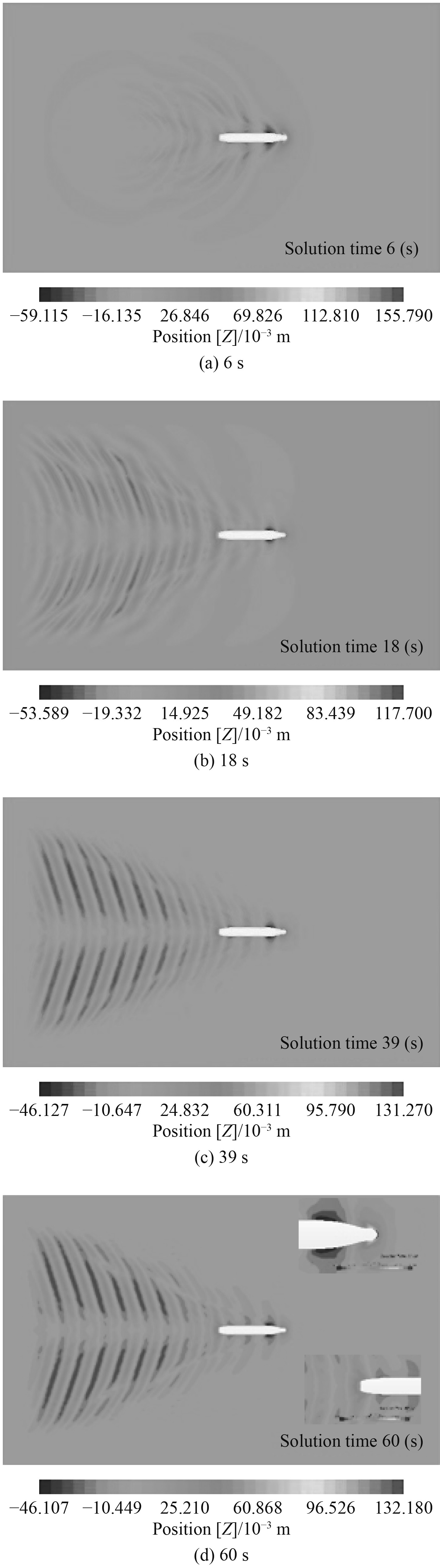
3 数值计算方法验证 3.1 数值计算结果可视化分析以表2中6倍船长计算结果为例,图3为船舶数值计算过程中的波形图。可知,随着时间的增加,船舶航行过程中的开尔文波形逐渐扩大成型并且趋于稳定状态,波形图符合船舶实际航行过程中的开尔文波形。从图4(d)中船首、尾放大图知,船首波高大于船尾波高,这也是粘压阻力产生的重要原因。
|
图 3 船舶航行波形图 Fig. 3 Ship motion waveform |
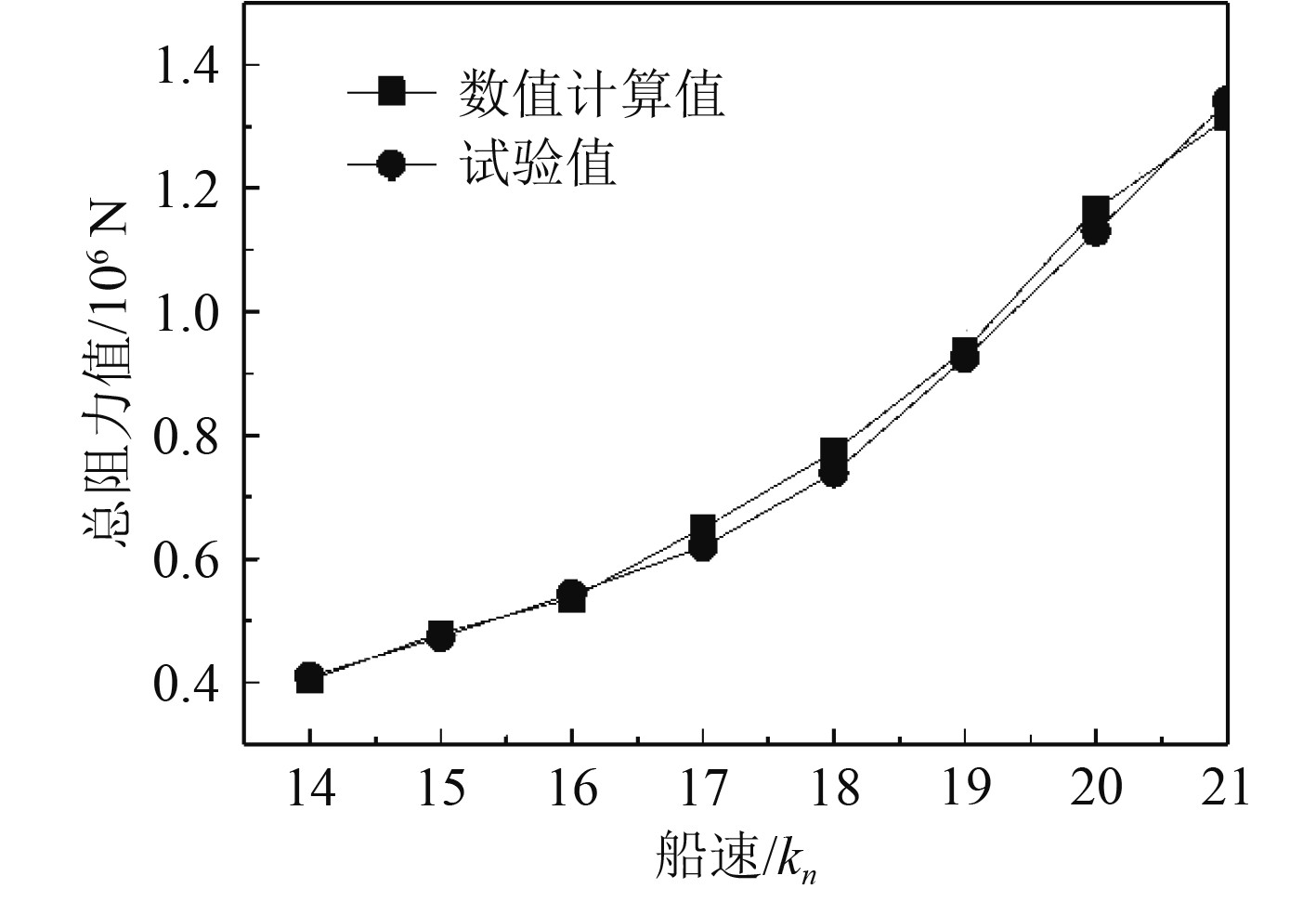
为了验证上述数值模拟的准确性以及适用性,对船舶在14~21 kn,即船模速度为1.3312~1.9968 m/s海况下的阻力进行数值计算,实船与船模的船速采用傅汝德换算法[2],船模到实船阻力值采用三因次换算法,计算结果如图4所示。随着船速的增加,船舶总阻力逐渐增大。数值模拟得到的船舶航行阻力变化趋势和试验值一致,误差均在5%以内。导致误差的原因可能是实船到船模尺寸阻力换算过程中产生的尺度效应。由于误差较小,表明该方法对船舶静水阻力的计算精确度较高,满足工程要求。
|
图 4 数值计算结果对比 Fig. 4 Comparison of numerical calculation results |
船舶静水阻力可以分为摩擦阻力和粘压阻力,根据相关的平板拖曳试验结果,摩擦阻力系数计算有以下几种常用的经验公式。
桑海公式:
| $ {C_f} = \frac{{0.4631}}{{{{({\rm{lg}}{Re} )}^{2.6}}}} ,$ | (4) |
柏兰特-许立汀公式:
| $ {C_f} = \frac{{0.455}}{{{{({\rm{lg}}{Re} )}^{2.58}}}},$ | (5) |
休斯公式:
| $ {C_f} = \frac{{0.066}}{{{{({\rm{lg}}{Re} - 2.03)}^2}}},$ | (6) |
ITTC1957公式:
| $ {C_f} = \frac{{0.075}}{{{{({\rm{lg}}{Re} - 2)}^2}}} 。$ | (7) |
式中:
图5为船模尺寸下数值模拟值摩擦阻力与各个经验公式值的对比。可知,桑海公式与仿真计算值更接近,这是由于经验公式都是根据船舶试验值分析得到,桑海公式更适合与本文相似船型的船舶。因此对同本文相似类型的船舶阻力进行经验公式计算时,推荐采用桑海公式进行船舶摩擦阻力的计算。图6为数值计算中不同航速情况下船舶摩擦阻力和粘压阻力的阻力值以及占比情况。可知,随着船速的增加,船舶摩擦阻力和粘压阻力逐渐增大,但是随着船速增加摩擦阻力占总阻力比值逐渐减小,粘压阻力逐渐增大。这是因为摩擦阻力主要和雷诺数有关,航速越大,雷诺数越大,摩擦阻力系数越小,而粘压阻力是因为粘性引起的船体前后压力不平衡而产生,船速越高,压差越大,粘压阻力越大,但是摩擦阻力还是处于主体地位。

|
图 5 摩擦阻力对比 Fig. 5 Friction resistance comparison |

|
图 6 阻力占比 Fig. 6 Resistance ratio |
为了验证本文的建模方法对其他船舶阻力计算同样适用,因此本文对KSC船舶进行数值模拟,采用了6倍船长计算区域,由于该船模长度略长于上述船模,故等比例采用0.15 m的基础尺寸,SST K-Omega湍流模型。模型尺度和实船尺度比例为31.6∶1,表5为KCS船舶实船尺度相关参数。
|
|
表 5 KCS船舶参数 Tab.5 KCS ship parameters |
KCS船舶实验数据来自文献[17],由于文献中将实验数据转化为阻力系数,因此本文也将计算结果按照相同方法转换为阻力系数进行对比。
| $ {C_d} = \frac{{{F_d}}}{{\dfrac{\rho }{2}{{{v}}^2}{{A}}}} 。$ | (8) |
式中:
数值模拟误差如表6所示。船舶数值计算误差均在3.5%以内,满足实际工程需求,说明本文计算策略适合和本文船型相似的船舶。
|
|
表 6 KCS船舶模型计算对比 Tab.6 Comparison of KCS ship model calculation |
1)在船舶数值模拟过程中,数值计算精确度并不是随着网格密度的增大而增大,但是随着计算区域的增加,网格密度对计算结果的影响减小。可以适当地采用较大的计算区域和较小的网格密度,以节省计算时长。对于和本文相似的散货船,推荐网格基础尺寸为0.14,计算区域为6倍船长,并采用SST K-Omega湍流模型。
2)采用经验公式法计算和本文船型相似的船舶静水阻力时,建议采用桑海公式可取得更高精度。
3)采用30 000 t散货船以及KCS船,对本文提出的数值计算策略进行验证分析,实验误差均在5%以内,满足实际的工程需求。
| [1] |
方海鹏, 陆梅兴, 黄超. 75000 t散货船阻力预报方法[J]. 船舶工程, 2017, 39(8): 10-12+29. |
| [2] |
曾帅. 典型海况下的船舶阻力预报研究[D] . 大连: 大连海事大学, 2020.
|
| [3] |
杨帆, 张青山, 杜云龙, 等. 船模阻力评估模块开发[J]. 船舶工程, 2019, 41(11): 19-23+97. DOI:10.13788/j.cnki.cbgc.2019.11.04 |
| [4] |
TEZDOGAN T, DEMIREL Y K, KELLETT P, et al. Full-scale unsteady RANS CFD simulations of ship behaviour and performance in head seas due to slow steaming[J]. Ocean Engineering, 2015, 97: 186-206. DOI:10.1016/j.oceaneng.2015.01.011 |
| [5] |
尹辉, 齐来保, 江梓丹, 等. 基于STAR CCM+对5415船模的阻力研究[J]. 中国水运(下半月), 2019, 19(5): 55-57. |
| [6] |
徐伟桐, 蒋一, 眭爱国. 基于STAR-CCM+平台的双体槽道滑行艇水动力性能研究[J]. 中国造船, 2022, 63(2): 137-144. DOI:10.3969/j.issn.1000-4882.2022.02.014 |
| [7] |
刘飞. 基于CFD方法的破损船舶阻力预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2021 .
|
| [8] |
罗良. 基于一维方法和三维方法的模型尺度及实船尺度船舶阻力预报[J]. 舰船科学技术, 2022, 44(6): 18-21. LUO L. Prediction of ship resistance based on one-dimensional and three-dimensional methods at model scale and real ship scale[J]. Ship Science and Technology, 2022, 44(6): 18-21. DOI:10.3404/j.issn.1672-7649.2022.06.004 |
| [9] |
倪崇本, 朱仁传, 缪国平, 等. 一种基于CFD的船舶总阻力预报方法[J]. 水动力学研究与进展A辑, 2010, 25(5): 579-586. NI C B, ZHU C R, MIAO G P, et al. A prediction method of ship total resistance based on CFD[J]. Chinese Journal of Hydrodynamics, 2010, 25(5): 579-586. |
| [10] |
VISONNEAO M, QUEUTEY P, DENG G B. Model and full-scale free-surface viscous flows around fully-appended ships[C]//ECCOMAS CFD 2006: Proceedings of the European Conference on Computational Fluid Dynamics, Egmond aan Zee, The Netherlands, September 5-8, 2006. Delft University of Technology. European Community on Computational Methods in Applied Sciences (ECCOMAS), 2006.
|
| [11] |
LE T H, VU M T, BICH V N, et al. Numerical investigation on the effect of trim on ship resistance by RANSE method[J]. Applied Ocean Research, 2021, 111: 102642. DOI:10.1016/j.apor.2021.102642 |
| [12] |
ANDREA FARKAS, NASTIA D, IVANA M. Assessment of hydrodynamic characteristics of a full-scale ship at different draughts[J] . Ocean Engineering, 2018, 156:135−152
|
| [13] |
Tezdogan T, Incecik A, Turan O. Full-scale unsteady RANS simulations of vertical ship motions in shallow water[J]. Ocean Engineering, 2016, 123: 131-145. DOI:10.1016/j.oceaneng.2016.06.047 |
| [14] |
KIM Y C, KIM K S, KIM J, et al. Analysis of added resistance and seakeeping responses in head sea conditions for low-speed full ships using URANS approach[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(6): 641-654. DOI:10.1016/j.ijnaoe.2017.03.001 |
| [15] |
SAYDAMA Z, GOKCAY S, INSEL M. CFD based vortex generator design and full-scale testing for wake non-uniformity reduction[J]. Ocean Engineering, 2018, 153: 282-296. DOI:10.1016/j.oceaneng.2018.01.097 |
| [16] |
杜云龙, 陈伟民, 董国祥. 典型油船船模静水阻力CFD计算策略探讨[J]. 江苏科技大学学报(自然科学版), 2017, 31(5): 661-665. |
| [17] |
陈永博. 船舶波浪增阻预报数值方法比较研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
 2023, Vol. 45
2023, Vol. 45
