2. 宁波舜宇光电信息有限公司,浙江 宁波 315211
2. Ningbo Sunny Optical Technology Company Limited, Ningbo 315211, China
圆柱壳结构作为舰艇推进器、潜艇舱室等水下航行器基础结构,广泛应用于海洋工程领域[1−2]。其受内外部复杂载荷激励产生的振动,影响机械结构寿命,降低设备可靠性,且严重恶化工作人员工作环境。
在船舶与海洋工程领域,圆柱壳作为大型机械结构,尺寸达数百米。在保证圆柱壳振动控制任务的同时,需考虑传感器和执行器在空间上的分布问题,否则将导致控制系统庞大复杂[3]。对大型结构的振动控制而言,分布式减振控制可降低中心控制器的计算负荷,控制节点扩展灵活[4],是复杂激励智能减振的研究热点。目前分布式减振控制系统大多应用可控性、可观性等性能指标进行作动器位置设计。以H∞、衰减率等控制性能指标进行减振控制器设计,同时考虑分布式控制系统中多智能体的一致性问题,使控制器具有更好协调控制性能[5,6]。Sun等[7]针对具有分布式执行器和传感器的大型挠性航天器,设计了分布式一致性观测器估计系统模态坐标,设计主从积分一致性振动控制器减小了柔性结构的振动。耿小明等[8]对振动主动控制中作动器位置优化问题进行了研究,基于可控性优化配置原则,利用遗传算法完成了圆柱壳体内作动器位置优化。周威亚等[9]基于一致性理论分布式振动控制方法,针对卫星太阳能帆板振动控制问题,通过数值算例验证了分布式控制方法的有效性。
然而,大型结构减振控制系统,激励形式及位置具有随机性。在假定需要控制的模态阶数下,当激励形式超出了模态截断阶次,存在着控制溢出的风险。且用H∞范数指标直接限定对外激励的减振衰减,相比可控、可观的作动器位置优化,更直观反应控制器的控制能力。基于此,本文假定在圆柱壳上以网格形式,成对布置压电传感器和作动器。基于数据驱动方法,在线对控制阶次进行模态截断。且通过H∞范数指标和粒子群优化算法,对作动器进行在线迭代优化选取,以实现分布式多智能体减振的自组织和自适应能力。
1 控制方程 1.1 动力学方程图1为具有坐标系的压电-圆柱壳耦合结构动力学模型,其中
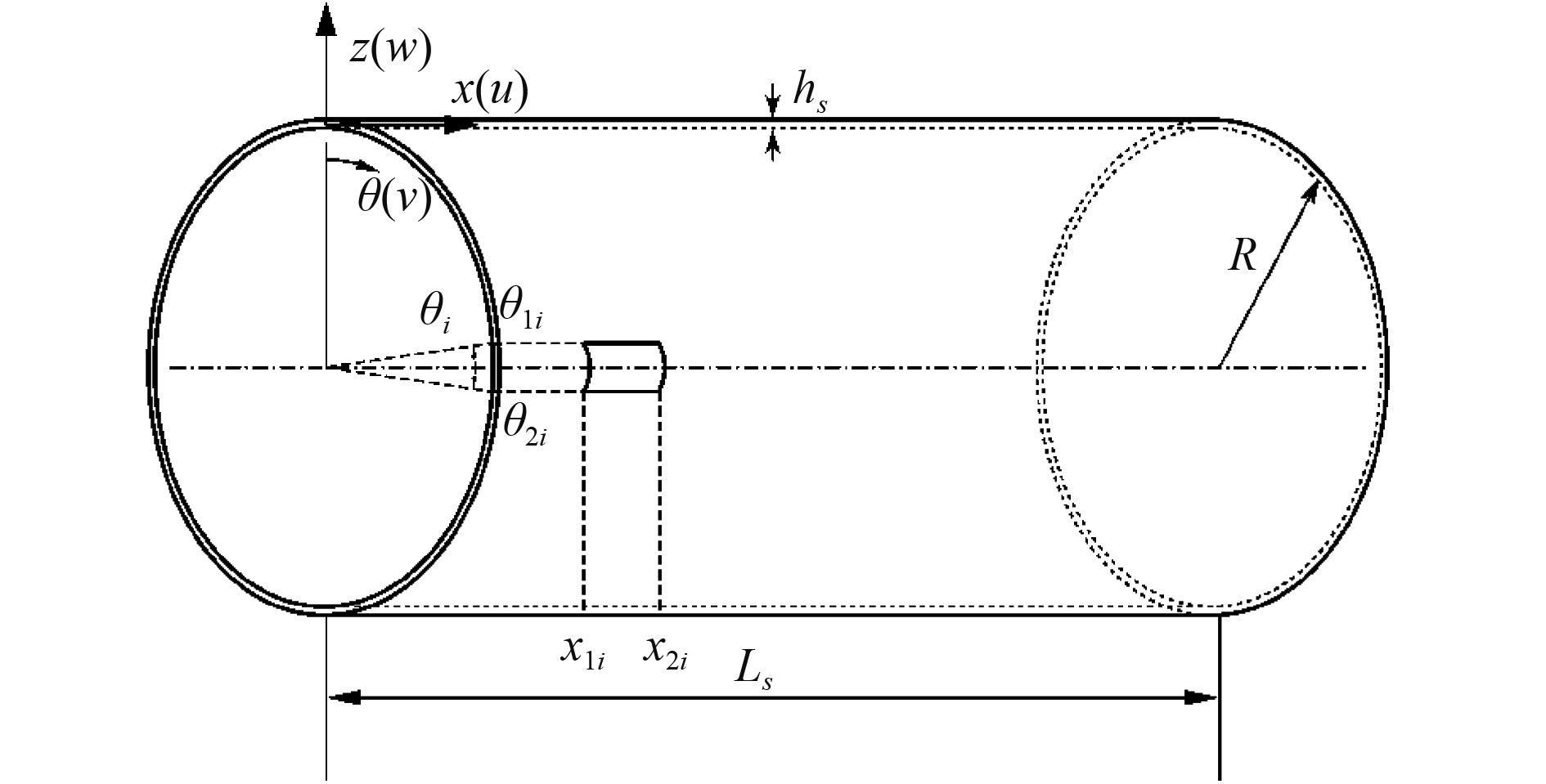
|
图 1 圆柱壳和压电模型示意 Fig. 1 Schematic diagram of cylindrical shell and piezoelectric model |
圆柱壳系统的动力学方程由Hamilton原理导出:
| $ \int_{{t_1}}^{{t_2}} {\delta \left( {T - V} \right)} {\text{d}}t + \int_{{t_1}}^{{t_2}} {\delta W} {\text{d}}t = 0。$ | (1) |
式中:
| $ T = \frac{1}{2}{\rho _s}\int\limits_{{V_s}} {\left( {{{\dot u}^2} + {{\dot v}^2} + {{\dot w}^2}} \right){\text{d}}} {V_s} + \frac{1}{2}\sum\limits_{i = 1}^{{N_p}} {{\rho _{pi}}\int\limits_{{V_{pi}}} {\left( {{{\dot u}^2} + {{\dot v}^2} + {{\dot w}^2}} \right){\text{d}}} {V_{pi}}} 。$ | (2) |
式中,
| $\left[ \begin{array}{*{20}{c}} {\sigma _x^p} \\ {\sigma _\theta ^p} \\ {\sigma _{x\theta }^p} \end{array} \right] = \left[ \begin{array}{*{20}{c}} {c_{11}^p}&{c_{12}^p}&0 \\ {c_{12}^p}&{c_{22}^p}&0 \\ 0&0&{c_{66}^p} \end{array} \right]\left[ \begin{array}{*{20}{c}} {\varepsilon _x^p} \\ {\varepsilon _\theta ^p} \\ {\varepsilon _{x\theta }^p} \end{array} \right] - \left[ \begin{array}{*{20}{c}} 0&0&{{h_{13}}} \\ 0&0&{{h_{23}}} \\ 0&0&0 \end{array} \right]\left[ \begin{array}{*{20}{c}} {{\delta _x}} \\ {{\delta _\theta }} \\ {{\delta _z}} \end{array} \right],$ | (3) |
| $ \left[ {\begin{array}{*{20}{c}} {{E_x}} \\ {{E_\theta }} \\ {{E_z}} \end{array}} \right] = - \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&0 \\ {{h_{13}}}&{{h_{23}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\varepsilon _x^p} \\ {\varepsilon _\theta ^p} \\ {\varepsilon _{x\theta }^p} \end{array}} \right] +\left[ {\begin{array}{*{20}{c}} {{\beta _{11}}}&0&0 \\ 0&{{\beta _{22}}}&0 \\ 0&0&{{\beta _{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta _x}} \\ {{\delta _\theta }} \\ {{\delta _z}} \end{array}} \right]。$ | (4) |
式中:
| $ {\sigma _p} = {{\boldsymbol{E}}_p}{\varepsilon _p} - {\boldsymbol{H}}\delta,$ | (5) |
| $ E = - {{\boldsymbol{H}}^{\text{T}}}{\varepsilon _p} + {\boldsymbol{D}}\delta,$ | (6) |
| $ \begin{split} V = &\frac{1}{2}\int\limits_{{V_s}} {{\varepsilon ^{\text{T}}}} {{\boldsymbol{E}}_s}\varepsilon {\text{d}}{V_s} +\\ & \sum\limits_{i = 1}^{{N_p}} {\int\limits_{{V_{pi}}} {\left( {\frac{1}{2}{\varepsilon ^{\text{T}}}{{\boldsymbol{E}}_{pi}}\varepsilon - {\varepsilon ^{\text{T}}}{{\boldsymbol{H}}_i}{\delta _i} + \frac{1}{2}\delta _i^{\text{T}}{{\boldsymbol{D}}_i}{\delta _i}} \right)} } {\text{d}}{V_{pi}} 。\\ \end{split} $ | (7) |
式中:
| $ {\delta _i} = {{\boldsymbol{B}}_i}{q_p},$ | (8) |
| $ {q_p} = {\left[ {\begin{array}{*{20}{c}} {{q_{p1}}}&{{q_{p2}}}& \cdots &{{q_{p{N_p}}}} \end{array}} \right]^{\text{T}}},$ | (9) |
| $ {{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0& \cdots &0 \\ 0&0& \cdots &0 \\ {\dfrac{1}{{{S_1}}}}&0& \cdots &0 \end{array}} \right],...,{{\boldsymbol{B}}_{{N_p}}} = \left[ {\begin{array}{*{20}{c}} 0&0& \cdots &0 \\ 0&0& \cdots &0 \\ 0&0& \cdots &{\dfrac{1}{{{S_{{N_p}}}}}} \end{array}} \right]。$ | (10) |
式中,
| $ \delta W = \delta {W_f} + \delta {W_c} = {f_d}\delta w + \sum\limits_{i = 1}^{{N_a}} {V_{ai}^{}\delta q_{acti}^{}} 。$ | (11) |
其中:
假定圆柱壳的边界条件为简支-简支。圆柱壳模型3个方向上位移可表示为[11]:
| $ \left\{ {\begin{array}{*{20}{l}} {u\left( {x,\theta ,t} \right) = \displaystyle\sum\limits_{n = 1}^N {\displaystyle\sum\limits_{m = 1}^M {\cos \left( {\frac{{m{\text{π}} x}}{L}} \right)} } \cos \left( {n\theta } \right)q_{mn}^u} ,\\ {v\left( {x,\theta ,t} \right) = \displaystyle\sum\limits_{n = 1}^N {\displaystyle\sum\limits_{m = 1}^M {\sin \left( {\frac{{m{\text{π}} x}}{L}} \right)} } \sin \left( {n\theta } \right)q_{mn}^v} ,\\ {w\left( {x,\theta ,t} \right) = \displaystyle\sum\limits_{n = 1}^N {\displaystyle\sum\limits_{m = 1}^M {\sin \left( {\frac{{m{\text{π}} x}}{L}} \right)} } \cos \left( {n\theta } \right)q_{mn}^w} 。\end{array}} \right. $ | (12) |
3个方向上的位移用向量表达并写成线性组合的形式:
| $ \left[ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{N_u}}&0&0 \\ 0&{{N_v}}&0 \\ 0&0&{{N_w}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{q_u}} \\ {{q_v}} \\ {{q_w}} \end{array}} \right] = {{N}}{q_s} 。$ | (13) |
采用Sanders壳体理论描述圆柱壳应变和位移之间的关系。导出基于Sanders壳体理论应变方程并改写为矩阵形式[11],将式(13)代入得:
| $ \begin{split} \varepsilon =& \left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}} \\ {{\varepsilon _\theta }} \\ {{\varepsilon _{x\theta }}} \end{array}} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {N_u}}}{{\partial x}}}&0&0 \\ 0&{\dfrac{1}{R}\dfrac{{\partial {N_v}}}{{\partial \theta }}}&{\dfrac{{{N_w}}}{R}} \\ {\dfrac{1}{R}\dfrac{{\partial {N_u}}}{{\partial \theta }}}&{\dfrac{{\partial {N_v}}}{{\partial x}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{q_u}} \\ {{q_v}} \\ {{q_w}} \end{array}} \right]- \\ & z\left[ {\begin{array}{*{20}{c}} 0&0&{\dfrac{{{\partial ^2}{N_w}}}{{\partial {x^2}}}} \\ 0&{ - \dfrac{1}{{{R^2}}}\dfrac{{\partial {N_v}}}{{\partial \theta }}}&{\dfrac{1}{{{R^2}}}\dfrac{{{\partial ^2}{N_w}}}{{\partial {\theta ^2}}}} \\ {\dfrac{1}{{2{R^2}}}\dfrac{{\partial {N_u}}}{{\partial \theta }}}&{ - \dfrac{3}{{2R}}\dfrac{{\partial {N_v}}}{{\partial x}}}&{\dfrac{2}{R}\dfrac{{{\partial ^2}{N_w}}}{{\partial x\partial \theta }}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{q_u}} \\ {{q_v}} \\ {{q_w}} \end{array}} \right] =\\ &{{\boldsymbol{B}}_{q1}}{q_s} + z{{\boldsymbol{B}}_{q2}}{q_s}。\\[-10pt] \end{split} $ | (14) |
将式(14)代入到系统能量方程中,圆柱壳系统的总动能、总势能和外力功变化可进一步表示为:
| $ \begin{split} T =& \frac{1}{2}\dot q_s^{\text{T}}\left( {{\rho _s}{h_s}\int_0^{{L_s}} {\int_0^{2{\text{π}} } {{\boldsymbol{N}}_{}^{\text{T}}{{\boldsymbol{N}}_{}}} } {\text{d}}\theta {\text{d}}x} \right){{\dot q}_s} +\\ & \frac{1}{2}\dot q_s^{\text{T}}\left( {\sum\limits_{i = 1}^{{N_p}} {{\rho _p}{h_p}\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {{\boldsymbol{N}}_{}^{\text{T}}{{\boldsymbol{N}}_{}}} } {\text{d}}\theta {\text{d}}x} } \right){{\dot q}_s}。\end{split} $ | (15) |
| $ {\begin{split} V =& \frac{1}{2}q_s^{\text{T}}\left( {\int_0^{{L_s}} {\int_0^{2{\text{π}} } {\int_{ - \frac{{{h_s}}}{2}}^{\frac{{{h_s}}}{2}} {{{\left( {{{\boldsymbol{B}}_{q1}} + z{{\boldsymbol{B}}_{q2}}} \right)}^{\text{T}}}} } } {{\boldsymbol{E}}_s}\left( {{{\boldsymbol{B}}_{q1}} + z{{\boldsymbol{B}}_{q2}}} \right){\text{d}}z{\text{d}}\theta {\text{d}}x} \right){q_s}+ \\ & \frac{1}{2}q_s^{\text{T}}\left( {\sum\limits_{i = 1}^{{N_p}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{{\left( {{{\boldsymbol{B}}_{q1}} + z{{\boldsymbol{B}}_{q2}}} \right)}^{\text{T}}}} } } {{\boldsymbol{E}}_{pi}}\left( {{{\boldsymbol{B}}_{q1}} + z{{\boldsymbol{B}}_{q2}}} \right){\text{d}}z{\text{d}}\theta {\text{d}}x} } \right){q_s}- \\ & q_s^{\text{T}}\left( {\sum\limits_{i = 1}^{{N_p}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{{\left( {{{\boldsymbol{B}}_{q1}} + z{{\boldsymbol{B}}_{q2}}} \right)}^{\text{T}}}{\boldsymbol{H}}{{\boldsymbol{B}}_i}} } } {\text{d}}z{\text{d}}\theta {\text{d}}x} } \right){q_p} +\\ & \frac{1}{2}q_p^{\text{T}}\left( {\sum\limits_{i = 1}^{{N_p}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{{\boldsymbol{B}}_i}^{\text{T}}{\boldsymbol{D}}{{\boldsymbol{B}}_i}} } } {\text{d}}z{\text{d}}\theta {\text{d}}x} } \right){q_p},\\[-15pt] \end{split}} $ | (16) |
| $ \delta W = \delta {W_f} + \delta {W_c} = \delta q_s^{\text{T}}{\boldsymbol{N}}_{}^{\text{T}}{F_d} + \delta q_{act}^{\text{T}}{V_a}。$ | (17) |
其中,
| $ \int_{{t_1}}^{{t_2}} {\left\{ \begin{gathered} \delta q_s^{\text{T}}\left[ \begin{gathered} - \left( {{{\boldsymbol{M}}_s} + {{\boldsymbol{M}}_p}} \right){{\ddot q}_s} - \left( {{{\boldsymbol{K}}_s} + {{\boldsymbol{K}}_p}} \right){q_s} \\ + {{\boldsymbol{L}}_{act}}{q_{act}} + {{\boldsymbol{L}}_{sen}}{q_{sen}} + {\boldsymbol{N}}_{}^{\text{T}}{F_d} \\ \end{gathered} \right] \\ + \delta q_{act}^{\text{T}}\left( {{\boldsymbol{L}}_{act}^{\text{T}}{q_s} - {{\boldsymbol{P}}_{act}}{q_{act}} + {V_a}} \right) \\ + \delta q_{sen}^{\text{T}}\left( {{\boldsymbol{L}}_{sen}^{\text{T}}{q_s} - {{\boldsymbol{P}}_{sen}}{q_{sen}}} \right) \\ \end{gathered} \right\}{\text{d}}t} = 0。$ | (18) |
| $ \begin{split} {{\boldsymbol{M}}_s} + {{\boldsymbol{M}}_p} =& {\rho _s}{h_s}\int_0^{{L_s}} {\int_0^{2{\text{π}} } {{\boldsymbol{N}}_{}^{\text{T}}{{\boldsymbol{N}}_{}}} } {\text{d}}\theta {\text{d}}x +\\ & \sum\limits_{i = 1}^{{N_p}} {{\rho _p}{h_p}\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {{\boldsymbol{N}}_{}^{\text{T}}{{\boldsymbol{N}}_{}}} } {\text{d}}\theta {\text{d}}x} ,\end{split} $ | (19) |
| $ \begin{split} {{\boldsymbol{K}}_s} =& \int_0^{{L_s}} {\int_0^{2{\text{π}} } {\int_{ - \frac{{{h_s}}}{2}}^{\frac{{{h_s}}}{2}} {{\boldsymbol{B}}_{q1}^{\text{T}}} } } {{\boldsymbol{E}}_s}{{\boldsymbol{B}}_{q1}}{\text{d}}z{\text{d}}\theta {\text{d}}x +\\ & \int_0^{{L_s}} {\int_0^{2{\text{π}} } {\int_{ - \frac{{{h_s}}}{2}}^{\frac{{{h_s}}}{2}} {{\boldsymbol{B}}_{q1}^{\text{T}}z} } } {{\boldsymbol{E}}_s}{{\boldsymbol{B}}_{q2}}{\text{d}}z{\text{d}}\theta {\text{d}}x +\\ & \int_0^{{L_s}} {\int_0^{2{\text{π}} } {\int_{ - \frac{{{h_s}}}{2}}^{\frac{{{h_s}}}{2}} {{\boldsymbol{B}}_{q2}^{\text{T}}} } } z{{\boldsymbol{E}}_s}{{\boldsymbol{B}}_{q1}}{\text{d}}z{\text{d}}\theta {\text{d}}x +\\ & \int_0^{{L_s}} {\int_0^{2{\text{π}} } {\int_{ - \frac{{{h_s}}}{2}}^{\frac{{{h_s}}}{2}} {{\boldsymbol{B}}_{q2}^{\text{T}}} } } {z^2}{{\boldsymbol{E}}_s}{{\boldsymbol{B}}_{q2}}{\text{d}}z{\text{d}}\theta {\text{d}}x ,\end{split} $ | (20) |
| $ \begin{split} {{\boldsymbol{K}}_p} =& \sum\limits_{i = 1}^{{N_p}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q1}^{\text{T}}} } } {{\boldsymbol{E}}_p}{{\boldsymbol{B}}_{q1}}{\text{d}}z{\text{d}}\theta {\text{d}}x} +\\ & \sum\limits_{i = 1}^{{N_p}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q1}^{\text{T}}} } } z{{\boldsymbol{E}}_p}{{\boldsymbol{B}}_{q2}}{\text{d}}z{\text{d}}\theta {\text{d}}x} +\\ & \sum\limits_{i = 1}^{{N_p}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q2}^{\text{T}}z} } } {{\boldsymbol{E}}_p}{{\boldsymbol{B}}_{q1}}{\text{d}}z{\text{d}}\theta {\text{d}}x} +\\ & \sum\limits_{i = 1}^{{N_p}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q2}^{\text{T}}{z^2}} } } {{\boldsymbol{E}}_p}{{\boldsymbol{B}}_{q2}}{\text{d}}z{\text{d}}\theta {\text{d}}x} ,\end{split} $ | (21) |
| $ \begin{split} {{\boldsymbol{L}}_{act}} =& \sum\limits_{i = 1}^{{N_a}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q1}^{\text{T}}} } } {\boldsymbol{H}}{{\boldsymbol{B}}_i}{\text{d}}z{\text{d}}\theta {\text{d}}x} +\\ & \sum\limits_{i = 1}^{{N_a}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q2}^{\text{T}}} } } z{\boldsymbol{H}}{{\boldsymbol{B}}_i}{\text{d}}z{\text{d}}\theta {\text{d}}x} ,\end{split} $ | (22) |
| $ \begin{split} {{\boldsymbol{L}}_{sen}} =& \sum\limits_{i = 1}^{{N_s}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q1}^{\text{T}}} } } {\boldsymbol{H}}{{\boldsymbol{B}}_i}{\text{d}}z{\text{d}}\theta {\text{d}}x} +\\ & \sum\limits_{i = 1}^{{N_s}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{\boldsymbol{B}}_{q2}^{\text{T}}} } } z{\boldsymbol{H}}{{\boldsymbol{B}}_i}{\text{d}}z{\text{d}}\theta {\text{d}}x} ,\end{split} $ | (23) |
| $ {{\boldsymbol{P}}_{act}} = \sum\limits_{i = 1}^{{N_a}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{{\boldsymbol{B}}_i}^{\text{T}}{\boldsymbol{D}}{{\boldsymbol{B}}_i}} } } {\text{d}}z{\text{d}}\theta {\text{d}}x},$ | (24) |
| $ {{\boldsymbol{P}}_{sen}} = \sum\limits_{i = 1}^{{N_s}} {\int_{{x_{1i}}}^{{x_{2i}}} {\int_{{\theta _{1i}}}^{{\theta _{2i}}} {\int_{h_p^{1i}}^{h_p^{2i}} {{{\boldsymbol{B}}_i}^{\text{T}}{\boldsymbol{D}}{{\boldsymbol{B}}_i}} } } {\text{d}}z{\text{d}}\theta {\text{d}}x}。$ | (25) |
由于式(18)中变分运算
| $ \left\{ {\begin{array}{*{20}{l}} \left( {{{\boldsymbol{M}}_s} + {{\boldsymbol{M}}_p}} \right){{\ddot q}_s}+ \left( {{{\boldsymbol{K}}_s} + {{\boldsymbol{K}}_p}} \right){q_s} = {{\boldsymbol{L}}_{act}}{q_{act}} +\\ {{\boldsymbol{L}}_{sen}}{q_{sen}} + {\boldsymbol{N}}_{}^{\text{T}}{F_d} ,\\ {{\boldsymbol{L}}_{act}^{\text{T}}{q_s} - {{\boldsymbol{P}}_{act}}{q_{act}} + {V_a} = 0},\\ {{\boldsymbol{L}}_{sen}^{\text{T}}{q_s} - {{\boldsymbol{P}}_{sen}}{q_{sen}}=0} 。\end{array}} \right.$ | (26) |
得执行器和传感器电荷量为:
| $ \left\{ {\begin{array}{*{20}{l}} {{q_{act}} = {\boldsymbol{P}}_{act}^{ - 1}{\boldsymbol{L}}_{act}^{\text{T}}{q_s} + {\boldsymbol{P}}_{act}^{ - 1}{V_a}},\\ {{q_{sen}} = {\boldsymbol{P}}_{sen}^{ - 1}{\boldsymbol{L}}_{sen}^{\text{T}}{q_s}} 。\end{array}} \right. $ | (27) |
将式(27)代入式(26)中得到系统总动力学方程:
| $ \begin{split} & \left( {{{\boldsymbol{M}}_s} + {{\boldsymbol{M}}_p}} \right){{\ddot q}_s}{\text{ + }}\left( {{\boldsymbol{K}}_s} + {{\boldsymbol{K}}_p} - {{\boldsymbol{L}}_{act}}{\boldsymbol{P}}_{act}^{ - 1}{\boldsymbol{L}}_{act}^{\text{T}} -\right. \\ &\left. {{\boldsymbol{L}}_{sen}}{\boldsymbol{P}}_{sen}^{ - 1}{\boldsymbol{L}}_{sen}^{\text{T}} \right){q_s} = {{\boldsymbol{L}}_{act}}{\boldsymbol{P}}_{act}^{ - 1}{V_a} + {\boldsymbol{N}}_{}^{\text{T}}{F_d} 。\end{split} $ | (28) |
传感器经电荷放大增益
| $ y = {\boldsymbol{G}}{q_{sen}} = {\boldsymbol{GP}}_{sen}^{ - 1}{\boldsymbol{L}}_{sen}^{\text{T}}{q_s} 。$ | (29) |
给定圆柱壳几何参数:长度Ls=0.51 m,半径R=0.15 m,厚度hs=0.002 m;材料参数:密度ρs=2770 kg/m3,泊松比μs=0.3,杨氏模量Es=7.4×1010 Pa;边界条件:简支-简支。使用Ansys软件仿真计算,定义误差
|
|
表 1 圆柱壳结构固有频率对比 Tab.1 Comparison of natural frequencies of cylindrical shell structures |

|
图 2 圆柱壳结构前6阶模态 Fig. 2 The first six modes of cylindrical shell structure |
由表1可知,本文圆柱壳振动理论模型与仿真结果在前8阶固有频率对比中,相对误差最大为1.05%,表明理论模型准确度较高。
1.3 状态空间针对式(28)的系统总动力学方程,由于压电元件对圆柱壳结构的质量和刚度影响较小,假设忽略压电元件对结构质量、刚度的影响,简化可得:
| $ {{\boldsymbol{M}}_s}{\ddot q_s}{\text{ + }}{{\boldsymbol{K}}_s}{q_s} = {{\boldsymbol{L}}_{act}}{\boldsymbol{P}}_{act}^{ - 1}{V_a} + {\boldsymbol{N}}_{}^{\text{T}}{F_d} 。$ | (30) |
引入式(31)的坐标变换,使坐标转换到正则模态坐标下,满足特征值和特征向量的正交性原则,使动力学方程解耦。
| $ {q_s}\left( t \right) = {{\boldsymbol{H}}_\eta }\eta \left( t \right) 。$ | (31) |
质量矩阵和刚度矩阵转换为对角阵形式,
| $ \ddot \eta {\text{ + 2}}{\boldsymbol{Z\Omega }}\dot \eta {\text{ + }}{{\boldsymbol{\Omega }}^2}\eta = {\boldsymbol{H}}_\eta ^{\text{T}}{{\boldsymbol{L}}_{act}}{\boldsymbol{P}}_{act}^{ - 1}{V_a} + {\boldsymbol{H}}_\eta ^{\text{T}}{\boldsymbol{N}}_{}^{\text{T}}{F_d},$ | (32) |
| $ y = {\boldsymbol{GP}}_{sen}^{ - 1}{\boldsymbol{L}}_{sen}^{\text{T}}{{\boldsymbol{H}}_\eta }\eta。$ | (33) |
其中,
| $ \begin{split} & \dot x\left( t \right) = {\boldsymbol{A}}x\left( t \right) + {{\boldsymbol{B}}_{act}}{V_a}\left( t \right) + {{\boldsymbol{D}}_f}{F_d}\left( t \right),\\ & y\left( t \right) = {{\boldsymbol{C}}_{sen}}x\left( t \right) 。\end{split} $ | (34) |
其中,式(34)、式(35)各参数矩阵表示为:
| $ \begin{aligned} &{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&{\boldsymbol{I}} \\ { - {{\boldsymbol{\varOmega }}^2}}&{ - 2{\boldsymbol{Z\varOmega }}} \end{array}} \right] \text{,} {{\boldsymbol{{B}}}_{act}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{\boldsymbol{H}}_\eta ^{\text{T}}{{\boldsymbol{L}}_{act}}{\boldsymbol{P}}_{act}^{ - 1}} \end{array}} \right] \text{,} \\ &{{\boldsymbol{D}}_f} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{\boldsymbol{H}}_\eta ^{\text{T}}{\boldsymbol{N}}_{}^{\text{T}}} \end{array}} \right] \text{,} {{\boldsymbol{C}}_{sen}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{GP}}_{sen}^{ - 1}{\boldsymbol{L}}_{sen}^{\text{T}}{{\boldsymbol{H}}_\eta }}&0 \end{array}} \right] 。\end{aligned} $ |
多智能体分布式协同控制的一个基本问题是一致性,即设计一个仅基于本地信息交换的分布式控制协议,使所有控制代理以协调的方式实现一个共同目标[12−13]。
压电执行器传感器组成的多智能体通信拓扑可用
考虑一般线性多智能体系统中N个相同的智能体:
| $ {\dot x_i} = {\boldsymbol{A}}{x_i} + {\boldsymbol{B}}{u_i} + {\boldsymbol{D}}{\omega _i},i = 1,2, \ldots ,N。$ | (35) |
式中,
| $ {u_i} = c{\boldsymbol{K}}\sum\limits_{j = 1}^N {{a_{ij}}\left( {{x_i} - {x_j}} \right)} ,\quad i = 1,2, \ldots ,N 。$ | (36) |
其中,
| $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&{\boldsymbol{I}} \\ { - {{\boldsymbol{\Omega }}^2}}&{ - 2{\boldsymbol{Z\Omega }}} \end{array}} \right]。$ | (37) |
其中,
| $ \begin{split} &{\dot x = \left( {{{\boldsymbol{I}}_N} \otimes {\boldsymbol{A}} + c{\mathcal{L}_s} \otimes {\boldsymbol{BK}}} \right)x + \left( {{{\boldsymbol{I}}_N} \otimes {\boldsymbol{D}}} \right)\omega },\\ & {z = \left( {{\boldsymbol{M}} \otimes {\boldsymbol{C}}} \right)x} 。\end{split} $ | (38) |
其中,
| $ {{\boldsymbol{M}}}_{ij}=\left\{\begin{array}{c}\dfrac{N-1}{N}\text{,}i=j,\\ -\dfrac{1}{N}\text{,}i\ne j。\end{array} \right.$ | (39) |
用
定义1[15,17]综合考虑衰减外部干扰和初始状态干扰意义上的最优控制率,定义权重矩阵
| $ {\left\| {{T_{\omega {x_0}z}}} \right\|_t} = \mathop {\sup }\limits_{{{\left\| \omega \right\|}^2} + x{{\left( 0 \right)}^{\text{T}}}Rx\left( 0 \right) \ne 0} \frac{{\left\| z \right\|}}{{{{\left( {{{\left\| \omega \right\|}^2} + x{{\left( 0 \right)}^{\text{T}}}Rx\left( 0 \right)} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}}} $ | (40) |
定义2[15]对于给定值
1)当
2)当
定义3[14,15]对于给定的
| $ \begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {{\bf{AP}} + {\bf{P}}{{\bf{A}}^{\rm{T}}} - \tau {\bf{B}}{{\bf{B}}^{\rm{T}}}}&{\bf{D}}&{{\bf{P}}{{\bf{C}}^{\rm{T}}}} \\ {{{\bf{D}}^{\rm{T}}}}&{ - {\gamma ^2}{\bf{I}}}&0 \\ {{\bf{CP}}}&0&{ - {\bf{I}}} \end{array}} \right) < 0},\\ {\left( {\begin{array}{*{20}{c}} {\boldsymbol{P}}&{\boldsymbol{I}} \\ {\boldsymbol{I}}&{{\gamma ^2}{\boldsymbol{R}}} \end{array}} \right) > 0} 。\end{array} $ | (41) |
当
1)对于给定的
2)求解反馈增益矩阵
3)选择耦合强度
在有限执行器、传感器的前提下,针对某一扰动情况,在全定义域内进行控制位置寻优,假定选择N对压电执行器、传感器,则需对压电位置参数
步骤1 初始化算法参数,生成粒子初始位置参数。
步骤2 导出各粒子对应的状态空间。
步骤3 求解该组粒子位置参数下的LMIs,导出
步骤4 在该定值
步骤5 依据上一代粒子的历史最优位置和历史最优目标函数值,更新粒子群速度与位置参数。
步骤6 若新粒子群代数G未超过迭代上限Gen,则返回步骤2;否则输出最优位置参数,并导出控制器。
2.3 分布式减振控制流程本文圆柱壳结构干扰自适应分布式减振控制方法流程,如图3所示。
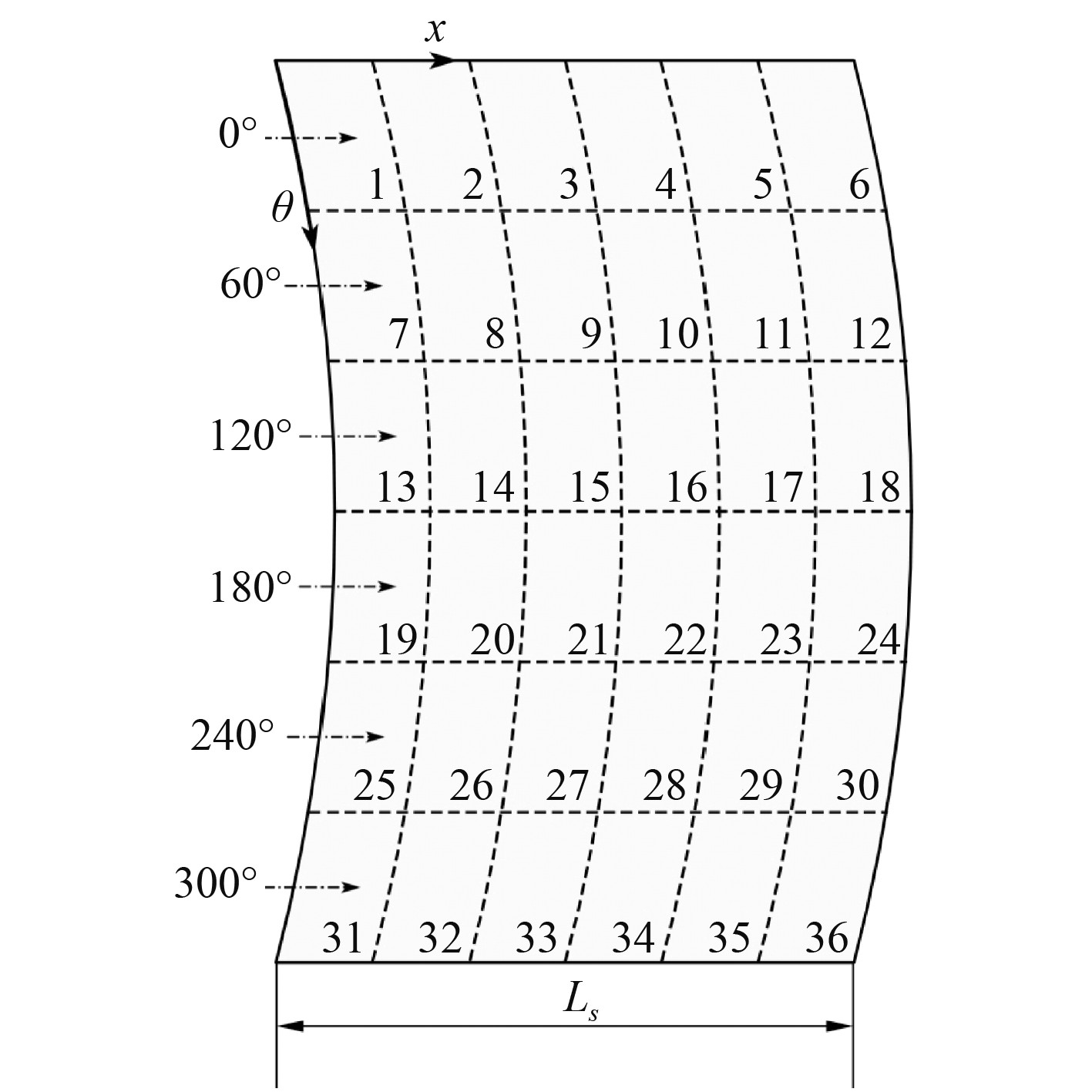
|
图 3 圆柱壳展开模型 Fig. 3 Cylindrical shell expansion model |
步骤1 进行圆柱壳控制区块划分,区块作为压电元件的预选择位置,分别对位安装压电执行器和压电传感器。
步骤2 不同激励位置和形式,系统振动响应不同,采用傅里叶变换(FFT)进行振动能量时频分析,一般取振动能量占系统振动总能量90%以上的前n阶模态作为系统控制阶数。
步骤3 根据步骤2中给定的控制阶数进行H∞一致性性能指标优化,利用BPSO算法进行控制位置参数迭代优化,导出该激励参数下,全局最优控制位置和控制器参数。
步骤4 导出该激励参数下的控制器,进行振动控制仿真。
步骤5 当激励参数改变时,重新进行步骤2~步骤4的优化和振动控制仿真过程。
3 仿真实验与分析将圆柱壳结构划分为6×6的控制区块,图3为圆柱壳展开模型。
圆柱壳和压电元件的各仿真参数如表2所示,其中压电执行器和压电传感器结构参数相同。为验证控制器在结构受激励形式、激励位置变化时,减振控制的自适应性,第一组和第二两组仿真实验分别设置同一位置参数的3个脉冲激励和同相位持续激励。第三组仿真实验设置4个点激励,其形式分别为结构前四阶模态频率同相位正弦函数。
|
|
表 2 圆柱壳结构和压电元件参数 Tab.2 Cylindrical shell structure and piezoelectric element parameters |
仿真实验1中,设置结构所受激励位置分别为
针对图3所示的控制区块模型,进行圆柱壳结构振动控制自组织优化。同时为避免结构振动节线位置,取第15区块作为系统振动能量对比位置以及减振控制效果对比位置。
该激励参数下,圆柱壳结构第15区块的振动能量分布如图4所示。圆柱壳结构第四阶固有频率振动能量最高,且结构振动能量主要分布在前四阶模态,故选择压电对元件数量为4组。Laplacian矩阵
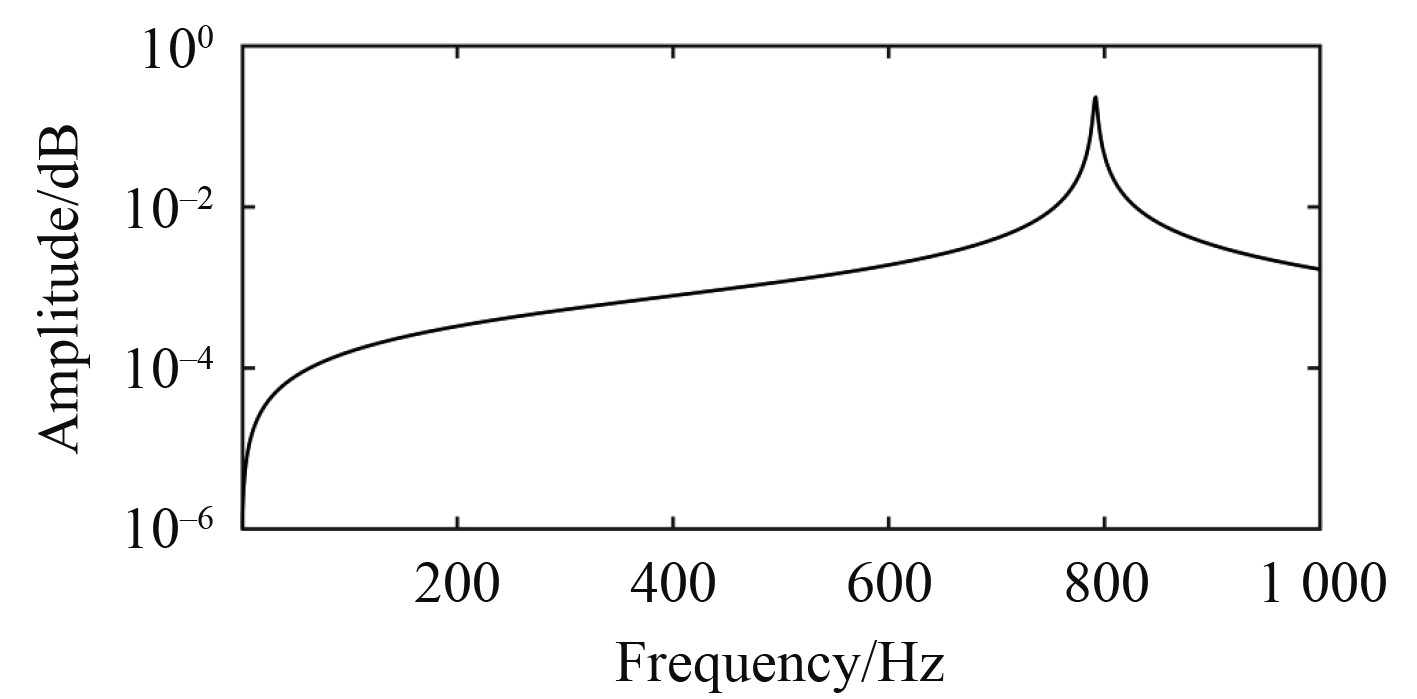
|
图 4 实验1圆柱壳振动能量分布 Fig. 4 Cylindrical shell vibration energy distribution of experiment 1 |
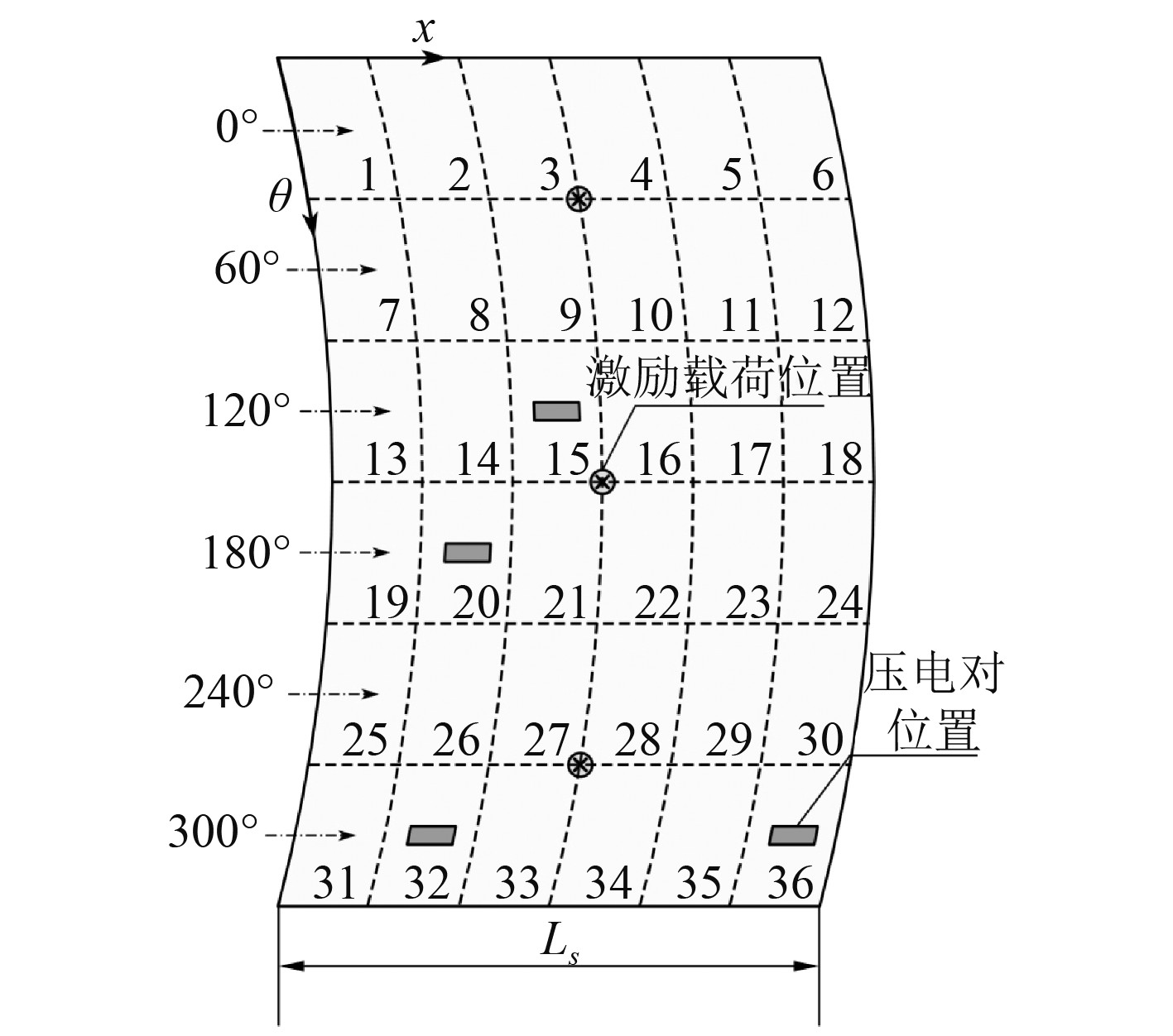
|
图 5 实验1位置优化的壳模型示意图 Fig. 5 Schematic diagram of shell model with optimized position in experiment 1 |
|
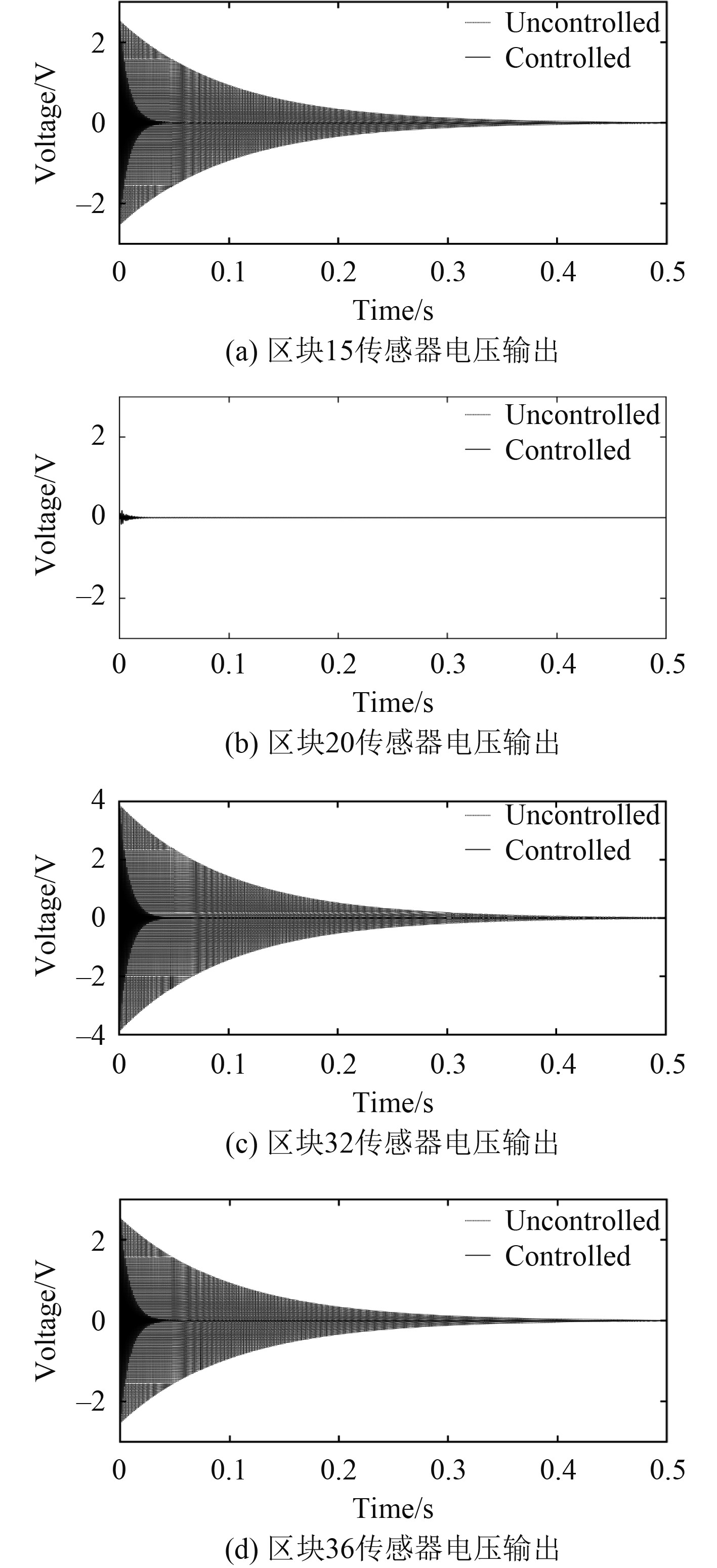
图 6 实验1传感器电压输出 Fig. 6 Sensor voltage output of experiment 1 |
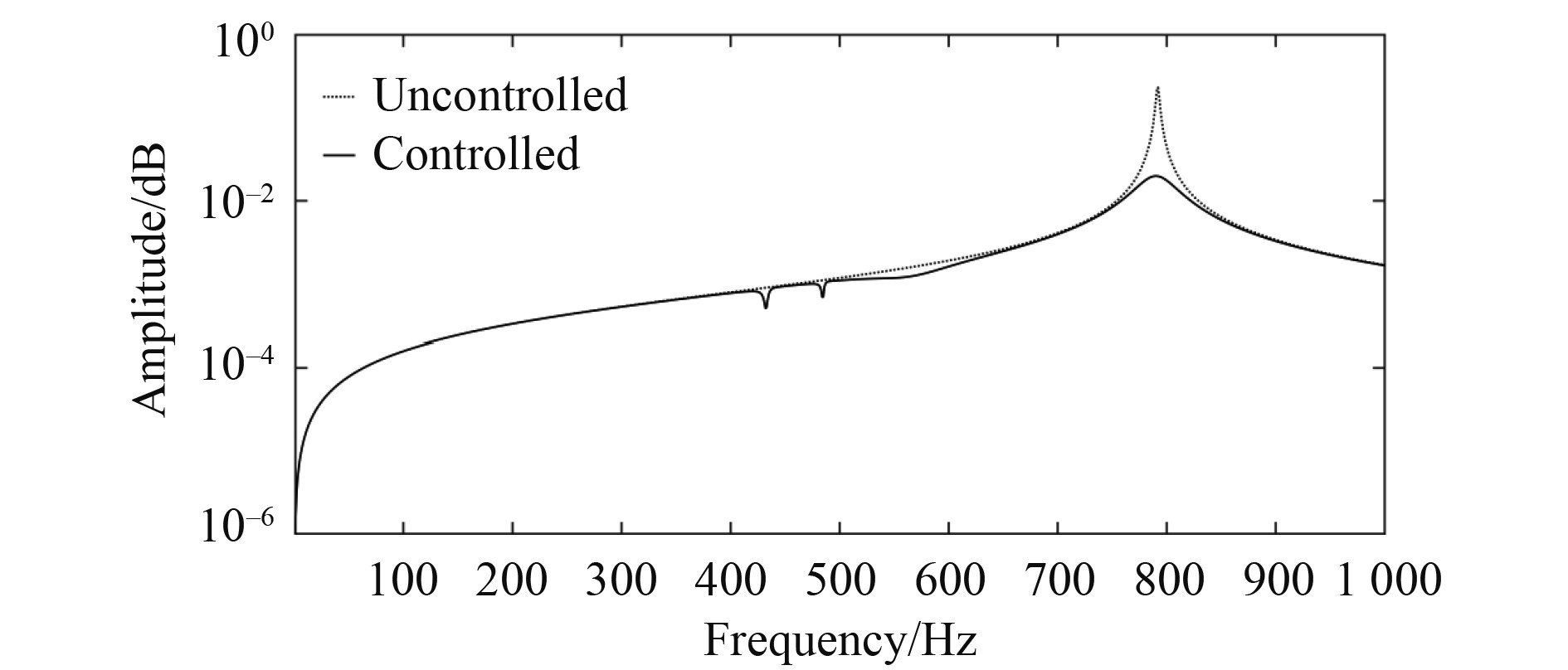
可知,区块20传感器位于第四阶模态振型的节线处。结合图7可知,对于系统结构的第四阶模态振动控制器有较好抑制效果,圆柱壳结构的振动能量降低了91.5%。仿真实验1中一致性输出度量Z如图8所示,通过设计的一致性项,各输出度量能在0.1 s内达到同一输出频率且收敛。
|
图 7 实验1圆柱壳结构振动能量对比 Fig. 7 Comparison of cylindrical shell vibration energy distribution of experiment 1 |

|
图 8 实验1一致性输出项Z Fig. 8 Consistency output item Z of experiment 1 |
仿真实验2中,外激励形式为圆柱壳结构第四阶固有频率的同相位正弦函数,作用位置及其他条件与实验1相同。圆柱壳结构受该激励影响振动能量分布如图9所示。
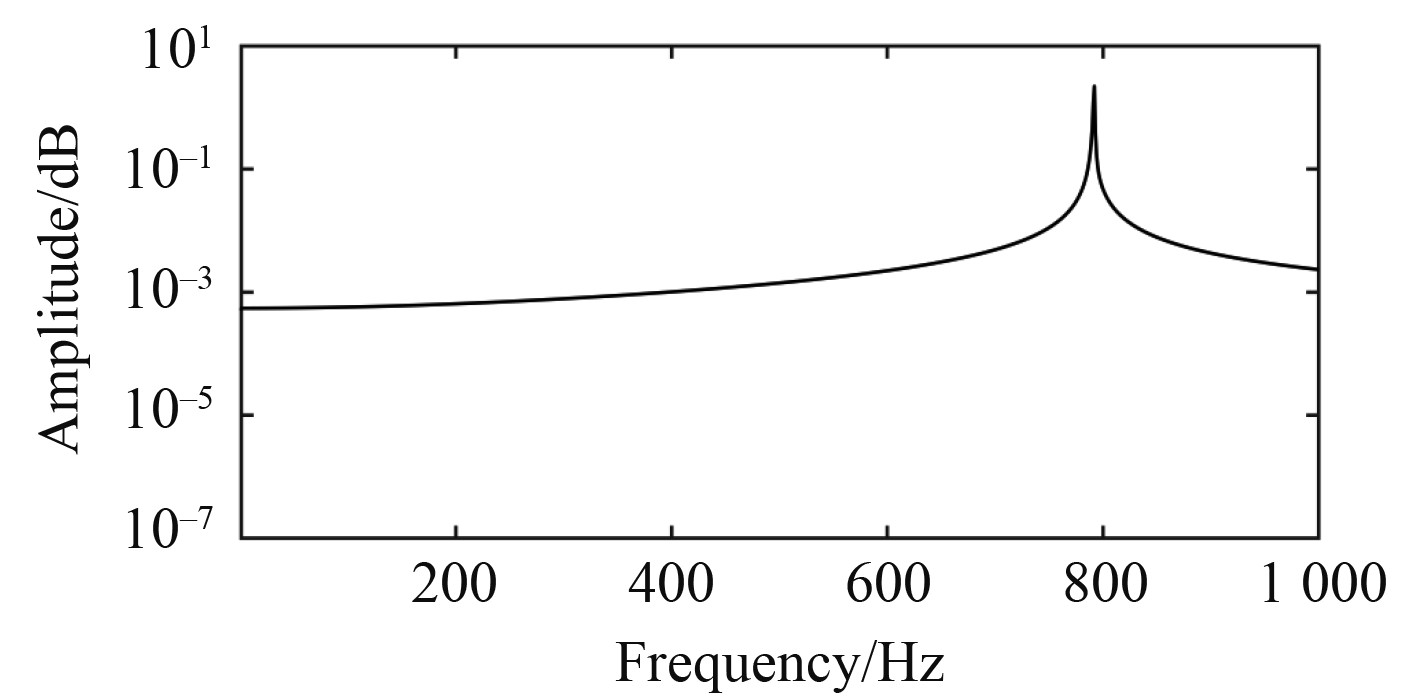
|
图 9 实验2圆柱壳振动能量分布 Fig. 9 Cylindrical shell vibration energy distribution of experiment 2 |
图10中峰值频率为结构第四阶固有频率,即结构做第四阶固有频率下的共振,选择控制前4阶

|
图 10 实验2传感器电压输出 Fig. 10 Sensor voltage output of experiment 2 |
模态振动。由于仅改变了外激励形式,故仅影响H∞一致性性能指标上界,即当
由图11和图12可知,在实验2激励载荷下,圆柱壳振动形式为第四阶固有频率的共振,控制器能在0.1 s内使振动收敛到较低幅值,圆柱壳结构的振动能量相较于未控制时降低90.9%。其中,区块20位于第四阶模态振型的节线处。

|
图 11 实验2圆柱壳结构振动能量分布对比 Fig. 11 Comparison of cylindrical shell vibration energy distribution of experiment 2 |
仿真实验3中,设置圆柱壳结构所受外激励的位置为
该激励参数下,圆柱壳结构第15区块的振动能量分布如图12所示,圆柱壳结构受到前4阶模态频率的正弦函数激励,其振动形式主要为前4阶共振的叠加,且结构振动能量主要分布在前4阶模态,选择压电对的元件数量为4组。Laplacian矩阵

|
图 12 实验3圆柱壳振动能量分布 Fig. 12 Cylindrical shell vibration energy distribution of experiment 3 |
压电控制区块为(6,20,23,25),如图13所示。导出该激励下的最优一致性控制器(36)并进行振动控制仿真,各区块压电传感器电压输出如图14所示。
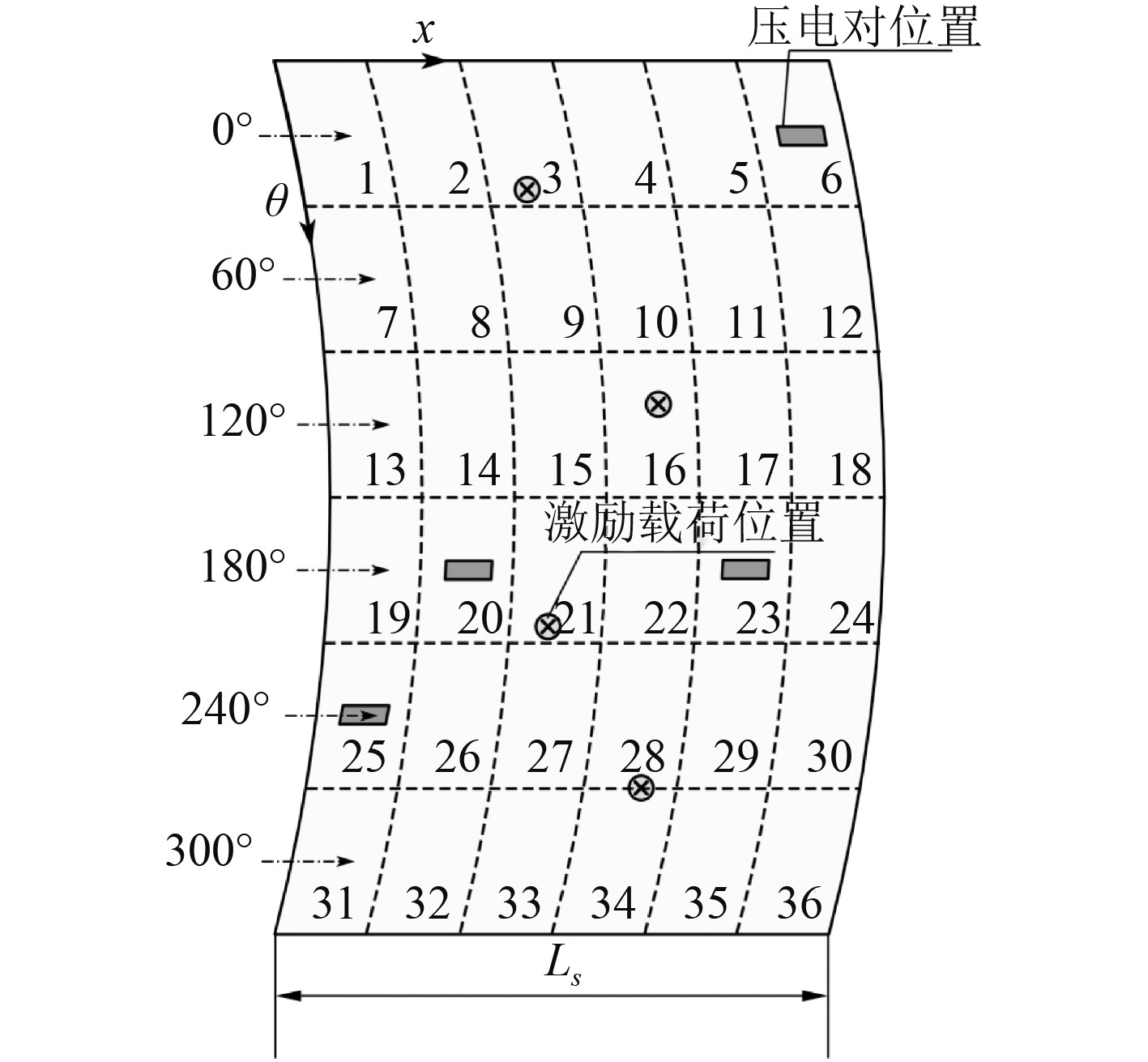
|
图 13 实验3位置优化的壳模型示意图 Fig. 13 Schematic diagram of shell model with optimized position in experiment 3 |
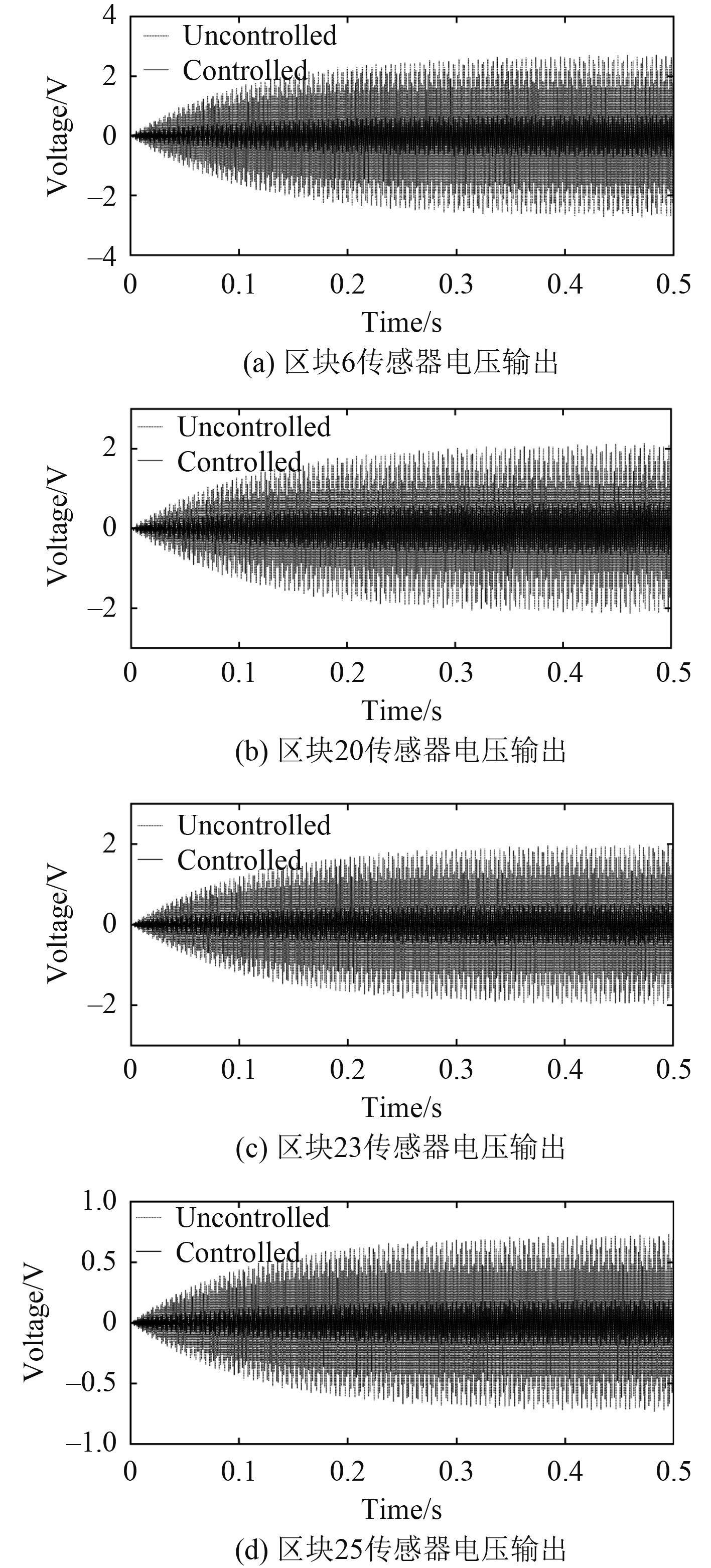
|
图 14 实验3传感器电压输出 Fig. 14 Sensor voltage output of experiment 3 |
由图14可知,圆柱壳结构受到复杂激励时,经自组织的控制器能在0.1 s内,使结构振动收敛到稳定区域。结合图15可知该激励形式下,对于系统结构第二、四阶模态振动控制器有较好抑制效果,圆柱壳结构振动能量相较于未控制时降低了91.2%。

|
图 15 实验3圆柱壳结构振动能量分布对比 Fig. 15 Comparison of cylindrical shell vibration energy distribution of experiment 3 |
1)基于Sanders壳理论和Hamilton变分法建立圆柱壳和压电元件耦合动力学模型,验证了该模型的准确性。
2)根据外激励位置和形式变化的特点,设计了压电多智能体分布式H∞一致性减振控制器干扰自适应优化策略。
3)本控制策略下,圆柱壳结构受3个初始脉冲激励时,能较快使振动收敛到0,且振动能量相较于未控制时降低91.5%;持续激励时,振动能量降低了90.9%;多模态激励时,振动能量降低91.2%。
综上,圆柱壳受到脉冲激励、持续激励、多模态持续激励时,经优化的控制器能有效抑制结构振动,使分布式控制器对外激励有较好的自适应能力。
| [1] |
刘文玺, 周其斗. 基于振动分析技术的潜艇舱段结构优化设计[J]. 舰船科学技术, 2017, 39(7): 54-59. DOI:10.3404/j.issn.1672-7649.2017.07.011 |
| [2] |
GOHARI H D, ZARASTVAND M R, TALEBITOOTI R, et al. Radiated sound control from a smart cylinder subjected to piezoelectric uncertainties based on sliding mode technique using self-adjusting boundary layer[J]. Aerospace Science and Technology, 2020, 106: 106141. DOI:10.1016/j.ast.2020.106141 |
| [3] |
李东旭. 大型挠性结构分散化振动控制: 理论与方法[M]. 北京: 科学出版社, 2013.
|
| [4] |
ZHOU W, ZHANG K, WU S, et al. Distributed cooperative control for vibration suppression of a flexible satellite[J]. Aerospace Science and Technology, 2022, 128: 107750. DOI:10.1016/j.ast.2022.107750 |
| [5] |
ZHANG N, NIU W, LI T. Consistency control of multi-agent system based on unknown input observer[J]. IFAC-Papers OnLine, 2018, 51(31): 566-571. DOI:10.1016/j.ifacol.2018.10.138 |
| [6] |
纪良浩, 王慧维, 李华青. 分布式多智能体网络一致性协调控制理论[M]. 北京: 科学出版社, 2015.
|
| [7] |
SUN Jun, LI Shuang, HUANG Jing, et al. Robust coordinated control for large flexible spacecraft based on consensus theory[J]. Journal of the Franklin Institute, 2020, 357(9): 5359-5379. DOI:10.1016/j.jfranklin.2020.02.049 |
| [8] |
耿小明, 尹韶平, 周景军, 等. 圆柱壳体振动主动控制作动器位置优化方法[J]. 水下无人系统学报, 2020, 28(6):650−656.
|
| [9] |
周威亚, 邬树楠, 王恩美. 基于一致性理论的卫星太阳能帆板分布式振动控制[J]. 南京航空航天大学学报, 2021, 53(6):909−917.
|
| [10] |
J. LEO DONALD. Engineering analysis of smart material systems[M]. New York: John Wiley & Sons, Inc, 2007.
|
| [11] |
A. LEISSA. Vibration of Shells[M]. Washington: NASA, 1973.
|
| [12] |
刘学良, 胥布工. 具有多个通信时延的多智能体系统分布式H∞一致性控制
[J]. 控制与决策, 2012, 27(4): 494-500. |
| [13] |
LIN Peng, JIA Yingmin, LI Lin. Distributed robust H∞ consensus control in directed networks of agents with time delay
[J]. Systems & Control Letters, 2008, 57(8): 643-653. |
| [14] |
DMITRY V. BALANDIN, MARK M. KOGAN. LMI-based H∞-optimal control with transients
[J]. International Journal of Control, 2010, 83(8): 1664-1673. DOI:10.1080/00207179.2010.487222 |
| [15] |
WANG Jingyao, DUAN Zhisheng, ZHAO Yu, et al. H∞ and H2 control of multi-agent systems with transient performance improvement
[J]. International Journal of Control, 2013, 86(12): 2131-2145. DOI:10.1080/00207179.2013.802371 |
| [16] |
LIU Yang, JIA Yingmin. H∞ consensus control for multi-agent systems with linear coupling dynamics and communication delays
[J]. International Journal of Systems Science, 2012, 43(1-3): 50-62. |
| [17] |
PRAMOD, P. KHARGONEKAR, KRISHAN, et al. H∞ Control with transients
[J]. Siam Journal on Control & Optimization, 1991, 29(6): 1373-1393. |
 2023, Vol. 45
2023, Vol. 45
