目前在船体建造各阶段存在很多结构装配缺陷,如接缝重合、对接板缝间隙过大及结构对接错位等问题,这些缺陷引起的焊接变形很大程度上会影响焊接质量,进而影响船舶建造精度。国内学者对船体结构装配缺陷进行了大量的研究工作,主要利用数值模拟方法预报结构在装焊过程中产生的变形和应力,孙鹏等[1]基于热弹塑性有限元分析理论,采用平均热循环曲线代替瞬态移动热源加载焊缝的方法,对船舶建造合拢中焊缝间隙超差的问题进行数值模拟分析,并通过试验进行验证。向祖权等[2]对不同焊缝间隙下板材的温度场及应力场进行数值仿真,总结了不同焊缝间隙对温度场、横向收缩量以及焊后残余应力的影响规律。邓德安等[3]采用热弹塑性有限元方法对大型船体板架结构的焊接变形和残余应力进行预测,对考虑/未考虑装配间隙2种情况进行焊接模拟,并通过实验对模拟结果进行验证。但在船舶实际建造中,较大的划线误差和安装误差等因素导致的船体板架纵骨错位问题,往往也会造成较大的焊接变形和焊后残余应力,且现有的工作鲜有涉及纵骨错位的研究,因此研究船舶建造阶段中的纵骨错位问题具有重要的工程意义。
本文基于热弹塑性有限元方法对纵骨错位问题进行数值模拟分析,利用生死单元技术构造不同错位量下的船体板架结构模型,对各错位量下船体板架的温度场及应力场进行模拟仿真,总结了不同纵骨错位量对板架焊接变形和应力的影响规律。
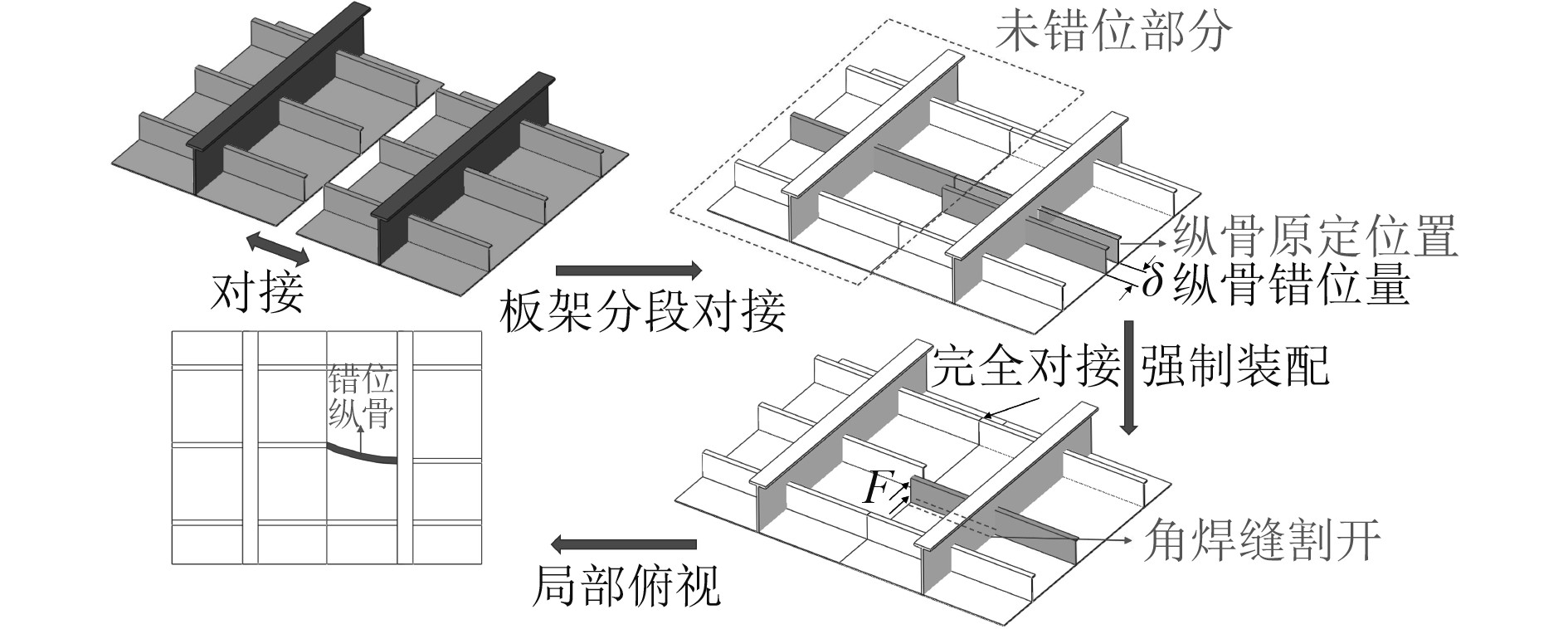
1 概 述船体板架主要由外板、纵向构件及横向构件组装而成,其建造过程中若存在过大的划线误差、安装及加工误差或分段间纵骨间距的补偿量不一致等情况,将导致纵向骨架安装不准的分段在合拢进行定位焊时产生错位问题[4]。如图1所示,将2根纵骨错开的距离定义为纵骨错位量
|
图 1 船体板架纵骨错位示意图 Fig. 1 Longitudinal dislocation of hull grillage |
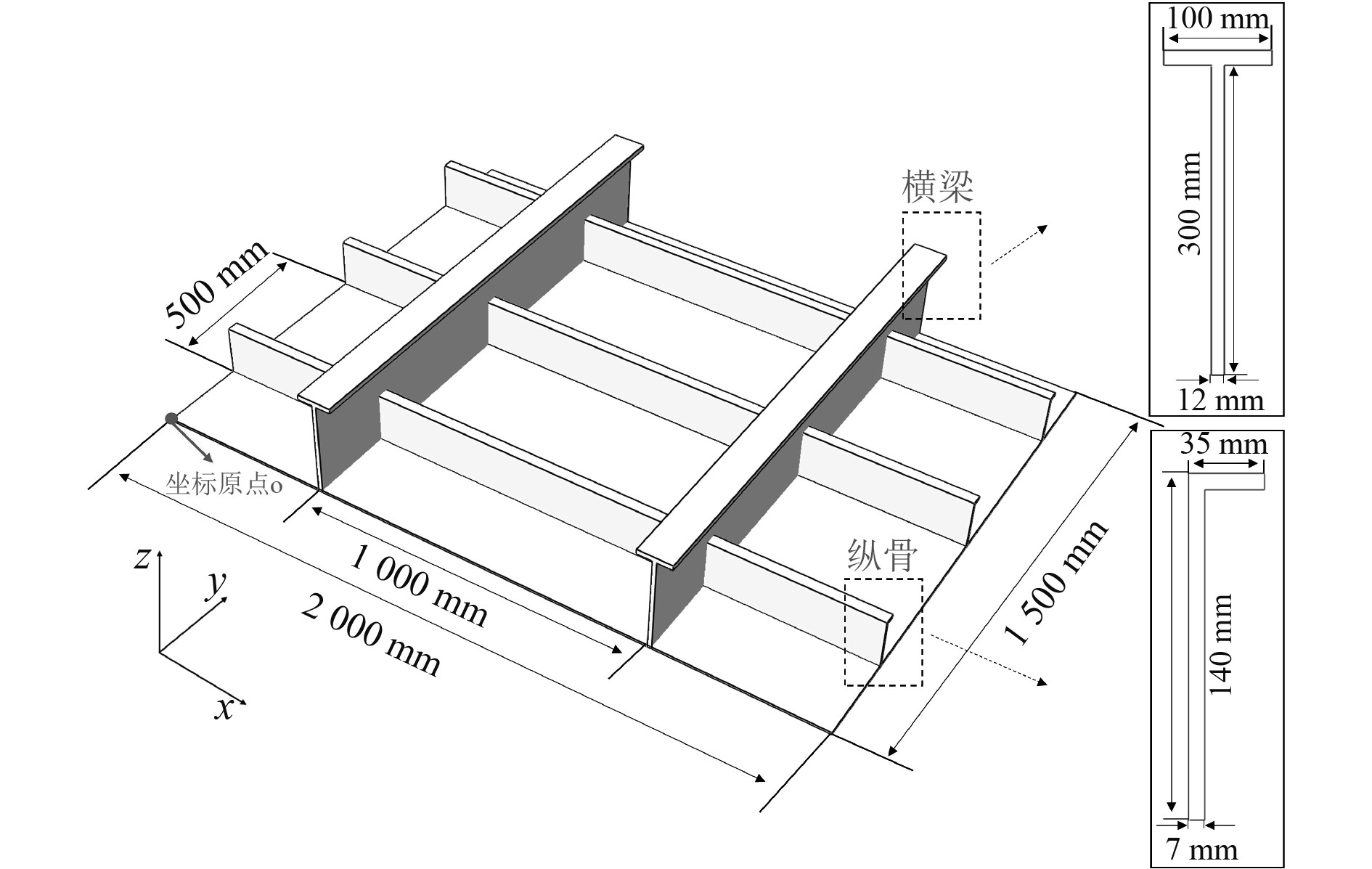
本文以船体结构中典型的纵骨架式板架作为研究对象,该板架由外板、3根纵骨和2根横梁组成。几何尺寸如图2所示,坐标原点建立在图中O点。
|
图 2 船体板架几何尺寸 Fig. 2 Geometry of hull grillage |
根据船体板架结构的几何尺寸及纵骨和横梁的布置情况,利用Patran软件建立三维有限元计算模型。由于焊接是一个温度随时间和空间急剧变化的过程[5],网格划分质量会直接影响到数值模拟精度。为了能准确模拟焊缝附近高度集中的热流密度输入情况,在温度变化剧烈的焊缝附近采用细密网格进行划分,最小单元尺寸为4 mm×2 mm,焊脚高度为4 mm,而远离焊缝区温度迅速降低,可将细网格逐步过渡至粗网格,采用此划分方式既可以满足计算精度的要求,同时又兼顾计算效率。划分完成后的有限元模型如图3所示,整个模型的单元数量为63255个,节点数量为84145个。通过有限元分析软件Abaqus对板架结构模型进行焊接数值模拟,其中热传导分析中的单元类型为DC3D8,应力场分析的单元类型为C3D8I单元,同时假定板材在焊接过程中完全焊透,并忽略点焊定位对变形结果的影响。

|
图 3 有限元模型 Fig. 3 Finite element model |
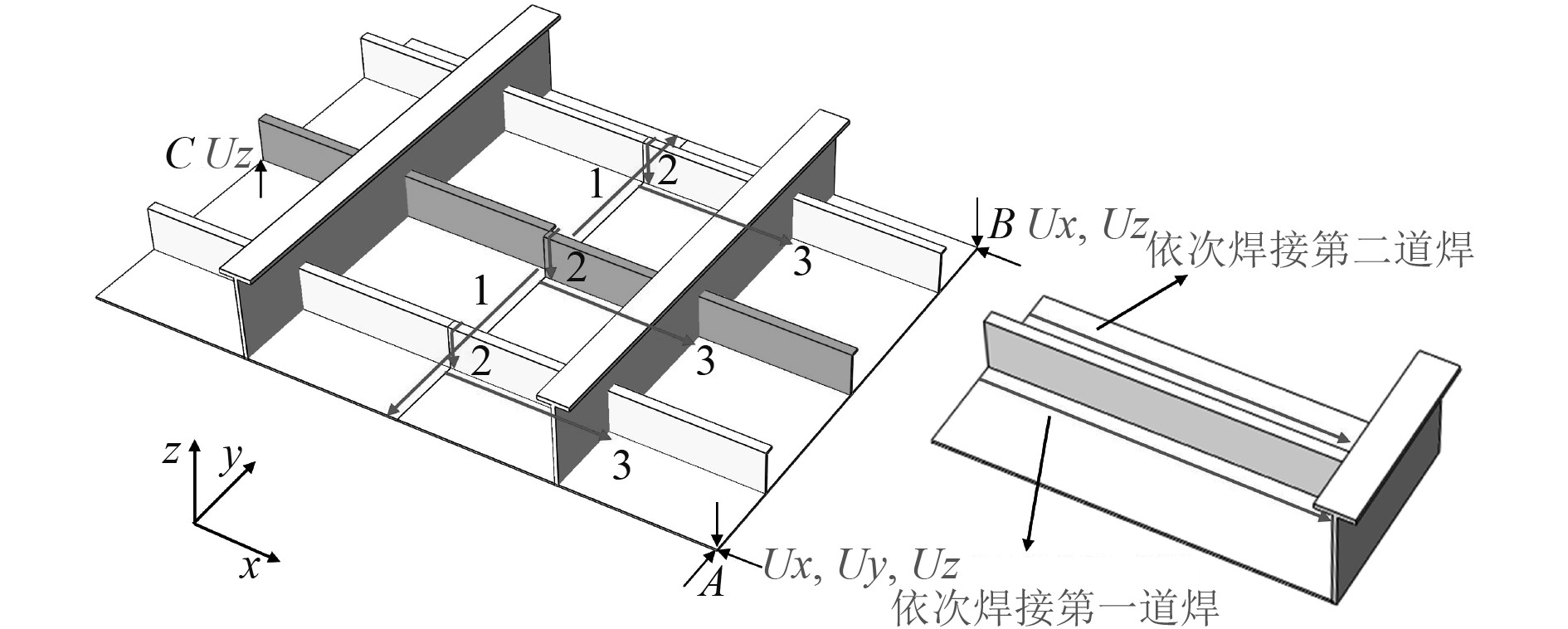
船体板架加强筋的焊接顺序对最终变形有着重要的影响,为了减小焊接变形和残余应力,在进行装焊工作前需要制定合理的焊接顺序。模拟中仅对外板与外板之间的拼板焊缝及图4中标注焊接顺序的纵骨焊接过程进行模拟,根据生产工艺对船体结构焊接顺序的要求,本文采用的焊接顺序如图4所示,图中“1、2、3”为焊接的先后次序。具体的焊接顺序如下:先从中间向左右两端对外板施焊,再对纵骨之间的连接处进行焊接,最后依次焊接纵骨与外板左右两侧的角焊缝。
|
图 4 焊接顺序及边界条件 Fig. 4 Welding sequence and boundary conditions |
板架在无约束条件下进行焊接工作,为避免结构模型产生刚体位移导致计算结果不收敛,在应力场分析中采取三支点自由约束[6]模拟自由焊过程,即在节点A施加x、y、z方向上的刚性约束,在节点B施加x、z方向上的刚性约束,在节点C施加z方向上的刚性约束。
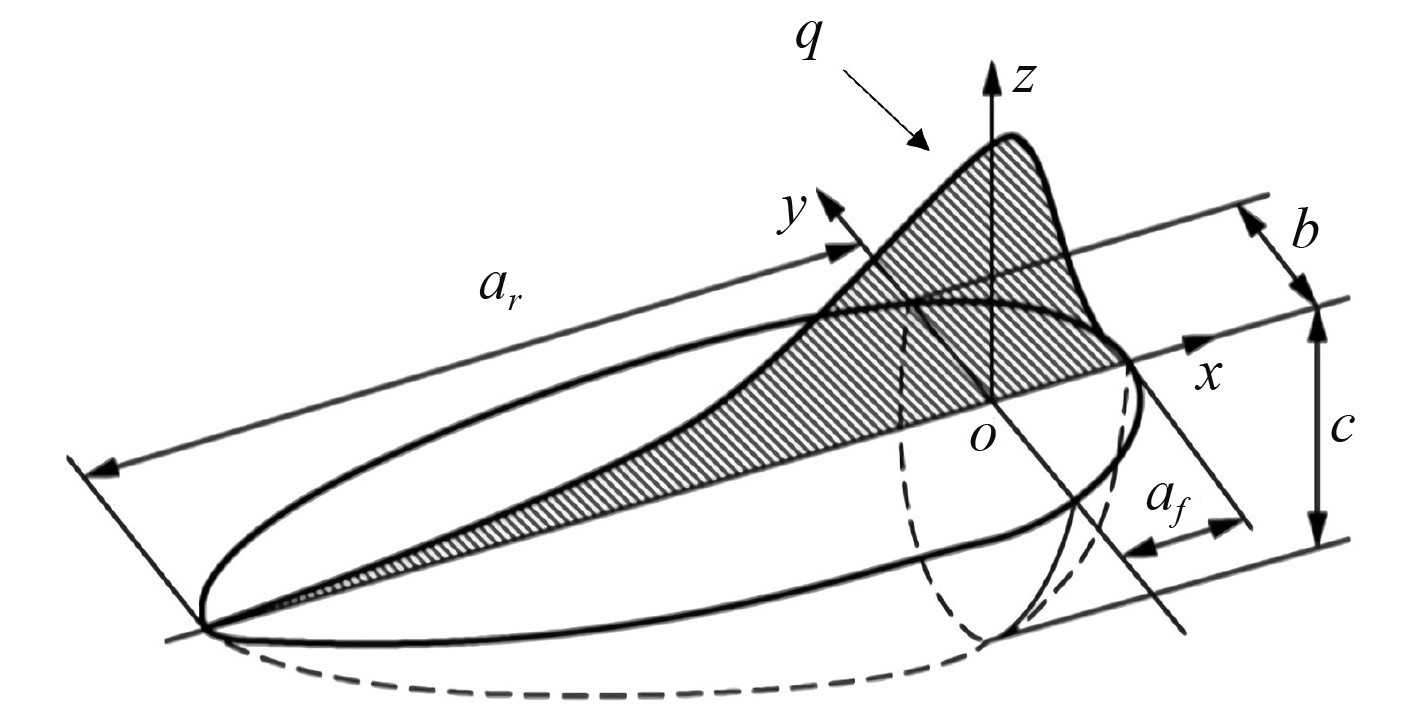
2.4 热源模型与材料属性热源模型选择的合理性直接关系到焊接过程数值仿真结果的准确性。在进行板架的焊接模拟时,通常将外界的能量输入等效为焊接热源模型并作用于焊缝处,利用Fortran语言编写的用户子程序实现热源的加载和移动。本文采用双椭球热源模型[7]描述焊接时的热流密度分布情况,该模型考虑了焊接热源中心前后端的温度梯度和沿板厚方向的分布特点,可以准确地模拟电弧焊的焊接热输入。双椭球热源模型如图5所示,该模型由前后2个1/4椭球组成,前后球体的长轴、短轴长度各不相同,其中
|
图 5 双椭球热源模型 Fig. 5 Double ellipsoid heat source model |
沿
| $ {q}_{f}(x,y,z)=\frac{6\sqrt{3}({f}_{f}Q)}{{a}_{f}bc {\text{π}} \sqrt{{\text{π}} }}\mathrm{exp}\left(-\frac{3{x}^{2}}{{a}_{f}{}^{2}}-\frac{3{y}^{2}}{{b}^{2}}-\frac{3{z}^{2}}{{c}^{2}}\right),x > 0 。$ |
沿
| $ {q}_{r}(x,y,z)=\frac{6\sqrt{3}({f}_{r}Q)}{{a}_{r}bc{\text{π}} \sqrt{{\text{π}} }}\mathrm{exp}\left(-\frac{3{x}^{2}}{{a}_{r}{}^{2}}-\frac{3{y}^{2}}{{b}^{2}}-\frac{3{z}^{2}}{{c}^{2}}\right),x\leqslant0。$ |
式中:
|
|
表 1 焊接参数 Tab.1 Welding parameters |
有限元模型中采用的材料为各向同性的AH32低碳钢[8],其力学性能遵循线性随动强化准则与Von Mises屈服准则。AH32钢材的物理特性和力学特性包括热传导系数、密度、比热、热膨胀系数、杨氏模量、屈服极限随温度变化的曲线如图6所示,该材料的泊松比为0.28。

|
图 6 材料属性 Fig. 6 Material properties |
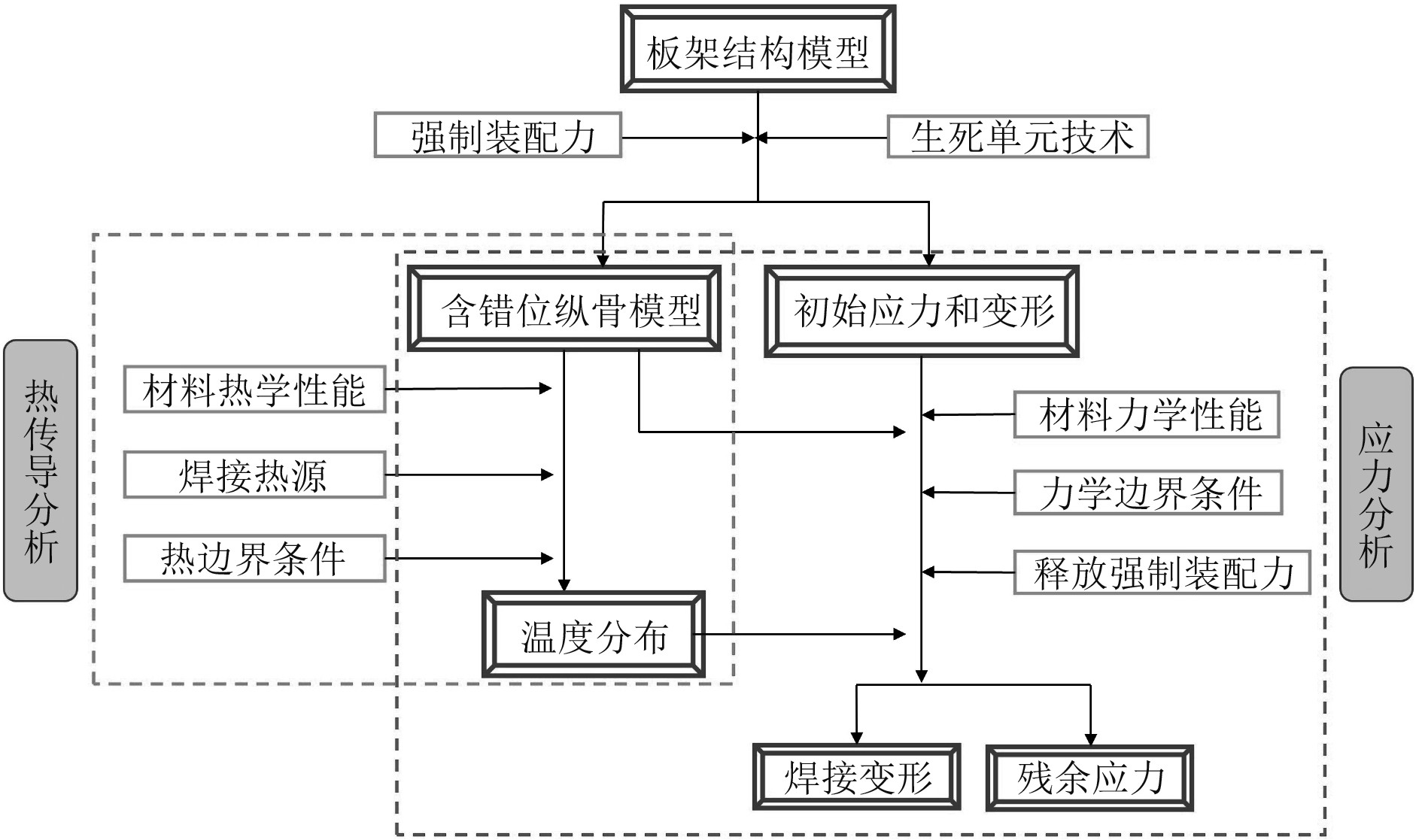
本文船体板架纵骨错位数值模拟方法采用基于顺序耦合的热弹塑性有限元方法[9],主要包括以下4个步骤:1)通过生死单元技术构造含错位纵骨的船体板架结构模型,采用不含有材料属性信息的“空气单元”建立未错位部分的板架结构,在错位纵骨端部施加外力使其达到装配位置后激活模型中的空气单元,最终形成含纵骨错位的船体板架结构模型;2)根据确定的焊接热源模型、材料的热学性能及边界条件,求解出随时间变化的焊接温度场;3)将温度场结果以外载荷的形式施加到力学模型中,同时施加力学边界条件,进行应力场分析;4)在焊接完成后释放强制装配力,得到板架结构的焊接变形及残余应力。
|
图 7 计算流程图 Fig. 7 Flowchart of analysis |
热弹塑性有限元方法被广泛应用于焊接数值模拟分析中,Bai-Qiao Chen等[10]采用该方法对T形接头进行数值模拟,计算过程中施加双椭球体热源,针对温度相关性能数据采集困难的问题,提出一种有效的简化模型,分别将仿真中的变形和温度结果与试验的实测值进行对比,发现两者吻合较好。王江超[11]为研究薄板加筋板的焊接变形特性,对其进行了焊接仿真与试验研究,计算结果与实验相比具有足够的精度。邓德安等[12]采用试验手段和热弹塑性有限元方法研究了厚板焊接残余应力分布特征,计算得到的横向与纵向残余应力与实验值比较吻合。以上文献均采用数值模拟与试验实测相结合的方式,验证了采用热弹塑性有限元数值模拟方法可有效预测焊接温度场和应力场结果。
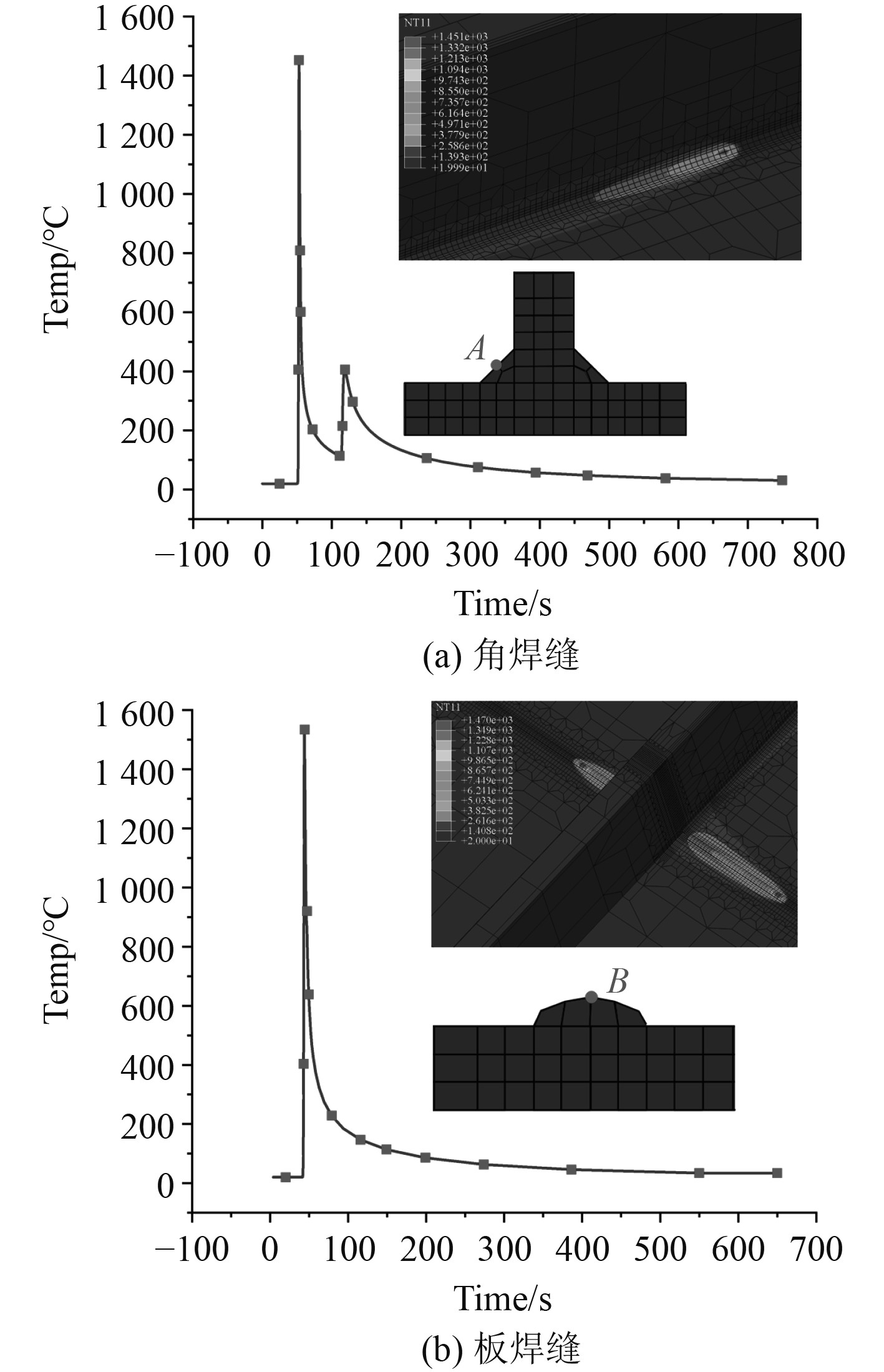
4 数值模拟结果与分析 4.1 温度场结果在焊接加热过程中,焊缝附近的瞬态温度分布云图如图8所示。热源中心沿着焊缝匀速移动,热源前端等温线密集,温度梯度大,后端等温线较为稀疏,温度梯度小。选取1 250 mm处角焊缝上的点A与500 mm处外板焊缝上的点B,绘制其温度时历曲线。当热源经过A点时,温度迅速上升至最大值1500℃后迅速降低,但由于纵骨的焊接方式是左右两侧依次焊接,因此当热源经过与A点相对的另一侧焊缝时,温度出现小幅度升高随后缓慢降至室温。当热源经过B点时,温度迅速上升至1540℃后缓慢降至室温。
|
图 8 瞬态温度分布及热循环曲线 Fig. 8 Transient temperature distribution and thermal cycle curve |
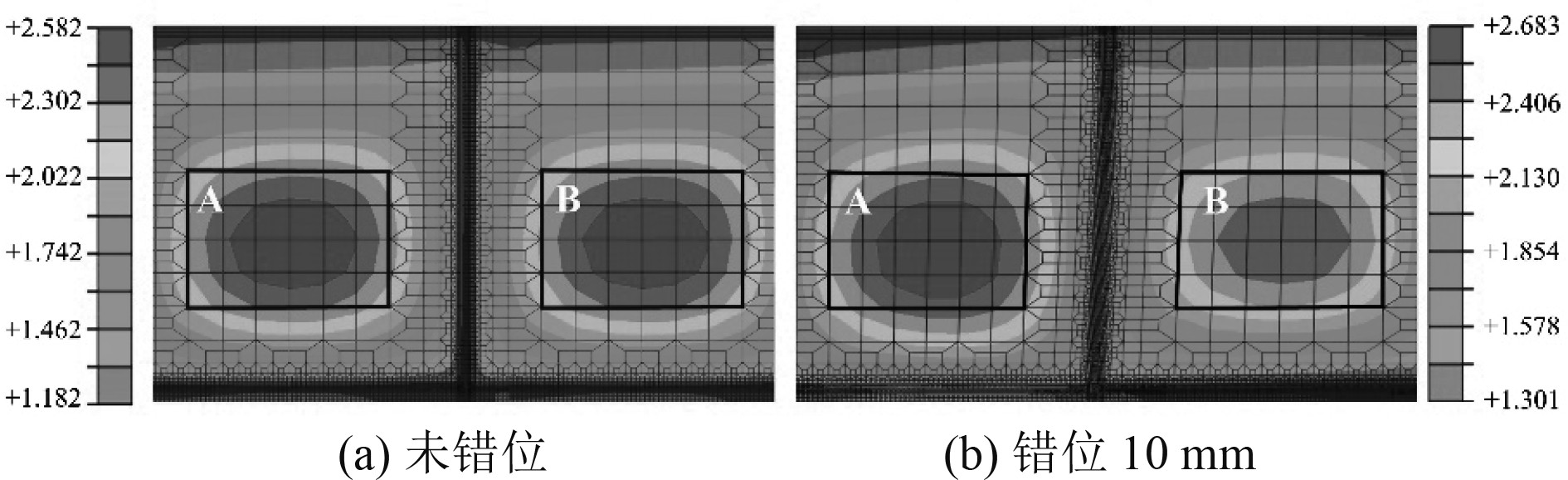
图9为焊接完成后船体板架结构垂向变形云图。可以看出,纵向加强筋之间的板格呈现波浪形,最大的板格垂向变形发生在自由边中部。本文重点关注中间纵骨两侧板格的焊接变形,即图中S区域,分析纵骨错位量对板格焊接变形的影响规律。从图10可以看出,未错位纵骨两侧板格的焊接变形总体上对称分布,而对于纵骨发生错位的板架,错位纵骨两侧板格的焊接变形分布具有明显的不对称性,这主要是由于纵骨错位改变了板架结构的力学性能,进而影响焊接变形。

|
图 9 整体结构垂向变形云图 Fig. 9 Overall vertical deflection |
|
图 10 S区域焊接变形图 Fig. 10 Welding deformation in S region |
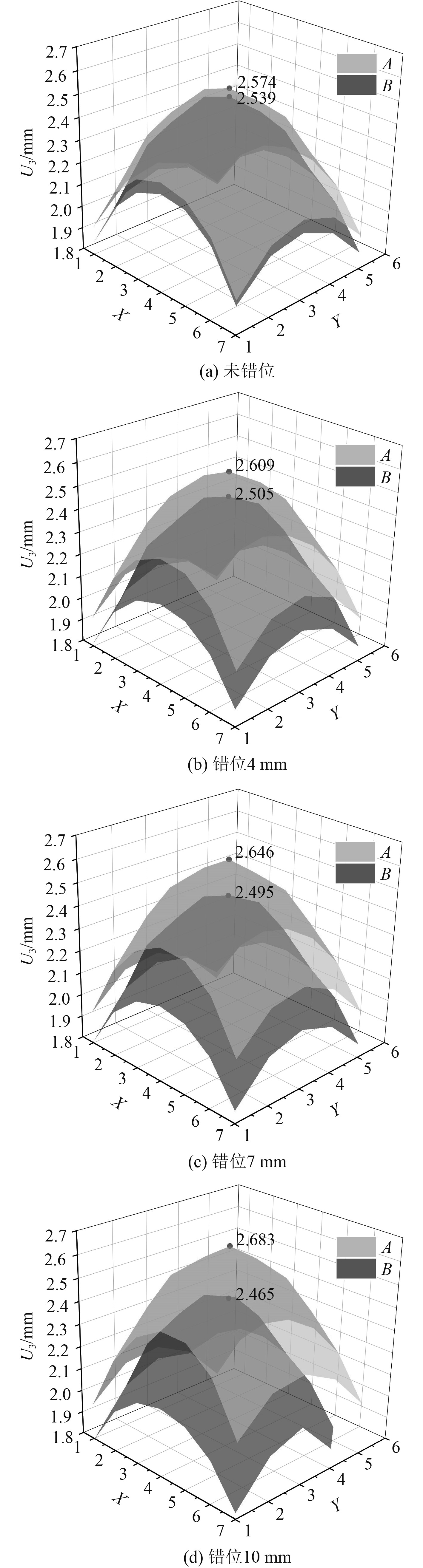
为了更直观地对比错位纵骨两侧板格焊接变形的差异性,图11基于A、B区域焊后网格节点空间坐标绘出了其三维变形曲面。由图可知,当纵骨未发生错位时,2个曲面的间距较小;随着错位量的增加,其间距亦明显增大。因此,错位现象对板格变形分布的不对称性具有加剧作用。
|
图 11 A、B区域三维变形图 Fig. 11 3D deformation of regions A and B |
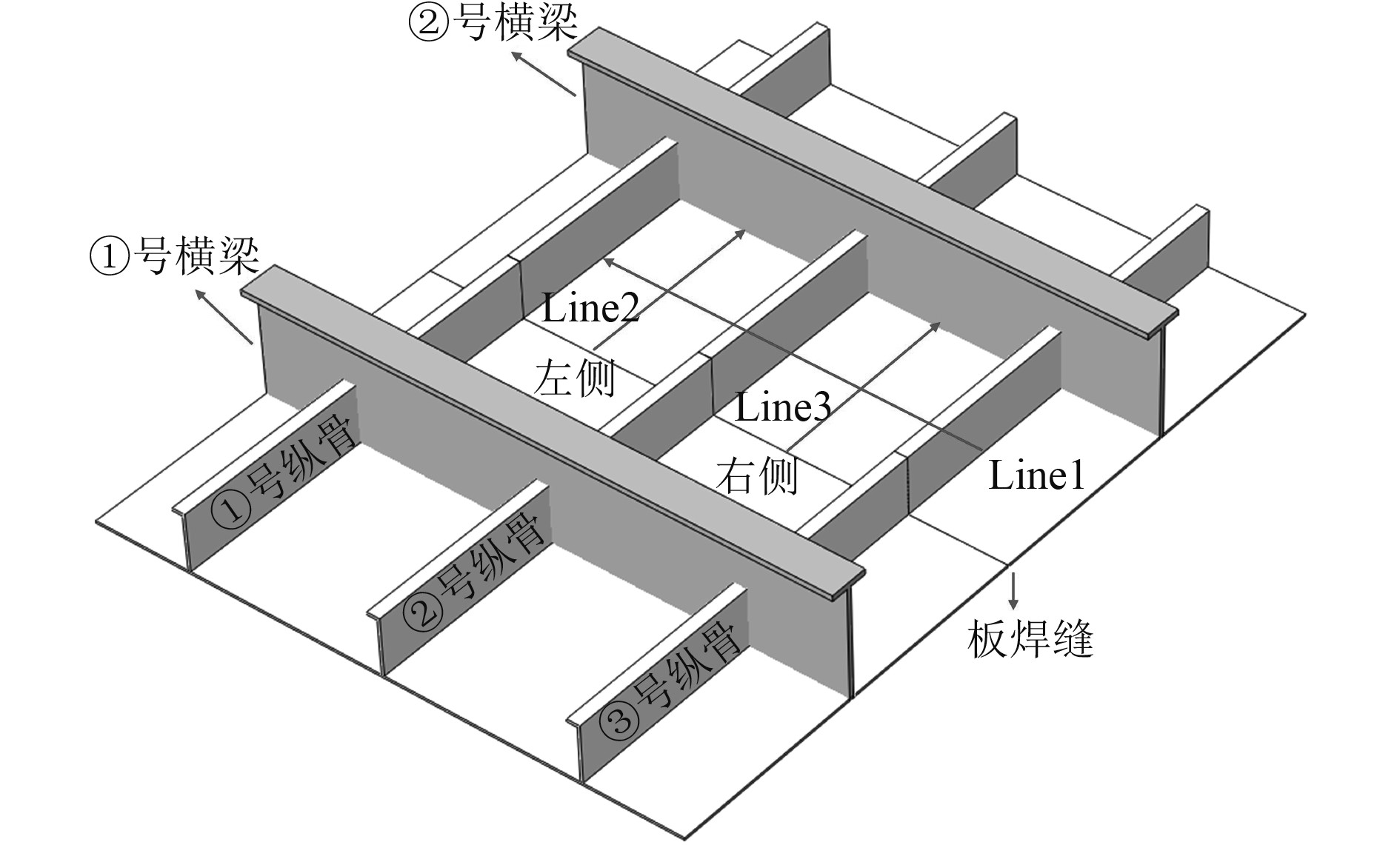
为进一步了解错位量对船体板架焊接变形量的影响,在模型上选取直线Line1~Line3,如图12所示,分析不同错位量下各直线所在位置处的板格垂向变形。其中Line1 位于外板焊缝与②号横梁之间的中线处,Line2位于①号和②号纵骨之间左侧板格的中线处,Line3位于②号和③号纵骨之间右侧板格的中线位置。
|
图 12 直线位置 Fig. 12 Position of lines |
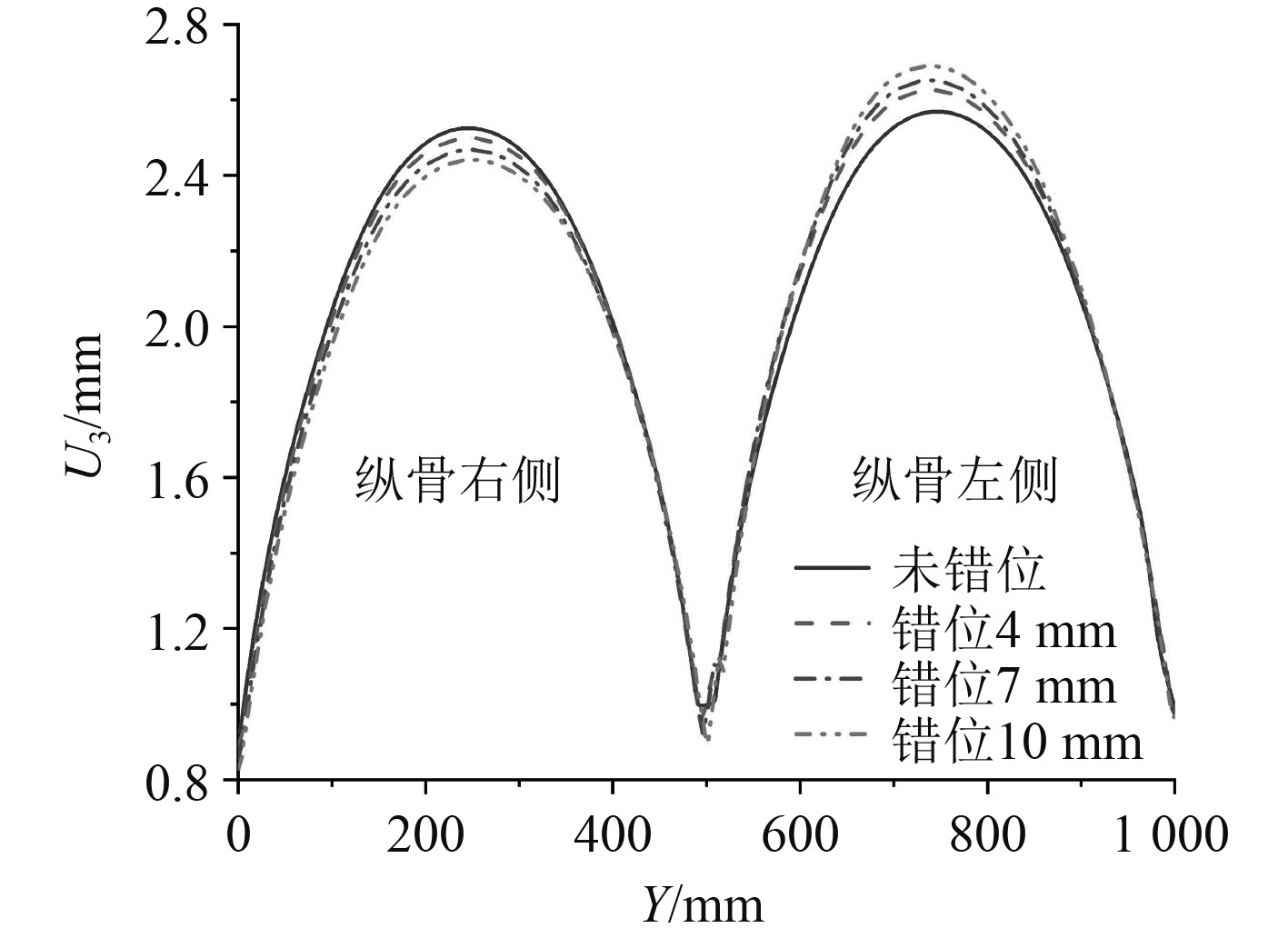
图13为焊接完成后Line1处板格的垂向变形沿Y方向的变化曲线。可知,最大垂向变形发生在板格中央位置,相邻纵骨之间的板格呈现中部向上拱的变形趋势,且错位纵骨左侧板格的最大变形量大于右侧板格。结合表2变形量的数据还可得出结论:当错位量增大时左右两侧板格的变形量呈相反的变化趋势,且两者差值逐渐增大。对于左侧板格,变形量随着错位量的增加而增加;对于右侧板格,变形量随着错位量的增加而减小。
|
图 13 Line1处焊接垂向变形 Fig. 13 Deflection on line1 |
|
|
表 2 各错位量下板格最大变形量 Tab.2 Maximum deformation of the lattice |
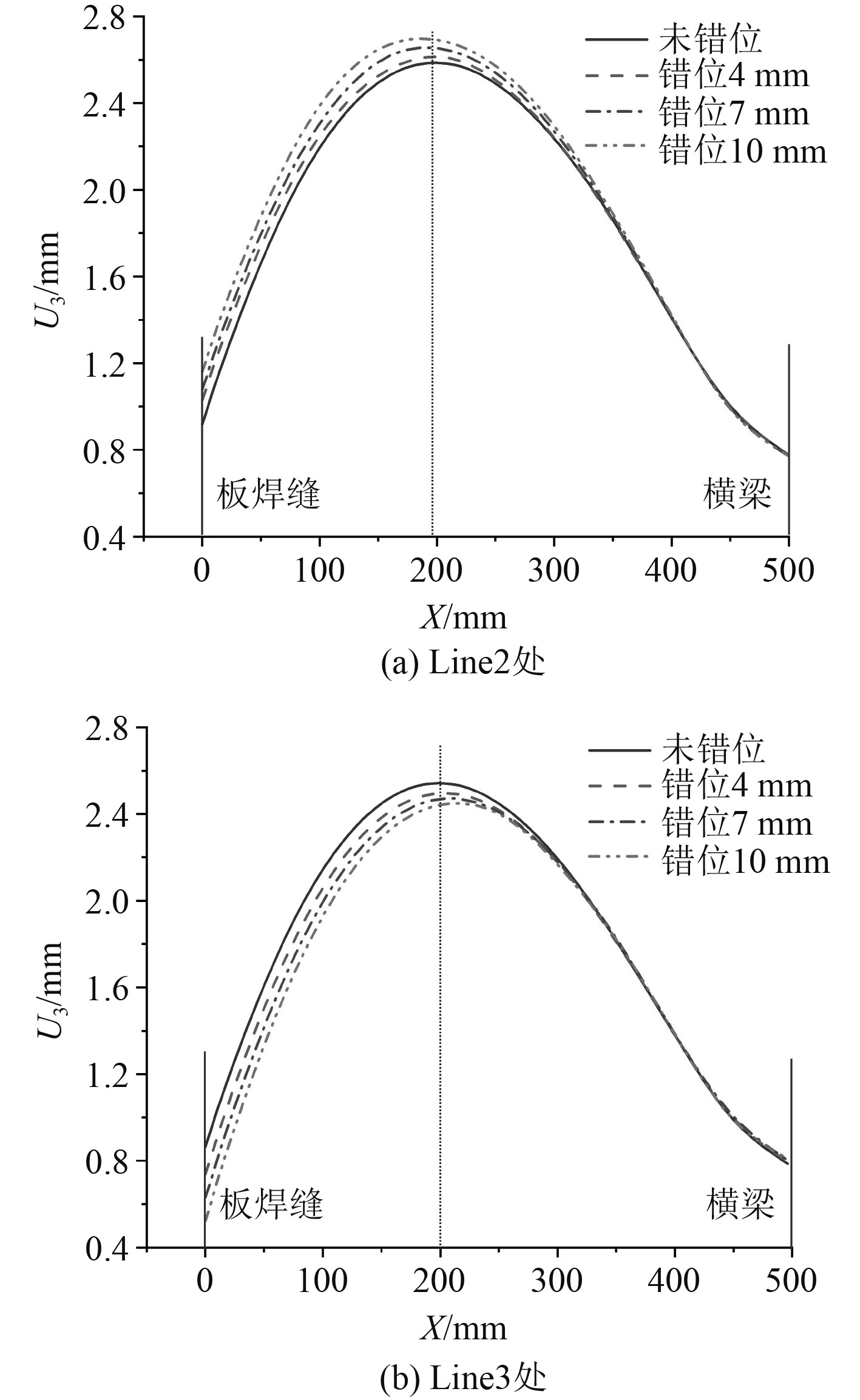
图14为 Line2和Line3处板格垂向变形在不同错位量下的变化曲线。可以看出,2条直线所在位置处的焊接变形沿X方向均先增大后减小,在距离板焊缝200 mm附近达到最大变形量。在同一位置处,Line2的变形随着错位量的增加而变大,Line3的变形随着错位量的增加反而减小。当Line2和Line3两条直线靠近横梁时,由于约束作用的增强,不同错位量之间产生的变形差异逐渐减小。
|
图 14 Line2和Line3处焊接垂向变形 Fig. 14 Deflection on line2 and line3 |
根据上述结果可知,纵骨错位对板格变形具有一定影响。除此之外,外板厚度也是影响焊接变形的重要因素之一。图15表示纵骨错位量为10 mm时,不同板厚的船体板架在Line1处的垂向变形,结合表3数据可知,随着板厚的减小,左右两侧板格的焊接变形和分布差异均明显增大,即板厚减小会加强纵骨错位对板格变形分布的影响,相反,板厚增加起到削弱作用,这是因为板厚增加导致结构刚度增强,进而对焊接变形产生抑制作用[13]。

|
图 15 各板厚下Line1处垂向变形 Fig. 15 Deflection at Line1 under each plate thickness |
|
|
表 3 各板厚下板格最大变形量 Tab.3 Maximum deflection under each plate thickness |
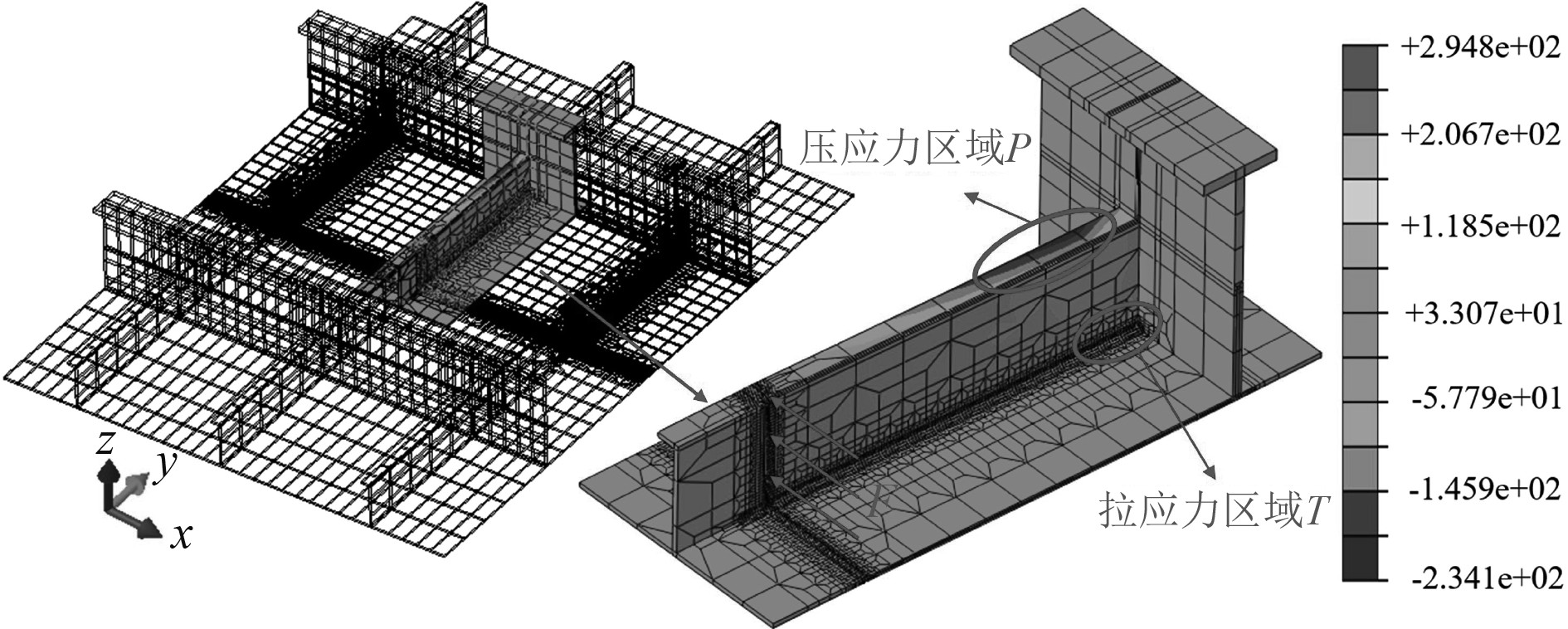
在图16所示的错位纵骨端部施加强制装配力F使其达到装配位置,该外力导致纵骨产生变形和应力,进而影响结构的力学性能。在焊接数值模拟时,将强制装配产生的变形和应力作为板架的初始变形和初始应力。以纵骨错位10 mm的板架为例,纵骨受外力F的强制作用及横梁的约束作用,在纵骨、横梁及外板的交界区域T因受拉产生拉应力,纵骨面板上的区域P因受压产生压应力,拉应力和压应力的最大值分别为294.8 MPa和234.1 MPa。对于其他的错位量情况,应力分布规律与纵骨错位10 mm的板架基本一致,仅在应力的数值上有所区别,错位量为4 mm和7 mm的拉压应力分别为119.8 MPa、93.5 MPa和211.2 MPa、163.7 MPa。结果表明,在错位纵骨强制装配的过程中产生的拉应力大于压应力,而且应力随着错位量的增加而增大。
|
图 16 强制装配产生的应力 Fig. 16 Stresses due to forced assembly |
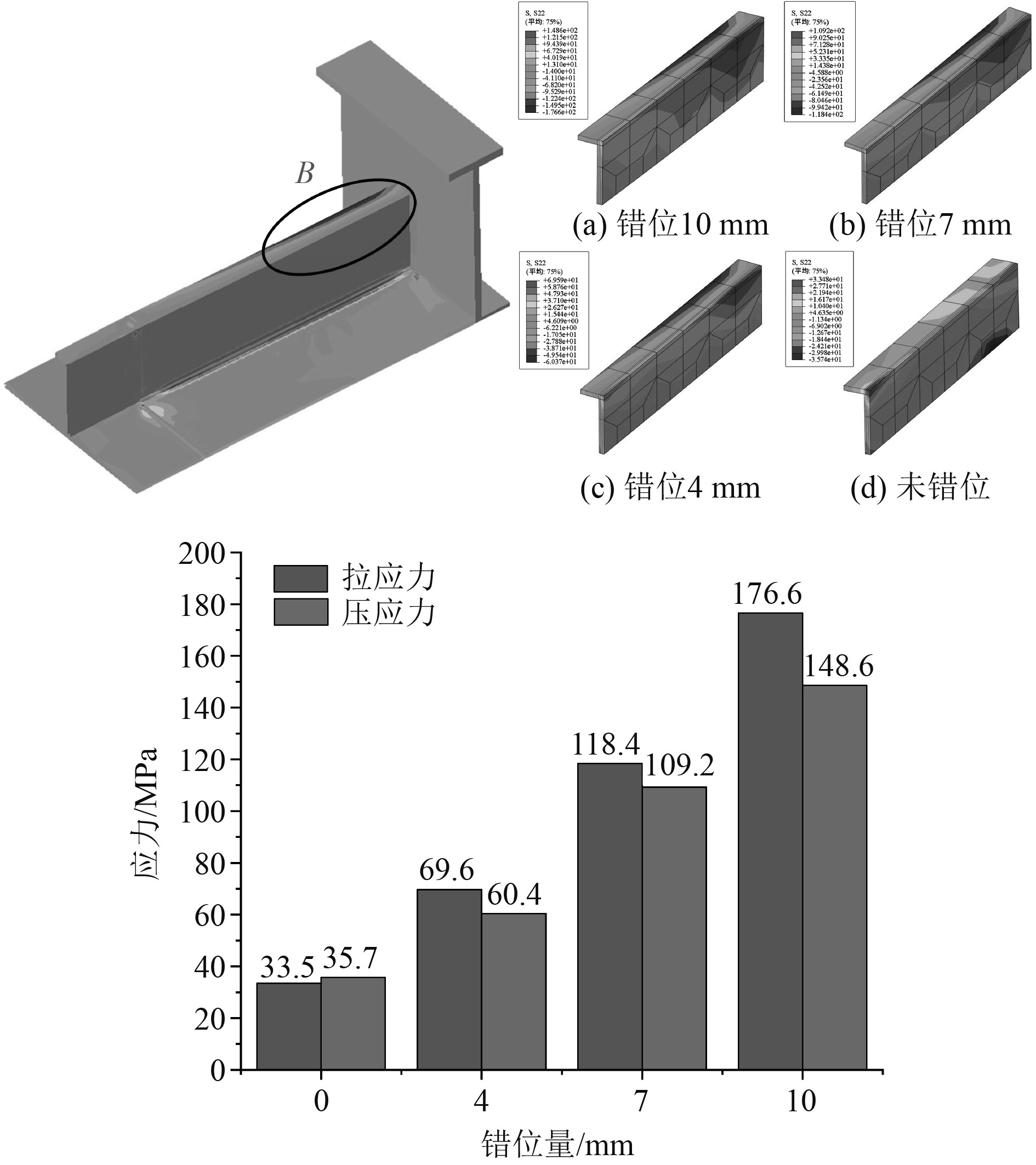
在焊接完成并释放外力后,各个错位量下板架残余应力的差别主要体现在错位纵骨上,如图17所示。对纵骨发生错位的板架而言,其残余应力分布规律在不同错位量下基本一致,拉应力与压应力主要分布在纵骨腹板和纵骨面板处。可知,焊接残余应力随着错位量的增加而增大。
|
图 17 焊后残余应力 Fig. 17 Residual stress after welding |
1)纵骨错位现象使得该纵骨两侧板格的焊后变形分布不一致,随着错位量的增加,两侧板格焊后变形差异愈加明显,最大可相差5.3倍。
2)错位纵骨左右两侧板格的焊接变形与纵骨错位量的关系呈相反变化趋势,其中左侧板格的焊接变形与错位量呈正比。纵骨错位10 mm与纵骨未错位相比,左右两侧板格变形差值增加3.7倍。
3)当错位量一定时,外板厚度越小,纵骨错位对船体板架焊接变形的影响越大。
4)随着错位量的增加,焊接初始应力与焊接残余应力均增加。初始拉应力与压应力最大可达到294.8 MPa和 234.1 MPa;对于焊接残余应力而言,当错位量为10 mm时,最大拉应力与压应力分别是纵骨未错位的4.4倍与4.9倍。
| [1] |
孙鹏, 金雁, 张建交, 等. 船体大焊缝间隙对接焊横向收缩变形数值模拟[J]. 武汉理工大学学报, 2017, 41(02): 355-358. |
| [2] |
向祖权, 刘彬, 郭纯轩, 等. 板材焊缝间隙差异对温度场及应力场的影响[J]. 船舶工程, 2015, 37(10): 89-93. DOI:10.13788/j.cnki.cbgc.2015.10.089 |
| [3] |
DEND D, MURAKAWA H, LIANG W. Numerical simulation of welding distortion in large structures[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(45−48): 4613-4627. DOI:10.1016/j.cma.2007.05.023 |
| [4] |
黄浩. 船体工艺手册[M] . 北京: 国防工业出版社, 2013: 793−794
|
| [5] |
董志波, 魏艳红, 刘仁培, 等. 不锈钢焊接温度场的三维数值模拟[J]. 焊接学报, 2004, 25(02): 9-14. DOI:10.3321/j.issn:0253-360X.2004.02.003 |
| [6] |
周宏, 李敢, 朱红娟. 船舶板材边界条件对高频感应弯板成形的影响[J]. 焊接学报, 2010, 31(11): 101-104. |
| [7] |
GOLDAK J, CHAKRAVARTI A, BIBBY M. A new finite element model for welding heat sources[J]. Metallurgical Transactions B, 1984, 15(2): 299-305. DOI:10.1007/BF02667333 |
| [8] |
YONGZHI L, KAIYUN W, YUJING J, et al. Prediction of welding deformation in stiffened structure by introducing thermo-mechanical interface element[J]. Journal of Materials Processing Tech, 2015, 216: 440-446. DOI:10.1016/j.jmatprotec.2014.10.012 |
| [9] |
UEDA Y, YAMAKAWA T. Analysis of thermal elastic-plastic stress and strain during welding by finite element method[J]. Transactions of the Japan Welding Society, 1971, 2(2): 186-196. |
| [10] |
CHEN B, GUEDES SOARES C. Experimental and numerical investigation on welding simulation of long stiffened steel plate specimen[J]. Marine Structures, 2021, 75: 102824. DOI:10.1016/j.marstruc.2020.102824 |
| [11] |
WANG J, SHIBAHARA M, ZHANG X, et al. Investigation on twisting distortion of thin plate stiffened structure under welding[J]. Journal of Materials Processing Technology, 2012, 212(8): 1705-1715. DOI:10.1016/j.jmatprotec.2012.03.015 |
| [12] |
邓德安, 清岛祥一. 焊接顺序对厚板焊接残余应力分布的影响[J]. 焊接学报, 2011, 32(12): 55-58+115-116. |
| [13] |
张凯. 基于数值模拟的角焊缝焊接变形特点和控制研究[D]. 武汉: 武汉理工大学, 2017: 39−40
|
 2023, Vol. 45
2023, Vol. 45
