0 引　言

高强聚乙烯夹层结构在抗弹片侵彻方面具有优良性能。Chen等^[1]通过实验和有限元软件Abaqus数值仿真相结合的方法分析了超高分子量聚乙烯(UHMWPE)编织材料和单向材料(UD)在弹道冲击下的失效模式和动态响应。结果表明，编织结构具有较好的抗剪切性能，UD结构具有较好的抗拉伸性能和较大的横向挠度。王晓强等^[2]通过实验研究了4种不同面密度的超高分子量聚乙烯纤维增强层合板的抗高速立方体破片侵彻性能，探究了超高分子量聚乙烯在中高速冲击作用下出现的拉伸变形、剪切以及层间分层等不同破坏模式。高恒等^[3]发现将UHMWPE纤维单向布和二维平纹布复合后，对抵御多发弹体侵彻更为有利。陈长海等^[4]将整个侵彻过程分为开坑镦粗、剪切压缩和拉伸变形3个阶段。基于能量守恒原理建立了超高分子量聚乙烯纤维增强塑料层合厚板抗高速钝头弹侵彻的弹体侵彻深度和靶板弹道极限的计算模型。

结构抗侵彻性能数值计算一般非常耗时，若采用优化算法对其抗侵彻性能进行优化设计，由于此过程中要进行成百上千次迭代计算，其时间成本难以承受。因此，研究提出结构抗侵彻性能快速预报方法对于其优化设计具有重要的价值。目前，利用代理模型技术开展结构抗侵彻性能快速预报研究鲜见报道，但在结构抗爆性能快速预报方面已陆续有学者开展了相关研究。Cai等^[5]利用所建立的Kriging代理模型对梯形波纹芯夹芯板在特定爆距下进行了多目标优化设计，并将优化设计与初始设计的抗爆性能进行比较。结果表明，在性能改进上存在很大潜力。Lan等^[6]研究设计了一种新型双箭头夹层板芯，基于拉丁超立方体采样方法、人工神经网络模型和非支配排序遗传算法进行参数研究和优化设计。

本文以高强聚乙烯-负泊松比效应复合结构为研究对象，利用代理模型技术开展其抗侵彻性能的快速预报方法研究，建立了高强聚乙烯-负泊松比效应复合结构抗侵彻性能分析的数值模型，构建其弹道极限快速预报代理模型，分析了代理模型类型和采样方式对代理模型精度的影响规律。

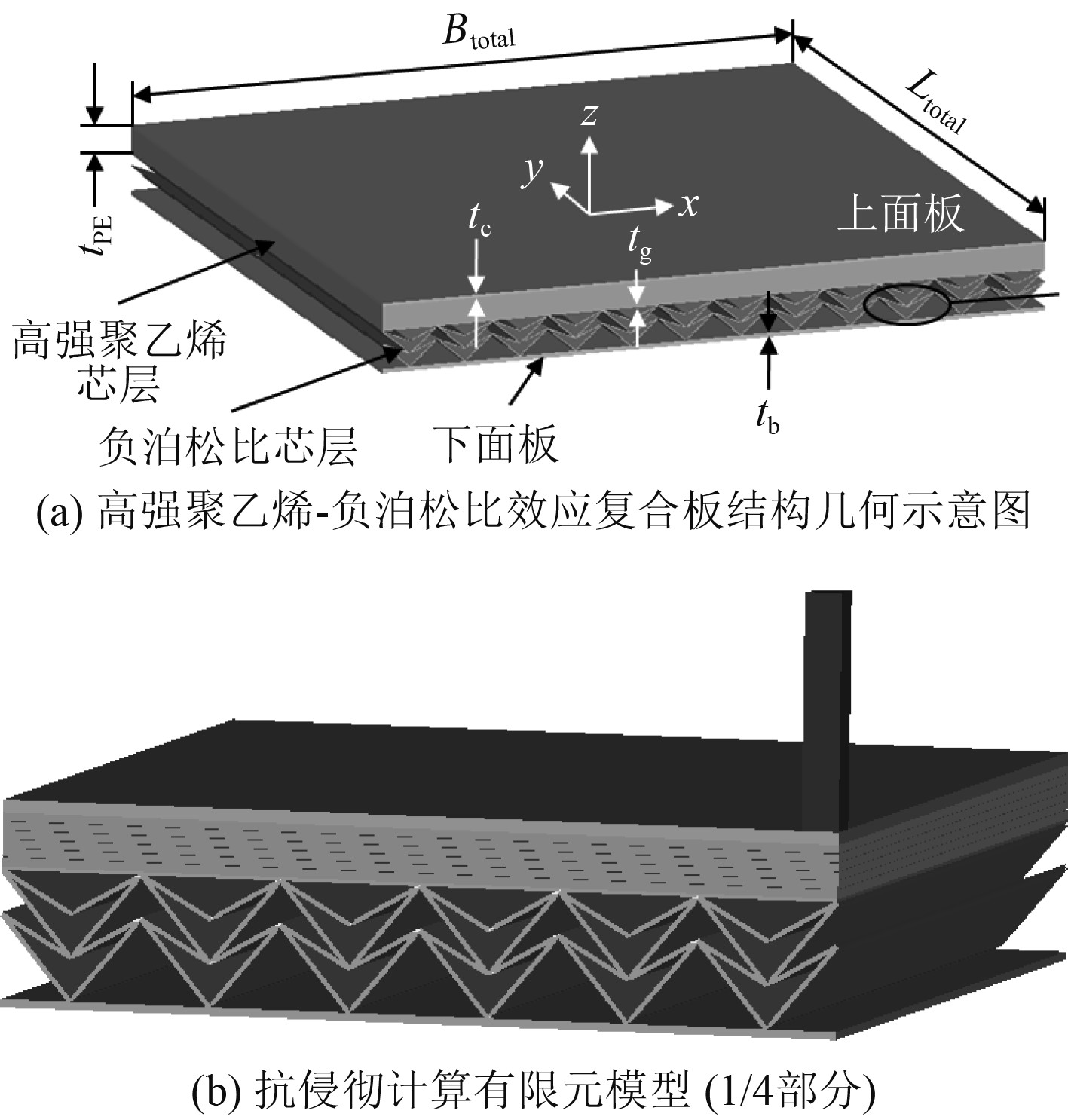
1 抗侵彻分析有限元模型及数值方法验证 1.1 抗侵彻分析有限元模型

本文研究对象是高强聚乙烯-负泊松比效应复合板结构，长度为300 mm，宽度为280 mm，其组成主要包括上面板、高强聚乙烯芯层、隔板、双箭头负泊松比结构、下面板，如图1(a)所示。有限元模型相关信息如下：

1）采用形状为圆柱体的破片模拟弹，弹体直径为12.8mm，高度为40mm，质量为40g，材料为35CrMnSiA钢。采用Cowper-Symonds材料模型描述35CrMnSiA钢在冲击载荷作用下的动态屈服应力 $ {\sigma }_{d} $ ，表达式如下：

$ {\sigma }_{d}=\left({\sigma }_{y}+B{\epsilon }_{p}^{n}\right)\left(1+{\left(\frac{\dot{{\varepsilon }_{p}}}{D}\right)}^{1/q}\right) 。$

(1)

式中：第1项用于考虑应变强化效应；第2项用于考虑应变率强化效应。 $ {\sigma }_{y} $ 为静态屈服强度；B为应变硬化系数； $ {\varepsilon }_{p} $ 为等效塑性应变；n为应变硬化指数； $ \dot{{\varepsilon }_{p}} $ 为塑性应变率；D为参考应变率；q为常数。35CrMnSiA钢材料具体参数参考文献[7]。

2）为节约计算资源，建立1/4有限元模型，如图1(b)所示。在网格划分上，考虑到着弹区域层合板单元的长宽高之比接近于1，且弹体的网格尺寸和着弹区域网格尺寸相当，参考文献[7]将弹体与复合结构整体网格大小确定为1.4mm。

3）除了高强聚乙烯芯层，其余板材为304不锈钢，具体材料参数参考文献[8]。

1.2 抗侵彻分析数值方法验证

鉴于高强聚乙烯-负泊松比效应复合结构包含高强聚乙烯材料和金属材料，而金属材料的抗侵彻数值仿真方法比较成熟。因此，高强聚乙烯抗侵彻数值仿真方法准确与否是本文计算工作的关键一环，利用限元分析软件Autodyn建立高速破片侵彻载荷下高强聚乙烯层合板动响应数值仿真模型，并将计算结果与Nguyen等^[9]实验结果进行对比，验证高强聚乙烯抗侵彻数值仿真方法的正确性。

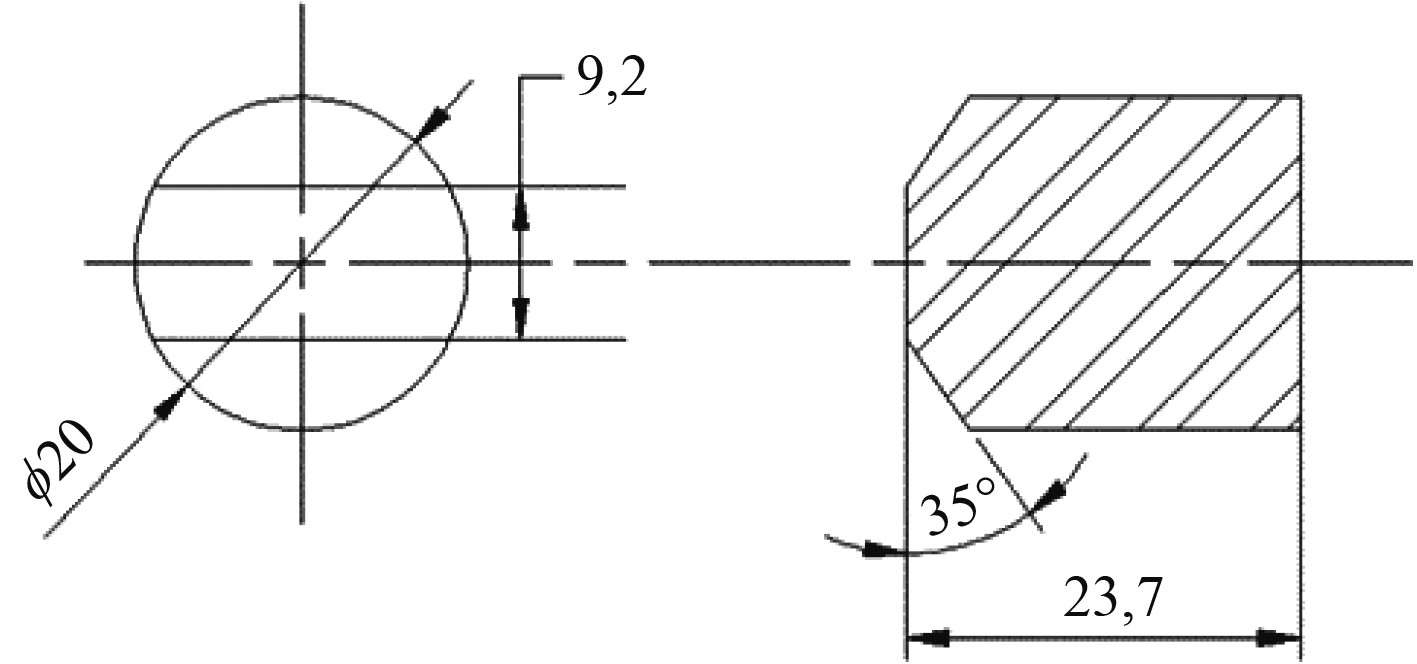
选择参考文献[9]中2种不同厚度的高强聚乙烯层合板作为计算对象，分别为10 mm和20 mm。靶板面内尺寸为300 mm×300 mm。侵彻弹体为美军标破片模拟弹，其直径为20 mm，质量为55 g，具体形状尺寸如图2所示。

由于破片模拟弹的不对称性，建立破片模拟弹侵彻作用下高强聚乙烯层合板的全几何模型，如图3所示。

高强聚乙烯层合板和弹体都采用非结构化拉格朗日三维实体单元离散，网格尺寸大小与上文保持相当。由于高速破片侵彻下靶板响应非常局部，当靶板的面内尺寸达到一定大小后，边界条件对计算结果的影响较小。因此，模型不施加任何边界条件（与文献中的实验状态保持一致）。

高强聚乙烯与破片模拟弹的材料参数均参照文献[9]。

为验证数值方法的准确性，主要从弹道极限结果开展对比验证工作。针对2种工况设置3 ~ 4个不同破片入射速度，利用Lambert–Jonas公式预测靶板弹道极限。

$ {V}_{R}=a{({V}_{l}^{p}-{V}_{BL}^{p})}^{1/p}。$

(2)

式中： $ {V}_{R} $ 为弹体剩余速度，m/s； $ {V}_{l} $ 为弹丸入射速度，m/s； $ {V}_{BL} $ 为预测的弹道极限；a和p为拟合常数。

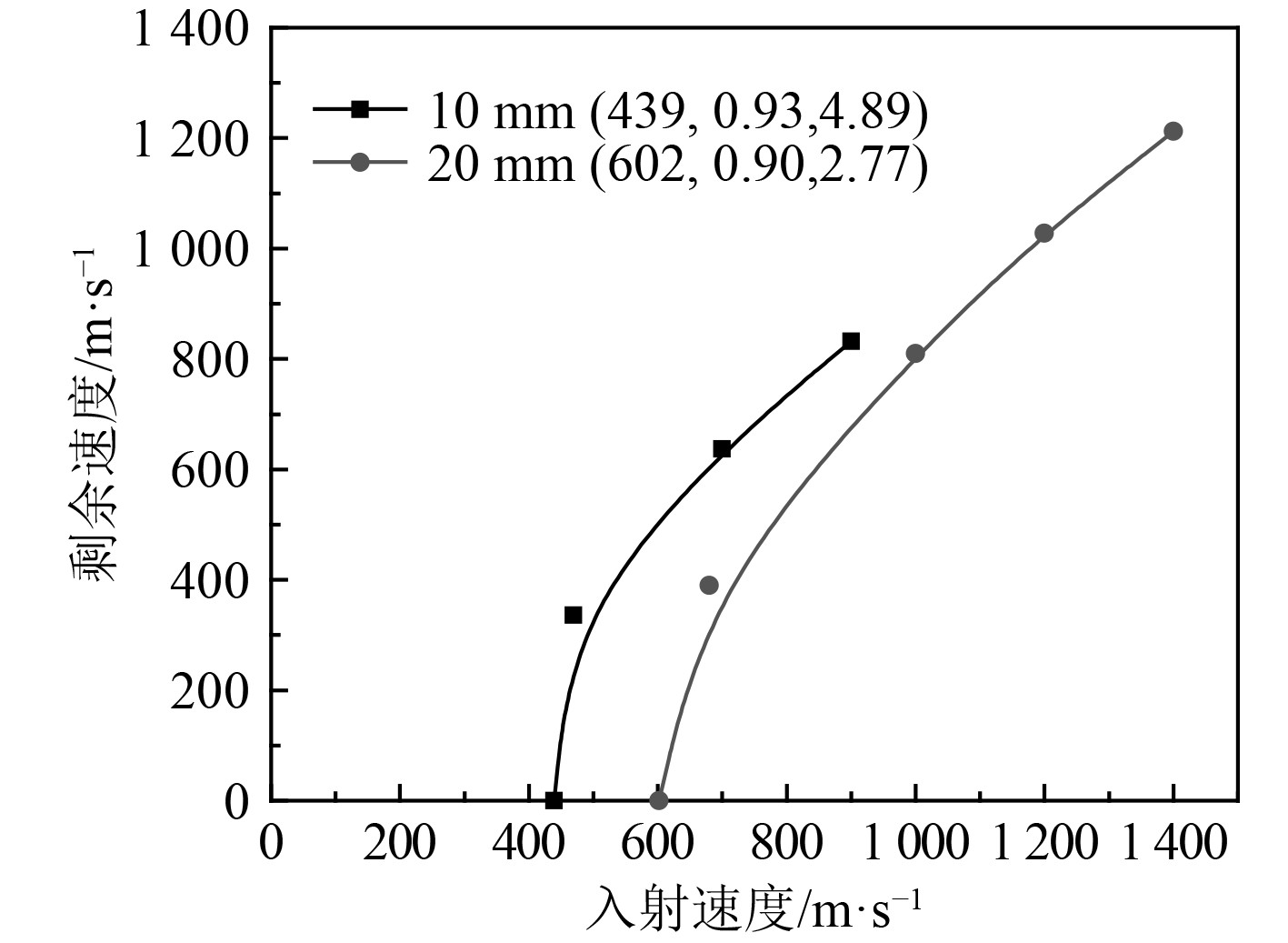
通过有限元计算获得每个工况下弹体剩余速度，利用Lambert–Jonas公式对2种板厚的高强聚乙烯层合板在20 mm破片模拟弹侵彻作用下的入射速度和剩余速度进行拟合，如图5所示。

预测的弹道极限值以及相对应文献中实验和数值预测的弹道极限值统计在表1中。可看出，预测弹道极限速度值与文献中实验值及拟合值吻合较好，最大误差约11%。因此，本文所采用的高强聚乙烯-负泊松比复合结构抗侵彻动态响应数值模拟方法准确可靠。

2 高强聚乙烯-负泊松比复合结构抗侵彻性能代理模型构建 2.1 设计变量及样本点

代理模型的设计变量确定为4个，分别是上面板厚度(t_f)、下面板厚度(t_b)、高强聚乙烯芯层厚度(t_PE)和负泊松比芯层板厚(t_c)，设计方案采用4因素4水平的正交试验设计。各设计变量的具体取值见表2。

采用正交试验设计生成共64个样本点。侵彻响应值为弹道极限速度v_BL，即针对每一个样本点，首先设置4个不同的破片入射速度。入射速度设置为500 m/s 、700 m/s、900 m/s、1100 m/s和1300 m/s。综合5个不同的破片入射速度及剩余速度，利用式（2）预测样本点的弹道极限速度v_BL。

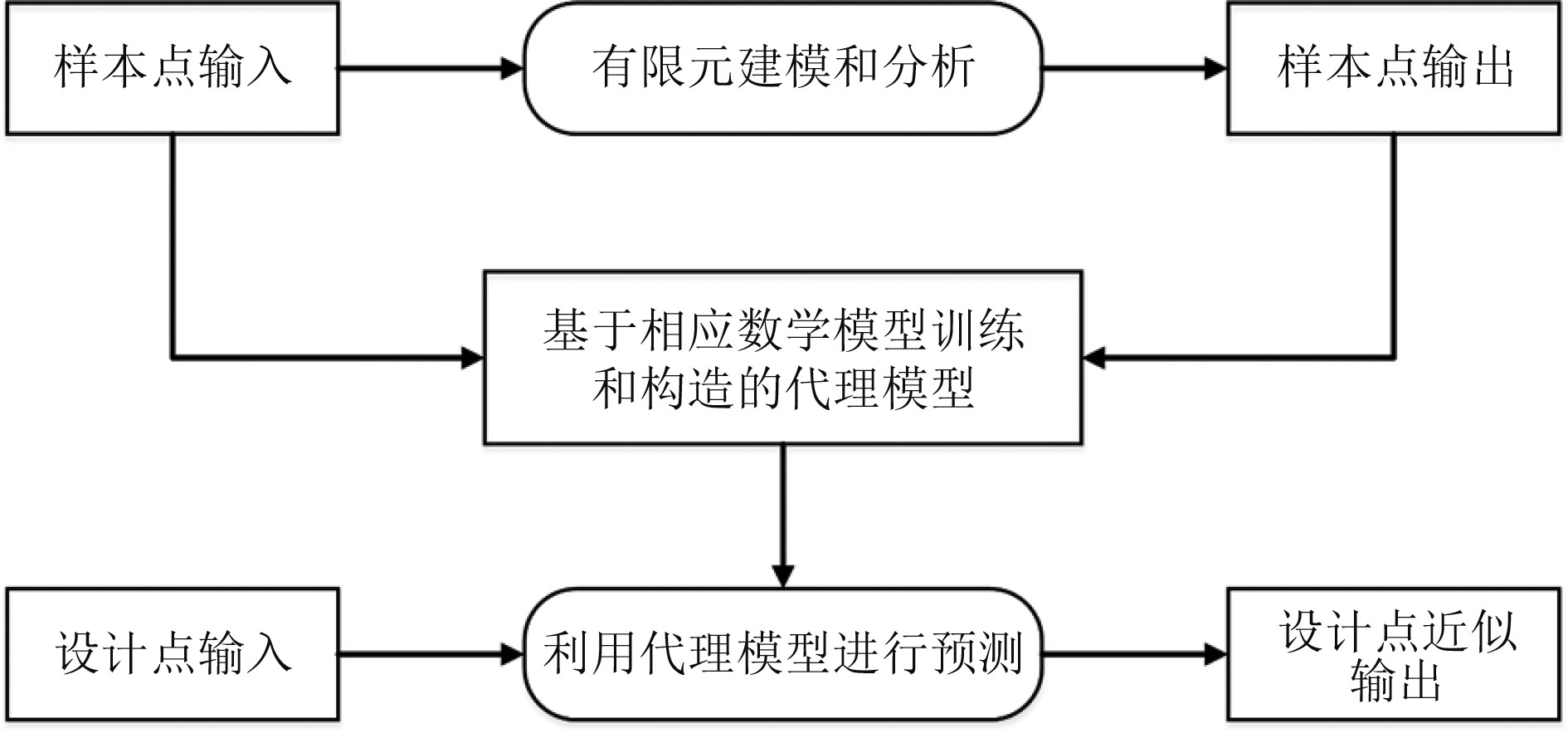
2.2 不同代理模型的精度分析

同样采用Kriging模型、多项式响应面模型和径向基函数模型3种数学模型分别构建复合结构抗侵彻响应代理模型，构造流程如图6所示。

对于构造完成的代理模型需进行精度检验，精度检验分3个层次进行。层次1：随机选取8个样本点作为检验点进行近似误差检验；层次2：随机选取6个由设计变量具体取值组成的检验点进行近似误差检验；层次3：随机选取4个由设计变量具体取值之间数值组成的检验点进行近似误差检验，要求取值尽可能分散。同样，针对以上3种层次的每一个检验样本点，通过设置4 ~ 5个不同破片入射速度，采用数值模型计算获得对应入射速度下破片剩余速度，再利用式（2）获取检测点的弹道极限速度，将此弹道极限速度与基于代理模型获取的弹道极限速度进行对比，以检验代理模型精度。

采用相对误差(RE)、归一化均方根误差(NRMSD)和相关系数 $ \left({\rho }_{xy}\right) $ 3个指标量来评估代理模型的精度。RE和RNSMD误差定义如下：

$ RE=\frac{{\widehat{y}}_{i}-{y}_{i}}{{y}_{i}}\times 100 \text%，$

(3)

$ NRMSD=\frac{\sqrt{\displaystyle\frac{1}{n}{\sum }_{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}}}{\stackrel-{y}}\times 100\text% 。$

(4)

式中： $ {y}_{i} $ 和 $ {\widehat{y}}_{i} $ 分别为有限元结果和代理模型预测结果； $ \stackrel{-}{y} $ 为 $ {y}_{i} $ 的均值。RE和NRMSD分别用于衡量代理模型的局部精度和整体精度。通常来说，两者的值越接近0，对应的代理模型预报精度越高。

相关系数( $ {\rho }_{xy}) $ 定义如下：

$ {\rho }_{xy}=\frac{Cov(X,Y)}{\sqrt{Var\left(X\right)}\sqrt{Var\left(Y\right)}} 。$

(5)

其中：Cov(X,Y)为2个变量的协方差；Var(X)，Var(Y)分别为2个变量的方差。

$ Cov\left(X,Y\right)=E\left(X,Y\right)-E\left(X\right)E\left(Y\right) ，$

(6)

其中，E(X)为变量X的期望值；E(Y)为变量Y的期望值。变量X和变量Y的方差定义如下：

$ \sqrt{Var\left(X\right)}=\sqrt{\frac{\displaystyle\sum _{i=1}^{n}({x}_{i}-\bar{{x}_{i}})^{2}}{n-1}}，$

(7)

$ \sqrt{Var\left(Y\right)}=\sqrt{\frac{\displaystyle\sum _{j=1}^{n}({y}_{i}-\bar{{y}_{i}})^{2}}{n-1}} 。$

(8)

相关系数 $ {\rho }_{xy} $ 的取值在(−1,1)之间，| $ {\rho }_{xy} $ |越大则表示2个变量之间的相关性越强，系数 $ {\rho }_{xy} $ 的正负号表示2个变量之间相关性质，若为负值则表示变量之间负相关，正值则表示变量之间正相关。

3种代理模型的精度检验如表3所示。

从表3可看出，Kriging代理模型的最大误差为18.1%，出现在层次3中，整体均方根误差为8.8%，相关系数为0.85。多项式响应面代理模型的最大误差为17.8%，出现在层次1中，整体均方根误差为9.7%，相关系数为0.73。径向基函数代理模型的最大误差为30.9%，出现在层次3中，整体均方根误差为11.2%，相关系数为0.76。

上述结果表明，径向基函数代理模型精度最差；与多项式响应面代理模型相比，Kriging代理模型预测结果的最大误差略高，但均方根误差更低，且相关系数更高。因此，综合来看，Kriging代理模型的预测精度更高。

2.3 不同采样方式对代理模型精度的影响分析

为比较不同采样方式可能对代理模型精度的影响，采用拉丁超立方采样方式构建Kriging代理模型，设计变量及取值范围与上文保持一致，将模型预测结果进行比较分析。

从表4可看出，采用拉丁超立方采样方式构建的Kriging代理模型最大误差值为34.0%，整体归一化均方根误差为18.5%，相关系数为0.43，与正交试验设计采样方式相比，其误差偏大。因此，采用正交试验设计采样方式对提高代理模型精度更有利。

3 结　语

本文建立高强聚乙烯-负泊松比效应复合结构抗侵彻性能分析的数值模型，构建其弹道极限快速预报代理模型，分析了代理模型类型和采样方式对代理模型精度的影响规律，得到以下结论：

1）相较多项式响应面和径向基函数代理模型，Kriging代理模型的预报精度最高，更适用于结构抗侵彻弹道极限代理模型构建。

2）相较于拉丁超立方采样方式，采用正交设计试验方法采样获得的代理模型精度更高，更适合复合结构弹道极限代理模型的构建。