2. 沈阳工业大学 机械工程系,辽宁 沈阳 110870
2. School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China
随着反舰导弹突防能力及毁伤威力大幅提升,反舰导弹已成为水面舰船主要威胁[1]。反舰导弹战斗部侵彻穿入舰船内部舱室,并在舱室内部爆炸,产生冲击波、准静态压力、破片,对舰船内部结构造成严重破坏[2]。开展反舰导弹舱内爆炸载荷特性研究对于舰船水上防护结构设计和评估至关重要[3]。
与自由场环境相比,由于舰船舱室结构的反射作用,舱室内部爆炸冲击波传播过程非常复杂[4]。在舱室内壁面上,爆炸冲击波首先会发生正反射、斜反射以及马赫反射等,同时还伴随反射波追赶入射波等。其次,经舱壁反射后的冲击波会在舱壁中心汇聚,再次形成入射脉冲,随后载荷特性将更为复杂[5-6]。针对舰船舱室内部爆炸冲击波载荷分布的问题:F Yang等[7]通过有限元仿真,得到了密闭舱室内部典型测点处的超压时程曲线,分析得出当炸药位于箱形结构几何中心时,舱壁中心和角隅处承受的超压最大。朱建方[8]对舱室在爆炸载荷下的响应过程进行了数值模拟,得出角隅处是舱室的薄弱区域。李伟等[9]开展缩比舱室内部爆炸模型试验,分析得出舱内爆炸冲击波在传播过程中遇到舱壁会发生反射并在角隅处汇聚,使角隅处结构发生破坏。侯海量等[10]也针对典型舱室结构开展了舱内爆炸模型实验,对舱内爆炸载荷特性进行了分析,得出舰艇结构除承受初始冲击波作用外,还将承受冲击波多次反复作用,舱室角隅处承受强度远大于壁面反射冲击波的汇聚波作用。目前针对舱室内部典型位置处爆炸载荷特性分析相对较少,没有舱内爆炸冲击波载荷计算模型。因此,有必要开展舱内爆炸冲击波载荷特性及计算模型研究。
设计1∶2缩尺比舱室模型,开展不同装药量下缩比舱室内爆试验,获取了正规反射测点,两壁面交汇角隅处测点和三壁面交汇角隅处测点的压力载荷数据,分析了舱内不同位置测点处压力载荷特性,并总结了舱内爆炸冲击波载荷计算模型。
1 试验模型 1.1 舱室模型根据船舱典型舱室模型图纸,按照1∶2缩尺比设计缩比舱室模型。其外形尺寸为2 m×1.5 m×1.75 m,壁厚8 mm,外部焊接加强筋提高其刚度,材料为45号钢。
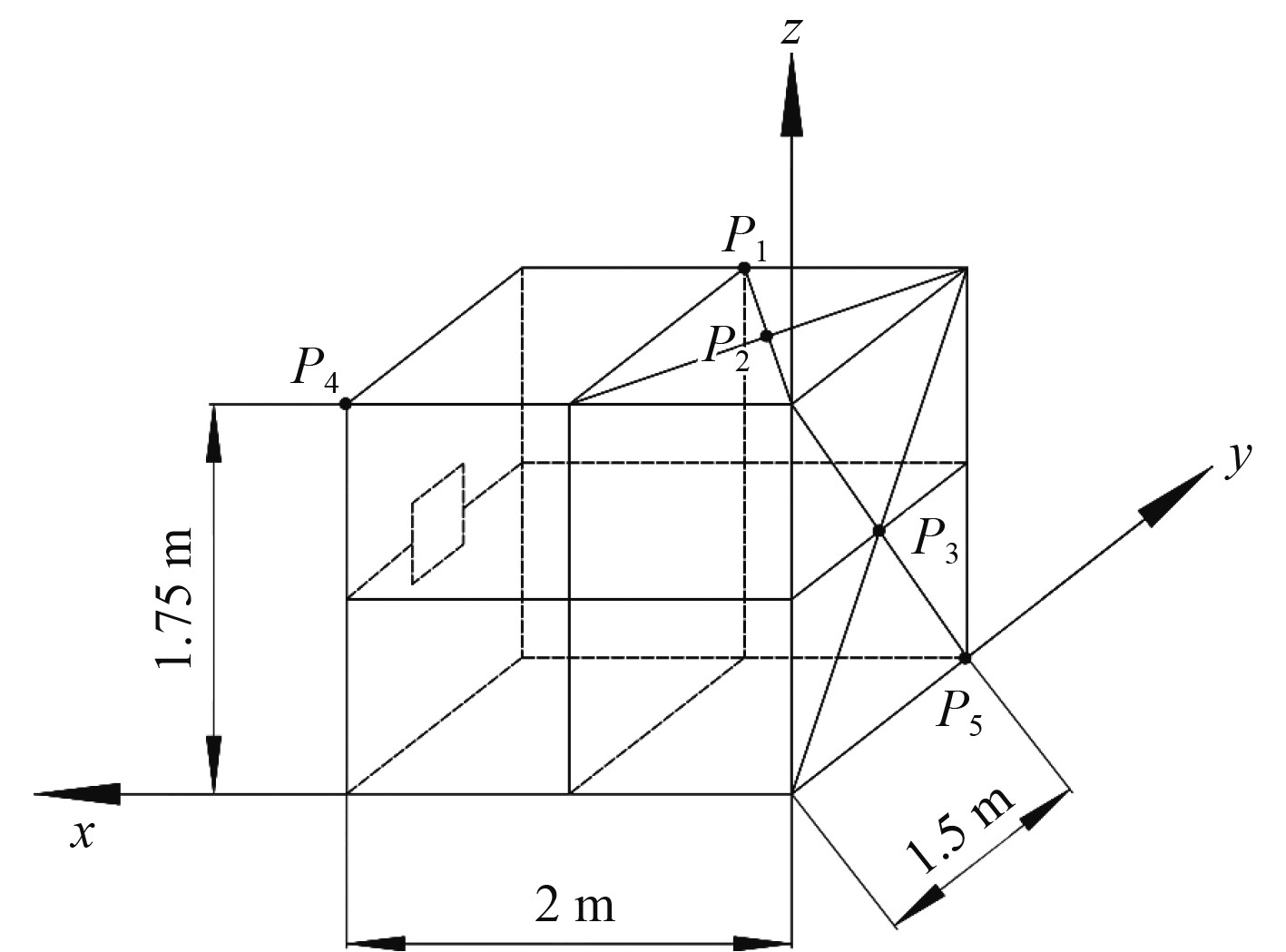
1.2 测点布置由于舱室内部壁面的反射作用使得密闭舱室内的冲击波变得复杂,不同特征点处呈现出不同的反射波形。为获得舱室内部不同位置的冲击波载荷特性,设置典型测点分别为正规反射测点、两壁面交汇角隅处反射冲击波测点和三壁面交汇角隅处反射冲击波测点。测点布置如图1所示,以舱室角隅处为原点建立直角坐标系,其中2号和3号为正规反射压力测点,1号为两壁面交汇角隅处压力测点,4号和5号为三壁面交汇角隅处压力测点。试验时,炸药位于模拟舱室中心,测点位置及爆距见表1。
|
图 1 测点设计图 Fig. 1 Design of measuring point |
|
|
表 1 测点位置 Tab.1 Measuring point location |
开展6种不同装药量试验,TNT当量分别为10 g、20 g、30 g、60 g、90 g和120 g。试验时使用8701炸药,密度为1.72 g/cm3,爆炸威力相当于1.5倍TNT当量,试验中8701炸药分别为6.7 g、13.3 g、20 g、40 g、60 g和80 g。
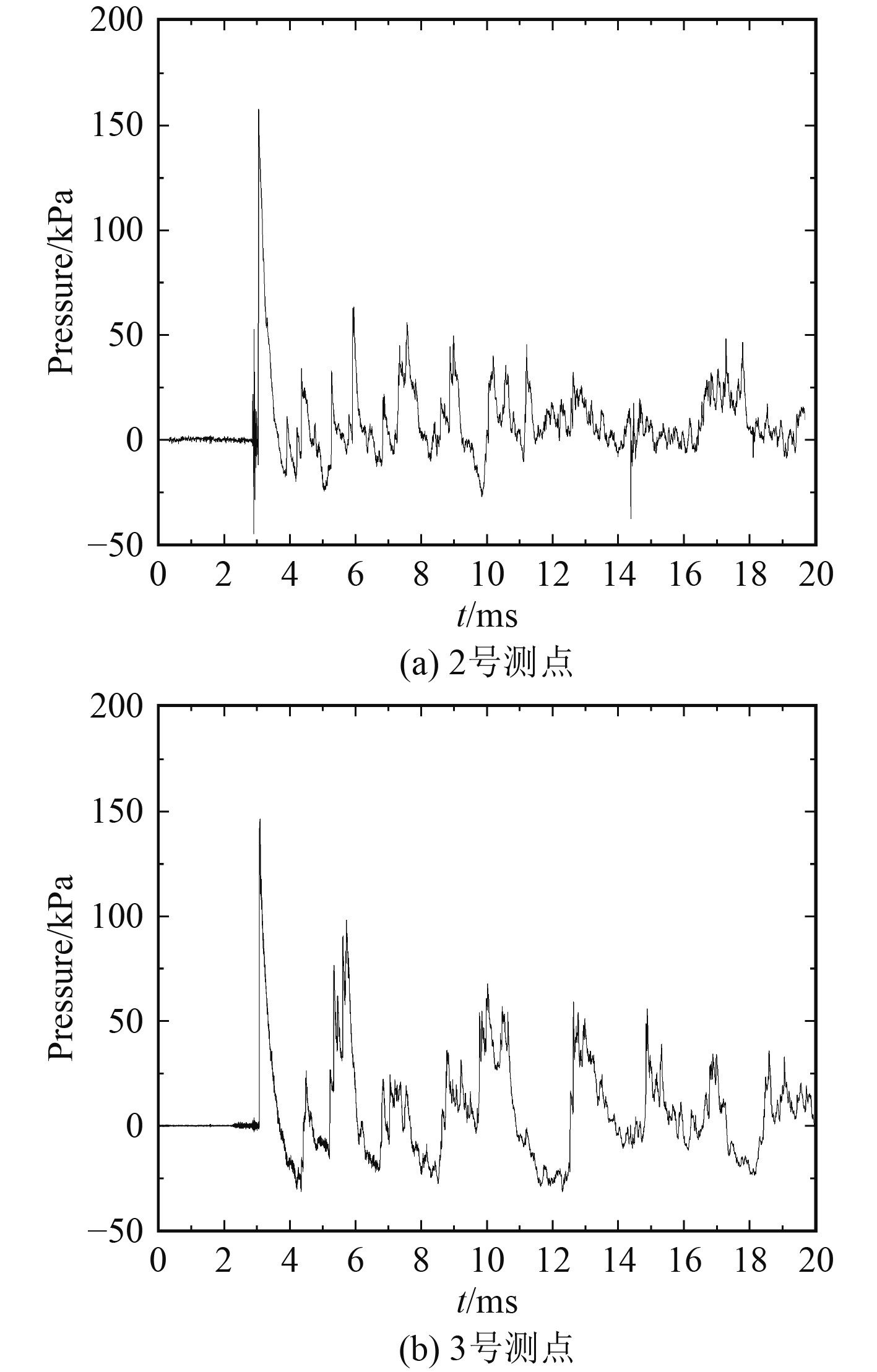
2 舱内爆炸压力载荷特性 2.1 单壁面反射超压图2为单壁面典型反射超压曲线,可看出,20 g TNT装药量下2号测点和3号测点都有一个较大的首峰峰值,且为最大峰值。2号测点和3号测点都发生正规反射。首次起跳压力是冲击波在舱室壁面上发生了正规反射所致,后续多峰现象是由于舱室其他壁面反射的冲击波分别作用于2号测点和3号测点所形成的。
|
图 2 单壁面典型反射超压曲线 Fig. 2 Typical reflection overpressure curves at the single wall |
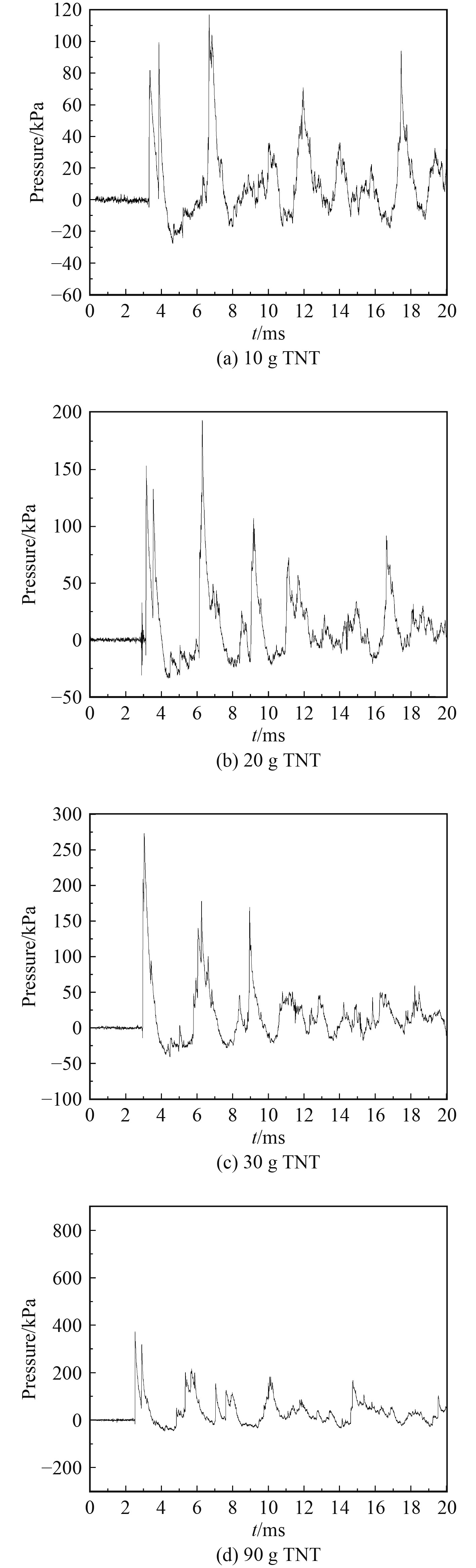
两壁面交汇角隅处典型反射超压曲线如图3所示。可看出,1号测点冲击波峰值压力首次起跳后还未衰减完毕时,会紧接着叠加一个和首峰峰值相当的冲击波,呈现出“双峰”结构,随后较长一段时间内还会出现多个峰值,且衰减比较缓慢。根据1号测点“双峰”超压时间差可判断“双峰”结构是冲击波在上壁面和侧壁面反射形成的,第1个峰值超压由上壁面反射冲击波引起,第2个峰值超压由侧壁面反射冲击波引起。随着装药量增加,冲击波初始能量越大,其传播速度也就越快,“双峰”结构时间间隔越小。
|
图 3 两壁面交汇角隅处典型反射超压曲线 Fig. 3 Typical reflection overpressure curves at the intersection of two walls |
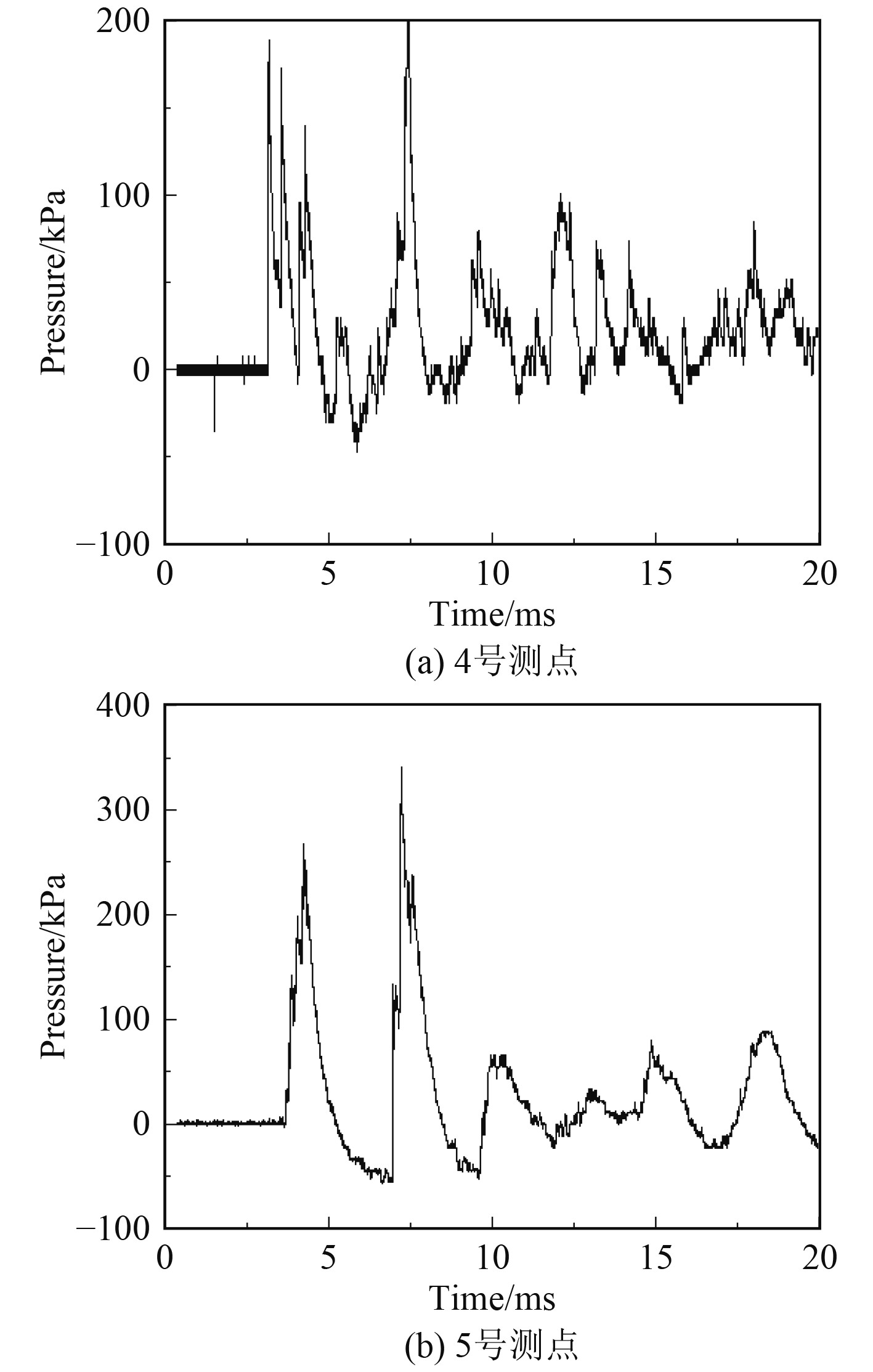
图4为三壁面交汇角隅处典型反射超压曲线。可看出,60 g TNT装药量下4号测点和5号测点呈现出明显的多峰现象,且接连出现多个峰值。由于三壁面交汇角隅处反射壁面较多,反射冲击波受到更多约束,因而4号测点和5号测点的峰值超压衰减都非常缓慢。4号测点的多个峰值中往往首峰是最大值,后续多峰是经过其他壁面多次反射所造成。5号测点相对于4号测点更加接近角隅处,5号测点超压峰值每次起跳都比上次起跳峰值要高。
|
图 4 三壁面交汇角隅处典型反射超压曲线 Fig. 4 Typical reflection overpressure curves at the intersection of three walls |
球状TNT在无限空气介质中,爆炸空气冲击波峰值超压经验公式为[10]:
| $\begin{split} \Delta {P}_{m}=&0.084\left(\frac{\sqrt[3]{W}}{r}\right)+0.27{\left(\frac{\sqrt[3]{W}}{r}\right)}^{2}+\\ &0.7{\left(\frac{\sqrt[3]{W}}{r}\right)}^{3}\text{,}1\leqslant \frac{r}{\sqrt[3]{W}}\leqslant 15。\end{split}$ | (1) |
式中:
空气冲击波在壁面正规反射后,峰值超压经验公式:
| $ \Delta {P_r} = 2\Delta {P_m} + \frac{{6\Delta P_m^2}}{{7 + \Delta {P_m}}} 。$ | (2) |
选取单壁面反射3号测点进行分析,其试验数据与理论计算结果见表2。
|
|
表 2 试验数据与理论计算结果3号测点 Tab.2 Experimental data and theoretical value |
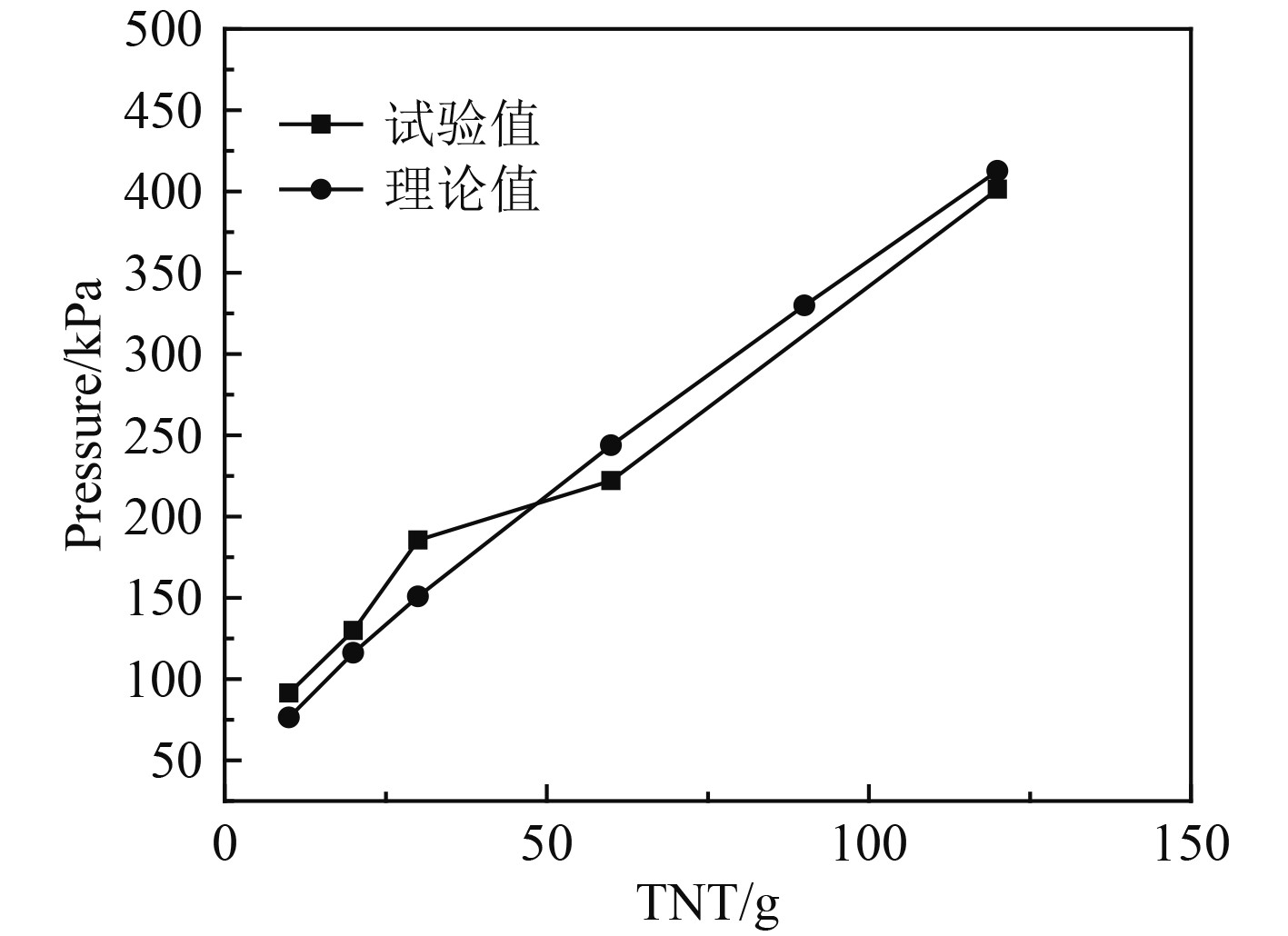
可看出,90gTNT装药量下实测峰值超压远大于120 g TNT装药量下实测峰值超压的2倍,判定为异常数据。图5为不同装药量下3号测点首峰峰值超压试验数据和理论计算结果对比,理论值与试验值相符较好,正规反射经验公式能有效计算舱内爆炸单壁面反射冲击波首峰峰值超压。
|
图 5 不同装药量下峰值超压试验值与理论值对比 Fig. 5 Comparison of experimental data and theoretical value under various charges |
当入射角超过一定角度时,入射波发生非正规反射,除了入射波和反射波以外,还会出现垂直于反射面的马赫波,这种非正规反射又被称为马赫反射,发生马赫反射时入射波的临界角称为马赫反射临界角[11]。马赫反射临界角不断减小,最后趋近极限值40°,当测点处于马赫反射区时,马赫反射超压经验公式为:
| $ \Delta {P_r} = \Delta {P_{mG}}\left( {1 + \cos {\phi _0}} \right)。$ | (3) |
式中,
| $ \Delta {P_{mG}} = 0.106\left( {\frac{{\sqrt[3]{W}}}{r}} \right) + 0.43{\left( {\frac{{\sqrt[3]{W}}}{r}} \right)^2} + 1.4{\left( {\frac{{\sqrt[3]{W}}}{r}} \right)^3} 。$ | (4) |
选取两壁面交汇角隅处1号测点进行分析,1号测点入射角为54°,当马赫反射临界角为54°时,
|
|
表 3 试验数据与理论计算结果 Tab.3 Experimental data and theoretical value |
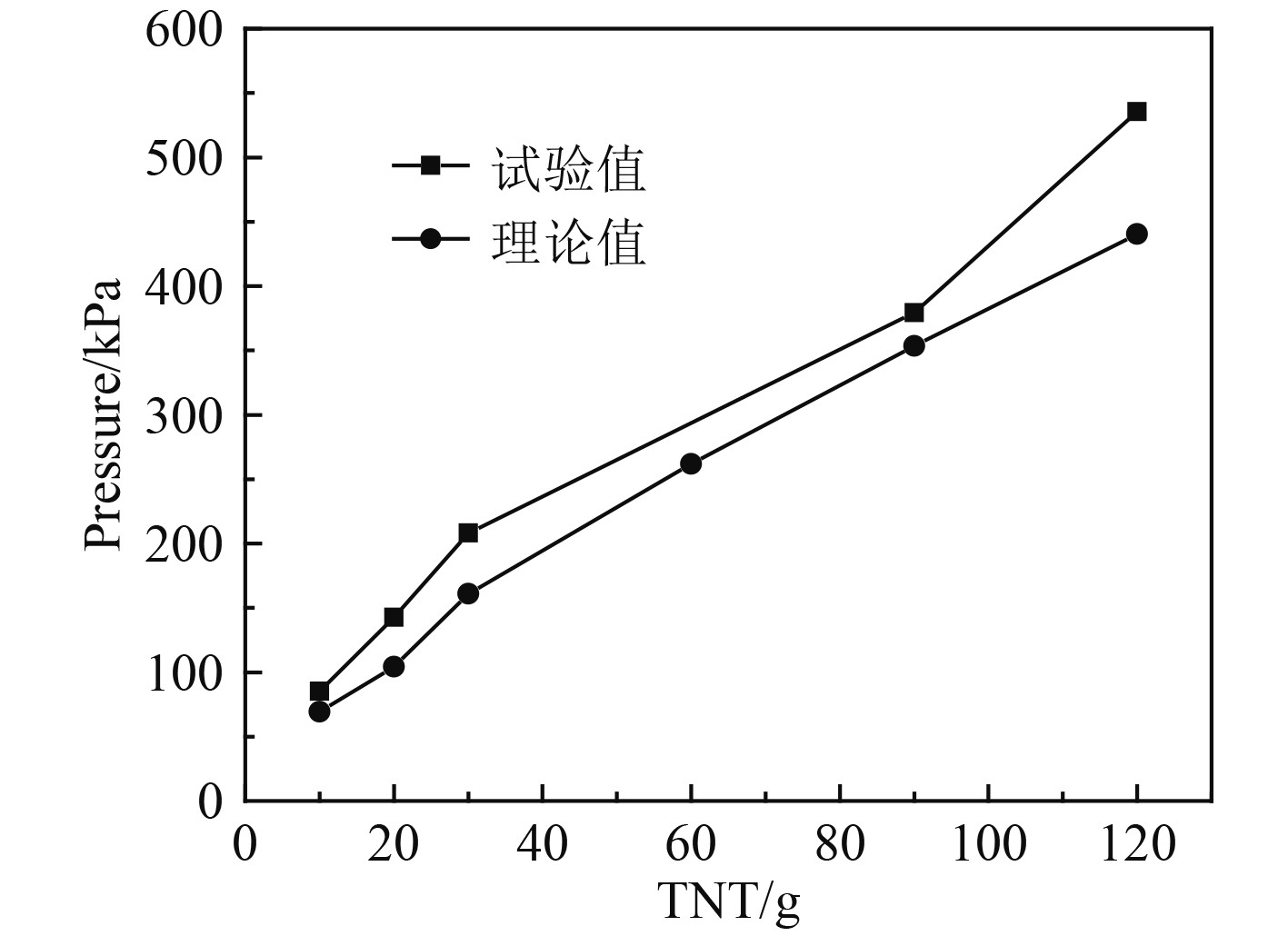
|
图 6 不同装药量下峰值超压试验值与理论值对比 Fig. 6 Comparison of experimental data and theoretical value under various charges |
利用正规反射和马赫反射对两壁面交汇角隅处反射冲击波首峰峰值超压进行计算。10 g和20 g按照正规反射计算,30 g以上装药量按照马赫反射计算,结果表明,试验值约为理论值的1.3倍左右,正规反射峰值超压
| $ \Delta {P_{r1}} = 1.3\left( {2\Delta {P_m} + \frac{{6\Delta P_m^2}}{{7 + \Delta {P_m}}}} \right) ,$ | (5) |
| $ \Delta {P_{r2}} = 1.3\left[ {\Delta {P_{mG}}\left( {1 + \cos {\phi _0}} \right)} \right]。$ | (6) |
选取三壁面交汇角隅处4号测点进行分析,4号测点入射角为47.4°,
|
|
表 4 试验数据与理论计算结果 Tab.4 Experimental data and theoretical value |
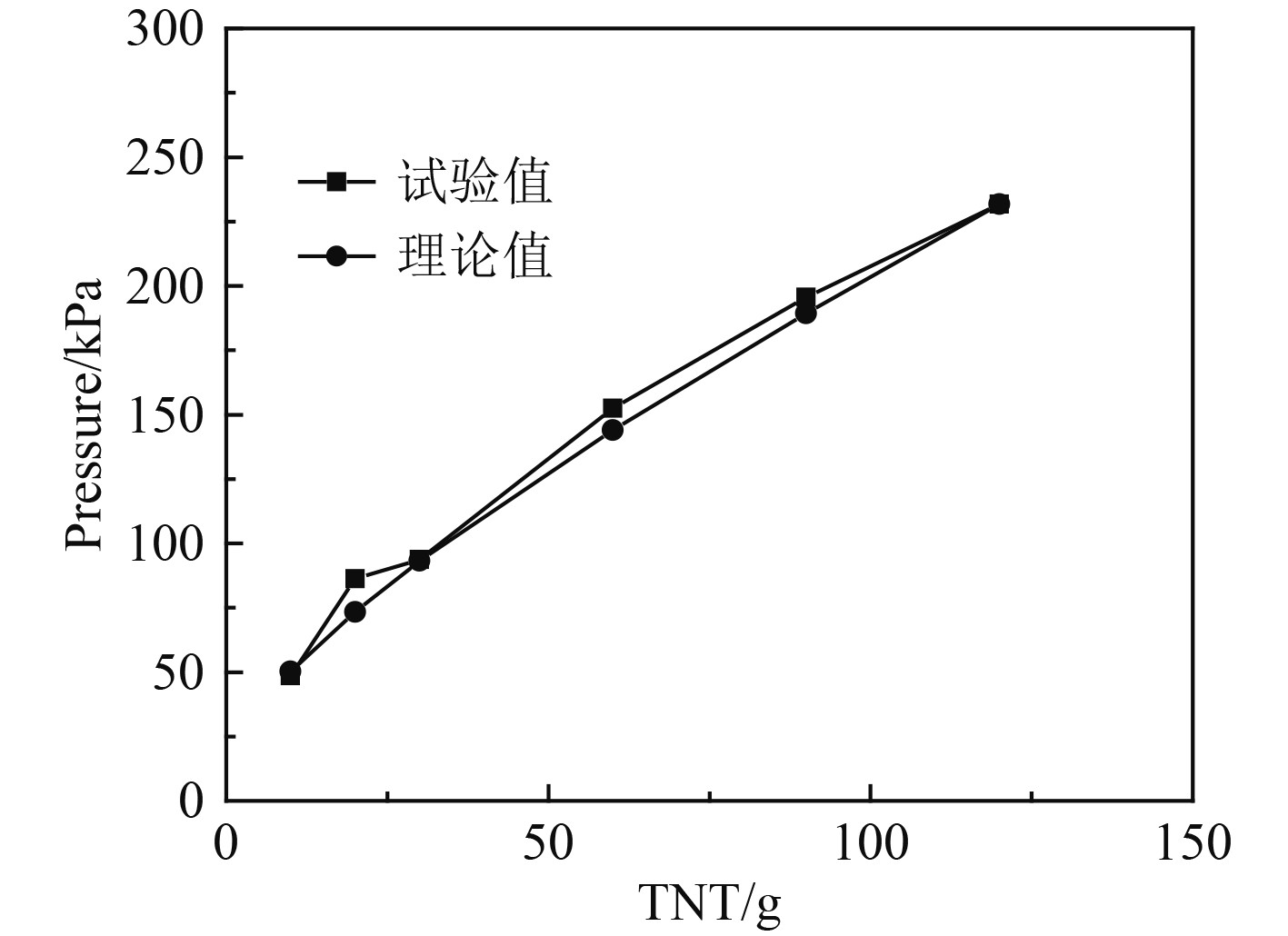
|
图 7 不同装药量下峰值超压试验值与理论值对比(4号测点) Fig. 7 Comparison of experimental data and theoretical value under various charges at No. 4 measuring point |
可看出,不同装药量下4号测点反射冲击波首峰峰值超压理论估算值和试验数据符合较好,装药量为60 g时误差最大为24.0%,装药量为120 g时误差不到0.05%,平均误差不超过10%。因此,正规反射经验公式能够计算三壁面交汇角隅处反射冲击波首峰峰值超压。
4 结 语1)单壁面测点压力载荷呈现明显多峰现象,首峰峰值最大,单壁面反射冲击波首峰峰值超压可采用正规反射经验公式进行计算。
2)两壁面交汇角隅处测点压力载荷呈现“双峰”结构,“双峰”结构时间间隔随装药量增加逐渐变小。若发生正规反射,反射冲击波首峰峰值超压为正规反射经验公式计算结果的1.3倍;若发生马赫反射,反射冲击波首峰峰值超压为马赫反射经验公式计算结果的1.3倍。
3)三壁面交汇角隅处测点压力载荷呈现明显多峰现象,且接连出现多个峰值,峰值超压衰减都非常缓慢。反射冲击波首峰峰值超压可采用正规反射经验公式进行计算。
| [1] |
姚迪, 罗刚, 谢伟, 等. 裸装药舱内爆炸压力载荷规律研究[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(1): 21-25. YAO Di, LUO Gang, XIE Wei, et al. Study on the law of explosive pressure load in bare charge cabin[J]. Journal of Wuhan University of Technology (Traffic Science and Engineering Edition), 2019, 43(1): 21-25. |
| [2] |
HU Y, WU C, LUKASZEWICZ M, et al. Characteristics of confined blast loading in unvented structures[J]. Protective Struct, 2011, 2(1): 21-43. DOI:10.1260/2041-4196.2.1.21 |
| [3] |
张磊, 杜志鹏, 高鹏, 等. 水面舰艇舱内爆炸毁伤载荷研究进展[J]. 中国科学:物理学 力学 天文学, 2021, 51(12): 1-11. ZHANG Lei, DU Zhipeng, GAO eng, et al. Research progress on damage load of surface ship cabin explosion[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2021, 51(12): 1-11. |
| [4] |
徐景林, 顾文彬, 刘建青, 等. 圆柱形爆炸容器内爆炸载荷的分布规律[J]. 振动与冲击, 2020, 39(18): 276-282. XU Jinglin, GU Wenbin, LIU Jianqing, et al. Distribution law of explosion load in cylindrical explosion vessel[J]. Journal of Vibration and Shock, 2020, 39(18): 276-282. DOI:10.13465/j.cnki.jvs.2020.18.038 |
| [5] |
王震, 胡可, 赵阳. 拱顶钢储罐内部蒸气云爆炸冲击荷载的数值模拟[J]. 振动与冲击, 2013, 32(20): 35-40. WANG Zhen, HU Ke, ZHAO Yang. Numerical simulation for internal vapor cloud explosion loading in dome-roof steel tanks[J]. Journal of Vibration and Shock, 2013, 32(20): 35-40. DOI:10.3969/j.issn.1000-3835.2013.20.008 |
| [6] |
庞崇安, 王震. 立式柱形钢储罐内部爆炸数值模拟及动力响应分析[J]. 爆破, 2015, 32(2): 54–58. PANG Chongan, WANG Zhen. Numerical simulation and dynamic response analysis of internal explosion in vertical columnar steel storage tank[J]. Blasting, 2015, 32(2): 54–58. |
| [7] |
FAN Yang, LI He, XIAO Liu, et al. Numerical simulation of explosion in a confined box-shaped structure[J]. Advanced Materials Research, 2013: 3204–3207.
|
| [8] |
朱建方, 王伟力, 曾亮. 舰艇舱室内爆毁伤的建模与仿真分析[J]. 系统仿真学报, 2009, 21(22): 7066-7072. ZHU Jianfang, WANG Weili, ZENG Liang. Modeling and simulation analysis of ship cabin implosion damage[J]. Journal of System Simulation, 2009, 21(22): 7066-7072. DOI:10.16182/j.cnki.joss.2009.22.049 |
| [9] |
李伟, 朱锡, 梅志远, 等. 战斗部舱内爆炸对舱室结构毁伤的实验研究[J]. 舰船科学技术, 2009, 31(3): 34-37. LI Wei, ZHU Xi, MEI Zhiyuan, et al. Robust watermarking of vector digital maps[J]. Ship Science and Technology, 2009, 31(3): 34-37. DOI:10.3404/j.issn.1672-7649.2009.03.005 |
| [10] |
侯海量, 朱锡, 李伟, 等. 舱内爆炸冲击载荷特性实验研究[J]. 船舶力学, 2010, 14(8): 901–907. HOU Hailiang, ZHU Xi, LI Wei, et al. Experimental study on impact load characteristics of explosion in cabinv [J]. Chinese Journal of Ship Research, 2010, 14(8): 901–907. |
| [11] |
黄寅生. 炸药理论[M]. 北京: 北京理工大学出版社, 2016: 257−258.
|
| [12] |
张国伟. 爆炸作用原理[M]. 北京: 国防工业出版社, 2006: 71−74.
|
 2023, Vol. 45
2023, Vol. 45
