2. 江南造船(集团)有限责任公司,上海 201913
2. Jiangnan Shipyard(Group) Co., Ltd., Shanghai 201913, China
目前,大多数反舰导弹携带的是半穿甲战斗部。半穿甲战斗部在打击舰船目标时,弹体基于其自身强度和动能侵彻船体防护板,从而达到毁伤船体内部设备的目标。
基于有限元仿真软件Ansys中的显示动力学模块,研究半穿甲战斗部打击舰船目标的侵彻深度。在此之前对有限元软件进行仿真的有效性验证,然后导入相关具体模型进行分析计算,研究弹体在不同初速度及不同攻角情况下对舰船的毁伤情况。在侵彻过程中,弹体会发生严重变形,出现早炸的情况导致武器失效,因此也同时研究分析了弹体侵彻过程中的安定性是否满足要求。
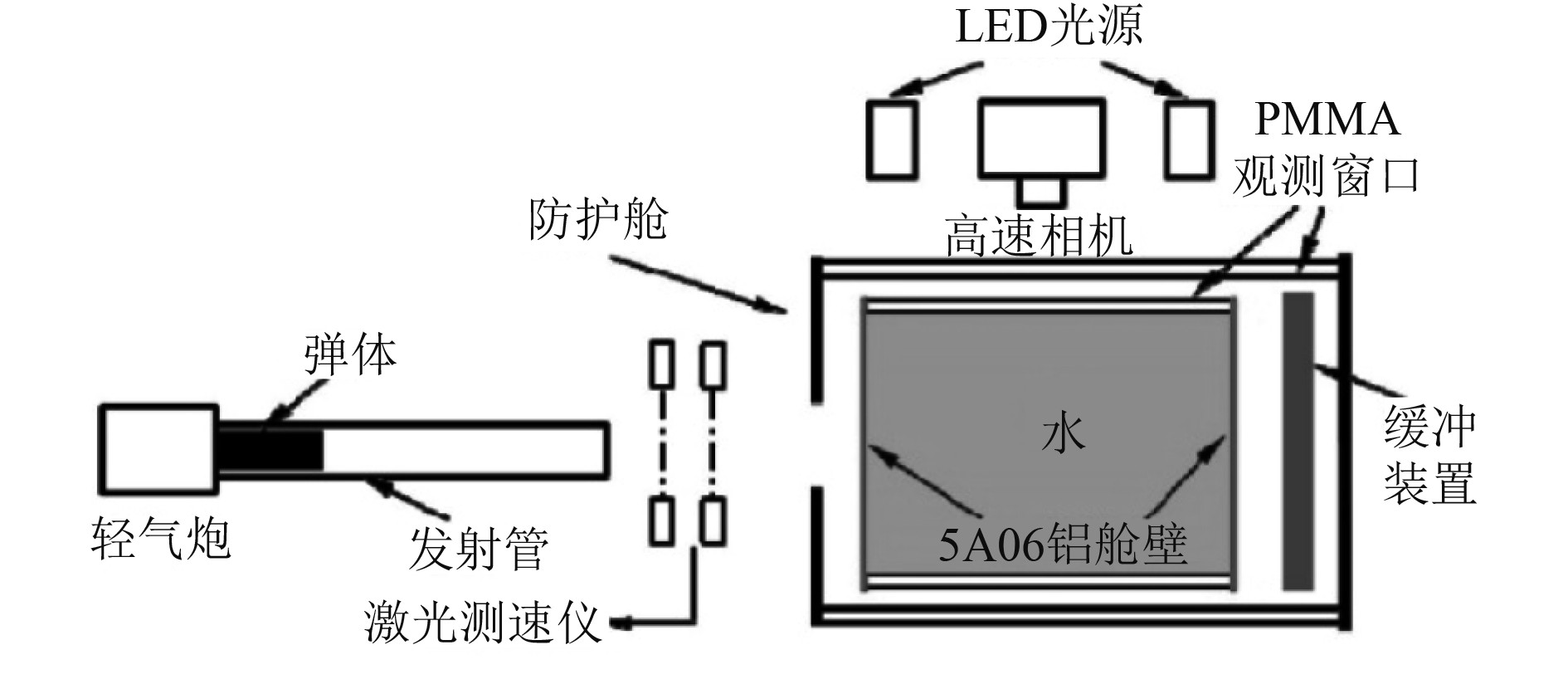
1 弹体侵彻液舱的有限元仿真有效性验证 1.1 几何模型基于Ansys有限元软件对舰船模型进行分析。首先,依照参考文献[1]中的试验数据从多个角度来验证有限元仿真的有效性。图1为该试验装置示意图,根据试验的具体结构,将几何模型简化为弹体、前靶板、流体区域和后靶板。几何模型的具体尺寸按照文献中试验模型的尺寸设置,前后靶板采用250 mm×180 mm×1.5 mm的5A06铝合金材料;弹体采用平头弹的形式,材料为直径为16 mm的45#钢材;流体区域体积为300 mm×180 mm×250 mm。
|
图 1 侵彻试验装置示意图 Fig. 1 Schematic diagram of the apparatus for the penetration test |
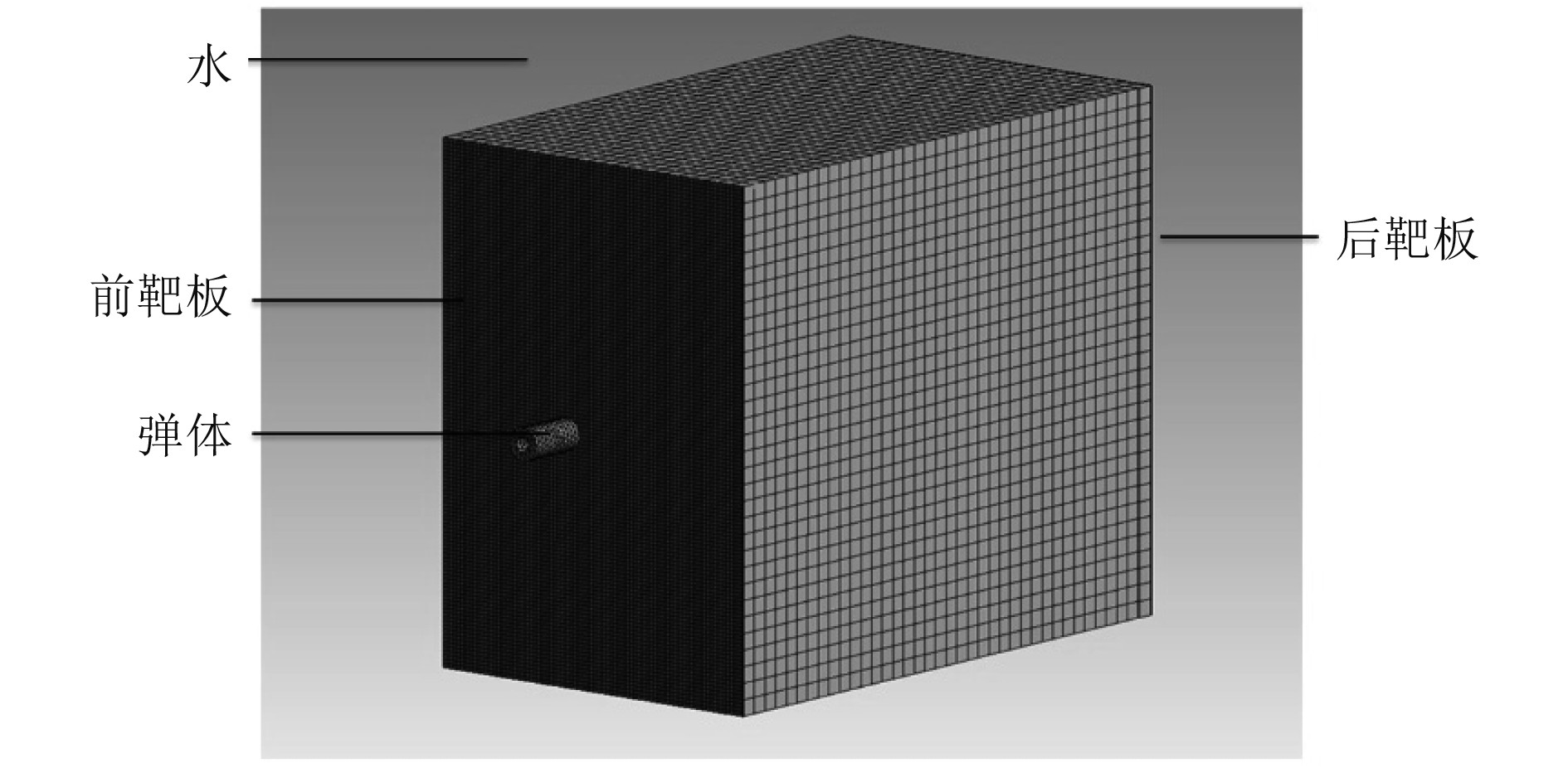
网格划分方面根据不同几何体的体积尺寸,采用不同的网格尺寸。弹体采用3 mm的四面体网格;由于要观察前后靶板的破损情况,因此将前后靶板的尺寸设置为2 mm;流体区域体积较大,设置为8 mm网格。弹体和前后靶板设置为拉格朗日网格。为保证流体区域的流动性,将流体区域设置为欧拉网格。具体模型如图2所示。
|
图 2 液舱的有限元模型 Fig. 2 Finite element modeling of liquid tank |
弹体和靶板采用Johnson-Cook本构模型。Johnson-Cook本构模型实质上将温度、应变和应变率这个3变量进行分开考虑,然后基于乘积关系将三者对动态屈服应力的影响建立联系。其本构关系可表示为[2]:
| $ {\sigma _Y} = \left( {A + B{{\mathop {\bar \varepsilon }\nolimits_p }^n}} \right)\left( {1 + C\ln {{\dot \varepsilon }^ * }} \right)\left( {1 - {T^ * }^m} \right)。$ | (1) |
式中:A、B、n、C、m分别为初始屈服应力常数、硬化模量、硬化指数、应变率相关系数和温度相关系数;
失效模型同样采用Johnson-Cook失效模型。当损伤度达到临界值时,应力和压力取为零值。单元的损伤度D定义为:
| $ D=\sum \frac{\Delta \varepsilon_{p}}{\varepsilon^{f}}。$ | (2) |
式中,D的取值在0~1之间,D=0为初始未损伤,当D=1时,材料发生失效。
| $ \varepsilon^{f} = \left[D_{1} + D_{2} + \exp \left(D_{3} \sigma^{*}\right)\right]\left[1 + D_{4} \ln \dot{\varepsilon}^{*}\right]\left[1 + D_{5} T^{*}\right]。$ | (3) |
式中,
|
|
表 1 固体材料参数表 Tab.1 Parameter table for solid material |
|
|
表 2 流体材料参数表 Tab.2 Parameter table for fluid materials |
1)空泡效应对比
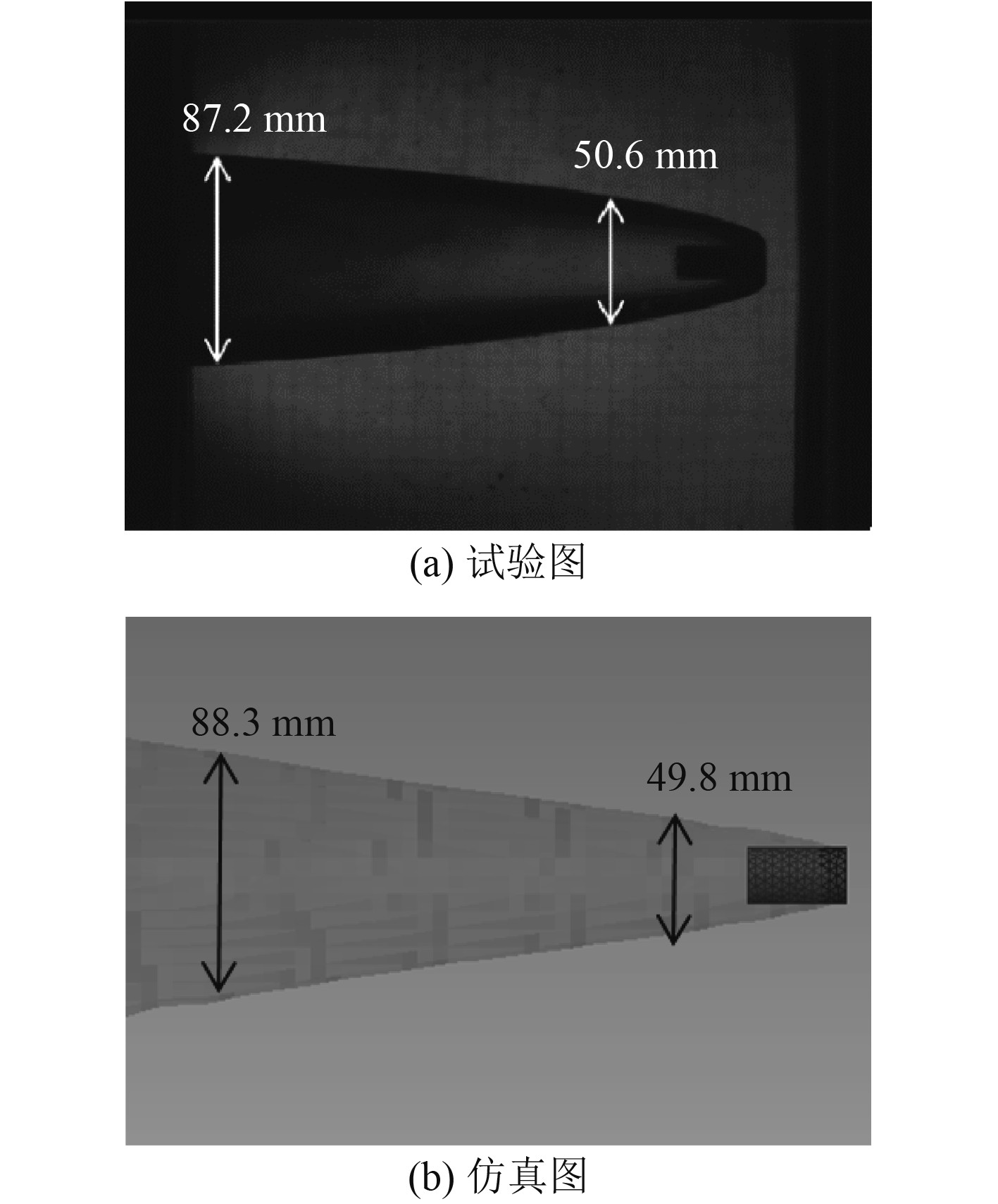
根据试验要求,将平头弹的速度设置为178.61 m/s。随着时间的增加,弹体的侵彻深度逐渐增加,同时空泡的直径也逐渐增加,如图3(b)所示。通过对比箭头标记位置的直径发现,试验和仿真产生的空泡大小基本吻合。
|
图 3 空泡试验与仿真对比图 Fig. 3 Comparison plot for air bubble test and simulation |
2)靶板破坏形态对比
以178.61 m/s的平头弹为例,通过对比前靶板的破坏形态来验证仿真结果的有效性。图4为试验和仿真所产生的弹孔对比图,在破坏机理和直径上基本吻合。

|
图 4 靶板的破坏形态对比图 Fig. 4 Comparison of the diagram pattern of the target plate |
3)水中弹体速度对比
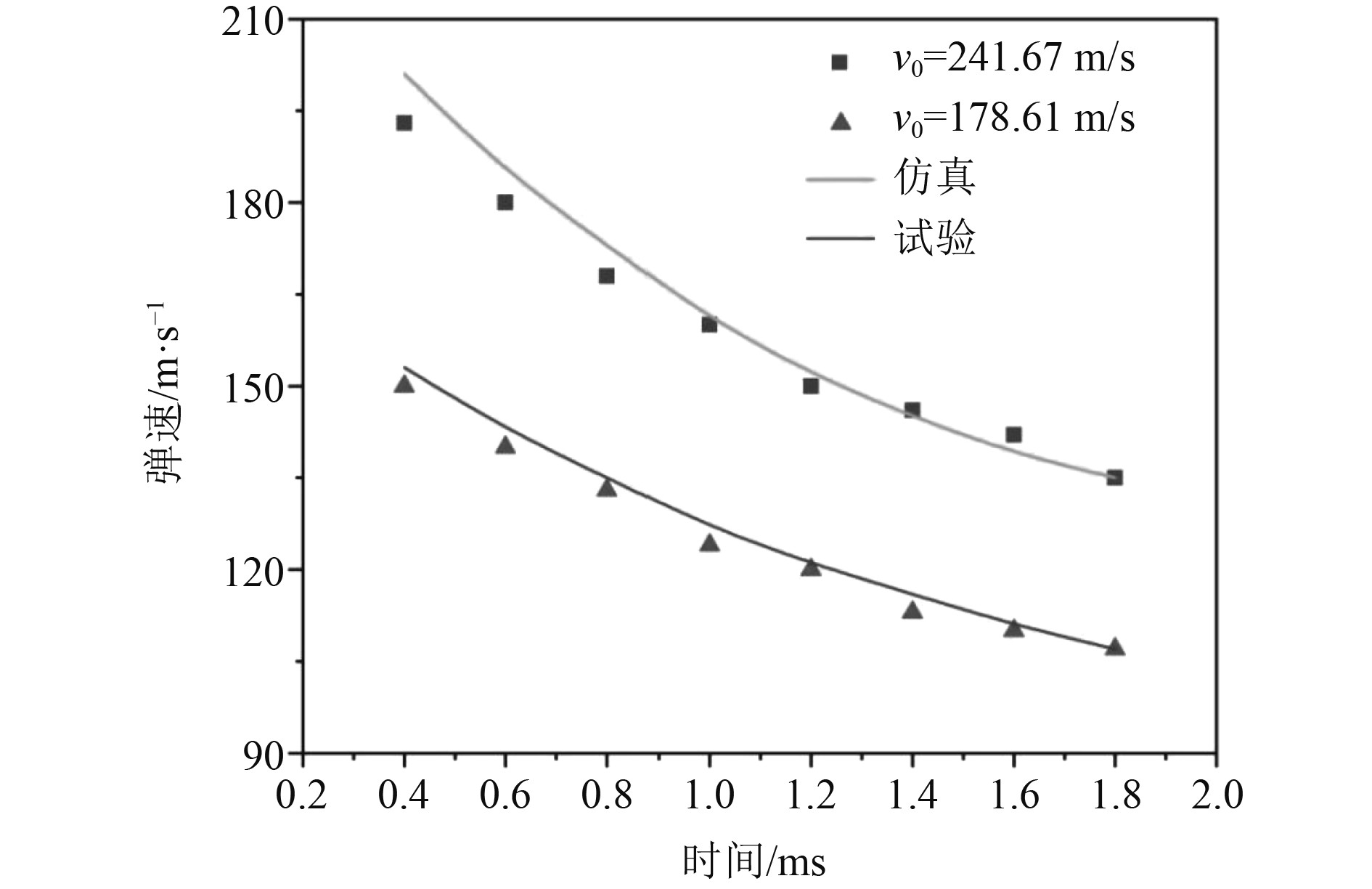
根据试验要求分别将仿真计算的弹体速度设为178.61 m/s和241.67 m/s,得到如图5所示的计算结果。通过图像可看出,弹体的初速度越高,其在水中的速度衰减也越大。整体误差在合理范围内,也进一步说明了显示动力学仿真的可靠性和有效性。
|
图 5 剩余速度仿真与试验对比图 Fig. 5 Comparison plot of simnlation and test for residual velocity |
1)半穿甲战斗部
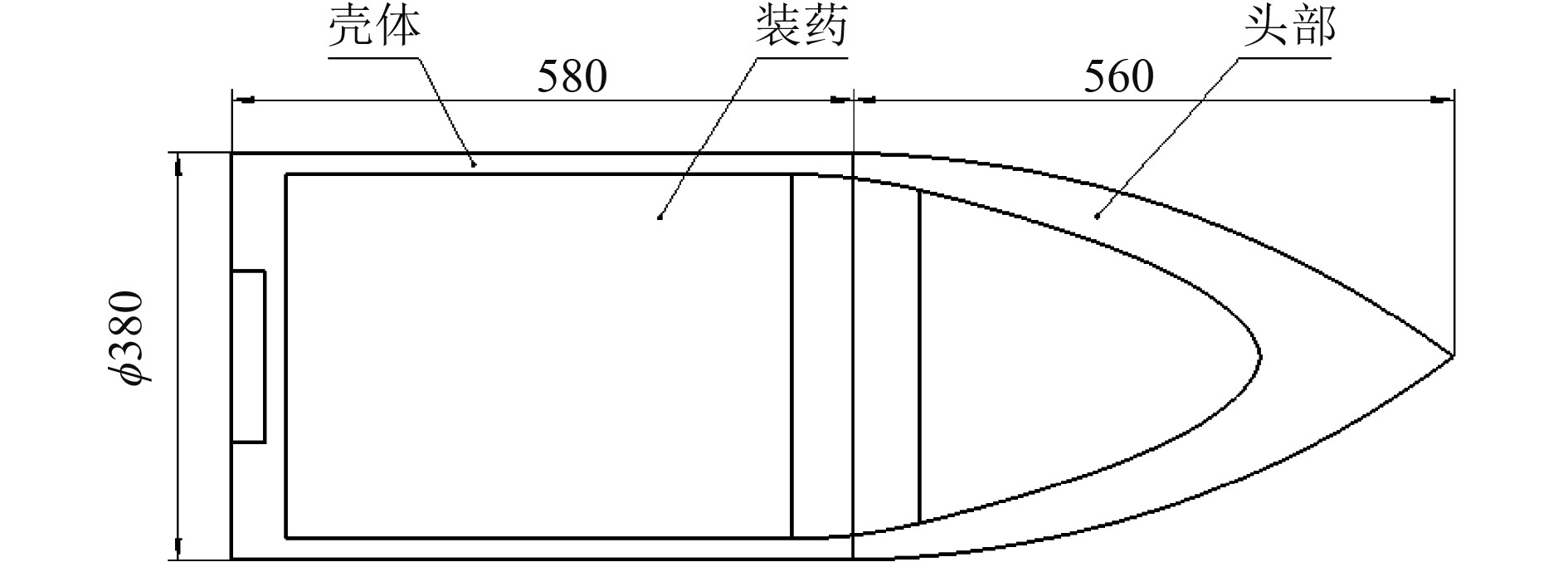
以典型的半穿甲尖卵型战斗部为研究对象。该型战斗部的壳体材料为45#钢,总长度1140 mm,壳体头部长度560 mm,圆柱筒体580 mm,直径380 mm。内装有105 kg的TNT炸药,战斗部总质量为375 kg。图6为该典型战斗部的结构示意图。
|
图 6 典型半穿甲战斗部的结构简图 Fig. 6 Structural sketch of a typical semi-armor-piercing combat eleent |
2)液舱结构
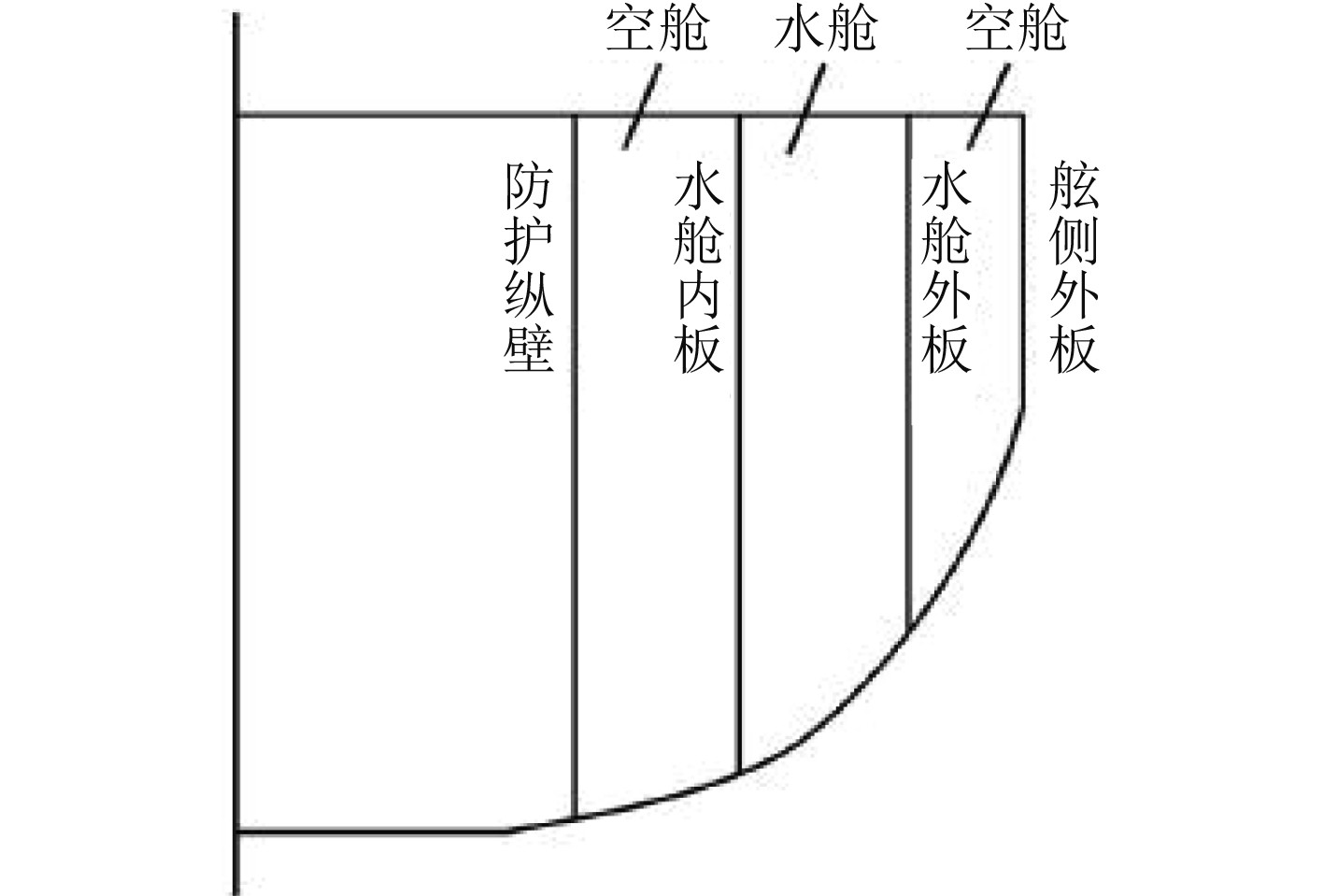
舰船作为军用船舶,在舷侧设有一定厚度的防护液舱。一般防护液舱由4层靶板构成,分别为舷侧外板、水舱外板、水舱内板和防护纵壁。具体结构如图7所示[4]。
|
图 7 舰船舷侧防护液舱示意图 Fig. 7 Schematic diagram of the ship's side protective liquid tanks |
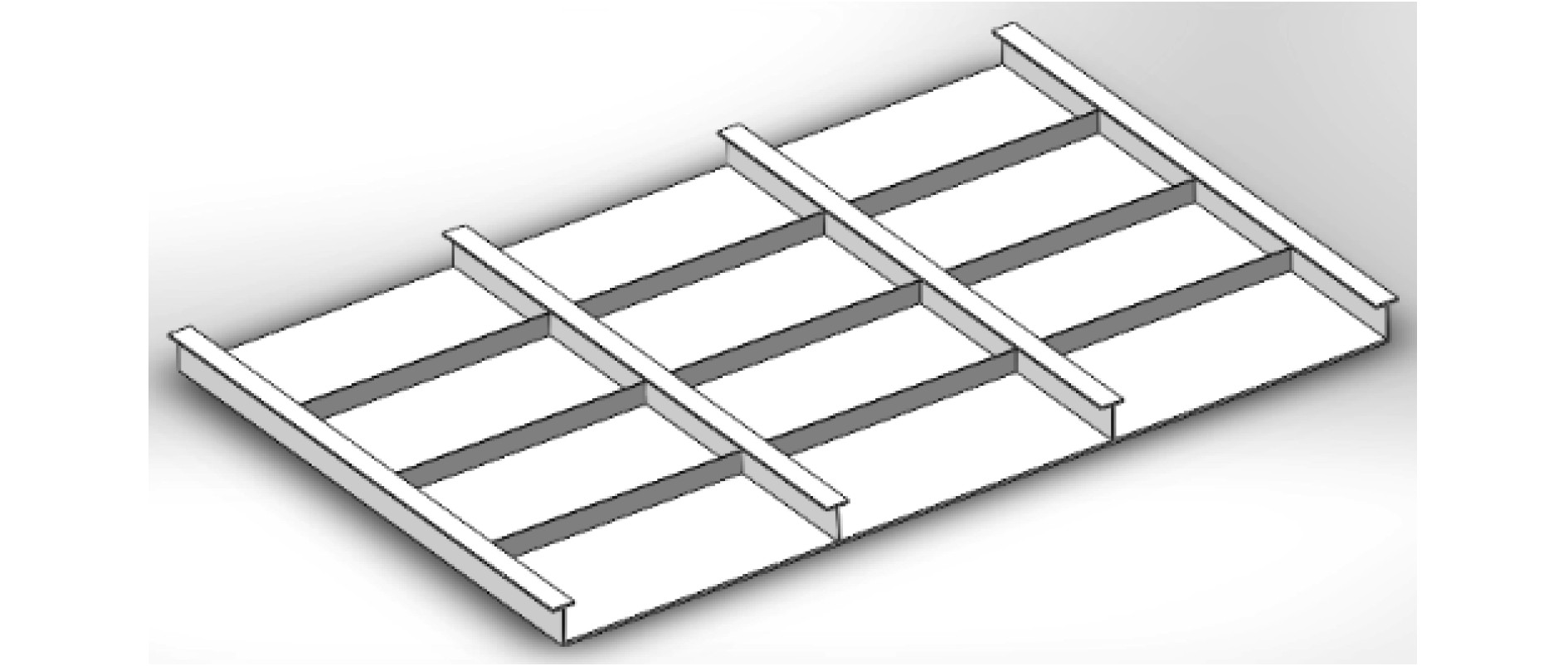
一般的船用钢板按结构可分为均质板和加筋板,舰船的液舱靶板皆采用加强筋板架结构,其面板厚度25 mm,全长6000 mm,宽4000 mm,面板宽160 mm,厚16 mm,腹板高240 mm,小筋腹板高180 mm,厚8 mm。具体模型如图8所示。
|
图 8 加强筋板架结构模型图 Fig. 8 Structural model diagram of reinforced rib plate frame |
将采用厚度等效法将加筋板等效为均质板,为后续的仿真实验做准备。厚度等效法是将靶板上的T型钢和L型钢等结构,按照强度或质量等效原则等效到靶板的厚度上,从而将加筋板转化为均质板来研究。
设平面靶板与靶板上的加强筋为相同材质,因此它们的密度相等。加强筋的体积为:
| $ V_{J}=S_{H} h_{H}+S_{G} h_{G}。$ | (4) |
式中,
加强筋的等效厚度为:
| $ H_{J}=\frac{V_{J}}{S_{B}} 。$ | (5) |
式中,
最终,加强筋板等效为均质靶板的厚度为:
| $ H=H_{B}+H_{J} 。$ | (6) |
式中,
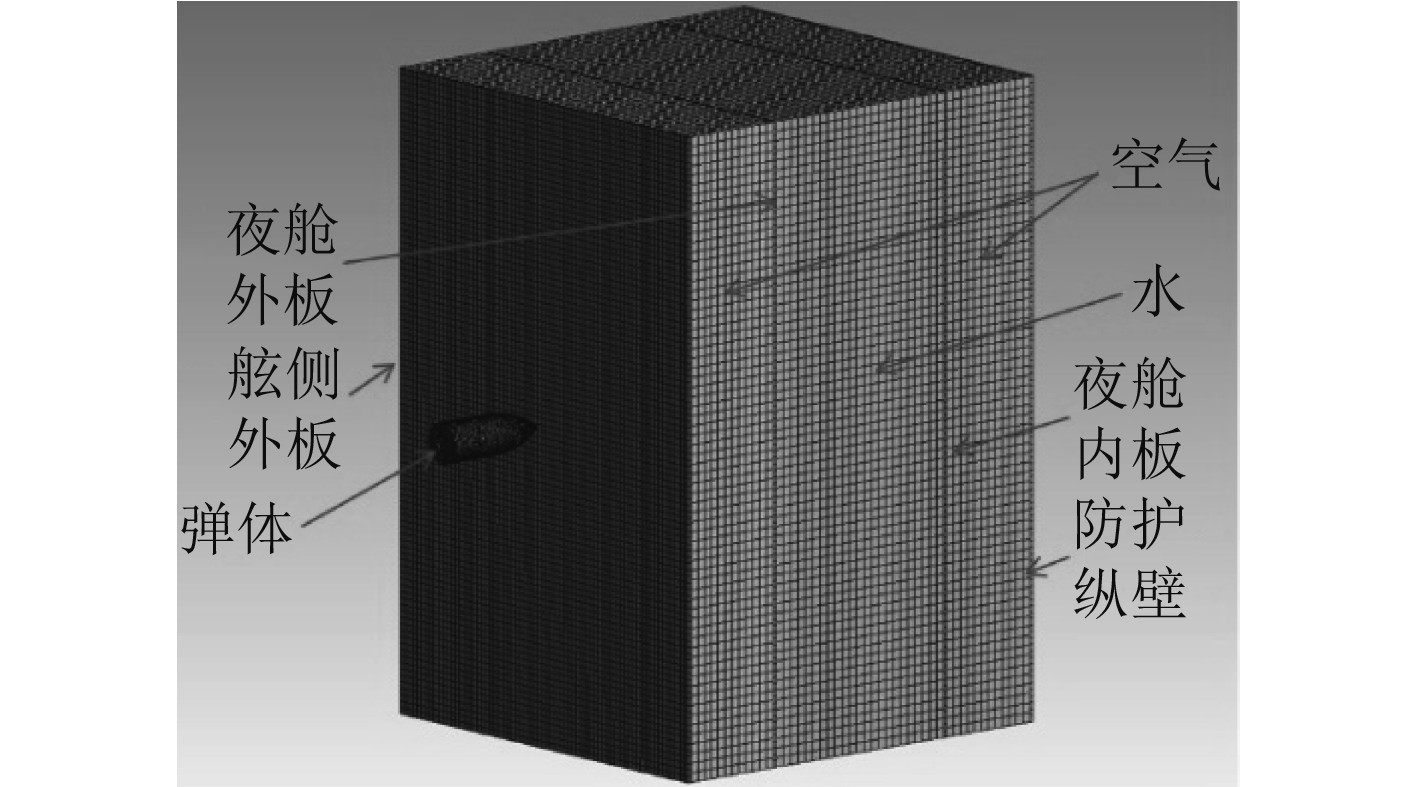
根据上述理论,该典型舰船的防护液舱靶板的厚度约为30 mm,包括半穿甲战斗部及靶板的其他尺寸均按原尺寸建立有限元模型。弹体和靶板分别设置为30 mm的四面体网格和六面体网格。同时设置为拉格朗日网格;液体区域设置为60 mm的四面体网格,同时设置为欧拉网格。每块靶板的4个侧面设置固定约束,并对欧拉域进行体积控制。具体有限元模型如图9所示。
|
图 9 船体舷侧防护液舱有限元模型图 Fig. 9 Finite element model of hull's outboard protection tank |
弹体和靶板同样采用J-C本构方程,水和空气将分别采用Shock EOS Linear和Ideal Gas EOS状态方程,相关材料参数如表3和表4所示[5-8]:
|
|
表 3 固体材料参数表 Tab.3 Parameter table of solid materials |
|
|
表 4 流体材料参数表 Tab.4 Parameter table of fluid materials |
图10为不同初速度下弹体在30 ms后的侵彻深度。首先,由于战斗部为尖卵型战斗部,所以靶板的破口为花瓣型破口。其次,战斗部在侵彻液舱时,产生了很明显的空泡现象,在不同初速度下,战斗部的侵彻深度存在明显差异。当初速度为300 m/s时,战斗部在30 ms后只能侵彻到液舱内部便不能继续侵彻;当初速度为400 m/s时,战斗部可击穿液舱,但剩余动能无法侵彻防护纵壁;当初速度为500 m/s时,战斗部刚好可侵彻整个舷侧结构;当初速度设为600 m/s时,战斗部可完全侵彻到舷侧结构,并还有一定的剩余速度。因此可得出结论,当弹体和目标结构确定的条件下,弹体初速度越高,侵彻深度和剩余速度越大。

|
图 10 不同初速度下的侵彻深度 Fig. 10 Depth of penetration at different initial velocities |
图11为不同初速度下弹体剩余速度的时历曲线,可以看出,随着计算时间的推移,弹体的剩余速度呈阶梯式下降,这是由于弹体在侵彻4层靶板时,每侵彻一层,弹体的剩余速度都会陡然下降。从不同的弹体初速度角度分析,初速度越高,弹体的剩余速度也越高。而初速度为300 m/s和400 m/s时,由于弹体没有足够多的动能,因此最终它们未能击穿液舱靶板,其剩余速度皆小于0。当弹体的初速度为300 m/s时,由于30 ms的时间弹体没有穿透靶板,并且剩余速度仍大于0,因此将计算时间延长到40 ms,直到弹体的击穿靶板或弹体速度小于0。
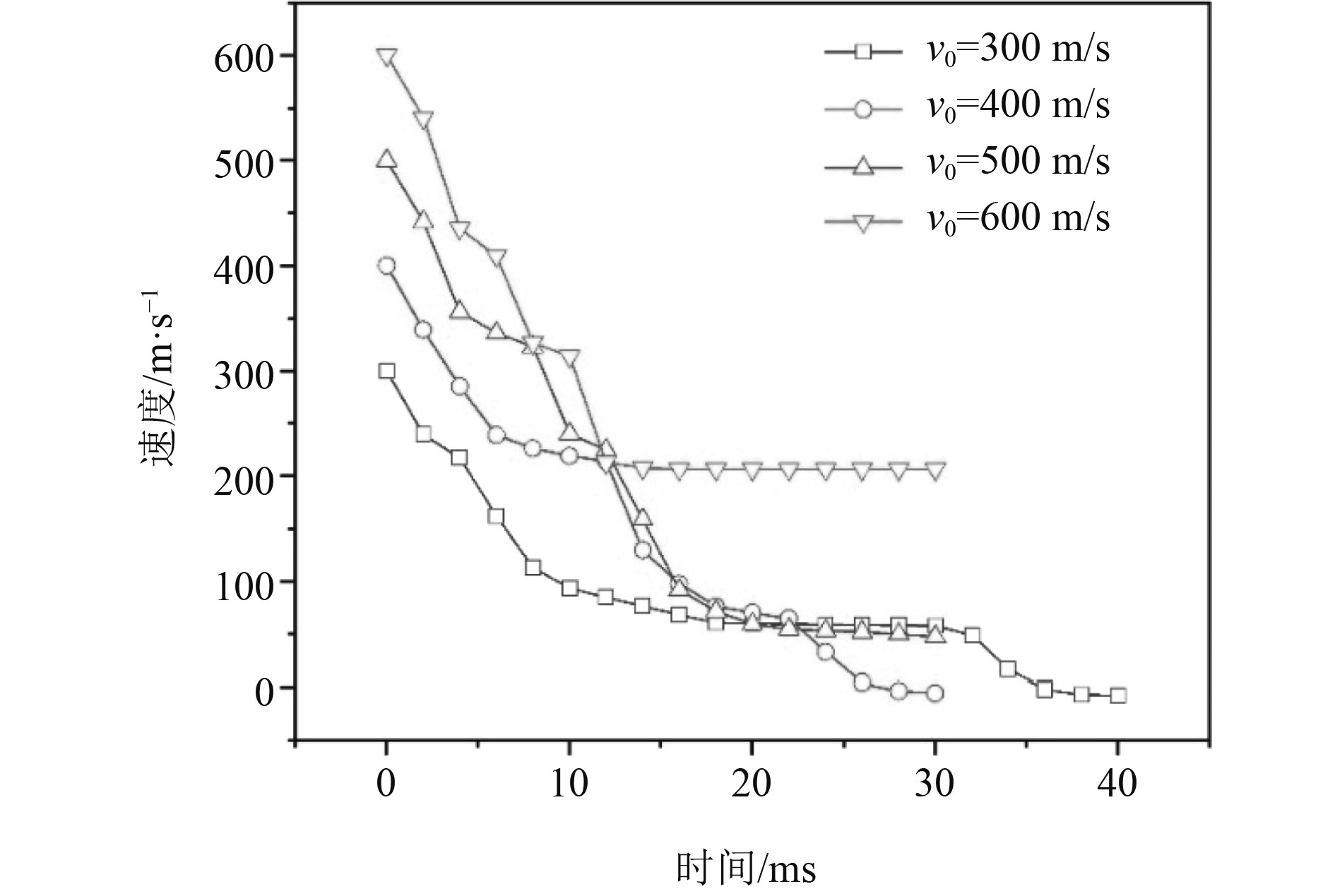
|
图 11 不同初速度下弹体剩余速度的时历曲线 Fig. 11 Time history curves of the residual velocity of the projectile at different initial velocities |
从不同初速度的时历曲线可以看出,弹体的初速度越高,最终的剩余速度也越高,当弹体的初速度呈线性变化时,弹体的最终剩余速度并不呈现线性变化。若想获得在一定区间内任意初速度所对应的剩余速度,只通过有限元仿真获得,工作量巨大很难实现。因此,在计算每个初速度所对应的剩余速度时,可采用近似拟合的方法计算。通过仿真实验获得较多的数据,然后将结果拟合成函数曲线求得在一定区间范围内任意初速度所对应的剩余速度,从而根据剩余速度判断出弹体能否击穿舷侧液舱靶板结构。
2.3 不同攻角下的侵彻深度分析弹体在打击舰船目标时,由于弹体飞行姿态的调整或者舰船目标的运动,弹体的速度方向不会总是与靶板的法线方向平行,速度方向和靶板的法线方向会形成一个夹角。讨论在相同初速度条件下,不同攻角下弹体的侵彻深度及剩余速度。
图12为初速度为500 m/s时,30 ms后弹体的侵彻深度。可知,随着攻角的增加,弹体的侵彻深度越来越小。为了进一步确定侵彻深度,同样以剩余速度作为弹体能否击穿靶板的判断依据。

|
图 12 不同攻角下的侵彻深度 Fig. 12 Depth of penetration at different argles of attack |
图13为相同初速度条件下,不同攻角的剩余速度时历曲线。可知,初速度相等的条件下,前15 ms的速度下降趋势变化不大。在15~30 ms时的速度变化存在明显差异,随着攻角的线性增加,弹体的剩余速度逐渐减小,剩余速度减小量呈非线性变化。
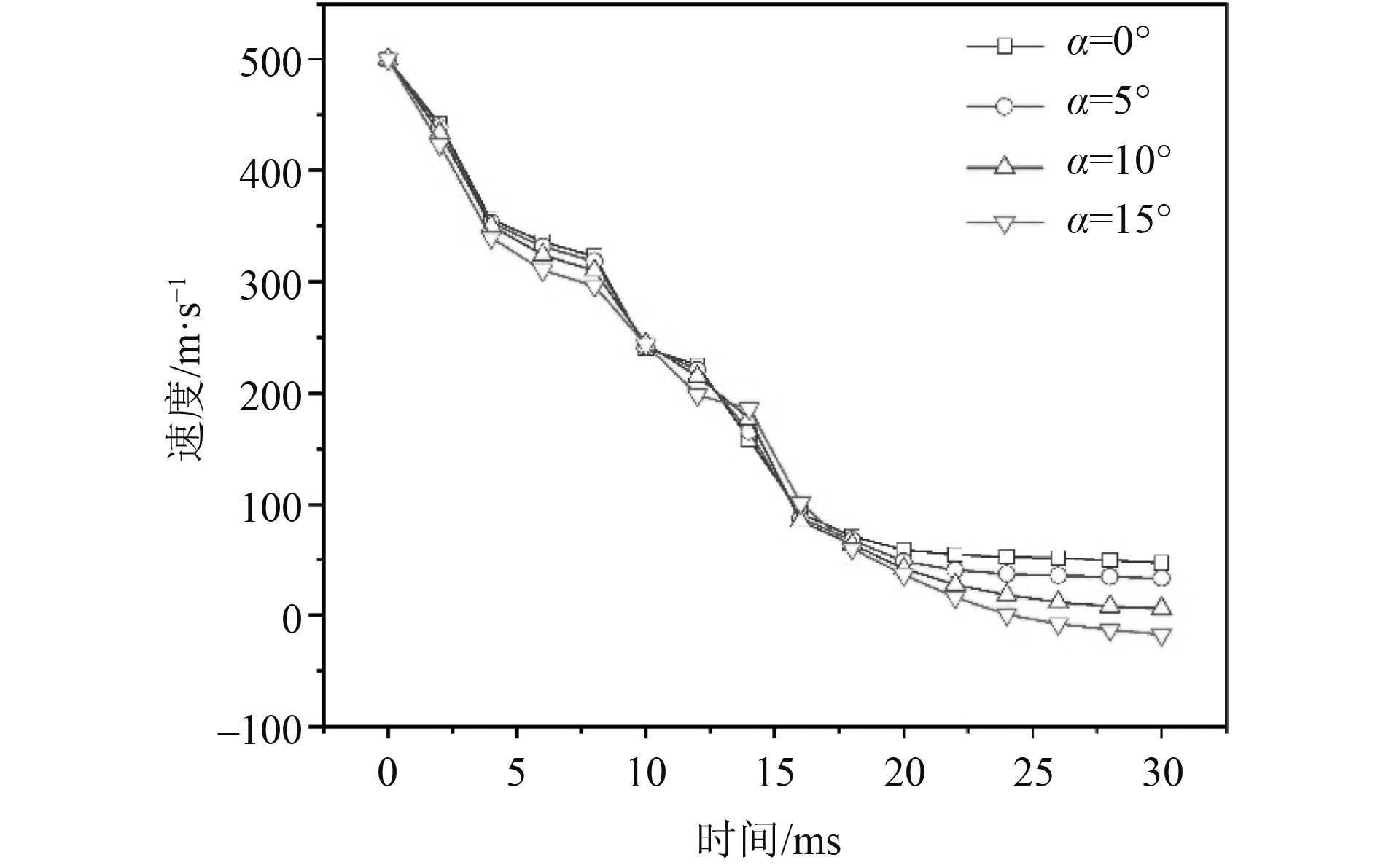
|
图 13 不同攻角下的剩余速度时历曲线 Fig. 13 Residual velocity time history curves at different angles of attack |
弹体的装药安定性是指弹体在受外界因素影响下,仍能保持其性质的能力。国内外学者在进行弹体安定性分析中,大多采用有限元仿真的方法进行弹体安定性评估。焦志刚等[9]基于Ls-dyna进行半穿甲战斗部斜侵不同厚度钢靶板的安定性分析,通过计算得到了壳体和装药的应力曲线。王伟力等[10]同样基于Ls-dyna分析了不同倾角下的弹体受力情况,得出了小倾角对安定性影响不大,大倾角影响较大的结论。本文主要研究的是弹体产生小倾角的情况,因此,将基于文献[11]的安定性计算方法进行弹体的安定性分析。
3.1 安定性理论计算侵彻过程中,装药受到应力的作用产生塑性应变能。用应力和应变率表示单位体积的塑性应变能变化率的能量守恒方程为:
| $ \begin{split} \rho \frac{{\rm{d}} e}{{\rm{d}} t}=\ & \sigma_{x x} \sigma_{x x}+\sigma_{y y} \sigma_{y y}+\sigma_{z z} \sigma_{z z}+2 \sigma_{x y} \sigma_{x y}+\\ & 2 \sigma_{x z} \sigma_{x z}+2 \sigma_{y z} \sigma_{y z}。\end{split} $ | (7) |
式中:
将(7)两边积分得到:
| $ \begin{split} \rho \varepsilon=\ & \int\left(\sigma_{x x} \varepsilon_{x x}+\sigma_{y z} \varepsilon_{y z}+\sigma_{z z} \varepsilon_{z z}+2 \sigma_{x y} \varepsilon_{x y} +\right.\\ & \left.2 \sigma_{x z} \varepsilon_{x z}+2 \sigma_{y z} \varepsilon_{y w}\right) {\rm{d }}t。\end{split} $ | (8) |
因为
| $ \rho \mathrm{e}=\int_{z_{0}}^{t_{m}} \sigma(\varepsilon) \mathrm{d} \varepsilon。$ | (9) |
式中:
| $ \rho \mathrm{e}=\int_{z_{0}}^{t_{m}} \sigma(\varepsilon) \mathrm{d} \varepsilon < \sigma_{\max} \cdot \varepsilon_{\max}。$ | (10) |
在侵彻过程中,由于相互作用的时间非常短,可认为装药的塑性应变能转化为内能是一个绝热升温的过程,故有方程:
| $ E=m C^{\prime \prime}\left(T-T_{0}\right)=\rho V C^{\prime \prime}\left(T-T_{0}\right)=\rho V e 。$ | (11) |
式中:
由上两式得:
| $ \rho C^{\prime \prime}\left(T-T_{0}\right)=\rho \mathrm{e}=\int_{\varepsilon_{0}}^{\varepsilon_{\max }} \sigma(\varepsilon) \mathrm{d} \varepsilon<\sigma_{\max } \cdot \varepsilon_{\text {max }}。$ | (12) |
取
图14为基于Ansys数值仿真的弹体应力应变云图。可知,尖卵型战斗部的尖部在撞击靶板时产生了较大的压缩变形,但这对弹体内部的装药影响程度较小。除此之外,随着初速度的增加,弹体的应变整体呈上升趋势,应变较大的区域面积也有所增大。

|
图 14 不同初速度下的弹体应变云图 Fig. 14 Strain map of the projectile at different initial velocities |
图15为弹体应力应变云图。可知,随着弹体攻角的变化,弹体的应力分布也存在差异。应力应变最大的位置,在弹体的由圆柱收缩为尖卵的拐角处。一旦此处的变形过大,将会对内部装药的安定性产生巨大影响。因此,可通过计算该位置的应力应变大小来评判弹体的安定性是否符合要求。

|
图 15 不同攻角下的弹体应变云图 Fig. 15 Strain maps of the projectlle at different angles of attack |
由于装药充满整个弹体内部,因此弹体在侵彻过程中所受的最大应变可近似为内部装药所受的最大应变。得出装药所受最大应变后,再求得最大应力便可通过式(12)得到弹体在侵彻过程中,由于碰撞所产生的内能,从而进一步判断弹体的安定性是否满足要求。
图16为TNT的应力应变曲线,将仿真计算得到的最大应变值代入到应力应变曲线中,即可得到相应的最大应力值。通过对比得知,该型半穿甲战斗部在一定范围内改变其初速度和攻角其安定性均满足要求[11]。
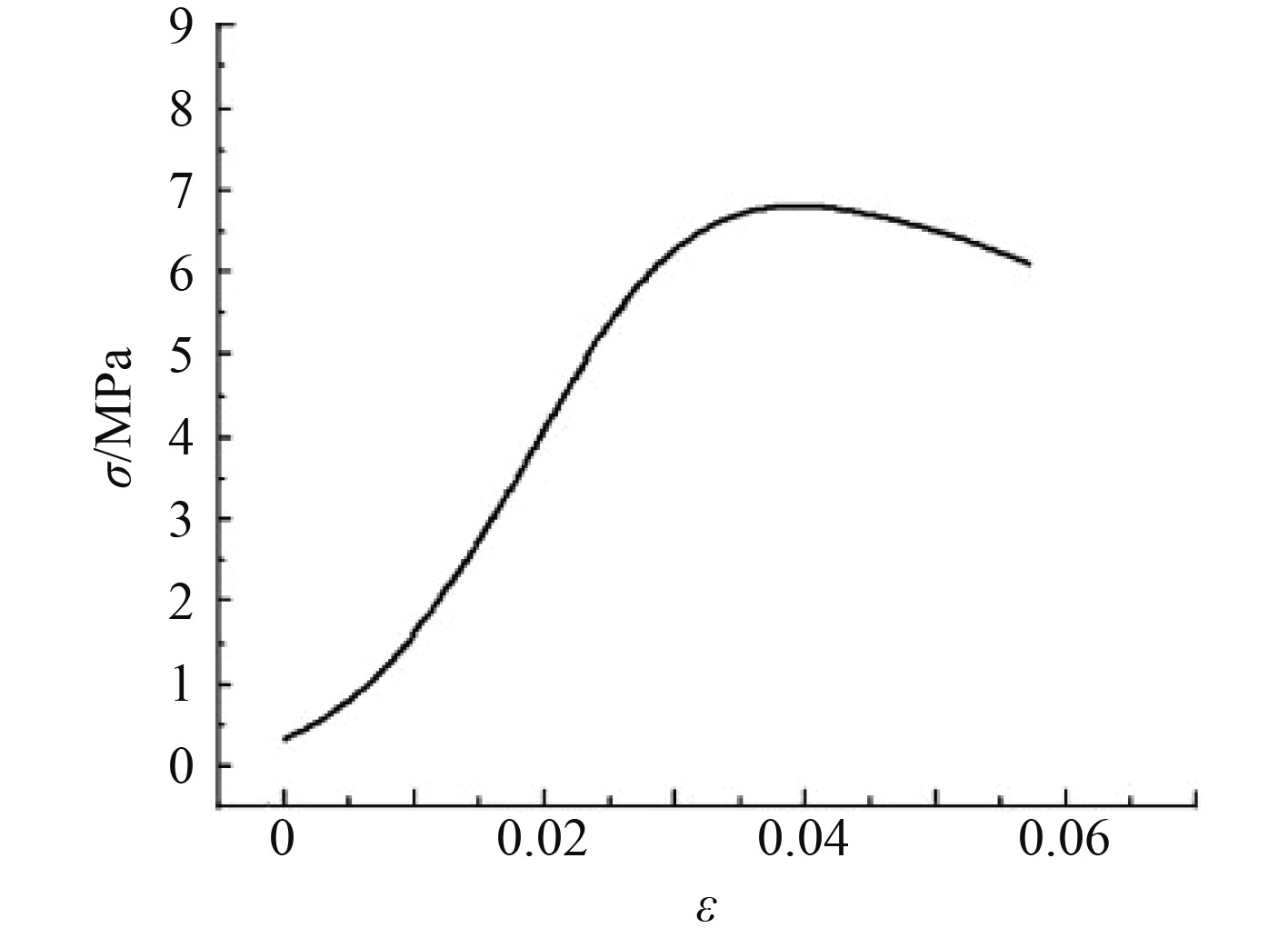
|
图 16 TNT的应力应变曲线 Fig. 16 Stress-strain curve of TNT |
图17为弹体产生最大应力应变时所在的位置。可知,弹体在不同的攻角下,最大应力应变的位置存在差异。当攻角为0°和5°时,弹体在侵彻第三层靶板时产生最大应力;当攻角为10°和15°时,弹体在侵彻第二层靶板产生最大应力。当弹体的安定性不符合要求时,便可得出引爆的相对位置,进而判断能否对舰船目标的内部设备造成毁伤。

|
图 17 最大应力应变时的侵彻位置 Fig. 17 Position of penetration at maximum stress-strain |
本文基于Ansys有限元仿真软件进行半穿甲战斗部侵彻舷侧液舱的仿真实验,通过改变弹体不同初速度与不同攻角进行仿真分析,得出以下结论:
当弹体和目标结构确定的条件下,初速度越高,侵彻深度和剩余速度越大。随着计算时间的推移,弹体的剩余速度呈阶梯式下降。当弹体的初速度呈线性变化时,弹体的最终剩余速度并不呈现线性变化。随着初速度的增加,弹体的应变整体呈上升趋势,应变较大的区域面积也有所增大。
随着攻角的增加,弹体的剩余速度越来越小,而随着攻角的线性增加,弹体剩余速度减小量呈非线性减小。随着弹体攻角的变化,弹体的应力分布也存在差异,应力应变最大位置,在弹体由圆柱收缩为尖卵的拐角处。最后根据弹体的最大应力应变仿真结果分析得到,装药安定性均满足要求。
| [1] |
拾路. 弹体撞击作用下液舱结构的毁伤失效研究[D]. 镇江: 江苏科技大学, 2019.
|
| [2] |
辛春亮, 薛再清, 涂建. 有限元分析常用材料参数手册[M]. 北京: 机械工业出版社, 2021.
|
| [3] |
杨砚世. 侵爆战斗部对航母毁伤评估方法研究[D]. 南京: 南京理工大学, 2015.
|
| [4] |
黄阳洋, 王志军, 赵鹏铎, 等. 射弹参数对侵彻防护液舱效果的影响研究[J]. 兵器装备工程学报, 2017, 38(12): 90-92+97. DOI:10.11809/scbgxb2017.12.021 |
| [5] |
熊飞, 石全, 朱艮春, 等. 半穿甲战斗部侵彻运动加筋板数值模拟[J]. 火力与指挥控制, 2015, 40(8): 74-77. DOI:10.3969/j.issn.1002-0640.2015.08.017 |
| [6] |
陈刚, 陈忠富, 陶俊林, 等. 45钢动态塑性本构参量与验证[J]. 爆炸与冲击, 2005(5): 69-74. DOI:10.3321/j.issn:1001-1455.2005.05.010 |
| [7] |
魏刚, 张伟, 邓云飞. 基于J-C模型的45钢本构参数识别及验证[J]. 振动与冲击, 2019, 38(5): 173-178. DOI:10.13465/j.cnki.jvs.2019.05.025 |
| [8] |
CZYRYCA E J. Advances in high strength Steel technology for naval hull construction[J]. Key Engineering Materials, 1993, 84−85: 491−520
|
| [9] |
焦志刚, 郭秋萍, 刘宗超. 半穿甲弹侵彻过程中装药安定性数值分析[J]. 弹箭与制导学报, 2012, 32(2): 92-94. DOI:10.3969/j.issn.1673-9728.2012.02.025 |
| [10] |
王伟力, 黄雪峰, 杨雨潼. 半穿甲战斗部侵彻过程中装药安定性研究[J]. 海军航空工程学院学报, 2010, 25(1): 79-82. |
| [11] |
廖学燕, 沈兆武, 姚保学, 等. 含铝纤维复合炸药的能量输出和力学强度[J]. 爆炸与冲击, 2010, 30(4): 424-428. DOI:10.11883/1001-1455(2010)04-0424-05 |
 2023, Vol. 45
2023, Vol. 45
