0 引　言

船舶图像弱小目标跟踪是计算机视觉领域的重要应用之一。对船舶目标进行准确、高效的跟踪与避障是实现智能感知、决策和控制的必要手段。然而，由于船舶目标在图像中往往呈现为尺寸较小、特征模糊的形象，给跟踪带来了极大的挑战。

因此众多专家学者对船舶图像弱小目标追踪展开了研究。林迅等^[1]研究通过LENET神经网络对弱小目标进行快速识别并提取其中特征，结合中分维度法与全局最近邻算法，最终实现弱小目标追踪。但此方法的条件过与特定，只有在碎云条件下才可以很好的实现弱小目标追踪。王俐云等^[2]研究通过高分四号卫星直接对船舶弱小目标进行检测并实现跟踪，此方法虽然简单便捷，但是由于云层遮挡等外界因素，容易丢失跟踪目标或产生误差。刘坤等^[3]研究通过在神经网络中引入全连接层，对新的目标函数进行学习，使用其对样本进行训练，利用目标函数的约束项使清晰样本与遮挡样本的特征共享，最终实现弱小目标追踪。但此方法在实际使用时会经常有较大误差，对应用产生较大影响。

视觉传达技术目的在于传达信息和意图，它依赖视觉并以影像呈现。本文研究基于视觉传达技术的船舶图像弱小目标跟踪方法，对船舶航行安全提供支持。

1 船舶图像弱小目标跟踪 1.1 基于视觉传达技术船舶图像预处理

在采集船舶图像时，图像不可避免的会有不同程度噪声污染，造成这些噪声的来源有光子噪声、电子噪声等，这些噪声可能会对图像的细节进行覆盖，从而使获取的图像无法使用，所以对获取的图像进行去噪预处理很有必要。本文使用均值滤波对获取的船舶图像进行降噪预处理。设 $ M \times M $ 个像素组成了船舶图像f(m,n)，对其使用均值滤波算法，可得去噪后的船舶图像g(m,n)，又可表达为：

$ g\left( {m,n} \right) = \frac{{\displaystyle\sum\limits_{\left( {a,b} \right) \in N}^{} {f\left( {m,n} \right)} }}{S} 。$

(1)

其中， $ N $ 的去心邻域表达为 $ \left( {\underline x ,\underline y } \right) $ ，集合 $ N $ 中的总像素数表达为 $ S $ 。在使用均值滤波方法去噪后，邻域随着 值的增大而增大， $ S $ 值越大，则其去噪效果会越好。

1.2 基于视觉传达技术的船舶图像弱小目标检测

目标检测是视觉传达技术的关键研究方向，通过分析图像的视觉信息，自动识别图像中的特定目标物体^[4]。基于视觉传达的目标检测技术主要利用图像处理、机器学习和深度学习等技术，通过多种方法实现目标检测。本文就图像处理技术使用二维最小均方滤波（TDLMS）方法对船舶图像弱小目标进行检测。传统的TDLMS算法检测船舶图像弱小目标就是对去噪后的船舶图像使用模板卷积，即

$ B\left( {m,n} \right) = \sum\limits_{h = 0}^{H - 1} {\sum\limits_{w = 0}^{W - 1} {{Q_i}\left( {x,y} \right)I\left( {x - h,y - w} \right)} } 。$

(2)

其中： $ B $ 为船舶图像弱小目标检测结果的图像； $ Q $ 与 $ I $ 为权重模板与原始船舶图像； $ x,h,y,w $ 与 $ i $ 为循环自变量与迭代次数；误差值为 $ {e_i} $ 。

$ {e_i} = {I_D}\left( {m,n} \right) - B\left( {m,n} \right) 。$

(3)

其中，期望船舶弱小目标图像表达为 $ {I_D} $ ，对于权重系数值的调整起到重要的调整。本文所使用的权重矩阵调整方法是误差值的负梯度方向，即

$ {Q_{i + 1}}\left( {h,w} \right) = {Q_i}\left( {h,w} \right) + \sigma {e_i}X\left( {x - h,y - w} \right), $

(4)

其中， $ \sigma $ 为控制迭代的步长表达。

由于在船舶图像检测区域内目标过于弱小，为了避免对背景弱小目标检测结果造成的影响，本文利用模板压缩法对减少弱小目标像素进行^[5]，从而使背景预测的精度有一定程度的提高。

由于船舶图像弱小目标的实际尺寸在远距离成像的时候十分弱小，为了得到与中心区域像素无关的方法，本文使用空心法，其映射公式表达为：

$ GD\left( r \right) = \left\{ \begin{gathered} 1\mathop {}\nolimits_{}^{} \left| r \right| \geqslant {r_0} \\ 0\mathop {}\nolimits_{}^{} \left| r \right| < {r_0} \\ \end{gathered} \right\} ，$

(5)

其中， $ r $ 与 $ {r_0} $ 分别为在模板中待计算像素点与模板中心的距离与模板参数，模板参数通常为模板的一半大小。

TDLMS迭代方法的修正公式表达为：

$ {Q_{{P_{i + 1}}}} = {Q_{{P_i}}}\left( {h,w} \right) + {\sigma _i}{e_i}X\left( {x - h,y - w} \right)GD\left( {x,y} \right) ，$

(6)

$ B\left( {m,n} \right) = \sum\limits_{h = 0}^{H - 1} {\sum\limits_{M = 0}^{W - 1} {{Q_{{p_i}}}\left( {x,y} \right)I\left( {x - h,y - w} \right)} }。$

(7)

利用式（6）获取最终检测到的船舶图像弱小目标。

1.3 船舶图像弱小目标跟踪

在识别出船舶图像弱小目标后，使用成像装置探测弱小目标，从而得到弱小目标状态参量的测量值，其中包括空间位置与运动速度等。使用滤波估值对弱小目标的运动状态进行最佳估计，根据其运动特性对弱小目标的运动模型进行建立，利用此模型，根据第 $ k $ 帧参数对第 $ k + 1 $ 帧参数进行预测，不断重复直至获取最终的船舶图像弱小目标跟踪结果。本文使用直线模型对弱小目标进行跟踪，由于现实中弱小目标的运动轨迹不一定为直线运动轨迹，所以在直线模型中加入卡尔曼滤波算法来对弱小目标的运动轨迹进行预测更新^[6]。动态直线模型为：

$ \begin{aligned} &X'\left( k \right) = AX'\left( {k - 1} \right) + \overline w \left( k \right)，\\& Z'\left( k \right) = HX'\left( k \right) + v\left( k \right) ，\end{aligned} $

(8)

卡尔曼滤波算法的标准方程如下式：

$ \begin{gathered} \hat X'{\left( k \right)^ - } = A\hat X'\left( {k - 1} \right) ，\\ P{\left( k \right)^ - } = AP\left( {k - 1} \right){A^{\rm{T}}} + O ，\\ P\left( k \right) = \left( {I - K\left( k \right)H} \right)P{\left( k \right)^ - }，\\ K\left( k \right) = P{\left( k \right)^ - }{H^{\rm{T}}}{\left[ {HP{{\left( k \right)}^ - }{H^{\rm{T}}} + R} \right]^{ - 1}}，\\ \hat X'\left( k \right) = \hat X'{\left( k \right)^ - } + K\left( k \right)\left[ {Z\left( k \right) - H\hat X'{{\left( k \right)}^ - }} \right] 。\\ \end{gathered} $

(9)

观测变量与状态变量分别表达为 $ Z\left( k \right) = {\left[ {x\left( k \right),y\left( k \right)} \right]^{\mathrm{T}}} $ 与 $ X'\left( k \right) = {\left[ {x\left( k \right),\hat x\left( k \right),y\left( k \right),\hat y\left( k \right)} \right]^{\mathrm{T}}} $ 。

状态转移矩阵与观测矩阵分别表达为 $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1\;\;T\;\;0\;\;0 \\ 0\;\;1\;\;0\;\;0 \\ 0\;\;0\;\;1\;\;T \\ 0\;\;0\;\;0\;\;1 \end{array}} \right] $ 与 $ {\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 1&0 \end{array}\mathop {}\limits_{}^{} \begin{array}{*{20}{c}} 0&0 \\ 1&0 \end{array}} \right] $ 。方差 $ O $ 的零均值高斯白噪声表达为 $ \overline w \left( k \right) $ ，也叫过程激励噪声；方差 $ R $ 的零均值高斯白噪声表达为 $ v\left( k \right) $ ，也做观测噪声；在 $ x $ 轴上弱小目标的位置与速度分别表达为 $ x\left( k \right) $ 与 $ \hat x\left( k \right) $ ；在 $ y $ 轴上弱小目标的位置与速度分别表达为 $ y\left( k \right) $ 与 $ y $ ；最优增益矩阵表达为 $ K\left( k \right) $ ；估计误差方差阵表达为 $ P\left( k \right) $ ； $ T $ 为阈值。

使用直线运动模型对弱小目标进行跟踪，得到船舶图像弱小目标的状态向量滤波值，从而对弱小目标在下一帧可能出现位置进行外推预测，这样当弱小目标被遮挡后再次出现时，依旧可以对弱小目标进行跟踪。

2 实验结果与分析

为了对本文方法的应用性进行验证，设一个船舶弱小目标做变速运动，对采集图像时间设置为每5 s采集一次，持续采集500 s。船舶弱小目标的初始时刻位置与初始速度分别为50 km与200 m/s；在0～100 s时，船舶弱小目标处在匀速直线运动中，在100～300 s时，船舶弱小目标做加速度为100 m/s²的加速非直线运动，在300～500 s时，船舶弱小目标做加速度为60 m/s²的加速非直线运动。使用本文方法对其进行弱小目标追踪，获取该船舶初始位置，运行100、300、500 s时位置的图像结果如图1所示。根据本文方法对该船舶图像弱小目标进行追踪，观察图1，可以发现使用本文方法在实验时间内均对船舶图像弱小目标进行了追踪，图1（b）到图1（c）此段时间内发现弱小目标移动距离最远，在追踪时间等量的情况下，说明此段时间内弱小目标移动速度最快，在弱小目标移动速度较快的情况下，本文方法仍然可以对船舶图像弱小目标进行追踪，进一步说明本文方法的实用性及对船舶图像弱小目标的追踪能力。

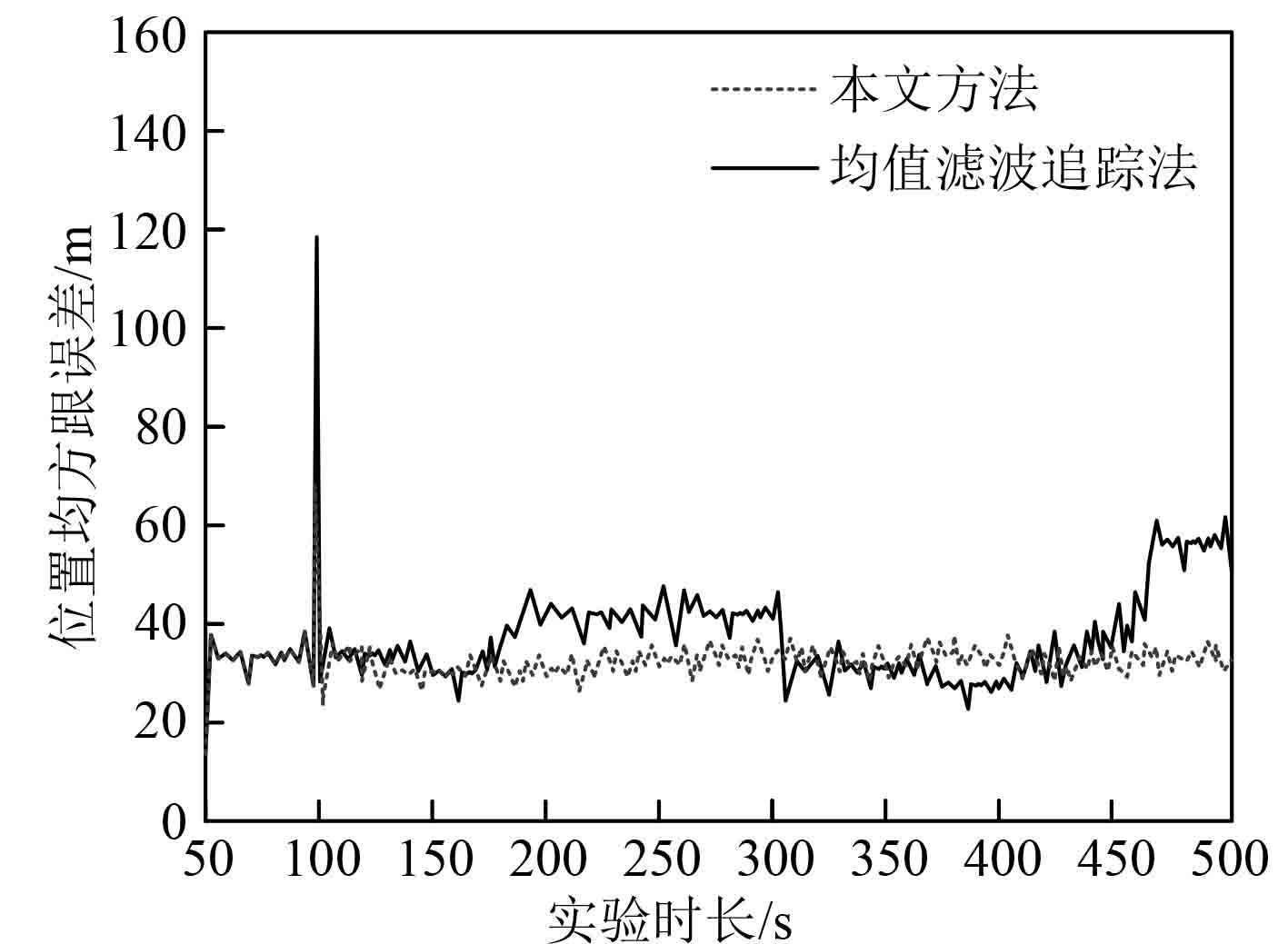
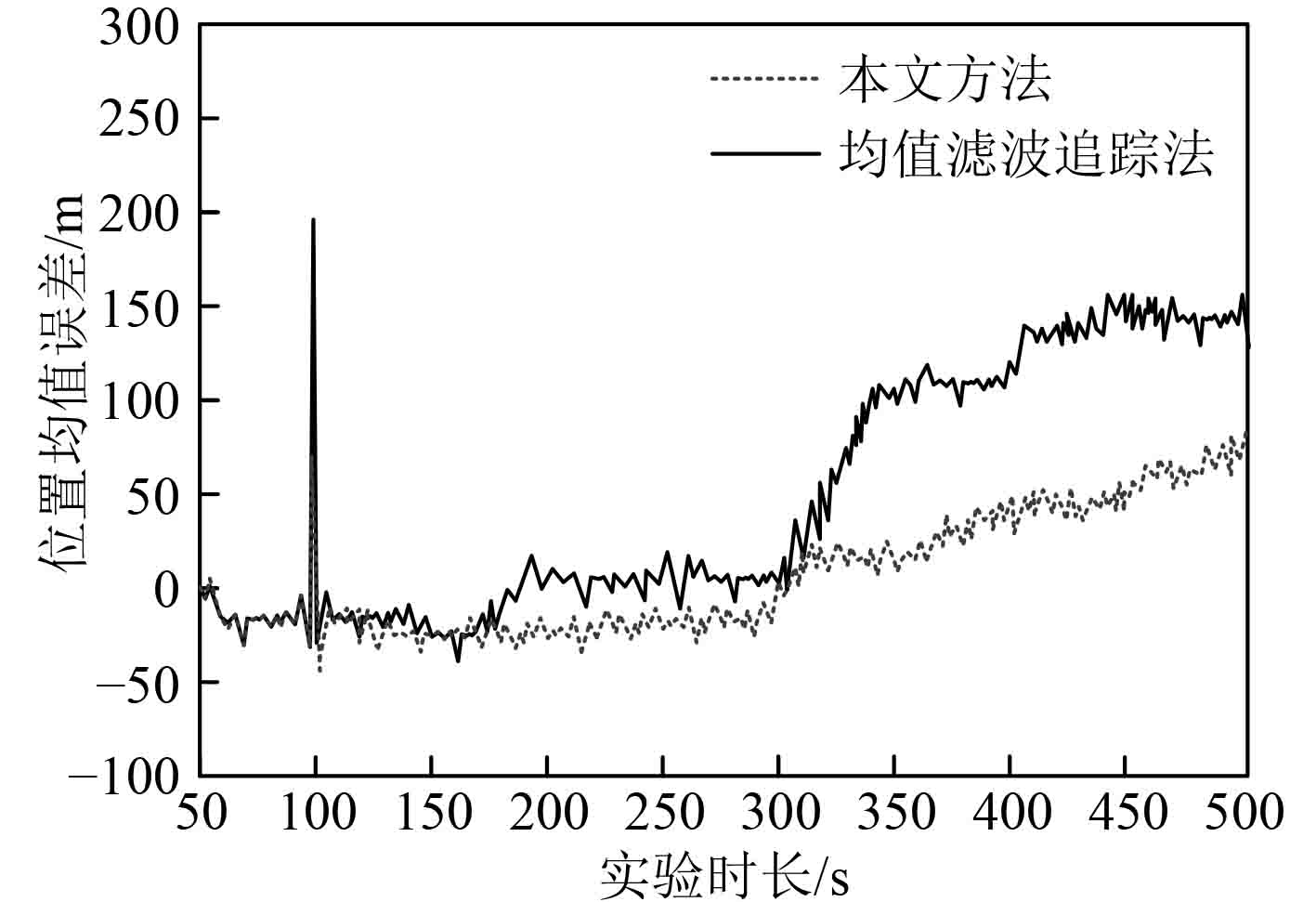
为了对本文跟踪算法进行验证，经过50次Monte Carlo仿真实验，分别使用本文方法与均值滤波方法得到船舶图像弱小目标位置的均方根误差与均值误差，如图2与图3所示。观察图2与图3可以发现，本文方法的追踪效果比均值滤波追踪算法的最终效果更好，尤其在船舶弱小目标加速度较大时，本文方法的追踪误差小于均值滤波追踪算法的追踪误差，且其追踪误差的收敛速度也更快。

由于采集的船舶图像中，弱小目标会存在模糊不清，以及出现一定程度上的变形现象，对弱小目标的追踪效果也会造成影响。为使本文方法可以精准对弱小目标进行追踪，使用视觉传达技术对船舶图像进行去噪预处理，对不同时间下，各个船舶图像的峰值信噪比PSNR、空间频率IE与信息熵SF这些指标进行考察，如表1所示。可以看出，本文方法的去噪效果在各个时间段的评价指标参数均较好，无论船舶进行匀速直线运动还是做非直线运动，使用本文方法去噪后船舶图像的PSNR、IE与SF均较为理想，说明无论船舶处于何种状态，本文方法均可将图像较好进行去噪预处理，不受船舶图像弱小目标的速度与路线影响。

3 结　语

卡尔曼滤波利用线性系统状态方程进行最优估计，本文将其应用于船舶图像弱小目标跟踪。在已知测量方差的情况下，能够从带噪声的测量数据中估计系统状态，并可对现场采集的数据进行实时更新和处理。本文方法可帮助船舶在航行过程中及时发现其他船舶与障碍，对其运动轨迹进行预测跟踪，保障船舶航行安全。