舰船卫星导航系统的误差来源主要包括钟差、轨道误差、大气延迟等。为了提高舰船卫星导航系统的精度,本文采用一种多系统的信号融合算法,可以减小各个系统的误差,提高导航的精度和可靠性。
1)信号建模。主要包括舰船卫星导航系统的坐标系建模、目标位置建模和噪声干扰信号建模,通过分析卫星导航系统的信号特征,实现更好的信号误差分析和信号融合。
2)信号融合平台搭建和误差估计。结合软硬件技术搭建卫星导航系统的信号融合平台,对平台的信号进行误差估计,包括对钟差、轨道误差和大气延迟等误差进行估计和补偿。
3)误差纠偏。结合分数阶fourier变换技术进行融合平台的导航信号误差纠偏,对纠偏后的信号进行位置解算,得到舰船的准确位置。
1 舰船卫星导航系统的定位坐标系舰船卫星导航以地球作为参照体,且解算过程中涉及多种坐标系,常用的坐标系包括以下几种:
1)地心地固坐标系。该坐标系以地球质心为原点,地球自转轴为Z轴,X轴指向经度0°的子午线,Y轴与X轴垂直,形成一个右手坐标系。该坐标系用于描述卫星在地球上的位置。
2)大地坐标系。大地坐标系是地理坐标系的一种扩展,考虑了地球的椭球形状和重力畸变。大地坐标系使用经度、纬度和高程来描述地球上的位置。
3)船体坐标系。船体坐标系以船体为原点,船体的前后、左右、上下分别对应X轴、Y轴和Z轴。船体坐标系用于描述船舶的运动和姿态。
本文在解算舰船卫星导航系统的位置信息时,建立坐标系如图1所示 。
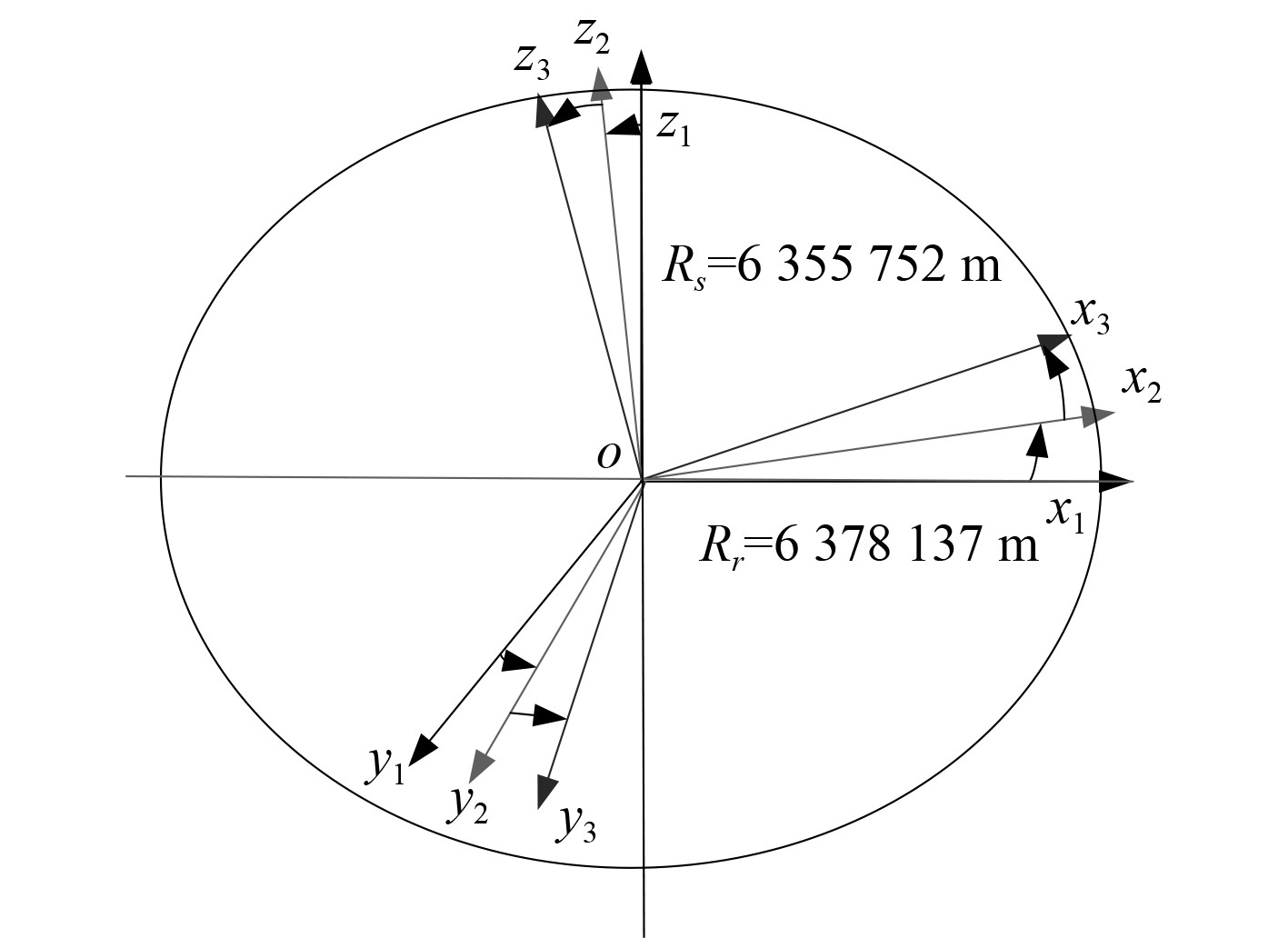
|
图 1 舰船卫星导航系统坐标系示意图 Fig. 1 Ship satellite navigation system coordinate system |
如图,载体坐标系
| $ f = \frac{{{R_r}}}{{{R_s}}} = 0.003\;35 \text{。} $ |
地球自转的角速度为
| $ \left\{ {\begin{array}{*{20}{l}} {{R_M} = \dfrac{{{R_s}{{(1 - f)}^2}}}{{{{\left[ {{{(1 - f)}^2}{{\sin }^2}L + {{\cos }^2}L} \right]}^{\sqrt 2 }}}}} ,\\ {{R_N} = \dfrac{{{R_r}}}{{{{\left[ {{{(1 - f)}^2}{{\sin }^2}L + {{\cos }^2}L} \right]}^{\sqrt 2 }}}}} 。\end{array}} \right. $ |
载体坐标系
| $ {\boldsymbol{A}}= {\boldsymbol{C}}_n^1{\boldsymbol{C}}_1^2{\boldsymbol{C}}_2^b{\boldsymbol{B}}\text{,} $ |
转换矩阵分别如下:
| $ {\boldsymbol{C}}_n^1 = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right]\text{,} $ |
| $ {\boldsymbol{C}}_1^2 = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \theta }&{\sin \theta } \\ 0&{ - \sin \theta }&{\cos \theta } \end{array}} \right]\text{,}{{{\boldsymbol{C}}}}_2^b = \left[ {\begin{array}{*{20}{c}} {\cos \phi }&0&{ - \sin \phi } \\ 0&1&0 \\ {\sin \phi }&0&{\cos \phi } \end{array}} \right]\text{。} $ |
其中:
导航坐标系
| $ {\boldsymbol{C}}_e^n = \left[ {\begin{array}{*{20}{c}} 0&{ - \sin L}&{\cos L} \\ 1&0&0 \\ 0&{\cos L}&{\sin L} \end{array}} \right]\text{。} $ |
在舰船卫星导航系统中,干扰信号以扫频干扰为主,由于扫频干扰信号的稳定性较差,频率难以准确定义,往往噪声抑制的效果较差。建立扫频干扰信号的时域模型为:
| $ S\left( t \right) = {A_1}{e^{j\left( {2{\text{π}} {f_0}t + {g_0}{t^2}} \right)}} \text{。} $ |
式中:
| $ f\left( t \right) = {f_0} + {g_0}\left( t \right) \text{,} $ |
扫频干扰信号的时宽如下:
| $ {\left( {\Delta f} \right)^2} = \frac{{\displaystyle\int\nolimits_{ - \infty }^\infty {{t^2}{{\left| {S\left( t \right)} \right|}^2}{\rm{d}}t} }}{{\displaystyle\int\nolimits_{ - \infty }^\infty {{{\left| {S\left( t \right)} \right|}^2}{\rm{d}}t} }} \text{,} $ |
扫频干扰信号的频宽如下:
| $ \begin{gathered} \\ {\left( {\Delta t} \right)^2} = \frac{{\displaystyle\int\nolimits_{ - \infty }^\infty {{f^2}{{\left| {S\left( f \right)} \right|}^2}{\rm{d}}t} }}{{\displaystyle\int\nolimits_{ - \infty }^\infty {{{\left| {S\left( f \right)} \right|}^2}{\rm{d}}t} }} 。\\ \end{gathered} $ |
图2分别为原始信号、增加了扫频干扰信号时宽和增加了扫频干扰信号频宽的信号,可见增加干扰后的信号噪声强度明显增加。
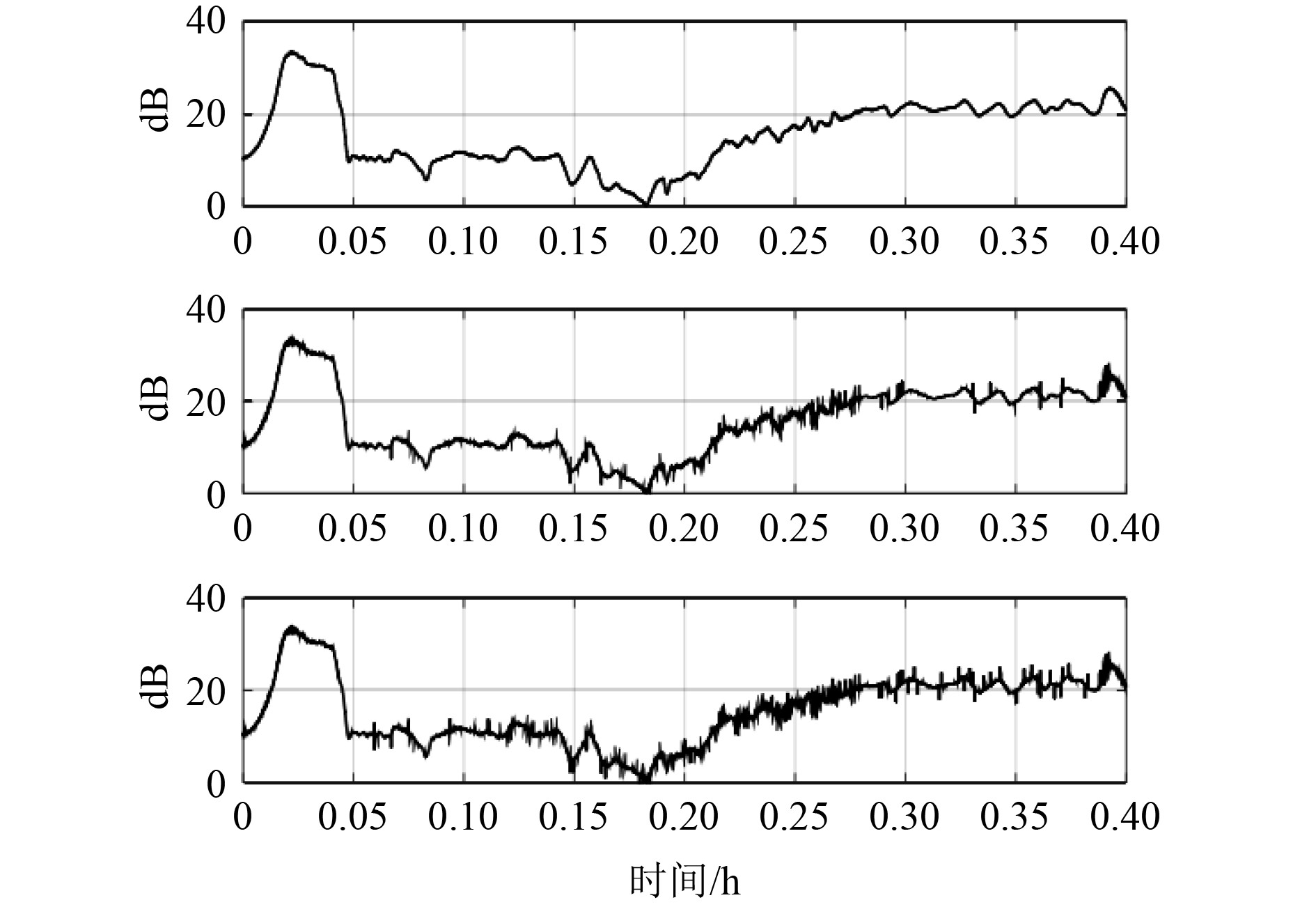
|
图 2 原始信号和增加扫频干扰的信号波形 Fig. 2 The original signal and the signal waveform with added sweep interference |
本文搭建的舰船卫星导航信号融合平台的功能包括:
1)多源信号接收。平台可以接收来自不同卫星导航系统(如GPS、GLONASS、北斗卫星等系统)的信号,实现多源信号的接收和处理[3]。
2)信号融合定位。平台通过融合多个卫星导航系统的信号,提供更加准确和可靠的舰船定位信息。通过使用多个卫星系统的信号,可以减少信号遮挡和多径效应对定位精度的影响。
3)时钟同步。平台可以通过接收多个卫星系统的信号,实现舰船内部各个设备的时钟同步,确保各个设备的数据同步和一致性。
4)信号强度监测。平台可以监测卫星导航信号的强度,提供实时的信号质量评估,以便舰船操作员能够及时了解信号质量情况,做出相应的调整和决策。
5)故障诊断和容错处理。平台可以监测卫星导航系统的故障情况,并提供相应的诊断和容错处理功能。当某个卫星导航系统发生故障时,平台可以自动切换到其他可用的卫星系统[2],确保舰船的导航功能不受影响。
6)数据记录和分析。平台可以记录舰船的导航数据,并提供数据分析功能,以便舰船操作员和管理人员对航行情况进行评估和分析,从而改进舰船的导航策略和决策。
信号融合平台包括硬件层和软件层。其中,硬件层又包括卫星雷达、变频器、滤波器、上位机和用户等;软件层包括监测模块和控制软件等,原理图如图3所示。

|
图 3 舰船卫星导航信号融合平台的功能原理图 Fig. 3 Functional schematic diagram of ship satellite navigation signal fusion platform |
分数阶Fourier变换是基于傅里叶变换的延伸形式,在信号优化、噪声抑制等方面有非常广泛的应用。
定义信号
| $ F\left( {x\left( {t,f} \right)} \right) = \int\nolimits_{ - \infty }^\infty {x\left( {t'} \right)\gamma \left( {{{t'}^{}} - t} \right){e^{ - jw{t^2}}}{\mathrm{d}}{t^{}}} \text{。} $ |
式中:
分数阶Fourier变换的定义为:
| $ {X_a}\left( u \right) = \left\{ {F\left( {x\left( t \right)} \right)} \right\} \cdot \left( u \right) = \int\nolimits_{ - \infty }^\infty {x\left( t \right){K_a}\left( {t,u} \right){\mathrm{d}}t} \text{。} $ |
其中,
式中:
分数阶fourier变换[4]的信号处理过程:
1)
| $ g\left( t \right) = x\left( t \right){e^{j{w^2}\cos \theta }} 。$ |
2)信号进行Fourier变换:
| $ G\left( u \right) = \int\nolimits_{ - \infty }^\infty {g\left( t \right){e^{ - jw{t^2}\cos \theta }}{\mathrm{d}}{t^{}}} 。$ |
3)将Fourier变换后的信号进一步进行分数阶调制,得到:
| $ {F_a}\left( u \right) = {A_0}\int\nolimits_{ - \infty }^\infty {G\left( u \right){K_a}\left( {t,u} \right){\mathrm{d}}t} 。$ |
图4为分数阶Fourier变换的信号处理示意图。
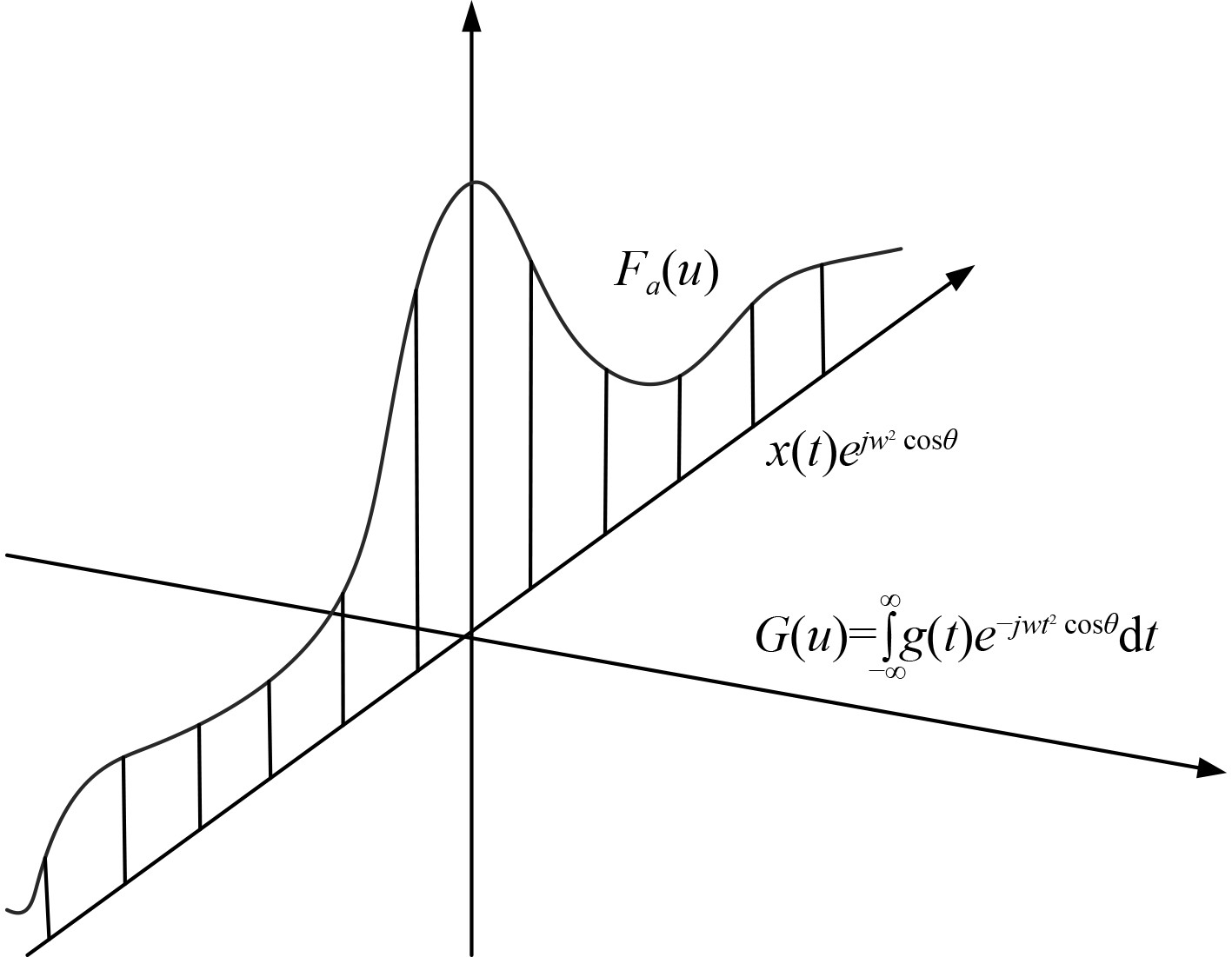
|
图 4 分数阶fourier变换的信号处理示意图 Fig. 4 Signal processing diagram of fractional fourier transform |
图中,分数阶Fourier变换将信号从时域坐标轴转化到频域坐标轴,得到调制后的函数曲线。
3.3 基于分数阶Fourier变换的误差纠偏与仿真本文结合分数阶Fourier变换和线性调频(LFM)信号进行导航卫星系统的信号误差纠偏与融合,线性调频(LFM)信号模型为:
| $ {L_p}\left( u \right) = A\frac{{{e^{jw}}}}{{\sqrt {j\sin \theta } }}{e^{ - j{w^2}\cot \theta }}\delta \left( {u\cos \theta - {f_0}} \right) 。$ |
在进行信号融合平台的测试仿真过程中,选取的信号频谱为1~3 G,选取的信号接收设备分辨率带宽为5 MHz,分别构建了3种幅值(5/10/15)的LFM信号

|
图 5 不同LFM信号下的舰船卫星系统位置信号误差曲线 Fig. 5 Error curves of ship satellite system position signals under different LFM signals |
由图5可知,调频信号的幅值越大,基于分数阶Fourier变换的舰船卫星位置信号的误差越小。
4 结 语本文针对舰船卫星导航系统的信号融合和信号干扰抑制问题进行了研究,并结合分数阶Fourier变换在信号时域与频域处理的优势,搭建了一种舰船卫星导航系统的信号融合平台,并对舰船卫星信号的干扰噪声过滤进行研究,有效实现了干扰信号的抑制,并进行了不同调频信号LFM下的信号误差仿真测试。
| [1] |
曾晓敏. 卫星导航系统中船舶无线通信信号截获方法[J]. 舰船科学技术, 2023, 45(6): 150-153. ZENG Xiao-min. Interception method of ship wireless communication signal in satellite navigation system[J]. Ship Science and Technology, 2023, 45(6): 150-153. |
| [2] |
申成良, 郭承军. 全球卫星导航系统中欺骗信号优化检测仿真[J]. 计算机仿真, 2019, 36(6): 109−113+119. SHEN Cheng-liang, GUO Cheng-jun. Computer Simulation, 2019, 36(6): 109−113+119. |
| [3] |
汪海伦, 丛爽, 尚伟伟, 等. 量子导航定位系统中光学信号传输系统设计[J]. 量子电子学报, 2018, 35(6): 714-722. WANG Hai-lun, CONG Shuang, SHANG Wei-wei, et al. Design of optical signal transmission system in quantum navigation and positioning system[J]. Journal of Quantum Electronics, 2018, 35(6): 714-722. |
| [4] |
艾腾飞, 吕晶, 周轩, 等. 卫星导航系统中多径信号干扰分析[J]. 通信技术, 2016, 49(12): 1607-1613. AI Teng-fei, LV Jing, ZHOU Xuan, et al. Interference analysis of multipath signal in satellite navigation system[J]. Communication Technology, 2016, 49(12): 1607-1613. |
| [5] |
唐毅, 钟文安, 李爽. 双源信号深组合导航在新一代运载火箭制导系统中应用初探[J]. 导航定位学报, 2015, 3(2): 62-66. TANG Yi, ZHONG Wenan, LI Shuang. Preliminary study on the application of dual-source signal deep combined navigation in the guidance system of a new generation of launch vehicle[J]. Journal of Navigation and Positioning, 2015, 3(2): 62-66. |
 2023, Vol. 45
2023, Vol. 45
