0 引　言

加速度计作为惯性导航系统中的核心惯性器件之一，主要用于观测运载体在测量参考坐标系下的线加速度，进而推算运载体在导航解算坐标系下的位置、速度以及姿态信息，其测量精度直接决定了系统的导航精度水平^[1-3]。目前，在中高精度导航系统中应用最为广泛的是石英挠性加速度计，其具有精度高、可靠性强、长期稳定性好等优点，相较于其他类型的加速计，在导航领域更受青睐。

理想情况下，加速度计的输出应与其敏感的加速度呈线性关系。但受到制造工艺、内部结构、采集线路等因素影响，不同元件间的输出模型存在一定差异，一般需要在实验室条件下对包括标度因数、偏值等参数进行标校后方能使用。然而，在实际工作环境下，温度的波动相较于实验室环境波动剧烈，其可能会引起加速度计内部结构发生改变，导致已标校的参数失效，最终导致测量精度下降，因此必须采用必要措施予以控制补偿^[4-6]。王淑娟等^[7]构建了石英挠性摆式加速度计的温度模型，并通过单轴十二位置翻滚实验及正交多项式拟合方法对模型参数进行了辨识与补偿后，在20℃~50℃范围内加速度计的测量精度提高了一个数量级。翁海娜等^[8]利用最小二乘法建立了五阶加速度计的偏值和标度因数误差模型，并在30℃~70℃范围内对模型参数进行了拟合补偿，补偿后水平状态下加速度计输出精度提高了一个数量级，垂直状态下也提升了60%以上。2018年，俞茂超等^[9]分析了石英加速度计的基本原理与温度误差特性，建立了多参量联合多项式模型对加速度计进行补偿，补偿后的加速度计偏值误差降低了75%。张金云等^[10]提出采用多项式样条函数回归方法对惯性平台系统内石英加速度计进行建模与补偿，补偿后加速计在20℃~50℃范围内的标度因数稳定性有2×10⁻⁴提升到8×10⁻⁶，偏值由1.5 LSB/s提升至0.3 LSB/s。总的来看，尽管基于多项式的温漂模型能够对加速度计参数与温度变化间的关系进行有效描述与补偿，但难以描述包括温漂滞环效应在内的多种非线性效应，导致补偿不完全，影响测量精度。近年来，随着机器学习研究的不断深入，支持向量机、神经网络、粒子群算法等先进算法被用于加速度计的温漂模型辨识与补偿，有效提升了现有加速度计在变温环境下的测量精度^[11-13]。

作为以一种衍生于支持向量机的稀疏概率模型，相关向量机(Relevance Vector Machine)被Tipping提出，其基于贝叶斯统计学习理论，通过移除不相关的点将模型稀疏化，从而极大减少了核函数所需的计算量，同时也克服了核函数必须满足Mercer条件的限制，在非线性模型的拟合应用中呈现出极大的优越性^[14]。本文在对加速度计温度模型进行分析的基础上，采用相关向量机对模型参数进行估计，并设计了实验对所述方法的有效性进行验证。实验结果表明，该方法能够有效提升变温条件下的加速度计输出精度，补偿后的温度误差相较于补偿前降低了50%以上。

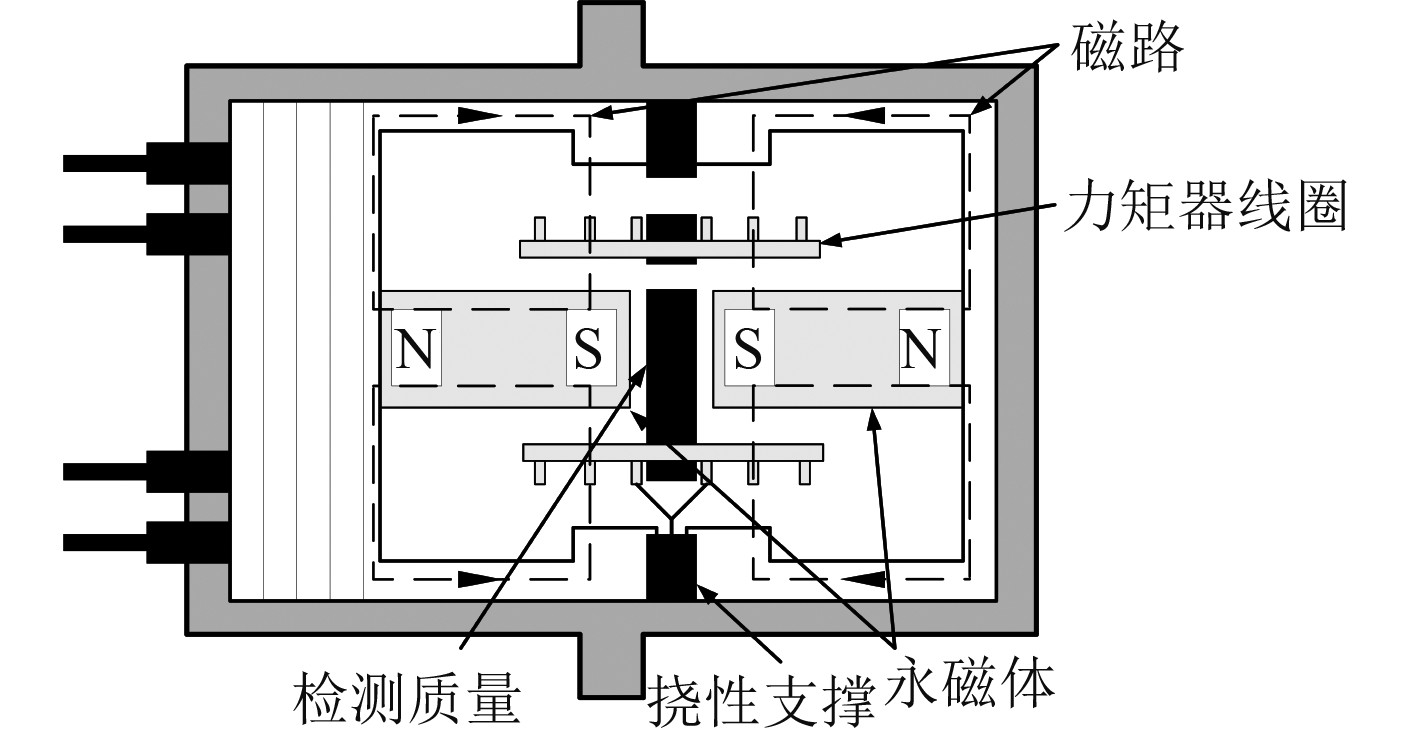
1 石英加速度计温度误差特性分析

典型的石英加速度计结构如图1所示，当加速度计的敏感方向存在加速度时，由石英摆片构成的检测质量将偏离平衡位置，进而引起平衡电容传感器输出发生改变，该信号经放大滤波后，一部分反馈至力矩器线圈，产生使检测质量回到平衡位置的电磁力，一部分经信号采集电路转换后作为加速度计的信号输出。因此，加速度计的输出精度受摆组件的摆性、力矩器电磁力矩系数以及结构材料的稳定性决定。

根据IEEE 1293-2018《线性单轴非陀螺加速度计标准规范格式及推荐测试流程》，加速度计的输出公式可表示为

$ \begin{split} E =& {K_1}\left\{ {K_0} + \frac{{{K_0}'}}{2}{\text{sign}}\left( a \right) + \left( {1 + \frac{{{K_1}'}}{2}{\text{sign}}\left( a \right)} \right)a + \right.\\ & \left.\sum\limits_{n = 2}^\infty {{K_n}{a^n} + \varepsilon } \right\}。\end{split} $

(1)

其中， $ E $ 为加速度计的输出； $ a $ 为加速度计敏感轴方向输入的加速度分量； $ {K_0} $ 为偏值， $ {K_n}\left( {n = 1,2,3...} \right) $ 为 $ n $ 阶标度因数； $ {K_n}' $ 为对应的标度因数不对称性； $ {\text{sign}}\left( {} \right) $ 为取符号运算函数； $ \varepsilon $ 为包括轴间耦合效应、门摆态变化等因素引起的误差。在中低精度的惯性导航系统中，除一阶标度因数与偏值外的其他因素对加速度计输出的影响极小，因此式(1)一般简化为式(2)的形式使用：

$ E = {K_1}\left( {{K_0} + a} \right) 。$

(2)

所以加速度值可根据式(3)计算：

$ a = \frac{E}{{{K_1}}} - {K_0} 。$

(3)

实际上，受加工装调精度以及线路特性影响，加速度计间的输出特性均会存在一定差异，为保证加速度计能够输出准确结果，需要预先对其标度因数与偏值进行精确标定，以构建式(2)的输出模型。然而在真实的应用条件下，加速度计的工作温度将随外界环境发生剧烈变化，特别是对于没有温控措施的捷联式系统，加速度计内部的元件特性，如永磁体的磁感应强度、挠性支撑的结构等均会发生改变，最终反映到加速度计的参数上。此时，在实验室条件下标定得到的参数将失效，在最终的测量结果中引入误差。

图2为某石英加速度计在变温条件下的加速度输出曲线，整个试验过程加速度计始终处于静止状态，因此加速度计敏感的加速度在测量过程中未发生变化。随着环境温度逐步升高，加速度计的输出随之改变，在整个温变过程中加速度计输出变化了1.2 mg，显然这将对导航精度造成严重影响。因此，对加速度计的温度误差特性进行分析研究，并进行合理补偿，对提升惯导系统的测量精度具有重要意义。

考虑加速度计的输出仅与标度因数与偏值相关，在变温条件下，式(2)应改写为：

$ E\left( T \right) = {K_1}\left( T \right)a + {K_1}\left( T \right){K_0}\left( T \right) 。$

(4)

将 $ {K_1}\left( T \right) $ 与 $ {K_0}\left( T \right) $ 关于 $ {T_0} $ 展开，表现为多项式形式：

$ \begin{gathered} {K_1}\left( T \right) = {K_1}\left( {{T_0}} \right) + \sum\limits_{n = 1}^\infty {\frac{{K_1^{\left( n \right)}\left( {{T_0}} \right)}}{{n!}}{{\left( {\Delta T} \right)}^n}}，\\ {K_0}\left( T \right) = {K_0}\left( {{T_0}} \right) + \sum\limits_{n = 1}^\infty {\frac{{K_0^{\left( n \right)}\left( {{T_0}} \right)}}{{n!}}{{\left( {\Delta T} \right)}^n}} 。\\ \end{gathered} $

(5)

其中， $ {T_0} $ 为标定参数的参考温度； $ K_1^{\left( n \right)}\left( {{T_0}} \right) $ 和 $ K_0^{\left( n \right)}\left( {{T_0}} \right) $ 为标度因数与偏值的n阶导数。加速度计温度误差 $ \Delta a $ 与温度变化量 $ \Delta T $ 存在一定近似线性关系，如图3所示，一般仅考虑一、二阶导数项即可加大降低温度误差影响。然而在实际应用过程中，该补偿方法仍存在一定缺陷。首先，在工作状态下，惯性导航系统内部复杂的温度场和外界环境温度的剧烈变化加上自身的内部器件发热，导致直接获取加速度计核心位置温度存在一定困难；其次，多项式温补模型存在高阶舍入误差，非线性温度效应的影响无法完全消除。最后，实际应用环境下，加速度计温度是自然连续变化的，传统的温度梯度标定方法忽略了温度变化率对结果的影响。因此，为进一步提升加速度计测量精度，建立温度采样数据与温度误差数据之间的非线性模型关系，而模型及参数的获取则成为解决这一问题的关键。

2 基于RVM的加速度计组件温度误差建模方法

传统的非线性模型建模方法包括多元回归，支持向量机、神经网络等，各有利弊。RVM是一种衍生于支持向量机的回归和分类算法，其基于概率学习思想，通过在权值ω上定义超参数α来控制Gaussian先验概率，在贝叶斯框架下进行机器学习，可以计算输出的概率分布、很自然的适用于复杂类温度误差模型，并利用判据来移除野值，从而获得稀疏化模型。

2.1 相关向量机函数拟合方法

设训练样本输入目标集为 $ \{ {x_n},{t_n}\} _{n = 1}^N $ ，即

$ {t_n} = y({x_n};\omega ) + {\varepsilon _n} $

(6)

式中， $ {\varepsilon _n} $ 为附加噪声。且满足高斯分布 ${\varepsilon _n}N(0,{\sigma ^2})$ ，则RVM的输出模型为：

$ y({x_n};\omega ) = \sum\limits_{i = 1}^N {{\omega _i}K(x,{x_i}) + } {\omega _0} 。$

(7)

式中， $ K(x,{x_i}) $ 为核函数， $ {\omega _i} $ 为权值，且 $ \phi ({x_i}) = K(x,{x_i}) $ 。

假设数据集 $ {t_n} $ 服从独立分布，则其条件概率为:

$ \begin{split} P(t|\omega ,{\sigma ^2}) = &\coprod\limits_{i = 0}^N N [{t_i}|y({x_i};\omega ),{\sigma ^2}] = \\ &{(2{\text{π}} {\sigma ^2})^{ - {N \mathord{\left/ {\vphantom {N 2}} \right. } 2}}}\exp \left\{ { - \frac{1}{{2{\sigma ^2}}}{{\left\| {t - \phi \omega } \right\|}^2}} \right\} 。\end{split} $

(8)

式中，向量 $t = {({t_1}, \cdots {t_N})^{\rm{T}}}$ ， $\omega = {({\omega _1}, \cdots {\omega _N})^{\rm{T}}}$ ， $ \phi $ 为 $ N \times (N + 1) $ 维矩阵， $\phi \left( {{x_n}} \right) = {\left[ {1,K({x_n},{x_1}), \cdots ,K({x_n},{x_N})} \right]^{\rm{T}}}$ 。

因此，对于给定样本集 $ {x_*} $ ，预测输出集 $ {t_*} $ 的条件概率为:

$ P({t_*}|t) = \iint P({t_*}|\omega ,{\sigma ^2})P(\omega ,{\sigma ^2}|t){\rm{d}}\omega {\rm{d}}{\sigma ^2} 。$

(9)

在贝叶斯框架下，该似然概率可设计到无限大，但为防止过拟合，为每个权值定义高斯先验概率分布来约束参数:

$ P(\omega |\alpha ) = \coprod\limits_{i = 0}^N N ({\omega _i}|0,\alpha _i^{ - 1}) 。$

(10)

式中， $\alpha = {({\alpha _0}, \cdots {\alpha _N})^{\rm{T}}}$ 为由超参数组成的(N+1)维向量。

因此，式(9)可转化为:

$ P({t_*}|t) = \iiint P({t_*}|\omega ,\alpha ,{\sigma ^2})P(\omega ,\alpha ,{\sigma ^2}|t){\rm{d}}\omega {\rm{d}}\alpha {\rm{d}}{\sigma ^2}。$

(11)

依据贝叶斯准则，通过已定义的先验概率，得到后验概率:

$ P(\omega ,\alpha ,{\sigma ^2}|t) = \frac{{P(t|\omega ,\alpha ,{\sigma ^2})P(\omega ,\alpha ,{\sigma ^2})}}{{P(t)}}。$

(12)

因无法直接计算后验概率 $ P(t|\omega ,\alpha ,{\sigma ^2}) $ ，将其分解为：

$ P(\omega ,\alpha ,{\sigma ^2}|t) = P(\omega |t,\alpha ,{\sigma ^2})P(\alpha ,{\sigma ^2}|t)。$

(13)

将式(13)代入式(11)有：

$ P({t_*}|t) = \iiint P({t_*}|\omega ,\alpha ,{\sigma ^2})P(\omega |t,\alpha ,{\sigma ^2})P(\alpha ,{\sigma ^2}|t){\rm{d}}\omega {\rm{d}}\alpha {\rm{d}}{\sigma ^2} 。$

(14)

则权重ω的后验概率分布为:

$ \begin{split} P(\omega |t,\alpha ,{\sigma ^2}) = & \frac{{P(t|\omega ,{\sigma ^2})P(\omega |\alpha )}}{{P(t|\alpha ,{\sigma ^2})}} = {(2{\text{π}})^{ - (N + 1)/2}}{\left| \sum \right|^{ - 1/2}}\\ & \exp \left\{ { - \frac{1}{2}{{(\omega - \mu )}^{\rm{T}}}{{\left| \sum \right|}^{ - 1}}(\omega - \mu )} \right\}。\end{split} $

(15)

后验协方差和均值分别为:

$ \sum = {({\sigma ^{ - 2}}{\phi ^{\rm{T}}}\phi + A)^{ - 1}} ，$

(16)

$ \mu = {\sigma ^{ - 2}}\sum {\phi ^{\rm{T}}}t 。$

(17)

式中， $A = {\rm{diag}}({\alpha _0}, \cdots {\alpha _N})$ 。

由于后验概率 $ P(\alpha ,{\sigma ^2}|t) $ 不能直接分解计算得到，采用狄拉克(Dirac Delta)函数近似计算：

$ P(\alpha ,{\sigma ^2}|t) = \delta ({\alpha _{MP}},\sigma _{MP}^2)。$

(18)

其中， $ {\alpha _{MP}},\sigma _{MP}^2 $ 为后验概率 $ P(\alpha ,{\sigma ^2}|t) $ 的最优解，即

$ {\alpha _{MP}} = \arg \max (P(\alpha |t)) ，$

(19)

$ \sigma _{MP}^2 = \arg \max (P({\sigma ^2}|t)) 。$

(20)

通过上述转化有:

$ P(\alpha ,{\sigma ^2}|t) \propto P(t|\alpha ,{\sigma ^2})P(\alpha )P({\sigma ^2})。$

(21)

因此有：

$ \begin{split} P(t|\alpha ,{\sigma ^2}) =& \int P (t|\omega ,{\sigma ^2})P(\omega |\alpha ){\rm{d}}\omega = \\&{(2\pi )^{ - N/2}}{\left| {{\sigma ^2}I + \phi {A^{ - 1}}{\phi ^{\rm{T}}}} \right|^{ - 1/2}}\\ & \exp \left\{ { - \frac{1}{2}{t^{\rm{T}}}{{({\sigma ^2}I + \phi {A^{ - 1}}{\phi ^{\rm{T}}})}^{ - 1}}t} \right\}。\end{split} $

(22)

对式(21)右边进行极大似然估计，可得:

$ L = \log (P(t|\log \alpha ,\log {\sigma ^2})) + \sum\limits_{i = 0}^N {\log } P({\alpha _i}) + \log P({\sigma ^2}) 。$

(23)

将式(17)代入式(23)整理得:

$ \begin{split} L =& \frac{1}{2}\left[ {\log \left| \sum \right| + \log \left| A \right| - {\sigma ^2}{t^{\rm{T}}}(t - \phi \mu )} \right] +\\ & \sum\limits_{i = 0}^N {(\alpha \log } {\alpha _i}) + N\log {\sigma ^2}。\end{split} $

(24)

对式(24)求偏导得:

$ \frac{{\partial L}}{{\partial \log {\alpha _i}}} = - \frac{1}{2}\left({\alpha _i}\sum\nolimits_{ii} + {\alpha _i}\mu _i^2 + 1\right)。$

(25)

式中： $ {\mu _i} $ 为式(17)中矩阵所对应的第i行平均权重值； $ {\sum _{ii}} $ 为式(16)后验协方差矩阵 $ \sum $ 的第i个对角元素。

假设 $ {r_i} = 1 - {\alpha _i}{\sum _{ii}} $ ，令式(25)为0，则有:

$ {\alpha _i}^\prime = \frac{{{r_i}}}{{\mu _i^2}} 。$

(26)

同理得:

$ {\sigma ^2}^\prime = \frac{{\left\| {t - \phi \mu } \right\|}}{{N - \sum\limits_{i = 0}^N {{r_i}} }} 。$

(27)

采用狄拉克(Dirac Delta)函数可将式(14)近似转化为：

$ P({t_*}|t) = \int P ({t_*}|\omega ,{\alpha _{MP}},\sigma _{MP}^2)P(\omega |t,{\alpha _{MP}},\sigma _{MP}^2){\rm{d}}\omega。$

(28)

又由于 $ P({t_*}|\omega ,{\alpha _{MP}},\sigma _{MP}^2) $ 和 $ P(\omega |t,{\alpha _{MP}},\sigma _{MP}^2) $ 均满足正态分布，因此：

$ P({t_*}|t) = N({t_*}|{y_*},\sigma _*^2) ，$

(29)

$ {y_*} = {\mu ^{\rm{T}}}\phi ({x_*})，$

(30)

$ \sigma _*^2 = \sigma _{MP}^2 + \phi {({x_*})^{\rm{T}}}\sum\nolimits_{} {\phi ({x_*})} ，$

(31)

$ \phi ({x_*}) = {[1,K({x_*},{x_1}), \cdots ,K({x_*},{x_N})]^{\rm{T}}}。$

(32)

选择合适的核函数对样本数据进行训练，将特征向量映射到高维空间。给定 $ \alpha $ ， $ {\sigma ^2} $ 初值，通过式(26)和式(27)进行迭代更新，待所有参数均满足收敛条件，迭代结束。此时，RVM回归预测模型确认完成。

2.2 加速度计温度误差建模与补偿

在RVM拟合方法中，核函数的选择对回归预测的计算复杂度和精确度产生直接影响。为兼顾精度与拟合速度，采用高斯核函数和多项式核函数构成的混合核函数，对加速度计的温度误差模型进行拟合:

$ K(x,{x_i}) = \lambda \exp ( - {\left\| {x - {x_i}} \right\|^2}/2{\sigma ^2}) + (1 - \lambda )(x \cdot {x_i} + 1)d。$

(33)

式中： $ {\sigma ^2} $ 为高斯核函数的宽度；d为多项式核函数参数； $ \lambda $ 为权重参数； $ {x_i} $ 为核函数中心。

基于RVM函数拟合的加速度计温度误差补偿方法主要包括数据归一、参数寻优和模型训练3个步骤进行。

1) 数据归一

为优化内存空间，加快参数寻优以及模型训练的速度，首先需要对加速度计组件温度数据和组件输出数据进行归一化处理，并记录归一化模型，处理方法如下式：

$ y = \frac{{{y_{\max }} - {y_{\min }}}}{{{x_{\max }} - {x_{\min }}}}(x - {x_{\min }}){\text{ + }}{y_{\min }}。$

(34)

式中， $ y $ 为归一化输出数据， $ {y_{\max }} = 1 $ ， $ {y_{\min }} = - 1 $ ， $ x $ 为归一化输入数据， $ {x_{\max }} $ 为输入数据的最大值， $ {x_{\min }} $ 为最小值。

2) 参数寻优

选择不同的核参数与权值参数将影响混合核函数的性能。采用网格寻优来优化混合核参数d和 $ {\sigma ^2} $ 以及权重参数λ的方法，来保证混合核函数具有更好的学习能力。根据经验，d，λ和 $ {\sigma ^2} $ 的取值范围为 $ \left[ {{2^{ - 10}},{2^{10}}} \right] $ ，取0.1为步长，将d，λ和 $ {\sigma ^2} $ 的取值以横、纵排列方式构成类似网格阵列。针对每个网格单元参数可得到对应的拟合函数模型，选取拟合准确率最高的一组参数作为最优参数，对应最优参数为 $ {d_{best}} $ ， $ {\lambda _{best}} $ 和 $ {\sigma ^2}_{best} $ 。

3) 模型训练

将归一化数据及最优参数代入进行训练，得到最佳拟合函数。此时根据实测数据温度变化即可推算对应的标度因数与偏值改变量，从而消除温度误差对测量结果的影响。

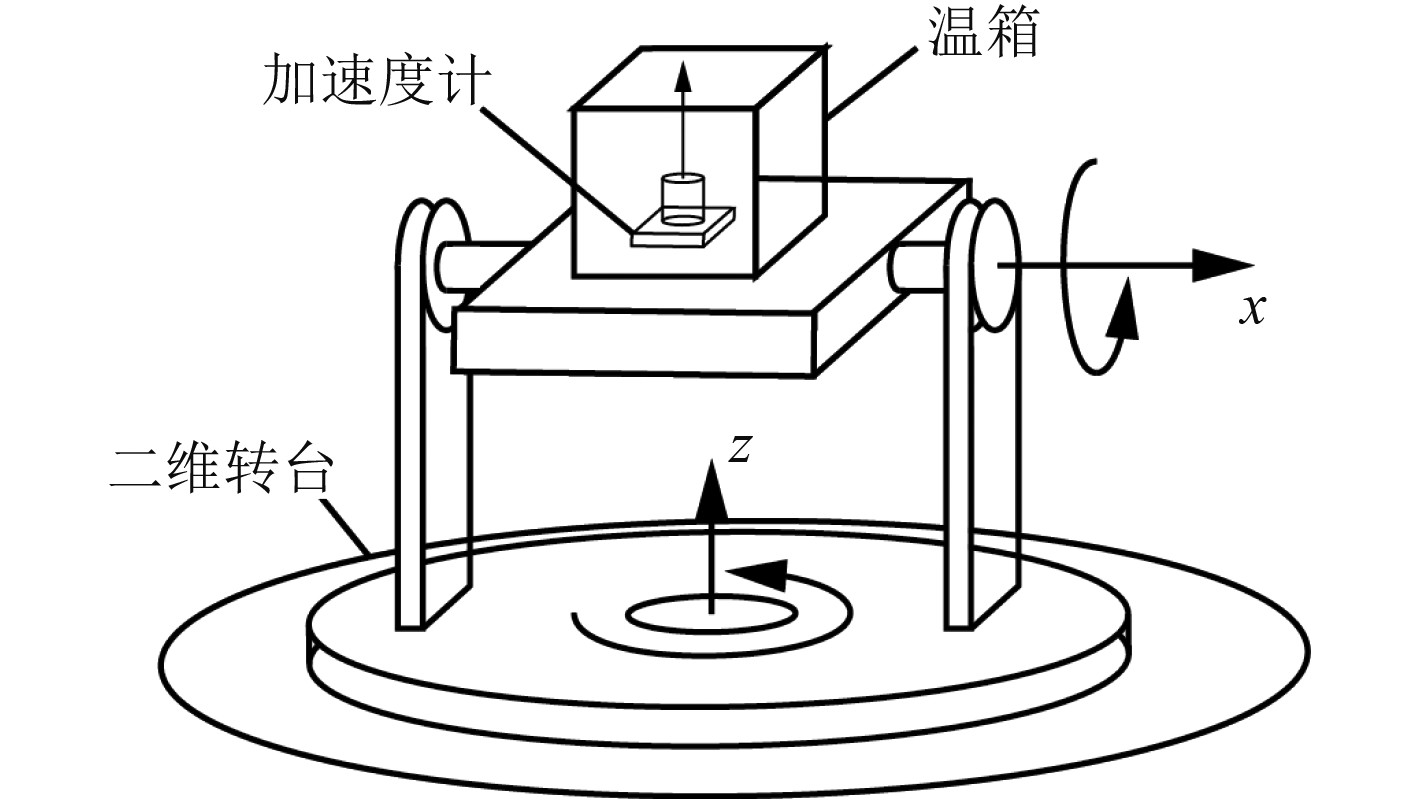
3 实　验

为验证所述方法，设计了实验对其有效性进行评估。具体实验装置如图4所示，待测加速度计通过安装孔固连在二维转台中央温箱内的台面上。调整工装，使加速度计的敏感轴方向在二维转台的外环与中环框架角度输出为0时，垂直指地。温箱的温度可通过外部控制电流在–30℃~+55℃的范围内随意调整，温度传感器测量温箱内的实时温度，并与加速度计输出的脉冲、二维转台的实时角度通过数据采集系统同步采集，发送到上位机。

根据式(4)，加速度计的偏值与标度因数均存在温度效应，二者的温度特性并不相同，因此在实验过程中，首先应考虑如何分离两项参数以避免耦合效应影响温度误差建模。当加速度计敏感轴方向位于水平面内时，其敏感的加速度应该为0，此时加速度计的输出仅受到偏值的影响；而加速度计敏感轴垂直本地水平面时，其敏感的加速度达到最大，为本地重力加速度G，从输出结果中扣除偏值温度误差，即可对标度因数的误差模型进行建模，从而实现二者的分离。具体的实验过程如下：首先控制二维转台x轴正向旋转90°，使加速度计敏感轴水平；控制温箱进行温度循环，温度循环范围设定为10℃~50℃，循环周期1 h，以100 Hz的频率同步记录温度传感器及加速度计的输出数据集为 $ \{ T_n^0,f_n^0\} _{n = 1}^N $ ，采用上位机软件通过相关向量机拟合加速度计偏值温度误差模型，并对加速度计的输出结果进行补偿。控制二维转台的x轴复位，此时加速度计敏感轴垂直指天，同样控制温箱进行相同的温度循环，并以100 Hz的频率同步记录温度及加速度计输出，并根据前面建立的加速度计偏值模型，扣除加速度计输出中偏值波动的影响，得到的数据集记作 $ \{ T_n^0,f_n^0\} _{n = 1}^N $ ，采用相关向量机建立加速度计标度因数温度误差模型，并对输出结果进行补偿。补偿前后的加速度计输出如图5所示，补偿前水平状态下加速度计的输出随温度变化发生明显改变，最大波动幅度达到了0.49 mG，经补偿后该误差被有效抑制，最大波动幅度降低了约50%，为0.27 mG。垂直状态下的数据同样可得到相同结论，补偿前的输出随温度变化的最大幅值为1.4 mG，补偿后该变化降低到0.28 mG，温度误差降低了一个数量级。

4 结　语

加速度计温度误差是惯性导航系统中不可忽视的误差之一，对导航精度有着重要影响，而自然工况下环境温度的变化可能引起加速度计标度因数以及零偏发生改变，造成测量精度严重下降，因此必须采取措施予以补偿。本文提出了一种基于相关向量机加速度计温度误差建模与补偿方法，并通过实验验证了该方法的有效性。经实验验证，补偿后的加速度计输出精度相较于补偿前提升了50%以上，温度误差得到了有效抑制。后续将进一步开展加速度计温度误差模型的分析研究，主要完成器件结构温度变形机理等工作，为加速度计的温度误差补偿提供理论支撑。