2. 中核武汉核电运行技术股份有限公司, 湖北 武汉 430074
2. China Nuclear Power Operation Technology Corporation, Ltd., Wuhan 430074, China
换热器是一种利用温度差来促进2种流体之间有效传热的装置[1]。在核能行业,换热器普遍用于设备冷却,支持安全相关设备执行功能,发挥重要功能[2]。换热设备经长时间运转后,由于介质的腐蚀、冲蚀、积垢等原因,使内外表面都有不同程度的结垢,甚至堵塞,严重影响换热器的性能[3]。对换热器性能指标建模和预测可提前判断换热器性能,优化换热器的维修策略,显著减少换热器停机时间[4]。
传统建模和预测算法主要基于经验方法或特定的热交换器动力学模型。例如污垢过程分析模型基于速率方程[5],其中污垢沉积增长速率被估计为一个确定性函数或一个随机近似[6]。污垢形成和物质沉积的过程是通过盐的结晶、流体流的颗粒沉积、生物物质的沉积和生长、工质中各种反应物的化学反应副产物和腐蚀等过程发生的,每一种单独的现象都以不同的速率(时间尺度)发生,因此,从基本原理建立准确的预测模型很困难[7-8]。
由于经验和基于模型预测技术的局限性,数据驱动预测方法得以发展。以数据驱动的方法,通过容易测量的热交换器参数来预测其性能。神经网络模型广泛用来模拟、优化和预测换热器的性能指标参数[9-11]。这些属于经典机器学习技术范畴的方法,通常受到数据规模的限制。
本文提出一种共享权重的长短时记忆神经网络,对换热器性能相关参数进行预测,有较高的预测精度,并能以较快速度收敛拟合。
1 换热器性能计算已知冷水和热水的进口温度、出口温度和流量,采用对数平均温差法(LMTD)计算相关性能参数,计算公式如下[12-13]:
| $ {Q}_{h}={{\rho }_{h}f}_{h}{C}_{ph}\left({T}_{hi}-{T}_{ho}\right),$ | (1) |
| $ {Q}_{c}={\rho }_{c}{f}_{c}{C}_{pc}\left({T}_{co}-{T}_{ci}\right),$ | (2) |
| $ {Q}_{e}=\frac{{Q}_{c}}{{Q}_{h}},$ | (3) |
| $ R=\frac{{T}_{hi}-{T}_{ho}}{{T}_{hi}-{T}_{ci}} ,$ | (4) |
| $ LMTD=\frac{\left({T}_{hi}-{T}_{co}\right)-\left({T}_{ho}-{T}_{ci}\right)}{\mathit{ln}\left(\dfrac{{T}_{hi}-{T}_{co}}{\left({T}_{ho}-{T}_{ci}\right)}\right)},$ | (5) |
| $ {U}_{h}=\frac{{Q}_{h}}{LMTD} ,$ | (6) |
| $ {U}_{c}=\frac{{Q}_{c}}{LMTD}。$ | (7) |
式中:
介绍方法中涉及的3种RNN和主要原理以及模型评估指标。
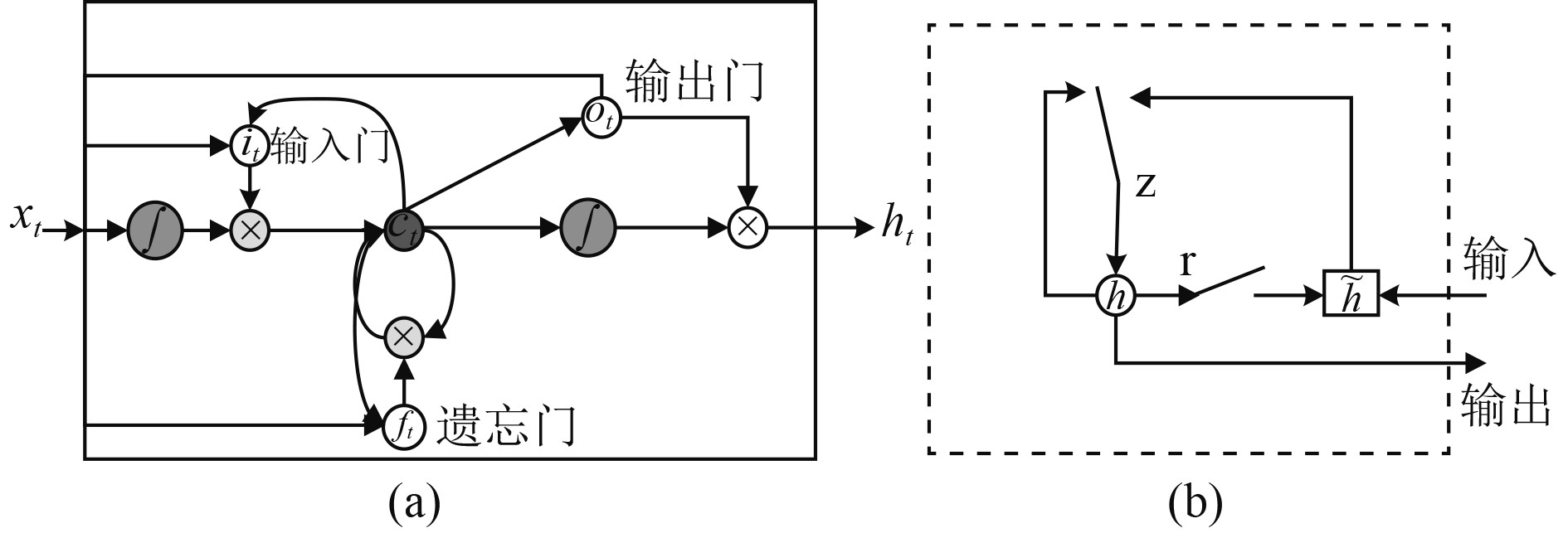
2.1 LSTM与GRU图1为LSTM和GRU算法模型示意图[14-15],LSTM结构包括输入门、忘记门和输出门。LSTM状态包含2个向量:一个隐藏的状态向量h和细胞状态c。在每个时间步, 输入门
|
图 1 LSTM和GRU算法模型示意图 Fig. 1 Schematic diagram of LSTM and GRU algorithm models |
| $ \begin{array}{c}{i}_{t}=\sigma \left({{\boldsymbol{W}}}_{{\boldsymbol{ih}}}{h}_{t-1}+{{\boldsymbol{W}}}_{{\boldsymbol{ix}}}{x}_{t}+{{\boldsymbol{b}}}_{{\boldsymbol{i}}}\right),\end{array} $ | (8) |
| $ \begin{array}{c}{f}_{t}=\sigma \left({{\boldsymbol{W}}}_{{\boldsymbol{fh}}}{h}_{t-1}+{{\boldsymbol{W}}}_{{\boldsymbol{fx}}}{x}_{t}+{{\boldsymbol{b}}}_{{\boldsymbol{f}}}\right),\end{array} $ | (9) |
| $ \begin{array}{c}{o}_{t}=\sigma \left({{\boldsymbol{W}}}_{{\boldsymbol{oh}}}{h}_{t-1}+{{\boldsymbol{W}}}_{{\boldsymbol{ox}}}{x}_{t}+{{\boldsymbol{b}}}_{{\boldsymbol{o}}}\right),\end{array} $ | (10) |
| $ \begin{array}{c}{g}_{t}={\rm{tan}}h\left({{\boldsymbol{W}}}_{{\boldsymbol{gh}}}{h}_{t-1}+{{\boldsymbol{W}}}_{{\boldsymbol{gh}}}{x}_{t}+{{\boldsymbol{b}}}_{{\boldsymbol{g}}}\right)。\end{array} $ | (11) |
其中:
| $ \begin{array}{c}{c}_{t}={f}_{t}\odot {c}_{t-1}+{i}_{t}\odot {g}_{t},\end{array} $ | (12) |
| $ \begin{array}{c}{h}_{t}={o}_{t}\odot {\rm{tan}}h\left({c}_{t}\right)。\end{array} $ | (13) |
其中,
GRU包括2个内部门变量中更新门z保护采用隐藏状态
| $ \begin{array}{c}{z}_{t}=\sigma \left({{\boldsymbol{W}}}_{z}{x}_{t}+{{\boldsymbol{U}}}_{z}{h}_{t-1}+{{\boldsymbol{b}}}_{z}\right),\end{array} $ | (14) |
| $ \begin{array}{c}{r}_{t}=\sigma \left({{\boldsymbol{W}}}_{r}{x}_{t}+{{\boldsymbol{U}}}_{r}{h}_{t-1}+{{\boldsymbol{b}}}_{r}\right),\end{array} $ | (15) |
| $ \begin{array}{c}{h}_{t}=\left(1-{z}_{t}\right)\odot {g}_{t}+{z}_{t}\odot {h}_{t-1}。\end{array} $ | (16) |
其中:
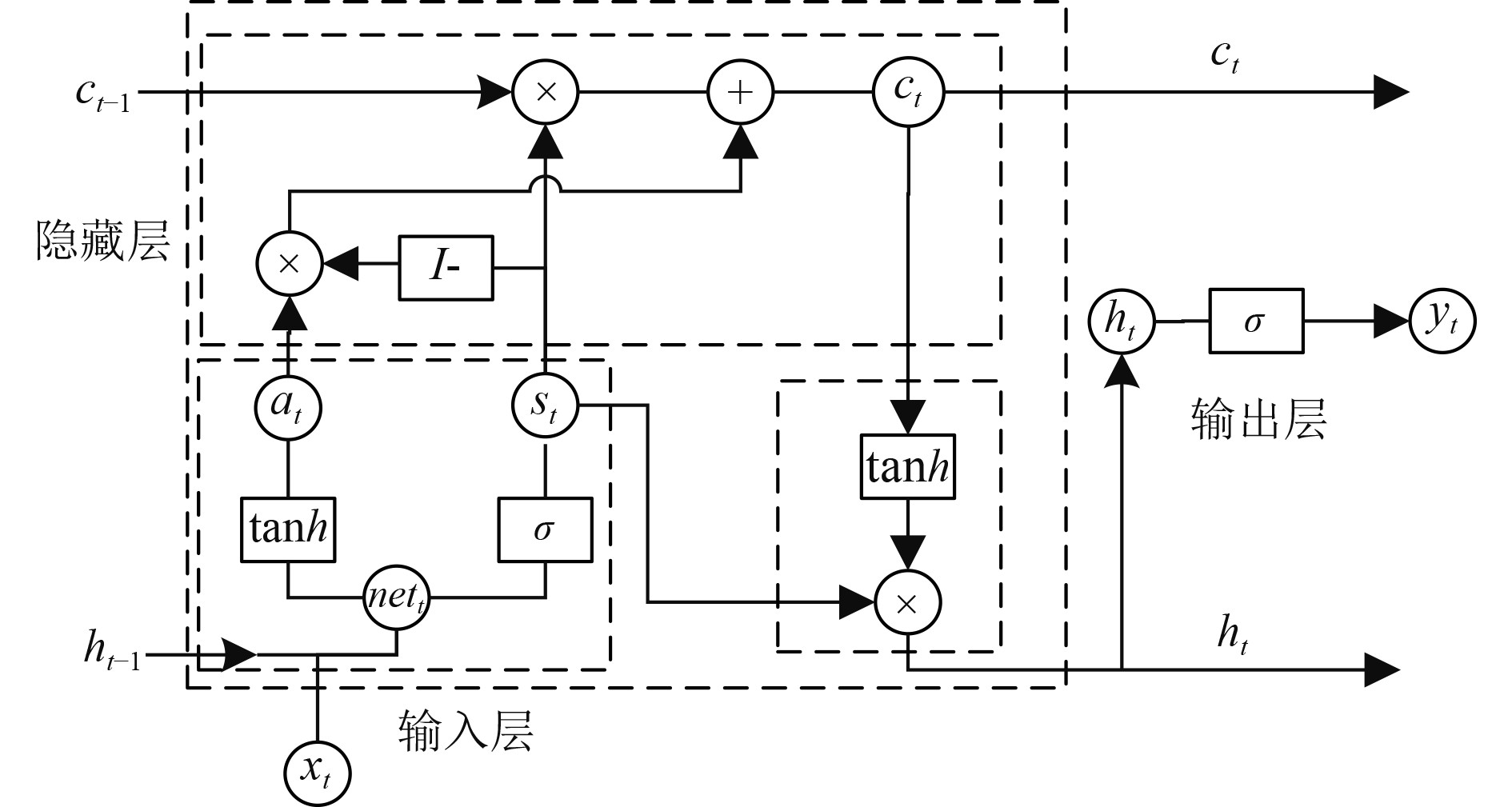
为了减少LSTM中需要优化的变量数量和训练时间,提出共享权长短期记忆网络(SWLSTM)。SWLSTM将输入门、输出门和遗忘门组合成一个新的门结构,称为共享门。SWLSTM网络结构如图2所示。
|
图 2 SWLSTM算法模型示意图 Fig. 2 Schematic diagram of SWLSTM algorithm model |
在时刻t时共享门和信息门的计算如下式:
| $ \begin{array}{c}{net}_{t}={w}_{h}{h}_{t-1}+{w}_{x}{x}_{t}+b,\end{array} $ | (17) |
| $ \begin{array}{c}{S}_{t}=\sigma \left({net}_{t}\right)=\sigma \left({w}_{h}{h}_{t-1}+{w}_{x}{x}_{t}+b\right),\end{array} $ | (18) |
| $ {a}_{t}=\tan h\left({net}_{t}\right)=\tan h\left({w}_{h}\cdot {h}_{t-1}+{w}_{x}\cdot {x}_{t}+b\right)。$ | (19) |
更新单元状态如下式:
| $ \begin{array}{c}{C}_{t}={s}_{t}*{C}_{t-1}+\left(1-{s}_{t}\right)*{a}_{t}。\end{array} $ | (20) |
计算隐藏层的输出如下式:
| $ {h}_{t}={s}_{t}*\tan h\left({C}_{t}\right)。$ | (21) |
输出层的预测值输出如下式:
| $ {y}_{t}=\sigma \left({z}_{t}\right)=\sigma \left({w}_{y}\cdot {h}_{t}+{b}_{y}\right) 。$ | (22) |
式中:
| $ \begin{array}{c}\left\{\begin{array}{c}\sigma \left(x\right)=y=\dfrac{1}{1+{e}^{-x}},\\ {\sigma }{{'}}\left(x\right)=y\left(1-y\right)。\end{array}\right.\\ \quad\; \left\{\begin{array}{c}\tan h\left(x\right)=y=\dfrac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}},\\ {\rm{tan}}{h}'\left(x\right)=1-{y}^{2}。\end{array}\right.\end{array} $ | (23) |
RMSE[16]定义为平方误差均值的平方根,公式如下:
| $ \begin{array}{c}RMSE=\sqrt{\dfrac{1}{{T}_{e}\displaystyle\sum _{i}^{Te}{\left({y}_{i}-{Y}_{i}\right)}^{2}}}。\end{array} $ | (24) |
式中:
1)数据集
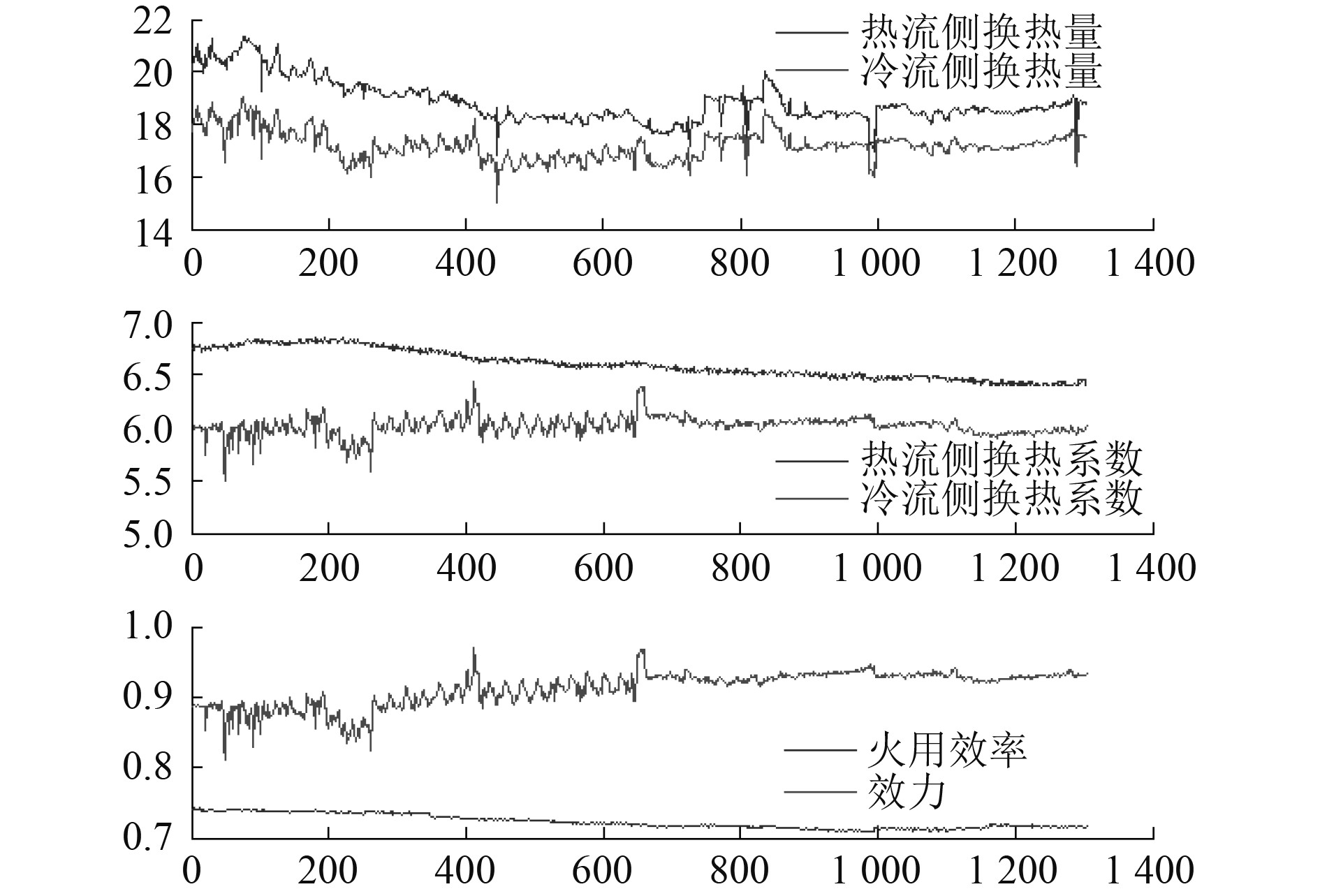
某换热器在线工艺监测参数冷水和热水的进口温度、出口温度和流量以每秒一次进行监测,本数据集获取到一个连续时间段的监测数据。由于原始数据采样较为频繁,首先针对明显异常的数据进行预处理(替代为前一取样值),按照每小时作为数据区间进行取平均值处理,获取得到按照小时间隔的工艺参数,各工艺参数随时间变化(h)如图3所示。

|
图 3 某换热器主要工艺参数监测值 Fig. 3 Monitoring values of main process parameters of a heat exchanger |
根据换热器性能计算公式,得到性能相关参数如图3。
2)输入数据构造
本文预测对象为图4中的火用效率和效力2个换热器无量纲性能指标,对其进行重组,以训练监督机器学习技术,其中最近的时间步长用作输入变量,下一个时间步长作为输出变量。
|
图 4 某换热器主要换热性能指标数据集 Fig. 4 Data set of main heat exchange performance indexes of a heat exchanger |
| $ \begin{array}{c}{{\boldsymbol{\beta }}}_{1}=\left[\begin{array}{cc}\begin{array}{cc}{s}_{\left(t1-k\right)}& \dots \\ {s}_{\left(t2-k\right)}& \dots \end{array}& \begin{array}{cc}{s}_{\left(t1-1\right)}& {s}_{t1}\\ {s}_{\left(t2-1\right)}& {s}_{t2}\end{array}\\ \begin{array}{cc}\dots & \dots \\ {s}_{\left(td-k\right)}& \dots \end{array}& \begin{array}{cc}\dots & \dots \\ {s}_{\left(td-2\right)}& {s}_{\left(td-1\right)}\end{array}\end{array}\right],\end{array} $ | (25) |
| $ \begin{array}{c}{{\boldsymbol{\beta}} }_{2}=\left[\begin{array}{c}\begin{array}{c}{s}_{t2}\\ {s}_{t3}\\ \dots \end{array}\\ {s}_{td}\end{array}\right],\end{array} $ | (26) |
| $ \begin{array}{c}{\boldsymbol{\varOmega}} =\left({{\boldsymbol{\beta}} }_{1}\text{,}{{\boldsymbol{\beta}} }_{2}\right)。\end{array} $ | (27) |
对上述数据做归一化处理:
| $ \begin{array}{c}{z}_{ij}=\dfrac{{\varOmega }_{ij}-{\min}\left(\varOmega \right)}{{\max}\left(\varOmega \right)-{\min}\left(\varOmega \right)}。\end{array} $ | (28) |
其中:
3)算法构造
在深度学习中,LSTM擅长解决时间序列问题,GRU是LSTM的变种。因此,选择LSTM、GRU作为与SWLSTM的比较模型。在python中的tensorflow框架中实现SWLSTM、LSTM、GRU。为确保比较的公平性,在这些模型中,将相同的参数设置为相等。这3种模型的参数详细情况见表1。
|
|
表 1 模型使用的参数设置 Tab.1 Parameter Settings used by the model |
4)收敛性参数设置
为了保证所提模型SWLSTM的预测精度,对其收敛性进行验证,然后进行比较。采用深度学习中常用的优化算法Adam验证收敛性,其参数设置如表2所示。为使每次运行的结果相同,设置收敛验证的SWLSTM的随机数种子相同。模型训练中RMSE作为损失函数。
|
|
表 2 模型训练中优化算法的参数设置 Tab.2 Parameter Settings of optimization algorithm in model training |
点预测结果评价是为了验证SWLSTM的精度。3个模型的点预测指标如表3所示。
|
|
表 3 3个循环神经网络的点预测指标 Tab.3 Point prediction indexes of three recurrent neural networks |
从表3可见,SWLSTM相对于另外2种循环神经网络,在预测精度并没有降低的情况下,训练时间减少。
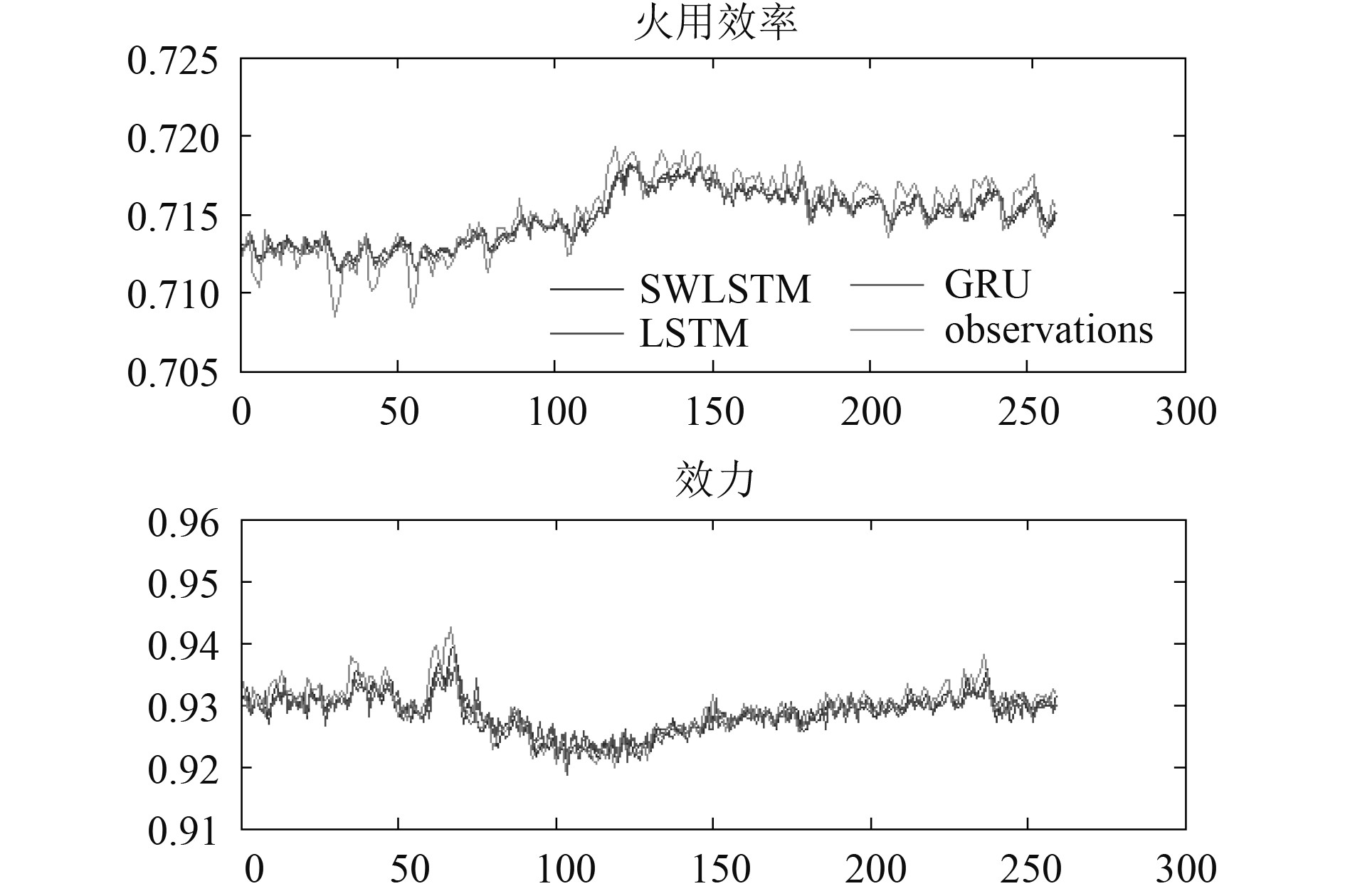
图5为3个模型在验证集上对换热器2个性能指标的点预测,3个循环神经网络模型的预测结果基本上都与观测值重合,具有很高的预测精度。
|
图 5 3个模型对换热器两个性能指标的点预测 Fig. 5 Point prediction of two performance indexes of heat exchanger by the three models |
典型的神经网络(RBFNN,BPNN,FFNN)被用于换热器相关参数的预测[17-19],神经网络模型的参数设置如表4所示。
|
|
表 4 神经网络模型[19]参数设置 Tab.4 Parameter Settings of neural network models |
图6为不同神经网络对换热器2个性能指标的预测。可见,RBFNN和FFNN对换热器2个性能指标的拟合效果较好。

|
图 6 不同神经网络模型对换热器两个性能指标的拟合 Fig. 6 Fitting of two performance indexes of heat exchanger with different neural network models |
3个典型神经网络的点预测指标如表5所示。与表3比较,尽管其预测精度不低,但训练时间上远逊于循环神经网络。
|
|
表 5 3个神经网络模型的点预测指标 Tab.5 Point prediction indexes of the three neural network models |
预知换热器未来的性能状态对其运维优化,提升核电机组的经济性十分重要。本文提出一种新的换热器性能预测方法共享权重长短时记忆网络模型,在不显著降低预测精度的情况下,减少了训练时间。SWLSTM保留了LSTM的功能,并通过共享权重减少了训练时间。相比于传统的神经网络模型,预测精度得到了提升,其训练时间更是大大减小。本文提出的方法应用于换热器2个无参量性能指标的预测,实验结果表明,SWLSTM能以较短的训练时间获得高精度的点预测。
利用壳管侧流体进口温度、出口温度和流量等在线测量值,计算系统与传热性能相关各个指标。实时训练历史数据,通过本模型提前预测换热器性能进行预测,主动预测换热器何时需要清洗可实现基于风险的维护计划,并优化处理速度、运行成本和维护成本,减少意外故障事件。
| [1] |
ZOHURI, B. Heat Exchanger Types and Classifications[J]. Compact Heat Exchangers, 2017(2): 19−56.
|
| [2] |
GTL Jr, ZIZZA M , DERIENZO P . Heat exchangers in nuclear power plants - ScienceDirect[J]. Advances in Nuclear Science and Technology, 1964: 41−106.
|
| [3] |
LIU Y , WANG X , MENG X , et al. A review on tube external heat transfer for passive residual heat removal heat exchanger in nuclear power plant[J]. Applied Thermal Engineering, 2018, 149.
|
| [4] |
UGWU H U , EBUNUOHA C , ORJI C U , et al. Maintenance optimization of a marine heat exchanger subject to fouling[J]. Journal of Emerging Trends in Engineering and Applied Sciences, 2010.
|
| [5] |
N. Epstein. General thermal fouling models[M]: fouling Science and Technology, 1988: 15–30 .
|
| [6] |
LALOT S, PALSSOR O, JONSSON G, et al. Comparison of neural networks and kalman filters performances for fouling detection in a heat exchanger[J]. International Journal of Exchanger, 2007, 8(1):151–168.
|
| [7] |
SS A , MCR A , HZ A , et al. Fouling modeling and prediction approach for heat exchangers using deep learning[J]. International Journal of Heat and Mass Transfer, 159.
|
| [8] |
张仲彬, 李煜, 杜祥云, 等. 水质对板式换热器结垢的影响权重及其机制分析[J]. 中国电机工程学报, 2012(32): 7. DOI:10.13334/j.0258-8013.pcsee.2012.32.015 |
| [9] |
MOHANRAJ M, JAYARAJ S, MURALEEDHARAN C. Applications of artificial neural networks for thermal analysis of heat exchangers – A review[J]. International Journal of Thermal Sciences, 2015(90): 150-172. DOI:10.1016/j.ijthermalsci.2014.11.030 |
| [10] |
IBRAHIM A H , NAFEY A S , HUSSAMI N . Prediction of the rate of heat transfer and fouling factor by using artificial neural network approach[J], 2007.
|
| [11] |
AHILAN C, KUMANAN S, SIVAKUMARAN N. Online performance assessment of heat exchanger using artificial neural networks[J]. International Journal of Energy & Environment, 2011, 2(5): 829-844. |
| [12] |
MAI T H, CHITOU N, PADET J. Method for the heat exchanger effectiveness calculation under variable dynamic conditions[J]. International Communications in Heat and Mass Transfer, 1999, 26(5): 739-748. DOI:10.1016/S0735-1933(99)00060-3 |
| [13] |
黄承明. 板式换热器循环水侧污垢系数计算及换热面积余量的选取[J]. 化工与医药工程, 2017, 38(3): 4. |
| [14] |
杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, 38(A02): 7. |
| [15] |
JOZEFOWICZ R , ZAREMBA W , SUTSKEVER I . An Empirical exploration of recurrent network architectures[C]// International Conference on Machine Learning. JMLR. org, 2015.
|
| [16] |
FRAPPIER V , NAJMANOVICH R J . Root Mean Square Error (RMSE) on the prediction of the effect of stabilizing mutations[J], 2014.
|
| [17] |
GUO Y , WANG F , JIA M , et al. Hybrid modeling method for predicting the cooling water outlet temperature in plate heat exchanger[C]// 2016 Chinese Control and Decision Conference (CCDC). IEEE, 2016.
|
| [18] |
CAO W, YOU X Y. The prediction of heat efficiency and pollutant emission of non-rated loaded condensing heat exchangers[J]. Clean Technologies and Environmental Policy, 2018, 20(10): 2299-2310. DOI:10.1007/s10098-018-1606-3 |
| [19] |
ŞAHIN F, OKBAZ A , ONBAŞ1OGLU H, et al. Prediction of the heat transfer rate of a fin and tube heat exchanger-using artificial neyral network trained and tested with experimental date[C]// 14th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, 2019.
|
 2023, Vol. 45
2023, Vol. 45
