0 引　言

船舶主机设备是船舶的核心，其正常运作对于船舶运行和安全性至关重要。而船舶主机设备振动对这些系统都会产生影响^[1]，传统的控制方法对设备振动的中心点无法精准定位，因此，需要对船舶主机设备的振动进行有效的控制和管理，以确保船舶的安全和稳定运行。

杨俊等^[2]提出船舶推进轴系振动控制方法，但该方法在不同的设备特性和环境条件下，无法进行灵活的调节和控制，减震效果一般。谢溪凌等^[3]提出船舶动力与传动装置振动控制方法，但该方法对低频率振动有控制效果，对中频和高频的振动达不到控制效果。

随着人工智能技术的高速发展，智能控制对设备能够进行更加精准地控制，在船舶主机设备振动控制领域，可以利用智能技术对设备的振动进行监测、分析和控制。为此，本文研究船舶主机设备振动智能控制方法，可以更精准，更快速地实现设备振动检测。

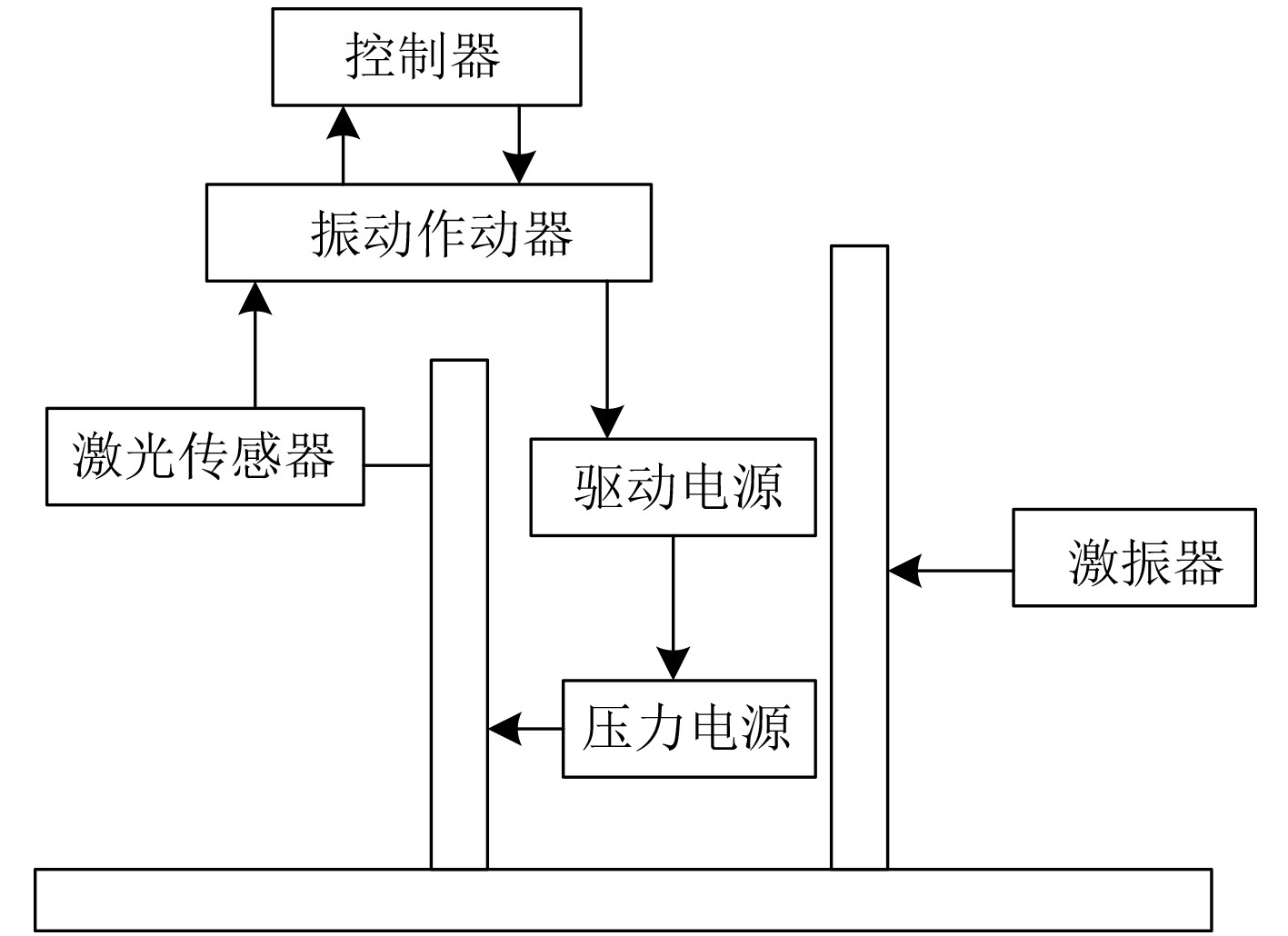
1 船舶主机设备振动控制方法

针对现有船舶主机设备振动控制方法，在实际应用中出现的问题，提出一种新型的振动控制方法。为确保应用新方法不影响船舶正常运行，需要安装硬件设备，作为实施此方法的基础^[4]。图1为新振动控制方法的硬件要求。为了确保新振动控制方法不影响船舶的正常运行，必须满足新振动控制方法的硬件要求。采用有限元分析法得到主机设备振动的详细数据，分析产生振动的主机设备具体位置，并结合振动作动器对产生振动的主机设备进行有效的振动控制处理。

1.1 基于有限元构建船舶主机设备模型

根据主机设备结构，构建基于有限元的主机设备模型，通过节点导入有限元建模方法，把CAD软件内的主机设备节点坐标数据先部署再提取。主机设备有限元建模操作步骤见图2。

有限元建模选用Ansys软件包参数化设计语言^[5]。APDL参数化编程与有限元批处理分析技术是有限元计算中最先进的技术之一，与Ansys软件具有良好的兼容性和包容性。通过使用APDL参数化编程，可以实现复杂有限元计算流程，提高分析效率。

常用的有限元模型结构基本都是三维结构，绘制或修改三维网格布局要求在三维环境下。应用Auto CAD软件在三维空间中实行船舶主机设备振动筛筛体网格布局，构建的主机设备有限元模型是一种简化模型，网格布局要求参考主机设备的工程图纸和简化要求，根据辅助线来完成精确的节点定位。在绘制好的单个三维网格布局图的每个交点处设立节点，区分构造复杂的不同图层。筛体由方梁、侧板和筋板等组成，建立节点后需要把其他无用层进行隐藏处理，保留需要的节点层。通过有限元模型来分析主机设备振动^[5]，由振动模态得知船舶结构大部分为多自由度的振动系统，主机设备安装基座 $ p $ 点到船体外板 $ l $ 点的传递函数 $ {H_{lp}}\left( \omega \right) $ 用公式表达为：

$ {H}_{lp}\left(\omega \right)={\displaystyle \sum _{i=1}^{n}\left[\frac{{\psi }_{pi}\cdot{\psi }_{li}}{{a}_{i}\left({\lambda }_{i}\right)}+\frac{{\psi }_{pi}^{*}\cdot{\psi }_{li}^{*}}{{a}_{i}^{*}\left({\lambda }_{i}^{*}\right)}\right]} 。$

(1)

式中： $ {\lambda _i} $ 为船舶结构振动的复模态频率； $ {\psi _i} $ 为复振型； $ {a_i} $ 为 $ {\lambda _i} $ 、 $ {\psi _{li}} $ 与船舶结构的复模态质量。

1.2 电力作动器控制策略的设计

应用电力作动器完成主机设备振动智能控制时，通过互相对称的2组偏心质量块式电力作动机构形成用于控制主机设备振动的振电力作动器。采用伺服三环控制对主机设备振动控制作动器进行环路设计，电流环调节器是 $ ACR $ ， $ {\rm{ASR}} $ 为转速环调节器， $ {\rm{APR }}$ 为位置环调节器， $ {\rm{PI}} $ 对转速环进行掌控，比例调节器控制位置环。基于电力作动器的主机设备振动输出力控制策略见图3。

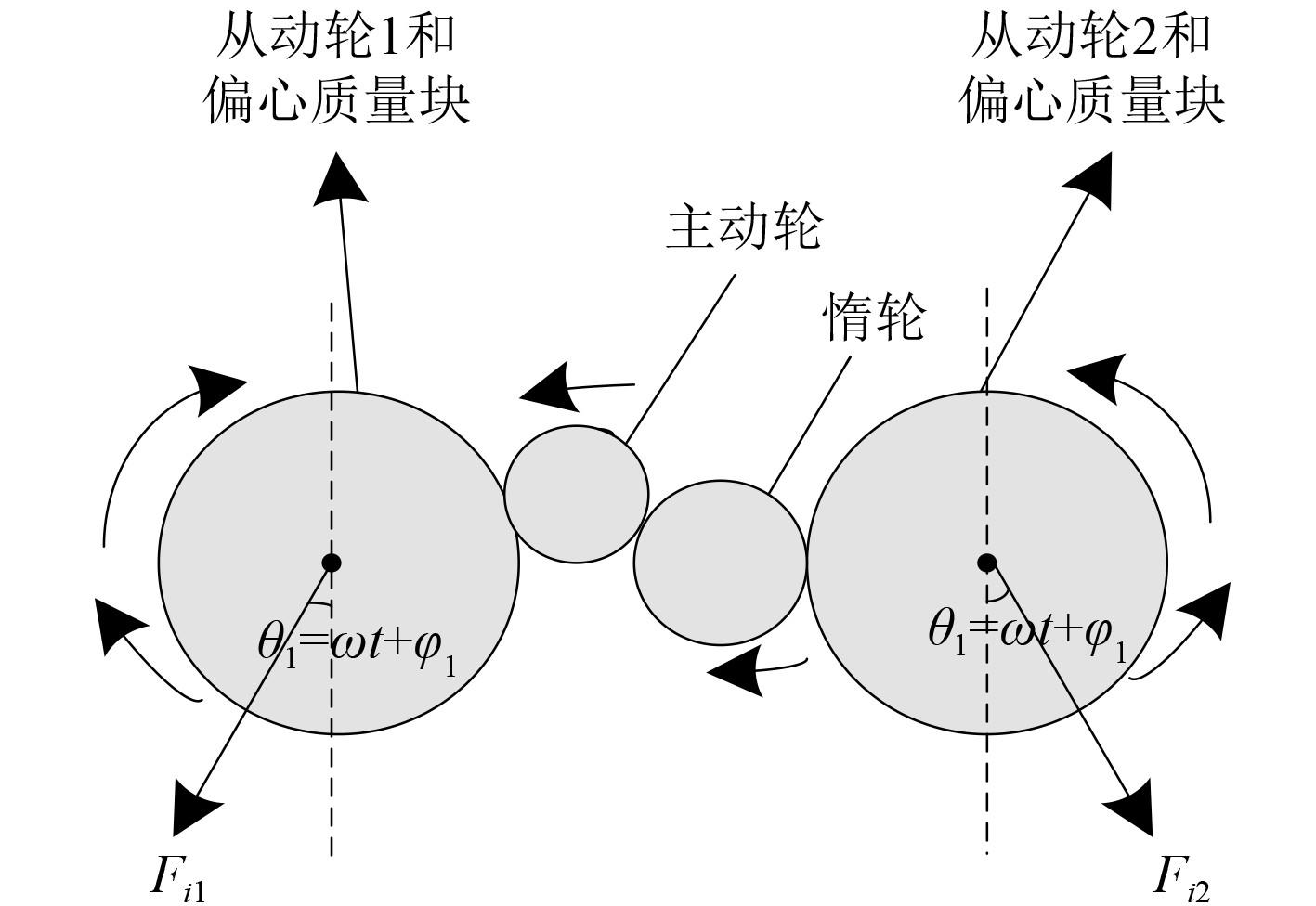
当需要控制输出的消振力时，通过电机主动轮启动偏心质量块，同时调整偏心质量块的位置来实现。图4为单组偏心质量块组件结构受力分析图。

图中，偏心质量块旋转角速度用 $ \omega $ 表示，第 $ i $ 组偏心质量块原始相位用 $ {\varphi _i} $ 表示， $ {\theta _i} $ 代表实际相位，2组偏心质量块输出的垂直消振力分别为F₁和F₂，第 $ i $ 组2个偏心质量块受离心力的影响分别用 $ {F_{i1}} $ 和 $ {F_{i2}} $ 表示（ $ i = 1,2 $ ）。如果2组电力作动器机构内偏心质量块产生同样的旋转频率，用公式表示为：

$ {F_1} = {F_{11}} + {F_{12}} = 2m{\omega ^2}r\cos \left( {\omega t + {\varphi _1}} \right)，$

(2)

$ {F_2} = {F_{21}} + {F_{22}} = 2m{\omega ^2}r\cos \left( {\omega t + {\varphi _2}} \right)。$

(3)

公式中偏心质量块的重量半径用 $ m $ 表示，偏心质量块的旋转半径用 $ r $ 表示。通过对式（2）和式（3）合成获得合成垂直消振力，用公式表达为：

$ F = 4m{\omega ^2}r\cos \left( {\frac{{{\theta _1} - {\theta _2}}}{2}} \right)\cos \left( {\frac{{{\theta _1} + {\theta _2}}}{2}} \right)。$

(4)

通过式（4）可知，控制2组偏心质量块的相位差与相位和，就是控制船舶主机设备垂直消振力的力幅与相位。

设计2台独立的方波电机，控制2台电机的转动速度就可以掌控偏心质量块的相位 $ {\theta _1} $ 和 $ {\theta _2} $ 。通过掌控 $ {\theta _1} $ 和 $ {\theta _2} $ 实现控制输出消振力力幅， $ {\theta _1} = {\theta _2} $ 时，2组偏心质量块输出组件力F₁和F₂处在同一个相位，最大消振力的输出幅值是 $ 4m{\omega ^2}r $ ； $ {\theta _1} = - {\theta _2} $ 时，2组不同相位的偏心质量块输出组件力F₁和F₂，0代表F₁和F₂输出的消振力，完成船舶主机设备振动控制。

2 结果与分析

为了验证本文方法对船舶主机设备振动的控制能力，以其船舶为实验对象，该船主机设备参数如表1所示。用电力作动器对实验对象的主机设备进行消振控制实验，采用轴系振动控制、传动装置振动控制和本文方法进行实验对比。电力作动器基本指标如表2所示。

2.1 有限元建模效果

通过有限元建立主机设备模型，如图5所示。通过本文方法建立的有限元模型可以可视化展现的主机电磁性能、振动和热特性等，更准确地模拟主机的工作过程，可以更好模拟设备振动情况。

2.2 振动控制效果分析

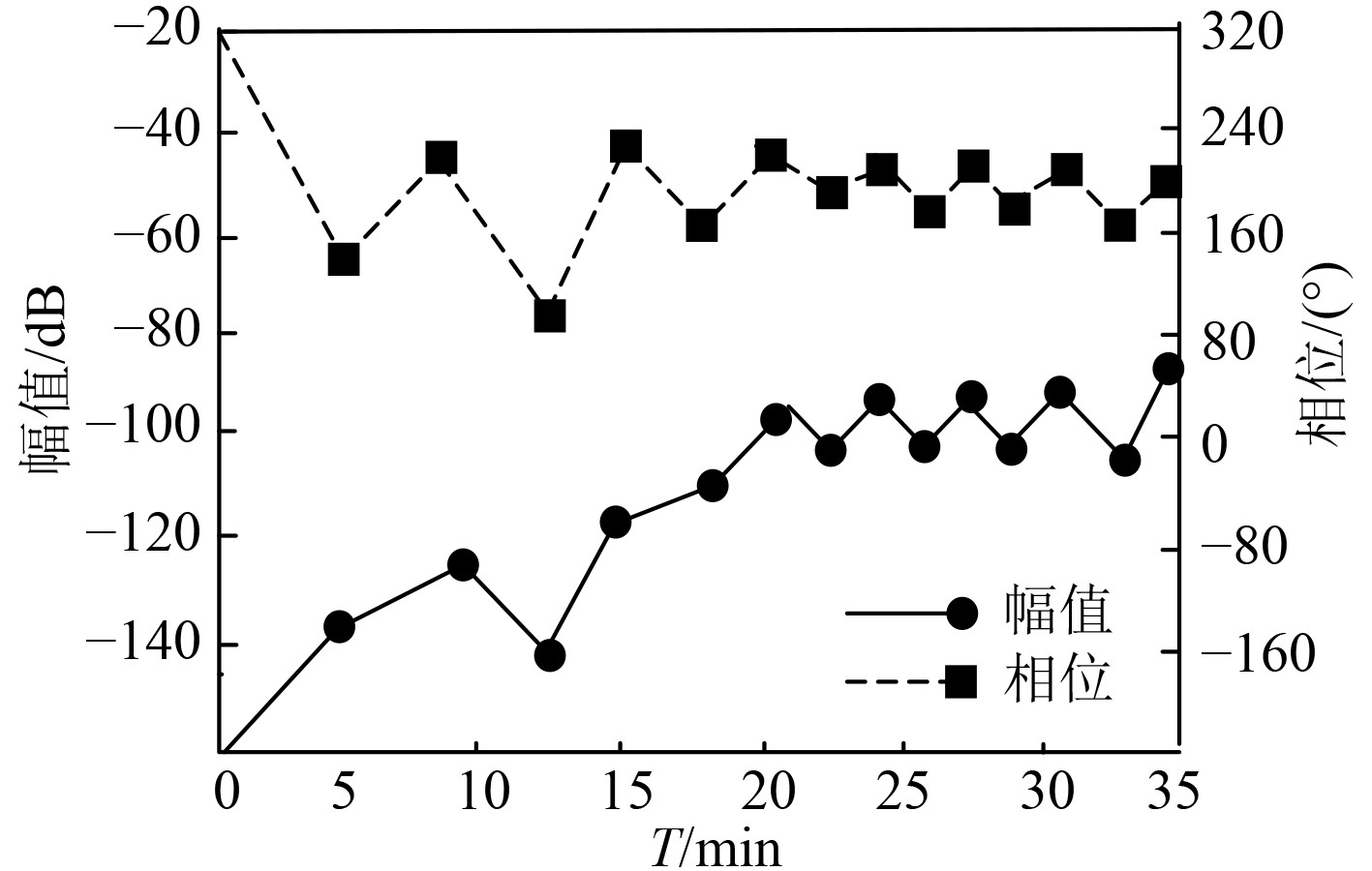
对本文方法控制振动后的船舶齿轮箱的稳定性进行实验分析，前15 min没有加入控制，后15 min加入控制，实验结果如图6所示。通过图6可知，在控制齿轮箱振动前的幅值波动幅度大且不稳定，在第15 min时，加入本文方法控制后的齿轮箱幅值波动慢慢稳定，相位也是同样情况。实验证明，采用本文方法可有效控制齿轮箱的震动，保证其稳定运行。

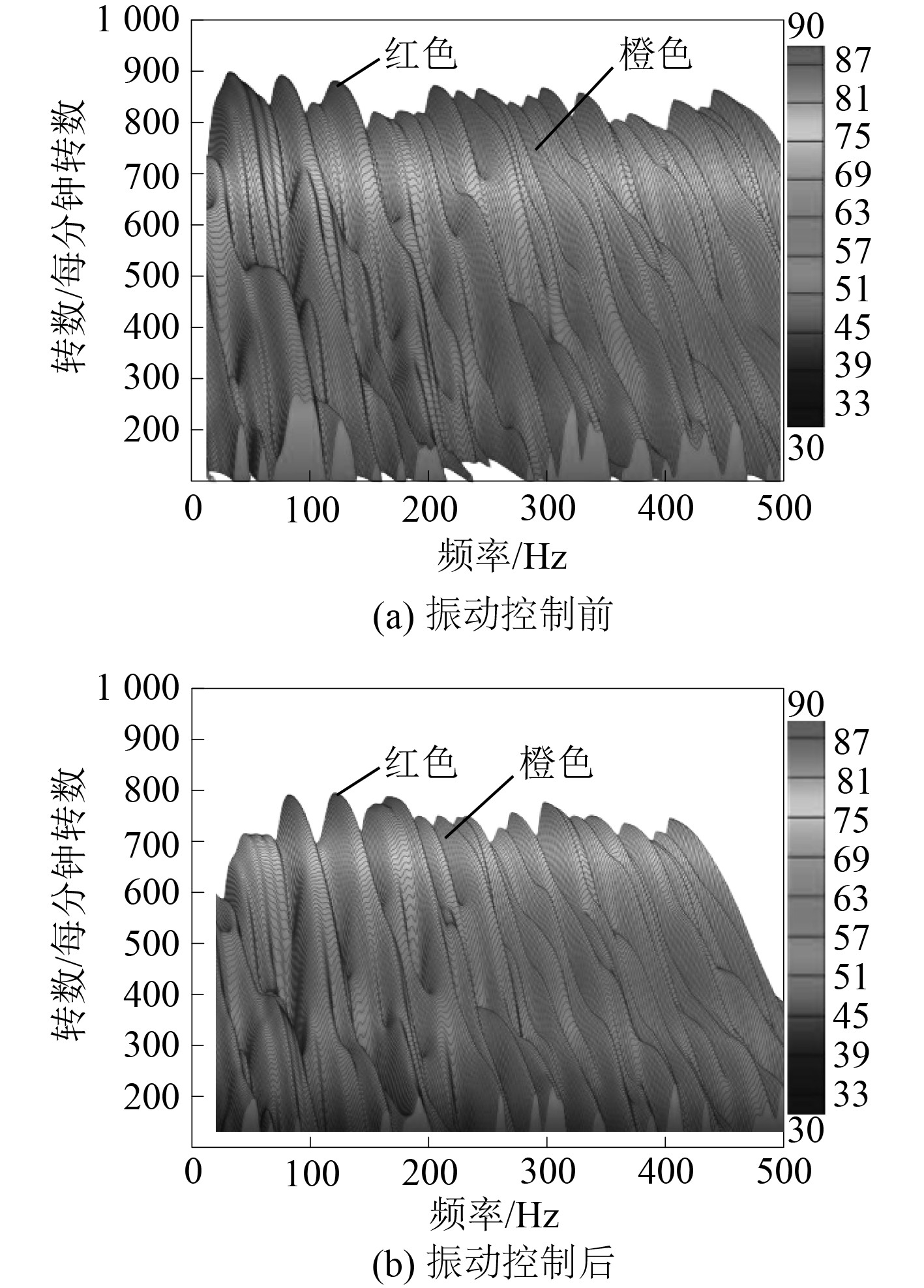
图7为船舶主机振动控制前后的对比结果。可以看出，振动控制前主机转数波动大，振动控制后机转数波动小，显著降低了红色及橙色分布面积。实验证明，本文方法可以有效控制船舶主机振动，控制振动的效果好。

3 结　语

为了解决船舶主机设备振动问题，对主机设备振动进行实验分析。结果表明，采用本文方法后的主机设备振动显著降低，对主机设备振动的智能控制效果好，能够获取更精准的振动位置及振动数据，不影响船舶的正常运行。