2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
船舶作为主要水上运输工具,在航运中起着极其重要的作用[1]。在这种情况下,长期在海上作业面对瞬息间千变万化的海洋各种水运环境的船舶所承受的强度非常大。船体在航行中不断受到海水的侵蚀,长期积累后会导致船舶的结构疲劳,致使船舶出现结构质量问题[2]。疲劳损伤被认为是船舶和海洋工程结构的主要损伤形式之一[3]。
在船体结构疲劳强度计算时,一般仅考虑船舶受到的波浪载荷作用,忽略了局部结构受到的高频载荷,如主机基座结构会受到高频主机振动载荷的作用。因此,为了能准确的预报恶劣海况下的主机基座结构疲劳强度,有必要考虑波浪载荷和主机振动载荷联合作用下对疲劳强度的影响。通常情况下,如果仅考虑线性波浪载荷的作用时,船舶的应力响应峰值是一个窄带过程,频率分布在一个较小的范围内[4]。对于这样一个窄带随机平稳过程,应力峰值或者说应力幅值的2倍可以看作等于应力范围,Bendat等[5]学者推导出了疲劳损伤的计算表达式。当作用的载荷为高低频载荷联合作用时,此时的窄带过程变成了宽带过程,窄带过程的计算方法不再适用。高低频载荷联合作用下的应力响应谱多呈现出双峰谱的形式,对于这种双峰谱的处理,工程上通常直接在2个峰之间的某一个频率下将其分成2个单峰窄带谱,接着对这两个窄带谱分别进行分析计算,计算每个谱的相关谱参数如零阶矩、一阶矩、二阶矩和四阶矩等来与整个宽带的各阶矩联系起来,中国CCS船级社、美国ABS船级社等[6-8]的相关规范多是采用这种叠加谱距的思想来进行双峰谱密度函数的计算。除此之外,还可以采用时域统计计数的方法计算高低频应力同时存在时的船体结构应力响应,然后则可以采用线性累积损伤理论的疲劳计算方法,再结合雨流计数法和S-N曲线进行疲劳强度的计算和分析[9]。
因此,本文开展了高低频载荷联合作用下的主机基座结构的疲劳强度计算研究,结合双峰谱疲劳计算理论,提出一种计及主机振动载荷的高低频载荷联合作用下主机基座疲劳强度计算方法。首先,采用线性频域的谱分析法直接计算波浪载荷作用下的主机基座结构热点疲劳损伤;然后采用时域分析计算法和S-N曲线计算出主机振动载荷作用下的热点疲劳损伤;其后,结合双峰谱疲劳计算理论,对高低频载荷耦合作用下的应力响应谱进行计算。
1 理论阐述 1.1 基于频域内谱分析法的疲劳强度理论通常将船舶在某一海况下受到的波浪载荷进行加载计算,得到船体结构的应力响应,然后进行应力响应谱的计算。关于应力的响应谱,首先就必须做好波浪谱的选择,通常在设计中使用的是Pierson-Moskowitz谱(简称P-M谱),即ISSC双参数谱,这是国际船舶结构会议(ISSC)所建议采用的标准波浪谱。该波浪谱可以通过不同的控制参数而被记入不同的形式,如果2个参数分别用平均跨零周期和有义波高来表示,波浪谱的表达式为:
| $ G_{\eta\eta}(\omega)=\frac{H_S^2}{4\pi}\left(\frac{2\pi}{T_z}\right)^4\omega^{-5}\exp\left(-\frac{1}{\pi}\left(\frac{2\pi}{T_z}\right)^4\omega^{-4}\right), $ | (1) |
在计算中,船舶受到的波浪响应频率应该选取遭遇频率
| $ \omega_e=\omega\left(1+\frac{2\omega U}{g}\cos\theta\right),$ | (2) |
式中:
对应的波能谱
| $ G_{\eta\eta}(\omega)d\omega=G_{\eta\eta}(\omega_e,\theta)d\omega_e,$ | (3) |
对于航向角为
| $ G_{XX}(\omega_e,\theta)=|H_{\sigma}(\omega_e,\theta)|^2\cdot G_{\eta\eta}(\omega_e,\theta),$ | (4) |
式中,
一般认为,应力交变过程中的应力峰值服从统计上的Rayleigh分布,在每一个短期海况下,因此其概率密度函数可以表示为:
| $ f_{\sigma}(\sigma)=\frac{\sigma}{m_0}\exp\left(-\frac{\sigma^2}{2m_0}\right),\;\;0\leqslant\sigma\leqslant\infty。$ | (5) |
式中:
在计算得到应力范围的长期分布后,进行相应的疲劳累积损伤度的计算。疲劳累积损伤度可直接由下式计算得到:
| $ D=\frac{N_L}{A}\int_0^{+\infty}S^m\frac{\xi}{\alpha}\left(\frac{S}{\alpha}\right)^{\xi-1}\exp\left[-(\frac{S}{\alpha})^{\xi}\right]\mathrm{d}S,$ | (6) |
考虑
| $ \begin{split} D =& \frac{{{T_d}}}{A}\Gamma (1 + m/2)\sum\limits_{n = 1}^{{N_{load}}} {{p_n}\sum\limits_{i = 1}^{{n_S}} {\sum\limits_{j = 1}^{{n_H}} {{p_i}{p_j}{\nu _{ijn}}{{(2\sqrt {2{m_{0ijn}}} )}^m}} } } =\\& \frac{{{\nu _0}{T_d}}}{A}\Gamma (1 + m/2)\sum\nolimits_{n = 1}^{{N_{load}}} {p_n}\sum\nolimits_{i = 1}^{{n_S}} \sum\nolimits_{j = 1}^{{n_H}},\\&{{p_i}{p_j}{r_{ijn}}{{(2\sqrt {2{m_{0ijn}}} )}^m} \leqslant \eta }。\\[-15pt] \end{split} $ | (7) |
式中:
计算双峰谱概率密度函数疲劳强度的基本思路首先设
| $ Y(t)=X_1(t)+X_2(t),$ | (8) |
因此,两者加和后的
| $ G_Y(f)=G_1(f)+G_2(f),$ | (9) |
同样,
| $ m_{n,Y}=\int_0^{\infty}f^nG_Y(f)\mathrm{d}f=m_{n,1}+m_{n,2}。$ | (10) |
假设
| $ P(t)=X_1(t)+R_2(t),$ | (11) |
对于窄带高斯过程,
当暂时不考虑高频部分的高应力区时,
| $ \begin{split}\overline{D}_P= & \frac{\nu_{0,p}T\overline{S}_P^m}{K}=\frac{\nu_{0,p}T}{K}(2\sqrt{2})^m\Gamma\left(\frac{m}{2}+1\right)\times \\ & \left[m_1^{*\frac{m}{2}+2}\times \left(1-\sqrt{\frac{m_2^*}{m_1^*}}\right)+\sqrt{\text{π}m_1^*m_2^*}\dfrac{m\Gamma\left(\dfrac{m}{2}+\dfrac{1}{2}\right)}{\Gamma\left(\dfrac{m}{2}+1\right)}\right],\\ & \end{split} $ | (12) |
窄带过程
| $ \overline{D}_{HF}=\frac{\nu_{0,2}T}{K}(2\sqrt{2})^mm_2^{*\frac{m}{2}}\Gamma\left(\frac{m}{2}+1\right)。$ | (13) |
基于窄带假设,基于双峰谱密度函数的疲劳损伤
| $ \overline{D}_Y=\frac{\nu_{0,Y}}{K}(2\sqrt{2})^m\Gamma\left(\frac{m}{2}+1\right)=\overline{D}_P+\overline{D}_{HF}=\rho\overline{D}_{Y,NB}。$ | (14) |
以1艘长约135 m的某船舶为例进行计及主机振动载荷的高低频载荷联合作用下主机基座结构疲劳损伤直接计算。表1和表2分别为该船所选的计算点信息以及波浪载荷基本参数。
|
|
表 1 疲劳计算热点位置 Tab.1 Location of fatigue calculation hotspot |
|
|
表 2 疲劳计算基本参数 Tab.2 Basic parameters of fatigue calculation |

|
图 1 主机基座有限元模型 Fig. 1 Finite element model of main engine base |
算例目标船的主机基座结构所用高强度钢材料的理论屈服极限为390 MPa,相关疲劳强度计算规范如CCS规范中给出的S-N曲线只适用于普通钢材料的疲劳计算,同时没有对应节点形式的S-N曲线,故通过试验得到对应高强度钢材料节点的S-N曲线。试验所得S-N曲线如表3所示。表中,
|
|
表 3 S-N曲线参数参数 Tab.3 Experimental S-N curve parameters |
波浪载荷计算的相关波浪参数确定后,即可利用三维水动力波浪载荷的计算程序软件进行波浪载荷作用下的响应计算,在软件中可以计算得到各规则波中的运动响应、选取的计算剖面载荷、水动压力等载荷成分。
本船为北大西洋航线,选取的海况为北大西洋海况。通过求出的应力响应传递函数及该船的航行海况,依据式(5)可得到应力响应谱,应力传递函数如图2和图3所示。
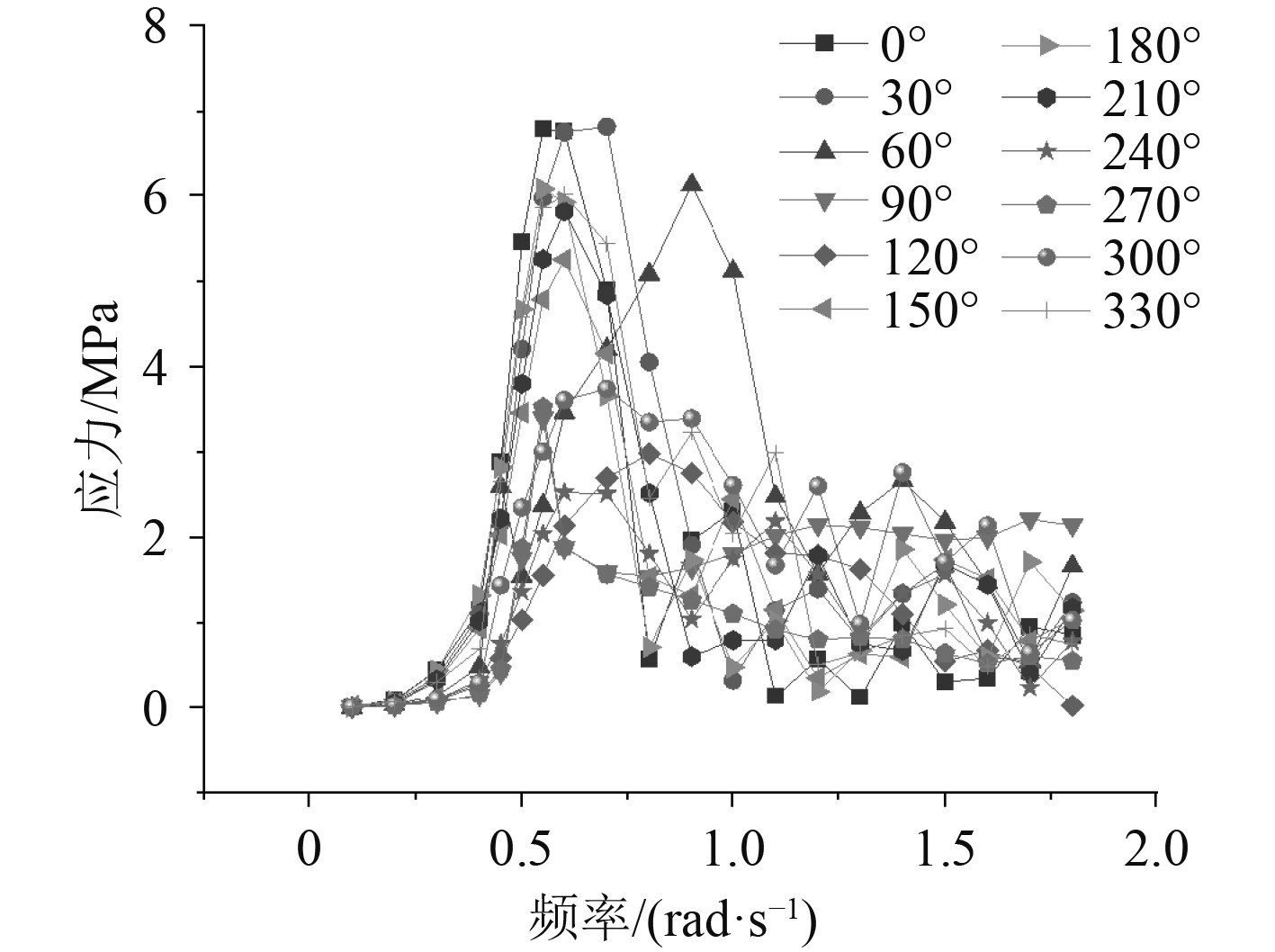
|
图 2 计算热点hotspot1应力传递函数 Fig. 2 The stress transfer function of hotspot1 |
根据谱分析法的理论,编写循环语句可计算得到各个短期海况的损伤并根据累积损伤理论进行线性叠加,最终完成7个计算热点在全海况的疲劳损伤度
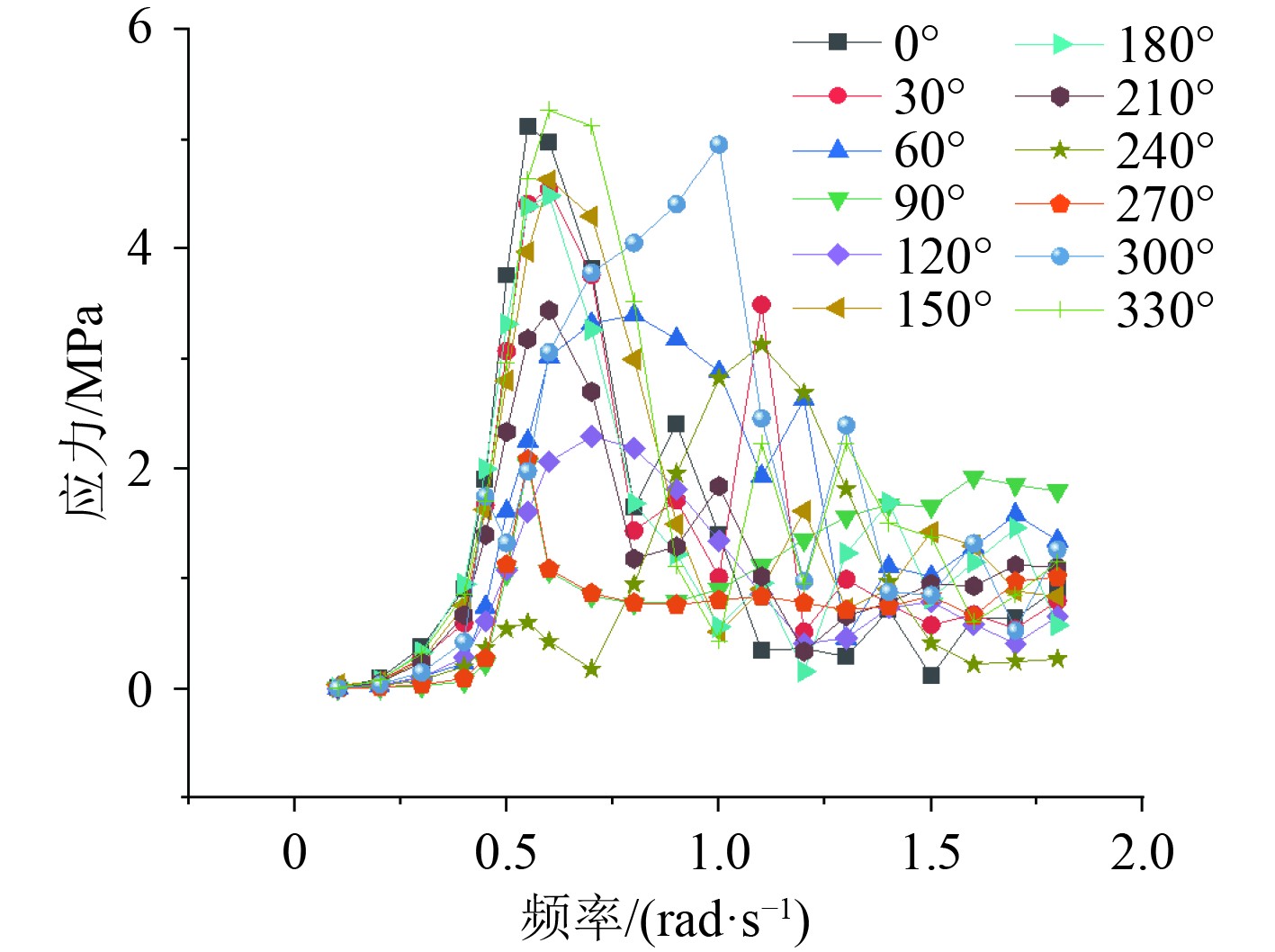
|
图 3 计算热点hotspot4应力传递函数 Fig. 3 The stress transfer function of hotspot4 |

|
图 4 趾端热点细化有限元模型图 Fig. 4 Fingertip hot spot refinement finite element model diagram |
|
|
表 4 低频波浪载荷作用下的谱分析法疲劳损伤计算结果 Tab.4 Fatigue damage calculation results of spectral analysis under low frequency wave load |
高频振动载荷有随机载荷和简单载荷等形式,而船舶主机的振动形式多为简单正弦振动,在本文的计算中,采用简单振动载荷中的正弦形式的振动载荷进行高频振动载荷作用下的疲劳强度计算研究。
对主机基座模拟施加稳态正弦形式的振动载荷,计算得到主机基座结构热点位置的应力响应图,计算时假定船舶航行主机以同一振动频率产生振动载荷作用。对于正弦形式的振动来说,需要频率(周期)和幅值来确定整个振动形式,利用有限元软件进行模拟加载。结合实际工作需求和主机基座结构特点,通过查阅相关资料,目标计算船的主机内部含有2个转子,分别为:燃气发生器转子,质量为352.25 kg;动力涡轮转子,质量为275.44 kg,故主机转子总质量为627.69 kg,偏心距为6×10−5m,计算选取激励振动频率为40 Hz。则在相应频率下的主机激励振动力幅值按下式计算:
| $ F_z=me\times(2\text{π}n)^2。$ | (15) |
实际情况下,主机会整体放置在基座结构上工作并对基座结构产生影响,为了模拟主机对基座结构的作用,将基座结构表面用有限元软件里的MPC点连接于主机基座结构重心附近处一点(图5中箭头所指位置),即将作用力施加到该点就可模拟主机对基座结构垂向的激振作用,同时计算时边界条件为双层底结构四周刚性固定。具体加载方式为稳态激励加载,求解时结构阻尼系数为0.02。
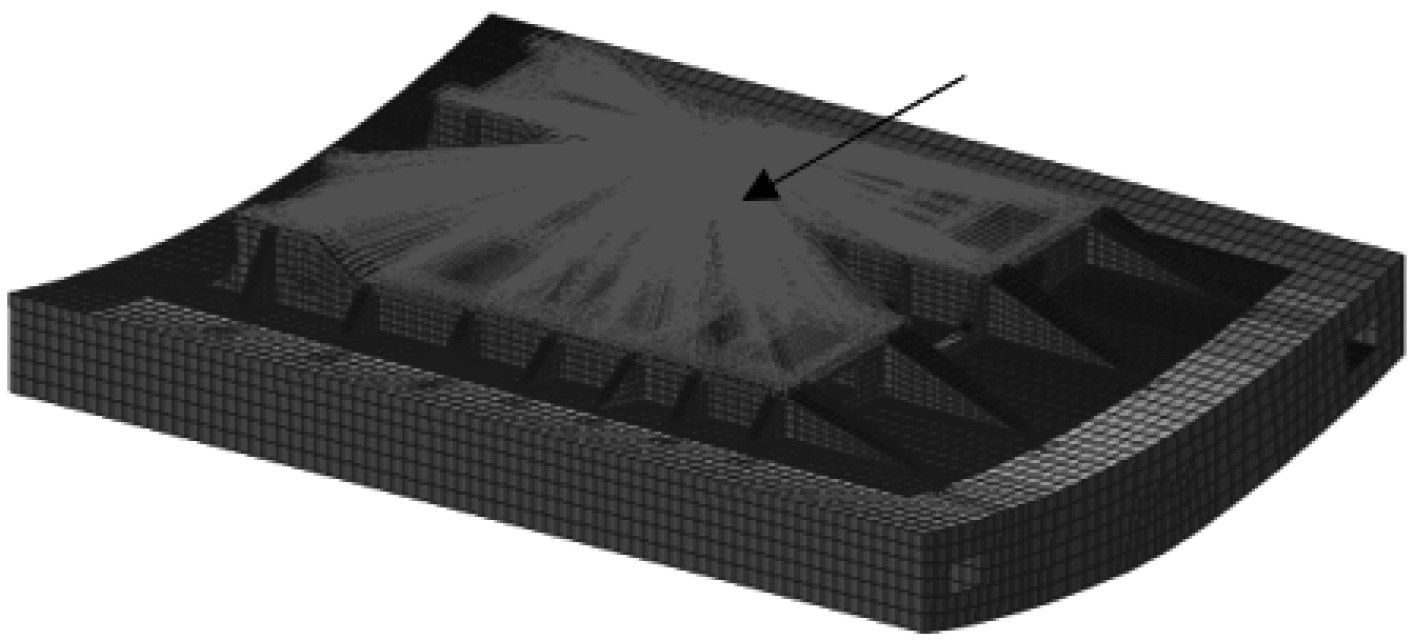
|
图 5 主机对基座结构的作用 Fig. 5 The effect of the main engine on the base structure |
计算得到的主机振动载荷作用下的肘板趾端热点应力响应曲线如图6所示,应力范围如表5所示。

|
图 6 热点应力响应曲线 Fig. 6 Hotspot stress response curve |
|
|
表 5 热点应力范围 Tab.5 Hotspot stress range |
将应力响应结果结合试验S-N曲线即可计算得到主机振动载荷作用下的结构产生疲劳破坏时的疲劳损伤度,如表6所示。
|
|
表 6 主机振动载荷作用下热点疲劳损伤计算结果 Tab.6 Calculation results of hotspot fatigue damage of main engine under vibration load |
在双峰谱疲劳计算方法推导中,假设
| $ \overline{D}=\overline{D}_P+\overline{D}_{HF}。$ | (16) |
可知,低频波浪载荷的过程的应力峰值分布服从瑞利分布,正弦振动下的应力响应过程是恒幅的,应力峰值一定,同时相较于波浪载荷其频率很高,所以最后高低频载荷耦合后的应力峰值的包络曲线的可以看作是原有曲线的基础上加上正弦振动的应力峰值,即此时应力峰值概率密度函数可以表示为:
| $ f(S)=\frac{(S-a)}{4m_0}\exp\left(-\frac{(S-a)^2}{8m_0}\right),$ | (17) |
式中,
因此,根据上式得到的应力峰值概率密度函数,可根据Miner累积损伤理论计算短期海况下的疲劳累积损伤,最后对于某一个短期海况疲劳损伤度为:
| $ \overline{D}_{ij}=\dfrac{T_{ij}f_{0ij}}{A}\int_s^{\infty}S^m\dfrac{(S-a)}{4m_0}\exp\left(-\dfrac{(S-a)^2}{8m_0}\right)\mathrm{d}S 。$ | (18) |
式中:
计算得到短期海况下的疲劳损伤度之后,总的损伤度计算即为所有短期海况下的疲劳损伤按照其出现的短期海况概率进行计算后的代数和,这里的计算方法与谱分析法疲劳强度直接计算类似,则整个结构在长期时间
| $ \overline{D}_P=\sum\limits_{n=1}^Np_n\sum\limits_{i=1}^{n_S}\sum\limits_{j=1}^{n_H}\overline{D}_{ij}。$ | (19) |
最后,计及主机振动载荷的高低频载荷联合作用下的疲劳损伤计算为高低频包络损伤加上高频振动损伤的和,具体计算表达式为:
| $ \overline{D}=\overline{D}_P+\overline{D}_{HF}。$ | (20) |
采用时域法对提出的计及主机振动载荷的高低频载荷联合作用疲劳直接计算法进行验证,通过将时域法计算得到的损伤结果与疲劳直接计算法计算的结果对比,说明采用直接计算方法计算结果的合理正确。时域法高低频载荷联合作用下的疲劳强度计算方法的具体思路流程是,首先在波浪载荷作用下对船体结构热点进行计算,得到某个短期海况下的热点位置的应力响应谱,然后基于频域转时域的方法,得到波浪载荷作用下的热点应力时历曲线,接着在曲线基础上叠加加上正弦振动的时历曲线,最后得到高低频载荷联合作用下的应力时历曲线。再利用雨流计数法对曲线进行统计计数,并得到最终损伤。
根据不规则波理论,通过计算频域上的应力响应谱,得到时域上不规则波下一个短期海况的应力响应时历曲线如图7所示。

|
图 7
一个短期海况的应力时历曲线(
|
对波浪载荷和主机振动载荷作用下的时历曲线进行统计计数即可得到该短期海况的疲劳损伤,这里采用最常使用的雨流计数法。用雨流计数法将短期海况下的应力-时间历程提取全部整循环之后,分别按照不同的应力峰值和应力范围进行排序并统计计数。将统计得到的不同应力范围下的计数结果结合材料的疲劳寿命S-N曲线,利用线性累积损伤理论,即可求得最后的损伤度
|
|
表 7 不同疲劳损伤计算方法计算结果对比 Tab.7 Comparison of calculation results of different fatigue damage calculation methods |
表7给出的计算结果中,第1列为雨流计数时历损伤计算结果,第2列为计及主机振动载荷的高低频载荷联合作用疲劳直接计算法损伤计算结果,第3列为波浪载荷和振动载荷分别作用下的损伤直接叠加结果。可以看到,前2种的方法计算结果都比直接叠加后的大,雨流计数时历计算损伤最大,其次是使用直接计算方法计算的损伤,最小的是直接叠加后的损伤结果。通常认为时历计算的结果更加准确与实际结果最为符合,而采用直接计算方法计算的结果比直接叠加的损伤大更接近时历计算结果,虽与时历的还存在一点误差,但也能够说明采用直接计算方法的计算比较准确,计算结果更加保守,验证了直接计算方法的正确合理。
2.4 疲劳损伤计算结果对比分析将计及主机振动载荷的高低频载荷联合作用疲劳计算方法计算的损伤,与高低频载荷单独作用下直接叠加的损伤进行对比,最后的计算结果见表8。
|
|
表 8 疲劳损伤计算结果对比 Tab.8 Comparison of fatigue damage calculation results |
从对比结果来看,在使用计及主机振动载荷的高低频载荷联合作用疲劳计算方法计算波浪载荷和主机振动载荷联合作用时的疲劳损伤时,比高低频载荷单独作用时的损伤结果直接叠加后的大,说明波浪载荷和主机振动载荷联合作用下的损伤不能单纯地直接叠加计算,采用计及主机振动载荷的高低频载荷联合作用疲劳计算方法计算得到的疲劳损伤结果更加保守,对结构的疲劳寿命估计更符合实际,为高低频载荷联合作用下的结构特别是主机基座结构疲劳计算提供一定的指导性方法。
3 结 语本文提出了一种计及主机振动载荷的高低频载荷联合作用疲劳直接计算方法,基于谱分析法的船舶结构疲劳强度直接计算理论,对主机基座结构进行热点位置的疲劳强度计算,得到了低频波浪载荷作用下主机基座结构的疲劳特性;然后基于振动理论和累积损伤理论,对主机基座结构进行主机振动载荷作用下的疲劳计算;最后开展了高低频载荷联合作用下的主机基座结构的疲劳强度计算研究,结合双峰谱疲劳计算理论,进行了计及主机振动载荷的高低频载荷联合作用下的疲劳强度计算,主要得到如下结论:
1)在考虑主机振动载荷与波浪载荷共同作用的情况下,各热点的疲劳损伤度较2种载荷直接叠加的结果增加约为15%~50%,影响较大,因此这种高低频载荷联合作用时的耦合效应对疲劳强度的计算不可忽略。
2)主机基座结构不同部位所受主机振动载荷和波浪载荷联合作用下的损伤度不同,产生差异的原因除了沿船长方向的位置不同外,还与热点处的结构不同有关。
3)所提方法可以应用于正弦振动形式的高频载荷与波浪载荷共同作用下的疲劳强度计算研究,可以更好提高计算的精确度同时不增加计算时长。
| [1] |
张清越. 大型小水线面双体船结构疲劳强度分析[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [2] |
MRSNIK M, SLAVIC J, BOLTEZAR M. Frequency domain methods for a vibration fatigue life estimation application to real data[J]. International journal of fatigue, 2013, 47: 8-17. DOI:10.1016/j.ijfatigue.2012.07.005 |
| [3] |
甄春博, 栾剑, 任慧龙. 小水线面双体船疲劳强度评估的简化方法[J]. 武汉理工大学学报, 2014, 36(10): 69-73. |
| [4] |
顾学康. 波激振动的理论预报及与实船试验结果的比较[J]. 船舶力学, 2003(06): 100-115. DOI:10.3969/j.issn.1007-7294.2003.06.012 |
| [5] |
BENDAT J S, PIERSOL A G. Random Data: Analysis and Measurement Procedure[J]. Measurement Science & Technology, 2000, 11(12): 1825. |
| [6] |
中国船级社. 波激和砰击振动对船体结构疲劳强度影响计算指南[S]. 2014.
|
| [7] |
ABS. Guidance notes on Springing Aeeseement for Container Vessel[S]. 2010.
|
| [8] |
ABS. Commentary on the Guide for Fatigue Assessment of Offshore Structures[S]. 2013.
|
| [9] |
MINER, MA. Cumulative Damage in Fatigue[J]. Journal Applied Mechanics 1945, 12.
|
| [10] |
JIAO G , MOAN T . Probabilistic analysis of fatigue due to Gaussian load processes[J]. Prob Engng Mech, 1990, 5(2): 76−83.
|
 2023, Vol. 45
2023, Vol. 45
