2. 天津大学 水利仿真与安全国家重点实验室,天津 300072
2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China
我国风能储备丰富,特别是海上风电发展前景广阔,是未来风电发展的核心。近年来,浮式风电发展迅速受到广泛关注,发展海上浮式风电会加快我国绿色能源开发利用的步伐。人们提出了多种海上浮式风机基础形式,常用的有Spar式、半潜式、TLP式等。半潜型浮式风机基础因其稳定性好、适用水深范围广和建造运输方便等优点而备受关注,特别适用于我国浮式风电的发展。
Bulder等[1] 最早提出三角形浮式基础(半潜型)的概念设计方案,从平台的稳定性、运动响应特性、用钢量、建造成本、维护等方面,研究了其在水深50 m以上海域的可行性。Robertson[2]分析了5 MW浮式风机的驳船型、半潜型、TLP型、SPAR型等的动力响应,结果显示,驳船型浮式风机的载荷最大。OC4项目是国际上多个单位共同参与的海上浮式风机验证项目,其风机下部为半潜型浮式基础上部为NREL 5 MW风机,用于美国“DeepCwind”基础项目。肖昌水[3]以OC4-DeepCwind浮式风机为研究对象,建立了浮式风机的刚柔耦合动力学模型,对旋转叶片的“动力刚化”现象进行模拟研究。刘周等[4]对比了OC4-deepCwind半潜式基础、Windfloat、Ideol三种不同类型浮式基础的水动力性能及时域响应,结果表明,OC4-deepCwind半潜式基础具有优良的深水适应性。张洪建等[4]设计了一种具有倾斜立柱的新型半潜式平台,对其频域、时域进行对比验证并研究了系泊系统的优化方案,结果显示,新平台垂荡固有周期增加,有效避免共振,浮式基础运动响应及缆索张力明显降低。Thanh等[5]针对 OC4-DeepCwind半潜浮式风机,研究了 DFBI 方法在浮式风机运动响应预报中的准确性,结果表明,风机气动性能、平台动力响应和系泊缆张力的预测结果与FAST响应结果相吻合。Wang[6]建立了FVAWT和FHAWT的气动–水–伺服–弹性耦合模型,在不同环境下进行了衰减实验、纯波条件、纯风条件、风波结合条件的时域模拟,并对结果进行了校核比对,结果表明,在低风速下,FVAWT的纵摇运动与FHAWT的纵摇运动非常接近。FVAWT的纵荡运动小于FHAWT的纵荡运动。此外,由于没有桨叶控制器,在风速过大的情况下,FVAWT的平台运动、系泊缆张力和结构响应会更大。
目前的半潜式浮式风机基础有两大类,一种是将塔柱和风机置于半潜式浮式基础的中心,如OC4-deepCwind浮式(见图1(a))、OO-Star浮式风机(见图1(b));另一种是将塔柱和风机置于半潜式浮式基础的三角浮筒上,如WindFloat浮式风机(见图1(c))、中国的峡引领号浮式风机(见图1(d))。

|
图 1 半潜式浮式风机 Fig. 1 Semi-submersible floating wind turbine |
采用数值模拟或模型试验方法对这2种浮式风机系统各自的动力性能做过详细的研究[5-7]。然而,这2种浮式风机运动性能有什么差异,哪种形式更好,对于这些问题目前缺乏有效的研究。本文以OC4-deepCwind浮式风机系统参数为基础,考虑塔柱和风机置于半潜式浮式基础的中心(原OC4-deepCwind浮式风机形式)以及塔柱和风机置于半潜式浮式基础的三角浮筒上(类似于WindFloat浮式风机)2种情况,对比研究浮式风机系统的动力响应,对比分析塔柱和风机位置对浮式风机系统动力性能的影响,为浮式风机设计提供参考。
1 浮式风机系统动力学理论 1.1 结构动力学方程浮式基础的运动方程可以写为如下形式:
| $ \left[ {M + A\left( \omega \right)} \right]\ddot x + C\left( \omega \right)\dot x + Df\left( {\dot x} \right) + K\left( x \right)x = q\left( {t,x,\dot x} \right) 。$ | (1) |
式中:M代表浮体质量矩阵;A代表与频率相关的附连水质量矩阵;C代表与频率相关的势流阻尼矩阵;D代表其他非线性阻尼矩阵;K代表浮体自身恢复刚度矩阵;
浮式风机系统的系泊系统、塔柱、叶片等柔性结构基于有限元方法进行分析,采用空间杆单元对结构进行建模。假定结构为直线,初始横截面积A0沿元件长度为常数。2个节点中的每个节点都有3个平移自由度。结构长度分别表示为L0和L,表示初始和变形配置。变形单元长度由下式给出:
| $ L = \sqrt {\Delta {x^2} + \Delta {y^2} + \Delta {z^2}} ,$ | (2) |
其中,
基于全拉格朗日公式和线性位移函数,格林应变由下式确定:
| $ {E_f} = \frac{1}{2}\frac{{{L^2} - L_0^2}}{{L_0^2}} = \frac{1}{{2L_0^2}}\left( {\Delta {x^2} + \Delta {y^2} + \Delta {z^2} - L_0^2} \right),$ | (3) |
Piola-Kirchhoff应力Sf通过下式确定:
| $ {S_f} = {S_f}\left( {{E_f},{E_0},{S_0}} \right) 。$ | (4) |
式中:E0为初始应变;S0为初始应力。3个位移分量的线性位移函数(场函数)如下:
| $ N = {N_u} = {N_v} = {N_w} = [1 - \xi \xi ],$ | (5) |
式中,
在实际计算中,使用了小应变理论,并假设L0是初始无应力单元长度。因此,结构的轴向力由下式给出:
| $ N = \frac{{L - {L_0}}}{{{L_0}}}(EA) 。$ | (6) |
式中:EA为轴向刚度;
考虑的外载荷主要为风载荷、波浪载荷、流载荷,具体算法如下:
所有位于水面以上的浮体结构均受到风载荷的影响。对于塔柱及停机状态的叶片,采用绕流理论计算风压,即
| $ {f_{L,D}} = \frac{{\rho V_W^2{C_{L,D}}}}{2} 。$ | (7) |
式中:fL,D为升力、阻力风压;CL,D为截面升力与阻力系数;p表示气流密度;VW表示来流风速。可得任一分段上l的绕流风力:
| $ {F_{L,D}} = \int_l {{f_{L,D}}} {\rm{d}}l 。$ | (8) |
对于一般作业工况下的叶片,风载荷主要表现为气动载荷,本文使用经典叶素动量理论来求解,具体求解过程与理论可参考文献[8]。
对于波浪载荷,基于三维势流理论[8]计算,获得一阶波浪力、平均漂移力、附加质量、静水恢复刚度、势流阻尼的水动力传递函数后,将频域结果转换为时域结果,之后进行浮式风机系统动力响应的时域计算。海上浮式风机所受流载荷采用经验公式计算。
1.3 计算过程对于浮式风机系统动力响应的时域计算,全耦合分析考虑了浮体结构的刚体模型,塔架、叶片的弹性模型,系缆的细长体模型及控制系统的完整体,使用非线性方法同时求解,进行动态分析。可以实现风机系统各子结构间惯性、阻尼、刚度等的耦合,但计算比较复杂。基于此,提出了简化的耦合方法,通过在不同的结构之间传递载荷或运动实现系统的耦合,大大地提高了计算速度。
本文对于浮式风机动力响应的计算基于现有软件SESAM展开,用GENIE模块建立计算几何模型;用WADAM模块进行水动力分析,得到浮式基础的水动力参数,模型考虑了浮式基础、叶片、塔柱、机舱等结构的重量和惯性矩;基于SIMA软件,对浮式风机系统进行动力响应分析。
2 动力学建模 2.1 浮式风机基本参数以5 MW浮式风机系统为例进行分析,其中,上部为NERL-5 MW风力机,主要参数见表1;浮式基础为DeepCwind半潜浮式基础,主要参数见表2。风力机系统的其他详细参数,包括机舱、系泊系统等参数见文献[10]。
|
|
表 1 NREL 5 MW风机系统参数 Tab.1 Parameters of NREL 5 MW wind turbines system |
|
|
表 2 DeepCwind半潜浮式基础参数 Tab.2 Parameters of DeepCwind semi-submersible floating platform |
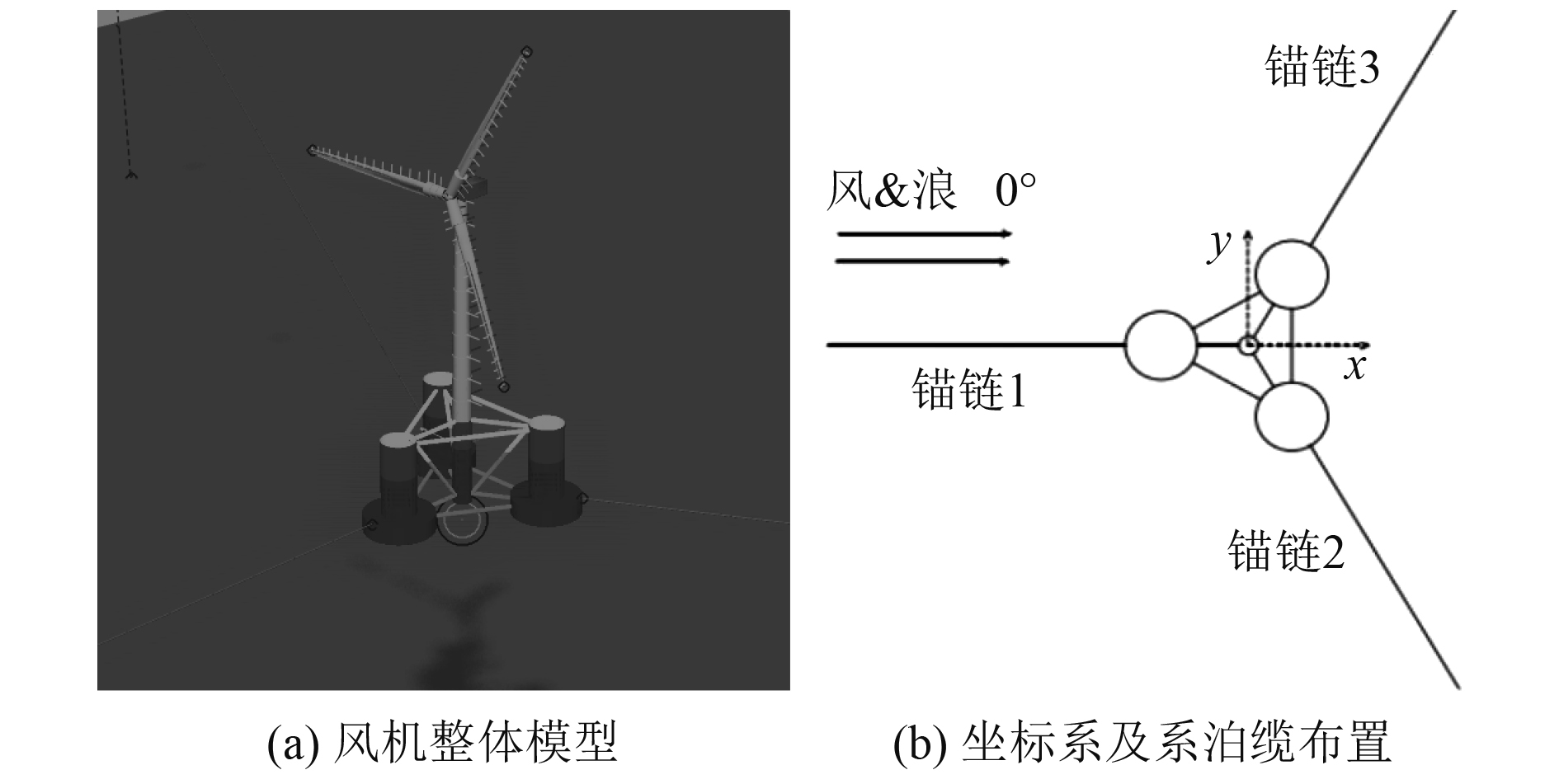
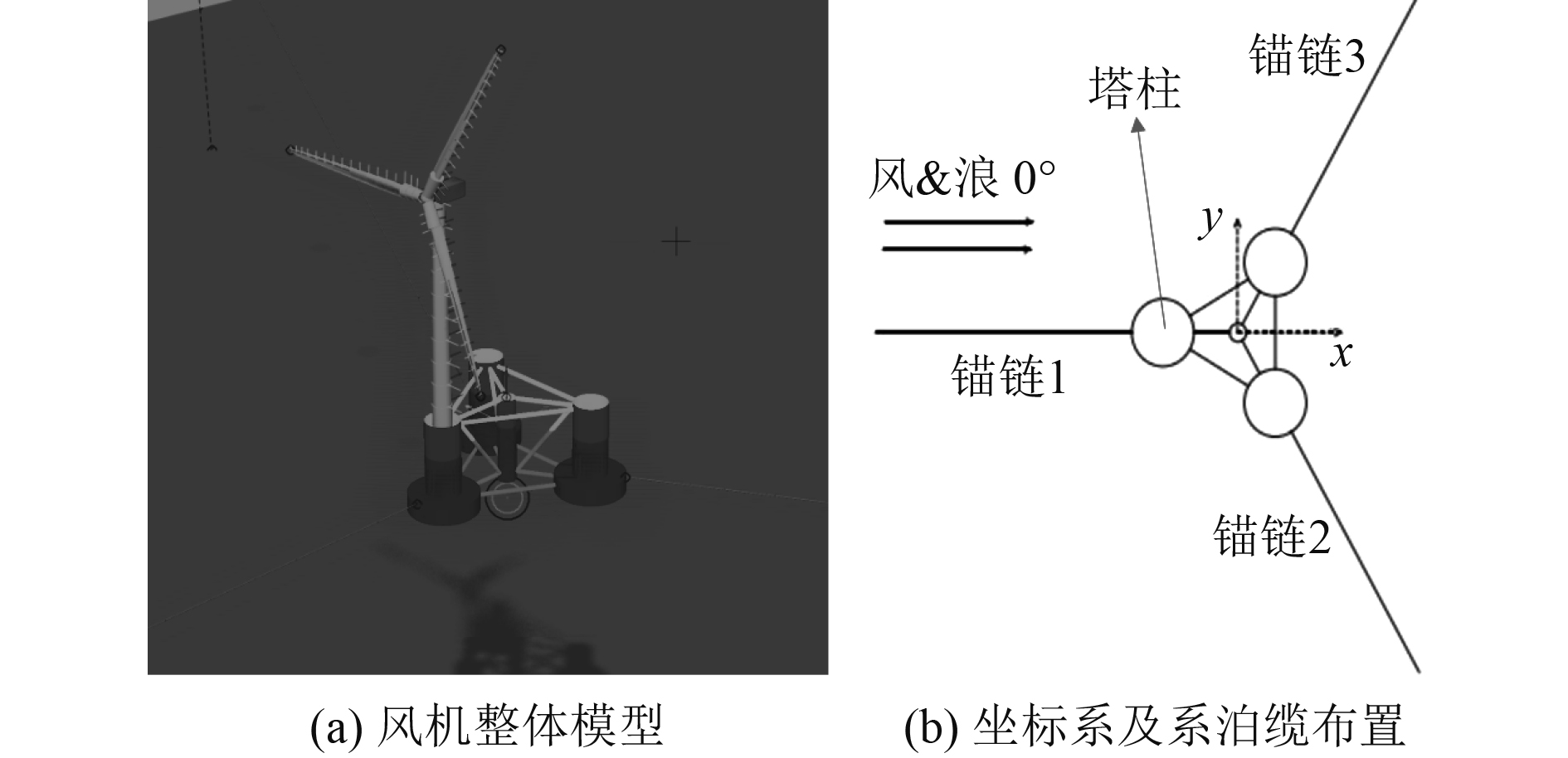
建立的浮式风力机系统耦合动力学模型如图2和图3所示。其中,叶片、塔柱为弹性体,浮式基础、轮毂、机舱为刚体。图2为原始的OC4-deepCwind风机,风机塔柱放在半潜式浮式基础的中心。图3为调整塔柱位置的浮式基础,风机塔柱放在三角形浮式基础的一个浮筒上。图2和图3中,浮式风机整机的重心位置、排水量、系缆参数等完全相同,由于塔柱和风机位置发生了变化,风机系统的惯性矩有所不同。两个模型采用同样的坐标系,坐标原点在整机的重心,风浪流的0°方向沿着缆1的方向,如图2(b)和3(b)所示。
|
图 2 原风机模型 Fig. 2 Original wind turbine model |
|
图 3 调整塔柱位置后的模型 Fig. 3 The model after adjusting the position of the tower |
针对2种风机分别进行计算,选取的计算工况如表3所示。其中LCY.1~3参考了CCS规范的1.1工况,LCY.4参考了CCS规范的6.1工况;LC2.X为风机塔柱调整位置的情况,LC1.X为原始浮式风机的情况。
|
|
表 3 工况设置 Tab.3 Conditions set |
流为剪切流,风为湍流风,取Davenport风谱,波浪为随机波,波浪谱为Jonswap谱。考虑风浪流同向,均为0°方向。
3 计算结果及对比分析针对2种模型,按照表3设置的工况分别进行计算,统计响应结果并进行对比,以分析塔柱位置对浮式风机动力性能的影响。在基础运动分析中,仅分析较为显著的纵荡、纵摇、垂荡、首摇4个自由度的运动。对于机舱加速度,仅分析响应结果较大的X向机舱加速度;2号和3号缆为对称,故仅取2号缆进行分析;气动力取与风方向一致的X方向进行分析。给出典型工况的时间历程,并统计、对比和分析4个工况的计算结果。
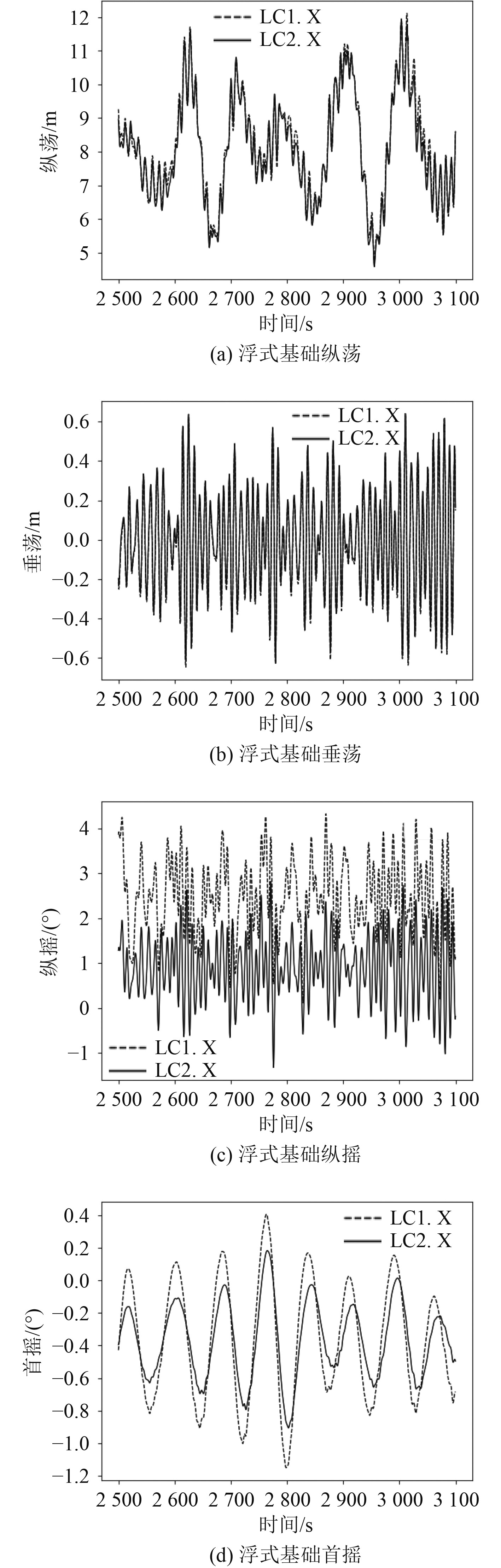
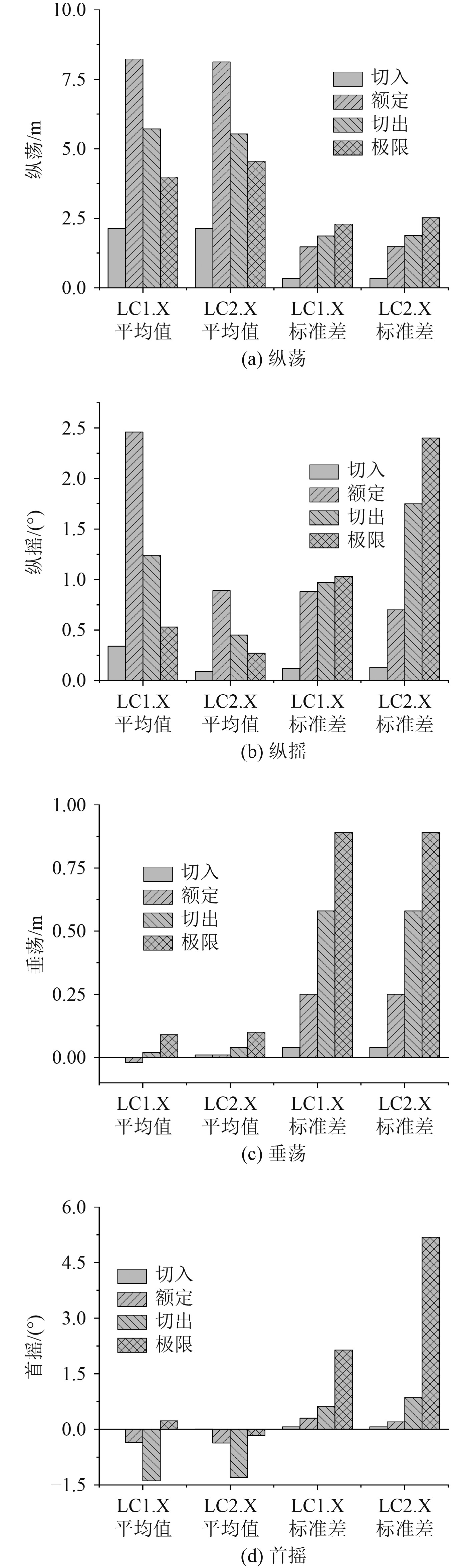
3.1 浮式基础运动给出额定工况和极限工况浮式基础运动时间历程,如图4和图5所示。对结果进行统计并对比,结果如图6所示。
|
图 4 浮式基础运动对比(额定工况) Fig. 4 Floating foundation motion comparison (Rated Condition) |

|
图 5 浮式基础运动对比(极限工况) Fig. 5 Floating foundation motion comparison (Extreme Condition) |
|
图 6 浮式基础运动统计 Fig. 6 The motion statistics of floating platform |
以上计算表明,对于浮式基础,其纵荡、垂荡受影响较小,纵摇受影响较大;调整塔柱位置后,浮式基础纵摇均值有一定减小,减小60%以上,标准差增大,最大增加约1倍,对应极限工况。此外,在前3个工况,首摇差异非常小,但在极限工况下,首摇的标准差大大增加约为1.4倍,最大首摇超过5°。
3.2 机舱加速度和叶片气动力
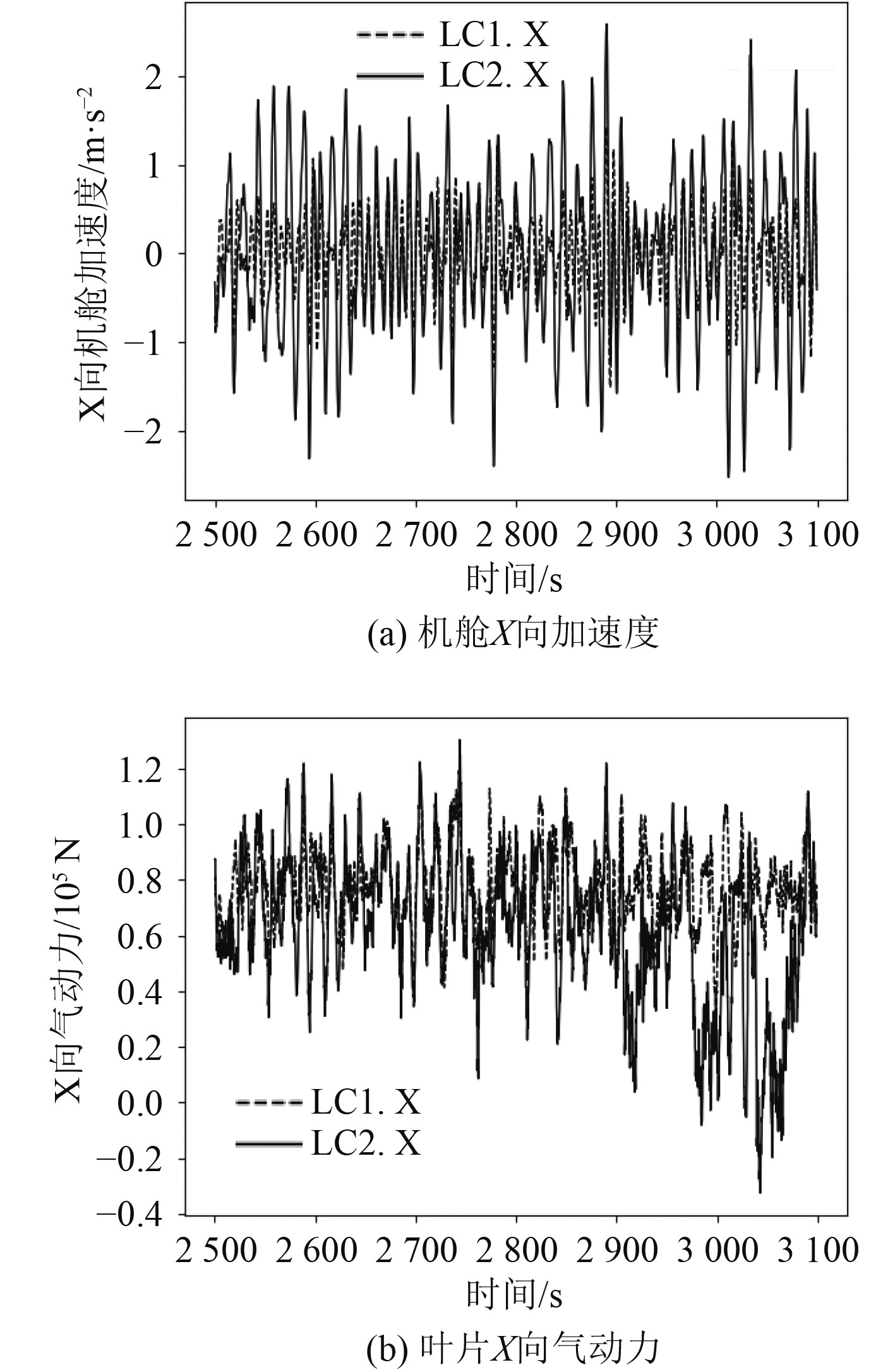
|
图 8 机舱加速度和叶片气动力时历对比(极限工况) Fig. 8 Comparison of nacelle acceleration and blade aerodynamic time domain results (extreme condition) |

|
图 9 机舱X向加速度对比 Fig. 9 The comparison of x direction nacelle |
由图7~图10可以看出,调整塔柱位置后,机舱X向加速度的平均值没有发生变化,其标准差增大,最大增大约1倍,对应极限工况;叶片X向气动力平均值变化较小,有减小的趋势,但差异较小,在20%以内;叶片X向气动力的标准差增大,最大增加约70%,也对应极限工况。
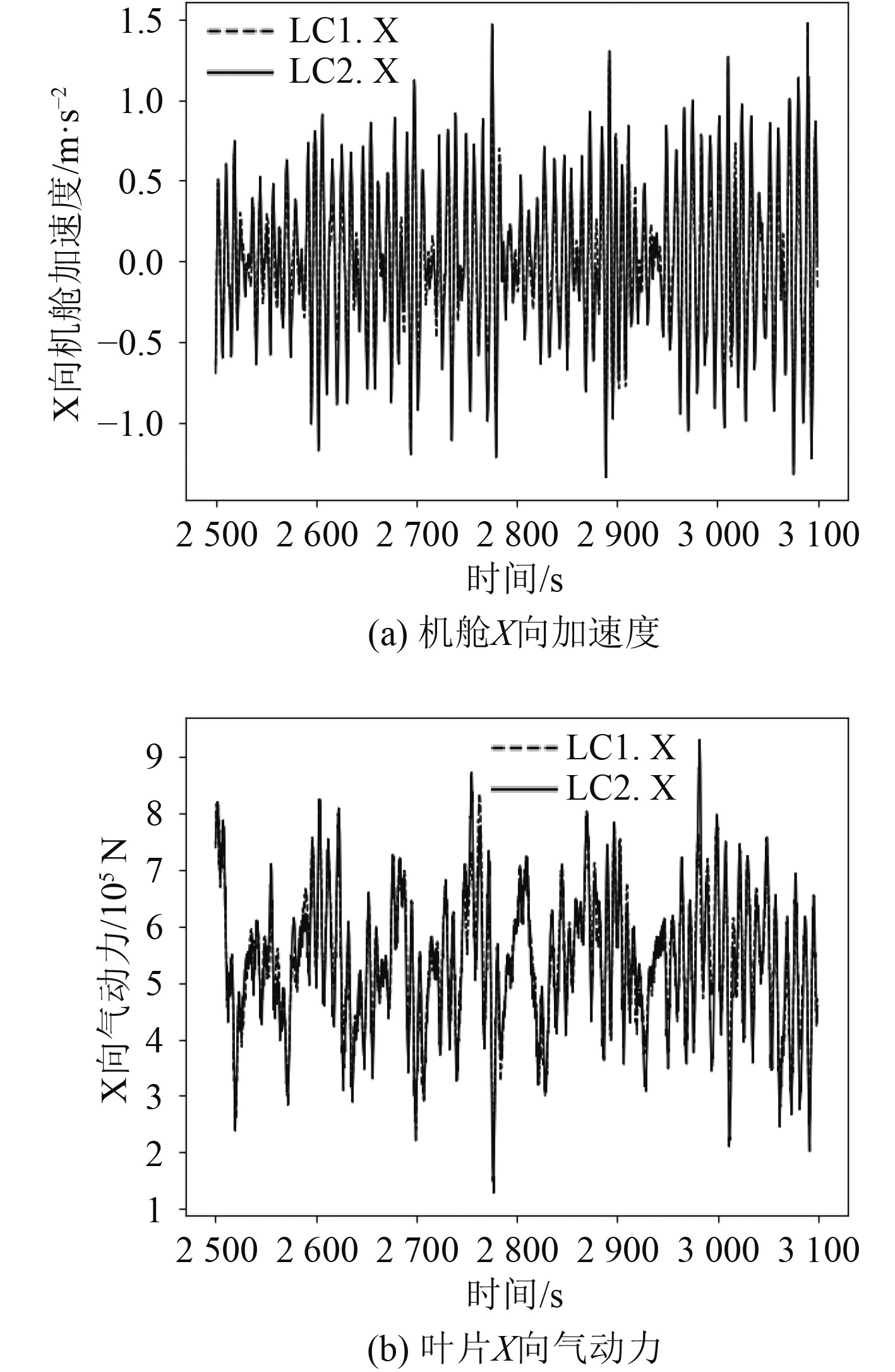
|
图 7 机舱加速度和叶片气动力时历对比(额定工况) Fig. 7 Comparison of nacelle acceleration and blade aerodynamic time domain results (rated condition) |
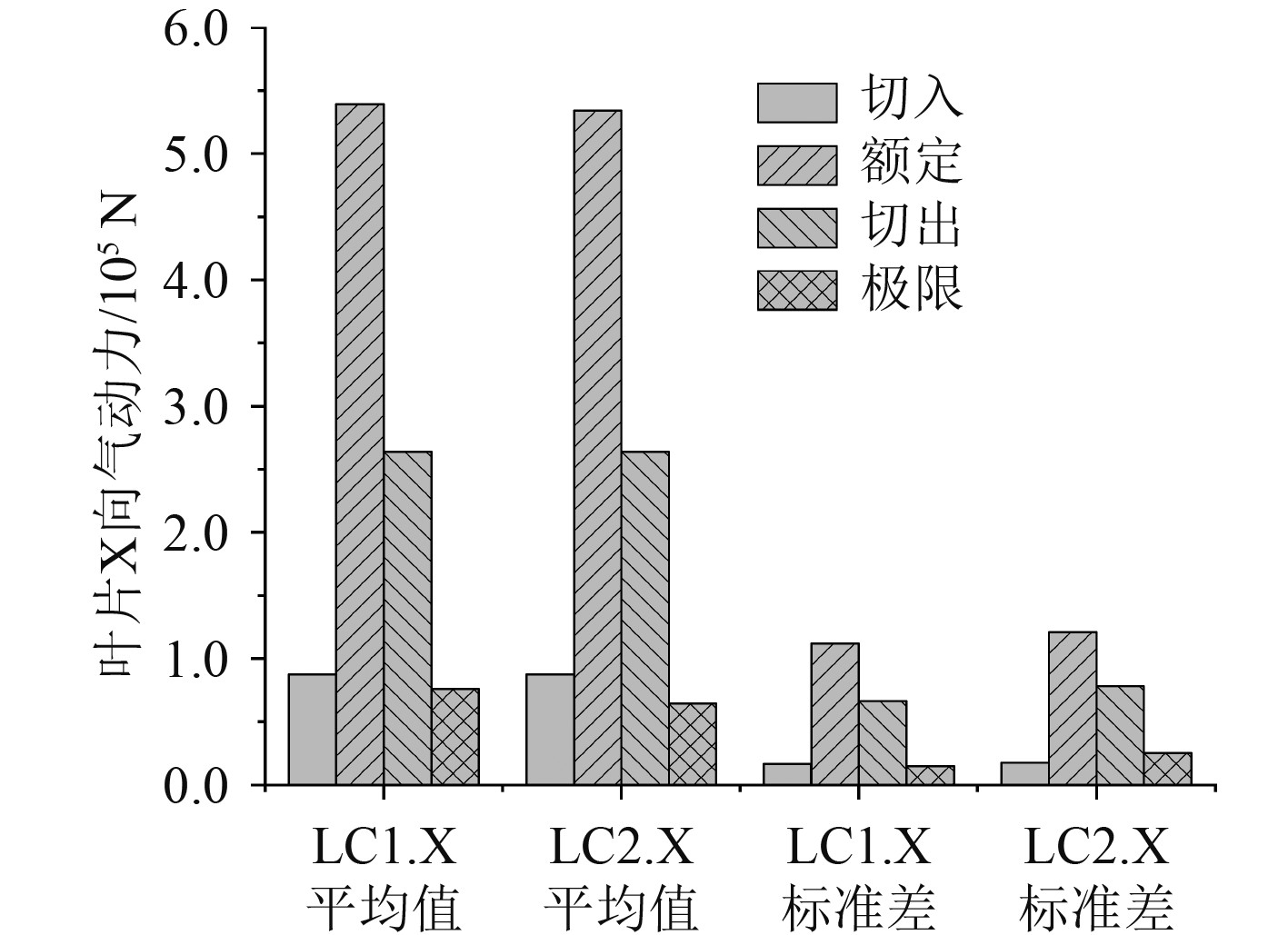
|
图 10 叶片 X 向动力对比 Fig. 10 The comparison of x direction aerodynamic force |
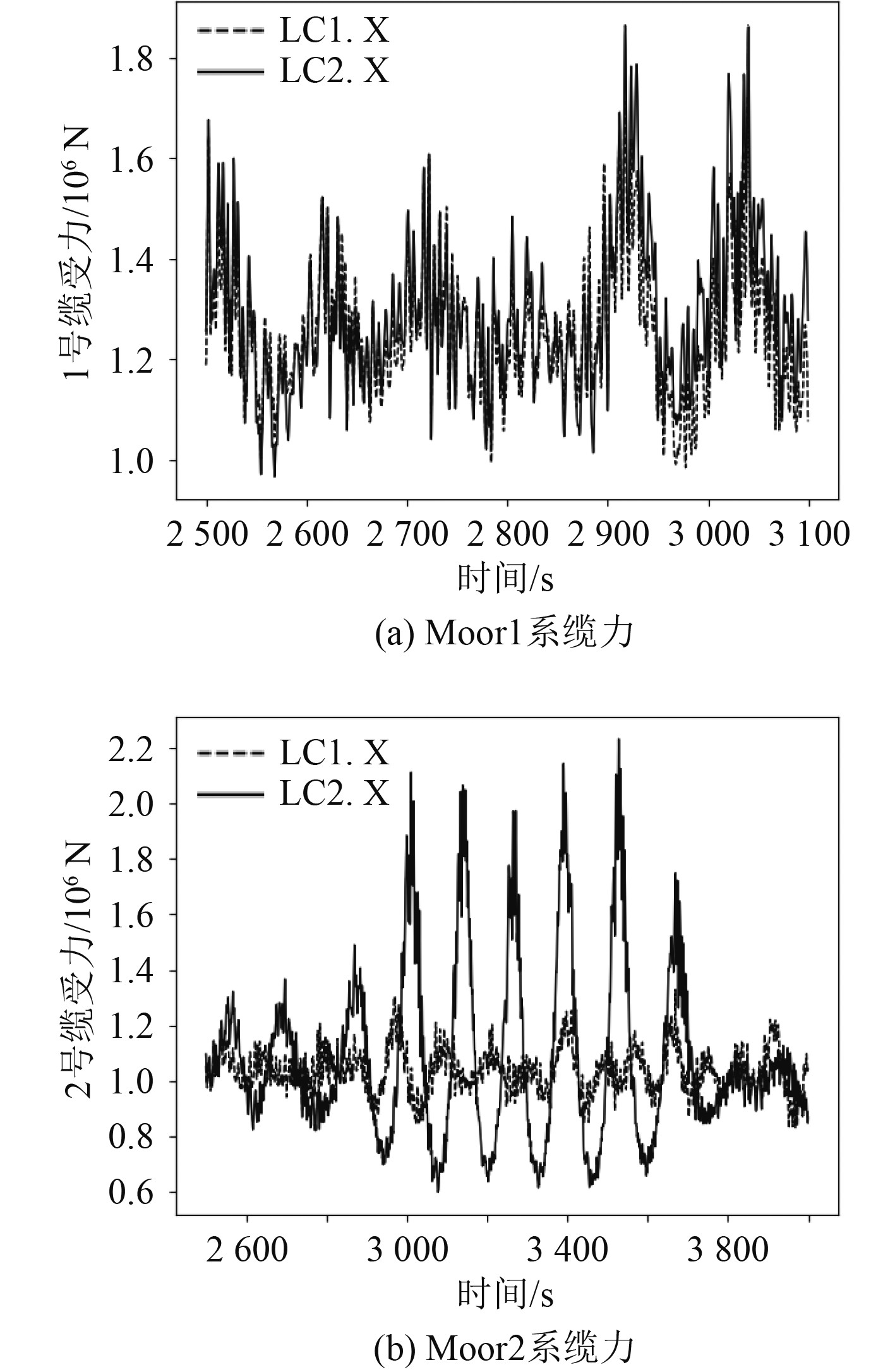
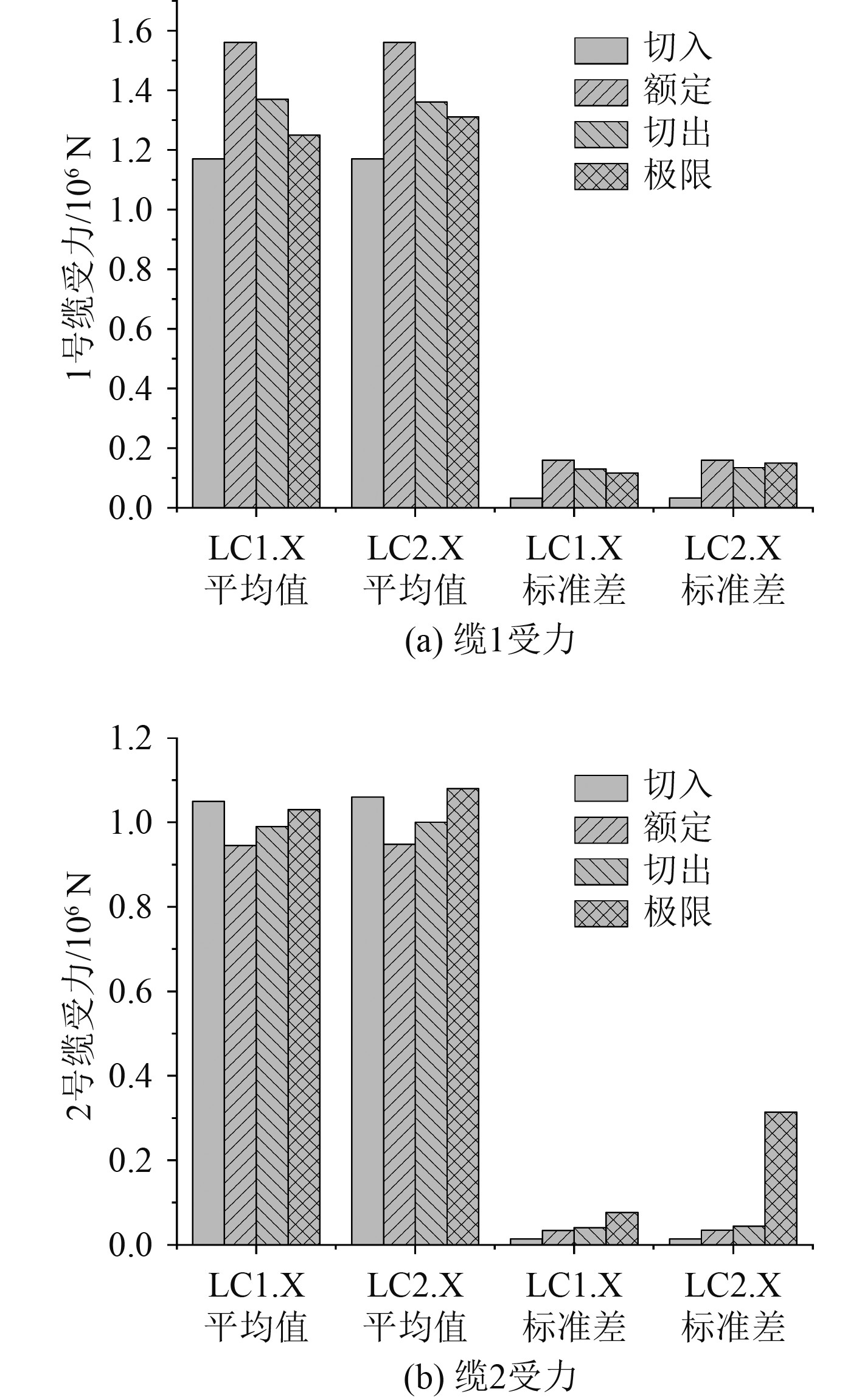
由图11~图13可以看出,调整塔柱后,1号和2号缆力的均值变化较小,均在5%以内,变化最大的工况是极限工况;1号和2号缆力的标准差变化较大,在极限工况的变化最为明显,1号和2号缆受力的标准差分别增大了29%和310%,这主要是由于风机发生了较大的首摇和横荡。
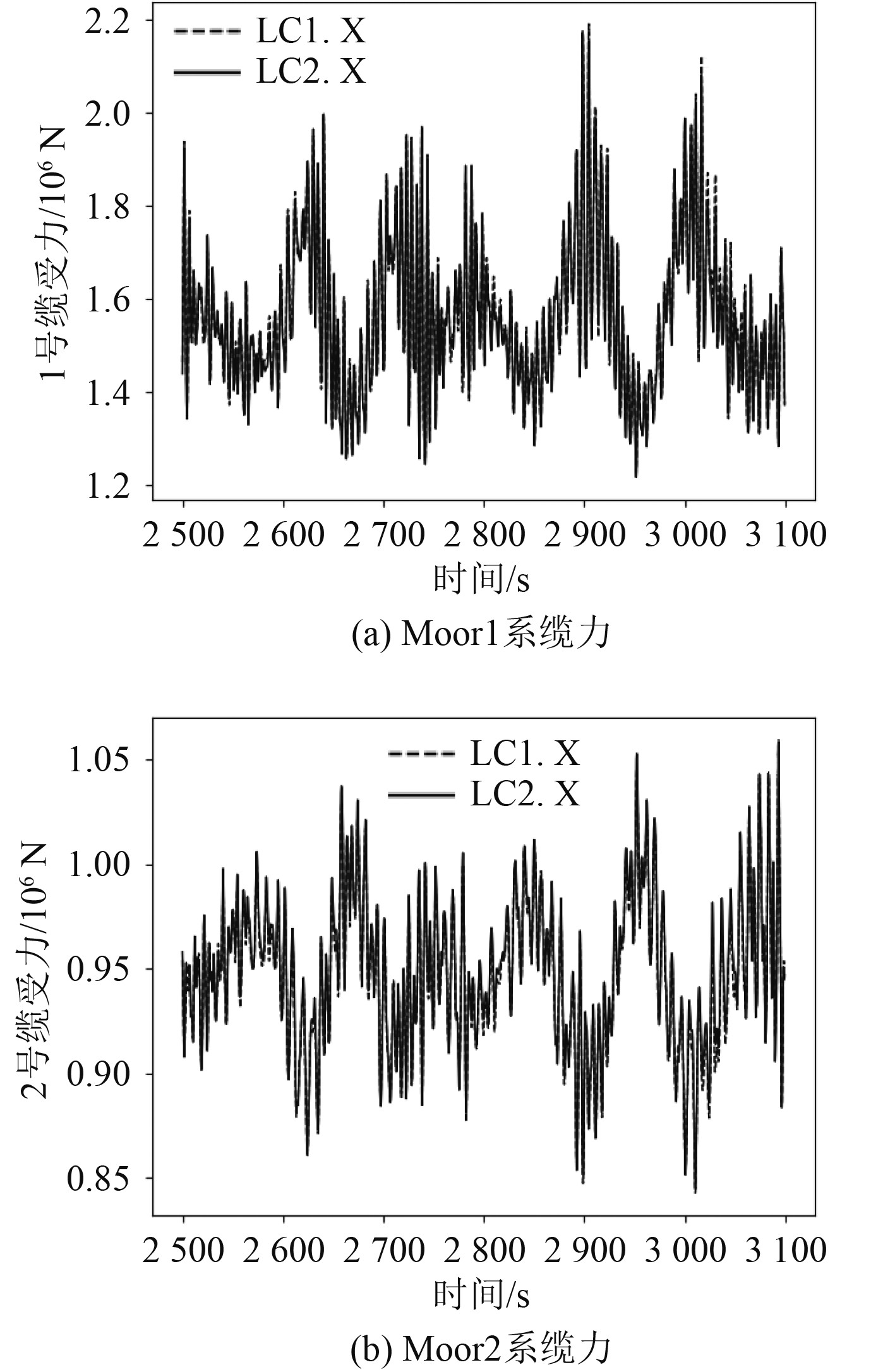
|
图 11 系缆力时历曲线(额定工况) Fig. 11 Time domain curve of mooring force (Rated Condition) |
|
图 12 系缆力对比时历曲线(极限工况) Fig. 12 Time domain curve of mooring force (Extreme Condition) |
|
图 13 系缆力结果统计 Fig. 13 Result statistics of mooring force |
本文建立浮式风机系统的耦合动力学模型,考虑切入、额定、切出、极限4种工况,对比研究了塔柱和风机布置位置对浮式风机系统动力性能的响应,结论如下:
1)浮式基础的纵荡、垂荡受影响较小,其纵摇受影响较大;调整塔柱和风机位置后,浮式基础纵摇均值有一定减小,标准差增大,最大增加约1倍,对应极限工况;在极限工况下,首摇的标准差大大增加,最大首摇角超过5°。
2)相较于原始的浮式风机,调节塔柱位置后机舱加速度均值没有明显变化,但标准差有提高;特别是极限工况,调整塔柱位置后,机舱X向加速度标准差增加了约1倍。
3)调整塔柱后,叶片气动力均值有小幅下降,标准差有明显增大且随着工况恶劣程度的提升,增大的更多;可见调整塔柱位置后叶片气动力波动变大,最大变化近1倍,对应于极限工况。
4)在切入、额定、切出工况下,LC1.X与LC2.X的1号和2号缆受力值相近,变化较小;而在极限工况下,由于首摇的影响,1号缆的标准差有较大变化,增加约30%。
| [1] |
BULDER B H, VAN HEES M T, HENDERSON A, et al. Study to feasibility of and boundary conditions for floating offshore wind turbines[R]. 2002.
|
| [2] |
ROBERTSON A N, JONKMAN J M. Loads analysis of several offshore floating wind turbine concepts[J]. Office of Scientific & Technical Information Technical Reports, 2011.
|
| [3] |
肖昌水. 海上浮式风机气动载荷及刚—柔耦合动力响应研究[D]. 天津: 天津大学, 2018.
|
| [4] |
刘周. 三种典型半潜式浮式风机基础水动力性能比较分析[D]. 广州: 华南理工大学, 2020.
|
| [5] |
Thanh Toan Tran, Dong-Hyun Kim. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach[J]. Renewable Energy, 2016, 92.
|
| [6] |
Wang K , Luan C , Moan T , et al. Comparative Study of a FVAWT and a FHAWT with a Semi-submersible Floater[C]. International ocean and polar engineering conference. 0.
|
| [7] |
张培智. 风浪耦合下的半潜式风机动力响应及塔基结构强度研究[D]. 江苏科技大学, 2021.
|
| [8] |
刘利琴, 肖昌水, 郭颖. 海上浮式水平轴风力机气动特性研究[J]. 太阳能学报, 2021, 42(01): 294-301. |
| [9] |
王涵. 浮式风机动力响应模型试验与数值计算对比研究[D]. 导师: 胡志强. 上海交通大学, 2019.
|
| [10] |
Robertson A, Jonkman J, Masciola M, et al. Definition of the semisubmersible floating system for phase II of OC4[J]. Offshore Code Comparison Collaboration Continuation (OC4) for IEA Task, 2012, 30.
|
 2023, Vol. 45
2023, Vol. 45
