0 引　言

拖曳线阵声呐具有良好的水下探测性能，是十分重要的水下目标探测手段之一。随着细线拖曳线阵声呐及UUV装备技术的快速发展，部分UUV已采用外挂式拖曳线阵声呐（直径小于40 mm）提升其水下探测能力^[1]。通常情况下，UUV由于体积及动力的限制，搭载的探测设备以前视声呐、侧扫声呐、下视多波束声呐等高频声呐为主，用于近距离静态目标探测，如反水雷、地形探测、水下搜救等。而外挂式细线拖曳线阵声呐，可一定程度摆脱UUV自身的体积限制，实现更大的探测距离（≥1 km），开展大范围的水下运动目标探测作业。

北约水下研究中心（NURC）在2007−2009年期间先后开展了新型被动拖曳阵SLITA（Slim Line Towed Array）及微型SLITA试验、主动发射声源TOSSA（Towed Sound Source for AUV）发射和接收声信号系统试验^[2,3]。SLITA拖曳线阵直径31 mm，长57.5 m；微型SLITA拖曳线阵直径12 mm，长13.5 m。TOSSA系统包含尾绳、BENS拖曳阵、拖曳源和OEX-C UUV等4个部分，其中拖曳线阵BENS线列直径31 mm，长57 m，拖曳源直径约16 cm，长约1.2 m。2009年4月OEX-C UUV搭载BENS拖曳阵和拖曳源，航行速度为2 kn，采用回声中继器模拟了一个潜艇的声信号，TOSSA发射出的声源被echo接收机连续接收，收发信号处理显示没有断点，实现了令人满意的探潜效果。

国内科研院所及高校开展了部分研究工作^[4−5]。其中，北京神州普惠科技股份有限公司已形成了成熟的UUV用光纤水听器拖曳线阵系统，常用基元数目为16/32/64/128/192/256等，线阵直径覆盖为26～30 mm，工作频带为5 kHz～10 kHz，系统噪声≤40 dB@1 kHz，阵列长度为≤300 m，最大工作深度为200 m，工作拖曳速度为2～6 kn，供电功耗≤40 W。

在UUV用光纤水听器拖曳线阵比较成熟的情况下，如何发挥其性能是UUV拖曳线阵声呐系统的重要研究课题之一。在拖曳线阵近百米、UUV自身推进动力仅数十千克的情况下，UUV的拖曳航速及转弯性能受限，同时在海流、海水密度变化等环境作用下，拖曳线阵必发生偏航及弯曲现象，并因此导致系统的测向精度下降^[6]。

本文以UUV外挂拖曳声呐直航及航向机动下，拖曳线阵形变化导致的波束响应变化为研究对象，采用Ablow和Schechter^[7]提出的缆索偏微分控制方程组对UUV拖曳线阵的阵形变化进行求解，采用经典波束形成方法得到拖曳线阵声呐发生阵形畸变后的波束响应，仿真计算得到对海流导致的线阵偏航、UUV航向机动导致的线阵弯曲，并就在拖曳过程中对阵型快速预报以提高平台测向精度的效果进行分析。

1 坐标系定义及模型建立 1.1 坐标系定义

大地坐标系为 $ E-\xi \eta \zeta $ 、随体坐标系为 $ b-xyz $ ，两坐标系原点重合， $ E-\xi \eta \zeta $ 坐标系依次绕z-y-x轴转动 $ \psi ,\theta ,\varphi $ 后，与 $ b-xyz $ 坐标轴重合。缆索局部坐标系为 $ c-tnb $ ， $ \mathit{t} $ 为缆索的切线方向，规定沿缆索长度s增长的方向为正；b与t垂直并位于水平面内（ $ {\psi }_{c}={\text{π}} /2 $ ）。 $ {\phi }_{c} $ 为t轴与 $ ij $ 平面夹角， $ {\theta }_{c} $ 为t轴在 $ ij $ 平面的投影与 $ i $ 轴的夹角。由大地坐标系 $ E-\xi \eta \zeta $ 依次绕z-x-z转动 $ -{\theta }_{c},-{\psi }_{c},{\phi }_{c} $ （欧拉角）获得。转换关系如下：

$ \left(\begin{array}{c}t\\ n\\ b\end{array}\right)=\left[\begin{array}{ccc} \cos{\phi }_{c}\cos{\theta }_{c}& \cos{\phi }_{c}\sin{\theta }_{c}& \sin{\phi }_{c}\\ -\sin{\phi }_{c}\cos{\theta }_{c}& -\sin{\phi }_{c}\sin{\theta }_{c}& \cos{\phi }_{c}\\ \sin{\theta }_{c}& -\cos{\theta }_{c}& 0\end{array}\right]\left(\begin{array}{c}i\\ j\\ k\end{array}\right)。$

(1)

1.2 UUV模型

UUV模型采用某重量约490 kg、长3.7 m的中小型AUV。位置及姿态用 $\mathit{\eta }={\left[n,e,d,\varphi ,\theta ,\psi \right]}^{{\rm{T}}}$ 表示，运动状态用 $\mathit{v}={\left[u,v,w,p,q,r\right]}^{{\rm{T}}}$ 表示。 $ n,e,d $ 表示在 $ E-\xi \eta \zeta $ 坐标系下沿北、东、向下指向的位置， $ \varphi ,\theta ,\psi $ 则表示相应的欧拉角（滚转、俯仰和偏航）； $ u,v,w,p,q,r $ 表示UUV在随体坐标系 $ b-xyz $ 下的广义速度。其水平面控制方程如下：

$ \begin{split} & m\left(\dot{u}-vr\right)=\frac{\rho }{2}{L}^{4}{X}_{uu}^{{'}}{r}^{2}+\frac{\rho }{2}{L}^{3}\left({X}_{\dot{u}}^{{'}}\dot{u}+{X}_{vr}^{{'}}vr\right)+\\ & \frac{\rho }{2}{L}^{2}\left({X}_{uu}^{{'}}{u}^{2}+{X}_{vv}^{{'}}{v}^{2}\right)+\frac{\rho }{2}{L}^{2}{u}^{2}\left({X}_{{\delta }_{r}{\delta }_{r}}^{{'}}{{\delta }_{r}}^{2}\right)+{X}_{T}+\\ & m\left(\dot{v}+ur\right)=\frac{\rho }{2}{L}^{4}{Y}_{\dot{r}}^{{'}}\dot{r}+\\ &\frac{\rho }{2}{L}^{3}\left({Y}_{\dot{v}}^{{'}}\dot{v}+{Y}_{r}^{{'}}ur+{Y}_{{\left|r\right|\delta }_{r}}^{{'}}u{\left|r\right|\delta }_{r}+{Y}_{v\left|r\right|}^{{'}}v\left|r\right|\right)+\\ & \frac{\rho }{2}{L}^{2}\left({Y}_{v}^{{'}}uv+{Y}_{v\left|v\right|}^{{'}}v\left|v\right|+{Y}_{{\delta }_{r}}^{{'}}{u}^{2}{\delta }_{r}\right)，\\ & {I}_{z}\dot{r}=\frac{\rho }{2}{L}^{5}\left({N}_{\dot{r}}^{{'}}\dot{r+{Y}_{r\left|r\right|}^{{'}}}r\left|r\right|\right)+\frac{\rho }{2}{L}^{4}{N}_{\dot{v}}^{{'}}\dot{v}+\\ &\frac{\rho }{2}{L}^{4}\left({N}_{r}^{{'}}ur+{N}_{{\left|r\right|\delta }_{r}}^{{'}}u{\left|r\right|\delta }_{r}+{N}_{\left|v\right|r}^{{'}}\left|v\right|r\right)+\\ &\frac{\rho }{2}{L}^{3}\left({N}_{v}^{{'}}uv+{N}_{v\left|v\right|}^{{'}}v\left|v\right|+{N}_{{\delta }_{r}}^{{'}}{u}^{2}{\delta }_{r}\right) 。\end{split} $

(2)

式中参数及水动力系数见文献[11]。

1.3 拖曳线阵模型

将拖曳线阵视为圆截面柔性拖曳缆索，假设其张力始终作用于缆索切向，且忽略弯曲、扭转和剪切力的影响。重力加速度记为 $ g\text{kg}\text{.}\text{m/}{\text{s}}^{2} $ ，水流密度记为 $ \rho \text{kg/}{\text{m}}^{3} $ ；缆索杨氏模量为 $ E $ ，缆索的等效直径为 $ dm $ ，单位长度质量为 $ m\text{kg/m} $ ，其法向和切向拖曳力系数分别为 $ {C}_{n} $ 和 $ {C}_{\iota } $ 。缆索系统的建模采用符号： ${\mathit{X}}_{c}= {\left[x,y,z\right]}^{{\rm{T}}}$ ， ${\mathit{Y}}_{c}={\left[T,{v}_{t},{v}_{n},{v}_{b},{\theta }_{c},{\phi }_{c}\right]}^{{\rm{T}}}$ 表示。其中， $ x,y,z $ 表示缆索上各点在大地坐标系 $ E-\xi \eta \zeta $ 的位置， $ {v}_{t},{v}_{n},{v}_{b} $ 为缆索上各点在随体坐标下的各个速度分量， $ T $ 为缆索上各点的缆索张力， $ {\theta }_{c},{\phi }_{c} $ 为缆索上各点的姿态角。

结合文献[7]可得考虑缆索收放速度变化的缆索偏微分方程组控制方程组：

$ \mathit{M}\left(s,t\right)\frac{\partial \mathit{Y}\left(s,t\right)}{\partial s}=\mathit{N}\left(s,t\right)\frac{\partial \mathit{Y}\left(s,t\right)}{\partial t}+\mathit{Q}\left(s,t\right) 。$

(3)

式中：

$ \mathit{M}\left(s,t\right)=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& -{v}_{b}{\cos}\phi & -{v}_{n}\\ 0& 0& 1& 0& -{v}_{b}{\sin}\phi & {v}_{t}\\ 0& 0& 0& 1& {v}_{t}{\cos}\phi +{v}_{n}{\sin}\phi & 0\\ 0& 0& 0& 0& T{\cos}\phi & 0\\ 0& 0& 0& 0& 0& T\end{array}\right]，$

$ \mathit{Q}\left(s,t\right)=\left[\begin{array}{c}w{\sin}\phi +0.5\sqrt{1+eT}\rho \pi d{C}_{\iota }{u}_{t}\left|{u}_{t}\right|\\ 0\\ 0\\ 0\\ 0.5\rho d\sqrt{1+eT}{C}_{n}{u}_{b}\sqrt{{u}_{n}^{2}+{u}_{b}^{2}}-\rho A{\dot{J}}_{b}\\ w \cos\phi +0.5\rho d{C}_{n}\sqrt{1+eT}{u}_{n}\sqrt{{u}_{n}^{2}+{u}_{b}^{2}}-\rho A{\dot{J}}_{n}\end{array}\right] ，$

$ \begin{split} & \mathit{N}\left(s,t\right)=\\ & \tiny\left[\begin{array}{cccccc}\frac{-me{v}_{t}}{1+eT}& m& 0& 0& -({m}_{1}{v}_{b}-\rho {\rm A}{J}_{b}){\cos}\phi & ({m}_{1}{v}_{n}-\rho {\rm A}{J}_{n})\\ e& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 1+eT\\ 0& 0& 0& 1& (1+eT){\cos}\phi & 0\\ \frac{-e({m}_{1}{v}_{b}-\rho {\rm A}{J}_{b})}{1+eT}& 0& 0& {m}_{1}& m{v}_{t}\mathit{cos}\phi +({m}_{1}{v}_{n}-\rho {\rm A}{J}_{n}){\sin}\phi & 0\\ \frac{-e({m}_{1}{v}_{n}-\rho {\rm A}{J}_{n})}{1+eT}& 0& {m}_{1}& 0& -({m}_{1}{v}_{b}-\rho {\rm A}{J}_{b}){\sin}\phi & m{v}_{t}\end{array}\right]。\end{split} $

其中： $A=0.25 {\text{π}}{d}^{2},w=(m-\rho A)g{\text{，}}{m}_{1}=m+\rho A{\text{，}} e= 1/EA$ 。

拖缆上端点与UUV尾部连接，拖缆上端点速度为UUV与拖缆连接点的速度，得到3个速度边界条件：

$ \left\{\begin{split}&{V}_{t}={V}_{i}\cos\theta cos\phi -{V}_{j}\sin\theta \cos\phi +{V}_{k}\sin\phi, \\ &{V}_{n}={V}_{i}\cos\theta \sin\phi -{V}_{j}\sin\theta \sin\phi -{V}_{k}\cos\phi ,\\ &{V}_{b}={V}_{i}\sin\phi -{V}_{j}\cos\phi。\end{split}\right. $

其中： $ {V}_{i}，{V}_{j}，{V}_{k} $ 为拖曳UUV的拖曳点在惯性系下沿3个轴的速度分量； $ {V}_{t}，{V}_{n}，{V}_{b} $ 为拖曳点处速度在缆索局部坐标系沿3个轴的速度分量。

拖曳下端点属于自由边界，张力为0，得到拖曳下端点的边界条件如下：

$ \left\{\begin{aligned} & T=0，\\ & -w \cos\phi -\frac{1}{2}\rho d{\left(1+\epsilon \right)}^{\frac{1}{2}}{C}_{n}{U}_{n}{\left({{U}_{n}}^{\frac{1}{2}}+{{U}_{b}}^{\frac{1}{2}}\right)}^{\frac{1}{2}}=\\ & {m}_{1}{\dot{V}}_{n}+m{V}_{t}\dot{\phi }-{m}_{1}{V}_{b}\dot{\theta }\sin\phi，\\ & -\frac{1}{2}\rho d{\left(1+\epsilon \right)}^{\frac{1}{2}}{C}_{n}{U}_{b}{\left({{U}_{n}}^{\frac{1}{2}}+{{U}_{b}}^{\frac{1}{2}}\right)}^{\frac{1}{2}}=\\ & {m}_{1}{\dot{V}}_{b}+m{V}_{t}\dot{\theta }\sin\phi +{m}_{1}{V}_{n}\dot{\theta }\sin\phi。\end{aligned}\right. $

1.4 拖曳线阵声呐波束响应

当拖曳阵形畸变后，各阵元的信号实际位置偏离理论位置，引起附加相位差，从而导致目标测向精度降低，也降低了波束形成的匹配性，导致波束形成器功能退化、指向性减小，空间滤波增益降低。接收阵列信号的权值采用复数形式表示为：

$ {w}_{m}\left(\theta ,f\right)={a}_{m}\left(\theta ,f\right){e}^{-j\phi \left(\theta ,f\right)}{\text{，}}m=\mathrm{0,1},\cdots ,M-1。$

(4)

其中， $ {a}_{m}\left(\theta ,f\right) $ 和 $ \phi \left(\theta ,f\right) $ 分别为权值的复制和相位。在特定频率下，基阵的增益表达式为：

$ P\left(\theta ,f\right)={\boldsymbol{w}\left(\theta ,f\right)}^{{\rm{H}}}\boldsymbol{a}\left(\boldsymbol{\theta },f\right),\boldsymbol{\theta }\in \mathbf{\Theta } 。$

其中， $ \mathit{w} $ 为特定频率下波束形成其观测方向的加权矢量， $ \mathit{a}\left(\mathit{\theta },f\right) $ 为在空间角度集合下的扫描阵列流形矢量。根据空间增益的定义，当目标方位角为 $ {\phi }_{0} $ 时，拖曳线阵声呐的波束响应函数表达式为：

$ \begin{split} & P\left(\phi ,f\right)=\frac{1}{M}\times\\ & \left|\sum _{m=1}^{M}{e}^{\frac{2{\text{π}} fj}{c}\{{x}_{m}\left(\cos\phi -\cos{\phi }_{0}\right)+{y}_{m}\left(\sin\phi -\sin{\phi }_{0}\right)-(M-1\left)d\left(\cos\phi -\cos{\phi }_{0}\right)\right\}}\right|。\end{split} $

(5)

其中， $ {x}_{m} $ ， $ {y}_{m} $ 为拖曳阵阵元位置。一般波束响应的能量描述用分贝表示， ${P}_{beam}\left(\phi ,f\right)=20\log10\left|P\left(\phi ,f\right)\right|$ 。

2 数值仿真 2.1 计算参数

以成熟的UUV用光纤水听器拖曳线阵为参考，取拖曳阵长为200 m，线阵直径为26 mm。取拖曳线阵法向、切向阻尼系数分别为 $ {C}_{n}=0.6 $ ， $ {C}_{\iota }=0.02 $ 。线阵杨氏模量为 $E=2.0\times {10}^{7}\text{Pa}$ ，重力系数为 $g=9.81\;\text{m/}{\text{s}}^{2}$ ，拖曳线阵为中性缆，计算可得其线密度为0.5437 kg/m。取线阵工作频率为0.5 kHz，半波长为1.5 m，考虑200 m拖曳阵长，采用128个阵元。

2.2 无阵形畸变下的波束响应

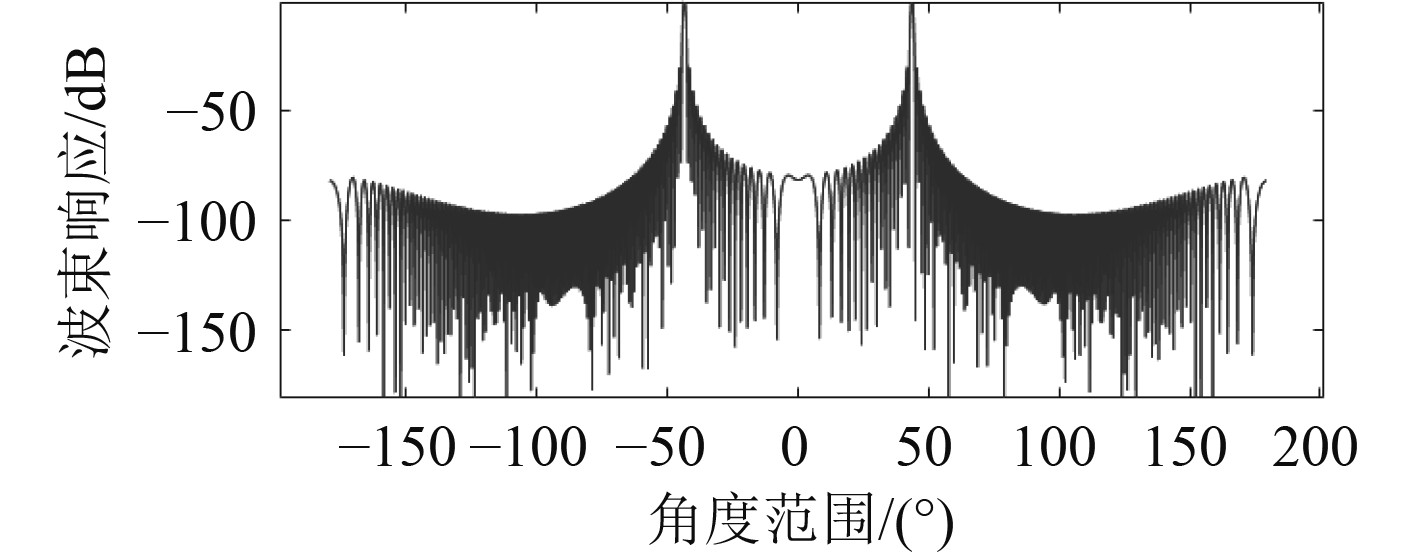
为不失一般性，计算波束响应曲线时，取探测目标所在舷角从0°～180°线性变化。不考虑噪声干扰及阵形畸变，以目标所在舷角为45°为例，其波束响应如图1所示，其镜像源位置为–45°，主瓣宽度在2°以内，具备较好的测向精度。

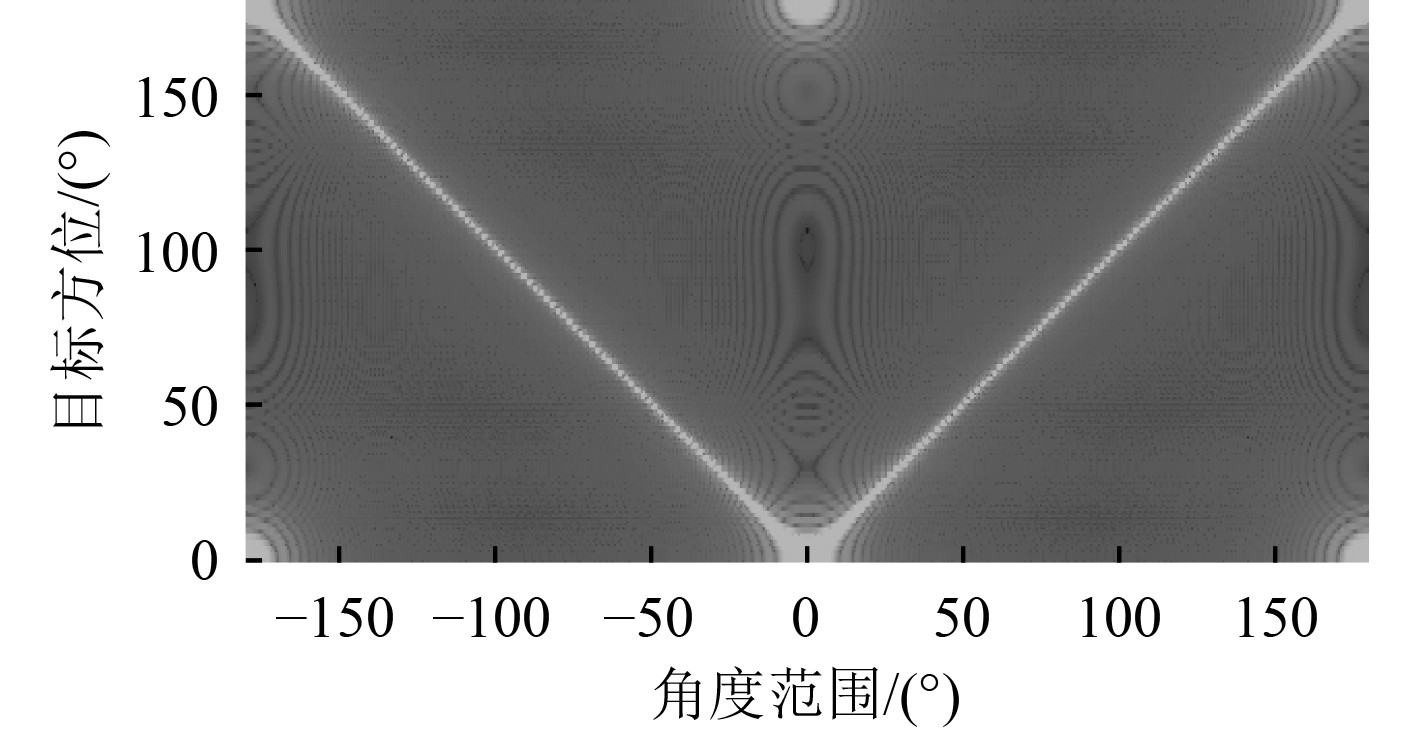
依次计算获取0°～180°目标角度下的波束响应曲线，并进行投影显示如图2。从图中深色线可看出，在−160°～−20°、20°～160°等目标角度下旁瓣较低，测向精度较高。在UUV头部及尾部方向上，测向精度差。该阵形下无法分辨目标的左右舷位置。

2.3 海流对线阵波束响应的影响分析

在直航工况下暂不考虑拖曳对UUV的影响，假定其始终以2 kn航速进行拖曳航行，在航行过程中遭遇稳定的0.2 m/s侧向海流作用。采用具有二阶精度的中心差分格式对该工况下拖曳线阵阵形计算，考虑计算效率，将200 m的线阵离散为20个单元开展计算，并通过样条插值的方式获得128个阵元的位置。

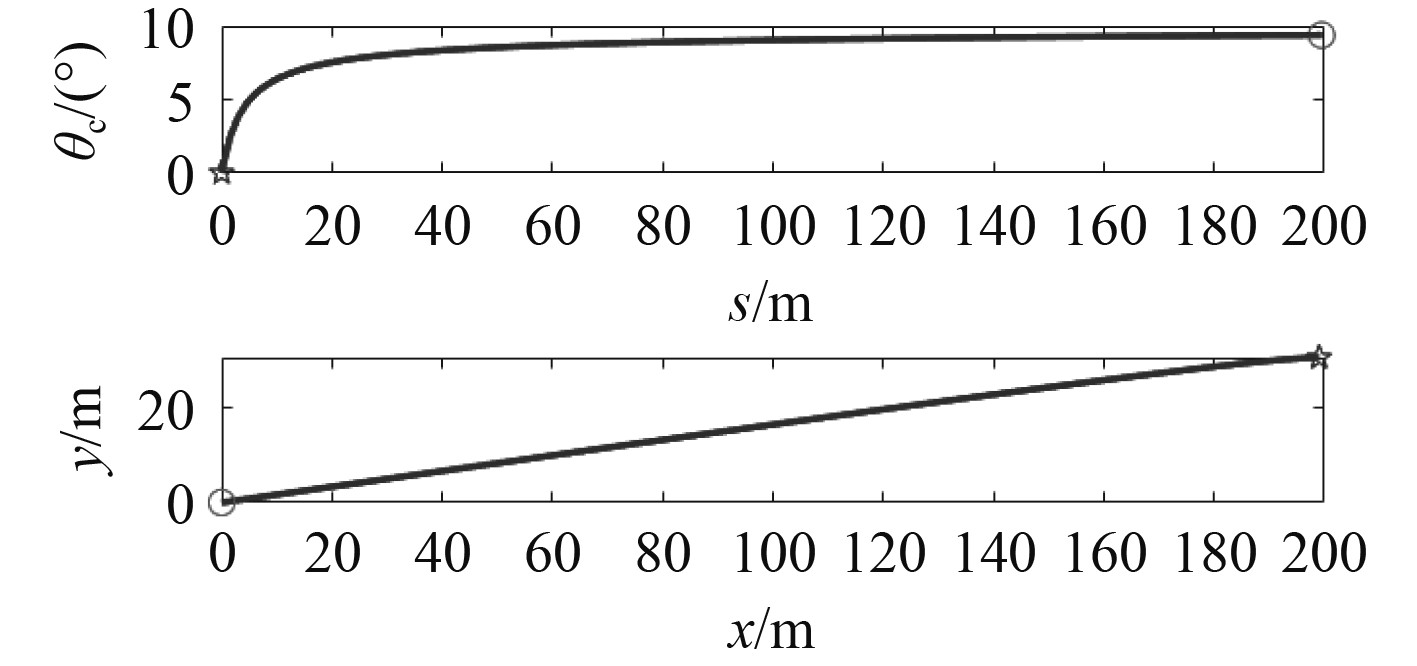
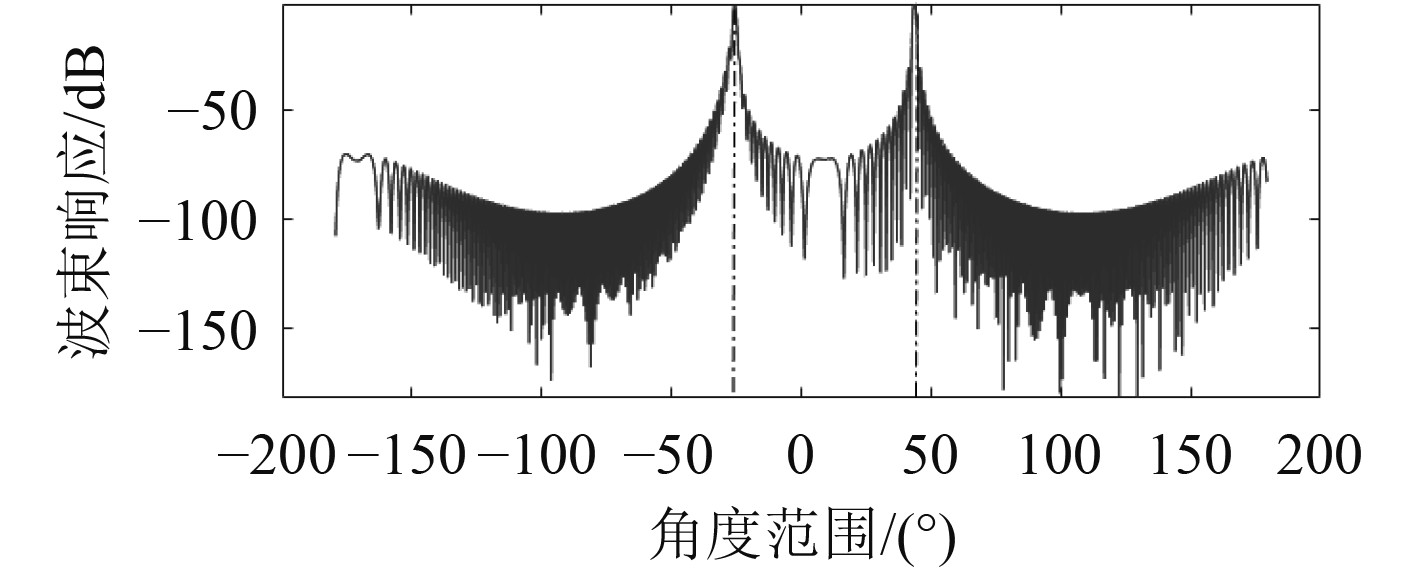
从图3可以看出，由于0.2 m/s的侧向海流作用，UUV后方的拖曳线阵向右舷方向偏转，后192 m段均匀分布128个阵元，偏转夹角约9°，但拖曳线阵几乎维持直线形状。从图4可看出，其镜像源位置由−45°偏转至−27°附近（UUV航向角为0°，右舷为正），但阵形基本维持直线型，主瓣宽度在2°左右，对目标的侧向精度影响较小。

拖曳线阵在稳定的侧向海流作用下，往右舷方向偏转，但基本维持直线阵形，并且主要由于拖曳线阵与UUV航向不一致，导致镜像源的探测角度不再关于0°近似对称。而关于线阵所在角度（9°附近）近似对称。由于阵形基本维持直线型，其主瓣宽度基本与理想阵形一致，对系统的测向精度影响较小。稳定的侧向海流下，虽然UUV左右舷相同角度下计算得到的波束响应不同，但其左右舷模糊问题依然无法解决。

2.4 UUV航向机动对线阵波束响应的影响分析

由于拖曳线阵列存在左右舷模糊问题，通常采用UUV作航向机动的方式，根据声呐时间-方位历程图中目标方位的变化或复杂目标跟踪算法实现目标位置左右舷的分辨。在航向机动过程实现左右舷分辨的过程中，UUV的航向机动较大，线阵阵形会产生较大畸变。

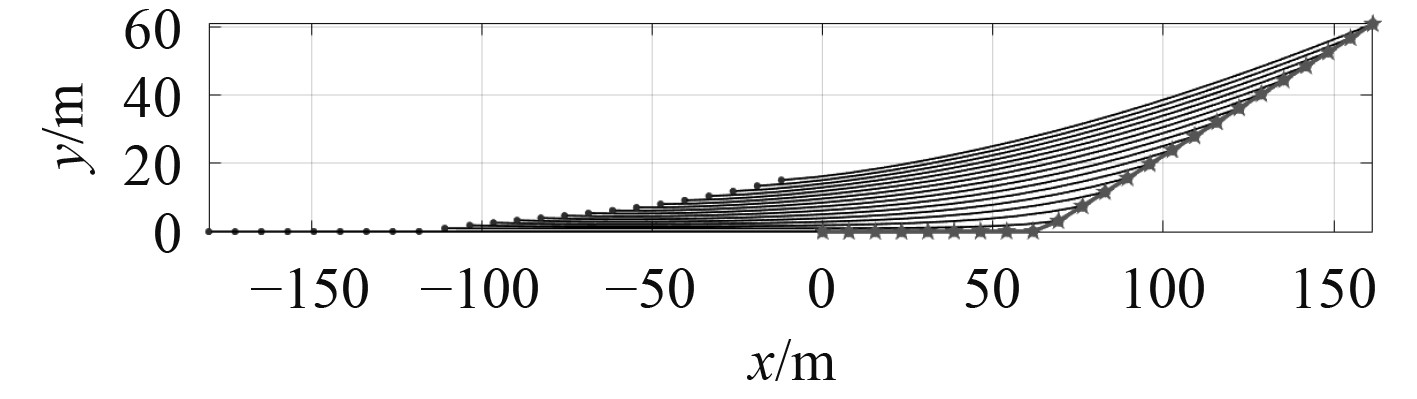
以无海流情况下在UUV拖曳直航一段时间后，进行30°航向机动分析。UUV航速2 kn，航行时间180 s，在60 s时进行左舷30°航向机动。同样为提高计算效率，将200 m的线阵离散为20个单元开展计算，获得20个节点后，通过样条插值的方式计算128个阵元的位置，进行畸变阵形的波束响应计算。计算获得的线阵阵形的变化情况如图6和图7所示。在60 s时，可以看出，UUV进行左舷30°航向机动，约5 s左右UUV航向角左转30°，在此过程中线阵上端点作用在UUV上的缆索张力减小。然后UUV沿新的航向航行，由于线阵的法向偏转，上端点作用在UUV上的缆索张力先增加，后减小，而后逐渐恢复至直线拖航时的状态。

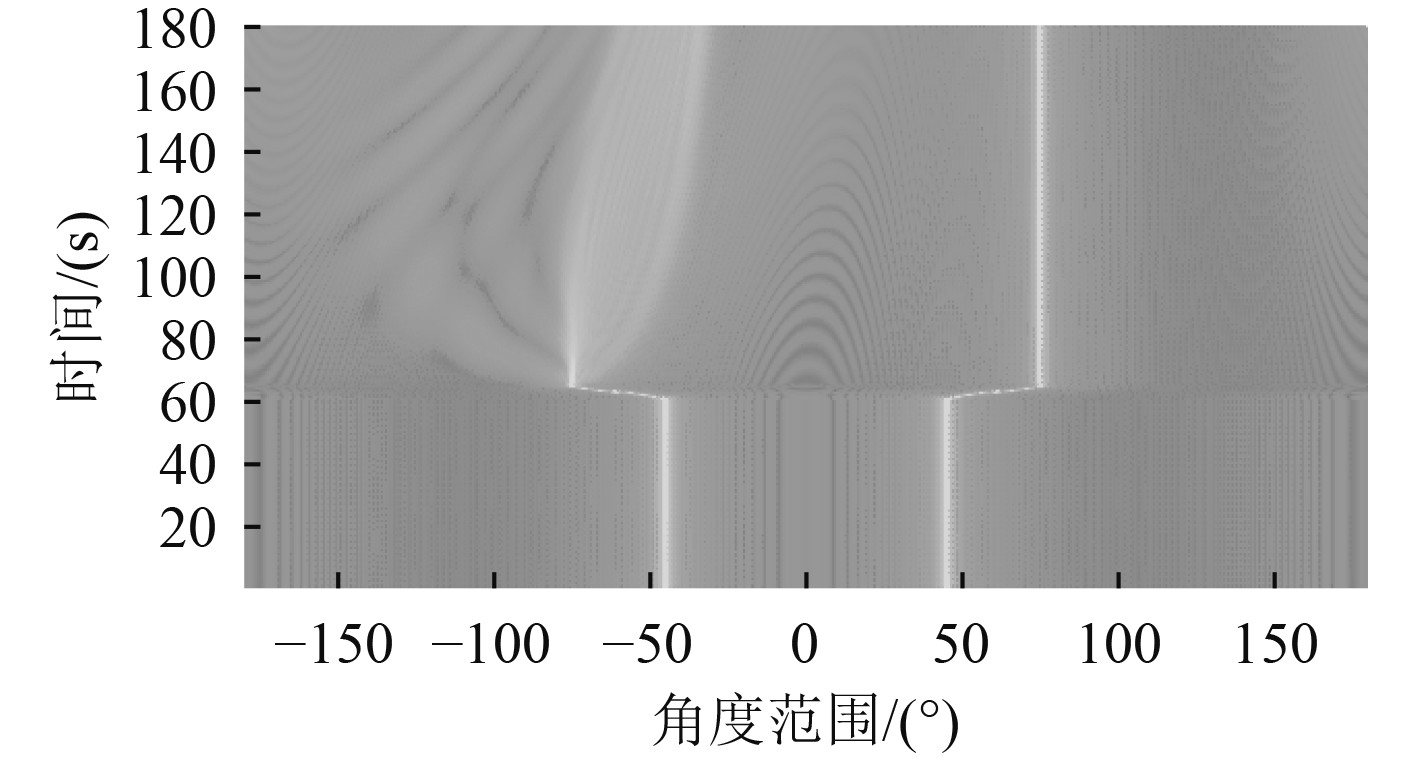
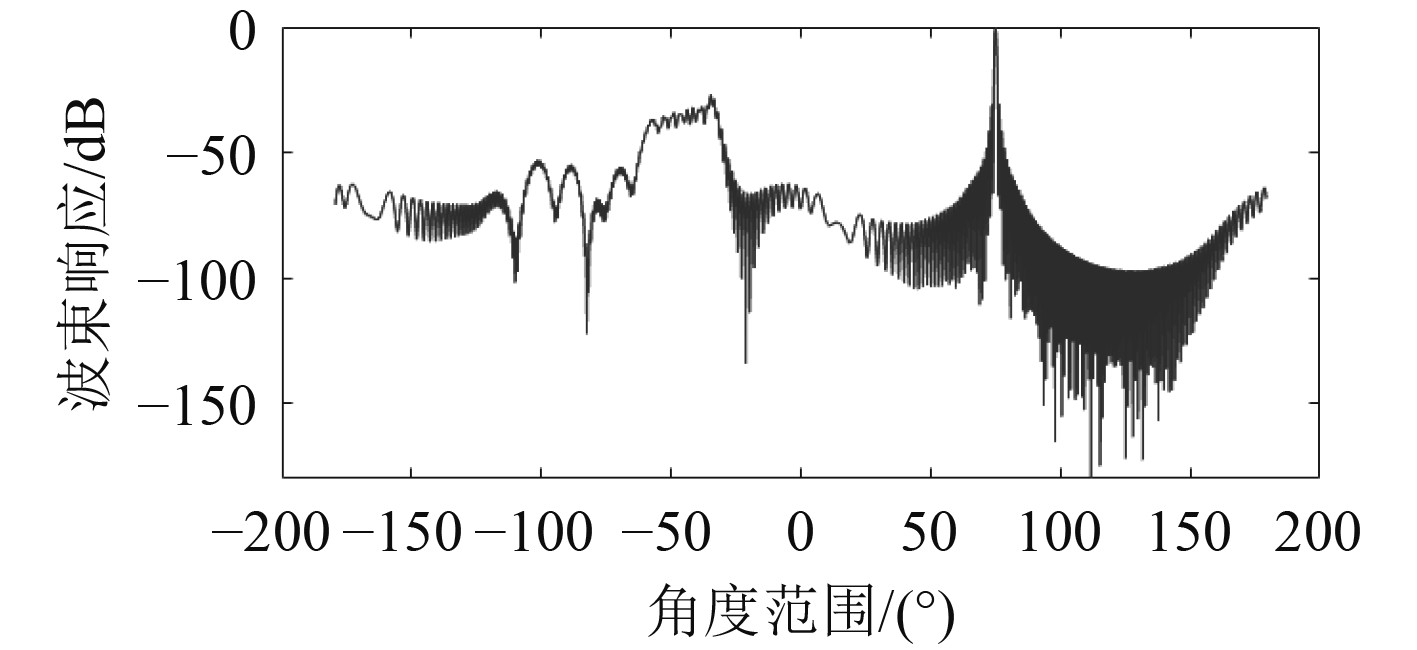
以目标所在舷角为45°为例，依次计算UUV航向机动过程中的波束响应曲线，并进行投影显示，如图8和图9 所示。可以看出，在60 s，UUV向左舷机动，因此其目标舷角从45°过渡至75°。利用UUV航向机动时阵形的畸变，可以解决左右舷位置分辨的问题。以180 s时的波束响应曲线为例，可清晰分辨出目标舷角为75°。

3 结　语

本文针对UUV拖曳线阵航速较慢，在遇到海流或航向机动进行左右舷分辨时，线阵阵形畸变现象导致的测向精度变化问题，通过采用Ablow和Schechter提出的缆索偏微分控制方程组对拖曳线阵的阵形变化进行数值求解，并采用经典的波束形成方法获得拖曳线阵声呐发生阵形畸变后的波束响应曲线。对海流导致的线阵偏航、UUV航向机动导致的线阵畸变现象引起的波束响应变化进行了仿真分析，并对线阵的测向精度以目标左右舷分辨问题进行了讨论。本文提出的线阵阵型预报方法，可用于对海流、航向机动时的阵形变化进行快速计算，以获得畸变列阵的波束形成权矢量。

1）在稳定的侧向海流作用下，线阵发生偏转，但基本维持直线型阵列。此时其主瓣宽度基本与理想阵形一致，对目标方位的估计精度影响较小，但由于拖曳线阵与UUV航向不一致，线阵探测获得的目标方位与目标相对UUV航向的方位有稳定的偏差角度（线阵方向与UUV方向的夹角）。并且线阵稳定偏转及畸变无法解决左右舷模糊的问题。

2）在UUV进行航向机动时，线阵发生畸变弯曲，波束主瓣有所变宽，一定程度增加了目标方位估计误差，但同时获得了畸变阵形对镜像源的抑制效果，实现了对目标的左右舷分辨。