2. 航天时代(青岛)海洋装备科技发展有限公司,山东 青岛 266200;
3. 中国航天科技集团有限公司智能无人系统总体技术研发中心,北京 100094;
4. 崂山实验室,山东 青岛 266237
2. Aero-Times (Qingdao) Marine Equipment Technology Development Co., Qingdao 266200, China;
3. China Aerospace Science and Technology Corporation Intelligent Unmanned System Overall Technology Research and Development Center, Beijing 100094, China;
4. Laoshan Laboratory, Qingdao 266237, China
无人艇(Unmanned Surface Vehicles, USV)是一种集环境感知、路径规划、导航控制功能为一体的无人水面平台,通过搭载相应任务载荷,能够执行不同的任务,尤其适用于各种单调或危险的任务场景[1]。但因其体量小、携带能源有限,一般由母船携带并通过收放装置投送至特定的海域执行相应任务。当前无人艇的布放与回收一般在慢航速与低海况下人工操作进行,存在较大风险且效率低,高效、安全、可靠的无人艇自主布放和回收系统是无人艇推广使用亟需突破的瓶颈[2]。路径跟踪控制技术是无人艇自主回收的关键技术之一,其控制精度深深影响着无人艇回收对接的成功率。无人艇回收过程中航速较慢,自身舵效较差,不仅易受外界风浪流环境干扰,而且受执行机构限制,控制输入易饱和,如不加以抑制会大幅降低无人艇回收对接成功率[3],因此要求回收路径跟踪控制器需具备较高的抗干扰能力与输入饱和调节能力。
目前国内外对于无人艇的路径跟踪控制已开展较多研究。Yu[4]基于传统视线法(Line-of-Sight, LOS)导引策略,设计了PD首向控制器跟踪滑道式回收直线路径,并未考虑环境干扰的影响。Lekkas[5]采用时变的前视距离LOS导引,并基于级联系统理论设计了首向控制器跟踪直线路径,并未考虑速度的控制以及曲线路径的跟踪。黄宏赟[6]基于积分视线(Integral LOS,ILOS)导引策略,采用反步法并通过扰动观测器设计了曲线路径跟踪控制器,但所用ILOS的前视距离参数固定不变。陈霄[7]考虑海流对侧滑角的影响,改进了2种ILOS导引策略,并应用反步法设计了速度与首向控制器跟踪曲线路径,但是并没有考虑除海流以外的其他环境干扰。周利[8]基于海流观测器估计侧滑角,设计了自适应ILOS导引策略,并基于扰动观测器与反步法设计了速度与首向控制器跟踪曲线路径,但其并未考虑控制输入饱和对控制器的影响。
本文针对无人艇自主回收场景,在导引律设计方面,将前视距离参数与横向位置跟踪误差相联系,设计了时变前视距离参数的ILOS导引方法。在控制器设计方面,考虑未知环境扰动,设计了指数收敛的扰动观测器,然后基于反步法设计了无人艇首向和速度控制器,为克服反步法解析导数求解的弊端,利于工程实现,设计了期望首向导数的二阶滤波器。此外,考虑回收路径跟踪过程中无人艇舵效较差而执行机构受限,控制输入易饱和的情况,设计了饱和补偿辅助系统。最后通过仿真对比实验,验证了算法的有效性。
1 USV路径跟踪数学模型 1.1 USV建模在进行USV建模前,作如下假设:USV结构左右对称,船体重心和艇体坐标系原点重合;USV是质量分布均匀的刚体;海面是一平面;重力加速度和海水密度为常值。同时只考虑线性阻尼,忽略惯性矩阵和阻尼矩阵非对角线元素,则USV三自由度运动学与动力学模型可表示为:
| $ \left\{ \begin{array}{l} \dot{x}=u \cos \psi-v \sin \psi, \dot{y}=u \sin \psi+v \cos \psi, \dot{\psi}=r,\\ \dot{u}=m_{22} v r / m_{11}-d_{11} u / m_{11}+\tau_{11}+d_{\nu} / m_{11},\\ \dot{v}=-m_{11} u r / m_{22}-d_{22} v / m_{22}+d_{v} / m_{22} ,\\ \dot{r}=\left(m_{11}-m_{22} / m_{33}\right) u v-d_{33} r / m_{39}+\left(\tau_{r}+d_{r}\right) / m_{39}。\end{array} \right. $ | (1) |
式中:
USV导引律的设计以位置跟踪误差模型为基础,假定期望回收路径是水平面一条参数化的自由曲线

|
图 1 USV位置跟踪误差示意图 Fig. 1 Diagram of USV position following error |
Serret-Frenet坐标系
定义USV在
| $ \begin{split}{\boldsymbol{\eta}}_{e}^{f}=&{\boldsymbol{R}}\left(\gamma_{p}\right) {\boldsymbol{\eta}}_{e}^{E}=\\ &\left[ \begin{array}{l} {x}_{e} \\ {y}_{e} \\ \psi_{v} \end{array} \right]=\left[ \begin{array}{ccc} \cos \gamma_{p} & \sin \gamma_{p} & 0 \\ -\sin \gamma_{p} & \cos \gamma_{p} & 0 \\ 0 & 0 & 1 \end{array} \right]\left[ \begin{array}{c} x-x_{p} \\ y-y_{p} \\ \psi+\beta-\psi_{p} \end{array} \right]。\end{split} $ | (2) |
USV的合速度
| $ \left[ \begin{array}{c} \dot{x}_{e} \\ \dot{y}_{e} \\ \dot{\psi}_{e} \end{array} \right]=\left[ \begin{array}{c} U \cos \left(\psi+\beta-\gamma_{p}\right)+y_{e} \dot{\gamma}_{p}-\dot{\omega} \sqrt{x_{p}^{\prime 2}+y_{p}^{\prime 2}} \\ U \sin \left(\psi+\beta-\gamma_{p}\right)-x_{e} \dot{\gamma}_{p} \\ r+\dot{\beta}-\dot{\gamma}_{p} \end{array} \right]。$ | (3) |
按照级联控制的思想,将USV回收路径跟踪控制分为导引律和控制器两方面分别进行设计,图2为系统框图。
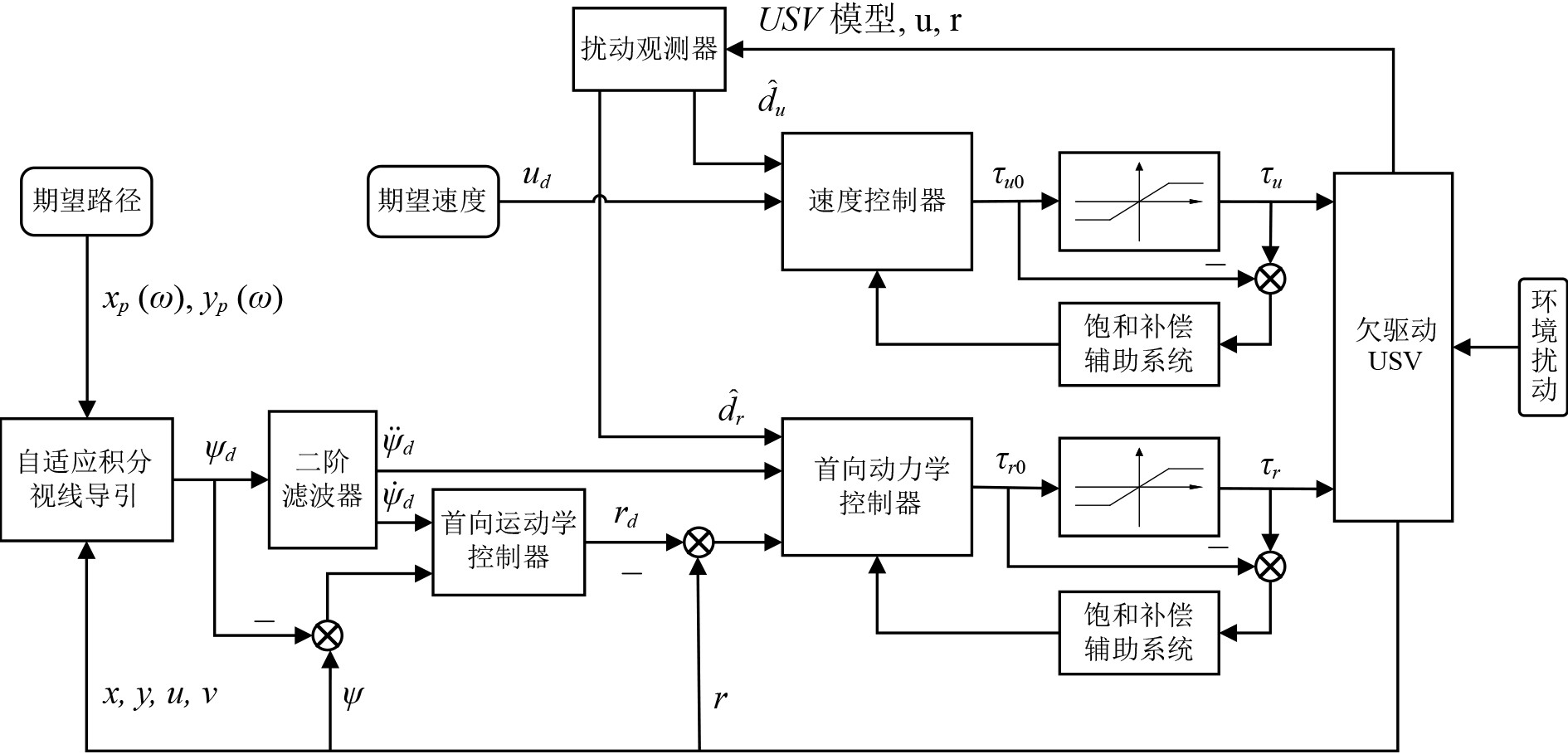
|
图 2 USV回收路径跟踪控制系统框图 Fig. 2 Block diagram of USV recovery path following control system |
ILOS导引是在LOS算法的基础上改进的,考虑了USV侧滑角的影响,作为一种经典的导引策略,在无人艇的路径跟踪中得到了广泛的应用。传统ILOS导引律一般形式为:
| $ \left\{\begin{split}&\psi_{ILOS}={\rm{arctan}}(-(y_e)+\lambda y_{eint}/\varDelta),\\ & \psi_d=\gamma_p-\beta+\psi_{ILOS},\\ & \dot \gamma_{eint}=Uy_e/\sqrt{\varDelta ^2+(y_e+\lambda y_{eint})^2}-\lambda y_{eint}。\end{split} \right. $ | (4) |
式中:
传统ILOS导引的前视距离
| $ \Delta\left(y_{e}\right)=\Delta_{\min }+\left(\Delta_{\max }-\Delta_{\min }\right) e^{-\alpha y_{e}^{2}}。$ | (5) |
式中,
为进行导引律稳定性设计,建立李雅普诺夫函数为:
| $\begin{split} \dot{V}_{e}=&x_{e}\left(U \cos \left(\psi+\beta-\gamma_{p}\right)-\dot{\omega} \sqrt{x_{p}^{\prime 2}+y_{p}^{\prime 2}}\right)+\\ &y_{e} U \sin \left(\psi+\beta-\gamma_{p}\right)+\lambda y_{eint} \dot{y}_{eint}。\end{split} $ | (6) |
为消除纵向位置跟踪误差,设计路径参数更新律为:
| $ \dot{\omega}=\left(U \cos \left(\psi+\beta-\gamma_{p}\right)+k_{x} x_{\mu}\right) / \sqrt{x_{p}^{\prime 2}+y_{p}^{\prime 2}}。$ | (7) |
式中,
| $ \begin{split}\dot {V}_e=&-k_x x_e^2-Uy^2_e/\sqrt{\varDelta(y_e)^2+(y_e+\lambda y_{eint})^2}-\\ &\lambda^2y^2_{eint}+U\phi(y_e,\tilde{\psi})\tilde{\psi} y_e。\end{split} $ | (8) |
其中,
为克服未知环境扰动,提高USV的抗干扰能力与路径跟踪精度,通过获取与分析USV控制输入和航行状态的实际关系,设计了扰动观测器来估计控制系统存在的未知环境扰动,并在控制器设计中加入相应的扰动补偿。假设外界海洋环境扰动
| $ \left\{\begin{array}{l} \hat{{\boldsymbol{\tau}}}_{d}={\boldsymbol{\sigma}}+{\boldsymbol{Q}} M v,\\ \dot{{\boldsymbol{\sigma}}}=-{\boldsymbol{Q \sigma}}-{\boldsymbol{Q}}(-C(v) v-D v+{\boldsymbol{Q}} M v+\tau)。\end{array}\right. $ | (9) |
式中:
估计误差
| $ \begin{split}\dot V_d=&\tilde d_u(\dot d_u-\dot{\hat d}_u)+\tilde d_r(\dot d_r-\dot{\hat d}_r)\leqslant \dot d^2_{\max}/(2q_{\min}-1)+\\ &(V_d(0)-\dot d^2_{\max}/(2q_{\min}-1))e^{-(2q_{\min}-1)t} 。\end{split}$ | (10) |
式中:
1) 首向运动学控制器设计
为使USV的首向收敛到期望首向,即
| $ r_{d}=-k_{y} \tilde{\psi}+\dot{\psi}_{d}-U \phi\left(y_{e}, \tilde{\psi}\right) y_{e}。$ | (11) |
式中,
| $ \begin{split}\dot{V}_{v}=&\tilde{\psi}\left(r-\dot{\psi}_{d}\right)=\tilde{\psi}\left(\tilde{r}+r_{d}-\dot{\psi}_{d}\right)=\\ &-k_{w} \tilde{\psi}^{2}-U_{\phi}\left(y_{e}, \tilde{\psi}\right) \tilde{\psi} \mathcal{F}_{e}+\tilde{\psi} \bar{r} 。\end{split}$ | (12) |
2) 首向饱和补偿辅助系统设计
在设计首向动力学控制器之前,考虑实际应用中执行器受限,控制输入饱和的情形。
| $ \tau_{r}=\left\{\begin{array}{ll} \tau_{r \max },& \tau_{r 0}>\tau_{r \max },\\ \tau_{r 0} ,& \tau_{r \min } \leqslant \tau_{r 0} \leqslant \tau_{r \max },\\ \tau_{r \min },& \tau_{r 0}<\tau_{r \min }。\end{array}\right. $ | (13) |
式中:
| $ \dot{\rho}_{r}=-k_{\rho r 1} \rho_{r}-\left(\left(0.5 \sigma_{r}^{2} \tilde{\tau}_{r}^{2}+\left|\bar{r}_{r}\right|\right) / \rho_{r}\right) \zeta\left(\rho_{r}\right)+\sigma_{r} \tilde{\tau}_{v} 。$ | (14) |
式中:
| $ \begin{split}&\zeta(x)= \\ &\left\{ \begin{array}{ll} 0 ,& |x|<a_{1},\\ 1 - \cos \left((\text{π} / 2) \sin \left((\text{π} / 2)\left(|x|^{2} - a_{1}^{2}\right) /\left(\alpha_{2}^{2} - a_{1}^{2}\right)\right)\right),& a_{1} \leqslant|x| \leqslant a_{2},\\ 1 ,& |x|>\omega_{2}。\end{array}\right.\end{split} $ | (15) |
3) 首向动力学控制器设计
为使USV的回转角速度能跟踪上虚拟控制律
| $ \begin{array}{l} k_{p r 1} \rho_{r}^{2}-\left(0.5 \sigma_{r}^{2} \tilde{\tau}_{r}^{2}+\left|\tilde{\kappa}_{r}\right|\right) \zeta\left(\rho_{r}\right)+\sigma_{r} \tilde{\tau}_{r} \boldsymbol{\rho}_{r} 。\end{array} $ | (16) |
设计首向控制器为:
| $ \tau_{r 0}=m_{33}\left(\dot{r}_{d}-k, \bar{r}-\bar{\psi}+k_{p r 2} \rho_{r}\right)-\left(m_{11}-m_{22}\right) z v+d_{33} r-\hat{d}_{r} 。$ | (17) |
式中:
| $ \begin{split} \dot{V}_{r} \leqslant &-k_{v} \dot{\psi}^{2}-U \phi\left(y_{r}, \dot{\psi}\right) \dot{\psi} y_{\psi}-(k_{r}-1 /(2 m_{33})-\\ &k_{p r} 2-1 / 2) \hat{r}^{2}- \left(k_{p r 1}-k_{p r} / 2-1 / 2\right) \rho_{r}^{2}+\\ &\left(\sigma_{r}^{2} / 2+1 / 2\right) \bar{t}_{r}^{2}+\dot{d}_{r}^{2} /\left(2 m_{33}\right)。\end{split} $ | (18) |
4) 二阶滤波器设计
在利用反步法设计首向控制器时,控制器中包含期望首向的一阶、二阶导数,但反步法自身存在“微分爆炸”的缺陷,所以为避免解析导数的直接求取,符合工程实际,通过设计二阶滤波器,获取期望首向的一阶、二阶导数估计。
| $ \left\{\begin{array}{l} \dot{z}_{1}=z_{2},\\ \dot{z}_{2}=-2 \xi \omega_{n} z_{2}-\omega_{n}^{2}\left(z_{1}-\psi_{d}\right)。\end{array}\right. $ | (19) |
式中:
1) 速度饱和补偿辅助系统设计
速度饱和补偿辅助系统的设计同首向饱和补偿辅助系统,表达式为:
| $ \dot{\rho}_{u}=-k_{p u 1} \rho_{u}-\left(0.5 \sigma_{u}^{2} \tilde{\tau}_{u}^{2}+\left|\tilde{u} \tilde{\tau}_{u}\right|\right) \zeta\left(\rho_{u}\right) / \rho_{u}+\sigma_{u} \tilde{\tau}_{u}。$ | (20) |
式中:
2) 纵向速度控制器设计
构造李雅普诺夫函数为:
| $ \begin{split}\dot V_u=&\tilde u(m_{22}vr/m_{11}-d_{11}u/m_{11}+(\tau_u+d_u)/m_{11}-\dot{u}_d)-\\ &k_{pu1}\rho^2_u-(0.5\sigma^2_u \tilde \tau^2_u+|\tilde u \tilde \tau_u|)\zeta (\rho_u)+\sigma_u\tilde \tau_u\rho_u。\end{split} $ | (21) |
设计首向控制器为:
| $ \tau_{x 0}=m_{11}\left(\dot{u}_{d}-k_{u} \tilde{u}+k_{p w 2} \rho_{u}\right)-m_{22} v r+d_{11} u-\hat{d}_{u} 。$ | (22) |
式中:
| $\begin{split} \dot V_u \leqslant &-(k_u-1/(2m_{11})-k_{\rho u2}/2-1/2)\tilde u^2-(k_{\rho u 1}-\\ &k_{\rho u 2}/2-1/2)\rho^2_u+(\sigma^2_u/2+1/2)\tilde \tau^2_u+d^2_u/(2m_{11})。\end{split} $ | (23) |
为分析路径跟踪控制系统全局稳定性,构造系统李雅普诺夫函数如下:
| $\begin{split} V=&\left(x_{e}^{2}+y_{t}^{2}+\lambda y_{\text {mit }}^{2}\right) / 2+\dot{\psi}^{2} / 2+\dot{r}^{2} / 2+\hat{u}^{2} / 2+\\ &\rho_{p}^{2} / 2+\rho_{s}^{2} / 2=V_{t}+V_{x}+V_{x},\end{split} $ | (24) |
对上式求导,并将式(8)、式(18)、式(23)代入得:
| $ \begin{split}\dot V\leqslant & -k_x x^2_e-Uy^2_e/\sqrt{\varDelta (y_e)^2+(y_e+\lambda y_{dint})^2}-\\ &\lambda^2 y^2_{eint}-k_{\Psi}\tilde \Psi^2-(k_r-1/(2m_{33})-k_{pr2}/2-\\ &1/2)\tilde r^2-\left(k_{w}-1 /\left(2 m_{11}\right)-k_{p w 2} / 2-1 / 2\right) \tilde{u}^{2}-\\ &\left(k_{p r 1}-k_{p r 2} / 2-1 / 2\right) \mu_{s}^{2}-(k_{p, 1}-k_{p o p} / 2-\\ &1 / 2) \mu_{\alpha}^{2}+ \left(\sigma_{r}^{2} / 2+1 / 2\right) \tilde{\tau}_{r}^{2}+\left(\sigma_{u}^{2} / 2+1 / 2\right) \tilde{\tau}_{u}^{2}+\\ &\tilde{d}_{r}^{2} /\left(2 m_{33}\right)+\tilde{d}_{H}^{2} /\left(2 k z_{11}\right) 。\end{split} $ | (25) |
由式(10)可知扰动观测器的估计误差指数收敛于一个很小的球域,则
| $ \dot{V} \leqslant-2 k V+\mu=\mu / 2 k+[V(0)-\mu / 2 k] e^{-2 k t} 。$ | (26) |
式中:
| $ k=\min\left\{\begin{array}{l} -k_x,U/\sqrt{\varDelta (y_e)^2+(y_e+\lambda y_{eint})^2},\lambda, k_{\psi},\\ k_r-1/(2m_{33})-k_{\rho r 2/2-1/2},\\ k_u-1/(2m_{11})-k_{\rho u2}/2-1/2,\\ k_{\rho r1}-k_{\rho r2}/2-1/2,k_{\rho u1}-k_{\rho u2/2-1/2} \end{array} \right\};$ |
且
由上式可以看出,通过选择合适的控制参数,就能保证V是有界的,则系统信号
为验证本文所设计的USV回收路径跟踪控制律的有效性,以CybershipII模型船为控制对象进行仿真,该USV的相关模型参数具体为
| $ \begin{split}t_{d}=&[0.2 \sin (t / 10)+0.5 \sin (t / 20), 0.05 \sin (t / 10)+\\ &0.1 \sin (t / 20), 0.1 \sin (t / 10)+0.2 \sin (t / 20)]^{t}。\end{split} $ | (27) |
USV路径跟踪控制器设计参数如表1所示。
|
|
表 1 USV路径跟踪控制器参数 Tab.1 USV path following controller parameters |
期望路径分为直线和曲线2种,将传统ILOS与本文设计的自适应ILOS方法进行对比,同时为验证输入饱和下控制器的性能,对比自适应ILOS 在有无加入饱和控制环节下的性能。
1) 直线路径跟踪
直线期望路径为
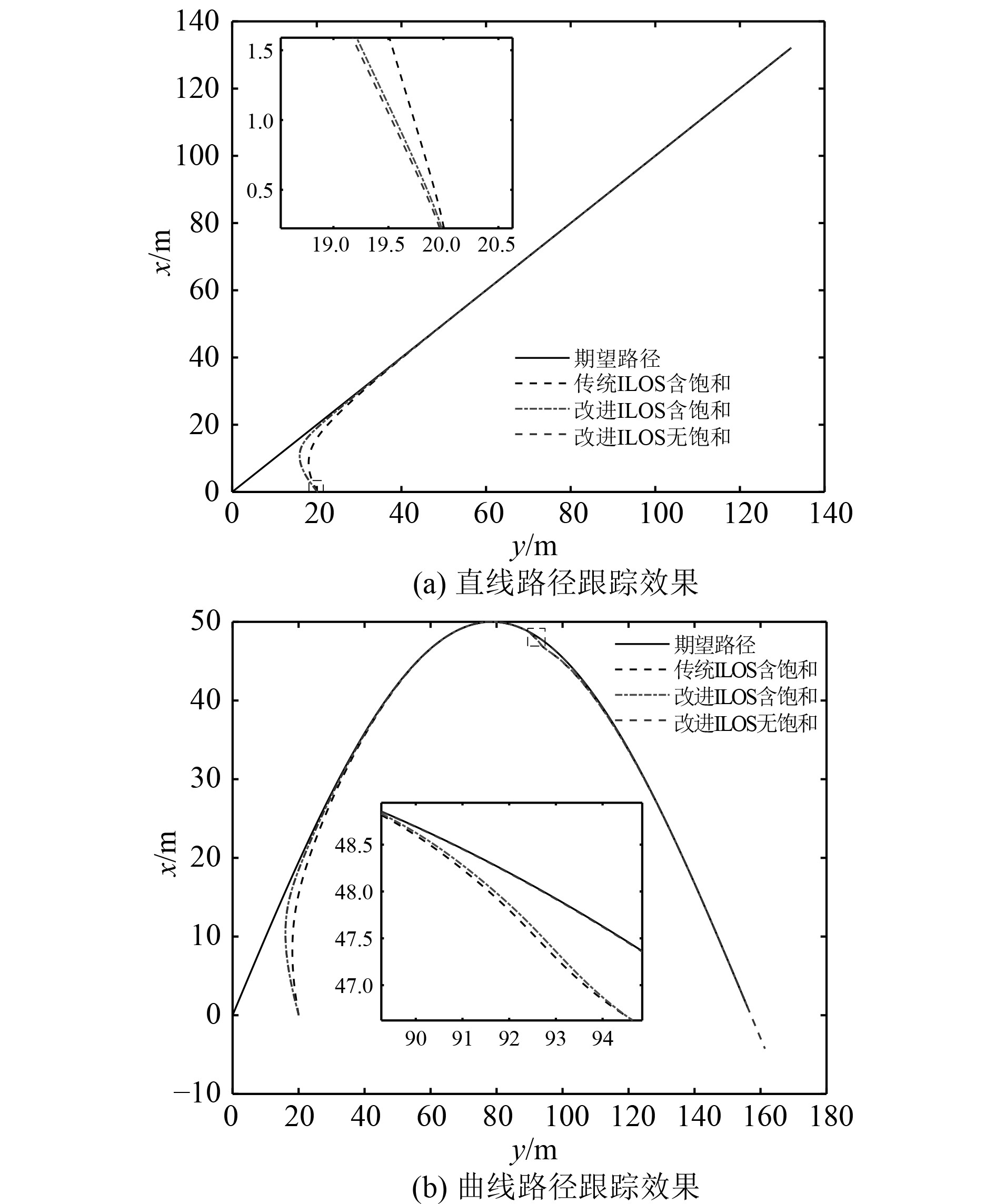
|
图 3 直线及曲线路径跟踪效果 Fig. 3 Straight and curve path following effect |

|
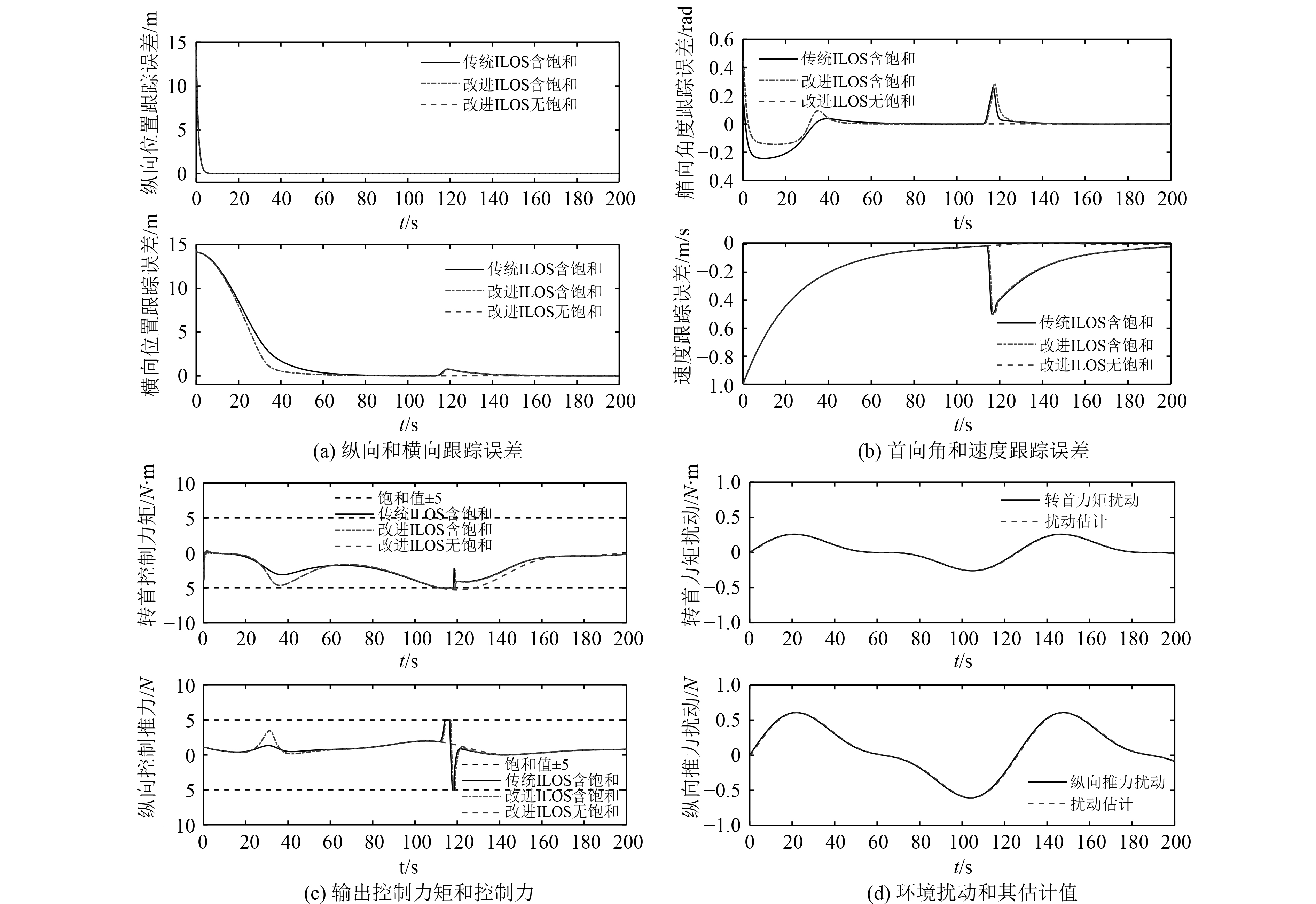
图 4 直线路径跟踪误差和控制输入对比及扰动观测器效果 Fig. 4 Comparison of linear path following error, control input and effect of disturbance observer |
由图3(a) USV直线跟踪效果可以看出,改进后ILOS相比传统ILOS具有较快的收敛速度。另外,未带控制输入饱和的ILOS由于没有输入饱和限制,相比带有控制输入饱和的ILOS具有更快的收敛速度。最终,3种方法都能跟踪到直线路径上。
由图4(a)和图4(b)可以看出,改进后的ILOS相比传统ILOS横向位置跟踪误差与首向角度跟踪误差均更小,收敛速度更快。而由图4(c)可以看出,改进后的ILOS为加快初始收敛速度,控制输入相比传统ILOS略大。另外,无饱和输入限制的ILOS在初始时刻具有较大的转首控制力矩,超出了执行器的最大调节范围,这与实际应用是不符的。综合图3和图4(c)可以看出,由于ILOS只在初始时刻存在瞬时的控制输入饱和,所以有无加入输入饱和控制环节并没有明显的差异。由图4(d)可以看出,扰动观测器具有很好的观测效果,扰动估计值与实际环境扰动只存在细微的差异。
2) 曲线路径跟踪
曲线期望路径为
|
图 5 曲线路径跟踪误差和控制输入对比及扰动观测器效果 Fig. 5 Comparison of curve path following error, control input and effect of disturbance observer |
由图3(b)USV曲线跟踪效果可以看出,改进后ILOS相比传统ILOS具有较快的收敛速度,但是带控制输入饱和的传统ILOS和改进ILOS在曲线路径拐弯处都存在少许偏差,不过该偏差很快就收敛到较小范围。而不加饱和环节的改进ILOS由于没有输入饱和限制,从初始收敛后就未再偏离跟踪路径。最终,3种方法都能跟踪到曲线路径上。
由图5(a)和图5(b)可以看出,改进后的ILOS相比传统ILOS横向位置跟踪误差与首向角度跟踪误差均更小,收敛速度更快。但是在120 s附近,带控制输入饱和的传统ILOS和改进ILOS首向角度跟踪误差都存在短暂小范围波动,受其影响,横向位置跟踪误差和速度跟踪误差也都存在误差波动的情况,但在短暂调节后误差又都收敛到较小范围。而不加饱和环节的改进ILOS从初始误差收敛后就未再出现波动。
而由图5(c)可以看出,改进后的ILOS由于为加快初始收敛速度,控制输入相比传统ILOS较大。另外,无饱和输入限制的改进ILOS在120 s附近,转艏控制力矩已经超出了执行器的最大调节范围,并不符合实际应用。综合图3(b)和图5(a)~图5(c)可以看出,带有控制输入饱和的改进ILOS,由于输入饱和的限制,存在控制输入饱和后短暂的误差波动,但是在饱和辅助补偿系统的调节下,可以快速地收敛到很小范围,这更符合实际工程应用。
4 结 语本文研究了USV在自主回收过程中的路径跟踪控制问题,提出了基于自适应ILOS导引及扰动观测器的鲁棒性跟踪控制方法,基于李雅普诺夫理论证明了系统的稳定性,并通过仿真实验验证了算法的有效性与优越性。
1) 自适应ILOS导引律设计。将传统ILOS导引方法的固定前视距离参数与横向位置跟踪误差相联系,设计了时变前视距离参数的ILOS导引方法,提高了USV回收中路径跟踪的响应速度。
2) 基于扰动观测器与反步法的鲁棒性控制器设计。考虑未知环境扰动,设计了渐进稳定的扰动观测器,并基于反步法设计了USV首向与速度控制器,提高了系统的抗干扰能力。为克服反步法解析导数求解的弊端,设计了期望首向导数的二阶滤波器,利于工程实现。
3) 饱和补偿辅助系统设计。考虑回收路径跟踪过程中USV舵效较差而执行机构受限,控制输入易饱和的情况,设计了饱和补偿辅助系统,具有较好的饱和调节效果。
| [1] |
胡常青, 朱玮, 何远清, 等. 无人水面艇自主导航技术[J]. 导航与控制, 2019, 18(1): 19-26. |
| [2] |
张晓东, 刘世亮, 刘宇, 等. 无人水面艇收放技术发展趋势探讨[J]. 中国舰船研究, 2018, 13(6): 50-57. DOI:10.19693/j.issn.1673-3185.01258 |
| [3] |
VOLDEN Ø, STAHL A, FOSSEN T I. Vision-based positioning system for auto-docking of unmanned surface vehicles[J]. International Journal of Intelligent Robotics and Applications, 2021.
|
| [4] |
Yu W Y, Wang J, Tang G Y, et al. Dual-attention-based optical terminal guidance for the recovery of unmanned surface vehicles[J]. Ocean Engineering, 2021, 239: 109852. DOI:10.1016/j.oceaneng.2021.109852 |
| [5] |
LEKKAS A M, FOSSEN T I. Integral LOS Path Following for curved paths based on a monotone cubic hermite spline parametrization[J]. IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY, 2014, 22(6): 2287-2300. DOI:10.1109/TCST.2014.2306774 |
| [6] |
黄宏赟. 欠驱动无人船路径跟踪控制研究[D]. 大连: 大连海事大学, 2020.
|
| [7] |
陈霄, 刘忠, 张建强, 等. 基于改进积分视线导引策略的欠驱动无人水面艇路径跟踪[J]. 北京航空航天大学学报, 2018, 44(3): 489-498. DOI:10.13700/j.bh.1001-5965.2017.0192 |
| [8] |
周利. 基于扰动补偿的无人艇路径跟踪控制算法研究[D]. 哈尔滨工程大学, 2018.
|
 2023, Vol. 45
2023, Vol. 45
