2. 中国船舶科学研究中心上海分部,上海 200011;
3. 上海海事大学 信息工程学院,上海 200135
2. Shanghai Branch, China Ship Scientific Research Center, Shanghai 200011, China;
3. Shanghai Maritime University, Shanghai 200135, China
随着船舶在吨位、航速以及数量上的快速提升,海上船舶碰撞事故越来越多,造成的人员伤亡和财产上的损失也越来越重大,而且对海洋环境也会造成极为严重的伤害[1]。目前船舶避让行为的决策主要依靠船员经验,不同的船长对船舶当前的会遇状况及危险度存在主观认知的偏差,进而在采取避让决策时存在误差和不协调性,这也是海上航行事故频发的主要原因之一。在航行过程中,尽管船舶有众多的通信设备、导航系统以及船舶监管设施等技术的支持,仍然发生较多水上交通事故。造成事故的主要原因是瞭望疏忽、对会遇态势判断错误、避碰决策的不当以及未以安全航速航行,因此船舶的自主化识别、碰撞危险度自主判断、智能决策以及智能化操纵相关的研究亟需推进[2]。
本文对人工势场法在静态环境中的全局路径规划进行研究。通过与模拟退火法相结合,提出自适应子目标对传统人工势场法进行优化改进,解决传统人工势场法在复杂环境中存在的局部极小值问题和目标不可达问题,提高了人工势场法的全局规划能力和规划效率。同时对船舶空间危险度(DCPA)及时间危险度(TCPA)模型进行深入研究。
1 人工势场法在静态环境的路径规划人工势场法广泛应用于机器人、车辆以及船舶的路径规划,其模型构造简洁,原理简单清晰,规划过程也不繁琐。但随着将其应用于越来越复杂的环境中,传统人工势场法本身存在的缺陷也暴露了出来[3]。人工势场法在模拟退火法帮助下能够使船舶逃离局部极值点,但模拟退火法消耗的时间较长。通过指向性自适应设置子目标点,引导船舶逃离局部极小点。
1.1 改进人工势场法函数目标不可达问题根本上来说是函数本身存在的漏洞,要解决这一问题,需要从函数入手,通过优化引力或斥力函数,对太过于接近目标点的斥力势场进行弱化或其缩小影响范围,但又不能太过于削弱,否则会发生碰撞危险。在势场模型构造方面,主要是通过构建合理的势场函数,消除或减少局部极小点,保证在目标点附近时引力作用占主导地位[4]。
| $ {U_{rep}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}\eta {{\left(\dfrac{1}{{\rho (q - {q_0})}} - \dfrac{1}{{{\rho _0}}}\right)}^{\text{2}}}} ,\\ {\rho (q - {q_0}) \leqslant {\rho _0},\rho ({q_{goal}} - {q_0}) > {\rho _0}} ,\\ {\dfrac{1}{2}\eta {{\left(\dfrac{1}{{\rho ({q_{goal}} - {q_0})}} - \dfrac{1}{{\rho (q - {q_0})}}\right)}^{\text{2}}}} ,\\ {\rho (q - {q_0}) \leqslant {\rho _0},\rho ({q_{goal}} - {q_0}) < {\rho _0}} ,\\ 0,\\ {\rho \left(q - {q_0}\right) > {\rho _0}} 。\end{array}} \right.\\ $ | (1) |
式中:
将改进的斥力势场函数在原斥力方向求负梯度运算可得斥力函数为:
| $ {F_{rep}} = \left\{ {\begin{array}{*{20}{l}} {\eta \left( {\dfrac{1}{{\rho \left( {q - {q_0}} \right)}} - \dfrac{1}{{{\rho _0}}}} \right)\dfrac{1}{{{\rho ^2}\left( {q - {q_0}} \right)}}} ,\\ {\rho (q - {q_0}) \leqslant {\rho _0},\rho ({q_{goal}} - {q_0}) > {\rho _0}} ,\\ {\eta \left( {\dfrac{1}{{\rho \left( {{q_{goal}} - {q_0}} \right)}} - \dfrac{1}{{\rho \left( {q - {q_0}} \right)}}} \right)\dfrac{1}{{{\rho ^2}\left( {q - {q_0}} \right)}}} ,\\ {\rho (q - {q_0}) \leqslant {\rho _0},\rho ({q_{goal}} - {q_0}) < {\rho _0}} ,\\ 0 ,\\ {\rho (q - {q_0}) > {\rho _0}}。\end{array}} \right. $ | (2) |
式中:
当目标点处于障碍物影响范围之内时,则将障碍物影响范围缩小,并保持障碍物相应范围内的斥力大小,避免在本船接近目标点时由于引力的减小,加上障碍物斥力的叠加,造成本船无法到达目标点,同时避免本船在靠近障碍物时由于影响范围的缩小而导致斥力的减小,最终与障碍物发生碰撞[5]。
1.2 改进人工势场法理论框架 1.2.1 模拟退火法模拟退火法计算过程简单、通用,鲁棒性强,适用于并行处理,可用于求解复杂的非线性优化问题。模拟退火方法由于其简单、易于实现而得到广泛应用,但非常耗时。只有在冷却速率无限慢的情况下才能收敛到全局最小值。与其他优化方法相比,模拟退火可以接受成本函数的暂时增加,而其他优化方法只能朝着导致成本函数减少的方向移动。因此,可以通过模拟退火法接受较差点来提升全局寻优能力,帮助人工势场法逃离局部极值点。
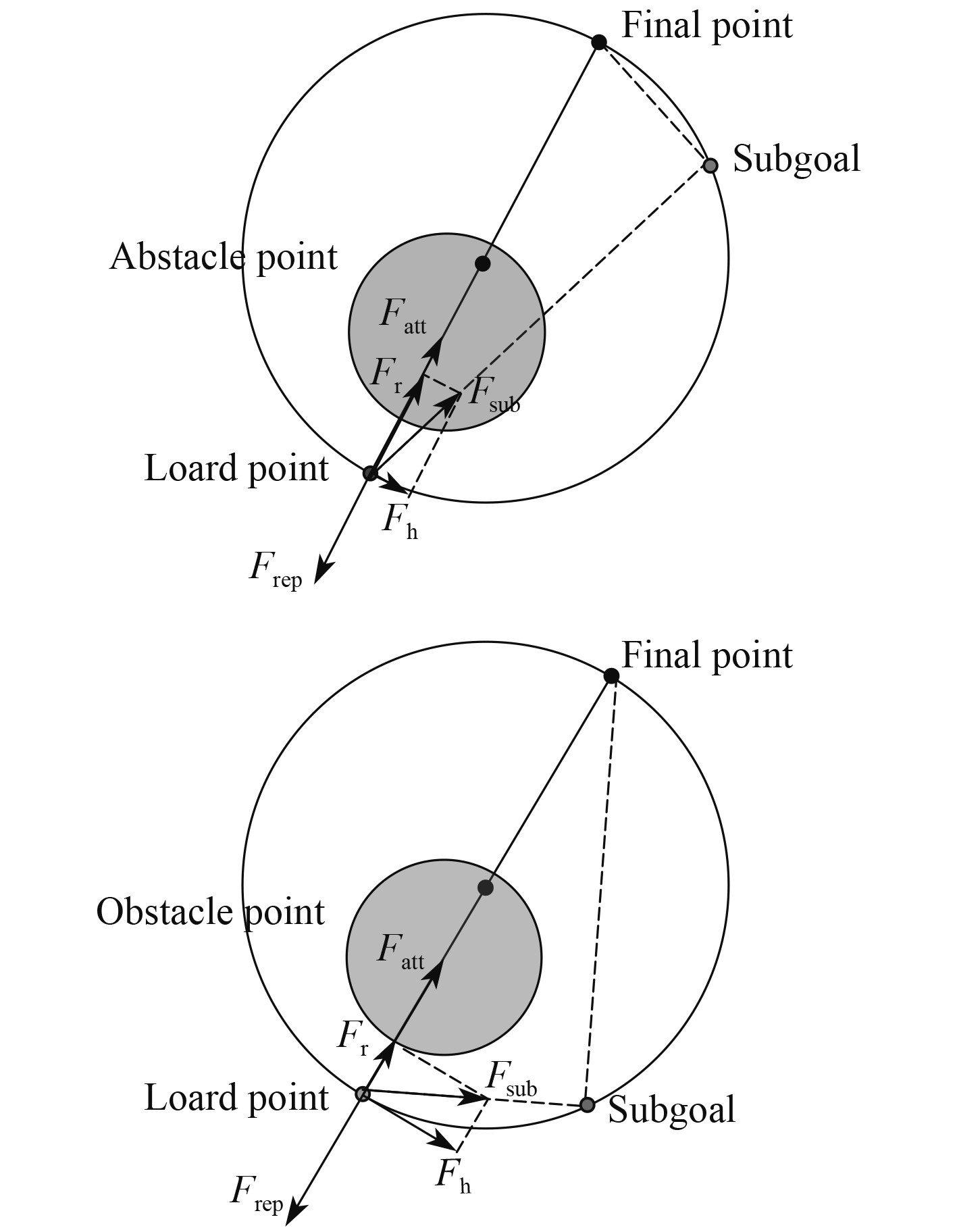
1.2.2 自适应子目标法由于模拟退火法生成新解的随机性较大,收敛速度慢,执行时间长,实时性差,所以通过生成子目标点对退火法的迭代范围进行约束。以局部极值点与目标点的中点作为圆心O,两点距离为直径作圆,通过自适应选取圆上的点作为子目标点,如图1所示。若该点处于障碍物内部,则以一定的角度梯度朝极值点方向生成新的子目标点。在船舶左右前方障碍物分布相差不大的情况下,根据船长的操船习惯,以船舶右舷转向作为优先选择。将极值点与目标点所在直线定义为L1,极值点与子目标点所在直线定义为L2,当L1与L2之间的夹角

|
图 1 自适应子目标 Fig. 1 Adaptive subgoals |
子目标点设置在距离目标点较近时,船舶受到的横向引力
|
图 2 子目标选取范围 Fig. 2 Subtarget selection range |
改进的人工势场法流程如图3所示:

|
图 3 改进人工势场法算法结构框图 Fig. 3 Structure Diagram |
采用Matlab仿真平台对改进后的人工势场法进行仿真验证,仿真结果均是在静态障碍物的前提下进行的。对仿真结果对比分析可得出,改进后的人工势场法拥有更好的的避障效果。算法主要参数设置如表1所示。
|
|
表 1 主要参数设置 Tab.1 Main parameter |
为了验证算法的可行性以及改进算法的优势,分别对传统人工势场法、人工势场法+模拟退火法和改进的势场法在复杂场景下进行仿真对比。
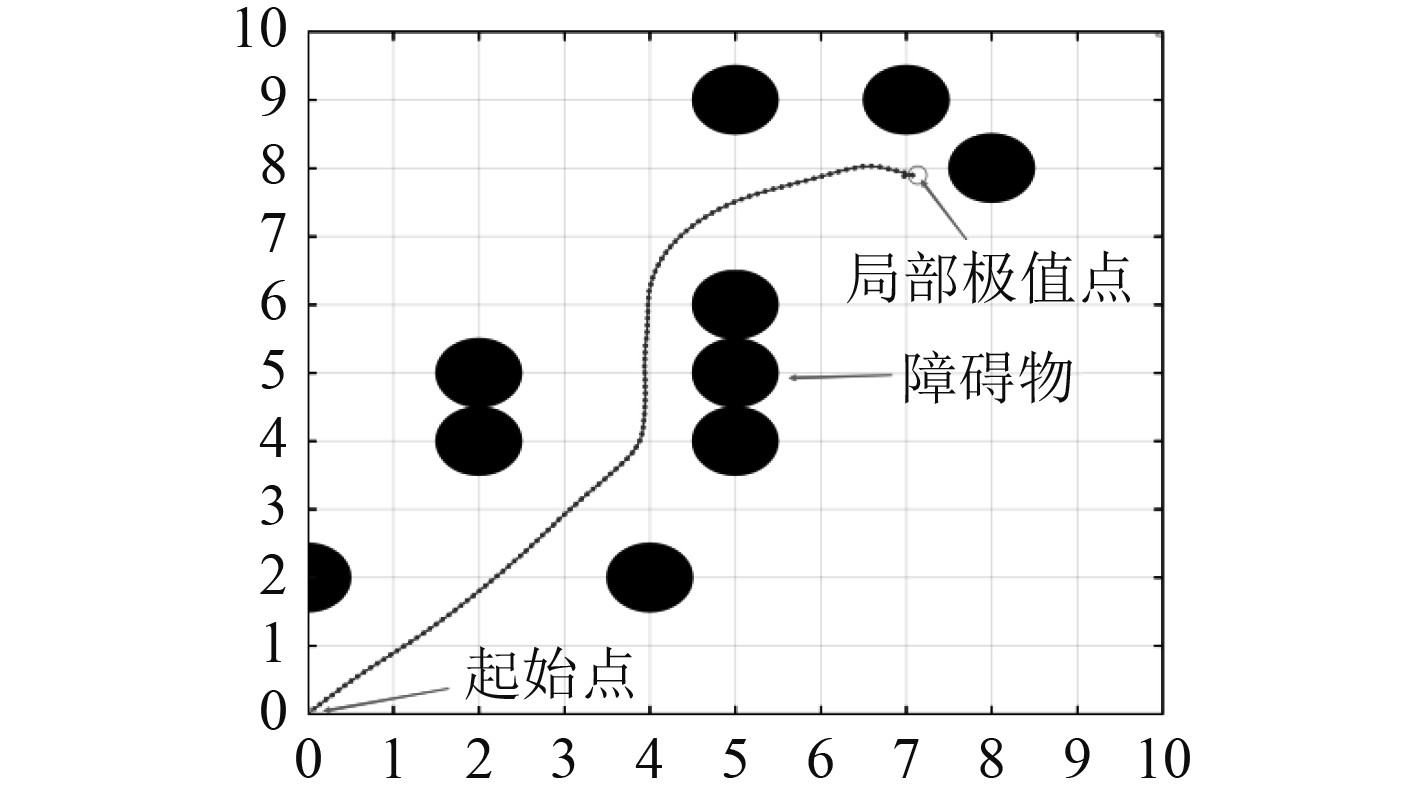
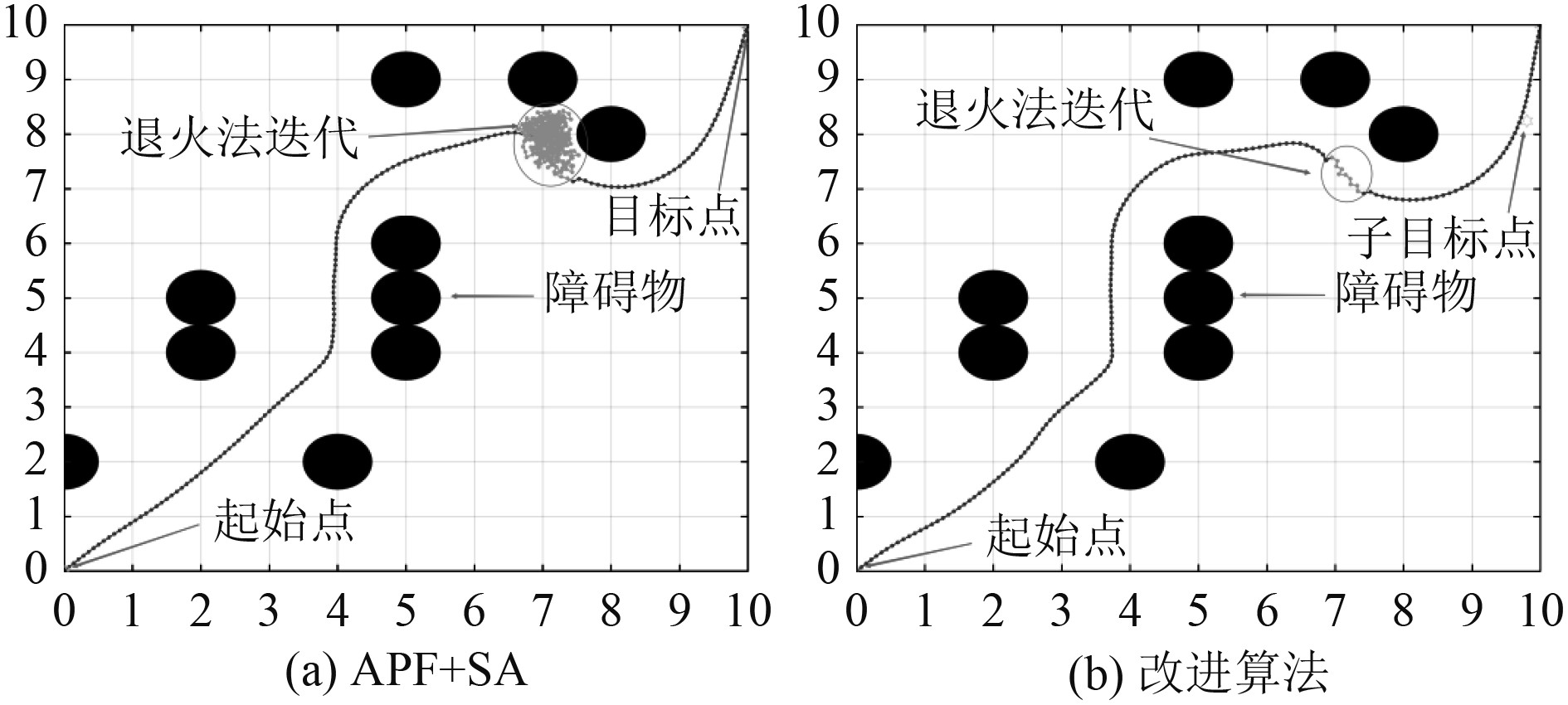
图4和图5仿真结果表明:当在复杂环境中时,传统人工势场法会在第1个局部极小点的位置停滞不前,无法到达目标点;人工势场法+模拟退火法在陷入局部极值点后通过不断进行退火操作,以步长为基础不断更新随机点为下一个前进点帮助船舶逃离局部极小点,顺利到达终点,但是其随机迭代的次数较多,消耗的时间过长,影响船舶避碰的时效性;本文算法通过设置合理的自适应子目标点,引导船舶以合理的转角逃离局部极值点,规划出合理路径的时间较短,路径也较为平滑。
|
图 4 传统人工势场法 Fig. 4 Traditional artificial potential field |
|
图 5 路径规划 Fig. 5 Path planning |
由图6可以看出,人工势场法+模拟退火法在随机生成路径时,角度变化较大,而且随机性也比较大,耗时较长。而本文采用的方法角度变化范围则主要集中在60°内,由子目标点引导船舶大大缩减的迭代时间。

|
图 6 转向角度 Fig. 6 Steering angle |
由表2可以看出,传统人工势场法无法规划出完整的路径,本文算法相较于人工势场法+模拟退火法,算法速度提高了将近6倍。
|
|
表 2 算法对比分析 Tab.2 Comparative analysis of algorithms |
针对船舶作为直航船在遇到紧迫局面时的紧急避碰场景,通过研究3种典型场景模型为紧急避碰研究提供建议。
2.1 危险度评判依据船舶航行过程中最大威胁来自其他船舶,在与他船会遇时需要保持安全的距离航行,如何判断两船是否有碰撞的风险,若有碰撞危险,危险的紧迫程度多大,则由碰撞危险度进行评判。避碰行动可行性及有效性的先行条件便是正确判断是否存在碰撞危险及预估碰撞危险的紧迫程度。
船舶空间危险度(DCPA)和时间危险度(TCPA)作为评判两船在会遇时的碰撞危险最重要依据,通常认为,当在DCPA小于安全会遇距离且TCPA较小的情况下,应当认为两船存在碰撞危险[6]。
2.2 船舶碰撞危险度空间碰撞危险度
| $ {{u_{dT}} = \left\{ {\begin{array}{*{20}{c}} 1,& {\left| {DCPA} \right| < {d_1}} ,\\ {\left( {\dfrac{{{d_2} - \left| {DCPA} \right|}}{{{d_2} - {d_1}}}} \right)}^{3.03},&{{d_1} < \left| {DCPA} \right| < {d_2}} ,\\ 0,& {\left| {DCPA} \right| > {d_2}} 。\end{array}} \right.} $ | (3) |
时间碰撞危险度
当
| ${ {u_{tT}} = \left\{ {\begin{array}{*{20}{c}} 1,&{TCPA < {t_1}} ,\\ {{\left( {\dfrac{{{t_2} - TCPA}}{{{t_2} - {t_1}}}} \right)}^2},& {{t_1} < TCPA \leqslant {t_2}} ,\\ 0,&{TCPA > {t_2}} 。\end{array}} \right.} $ | (4) |
当
| $ {{u_{tT}} = \left\{ {\begin{array}{*{20}{c}} 1,& {\left| {TCPA} \right| < {t_1}} ,\\ \dfrac{1}{{\left| {TCPA} \right|}}{{\left( {\dfrac{{{t_2} + TCPA}}{{{t_2} - {t_1}}}} \right)}^2},& {{t_1} < \left| {TCPA} \right| \leqslant {t_2}} ,\\ 0,& {\left| {TCPA} \right| > {t_2}} 。\end{array}} \right.} $ | (5) |
影响船舶碰撞危险度的决定性因素是DCPA和TCPA,所以碰撞危险度不能单纯依靠DCPA或TCPA 来决定。在一定条件下,DCPA和TCPA的变化之间存在确定的函数关系,而且在较大的范围内此函数关系呈线性关系。
| $ {u_T} = {u_{dT}} \oplus {u_{tT}}。$ | (6) |
式中
判断对遇态势最直接的方法是观察本船与来船是否处于对向航行。若两船的航向相差180°或者角度偏差±6°,则认为两船处于对遇态势。
对遇态势中,若两船间的距离小于碰撞危险阶段的上界值,即入侵了本船的领域范围,而且两船之间的DCPA小于安全会遇距离,则表示两船存在碰撞危险。对遇态势中DCPA与转向角度之间的关系如图7所示[6]。

|
图 7 对遇态势几何图 Fig. 7 Geometry of encounter situation |
设L=6 n mile,在不同船速比k和不同转向θ的情况下,DCPA的变化(DCPA <0则说明本船从来船船尾经过)。
由表3可知,在对遇场景中,当航速比K=1时,本船只需向右转10°即可,随着航速比的增大,船舶需要更大的舵角才可有效完成避碰操作。
|
|
表 3 船速比与DCPA关系表 Tab.3 Relationship between ship speed ratio and DCPA |
交叉会遇是指两船的航向在某点存在交叉,且来船与本船的航向角大于5°,小于112.5°。
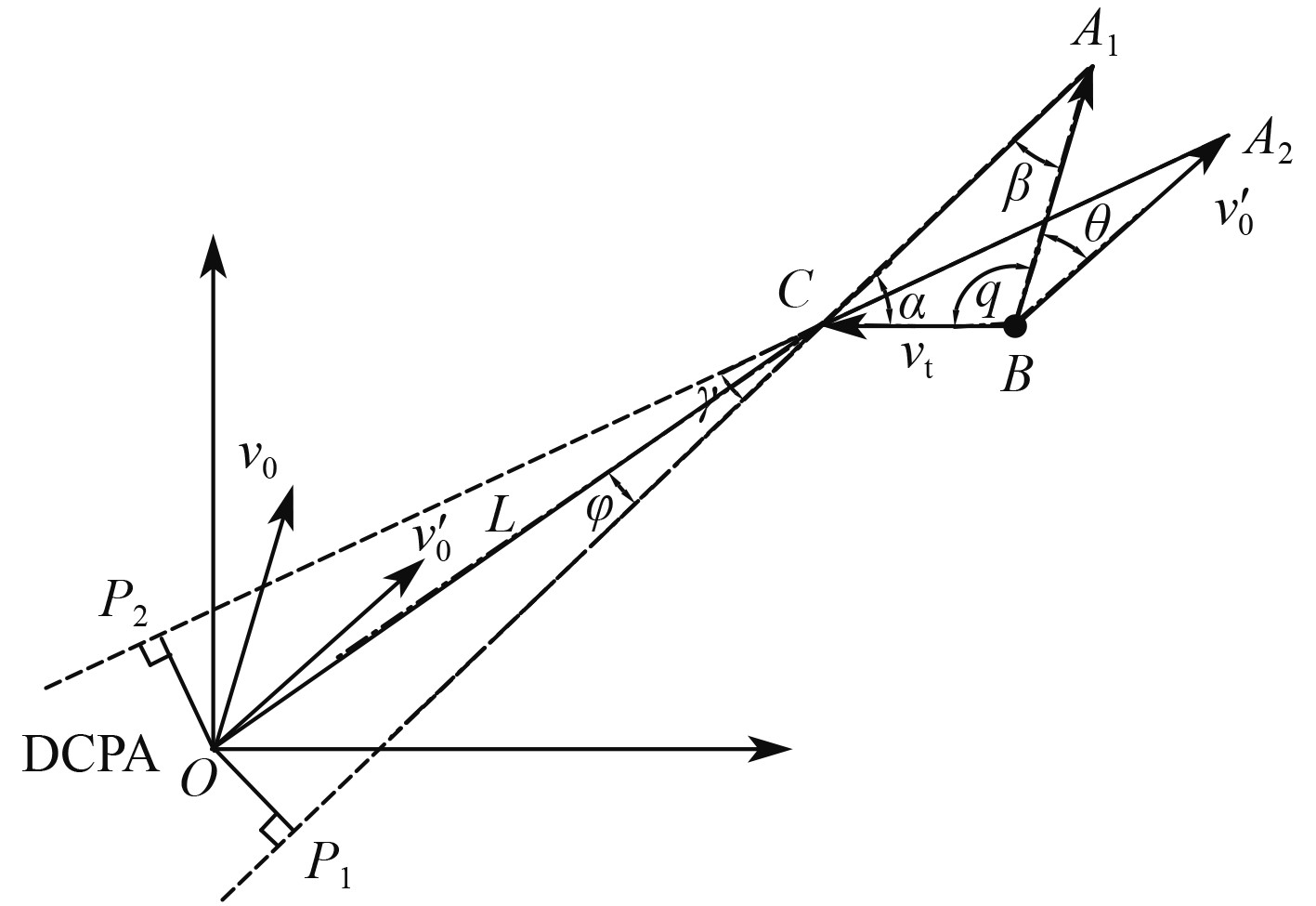
在雷达图中小角度交叉与大角度交叉的区别则体现在相对运动舷角
|
图 8 交叉会遇雷达图 Fig. 8 A cross will meet a radar map |
当来船入侵本船领域时,将产生碰撞危险,本船需根据《规则》采取适当的行动进行避让。因此,对于交叉会遇,依然以6 n mile作为两船的初始距离,会遇角度为30°,进行船速比、转向角以及DCPA之间关系研究。
由表4可得,在船速比K=1时,本船转向20°的DCPA与对遇态势中的DCPA相差较大,说明会遇角度对船舶避让影响较大。船速比对船舶碰撞的影响比对遇态势的要小很多。表5为大角度会遇船速比与DCPA关系表。
|
|
表 4 小角度会遇船速比与DCPA关系表 Tab.4 Small angle meeting the relationship between ship speed ratio and DCPA |
|
|
表 5 大角度会遇船速比与DCPA关系表 Tab.5 Relationship between ship speed ratio and DCPA |
大角度交叉会遇以相遇角45°为例,两船能够以安全距离避让,本船转向角随着船速比的增大而增加。与会遇角30°相比,船速比对转向幅度的影响更为明显,在船速比为1时转向角相差不大,但当船速比大于1时,其达到安全距离所需的转向角幅度之间相差较大。
2.3.3 追越危险在追越过程中,由于两船间的方位、距离将发生变化,当若追越船只过早复航可能会形成大角度交叉会遇的局面,产生碰撞危险。
追越过程中DCPA的变化如图9所示。
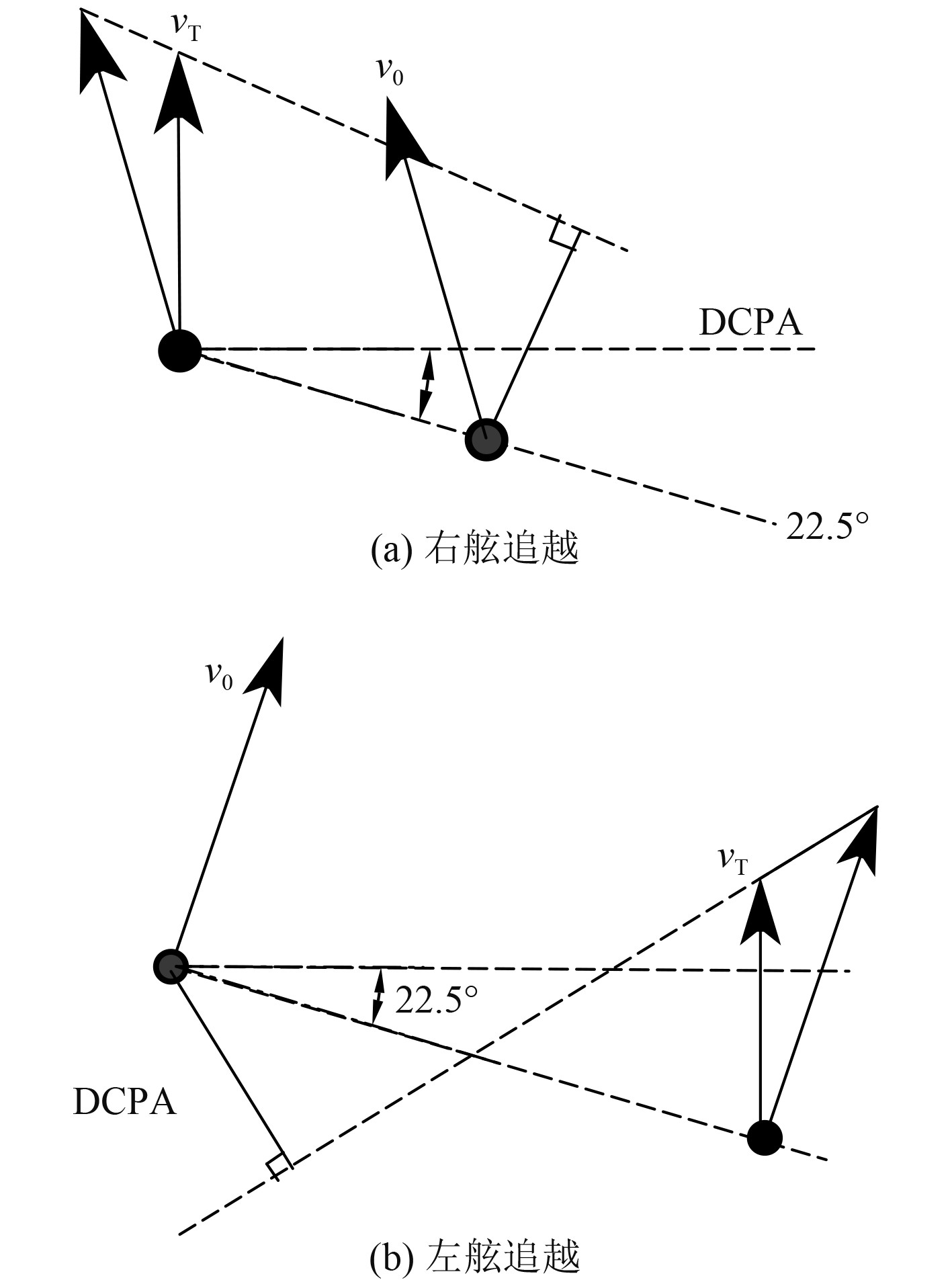
|
图 9 追越态势下DCPA Fig. 9 DCPA under overtaking situation |
对于追越态势的避碰方法主要有以下3种:
方法1当后船处于112.5°~150°时,前船左转,置后船于船尾方向(DCPA增大);当后船处于150°~210°时,前船左转约30°;当后船处于210°~247.5°,前船右转,置后船于船尾方向。
方法2相较于方法1方法提出的DCPA更大,在追越态势中也相对安全。
| $ {\left\{ \begin{array}{l}{D}=6\;\text{n}\;\text{mile},112.5\text{°},\sim 200\text{°},\text{前船左转50°},\sim 60\text{°},\\ 200\text{°},\sim 247.5\text{°},\text{前船右转50°},\sim 60\text{°};\\ {D}=4\;\text{n}\;\text{mile},112.5\text{°},\sim 200\text{°},\text{前船左转50°},\sim 60\text{°},\\ 200\text{°},\sim 247.5\text{°},\text{前船右转5°},\sim 60\text{°}。\end{array}\right. }$ |
方法3主要是指两船互见情况下的追越态势,让路船可根据两船的实际相对方位确定转向避让方案。当前船在让路船左前方时,采取右转避让;当前船位于让路船右前方时,采取左转避让;当前船位于让路船的正前方时,采取左转从前船左舷通过,且DCPA>0.5 n mile。
3 结 语1)通过改进人工势场法进行船舶避碰决策,并进行仿真验证。
2)人工势场法在模拟退火法帮助下能够使船舶逃离局部极值点,但模拟退火法消耗的时间较长。通过指向性自适应设置子目标点,引导船舶逃离局部极小点。相较于人工势场法+模拟退火法,算法速度提高了将近6倍。
3)根据船舶空间危险度(DCPA)及时间危险度(TCPA)模型,主要研究不同船速比下,转向角对DCPA的影响,并对典型船舶会遇和紧迫局面四种场景进行数学模型分析。
| [1] |
刘炯炯, 刘克中, 杨星, 等. 基于规则的多船协调避碰决策算法及仿真验证[J]. 中国航海, 2020, 43(4): 8-14. |
| [2] |
陈国权. 船舶避碰自动化关键技术研究[D]. 大连: 大连海事大学, 2016.
|
| [3] |
罗世民, 方泉根. 对1972年国际海上避碰规则的几点补充修改意见[J]. 中国航海, 1984(2): 1-7. |
| [4] |
吴兆麟, 郑中义. 船舶最佳避碰行动时机决策模型[J]. 大连海事大学学报:自然科学, 2000, 26(4): 1-4. |
| [5] |
罗乾又, 张华, 王姮, 等. 改进人工势场法在机器人路径规划中的应用[J]. 计算机工程与设计, 2011, 32(4): 1411-1413+1418. |
| [6] |
梁浩. 基于数据挖掘的船舶碰撞危险度研究[D]. 大连: 大连海事大学, 2017.
|
 2023, Vol. 45
2023, Vol. 45
