2. 上海海事大学 商船学院航运仿真技术教育部工程研究中心,上海 201306
2. Merchant Marine College, Engineering Research Center of Simulation Technology of the Ministryof Education, Shanghai Maritime University, Shanghai 201306, China
受到海浪、海风、洋流等综合环境因素的影响,船舶航行过程中会产生六自由度方向的复杂运动[1]。当船舶常态化运动状态被打破,尤其是在恶劣海况条件下,船舶摇荡加剧时,船舶的航行安全存在极大的安全隐患。因此,准确预测船舶摇荡运动状态,能够有效提升船舶航行的安全性,其研究意义极为重大[2]。
对船舶摇摆进行预测的主要方法包括首前波法、卡尔曼滤波方法、人工神经网络方法以及时间序列分析方法等[3]。时间序列分析方法主要用于短期预测,其将预测对象按照时间顺序进行属性值排序,使用相应的数学模型研究属性变化特性后进行短期预测。唐刚等[4]采用Newton方法对ARMA模型参数进行优化,并对船舶升沉运动进行了预测研究。王明瑞等[5]采用多维度的AR模型,对大型船舶的时间序列模型进行预测。彭秀艳等[6-7]采用基于卡尔曼滤波的算法对自回归模型(AR)预测模型进行参数估计,提升了模型预测的准确度和速度。为进一步提升AR模型对船舶运动预测的速度,采用了最小二乘法进行参数估计。马洁等[8]采用线性AR模型,基于水池实验环境进行了船舶运动的研究和预报。王培良[9]采用基于粒子群算法优化ARIMA模型进行了船舶摇摆运动的预测研究。
综上,基于时间序列分析方法研究预测船舶运动时,不同船舶类型、不同数学模型及不同参数的相同模型的研究结果不尽相同。同时航行环境的差异和波动性,均使得船舶运动尤其是船舶摇摆存在非平稳性,因此本文采用ARIMA模型对集装箱船舶的纵摇角度进行研究并预测[10],通过对比不同差分次数的ARIMA模型的预测结果,确定最终的预测模型及参数。
1 理论与方法 1.1 ARIMA模型当序列的自相关系数或偏相关系数至少有一个不是拖尾或者截尾,则为非平稳序列,需要进行差分运算。船舶的摇摆模型属于非平稳性时间序列,且随机性较大[9],因此本文使用ARIMA模型进行分析研究。
ARIMA模型由Box-Jenkins于20世纪70年代提出,其模型本质是在ARMA模型的基础上,将每个预测对象与相应的时间连接构建时间序列,用准确的数学模型描述该时间序列,并根据时间序列的性质预测未来值。
设
| $ {\nabla }^{d}{X}_{t}={W}_{t}{\text{,}} $ | (1) |
且
| $ {\phi }\left({B}\right){\nabla }^{d}{X}_{t}=\theta \left(B\right){\epsilon }_{t}{\text{。}} $ | (2) |
式中:p为AR模型的自回归项;d为差分次数;q为MA模型的移动平均项数;
| $ \left\{\begin{aligned} & B{X}_{t}\equiv {X}_{t-1}\text{,}B{\varepsilon }_{t}\equiv {\varepsilon }_{t-1}{\text{,}}\\ & \phi \left(B\right)=1-{\mathrm{\phi }}_{1}B-{\mathrm{\phi }}_{2}{B}^{2}-\cdots {\mathrm{\phi }}_{p}{B}^{p}{\text{,}}\\ & \theta \left(B\right)=1-{\theta }_{1}B-{\theta }_{2}{B}^{2}-\cdots {\theta }_{q}{B}^{q}{\text{。}} \end{aligned}\right. $ | (3) |
式中:
差分运算是指将序列t时刻的值与其后移值相减的运算,具有强大的确定性信息提取能力,能够使非平稳序列显示出平稳序列的性质,此时可称非平稳序列为差分平稳序列,差分平稳序列可以使用ARIMA模型进行拟合[12]。
式(1)中的d阶差分算子可表示为:
| $ \begin{split} {\nabla ^d} \equiv & {\left( {1 - {\rm{B}}} \right)^d} = 1 - \left( {\begin{array}{*{20}{c}} d\\ 1 \end{array}} \right)B + \left( {\begin{array}{*{20}{c}} d\\ 2 \end{array}} \right){B^2} + \cdots + \\ & {\left( { - 1} \right)^{d - 1}}\left( {\begin{array}{*{20}{c}} d\\ {d - 1} \end{array}} \right){B^{d - 1}} + {\left( { - 1} \right)^d}{B^d}{\text{,}} \end{split} $ | (4) |
其中常用的一阶差分和二阶差分分别如下:
| $ \left\{\begin{aligned} & \nabla {X}_{{\rm{t}}}={X}_{{\rm{t}}}-{X}_{{\rm{t}}-1}=(1-B){X}_{{{t}}}{\text{,}}\\ & {\nabla }^{2}{X}_{{\rm{t}}}={X}_{{\rm{t}}}-2{X}_{{\rm{t}}-1}+{X}_{{\rm{t}}-2}={(1-B)}^{2}{X}_{{{t}}}{\text{。}} \end{aligned}\right. $ | (5) |
经过差分后的序列需要检验其平稳性,单位根检验是其中常用的方法之一,其公式如下:
| $ {X}_{t}={c}+\mathrm{\alpha }{t}+{{\delta }X}_{{{t}}-1}+{\beta }_{1}\nabla {X}_{{{t}}-1}+\cdots +{\beta }_{p}\nabla {X}_{{{t}}-p}+{\epsilon }_{{{t}}} 。$ | (6) |
式中:c为常数项;
如果检验拒绝
传统差分运算次数取值为首次获得平稳序列的正整数d,而研究发现针对船舶摇摆角度的预测,使用不同次数d的ARMA(p,d,q)模型进行预测,获得的结果也不尽相同。因此,在传统检验的基础上,通过均方误差(mean squared error,MSE)分析模型的优劣。
| $ \mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{n}\sum _{t={\rm{1}}}^{n}{E}_{t}^{2}=\frac{1}{n}\sum _{{{t}}=1}^{n}{({X}_{{\rm{t}}}-\widehat{{X}_{{{t}}}})}^{2}{\text{。}} $ | (7) |
式中:
AIC准则是由日本统计学家Akaike于20世纪70年代提出,因此又称为Akaike信息准则。
AIC准则可描述为:
| $ \mathrm{min}AIC=n\mathrm{ln}{\widehat{{\sigma }_{\epsilon }}}^{2}+2(p+q+1){\text{。}} $ | (8) |
式中:n为样本容量;
根据Yule-Walker方程可知,式(3)中的自回归系数
| $ \left[\begin{array}{cc}\genfrac{}{}{0pt}{}{\begin{array}{cc}1& {\rho }_{1}\end{array}}{\begin{array}{cc}{\rho }_{1}& 1\end{array}}& \genfrac{}{}{0pt}{}{\begin{array}{cc}\cdots & {\rho }_{p-1}\end{array}}{\begin{array}{cc}\cdots & {\rho }_{p-2}\end{array}}\\ \genfrac{}{}{0pt}{}{\begin{array}{cc}⋮& ⋮\end{array}}{\begin{array}{cc}{\rho }_{p-1}& {\rho }_{p-2}\end{array}}& \begin{array}{c}\begin{array}{cc}⋮& ⋮\end{array}\\ \begin{array}{cc}\cdots & 1\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{\phi }_{1}\\ {\phi }_{2}\\ \begin{array}{c}⋮\\ {\phi }_{p}\end{array}\end{array}\right]=\left[\begin{array}{c}{\rho }_{1}\\ {\rho }_{2}\\ \begin{array}{c}⋮\\ {\rho }_{p}\end{array}\end{array}\right]{\text{,}} $ | (9) |
而移动平均系数
| $ \begin{aligned} & {\rm{cov}}\left({X}_{t}\text{,}{X}_{t-s}\right)={\gamma }_{t\text{,}} s=\\ &\left\{\begin{aligned} &{\sigma }^{2}({\theta }_{s}+{\theta }_{1}{\theta }_{s-1}+\cdots +{\theta }_{q}{\theta }_{s-q})\text{,}s < q{\text{,}}\\& 0\text{,}{\rm{others}}{\text{。}}\end{aligned}\right. \end{aligned}$ | (10) |
由式(9)和式(10)可求解获得
同时式(9)中的自相关系数与自协方差存在如下关系:
| $ {\rho }_{s}=\rho \left(t\text{,}t-s\right)=\frac{{\gamma }_{{\rm{t}}\text{,}s}}{{\sigma }_{{\rm{t}}}{\sigma }_{{\rm{t}}-s}}{\text{。}} $ | (11) |
因此,自相关系数也可以进行序列稳定性检验,平稳序列具有短期相关性,即短时间间隔的序列值之间相互影响较强,而长时间间隔的序列值之间影响较弱。同时在自相关系数衰减性方面,平稳序列的衰减速度明显快于非平稳序列,且其值在零附近随机波动。
1.5 模型构建流程图使用ARIMA模型进行序列预测的基本流程如图1所示。

|
图 1 ARIMA模型构建流程 Fig. 1 Flow chart of ARIMA model |
以某集装箱船船首摇摆角度数据为基础进行算法验证。船载传感器在某段时间内采集样本数据47次,每次采集100个样本值,为避免噪声干扰,取每次采样数据的样本均值作为纵摇角度序列,如图2所示。

|
图 2 船舶纵摇角度值序列 Fig. 2 Ship pitch angle value sequence |
分析可知,船舶纵摇角度序列呈现非平稳特性,且其序列单位根检验统计量对应的p值为0.6211,显著大于0.05,因此可认定角度序列为非平稳序列,需对其进行差分运算。同时为检验模型预报结果,选取前42次数据为拟合数据序列进行研究,最后5次数据为检验序列。
2.2 差分运算分析非平稳的角度序列进行差分后,数据将表现出平稳特性,后续分析以一阶差分为例,其差分数据的时序图和自相关图如图3所示。
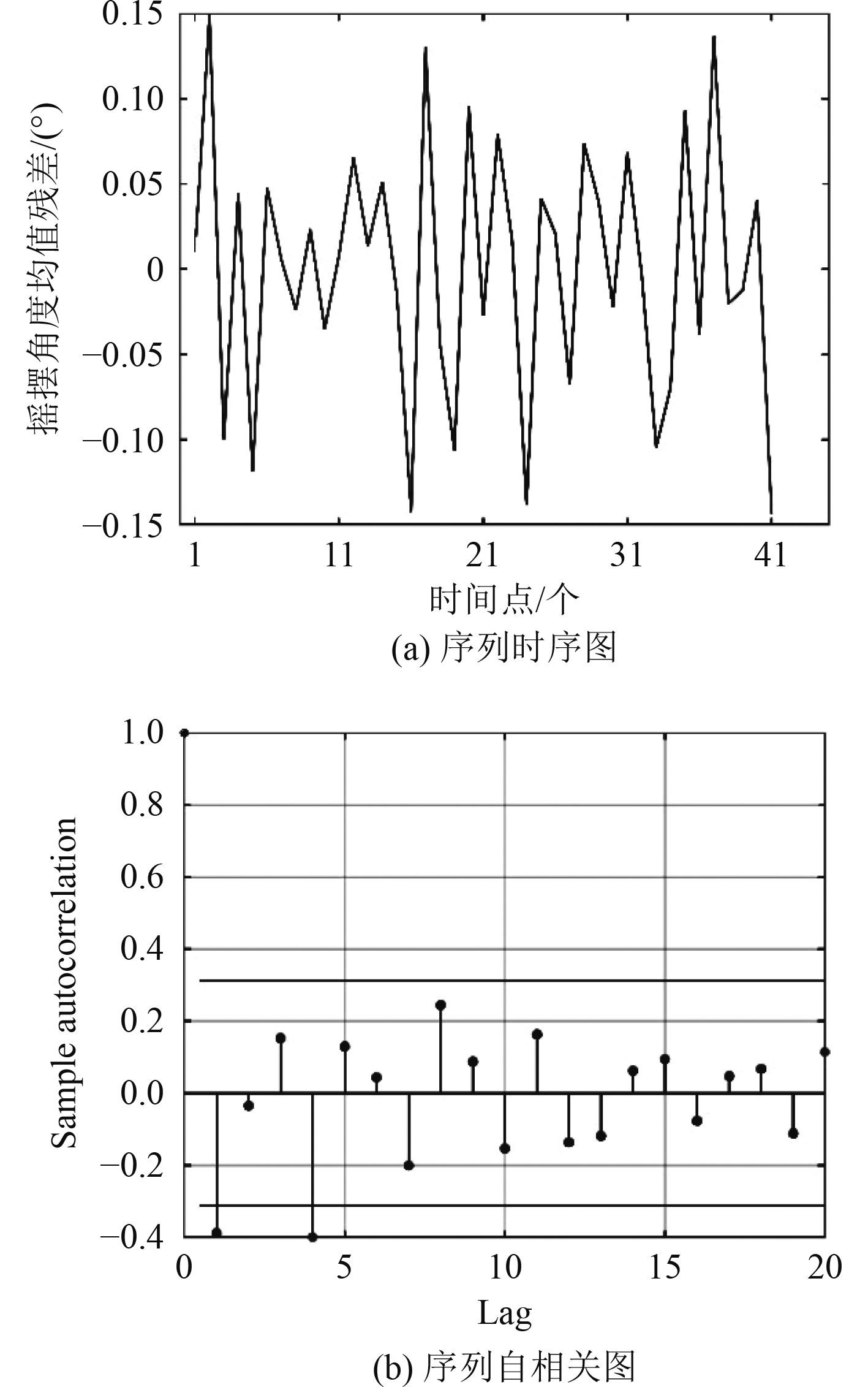
|
图 3 差分运算后角度值序列图 Fig. 3 Chart of angle value sequence differenced |
分析可知,一阶差分后的角度序列在均值附近波动较为平稳,序列呈现较强的短期相关性,在零均值附近波动,且此时序列的单位根检验p值为0.001,显著小于0.05,因此可认为此时的角度序列为平稳序列。
2.3 模型构建通过自相关图和单位根检验,可知差分次数
|
|
表 1 各阶数p和q组合对应的AIC值 Tab.1 AIC value corresponding to the different p and q |
分析可知,随着p值的增大,相应的AIC值基本呈现逐渐减小的趋势,随着q值的增大,相应的AIC值有起伏波动,最终确定最小的AIC值所对应的p值和q值分别为4, 2,即此时对应的模型为ARIMA(4, 1, 2)。
模型确定后,可根据式(9)和式(10)进行模型参数估计,其值如表2所示。
|
|
表 2 模型参数值 Tab.2 Model parameter value |
模型参数确定后,即可使用ARIMA模型进行角度序列预测,并与实际值进行对比,其结果如图4所示。

|
图 4 预测结果示意图 Fig. 4 Schematic diagram of prediction results |
分析可知,基于一阶差分的ARIMA模型能够对船舶纵摇角度序列进行预测。从图4(a)可知,其预测值与实际值的变化趋势相近;从图4(b)可知,预测误差均较小。表明ARIMA模型的预测较为准确,模型参数设置也较为合理。
为对比不同差分次数下的ARIMA预测结果,分别进行二次差分和三次差分运算,相应的模型参数如表3所示。
|
|
表 3 不同差分次数时模型参数值 Tab.3 Model parameter values at different times of difference |
模型参数确定后,分别使用ARIMA模型进行角度序列预测,其结果分别如图5和图6所示。

|
图 5 二次差分运算结果示意图 Fig. 5 Schematic diagram of the results of the second difference operation |

|
图 6 三次差分运算结果示意图 Fig. 6 Schematic diagram of the results of the triple difference operation |
预测结果分析可知,原始序列经过二次和三次差分运算后均获得平稳序列,所得ARIMA模型亦均可进行角度序列值的预测,但预测结果不尽相同,同时各预测模型对应的MSE值分别如表4所示。
|
|
表 4 各模型对应的MSE值 Tab.4 MSE value corresponding to each model |
结合预测误差图和MSE值分析,二阶差分所获模型的预测结果更为准确,即ARIMA(3,2,3)模型能更好的进行本文所述集装箱船的纵摇角度值预测。
3 结 语本文通过对集装箱船纵摇角度值的原始数据进行平稳性分析,采用具有差分运算的ARIMA模型进行时间序列值预测,并以误差和均方误差为指标,对比分析不同差分次数产生的不同估计参数ARIMA模型的预测效果。结果表明,优化差分次数获得的ARIMA模型具有更好的预测效果,验证了本文方法的科学性和适用性。
| [1] |
张春娜. 基于经验模态分解的舰船运动姿态预测模型研究[J]. 舰船科学技术, 2021, 43(2): 22-24. |
| [2] |
李远芳, 李俊彪, 张莉. 海洋环境预测数据在船舶航行控制中的应用[J]. 舰船科学技术, 2020, 42(16): 37-39. |
| [3] |
彭秀艳, 张彪. 基于EMD-PSO-LSTM组合模型的船舶运动姿态预测[J]. 中国惯性技术学报, 2019, 27(4): 421-426. |
| [4] |
唐刚, 姚小强, 胡雄. 基于Newton法优化ARMA模型参数的船舶升沉运动预测研究[J]. 海洋工程, 2020, 38(2): 27-38. |
| [5] |
王明瑞. 大型舰船运动交互预测中的多维度AR算法研究与仿真[J]. 舰船科学技术, 2021, 43(4): 10-12. |
| [6] |
彭秀艳, 王茂, 刘长德. AR模型参数自适应估计方法研究及应用[J]. 哈尔滨工业大学学报, 2009, 41(9): 12-16. |
| [7] |
彭秀艳, 刘长德. 基于格型递归最小二乘算法的船舶运动极短期预报[J]. 船舶力学, 2012, 16(Z1): 44-51. |
| [8] |
马洁, 韩蕴韬, 李国斌. 基于自回归模型的船舶姿态运动预报[J]. 舰船科学技术, 2006(3): 28-30. |
| [9] |
王培良, 张婷, 肖英杰. 基于改进PSO-ARIMA模型的船舶纵摇角度预测[J]. 上海海事大学学报, 2021, 42(1): 39-43. |
| [10] |
王培良, 吴晓芳, 张婷. 在航集装箱船摇摆姿态的概率模型[J]. 上海海事大学学报, 2017, 38(4): 21-25. |
| [11] |
曹俊波, 周任军, 邓学华, 等. 考虑优化ARIMA模型差分次数的风功率预测[J]. 电力系统及其自动化学报, 2019, 31(1): 105-111. DOI:10.3969/j.issn.1003-8930.2019.01.017 |
| [12] |
郑卓, 曹辉, 高鹤元, 等. 基于加权马尔可夫链修正的ARIMA预测模型的研究[J]. 计算机应用与软件, 2020, 37(12): 63-67. DOI:10.3969/j.issn.1000-386x.2020.12.010 |
 2023, Vol. 45
2023, Vol. 45

