0 引　言

高速排水型船舶通过采用更先进的船体设计、使用轻量化材料和先进的推进系统，可以减少船舶的阻力，提高航速和燃油效率，是一种非常具有潜力的新型船舶类型。

高速排水型船舶的尾浪对于环境和自身运行都会产生不同程度的影响，一方面，高速船舶航行产生的尾浪可能会冲刷堤岸、危害水工建筑。另一个方面，高速排水型船舶在产生尾浪时，由于波浪的作用力，船舶的航行稳定性可能会下降，这可能会对船舶的操纵和控制带来一定的挑战，特别是在恶劣海况下。因此，有些航行区域会限制高速船舶的行驶速度。

本文基于流体动力学理论^[1]，对高速排水型船舶的水动力特性进行分析，并通过建立流体有限元模型，结合广义边界元计算理论，对高速排水型船舶的尾浪特性进行研究，对于指导高速排水型船的优化设计有一定作用。

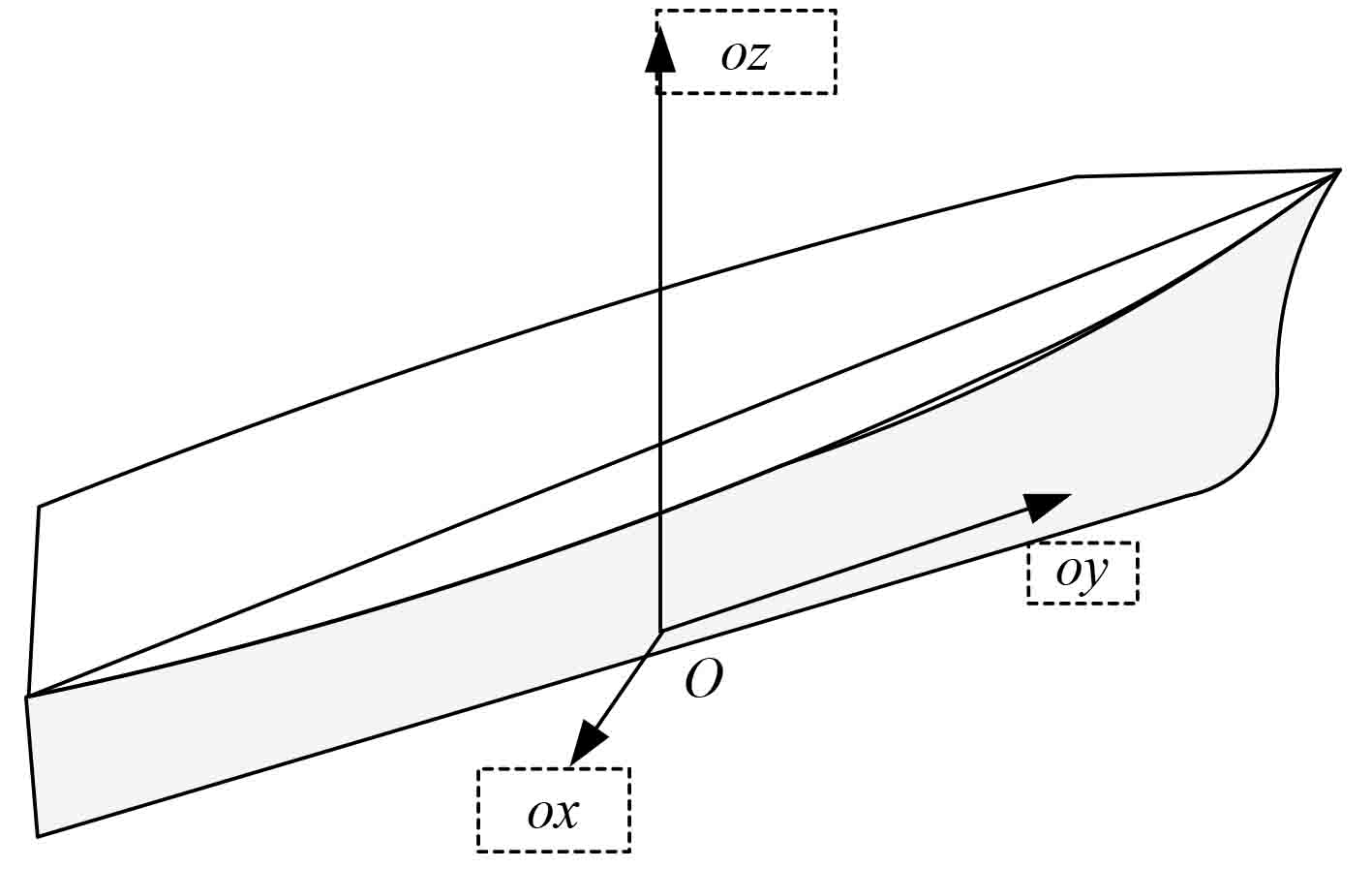
1 高速排水型船舶的控制方程

针对高速排水型船舶的运动特性，本文建立随动坐标系如图1所示：

图中，原点o在船舶质心，oz垂直向上，船舶前进方向为oy轴正向。

结合随动坐标系，建立高速排水型船舶的运动模型如下：

$\begin{gathered} {m_0}\frac{{{\partial ^2}}}{{\partial {t^2}}}{X_g} = \vec F ，\\ \vec T{{\vec I}_g}{{\vec T}^{ - 1}}\overrightarrow w + \overrightarrow w \times \vec T{{\vec I}_g}^{ - 1} = {{\vec M}_g} 。\end{gathered}$

式中： ${\vec I_g}$ 为船舶惯性转矩； $\overrightarrow w$ 为船舶的角速度； ${\vec M_g}$ 为所受的合力矩； ${m_0}$ 为高速排水型船舶的重量； ${X_g}$ 为船舶位移； $\vec F$ 为外在合力； $\vec T$ 为坐标系矩阵^[2]。

高速排水型船舶的摩擦系数 ${\mu _f}$ 与摩擦力 ${F_f}$ 如下：

$\begin{gathered} {\mu _f} = \frac{{0.075}}{{{{\left( {\log {R_n} - 3} \right)}^2}}} ，\\ {F_f} = \frac{1}{2}\rho {V_0}^2{S_0}{\mu _f} 。\end{gathered}$

其中： ${R_n}$ 为摩擦力学的雷诺常数； ${V_0}$ 为相对流场的船速度； ${S_0}$ 为摩擦力作用面积。

结合海水流场的特性，建立高速排水型船舶的流体连续性方程如下：

$\rho * \frac{{{\mathrm{d}}V}}{{{\mathrm{d}}t}} + \frac{{\delta \left( {\rho l} \right)}}{{\delta y}} + \frac{{\delta \left( {\rho m} \right)}}{{\delta z}} + \frac{{\delta \left( {\rho n} \right)}}{{\delta x}} = 0 \text{。}$

式中： $\rho$ 为流体密度； $l$ ， $m$ ， $n$ 为单位流体的速度分量。

建立高速排水型船舶的流体动量方程如下：

$\frac{{\partial \left( {\rho {u_x}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_x}{u_y}} \right)}}{{\partial x}} = - \frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial x}}\left[ {\mu \left( {\frac{{\partial {u_x}}}{{\partial y}} + \frac{{\partial {u_y}}}{{\partial x}}} \right)} \right] + {F_i}\text{。}$

式中： ${u_x}$ ， ${u_y}$ 分别为流体的动量在2个方向的分量； ${F_i}$ 为惯性力。

建立高速排水型船舶的流体湍流模型如下：

$\left\{ {\begin{array}{*{20}{c}} {\dfrac{{\partial k}}{{\partial t}} + {{\bar u}_{}}\dfrac{{\partial k}}{{\partial {x_{}}}} = \dfrac{\partial }{{\partial y}}\left[ {\left( {v + {\sigma _k}{v_t}} \right)\dfrac{{\partial k}}{{\partial {x_j}}}} \right] + {P_k} - {\beta ^*}k\omega } \text{，}\\ {\dfrac{{\partial \omega }}{{\partial t}} + {{\bar u}_{}} = \dfrac{\partial }{{\partial x}}\left[ {\left( {v + {\sigma _k}{v_t}} \right)\dfrac{{\partial \omega }}{{\partial {x_j}}}} \right] + 2(1 - {F_i}){\sigma ^{_{_{}}}}} 。\end{array}} \right.$

式中： ${\bar u_{}}$ 为平均速度； ${P_k}$ 为流体在所述位置的压力； ${\sigma _k}$ 为流体的粘度系数； ${\ \beta ^ * }$ 为误差系数。

高速排水型船舶在流场中的水动力性能与流体的基本特性密切相关，如图2所示，流体根据内部分子的运动状态分为层流、湍流和页面边界。

图中，页面边界又可分为静力学边界和动力学边界，本文在分析高速排水型船舶的流体特性时，采用动力学边界条件^[3]。

建立边界面方程为：

$F(x,y,z,t) = \eta (x,y,t) - z = 0 \text{，}$

质点的法向速度建模为：

${v_n} = \frac{{{v_x}{F_x} + {v_y}{F_y} + {v_z}{F_z}}}{{\sqrt {F_x^2 + F_y^2 + F_z^2} }} \text{，}$

进而可得边界面上的质点法向速度建模为：

${\phi _n} = \frac{{{\phi _x}{F_x} + {\phi _y}{F_y} + {\phi _z}{F_z}}}{{\sqrt {F_x^2 + F_y^2 + F_z^2} }} \text{，}$

由于 ${\phi _n} = {v_n}$ ，可知：

$\frac{{\partial \eta }}{{\partial t}} + \frac{{\partial \phi }}{{\partial x}}\frac{{\partial \eta }}{{\partial x}} + \frac{{\partial \phi }}{{\partial y}}\frac{{\partial \eta }}{{\partial y}} - \frac{{\partial \phi }}{{\partial z}} = 0 \text{，}$

根据等压条件和拉格朗日积分原理^[4]，可得：

$\begin{aligned} & \frac{{\partial \phi }}{{\partial t}} + \frac{1}{2}\nabla \phi \cdot \nabla \phi + g\eta = 0\text{，} \\ & \eta (x,y,t) = z 。\end{aligned}$

2 基于广义边界元法的高速排水型船舶尾浪数据模拟 2.1 流体广义边界元法

与传统边界元法相比，广义边界元法能够处理更加复杂的流体流动现象。广义边界元法基于边界积分方程，通过将流体领域划分为边界和内部2个区域，将流体力学问题转化为求解边界上的积分方程。在边界上，通过离散化边界上的节点，并利用边界元法的基本原理，将积分方程转化为代数方程组。在内部区域，通过使用有限元法或有限差分法等数值方法，求解流体的速度和压力分布。

广义边界元法的优点在于能够处理复杂的流体流动问题，如自由表面流动、多相流动、湍流等。由于只需要在边界上离散化节点，相对于有限元法等方法，广义边界元法的计算量较小，适用于大规模问题的求解。此外，广义边界元法还可以方便地处理边界条件的变化和流体领域的变形等问题。

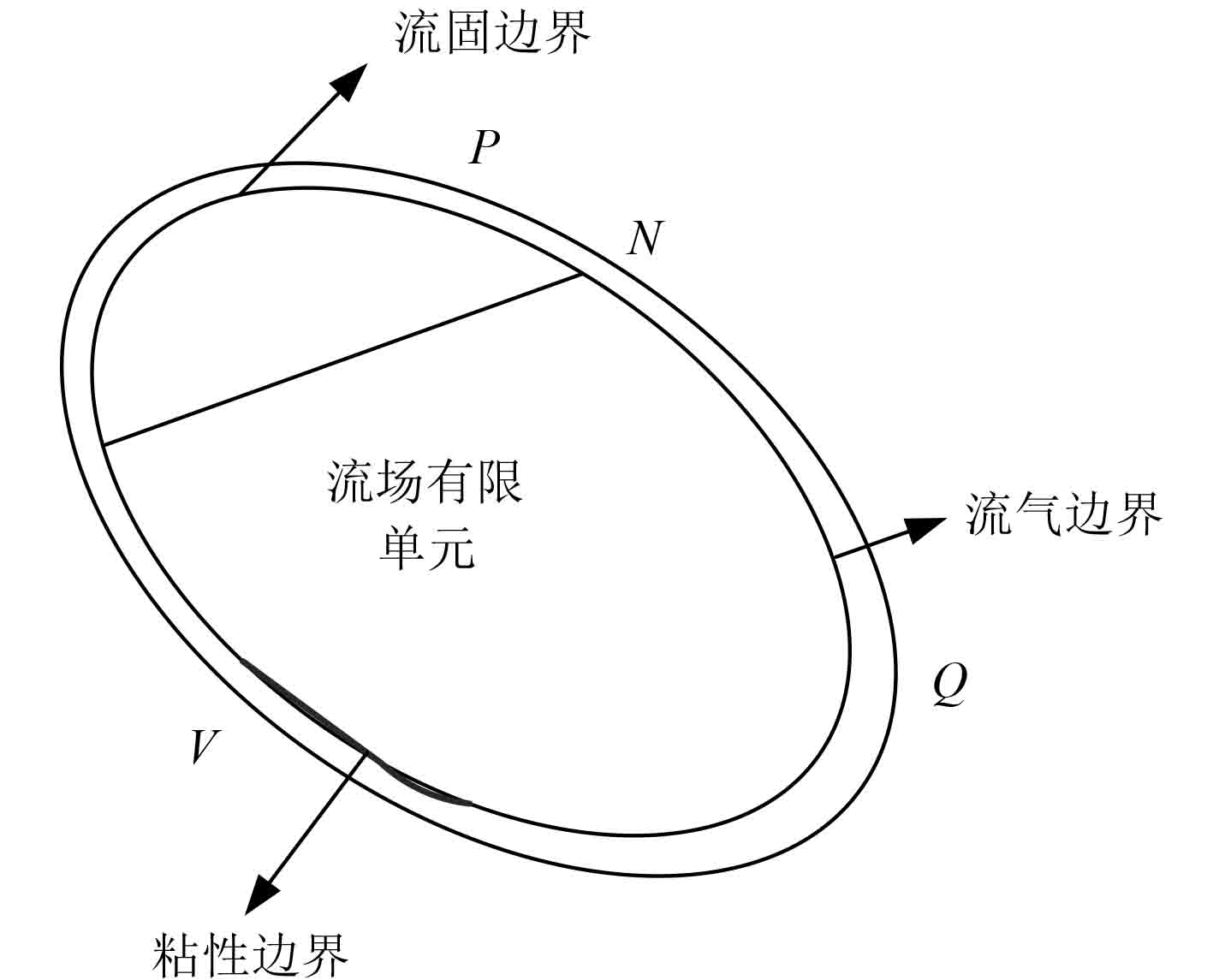
流体广义边界元的原理模型如图3所示。

流体广义边界元的边界包括粘性边界、流固边界和流气边界3种，建立流体广义边界元模型为：

$\frac{1}{2}P\left( {{r_P}} \right) = \int {\left( {G({r_P},{r_Q})\frac{{{\partial ^2}P\left( {{r_P}} \right)}}{{\partial n}} - 1} \right){\mathrm{d}}s} \text{，}$

流体边界的法向导数与速度有下式关系：

$\frac{{{\partial ^{}}P\left( {{r_Q}} \right)}}{{\partial {n_Q}}} = - j{\rho _0}\omega \left( {{r_Q}} \right) \text{，}$

流体边界元模型可简化为：

$- \frac{1}{2}P\left( {{r_P}} \right) = \int {\left( {G({r_P},{r_Q})j{\rho _0}\omega \left( {{r_Q}} \right) - 1} \right){\mathrm{d}}s} 。$

式中： $G({r_P},{r_Q})$ 为流体边界元的格林函数； $G({r_P},{r_Q}) = exp\dfrac{{\left( {j\omega {r_P}} \right)}}{{4{\text π} \sqrt 2 {r_Q}}}$ 。

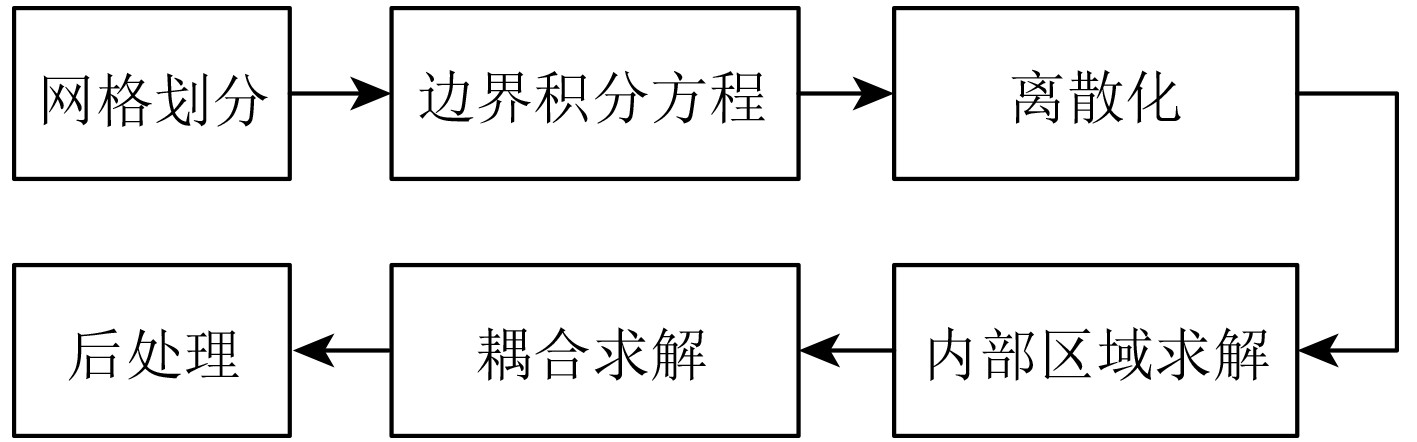
流体广义边界元法的计算流程如图4所示。

1）网格划分。将流体领域划分为边界和内部2个区域。在边界上离散化节点，并根据问题的要求选择适当的节点分布方式。

2）边界积分方程。根据流体力学问题的边界条件和物理方程，建立边界积分方程，通常使用格林公式将流体力学问题转化为边界上的积分方程。

3）离散化。将边界上的积分方程离散化，将积分方程中的未知量和积分变量用离散的节点和权重表示。通常使用基函数展开边界上的未知量，并将积分方程转化为代数方程组。

4）内部区域求解。在内部区域使用其他数值方法，如有限元法或有限差分法，求解流体的速度和压力分布。通常将流体的速度和压力表示为基函数的线性组合，并根据流体的动力学方程和边界条件建立代数方程组。

5）耦合求解。将边界上的代数方程组和内部区域的代数方程组耦合起来，通过迭代方法求解整个流体力学问题。

6）后处理。根据求解得到的速度和压力分布，可以计算流体的其他物理量，如流量、涡量等，并进行结果的分析和评估。

2.2 基于广义边界元法的高速排水型船舶尾浪数值计算

本文基于流体力学有限元分析软件Fluent进行高速排水型船舶的尾浪数值仿真，关键步骤如下：

1）广义边界元模型

建立船舶的广义边界元模型如下：

$\frac{1}{2}P\left( t \right) = \int {\left( {G(x,t)\frac{{{\partial ^2}P\left( t \right)}}{{\partial t}} - 1} \right){\mathrm{d}}t} \text{。}$

式中： $P\left( t \right)$ 为流体压力； $G(x,t)$ 为船舶相对流体的运动方程。

压力与船舶角速度关系满足：

$\frac{{{\partial ^{}}P\left( t \right)}}{{\partial t}} = - j{\rho _0}\omega \left( t \right) \text{，}$

可得简化后的广义边界元模型：

$f\left( t \right) = \frac{1}{2}\int {\left( {G(x,t)j{\rho _0}\omega \left( t \right) - 1} \right){\mathrm{d}}t} 。$

式中， ${\rho _0} = \exp\dfrac{{\left( {j\omega t} \right)}}{{4{\text π} \sqrt 2 t}}$ 。

2）有限元建模

为了提高高速排水型船舶的尾浪仿真精度，在进行有限元建模时，重点对以下2个方面进行网格的特殊处理：

1）网格细化。对船舶尾浪区域的网格进行细化处理，以更准确地捕捉尾浪的细节。尾浪区域通常是船舶尾部周围的区域，这是尾浪形成和传播的主要区域。通过细化网格，可以更好地模拟尾浪的形状和传播过程。尾浪区域的网格细化精度为10～30 μm逐渐过渡。

2）自适应性网格。Fluent软件^[5]支持网格的自适应性调整，在尾浪区域，可以使用网格适应性技术，根据流场的变化自动调整网格的密度。网格适应性可以根据流场的梯度、涡度等参数来判断网格的密度是否足够，如果不够，则自动细化网格；如果足够，则可以保持网格的密度不变或进行适当的稀疏。通过网格适应性，可以更好地捕捉尾浪形成和传播过程中的细节和变化。

建立高速排水型船舶尾浪仿真的有限元模型如图5所示。

3）入口边界参数施加

入口边界参数决定了有限元仿真是否发散和收敛，入口边界条件参数主包括海水速度，压力等，仅考虑沿水平ox方向的平面波，模型为：

$\zeta (x,t) = a\cos (kx - \omega \cdot t) \text{。}$

式中： $a$ 为幅值； $\omega$ 为角速度；k为波数。对于浅水情况下，存在：

${\omega ^2} = kg\tan h \text{，}$

式中，h为水深。此时，平面波的速度为：

${V_p} = \omega /k = \sqrt {g/k} \sqrt {\tanh (kh)} 。$

4）求解

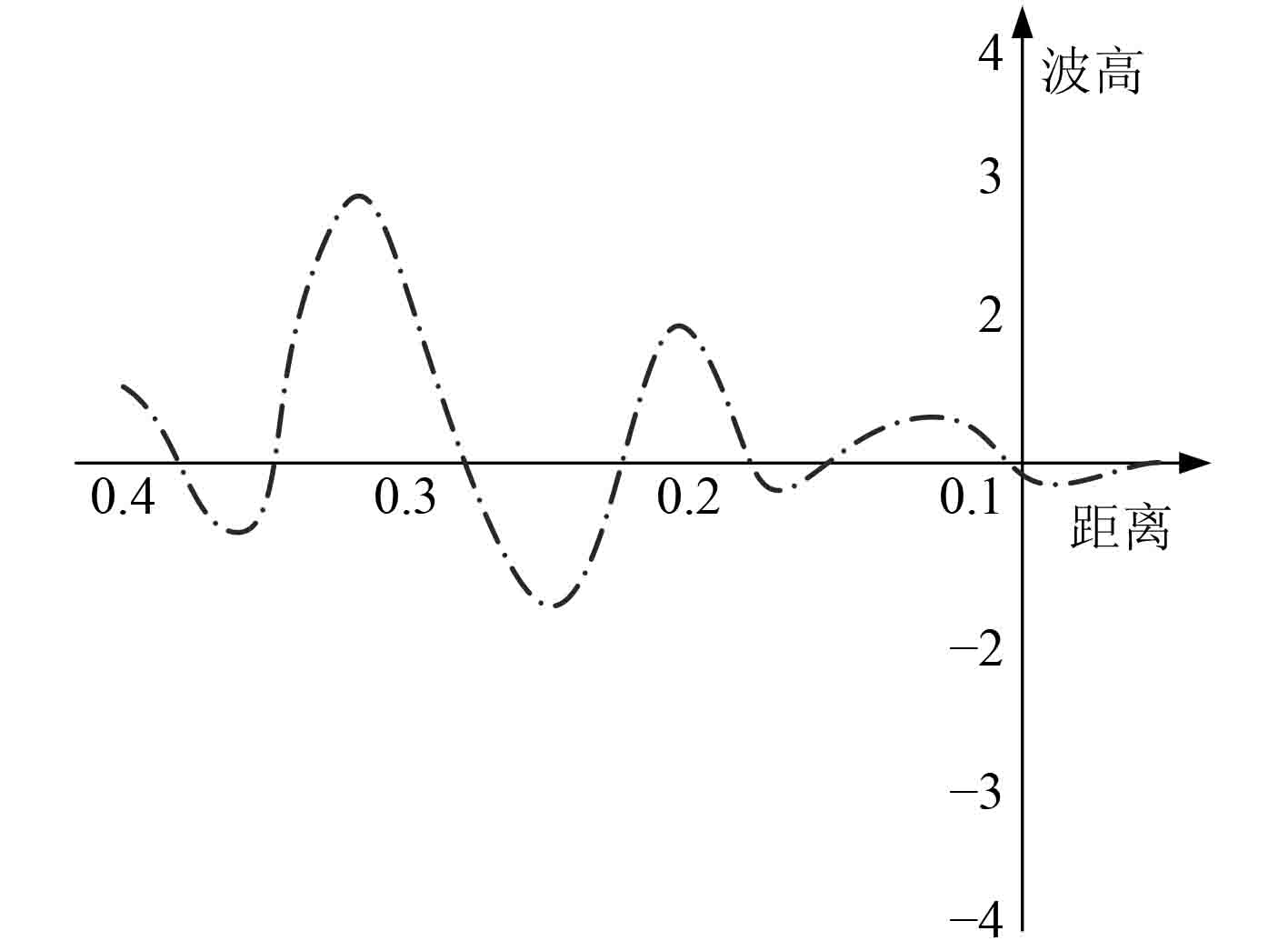
给定流场的来流速度为15 m/s，在Fluent求解器中高速排水型船舶的尾浪特性仿真曲线如图6所示。

图中可见，随着与船舶距离的增加，尾浪的波高从0.7 m逐渐增加至3 m左右。

3 结　语

高速排水型船舶的尾浪对环境和自身动力学性能均有影响，本文针对高速排水型船舶的尾浪特性仿真进行研究，通过建立高速排水型船舶的流动动力学模型，结合广义边界元法，在有限元仿真软件Fluent中进行有限元建模、边界模型建立、求解等，完成了高速排水型船舶的尾浪数值模拟与仿真。