2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
两相流与结构的流固耦合现象广泛存在,如LNG-FPSO船舶的复杂输流管道、海上石油开采平台的输送管道、动脉中的血液流动[1]等。在实际工程中,为了更改管路走向,水平U型管的应用十分广泛。流体在管道中流动时会产生脉动激励力作用于管道内壁,引发管道结构振动,可能对安全生产和生态环境造成威胁,因此有必要对管道中流体流动形态及其诱导的管道振动响应进行深入研究。
多位学者对于管内流体流动形态及流激振动已经有了一定的研究。刘行等[2]探讨了含冰率、流速、初始溶液浓度等因素对冰浆流动形态、流变特性及流动压降的影响。高岳等[3]研究了立管振动响应特性以及振动对管内气液两相流动的影响。王志伟等[4]分析了通过90°弯管后气液两相流的速度变化、截面含气率、压力分布及流型发展规律。
在水平管道中主要存在分层流、波状流、环状流、段塞流4种流型,一般而言,段塞流比其他流型更容易发生结构振动,但目前针对段塞流流体激励和振动响应数值仿真的相关研究较少。段塞流是一种不稳定的动态流动,通常表现为连续的无气液体或连续的无液气体[5]。Faiza Saidj等[6]研究了段塞流沿管道的发展和演变,Wang等[7]发现段塞速度和长度是影响管道振动冲击的重要因素。
本文基于计算流体力学和计算结构动力学基本原理,应用Ansys有限元分析软件,对水平U型管中多种气液两相流流型进行对比分析,明确了段塞流工况是诱发U型管振动最剧烈的流型工况,进而研究了段塞流工况下的流体动态激励特性及管道振动响应特性。
1 数值仿真方法及相关原理流体激励力作用下管道结构的基本动力学方程为:
| $ {\boldsymbol{M}}\ddot {\boldsymbol{u}} + {\boldsymbol{C}}\dot {\boldsymbol{u}} + {\boldsymbol{Ku}} = {\boldsymbol{F}}。$ | (1) |
式中:
| $ \begin{split} & {{{\dot {\boldsymbol{u}}}_t} = \frac{1}{{\Delta {t^2}}}\left( {{{\boldsymbol{u}}_{t - \Delta t}} - {{\boldsymbol{u}}_t} + {u_{t + \Delta t}}} \right)},\\ & {{{\ddot {\boldsymbol{u}}}_t} = \frac{1}{{2\Delta t}}\left( { - {{\boldsymbol{u}}_{t - \Delta t}} + {{\boldsymbol{u}}_{t + \Delta t}}} \right)} ,\\ & {{{\boldsymbol{u}}_{ - \Delta t}} = {{\boldsymbol{u}}_0} - \Delta t{{\dot {\boldsymbol{u}}}_0} + \frac{{\Delta {t^2}}}{2}{{\ddot {\boldsymbol{u}}}_0}} 。\end{split} $ | (2) |
式中:
| $ \bar {\boldsymbol{F}} = {\boldsymbol{F}} - \left( {{\boldsymbol{K}} - \frac{2}{{\Delta {t^2}}}{\boldsymbol{M}}} \right){{\boldsymbol{u}}_t} - \left( {\frac{1}{{\Delta {t^2}}}{\boldsymbol{M}} - \frac{1}{{2\Delta t}}{\boldsymbol{C}}} \right){{\boldsymbol{u}}_{t - \Delta t}},$ | (3) |
故
| $ \left( {\frac{1}{{\Delta {t^2}}}{\boldsymbol{M }}+ \frac{1}{{2\Delta t}}{\boldsymbol{C}}} \right){{\boldsymbol{u}}_{t + \Delta t}} = \bar {\boldsymbol{F}} 。$ | (4) |
流体域控制方程包含质量和动量守恒方程,如下式:
| $ \nabla \cdot {\boldsymbol{V}} = 0,$ | (5) |
| $ \rho \left( {\frac{{\partial {\boldsymbol{V}}}}{{\partial t}} + {\boldsymbol{V}}\nabla \cdot {\boldsymbol{V}}} \right) = - \nabla p + \rho {\boldsymbol{f}} + \mu {\nabla ^2}{\boldsymbol{V}} 。$ | (6) |
式中:
本文采用几何重构的VOF模型,其适用于求解具有较明显相界面的两相流,具有较高的精确度。在每个时间步内,根据流体域有限控制体内的空泡份额来捕捉相界面。湍流模型为标准
| $ \frac{\partial }{{\partial t}}\left( {{r_\alpha }\rho } \right) + \nabla \cdot \left( {{r_\alpha }\rho{\boldsymbol{ V}}} \right) = 0,$ | (7) |
| $ \begin{split} \frac{\partial }{{\partial t}}\left( {\rho {\boldsymbol{V}}} \right) + \nabla \cdot \left( {\rho {\boldsymbol{V}} \otimes {\boldsymbol{V}}} \right) =& \nabla \cdot \left( {\mu \left( {\nabla {\boldsymbol{V}}} \right) + {{\left( {\nabla {\boldsymbol{V}}} \right)}^{\rm{T}}}} \right) -\\ & \nabla p + \rho f + \sigma k{\boldsymbol{n}}。\end{split} $ | (8) |
式中:
| $ \sum\limits_{\alpha = 1}^2 {{r_\alpha }} = 1,$ | (9) |
流固耦合界面的位移协调和应力平衡方程如下:
| $ {d_{{f}}} = {d_{{s}}},$ | (10) |
| $ {n_{{f}}}{\tau _{{f}}} = {n_{{s}}}{\tau _{{s}}}。$ | (11) |
式中:
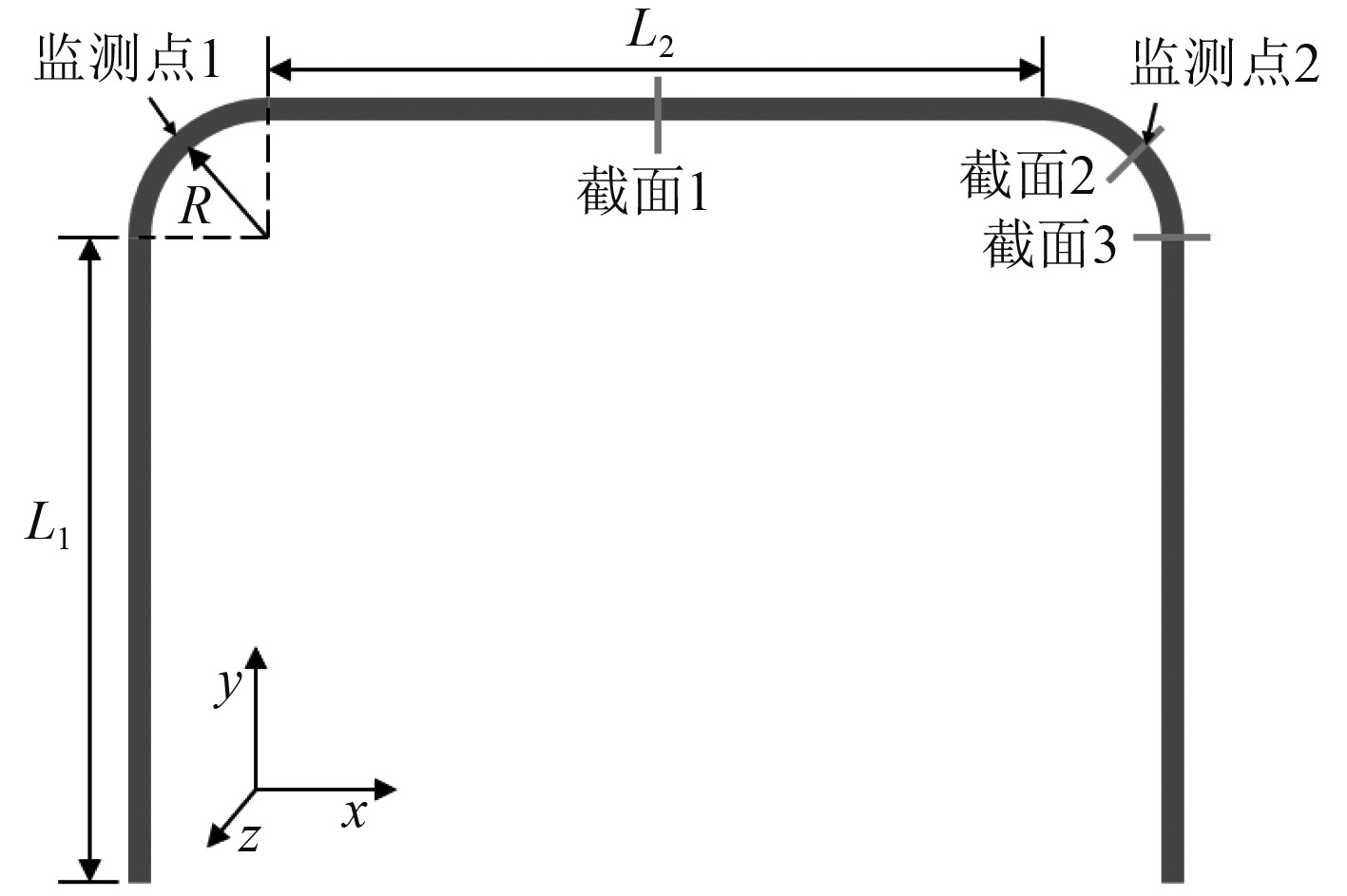
本文研究对象为水平U型管,其在需要更改管路走向的工程管道系统中应用广泛。如图1所示,管道位于水平面XOY内,重力加速度沿Z轴负方向,其值为9.81
|
图 1 U型管几何模型及监测面(点)设定 Fig. 1 U-tube geometric model and monitoring surface (point) setting |
|
|
表 1 流体物理特性 Tab.1 Physical properties of fluid |
| $ {J_{{w}}} = \frac{{{Q_{{w}}}}}{A} {J_{{v}}} = \frac{{{Q_{{v}}}}}{A} ,$ | (12) |
| $ J = \frac{{{Q_{{w}}} + {Q_{{v}}}}}{A} = {J_{{w}}} + {J_{{v}}} ,$ | (13) |
| $ \beta = \frac{{{Q_{{v}}}}}{{{Q_{{w}}} + {Q_{{v}}}}} = \frac{{{J_{{v}}}}}{J}。$ | (14) |
式中:
在均质流假设下,两相流在某一截面的动量通量
| $ M = A{J^2}\left( {{\rho _{\text{v}}}{\alpha ^A}\left( t \right) + {\rho _{\text{w}}}\left( {1 - {\alpha ^A}\left( t \right)} \right)} \right) ,$ | (15) |
| $ \Delta M = F\Delta t。$ | (16) |
式中:A为截面积;J为混合流体平均速度;
| $ \alpha _{RMS}^A = \sqrt {\frac{1}{3}{{\sum\limits_{i = 1}^3 {\left( {\alpha _i^A} \right)} }^2}} 。$ | (17) |
由表2可知,随着单元和节点数目的增多,相对误差越来越小,方案4与方案3的相对误差仅为0.1643%。对结果精度和计算代价进行权衡,选择方案3作为仿真网格,如图2所示。对其他工况下的管道气液两相流数值仿真,均进行了相应的网格无关性验证来确定网格密度。
|
|
表 2 四种网格方案对比 Tab.2 Comparison of four grid schemes |

|
图 2 流体域网格 Fig. 2 Fluid domain mesh |
为验证数值仿真框架的可靠性,参照Abdalellah[8]等的段塞流实验进行对比验证,数值仿真的边界条件依据实验条件设置,图3为实验与CFD模拟在相同管道段中段塞流形态的时序对比。其中,云图1表示气相,2表示液相,虚线3表示液塞边界。从液塞数量上看,实验和数值仿真的观测结果一致;从液塞形态上看,实验和数值仿真的观测结果基本吻合,说明了CFD模型的有效性。

|
图 3 实验与CFD模拟的段塞流形态对比 Fig. 3 Comparison of slug flow morphology between experiment and CFD simulation |
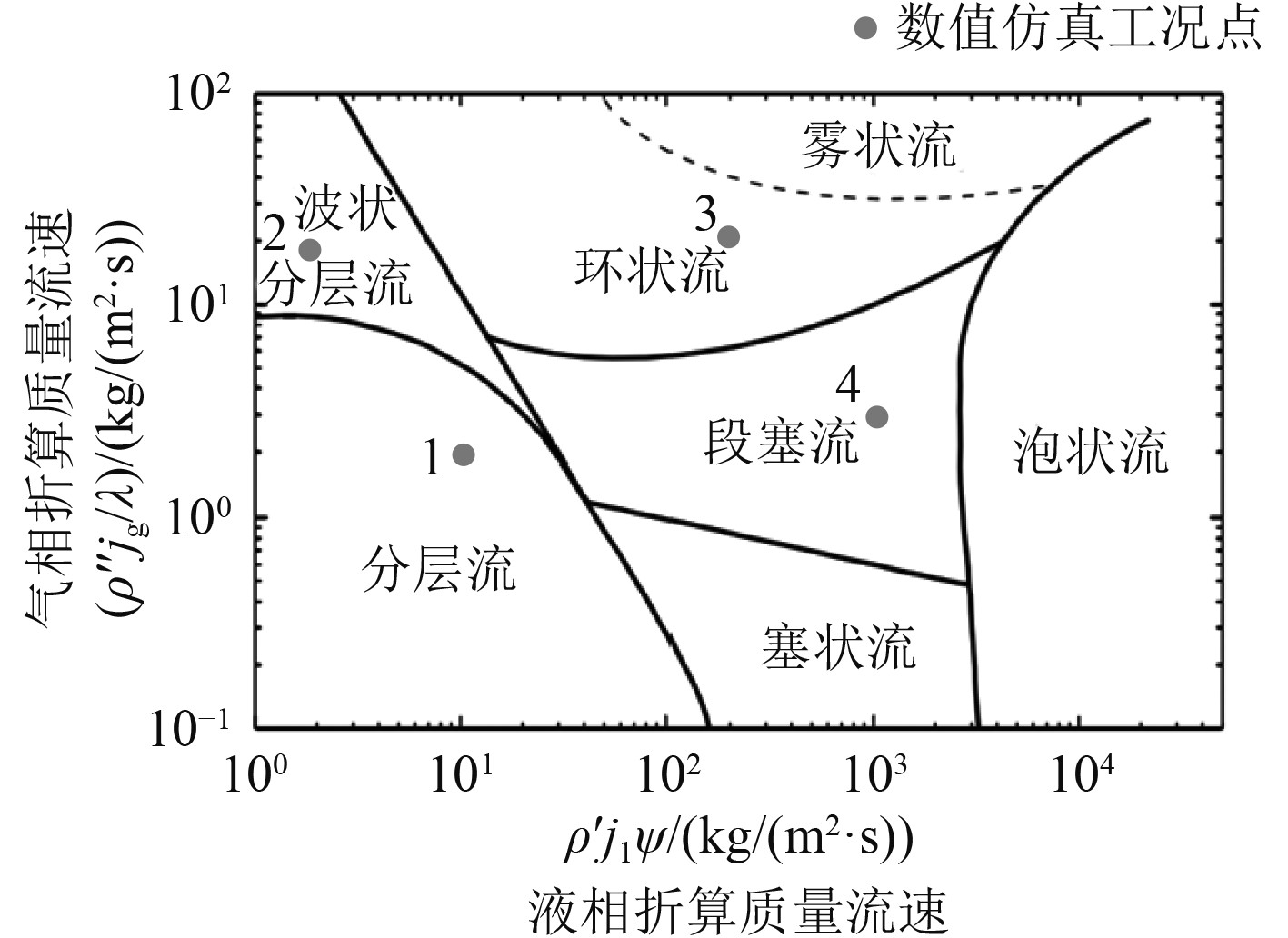
为了更直观地说明段塞流诱导管道振动的剧烈程度,对于水平U型管,设置不同的气液两相流入口边界条件,研究分层流、波状流、环状流的管内流动特性,并与段塞流的管内流动特性作对比。4种工况的选取依照Baker流型图,如表3和图4所示。
|
|
表 3 U型管气液两相流数值仿真工况 Tab.3 Numerical simulation of gas-liquid two-phase flow in U-tube |
|
图 4 仿真工况点示意图 Fig. 4 Schematic diagram of simulation operating points |
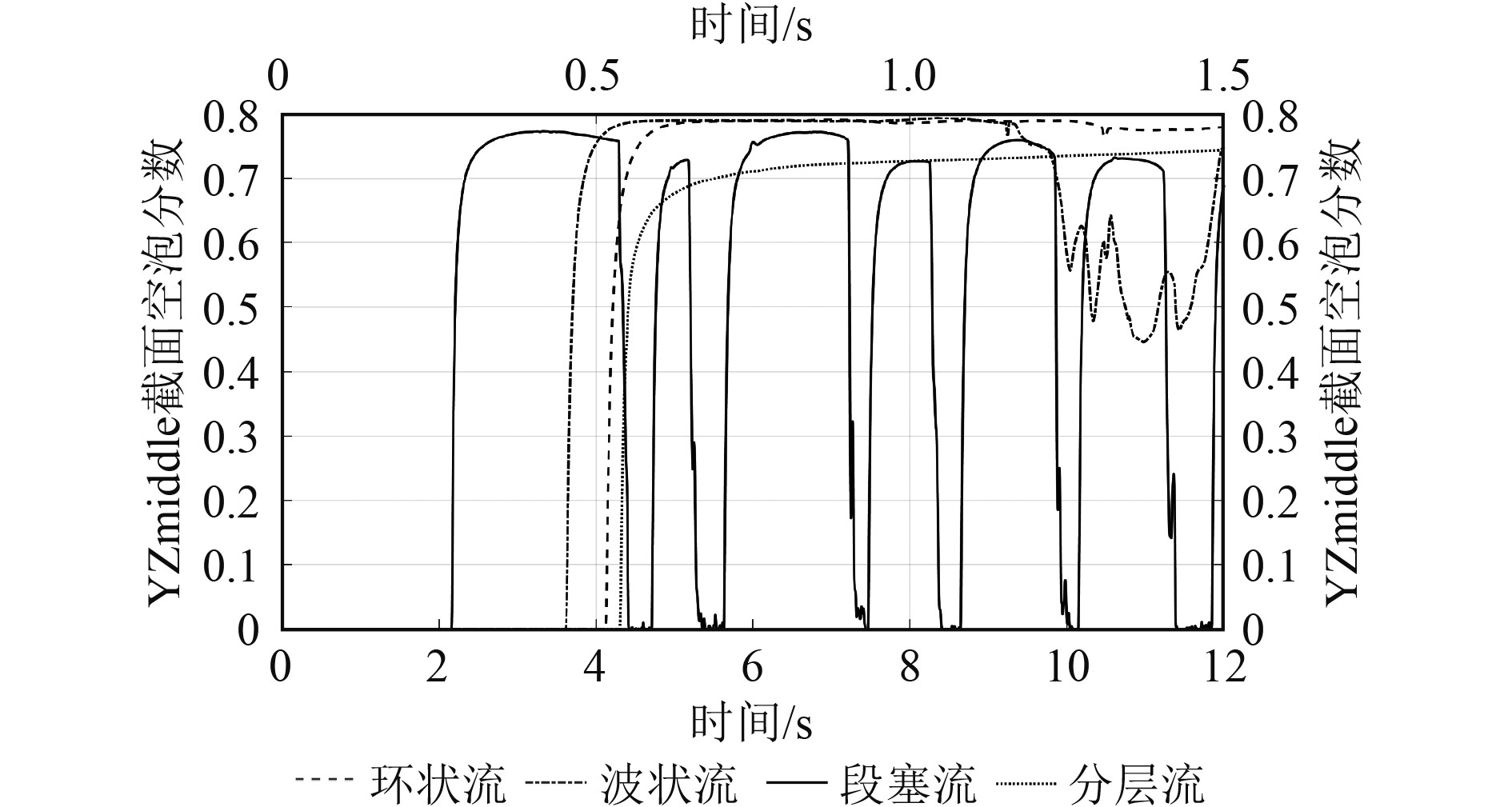
选取U型管跨中横截面,对比4种流型下空泡分数的时域特性,如图5所示。
|
图 5 空泡分数时域曲线 Fig. 5 Time domain curves of void fraction |
4种流型工况的混合流平均流速差别较大,仿真总时长设置不一。为便于展示,波状流和环状流参考上方横轴,段塞流和分层流参考下方横轴。由图5可知,分层流空泡分数稳定在0.74附近;环状流在流型充分发展后,空泡分数基本稳定在0.78附近,并伴随小范围波动;波状流相较环状流呈现出较大幅度的波动。段塞流具有与其他3种流型截然不同的特性,其空泡分数在0与0.75之间呈锯齿状反复交替,这与段塞流在管道中液塞与气体交替前进的特征相符。
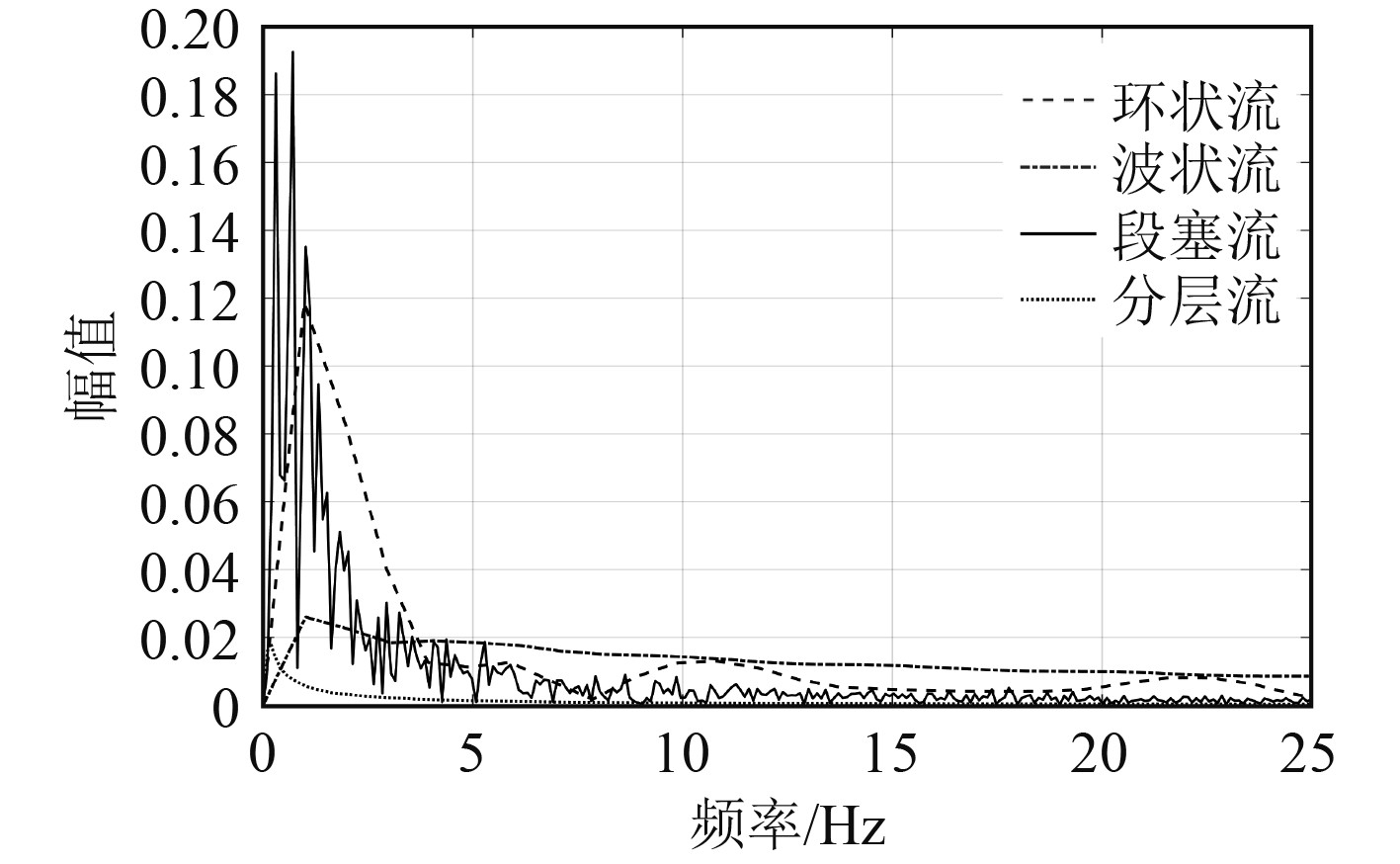
根据式(15)和式(16),截面空泡分数频域特征可反映激励力频域特征,4种流型下跨中横截面空泡分数频域曲线如图6所示。可以看出,段塞流诱导激励力幅值最大,分层流诱导激励力幅值最小。4种流型在水平U型管中诱发的流体激励力都属于低频激励力,主频均在5 Hz以下。其中,段塞流在0.71 Hz处达到空泡分数最大峰值。
|
图 6 空泡分数频域曲线 Fig. 6 Frequency domain curves of void fraction |
设定气相折算速度为
|
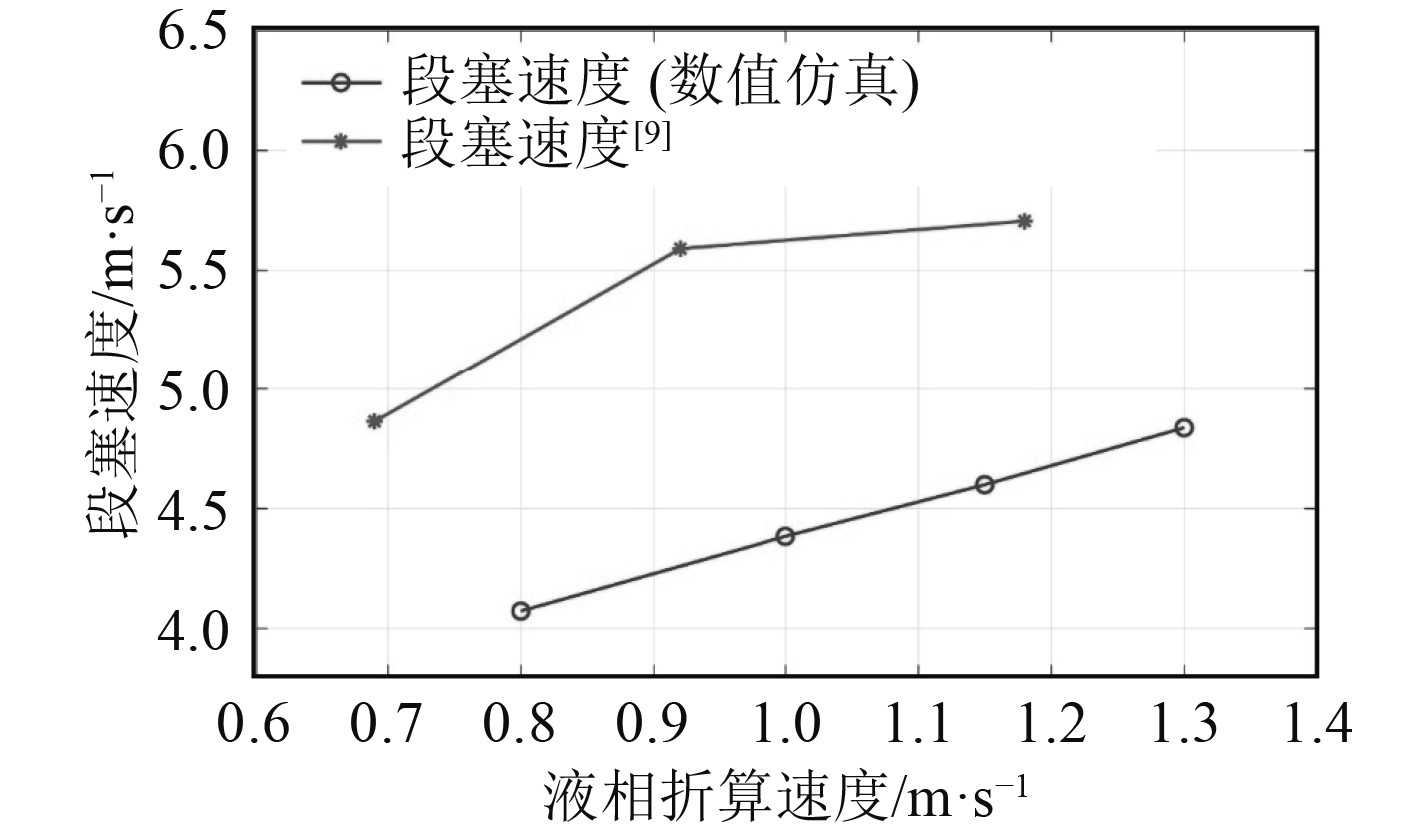
图 7 段塞速度随液相折算速度的变化关系(Jv = 2.44 m/s) Fig. 7 Relationship between slug velocity and superficial liquid velocity (Jv = 2.44 m/s) |
|
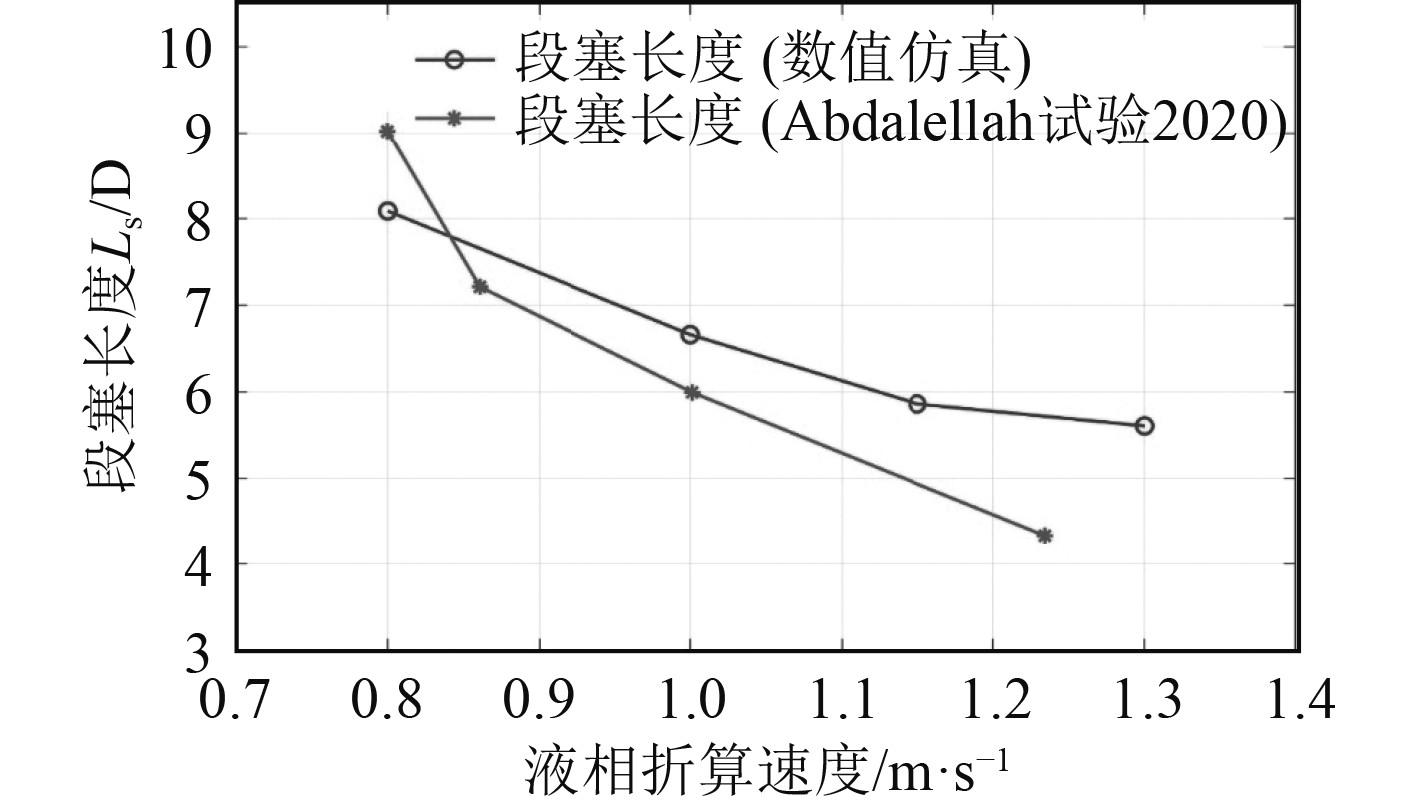
图 9 段塞长度随液相折算速度的变化关系(Jv = 2.44 m/s) Fig. 9 Relationship between slug length and superficial liquid velocity (Jv = 2.44 m/s) |
段塞速度是液塞在段塞流单元中的平均速度,其对液塞生长、发展和消失的机理研究起重要作用。从数值仿真结果中,每间隔0.5 s获取一次段塞流形态云图,取中部水平直管段捕获的所有液塞的平均速度为本次仿真的段塞速度(见图7),在气相折算速度不变的情况下,水平U型管中段塞速度随液相折算速度的增大而线性增大。
段塞流在管道中的流动是复杂的随机过程,并不具有规律的周期性,段塞频率只是用周期性来近似模拟段塞流流动。对中部水平管段的段塞进行追踪,在管道相同位置出现相同段塞时认为是段塞的一个周期。由图8可以看出,在气相折算速度不变的情况下,段塞频率随液相折算速度的增大而增大。此外,在气相和液相折算速度分别为2.44 m/s和1 m/s时,段塞频率为0.7 Hz,这与相同工况下获取的段塞流激励力主频0.71 Hz相吻合,表明段塞频率同流体诱导激励力主频是相对应的关系。

|
图 8 段塞频率随液相折算速度的变化关系(Jv = 2.44 m/s) Fig. 8 Relationship between slug frequency and superficial liquid velocity (Jv = 2.44 m/s) |
段塞长度和段塞频率是强相关参数,段塞频率增大,段塞长度减小。从数值仿真结果中,每间隔0.5 s获取一次管道段塞流形态云图,取中部水平直管段捕获的所有液塞的平均长度为本次仿真的段塞长度。由图9可以看出,在气相折算速度不变的情况下,随着液相折算速度的增大,段塞长度减小。
因管道形态、内径、壁厚等参数不一致,本文与其他学者的结果数值并不一致,但在特征参数随液相折算速度的变化趋势上是统一的,这揭示了段塞流包括段塞速度、频率及长度在内的特征参数变化规律在水平管道中具有一致性。
3.2 段塞流工况下管道振动特性分析 3.2.1 固体域模型及管道系统模态计算管道采用钢材料,壁厚为20 mm,弹性模量为200 GPa,泊松比为0.3,密度为7850 kg/m3,生成网格如图10所示。管道两端设定固定约束,将管道内壁设为流固耦合面进行数据交互。

|
图 10 结构域网格 Fig. 10 Structure domain mesh |
对管道进行干湿模态分析[11],前6阶结果对比如表4所示。由于水的密度和声速特性远大于空气,在湿模态分析时采用极端工况,即均为单相液态水,故气液两相流管道系统固有频率介于表中所列干湿模态固有频率之间。已知段塞流工况下空泡分数主频(流体激励力主频)为0.71 Hz,与管道固有频率的错开率大于78%,故流体与管道不会产生共振。
|
|
表 4 前6阶管道固有频率 Tab.4 First six natural frequencies of pipeline |
为探究水平U型管在段塞流作用下的振动响应特性,设定液速

|
图 11 两监测点位移及频谱 Fig. 11 Displacement and spectrum of two monitoring points |
可知:
1)监测点1和监测点2的时域、频域曲线基本重合,两监测点在几何上对称,在振动响应上也对称。
2)X和Y方向峰值振动频率为6 Hz,接近管道二阶固有频率,Z方向峰值振动频率为3.8 Hz,接近管道一阶固有频率。这与管道固有振型相对应,根据模态分析结果,管道一阶振型主要沿Z方向,二阶振型主要沿X和Y方向。
3)两端固定约束的水平U型管在段塞流工况下响应幅值呈现出X方向最大、Z方向次之、Y方向最小的特性。气液两相流以较大速度流入管道,沿着XOY平面冲击原有流场使其逐渐趋于段塞流分布,且管道在X方向上跨距较Y方向更大,故X方向的响应幅值也较大;而管道一阶振型主要沿Z方向,其振动响应幅值介于X和Y方向之间。
4 结 语本文基于计算流体力学和计算结构动力学方法,对气液两相流诱导水平U型管振动进行了数值仿真研究。在验证数值仿真框架可靠性的基础上,对比分析气液两相流典型流型,重点研究了振动最剧烈的段塞流的流体特征参数和其诱导的管道振动响应,主要结论如下:
1)基于Ansys几何重构VOF模型、
2)4种典型流型在水平U型管中诱发的流体激励力都属于低频激励力,主频均在5 Hz以下。段塞流诱导的激励力幅值最大,波状流和环形流次之,分层流最小。
3)对于水平U型管,在气相折算速度不变的情况下,随着液相折算速度的增大,段塞速度和段塞频率增大,段塞长度减小。此外,段塞流诱导激励力主频同段塞频率相互对应,二者从不同层面反映了段塞流诱导管道振动的原因。
4)U型管两弯头结构对称,振动响应也基本对称。X和Y方向峰值振动频率接近管道二阶固有频率,Z方向峰值振动频率接近管道一阶固有频率,与管道固有振型相对应。
| [1] |
MELKA B, GRACKA M, ADAMCZYK W, et al. Multiphase simulation of blood flow within main thoracic arteries of 8-year-old child with coarctation of the aorta[J]. Heat and Mass Transfer, 2018, 54(8): 2405-2413. DOI:10.1007/s00231-017-2136-y |
| [2] |
刘行, 王晓春, 李娟. 冰浆流动特性研究进展[J]. 低温与超导, 2021, 49(2): 89-98. DOI:10.16711/j.1001-7100.2021.02.015 |
| [3] |
高岳, 朱红钧, 王珂楠, 等. 弯曲柔性立管举升气液两相流时的流固耦合效应研究[J]. 海洋工程, 2022, 40(1): 39-49. |
| [4] |
王志伟, 何炎平, 李铭志, 等. 基于计算流体力学的90°弯管气液两相流数值模拟及流型演化[J]. 上海交通大学学报: 1−9[2022-07-20].
|
| [5] |
JAEGER J, SANTOS C M, ROSA L M, et al. Experimental and numerical evaluation of slugs in a vertical air–water flow[J]. International Journal of Multiphase Flow, 2018, 101: 152-166. DOI:10.1016/j.ijmultiphaseflow.2018.01.009 |
| [6] |
SAIDJ F, HASAN A, BOUYAHIAOUI H, et al. Experimental study of the characteristics of an upward two-phase slug flow in a vertical pipe[J]. Progress in Nuclear Energy, 2018, 108: 428-437. DOI:10.1016/j.pnucene.2018.07.001 |
| [7] |
WANG L, YANG Y, LI Y, et al. Dynamic behaviours of horizontal gas-liquid pipes subjected to hydrodynamic slug flow: Modelling and experiments[J]. International Journal of Pressure Vessels and Piping, 2018, 161: 50-57. DOI:10.1016/j.ijpvp.2018.02.005 |
| [8] |
MOHMMED A O, AL-KAYIEM H H, OSMAN A B, et al. One-way coupled fluid–structure interaction of gas–liquid slug flow in a horizontal pipe: Experiments and simulations[J]. Journal of Fluids and Structures, 2020, 97: 103083. DOI:10.1016/j.jfluidstructs.2020.103083 |
| [9] |
黄阿勇, 李艳红, 王经, 等. 水平管道油气二相段塞流稳态流动特性[J]. 化学工程, 2010, 38(5): 26-29. DOI:10.3969/j.issn.1005-9954.2010.05.007 |
| [10] |
FETTER C P. Development of a clamp-on acoustic two-phase flowmeter[J]. 1988.
|
| [11] |
陈玉涛. 气液两相流弹性管道流致振动数值建模与分析[D]. 上海: 上海交通大学, 2020.
|
 2023, Vol. 45
2023, Vol. 45

