船舶不仅需要满足基本的功能要求,如运输、作业等,还需适应不断变化的环境条件,如风、浪、流等。因此,如何提高船舶的性能和舒适性已成为当前研究的热点问题[1 − 3]。在船舶设计中,外部造型是影响其性能和舒适性的重要因素之一。传统的船舶设计方法主要依靠经验和工程判断,无法实现最优化设计。近年来,随着计算机技术和数值模拟方法的发展,船舶设计已经逐步走向数字化和智能化[4-5]。众多学者对船舶结构优化进行了研究,罗文俊等[6]从船舶结构可靠性角度出发,使用可靠性评估方法,获得兴趣子域范围,使用尽可能少的样本点组成感兴趣区域,拟合出动态代理模型,优化出全新的船舶结构,经过验证,该方法计算效率较高,适用性较强。但是该方法优化后的船舶结构还停留在模型分析阶段,缺乏实际试验结果。陈熠画等从细节角度出发,改善船舶结构硬点节点设计难度较大问题,优化船舶结构上的受力情况,该方法通过试验对比优化前后的节点受力情况,但是试验分析较少。
考虑到以上多种因素,本文基于仿生理论研究船舶外形设计优化。
1 仿鲸鱼鳍优化设计—船舶双尾鳍结构船舶结构上的双尾鳍是安装在船舶尾部,一方面能降低船舶航行时的黏压阻力,另一方面还能提升船舶的伴流,一般会沿着船舶推进器轴方向安装。按照以往仿生经验,这种双尾鳍设计成鱼鳍形状,提升船舶的速度。本文在此基础上,研究利用仿鲸鱼鳍的仿生理论方式优化双尾鳍结构,使得船舶在实际应用时具有更快的航行速度,同时提升航行稳定性。
1.1 仿生鲸鱼鳍几何模型构建通过构建几何模型,模拟出仿鲸鱼鳍的水动力特性。构建几何模型时,借助翼型相似化模拟鲸鱼鳍,获得鲸鱼鳍横截面形状。同时使用样条先绘制出鲸鱼鳍,经优化与筛选,获得鲸鱼鳍的前、后缘外轮廓。根据鲸鱼鳍的外轮廓形状以及横截面参数,利用CATIA软件构建出鲸鱼鳍的几何模型,构建步骤如下:
1)从图像素材库收集数张鲸鱼胸鳍图像(其中以座头鲸为代表),把这些图像导入到CAD软件之中,利用软件自带的样条曲线绘制模块绘制出鲸鱼鳍的外部轮廓,挑选这些轮廓线后,向CATIA软件导入这些轮廓线;
2)选择与鲸鱼鳍相近的翼型,利用专门仿真翼型的NACA机翼仿真软件,构建翼型二维模型,将该二维模型导入CATIA软件之中;
3)利用扫掠处理方法在CATIA软件中建立仿生鲸鱼鳍的几何模型(见图1)。

|
图 1 仿生鲸鱼鳍的几何模型 Fig. 1 Geometric model of the bionic whale fin |
借助仿生鲸鱼鳍优化设计船舶双尾鳍结构时,需要考虑鲸鱼鳍的运动学特性,以此模拟出应用在船舶的运动特性。在图1的仿生鲸鱼鳍的几何模型基础上,计算仿生鲸鱼鳍的运动学特性。ω(t)表示鲸鱼鳍侧向摆动速度,将仿生鲸鱼鳍应用在船舶双尾鳍结构中需要考虑3个限定条件:
鲸鱼鳍真实运动时会做出规律性运动,但是该运动也会伴随鱼鳍的扭动,因此鲸鱼鳍运动是一个较为复杂的多自由度运动,将仿生鲸鱼鳍应用在船舶双尾鳍结构时,可以把鲸鱼鳍运动简化成一种云角速度简谐摆动模型。设定鲸鱼鳍以规律性固定相位差云顶,鲸鱼鳍云角速度简谐摆动模型为:
| $ {\phi ^i} = A_{ray}^i\sin \left[ {2\text{π} {f_{ray}} + \left( {i - 1} \right){\phi _{lag}}} \right] - \psi 。$ | (1) |
式中,
鲸鱼鳍发生摆动能够帮助鲸鱼前进,将仿生鲸鱼鳍应用在船舶双尾鳍结构中,能够加速船舶推进。如果
应用在船舶双尾鳍结构的仿生鲸鱼鳍是一种柔性固态边界运动变化,所以划分模型网格时,使用非结构化网格。网格划分时考虑仿生鲸鱼鳍的运动是一种柔性运动,所以划分仿生鲸鱼鳍的网格时,使用DEFINE_GRID_MOTION描述仿生鲸鱼鳍几何模型表面上各个网格点的运动特征。仿生鲸鱼鳍具有生物特性,划分网格时会出现三维扭转变形,为了避免出现负体积网格,需要结合扩散光顺方法和局部网格重构方法划分仿生鱼鳍的网格。
扩散光顺是一种动网格划分,不会使网格拓扑结构发生改变,网格节点运动位移通过扩散方程求解得到,网格运动控制表达式为:
| $ \nabla *\left( {\gamma \nabla \vec u} \right) = 0 。$ | (2) |
式中,
使用网格中心加权平均距离倒数实现差值网格运动速度,根据该差值计算得到在下一个时间步长上的网格节点位置:
| $ {x_{{\mathrm{next}}}} = {x_{{\mathrm{now}}}} + \vec u*\Delta t。$ | (3) |
其中:xnow和
使用边界长度法求解扩散系数
| $ \gamma = 1/{d^4}。$ | (4) |
实际计算时为了增加运动扩散,设定扩散系数为1.6,设定局部重构方法时,设定1作为网格重构间隔数,以此保证网格重构速度。
对仿生鲸鱼鳍网格划分时,利用有限体积法离散控制方程,确保经过控制以后,不论何时刻都不会发生负体积网格,由于仿生鲸鱼鳍摆幅与展弦都较大,容易出现网格畸变,所以利用扩散光顺方式控制仿生鲸鱼鳍的四面体网格,再使用网格重构方式将超出规定倾斜率的网格重新构建出来。本文所构建的应用于船舶双尾鳍结构的仿生鲸鱼鳍网格划分结果如图2所示。将仿生鲸鱼鳍结构实际应用在船舶双尾鳍结构上,优化船舶外部造型。

|
图 2 仿生鲸鱼鳍网格划分结果 Fig. 2 Mesh division results of bionic whale fins |
本文以某多用途货船为研究对象,该船总长68.9 m,船身的长度与宽度分别为62.81 m和15 m,型深为6.5 m。设计满载吃水为2.3 m,空载吃水为2.75 m,总重与净重分别为2249 t和1188 t,该船的基本模型如图3所示。图3中,框中的区域是该研究对象未经优化的初始双尾鳍结构。能够看出,这种普通的双尾鳍结构是一种规则的几何形状,不具备特点,本文针对该区域实现基于仿生理论的船舶外部造型设计优化。

|
图 3 研究对象 Fig. 3 Research objects |
使用本文方法,优化后的模型如图4所示。由图4可知,优化后的双尾鳍,结合仿生鲸鱼鳍结构,设计成接近鲸鱼鳍形状的双尾鳍,使得双尾鳍具有弧度,改变船舶尾鳍流线。

|
图 4 船舶双尾鳍优化设计 Fig. 4 Optimal design of ship’s double stern fins |
在模型生成优化双尾鳍结构前后,船舶航行速度为20 m/s时的兴波阻力模拟结果如图5所示。兴波阻力是船舶航行时,在水体之中所受到的阻力,一般中心流速小于四周流速。从图5能够明显看出,未经过本文方法优化的船舶航行在水体中,兴波阻力更高。经过本文方法优化设计后的双尾鳍结构兴波阻力明显更低,说明使用本文方法优化之后的船舶外部结构实际航行时阻力更小,能够一定程度提升船舶的航行速度。
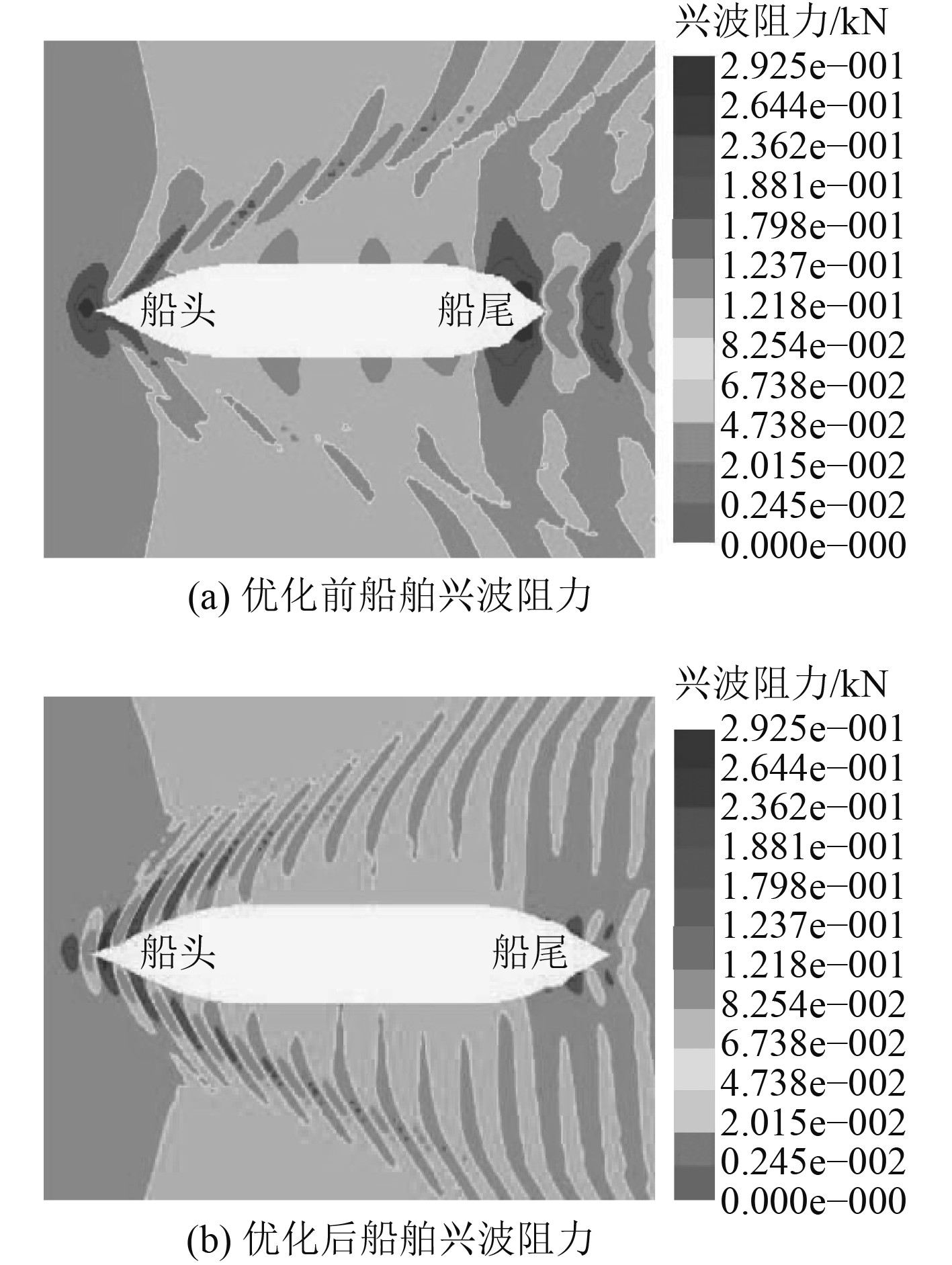
|
图 5 兴波阻力模拟结果对比 Fig. 5 Comparison of simulation results of wave generating resistance |
在模型中模拟计算并且测试优化前后船舶的各项阻力变化情况,对比结果如表1所示。从表1能够看出,与未优化的船舶结构相比,经过仿生鲸鱼优化双尾鳍后的船舶外部造型结构,各阻力系数均较低,且从表1能够获知,压阻力系数与摩擦阻力系数较低,导致最终总阻力系数降低,说明使用本文仿生方法优化后的船舶外部结构具有良好的航行性能。
|
|
表 1 阻力变化 Tab.1 Resistance changes |
分析船舶吃水情况,获得船舶稳定性变化。由于优化船舶双尾鳍会改变船舶的漂浮状态,因此分析优化前后船舶在不同航行时间的吃水情况,判断船舶稳定性变化,试验结果如图6所示。通常情况下船舶载重量增加,会导致船舶的吃水深度增加,但是从图6能够明显看出,未经优化的船舶吃水深度增加较为迅速,经过仿生理论优化设计后的船舶吃水深度随着船舶载货重量增加,上升趋势较为缓慢。由此可以确定,经过优化设计后,船舶具有较强稳定性。
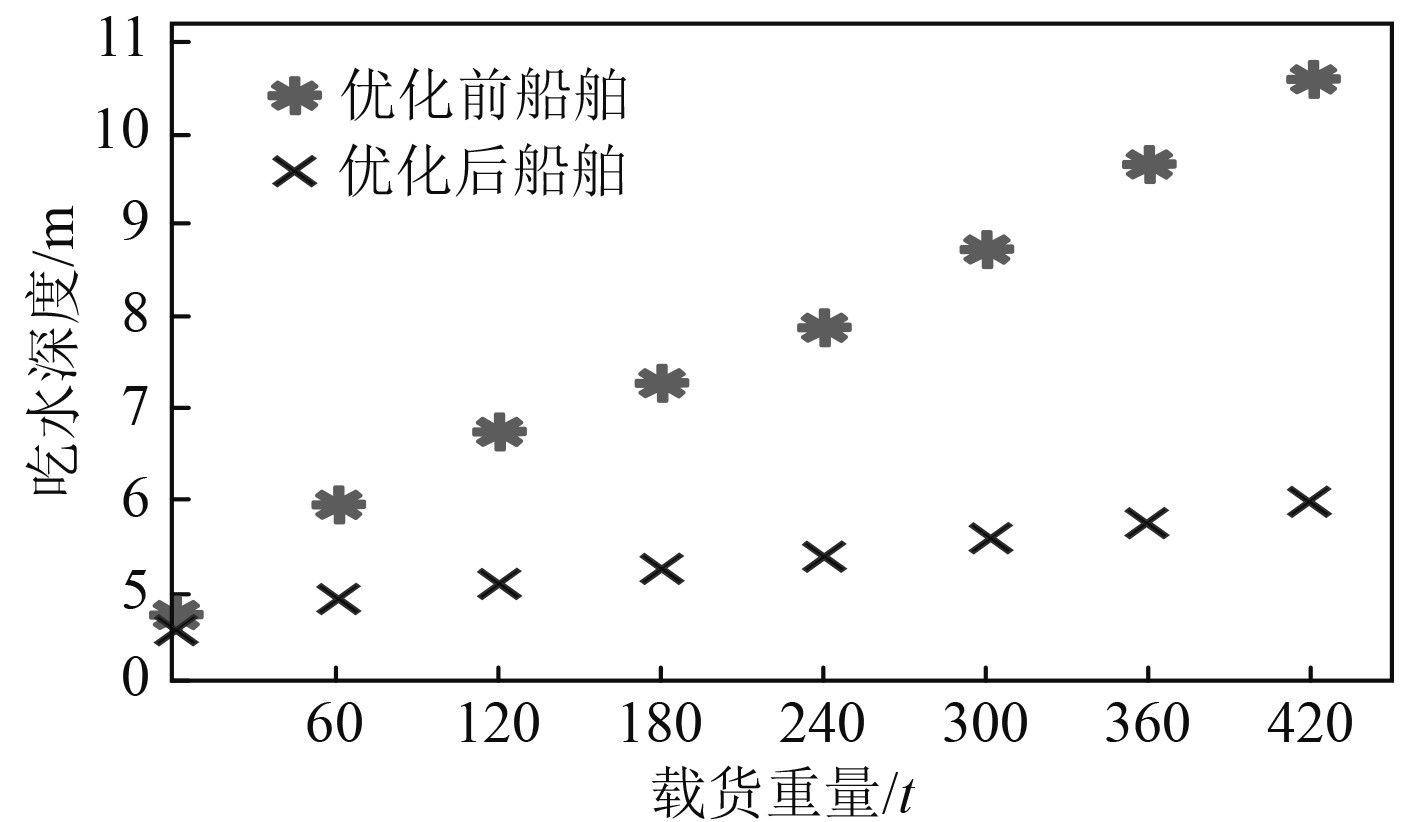
|
图 6 吃水情况分析 Fig. 6 Draft analysis |
结合仿生理论基本思路,研究船舶外部造型设计优化。本文研究以鲸鱼鳍为仿生对象,通过构建仿生鲸鱼鳍几何模型与运动学模型计算,确定仿生鲸鱼鳍的运动特性,再通过网格划分得到仿生仿生鲸鱼鳍结构,将该结构应用在船舶双尾鳍结构上,优化船舶结构。经过分析确定,优化双尾鳍之后,船舶的兴波阻力变小,综合阻力降低,即使在较大载重情况下仍具有较强稳定性,综合性能得到提升。
| [1] |
郭健, 潘彬彬, 崔维成, 等. 基于智能材料的深海执行器及海洋仿生机器人研究综述[J]. 船舶力学, 2022, 26(2): 301-313. GUO Jian, PAN Bin-bin, CUI Wei-cheng, et al. Review of deep-sea actuators and marine bionic robots based on intelligent materials[J]. Journal of Ship Mechanics, 2022, 26(2): 301-313. |
| [2] |
魏骁, 李恒, 黄晨冉. 基于PCE法和最大熵法的船舶不确定性优化设计[J]. 中国舰船研究, 2023, 18(3): 13-25. WEI Xiao, LI Heng, HUANG Chenran. Application of uncertainty design optimization based on polynomial chaos expansions and maximum entropy method in ship design[J]. Chinese Journal of Ship Research, 2023, 18(3): 13-25. |
| [3] |
刘磊, 孙卓文, 陈令仪, 等. 基于深度学习的仿生集群运动智能控制[J]. 控制与决策, 2021, 36(9): 2195-2202. LIU Lei, SUN Zhuo-wen, CHEN Ling-yi, et al. Intelligent control of bionic collective motion based on deep learning[J]. Control and Decision, 2021, 36(9): 2195-2202. |
| [4] |
李怡昕, 胡桥, 刘钰, 等. 水下航行器仿生侧线探测阵列优化布置模型及评估方法[J]. 西安交通大学学报, 2021, 55(11): 34-45. LI Yixin, HU Qiao, LIU Yu, et al. Optimal placement model and evaluation scheme of artificial lateral line detection array for underwater vehicle[J]. Journal of Xi'an Jiaotong University, 2021, 55(11): 34-45. |
| [5] |
许永生, 赵秦琨, 支锦亦, 等. 基于生物形态简化优化法的产品仿生设计研究[J]. 包装工程, 2021, 42(18): 188-193. XU Yong-sheng, ZHAO Qin-kun, ZHI Jin-yi, et al. Product bionic design based on simplified optimization method of biological form[J]. Packaging Engineering, 2021, 42(18): 188-193. |
| [6] |
罗文俊, 王德禹. 基于兴趣子域动态代理模型的船舶结构可靠性优化[J]. 中国舰船研究, 2021, 16(4): 96-107. LUO Wenjun, WANG Deyu. Reliability-based optimization of ship structure based on interest subdomain dynamic surrogate model[J]. Chinese Journal of Ship Research, 2021, 16(4): 96-107. |
 2023, Vol. 45
2023, Vol. 45
