浅水环境中船舶斜航运动是研究船舶操纵安全的重要课题之一,随着海运石油市场的发展,超大型油轮的靠泊操纵安全问题频出,对沿海海域的航行安全和环境污染带来比较严重的影响。近年来,国内外学者越来越关注浅水效应对超大型油轮的影响。RoyChoudhury等[1]模拟了在深水及浅水水域超大型油轮小漂角稳态运动,对比了深水和浅水稳态运动的水动力特性,分析了船体与螺旋桨、舵之间的相互作用,证明模拟数值是研究船舶水动力操纵性的有效工具。王化明等[2]以超大型油轮模型为模拟对象,设置了不同的水深吃水比,通过水动力值与试验结果的分析对比,发现极浅水域误差较大,其他水深水动力值与试验值相符。牙政谋[3]进行了浅水环境下超大型油轮的旋回性以及停船操纵实验,对比分析旋回进矩与纵向进矩在不同水深下的特性,发现随着水深的减少船舶旋回性能减弱,船舶下沉及纵倾变大,对船舶航行安全有较大的影响。伍海华等[4]通过仿真软件STAR-CCM+模拟了超大型油轮在漂角0°~180°下的黏性绕流,得出船舶在不同漂角下航行的水动力系数,可以发现其水动力系数随漂角的变化规律。
综上所述,在浅水环境中,浅水效应对超大型油轮的影响更加明显。为此,本文以超大型油轮为研究对象,首先开展网格收敛性研究和数值方法验证研究,并在此基础上对超大型油轮在不同水深、不同速度以及不同漂角的斜航运动进行数值模拟。最终对比分析所得水动力系数,研究超大型油轮在浅水环境下的水动力特性。
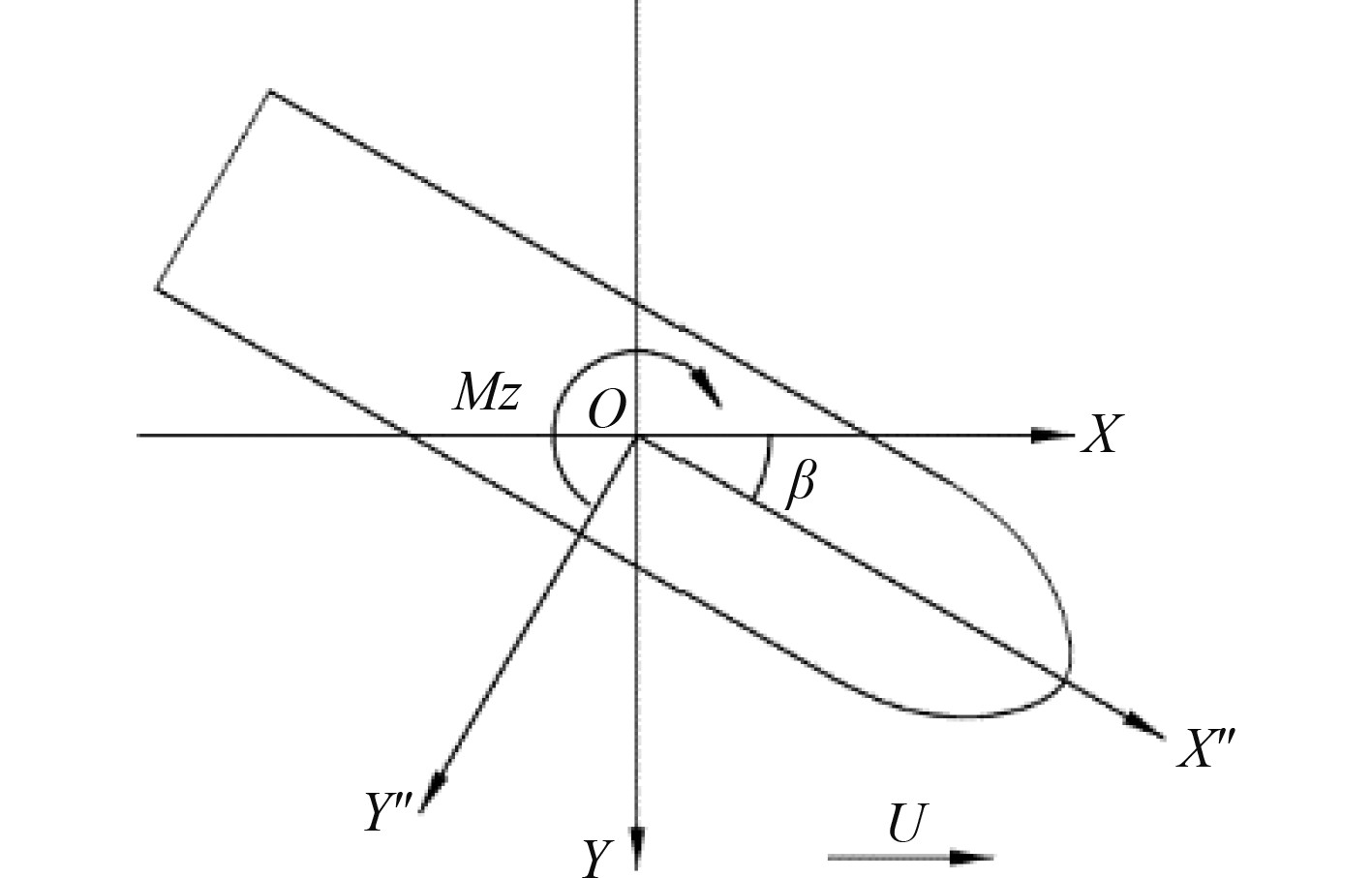
1 模型设置 1.1 坐标系为了便于对船舶运动问题的描述,采用总体坐标系和运动坐标系2套坐标系进行研究模拟,采用右手坐标法则。
运动坐标系:坐标原点是船舶中横剖面、中纵剖面与设计水线面的交点,Ox″轴沿着船长方向指向船首为正向, Oy″轴沿着船宽方向指向右舷为正向。
总体坐标系:坐标原点是与运动坐标系原点位于相同位置,其Ox轴为水平向右为正向,Oy轴为垂直于Ox轴竖直向下为正向。如图1所示,U为船舶航行速度,
|
图 1 坐标系的建立 Fig. 1 The establishment of coordinate system |
本文选取超大型油轮(VLCC)船模为研究对象,对其在深浅水域低速斜航行下的水动力性能进行数值模拟,模型缩尺比例1∶50,且考虑船体下沉和纵倾。超大型油轮船体模型如图2所示,船型参数见表1。

|
图 2 超大型油轮模型 Fig. 2 Geometry of VLCC model |
|
|
表 1 超大型油轮主尺度 Tab.1 Principal dimensions of VLCC |
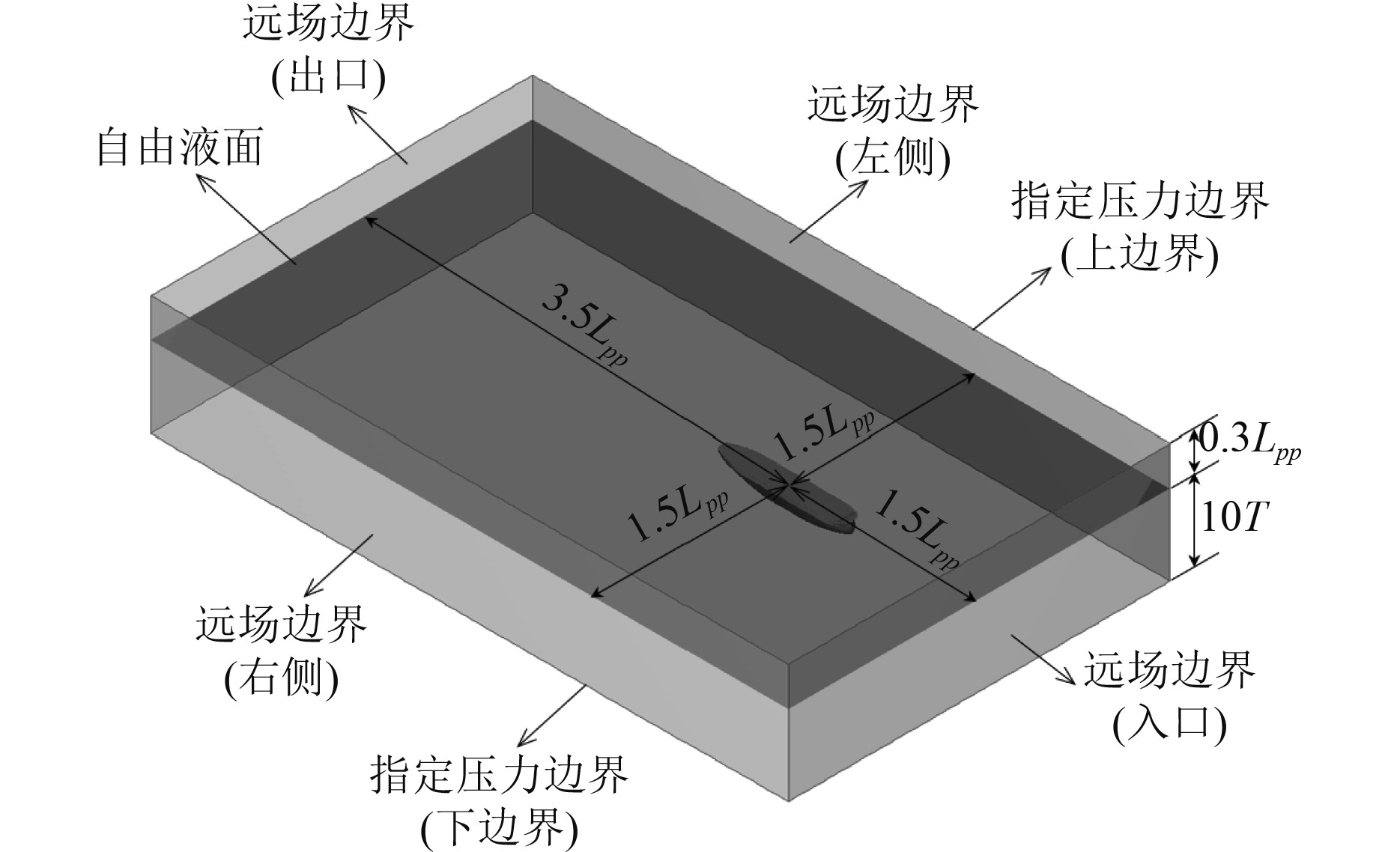
本文计算水域为静水域,考虑自由液面的影响,不同漂角是通过以原点为圆心旋转船体来实现。深水域计算域如图3所示,浅水域计算域如图4所示,设置各个边界条件如下。
|
图 3 深水域计算域与边界条件 Fig. 3 Calculation domain and boundary conditions of deep water area |

|
图 4 浅水域计算域与边界条件 Fig. 4 Calculation domain and boundary conditions of shallow water area |
上边界:指定压力边界,顶部距自由液面0.3Lpp。
下边界:深水域为指定压力边界,底部距自由液面10倍吃水。浅水域为壁函数壁面,底部距自由液面1.2到3倍吃水之间。
左边界:远场边界,左侧距船中1.5Lpp。
右边界:远场边界,右侧距船中1.5Lpp。
前边界:远场边界,距船中1.5Lpp。
后边界:远场边界,距船中3.5Lpp。
1.4 网格划分采用CFD计算软件NUMECA中的网格生成器Hexpress进行网格划分。本文所有计算的网格都采用全六面体非结构网格,对自由液面、船体结构以及周围的网格进行加密。船体网格如图5所示,深水计算域网格数量为116万如图6所示,浅水计算域网格如图7所示。

|
图 5 船体网格 Fig. 5 Hull grid |
|
图 6 深水域网格 Fig. 6 Deep water grid |

|
图 7 浅水域网格 Fig. 7 Shallow water grid |
为了同时考虑计算精度和效率,必须建立合适的网格尺寸和密度,因此对5套不同的网格进行收敛性验证。船体网格与空间域网格的拆分比例保持不变,通过近似为
网格验证工况:计算域水深h=1.5T;船模速度U=0.364 m/s;相应的傅汝德数为Fr=0.045;雷诺数为Re=2.24×106;漂角
|
|
表 2 浅水域网格收敛性验证结果 Tab.2 Verification results of grid convergence in shallow water area |
由韩国海洋工程研究所(Maritime and Ocean Engineering Research Institute,MOERI)设计改进的油轮KVLCC2(The Korean VLCC designed at MOERI)是研究船舶水动力性能的主要船型之一,拥有丰富的船模实验数据。由于本文研究对象为超大型油轮,与KVLCC2船型非常相似,故以该船的实验数据为参考进行方法有效性验证,两船型的主尺度对比见表3。
|
|
表 3 主尺度 Tab.3 Main dimensions |
由于深水域和浅水域的水动力特性不同,分别针对2种水域进行验证。通过模拟实验工况得到数值与实验结果的相对误差进行有效性验证,模拟数值与实验结果相对误差表示为E%D,EFD为试验数值,CFD为数值模拟值。
| $ {E}\mathrm{\%}{D}=\frac{CFD-EFD}{EFD}\times 100{\%}。$ | (1) |
模拟结果和实验结果按照以下公式进行无量纲化处理:
| $ X=\frac{{F}_{x}}{0.5\rho {U}^{2}{L}_{pp}T},$ | (2) |
| $ Y=\frac{{F}_{y}}{0.5\rho {U}^{2}{L}_{pp}T} ,$ | (3) |
| $ N=\frac{{M}_{z}}{0.5\rho {U}^{2}{L}_{pp}^{2}T} 。$ | (4) |
式中:X为阻力系数;Y为横向力系数;N为转首力矩系数;ρ为20° 海水密度。
2.2.1 深水域方法有效性验证深水域方法有效性验证工况参考实验[5]进行数值模型,通过对超大型油轮6个不同傅汝德数的深水直航进行数值模拟,阻力系数数值结果与实验结果如表4所示,曲线如图8所示。
|
|
表 4 深水域方法有效性验证 Tab.4 Validation of deep water method |

|
图 8 深水域阻力系数 Fig. 8 Resistance coefficient in deep water |
通过表4与图8可知,随着速度的增大,阻力系数相对误差值也稍有增加,最大相对误差为1.15%,平均误差小于1%,深水域数值计算得到的阻力系数与实验值非常吻合,所以深水域所采用的数值模拟方法对本文后续的计算有效。
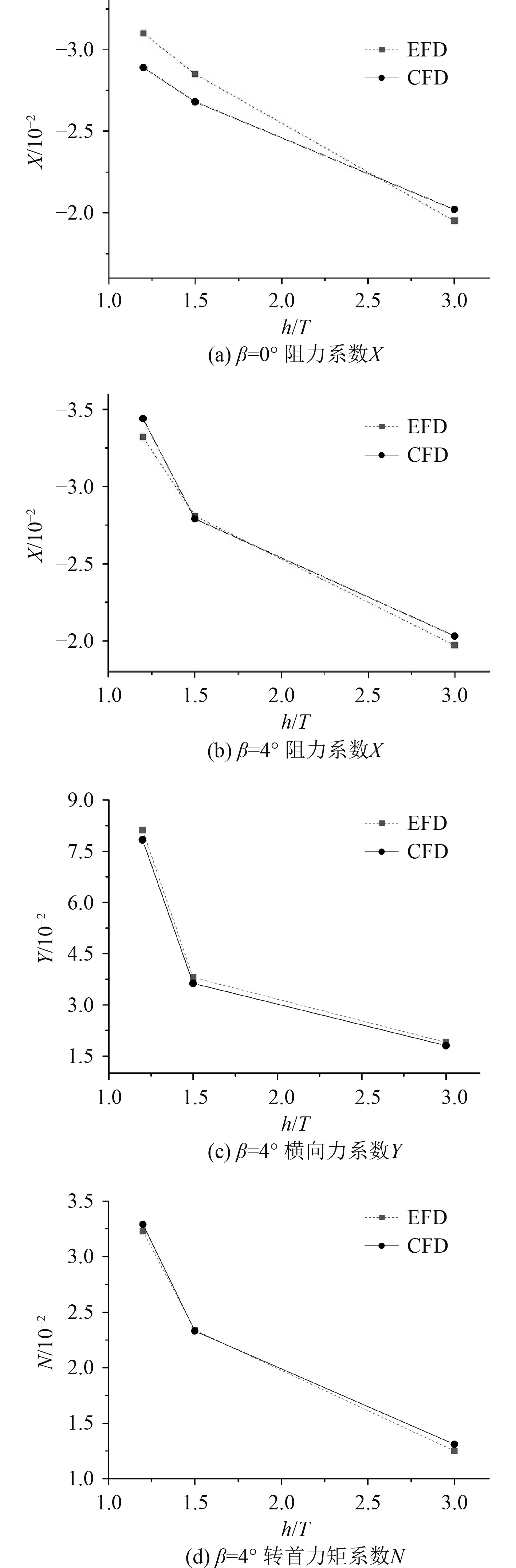
2.2.2 浅水域方法有效性验证浅水域将选取意大利罗马水池的KVLCC2实验数据[6]进行验证,船模速度为U=0.5328 m /s;傅汝德数为Fr=0.0643;漂角为
|
|
表 5 浅水域方法有效性验证 Tab.5 Validation of shallow water method |
|
图 9 浅水域水动力系数 Fig. 9 Hydrodynamic coefficient in shallow water |
由表5可知,浅水域模拟计算数值与实验结果吻合度较好,相对误差均小于5.5%。由图9可知,水动力系数与实验结果的变化趋势基本一致,说明该数值模拟方法对本文后续的浅水域水动力值计算方法可行。
3 数值结果与分析 3.1 计算工况为了研究超大型油轮在不同水深斜航工况下,浅水效应对水动力的影响规律,对超大型油轮在不同速度、不同水深吃水比,以及不同漂角下的船舶水动力数值进行模拟计算。模拟速度为极低速情况:水深吃水比h/T=1.2,1.5,3,10;U=0.364 m/s,0.218 m/s,0.073 m/s;相应的傅汝德数为Fr=0.045,0.027,0.009;雷诺数为Re=2.24×106,1.34×106,4.495×105 。其中,雷诺数Re=4.495×105小于转捩雷诺数Re=5×105,属于层流边界流动,所以本文计算模型采用湍流模型(SST-Menter)和层流(Laminar)模型2种模型模拟计算,计算工况如表6所示。
|
|
表 6 计算工况 Tab.6 Cases of simulation |
通过数值模拟得到3个不同傅汝德数情况下水深对水动力系数的影响。如图10、图11和图12所示,3种傅汝德数的水动力系数变化趋势基本一致。
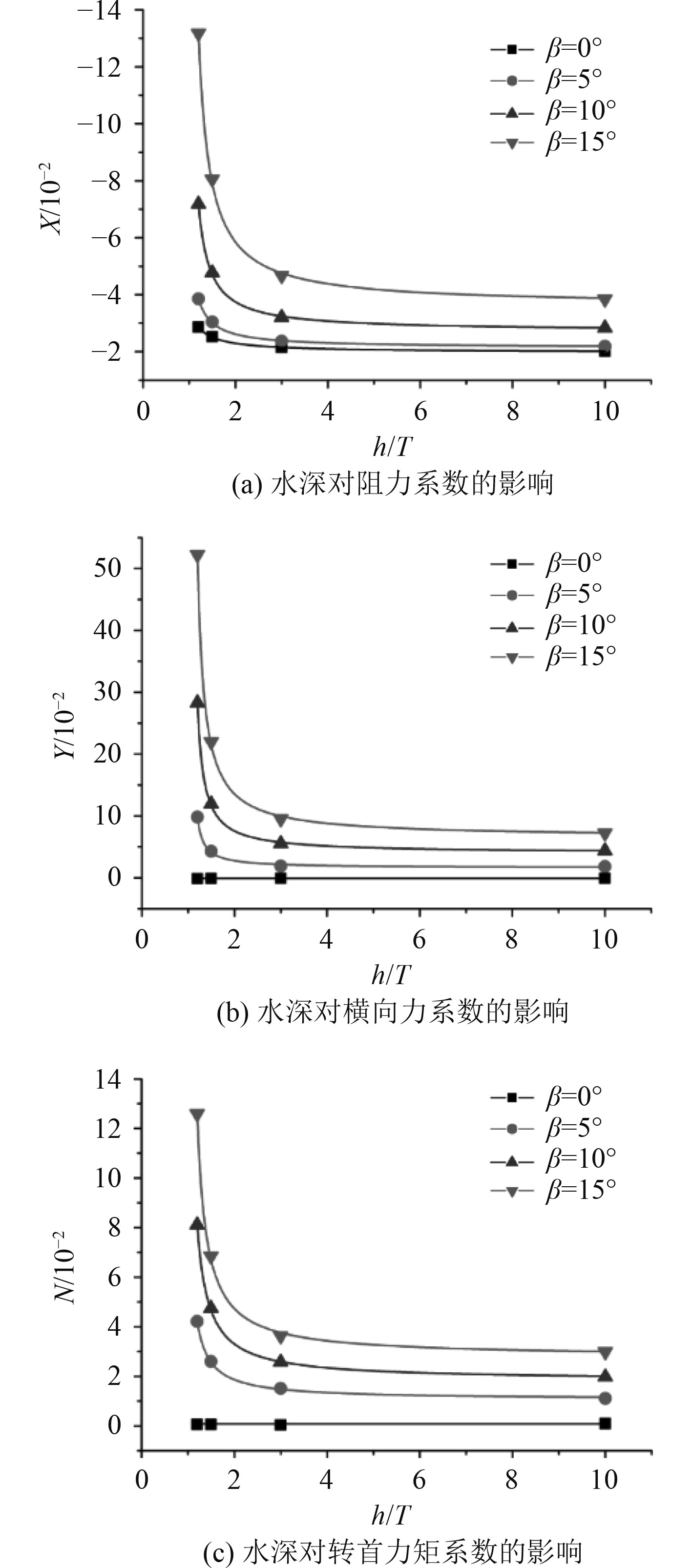
|
图 10 Fr=0.045时水深对水动力系数的影响 Fig. 10 Effect of water depth on hydrodynamic coefficient when Fr = 0.045 |
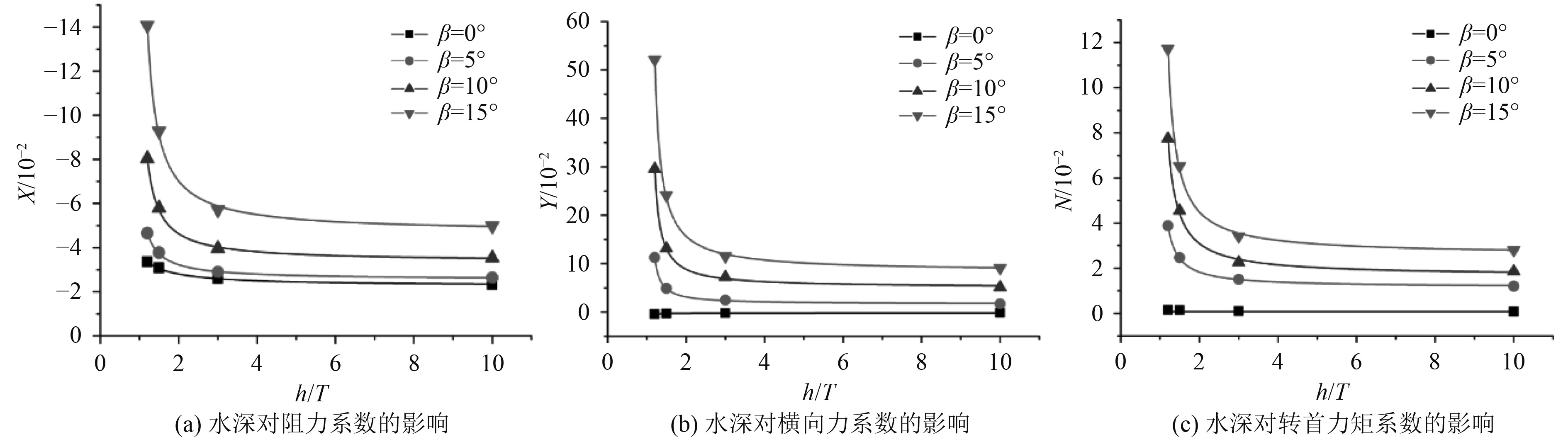
|
图 11 Fr=0.027时水深对水动力系数的影响 Fig. 11 Effect of water depth on hydrodynamic coefficient when Fr = 0.027 |
超大型油轮在不同水深条件下水动力随着漂角的变化规律,0°漂角的水动力系数随着水深的变化很小,由于当水深傅汝德数Frh<0.5时,浅水效应不明显。5°~15°漂角工况下的水动力系数随着水深的减少而增加,并且随着漂角的增大更加明显。由此可见,随着船舶航行角度的变化,浅水效应依旧舶水动力系数有着较大的影响。当水深吃水比大于3时,水动力系数变化较小,以水动力系数变化最大的工况为例,当β=15°,Fr=0.045时,水深从3倍吃水到10倍吃水,阻力系数X仅增大了1.2倍,横向力系数Y增大了1.3倍,转首力矩系数N增大了1.2倍。当水深吃水比小于3时,漂角β=10°,15°的水动力系数显著增加,以β=15°,Fr=0.045为例,水深从3倍吃水到1.2倍吃水,阻力系数X增大了2.8倍,横向力系数Y增大了5.5倍,转首力矩系数N增大了3.5倍。综上所述,在低速斜航环境下,水深对水动力系数依然有较大的影响。
由图13可知,由于本文计算的速度工况较小,水动力系数随着傅汝德数的增大变化不明显。
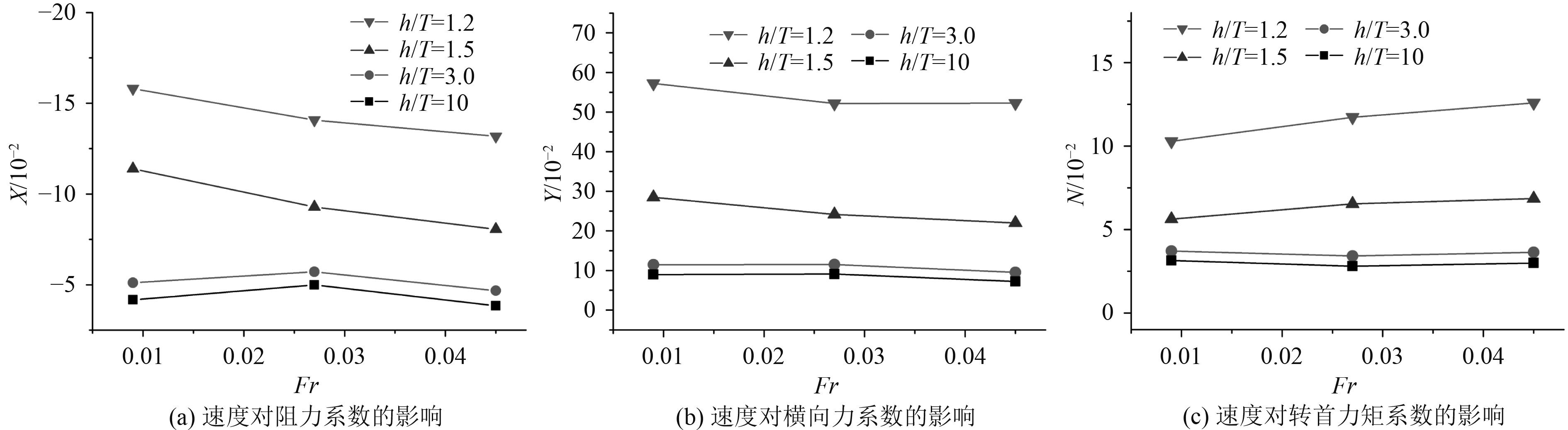
|
图 13 速度对水动力系数的影响 Fig. 13 Effect of speed on hydrodynamic coefficient |
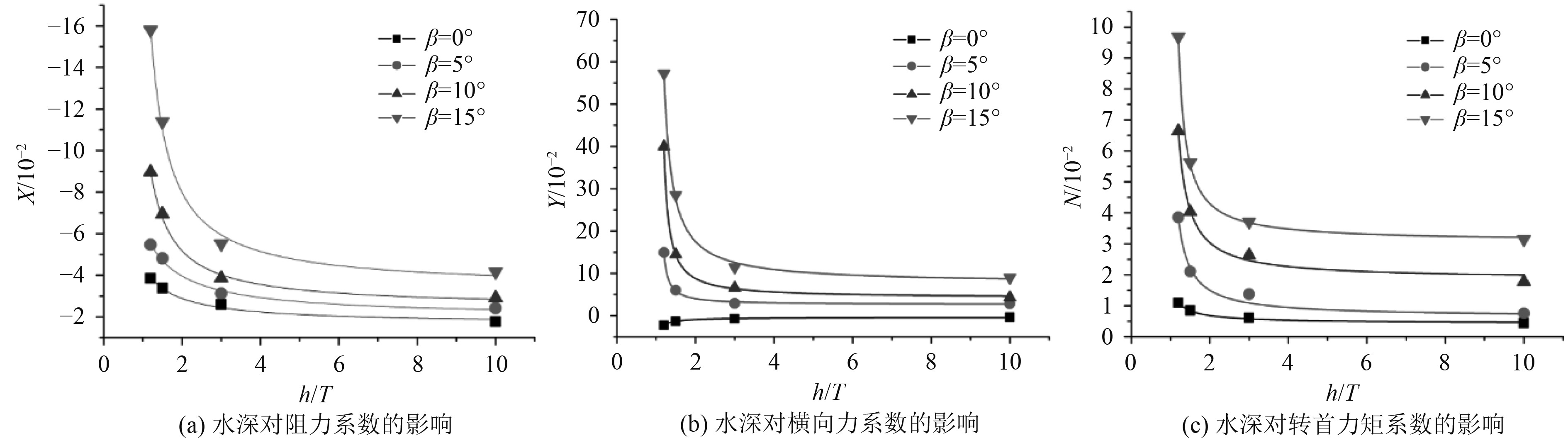
|
图 12 Fr=0.009时水深对水动力系数的影响 Fig. 12 Effect of water depth on hydrodynamic coefficient when Fr = 0.009 |
通过研究可知,不同的速度工况对水动力系数的影响不大,所以以速度U=0.364 m/s,傅汝德数为Fr=0.045的工况进行分析。如图14所示,通过以漂角为横轴,水动力系数为纵轴绘制曲线图。从图中可看出,漂角对水动力系数的影响规律,水动力系数随着漂角的增加均呈现出增大的趋势,随着水深的减小而出现更加明显的变化。
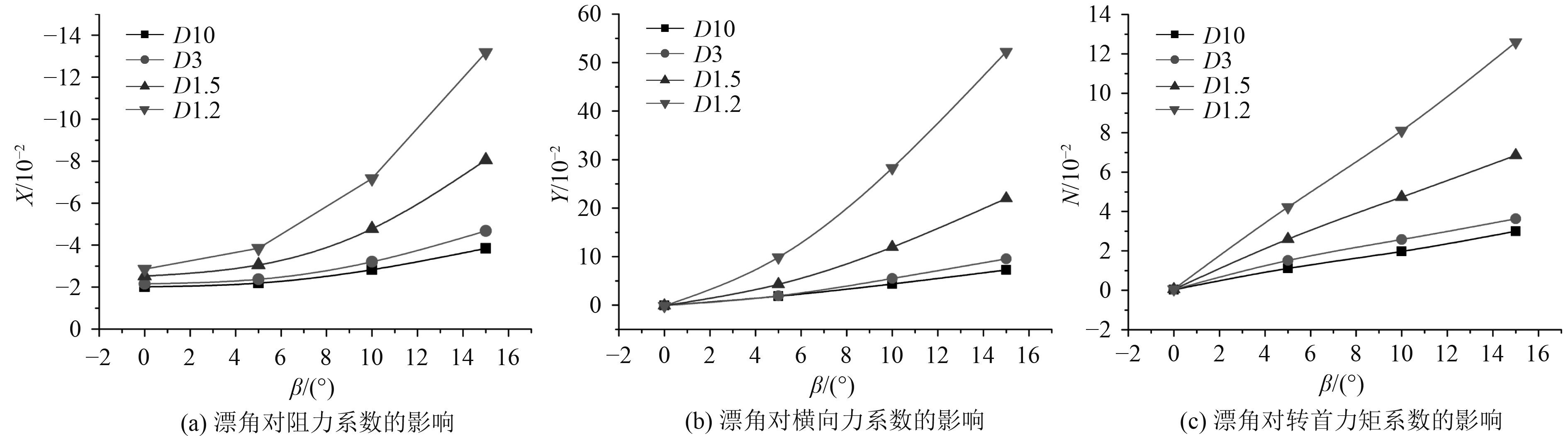
|
图 14 Fr=0.045时漂角对水动力系数的影响 Fig. 14 Effect of drift angle on hydrodynamic coefficient when Fr = 0.045 |
在水深吃水比h/T=10,3工况下,随着漂角的增加,水动力系数以比较小的趋势增加,说明在低速深水环境下,小漂角对水动力系数的影响不大。在水深吃水比h/T=1.5,1.2工况下,水动力系数随着漂角增加有较明显的增大,横向力系数的变化更加明显。综上所述,在低速情况下船舶在浅水水域斜航运动时,水深吃水比大于1.5出现浅水效应。
3.4 船体压力分布图15为水深吃水比h/T=1.2,傅汝德数为Fr=0.045工况下,不同漂角的船体压力分布对比图。图16为

|
图 15 不同漂角下船体压力分布 Fig. 15 Hull pressure distribution under different drift angles |

|
图 16
不同水深下的船体压力分布(
|
本文对超大型油轮模型在不同水深水域进行斜航运动的水动力进行模拟计算。首先,对浅水域分别进行网格收敛性验证,不同水域的网格分别设置了5套网格进行验证,确定了适合的网格密度。其次,对深水域设置了6个傅汝德数的工况,以及对浅水域设计了2个漂角,3种水深的试验工况。结果证明,通过将两者的计算数值与试验结果相对比,验证本文所采用的数值方法对2种水域的有效性。采用该数值方法对超大型油轮船模在4种水深情况下的斜航水动力进行模拟计算,分析了水深、漂角以及速度对船舶水动力系数的影响规律。
可知,在低速情况下浅水效应会受到船舶航行漂角的增大而更加显著,作用于船体的压力由于漂角和浅水效应的作用呈现出不对称性,船舶横向力与转首力矩都因此而产生了变化。超大型船舶在靠港时一般在浅水环境下以低速斜航运动,所以对其浅水环境下的水动力研究及靠泊操纵有一定指导意义。
| [1] |
ROYCHOUDHURY S, DASH A K, NAGARAJAN V, et al. CFD simulations of steady drift and yaw motions in deep and shallow water[J]. Ocean Engineering, 2017, 142: 161-184. DOI:10.1016/j.oceaneng.2017.06.058 |
| [2] |
Wang H, Zou Z, Tian X. Computation of the viscous hydrodynamic forces on a KVLCC2 model moving obliquely in shallow water[J]. Journal of Shanghai Jiaotong University, 2009, 14(2): 241-244. DOI:10.1007/s12204-009-0241-x |
| [3] |
牙政谋. 大型船舶浅水航行安全研究[J]. 中国水运, 2022(2): 117-119. DOI:10.13646/j.cnki.42-1395/u.2022.02.040 |
| [4] |
伍海华, 邹早建. 船舶大漂角斜航运动水动力数值预报[J]. 水动力学研究与进展(A辑), 2019, 34(3): 339-345. DOI:10.16076/j.cnki.cjhd.2019.03.009 |
| [5] |
LARSSON L, A workshop on numerical ship hydrodynamics[J]. Farkostteknik, 2010.
|
| [6] |
TOXOPEUS S L, SIMONSEN C D, GUILMINEAU E, et al. Investigation of water depth and basin wall effects on KVLCC2 in manoeuvring motion using viscous-flow calculations[J]. Journal of Marine Science and Technology, 2013, 18(4).
|
 2023, Vol. 45
2023, Vol. 45
