钝体绕流是自然界和工程领域中的经典流体力学问题,如桥墩、码头、海洋平台支柱、海底管线等。当水流流过钝体时,在钝体尾流中会形成周期性的漩涡脱落,对结构物施加不稳定的载荷并引起振动响应,这一过程将直接影响到结构物的稳定性和安全性。
国内外学者已开展的绕流研究主要针对圆柱及方柱,而对带圆形倒角的柱体研究较少。倒角柱体(倒角半径R+=R/D,其中R为倒圆角半径,D为柱体直径)因表面过渡平顺,其表面流动不会因柱体的几何突变而引起强制分离,从而减小了应力集中[1],降低结构失效的可能性。杜晓庆等[2]研究发现对方柱进行倒角修正能改变其绕流场结构,明显改善方柱的气动性能。Hu等[3]通过PIV、LDV技术研究了Re=2600、6000时倒角半径对柱体尾流流场的影响,研究发现随着倒角半径的增大,柱体截面从方柱过渡到圆柱,柱体后尾流宽度减少约25%。Kumar等[4]运用PIV技术对不同倒角柱体的流场特性进行了研究,发现不同的倒角半径对柱体的尾流形态有显著影响,R+越大,柱体近尾流处的涡脱落越均匀。Abdelhamid等[5]通过数值模拟研究了低雷诺数下(Re=40~180)不同倒角柱体(R+=0.0~0.5)的绕流特性,发现随着R+的增加,漩涡脱落出现的临界雷诺数不断减小。
在实际工程中,柱体/管线通常以不等直径的形式组合出现,如由主圆柱和附属圆柱组成的圆柱系统。当水流流经这样的组合结构时,由于结构之间的相互干扰,其流场形态和受力特性相比于单个结构更为复杂。国内外已有学者对并列不等直径圆柱绕流开展了部分研究工作。Yang等[6]、Dalton等[7]研究了并列圆柱中小圆柱对大圆柱受力特性的影响,研究表明小圆柱的存在能显著影响大圆柱的升阻力系数。Yokoi和Hirao[8]通过实验研究了并列不等直径双圆柱尾流形态随间距比的变化规律,并给出了不同尾流形态下斯特努哈尔数St的变化规律。高洋洋[9]通过PIV实验和数值模拟研究了不同间距比L/D(其中L为两圆柱的中心间距,D为大圆柱直径)下并列布置不等直径双圆柱的绕流特性,研究发现当L/D=1.2时,由于间隙流偏斜的影响,两柱后方形成一宽一窄的尾流;当L/D=2.4和3.6时,观察到两柱后方同相位与反相位脱落的漩涡交替出现。毕贞晓[10]对不等直径并列双圆柱绕流的研究发现:当L/D =1.2时,柱体间的间隙流出现交替偏斜的现象,两柱体后方的尾流形态为偏斜流态;当L/D =1.5时,两柱体间的间隙流偏斜现象消失,后方的尾流形态为双涡脱落流态。张艺鸣等[11]对不同间距比下的并列不等直径双圆柱进行了数值模拟,研究表明当L/D≤3.0时,双圆柱尾流涡相互融合,互扰效应造成斯特劳哈尔数偏低;当L/D>3.0时,两圆柱互扰较弱,圆柱水动力系数与单圆柱结果相差不大。
并列布置下的不等直径倒角柱体在工程领域已有应用,柱体间的互扰效应会对柱体后方尾流流态产生较显著影响,从而导致柱体的受力特性产生变化。虽然针对圆柱在不同排列方式和不等直径方面的研究已取得不少进展,但针对不等直径倒角柱体在并列布置时的尾流流态和受力情况尚未给出。本文采用大涡模拟方法研究3种间距比(L/D=1.2、1.5、2.0)下并列布置的5种倒角体的受力特性、后方瞬时和时均流场的变化规律。
1 计算模型及参数设置 1.1 控制方程在理想情况下,假设流体不可压缩,流体密度不变,温度变化亦可忽略,因此可不考虑能量方程,只考虑连续方程和动量方程,将滤波函数代入得到N-S方程:
| $ \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \frac{{\partial \overline {{u_i}} \overline {{u_j}} }}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \overline p }}{{\partial {x_i}}} + v\frac{{{\partial ^2}\overline {{u_i}} }}{{\partial {x_j}\partial {x_j}}} + \frac{{\partial \overline {{\tau _{ij}}} }}{{\partial {x_j}}},$ | (1) |
| $ \frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0 ,$ | (2) |
令
| $ \overline {{u_i}{u_j}} = \overline {{u_i}} \overline {{u_j}} + \left( {\overline {{u_i}{u_j}} - \overline {{u_i}} \overline {{u_j}} } \right) ,$ | (3) |
| $ \overline {{\tau _{ij}}} = - \left( {\overline {{u_i}{u_j}} - \overline {{u_i}} \overline {{u_j}} } \right)。$ | (4) |
式中,
| $ \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \frac{{\partial \overline {{u_i}} \overline {{u_j}} }}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \overline p }}{{\partial {x_i}}} + v\frac{{{\partial ^2}\overline {{u_i}} }}{{\partial {x_j}\partial {x_j}}} + \frac{{\partial \overline {{\tau _{ij}}} }}{{\partial {x_j}}} 。$ | (5) |
建立亚格子尺度模型(SGS模型)使式(5)封闭,选用Smagorinsky-Lilly模型:
| $ {\tau _{ij}} - \frac{1}{3}{\tau _{kk}}{\delta _{ij}} = - 2{\mu _t}\overline {{S_{ij}}} ,$ | (6) |
式中:
| $ {\mu _t} = \rho {\left( {{C_s}\Delta } \right)^2}\left| {\overline S } \right|,$ | (7) |
| $ \overline {{S_{ij}}} = \frac{1}{2}\left( {\frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} + \frac{{\partial \overline {{u_j}} }}{{\partial {x_i}}}} \right)。$ | (8) |
式中:Δ为滤波尺寸表示为
参照文献[15],本文计算模型和计算域的选取如图1所示。大柱为图中下方柱体,直径D=0.01m;小柱为上方柱体;直径d=0.005m,顺水流方向(x方向)长度为30D,垂直水流方向(y方向) 长度为20D,计算域展向(z方向)高度为πD,左边界为速度入口(velocity-inlet),右边界为自由出流(outflow),两侧为对称边界(symmetry),结构表面为无滑移边界条件(wall)。自由来流速度U0=0.391 m/s,水的运动粘度v =1.003×10−6 m2/s,得到雷诺数Re=U0D/v=3900。计算域网格如图2所示,在柱体周围1.5D范围内采用O型网格设置加密区域,首层网格厚度为0.003D,通过经验公式Y+=0.172×(Δy/D)×Re0.9得到底层网格Y+约为0.88,满足Y+≤1的要求。时间步长设置为ΔtU0/D =0.0391,以满足CFL数小于1[1]。

|
图 1 计算域 Fig. 1 Computational domain |

|
图 2 计算域网格 Fig. 2 Computational mesh |
为验证网格无关性及数值方法的准确性,采用3种不同的网格(A1、A2、A3)对单圆柱绕流进行数值模拟。表1给出了3套网格的设置情况,表2给出了本文与文献的对比结果。可以看出,A2、A3计算的Cd-ave和St结果与其他献的计算结果吻合较好,且A2、A3计算的回流长度与Wornom[16],站庆亮[17]的结果也较为接近。为提高计算效率,本文所有网格设置与A2网格相同。
|
|
表 1 网格设置情况 Tab.1 Detailed grid settings |
|
|
表 2 数值模拟结果验证(Re=3900) Tab.2 Verification of numerical simulations |
并列双圆柱的对比验证工况为Summer[18]的PIV物模实验,间距比L/D=3.0,图3为本文与文献的升力系数频谱图对比结果。可以看出,本文和文献的St数分别为0.219和0.21,St数接近且频谱峰值附近的升力系数波动程度也相当,说明本文的计算模型能很好地反映并列柱体绕流的真实情况,模拟结果与文献结果的一致性表明,本文采用的数值方法具有较高可靠性和准确性。
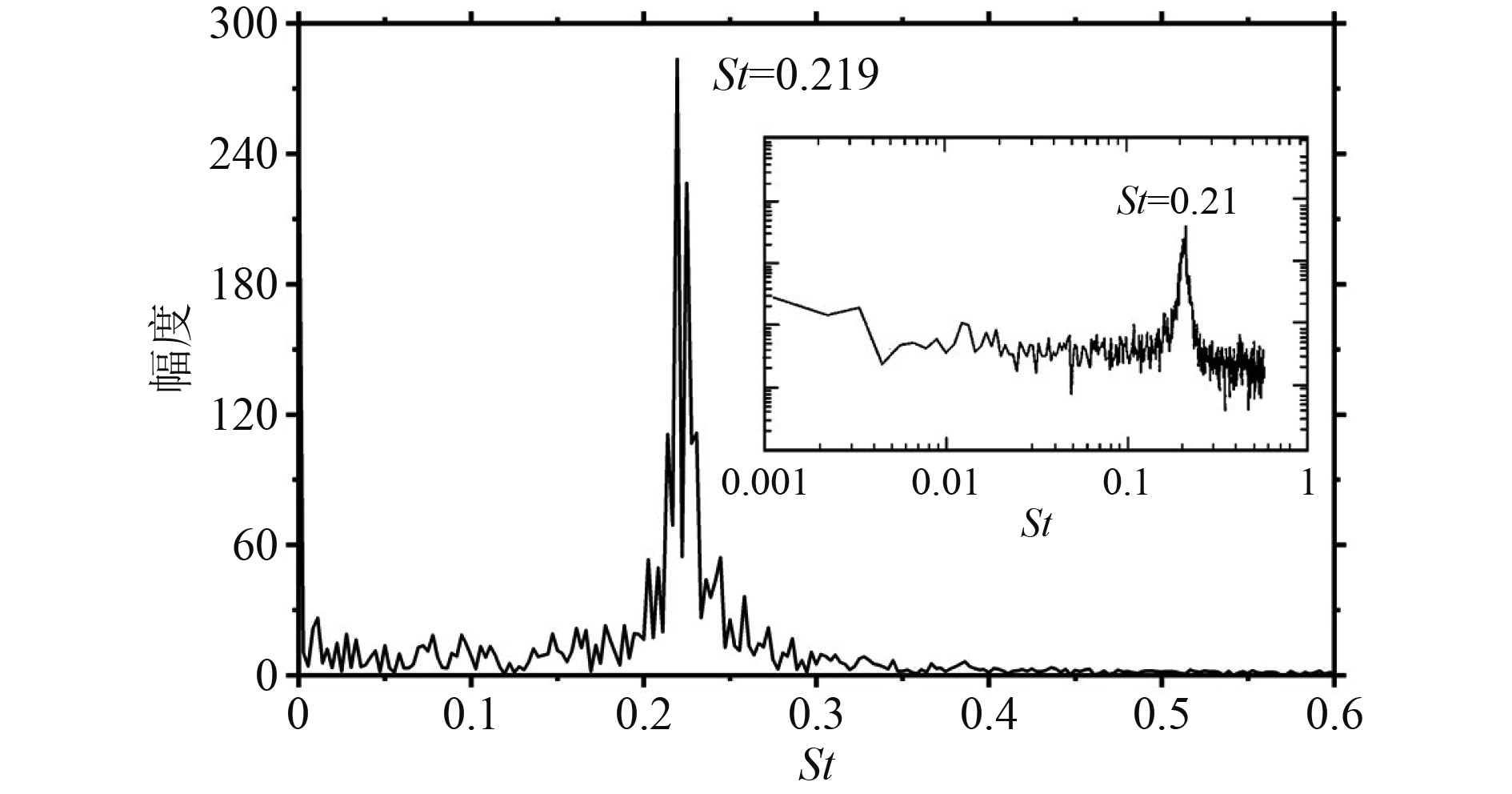
|
图 3 升力系数频谱图对比结果(Re=2200) Fig. 3 Comparison of spectrum of lift coefficient (Re = 2200) |
采用Hunt[21]提出的Q准则来进行表示瞬时流场特性。图4~图6为3种间距比L/D、5种倒角半径R+的两柱体展向截面(Z/D=0.5π)瞬时涡量云图,与大柱相比,小柱由于尺寸较小,其剪切层在沿柱体倒角或柱体截面分离时较为迅速,导致小柱的剪切层流速更大,柱体后方涡街的扰动更强。如图4所示,当L/D=1.2时,剪切层的初始分离均在两柱体前倒角转折处发生,受间隙流偏斜的影响,两柱体内侧分离的剪切层向小柱一侧偏斜。由于2个柱体离得足够近,互扰效应较强,从剪切层分离的漩涡相互混掺,在柱体后方形成较多的细小涡流。与小柱相比,大柱后方脱落的漩涡尺度更大,尾流形态为由大柱主导的偏斜流态。随着R+的增大,偏斜流态的尾流形态变化不大。

|
图 4 L/D=1.2时两柱体瞬时涡量云图(s−1) Fig. 4 Instantaneous vorticity contour of two cylinders at L/D=1.2 (s−1) |
如图5所示,当L/D=1.5,R+=0.1时,两柱内侧分离的剪切层受间隙流偏斜影响向上方偏斜,但由于间距比的增大,互扰效应减弱,剪切层的偏转程度与L/D=1.2时相比有所改善,但偏斜流态的尾流形态并未改变。随着R+增大到0.2,由于柱体表面过渡更平顺,观察到剪切层受间隙流的影响减弱,两柱体从前倒角转折处分离的剪切层几乎与自由流平行,尾流形态由偏斜流态向双涡脱落流态过渡,表明倒角变化能改善柱体剪切层的分离发展。

|
图 5 L/D=1.5时两柱体瞬时涡量云图(s−1) Fig. 5 Instantaneous vorticity contour of two cylinders at L/D=1.5 (s−1) |
如图6所示,随着L/D的进一步增大,当L/D=2.0时,两柱体分离的剪切层保持平行一同向下游发展,从剪切层分离的漩涡相互作用较弱,尾流形态为平行双涡脱落流态,但两柱的涡脱并不同步。这是因为小柱的涡脱落速度比大柱快,且涡脱落的尺度比大柱小,从而导致了大小柱尾流同相位涡脱落存在相位差。随着R+的增大,双涡脱落流态的尾流形态变化不大。
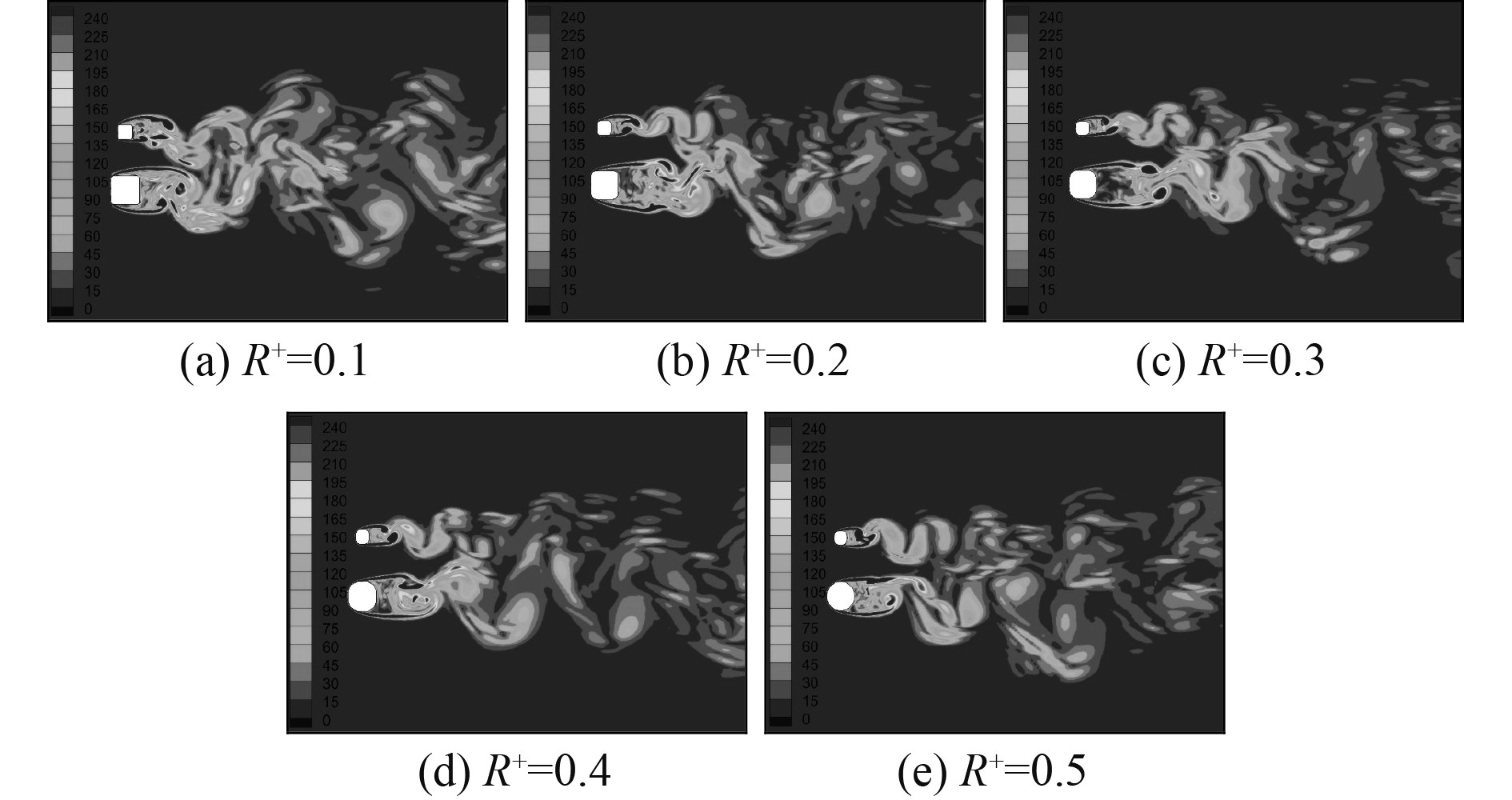
|
图 6 L/D=2.0时两柱体瞬时涡量云图(s−1) Fig. 6 Instantaneous vorticity contour of two cylinders at L/D=2.0 (s−1) |
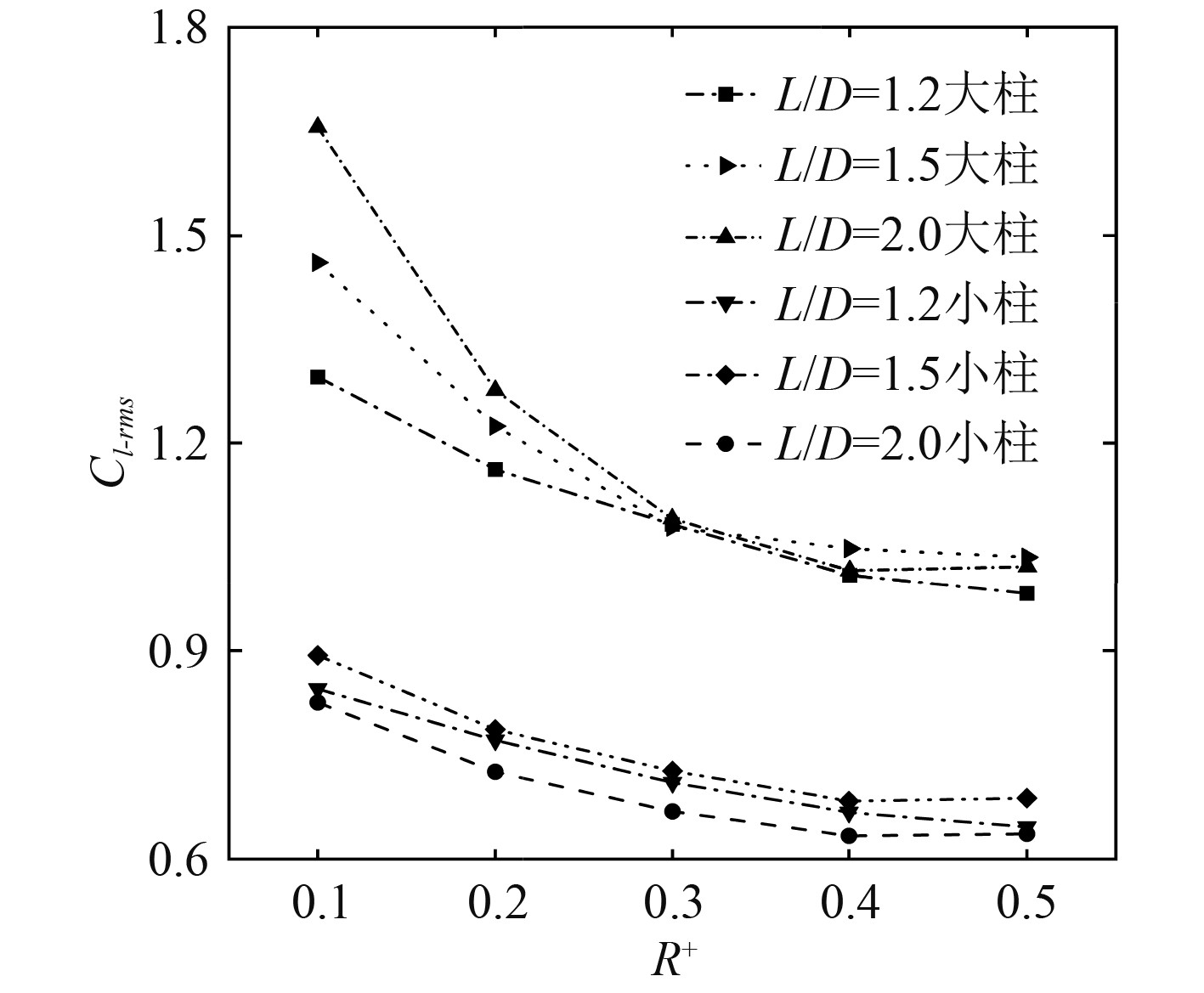
图7~图9分别给出了两柱体平均阻力系数Cd-ave、升力系数均方根Cl-rms和斯特劳哈尔数St随R+的变化曲线。由图7可看出,对于所研究的3种间距比,当R+从0.1增加到0.4时,大柱的Cl-rms均逐渐减小,到R+=0.4时达到最小值,最大降幅为92.3%,而当R+从0.4增加到0.5时,大柱的Cl-rms逐渐增大。随着R+的增加,小柱的Cl-rms呈现出先减小后增大的趋势。
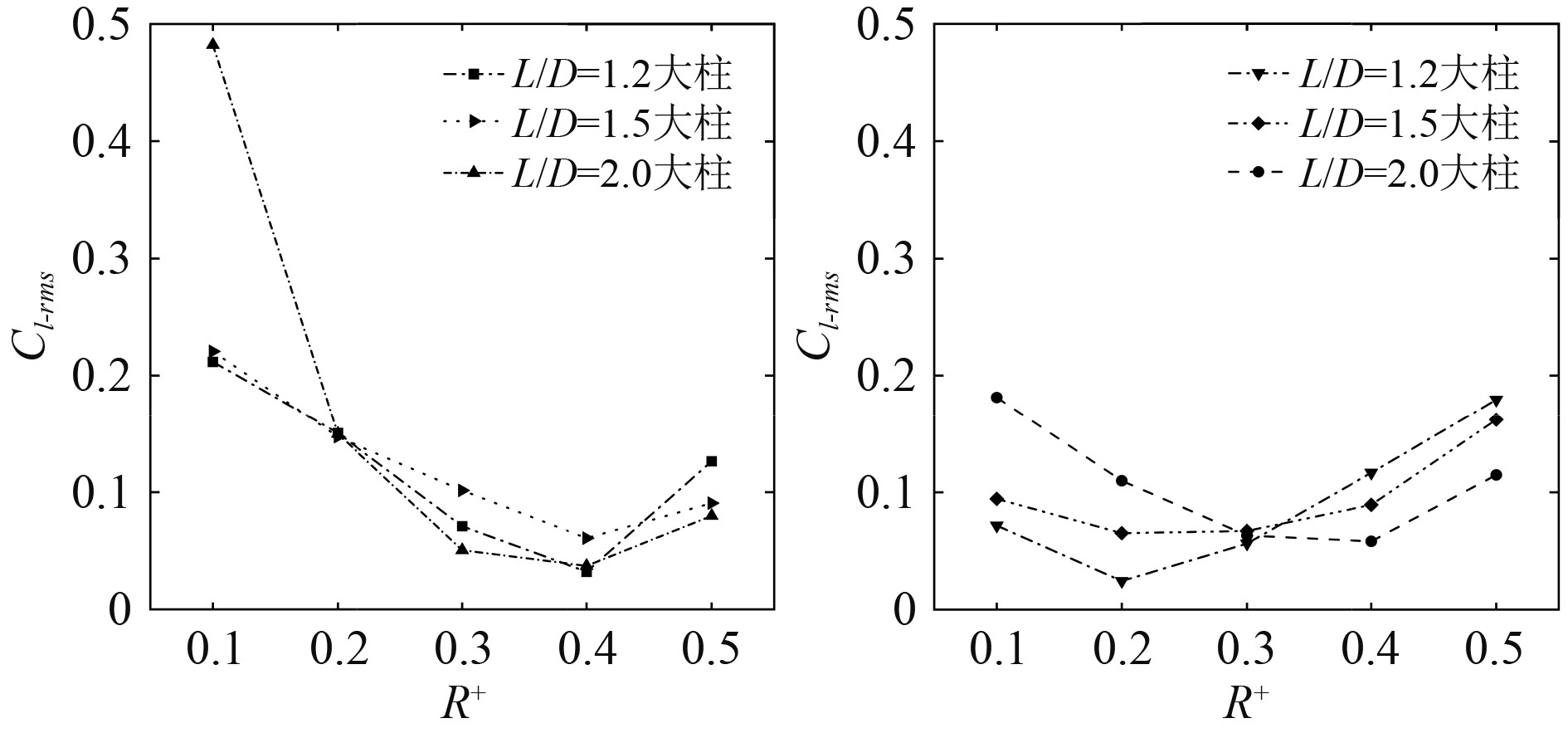
|
图 7 两柱体升力系数均方根 Fig. 7 Root mean square of lift coefficient of two cylinders |
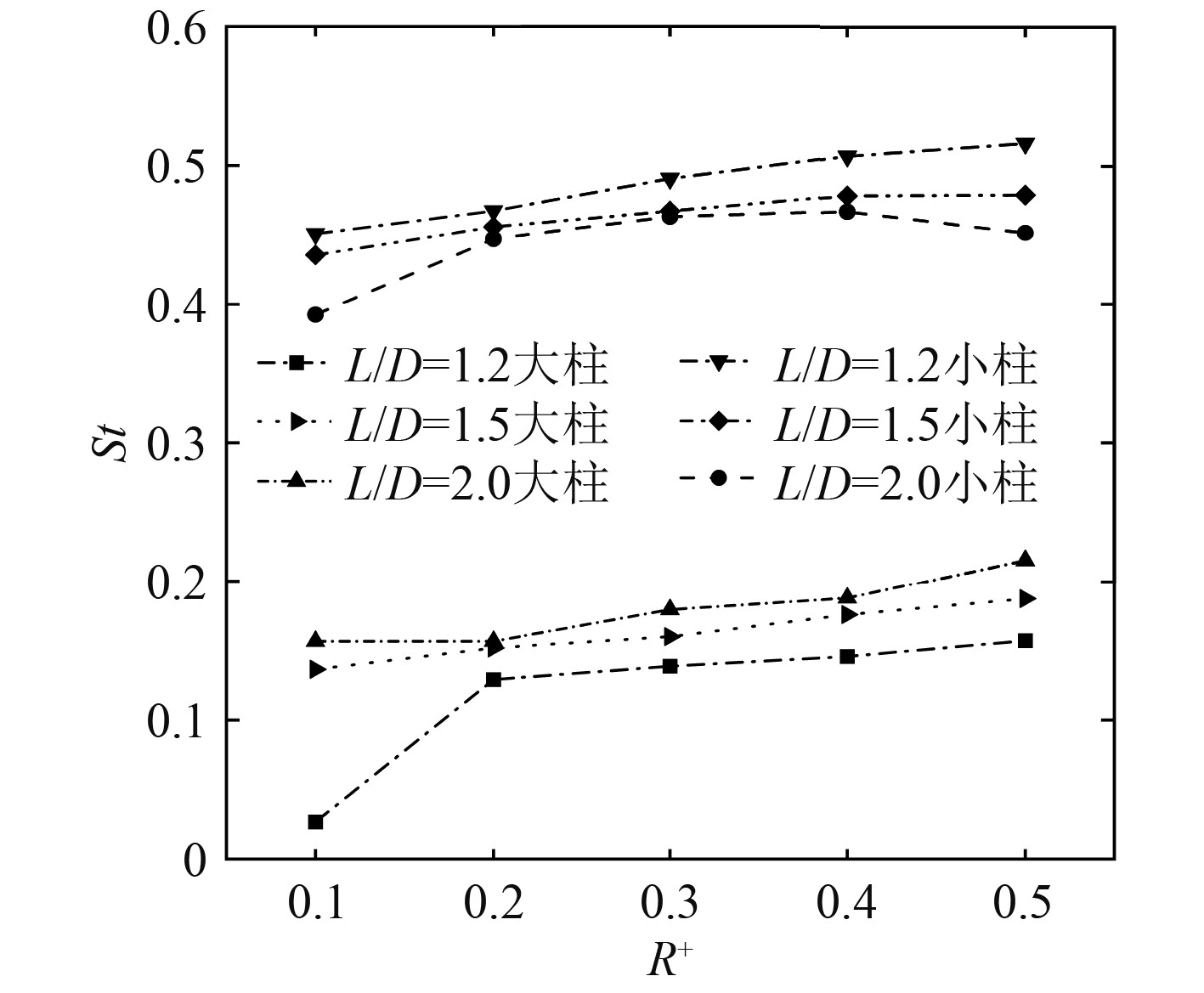
|
图 9 两柱体斯特劳哈尔数 Fig. 9 Strouhal number of two cylinders |
由图8可看出,大柱的Cd-ave明显大于小柱。对于所研究的3种间距比,当倒角半径R+从0.1增加到0.4时,大柱和小柱的Cd-ave均逐渐减小,且L/D越大,大柱的Cd-ave降幅越大,最大降幅为38.6%;当R+从0.4增加到0.5时,Cd-ave变化不大。当L/D=1.2和1.5时,由于互扰效应,脱落涡之间的强烈干扰,观察到两柱体涡脱落频率存在多个极值,此时选取峰值响应对应的涡脱频率计算St。如图9所示,小柱的St明显大于大柱,当L/D相同时,随着R+的增大,大柱、小柱的St均逐渐增大,表明倒角变化对柱体后方的涡脱落频率有较大影响;同时当R+相同时,随着L/D的增大,小柱的St逐渐减小,大柱的St逐渐增大。
|
图 8 两柱体平均阻力系数 Fig. 8 Averaged drag coefficient of two cylinders |
为更好获取两柱体下游的流速,参照文献[17],两柱体下游监测线布置见图10,截取展向Z=πD/2面,以两柱体中心处作为x/D=0的位置,设置6条横流向监测线,分别为x/D=0.58、1.06、1.54、2.02、3.0和5.0,在各圆柱尾流充分发展后开始进行时均统计,共统计约30个涡脱落周期,得到不同x/D处的顺流向及横流向速度分布。

|
图 10 两柱体下游监测线布置 Fig. 10 Layout of monitoring lines downstream of two cylinders |
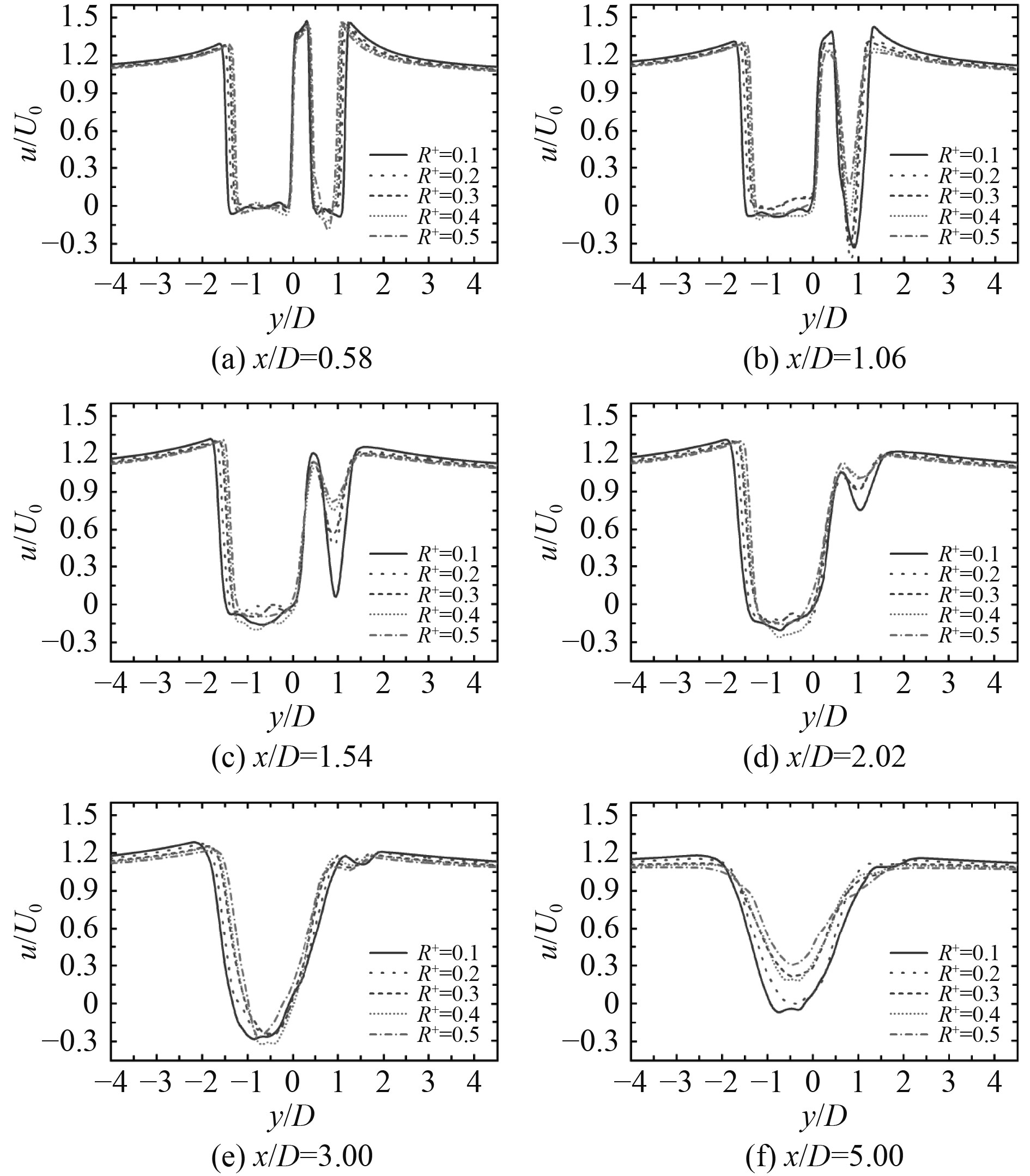
图11给出了L/D=1.2时,不同x/D条件下顺流向的时均速度曲线,两柱体在其中心线处的顺流向速度分布差异较大。如图11(a)~图11(e)所示,近尾迹处(0.58≤x/D≤3.0)各倒角下大柱尾流的顺流向时均流速分布差距不大,因此可认为倒角变化对大柱后方近尾迹以内的流场影响程度很小。从图11(c)可看出,随着R+的增大,小柱后方近尾迹处的顺流向速度曲线下切深度明显减少,表明倒角变化对小柱下游的流场影响程度较大。当0.58≤x/D≤1.06时,两柱体后方产生的漩涡被剪切层包裹而互不干扰,因此观察到大柱和小柱尾流的时均速度分别呈独立“深U型”和“深V型”分布;随着监测线离柱体越来越远,当1.06<x/D<3时,由于尾流宽度逐渐变窄,大柱尾流的时均速度向“深V型”发展,此时从两柱各自剪切层分离的漩涡相互混掺,小柱尾流的时均速度向“浅V型”分布发展;当x/D≥3.0时,顺流向时均速度呈现“单V型”分布,表明尾流的时均速度分布受大柱主导。
|
图 11 不同x/D条件下顺流向时均速度(L/D=1.2) Fig. 11 Time-averaged velocity in the streamwise direction with diffierent x/D (L/D=1.2) |
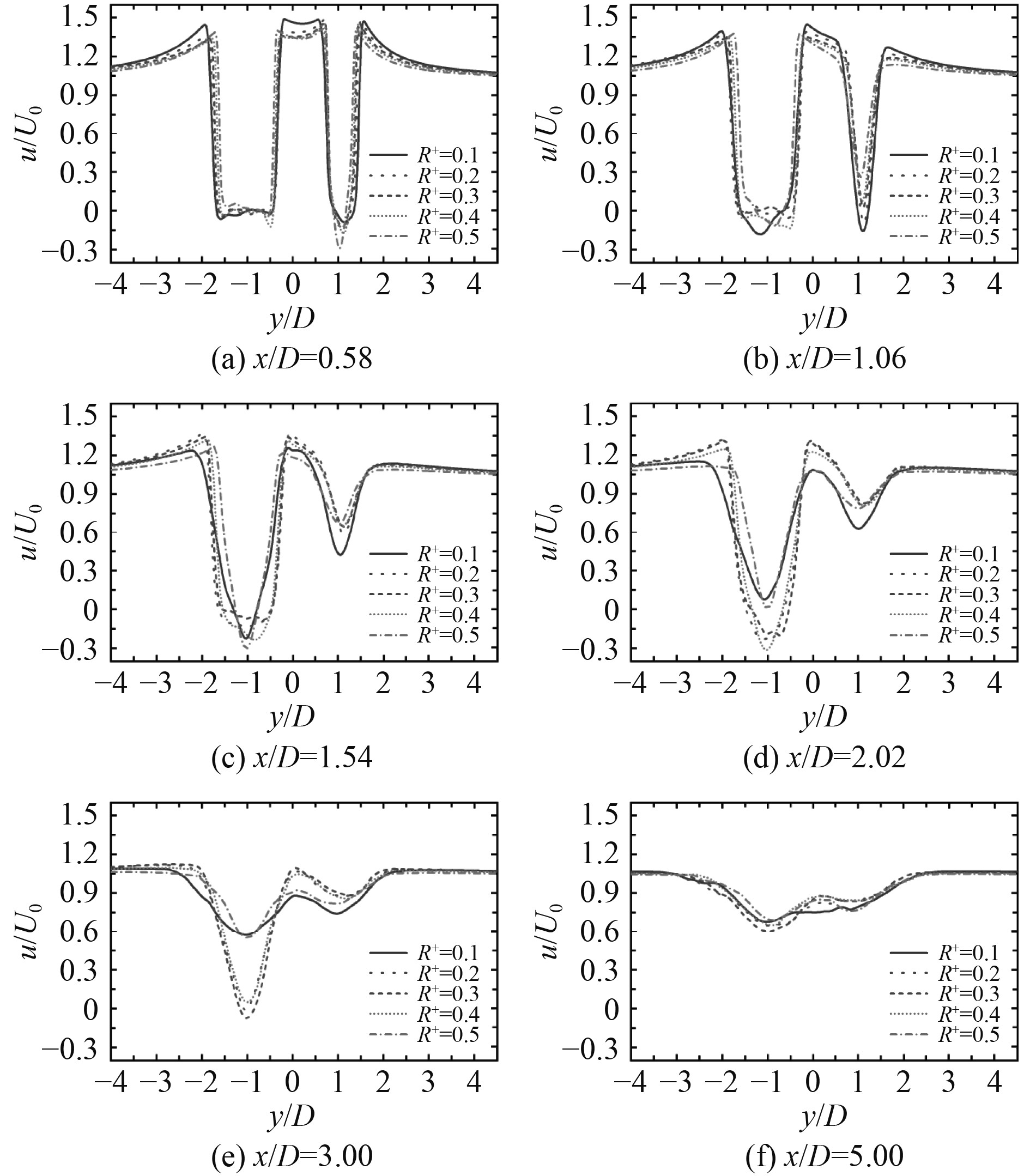
图12和图13分别给出了L/D=1.5和L/D=2.0时,不同x/D条件下顺流向的时均速度,L/D=1.5时柱体下游时均速度分布与L/D=2.0时基本相同。当0.58≤x/D≤1.06时,两柱体后方产生的漩涡被剪切层包裹而互不干扰,大柱后方顺流向时均速度呈“深U型”分布,小柱后方顺流向时均速度呈“深V型”分布;当1.06<x/D<3时,两柱后方的顺流向时均速度均向“浅双V型”分布过渡;当x/D≥3.0时,两柱后方的顺流向时均速度为“浅双V型”分布,与L/D=1.2时的“单V型”分布不同。这是因为随着间距比的增大,大柱与小柱之间的互扰效应减弱,尾流的时均速度分布受大柱和小柱共同主导。

|
图 12 不同x/D条件下顺流向时均速度(L/D=1.5) Fig. 12 Time-averaged velocity in the streamwise direction with diffierent x/D (L/D=1.5) |
|
图 13 不同x/D条件下顺流向时均速度(L/D=2.0) Fig. 13 Time-averaged velocity in the streamwise direction with diffierent x/D (L/D=2.0) |
本文采用大涡模拟方法研究雷诺数Re=3900、3种间距比L/D、5种倒角半径R+并列布置不等直径三维柱体受力特性、后方瞬时和时均流场的变化规律,主要结论如下:
1)倒角变化能改善柱体剪切层的分离发展,同时减小柱体所受的阻力和升力。随着R+的增大,3种间距比下大柱的Cd-ave和Cl-rms总体都呈现出减小的趋势,最优工况出现在R+=0.4,最大降幅分别为38.6%和92.3%。
2)L/D变化对柱体后方尾流形态有显著影响。当L/D=1.2时,由于间隙流偏斜的影响,各R+下两柱体后方的尾流形态均为由大柱主导的偏斜流态;当L/D=1.5时,随着R+的增大,并列两柱后方的尾流形态由偏斜流态向双涡脱落流态过渡;当L/D=2.0时,各R+下两柱体尾流形态均为平双涡脱落流态。
3)L/D变化对柱体后方流场有较大影响。当L/D=1.2时,并列柱体后方顺流向时均速度分布由“深UV型”到“单V型”过渡;当L/D=1.5和2.0时,并列两柱后方顺流向时均速度分布由“深UV型”向“浅双V型”过渡。
| [1] |
于定勇, 赵建豪, 黄东燕, 等. 不同倒角半径柱体绕流数值模拟及水动力特性分析[J]. 海洋工程, 2018, 36(5): 1-11. DOI:10.16483/j.issn.1005-9865.2018.05.001 |
| [2] |
杜晓庆, 刘延泰, 施定军, 等. 低雷诺数下类方柱绕流的数值模拟研究[J]. 重庆交通大学学报(自然科学版), 2020, 39(5): 49-57. |
| [3] |
HU J C, ZHOU Y, DALTON C. Effects of the corner radius on the near wake of a square prism[J]. Experiments in Fluids, 2006, 40(1): 106-118. DOI:10.1007/s00348-005-0052-2 |
| [4] |
KUMAR R A, SOHN C H, GOWDA B H L. Influence of corner radius on the near wake structure of a transversely oscillating square cylinder[J]. Journal of Mechanical Science and Technology, 2009, 23(9): 2390-2416. DOI:10.1007/s12206-009-0630-y |
| [5] |
ABDELHAMID T, ALAM M M, ISLAM M. Heat transfer and flow around cylinder: Effect of corner radius and Reynolds number[J]. International Journal of Heat and Mass Transfer, 2021, 171: 121105. DOI:10.1016/j.ijheatmasstransfer.2021.121105 |
| [6] |
YANG K, CHENG L, AN H, et al. The effect of a piggyback cylinder on the flow characteristics in oscillatory flow[J]. Ocean Engineering, 2013, 62: 45-55. DOI:10.1016/j.oceaneng.2013.01.017 |
| [7] |
DALTON C, XU Y, OWEN J C. The suppression of lift on a circular cylinder due to vortex shielding at moderate Reynolds number[J]. Journal of Fluids and Structures, 2001, 15 (3−4).
|
| [8] |
YOKOI Y, HIRAO K. Vortex shedding and vortex formation from a pair of in-line forced oscillating parallel arranged two circular cylinders[J]. Journal of Fluid and Science and Technology, 2009(4): 401-14. DOI:10.1299/jfst.4.401 |
| [9] |
高洋洋. 多柱体系统静止绕流与涡激振动的试验及数值研究[D]. 青岛: 中国海洋大学, 2011.
|
| [10] |
毕贞晓. 不等直径并列双圆柱绕流的受力分析和湍流特性研究[D]. 上海: 上海应用技术学院, 2015.
|
| [11] |
张艺鸣, 罗良, 陈威等. 不等直径并列双圆柱绕流数值模拟研究[J]. 舰船科学技术, 2021, 43(9): 48-52. DOI:10.3404/j.issn.1672-7649.2021.05.010 |
| [12] |
SMAGORINSKY J. General circulation experiments with the primitive equations: I. The basic experiment[J]. Mon. Wea. Rev. 1963, 91.
|
| [13] |
贾晓荷. 单圆柱及双圆柱绕流的大涡模拟[D]. 上海: 上海交通大学, 2008.
|
| [14] |
郭雷. 斜侧体三体船阻力计算及构型研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.
|
| [15] |
于定勇, 康骁, 赵建, 豪. 不同倒角半径四柱体绕流数值模拟及水动力特性分析[J]. 海洋工程, 2021, 39(1): 1-11. DOI:10.16483/j.issn.1005-9865.2021.01.001 |
| [16] |
WORNOM S, OUVRARD H, SALVETTI M V, et al. Variational multiscale large-eddy simulations of the flow past a circular cylinder: Reynolds number effects[J]. Computers and Fluids, 2011, 47(1): 44-50. DOI:10.1016/j.compfluid.2011.02.011 |
| [17] |
战庆亮, 周志勇, 葛耀君. Re=3900圆柱绕流的三维大涡模拟[J]. 哈尔滨工业大学学报, 2015, 47(12): 75-79. |
| [18] |
SUMNER D, WONG S S T, PRICE S J, et al. Fluid behavior of side-by-side circular cylinders in steady cross-flow[J]. Journal of Fluids and Structures, 1999, 13(3): 309-338. DOI:10.1006/jfls.1999.0205 |
| [19] |
LYSENKO D A, Ertesvåg I S, Rian K E. Large-Eddy Simulation of the Flow Over a Circular Cylinder at Reynolds Number 3900 Using the OpenFOAM Toolbox[J]. Flow Turbulence & Combustion, 2012, 89(4): 491-518. |
| [20] |
LOURENCO L M, SHIT C. Characteristics of the plan turbulent near wake of a circular cylinder: A partical image velocimetry study[R]. Private Communication, 1993.
|
| [21] |
HUNT J C R, WRAY A A, MOIN P. Eddies, streams, and convergence zones in turbulent flows [J]. Center for Turbulence Research CTR-S 88, 1988.
|
 2023, Vol. 45
2023, Vol. 45

