随着近代科技的发展,海军作战装备有了质的提升。在海军作战中,舰艇承担了主要进攻任务,同时也是受到攻击的主要目标,因此如何提升舰船的防护性能是现代舰船设计的重要考量因素。在舰船内部通常有储存液体的舱室,并且这些液体是保证舰船正常航行的重要物质基础,所以需要对液舱结构进行优化以防止其受到冲击损伤。
复合多层异质结构普遍应用于现代结构防护性能的优化技术中,主要有2种或以上的材料混合而成。近年来,许多学者对多层板和夹层板的抗侵彻性能进行了研究,并得出一些重要结论。肖新科等[1]研究了接触式双层钢靶板和间隙式双层钢靶板的抗侵彻性能,得出接触式双层钢靶板具有更大的弹道极限,而间隙式双层钢靶板抗侵彻性能具有较大分散性。李金柱等[2]通过对环氧树脂玻璃钢-聚氨酯泡沫夹层复合材料的抗侵彻性能进行研究,并讨论了这2种材料对抗侵彻性能的影响。蔡铉龙等[3]通过对不同弹体侵彻钢/尼龙夹层板得到其弹道极限,从而得出钢/尼龙夹层板的抗侵彻性能。焦凯等[4]研究了聚氨酯钢夹层板的抗侵彻性能,并同时讨论了其损伤和破坏机理。张伟等[5]进行了弹丸高速撞击容器的实验,分析了容器的穿孔和裂纹失稳破裂的界限。Xue Bing等[6]基于SPH-FEM方法,进行了面板厚度对金字塔网格结构抗水下冲击性能的影响研究。张志春等[7]基于SPH-FEM耦合法研究了30CrMnSiA钢板受到弹体冲击,并分析其破坏模式。柳春等[8]基于FEM-SPH耦合法研究落石冲击钢筋混泥土的过程。卞梁等[9]研究了钨合金长杆弹体冲击陶瓷复合靶,并采用了陶瓷和金属材料的本构模型。
本文采用SPH-FEM耦合法,通过使用Ls-dyna算法对泡沫铝夹层板进行抗侵彻的研究,利用SPH无网格的特性处理泡沫铝软质材料在大变形情况下出现负体积问题。通过数值仿真得出其弹道极限和变形损伤,将数值结果和实验结果进行对比分析其抗侵彻性能。
1 SPH-FEM理论 1.1 SPH方法介绍SPH全称为光滑粒子流体动力学,主要用来处理计算流体力学,近年来被广泛用于解决大变形、高速冲击等问题。由于采用有限元FEM方法时产生的大变形容易使得结构出现负体积从而使计算停止,因此运用SPH法在处理侵彻靶板时产生的大变形问题有巨大优势。
1.2 SPH基本原理光滑粒子流体动力学(SPH)为无网格粒子法,其核函数近似方程为[10]:
| $ < f(r) > = \int\limits_\varOmega {f({r'})} W(r - {r'},h){\rm{d}}{r'} 。$ | (1) |
式中:
式(2)为粒子近似方程,如下:
| $ < \nabla \cdot f({x_i}) > = \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}f({x_j}) \cdot {\nabla _i}{W_{ij}}}。$ | (2) |
式中:f(xi)为粒子i的近似值;N为紧支域中的粒子数量;mj和
| $ \left\{ \begin{aligned} & 1 - \frac{3}{2}{m^2} + \frac{3}{4}{m^3} \quad |m| < 1,\\ &\frac{1}{4}{(2 - m)^3} \qquad\quad 1 \leqslant |m| \leqslant 2,\\ & 0 \qquad\quad\qquad\qquad |m| < 2 。\end{aligned} \right. $ | (3) |
在计算过程中需要满足质量守恒、动量守恒和能量守恒,保证计算结果的有效性,其形式分别为:
| $ \frac{{{\rm{d}}{\rho _i}}}{{{\rm{d}}t}} = {\rho _i}\sum\limits_{j = 1}^N {{m_j} \cdot v_{ij}^b\frac{{\partial {W_{ij}}}}{{\partial x_i^b}}} ,$ | (4) |
| $ \frac{{{\rm{d}}v_i^a}}{{{\rm{d}}t}} = - \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}\left(\frac{{\sigma _i^{ab} + \sigma _j^{ab}}}{{{\rho _i}}} + {\prod _{ij}}\right)\frac{{\partial {W_{ij}}}}{{\partial x_i^b}}},$ | (5) |
| $ \frac{{{\rm{d}}{e_i}}}{{{\rm{d}}t}} = \frac{1}{2}\sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}\left(\frac{{\sigma _i^{ab} + \sigma _j^{ab}}}{{{\rho _i}}} + {\prod _{ij}}\right)} v_{ij}^b\frac{{\partial {W_{ij}}}}{{\partial x_i^b}} 。$ | (6) |
式中:v表示速度;e表示能量;t表示时间;a,b分别表示坐标轴方向。
1.3 SPH-FEM耦合理论对于SPH-FEM再计算的耦合过程中,在SPH粒子附近界面的近似半径以内,根据位置和离散模式不同,采用了不同的近似方法。对于靠近耦合界面的粒子,将支持域中的FE节点作为背景粒子的方式加入到求和中。对于远离耦合边界采用纯SPH粒子形式,对于有限元则采用纯有限元形式,以下分别为SPH,FEM和SPH-FEM 3种近似公式[12]。
| $ < f({x_i}) > = \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}f({x_{ij}}){W_{ij}}} ,$ | (7) |
| $ < f(x) > = \sum\limits_i {{N_i}(x)f({x_i})},$ | (8) |
| $ < f({x_i}) > = \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}f({x_j}){W_{ij}} + \sum\limits_{j = 1}^{{N_b}} {\frac{{{m_{bj}}}}{{{\rho _{bj}}}}f({x_j}){W_{ij}}} }。$ | (9) |
式(7)为纯SPH粒子方程,式(8)为纯有限元方程,式(9)为SPH-FEM耦合方程。式中:

|
图 1 SPH-FEM耦合过程流程图 Fig. 1 Shows the flow chart of SPH-FEM coupling process |
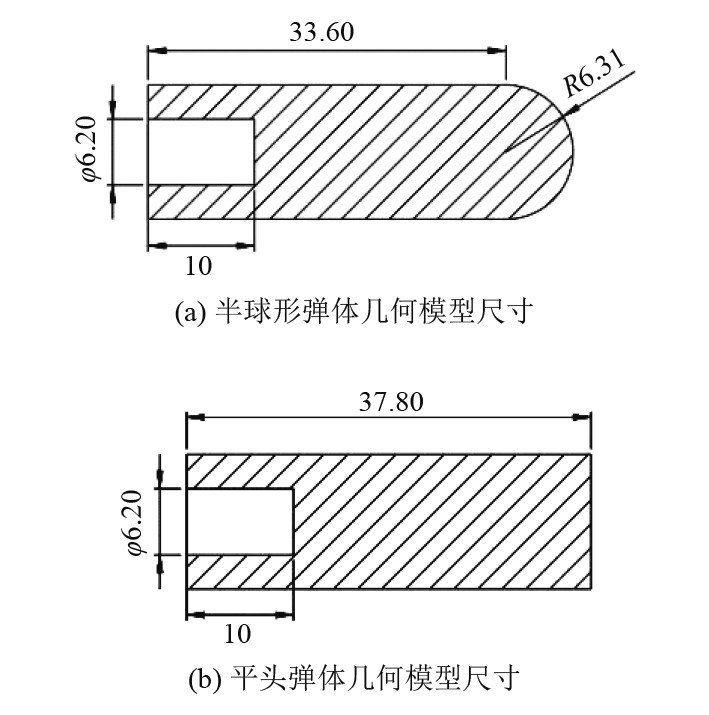
图2(a)为半球形弹体的几何尺寸,图2(b)为平头弹体的几何尺寸,且2个尺寸的单位都是mm,2个弹体尾部各挖出一个深10 mm,直径为6.2 mm圆柱孔。目的是为了弹体在冲击过程中,使其重心稳定。
|
图 2 不同弹体几何尺寸 Fig. 2 Geometric dimensions of different projectile bodies |
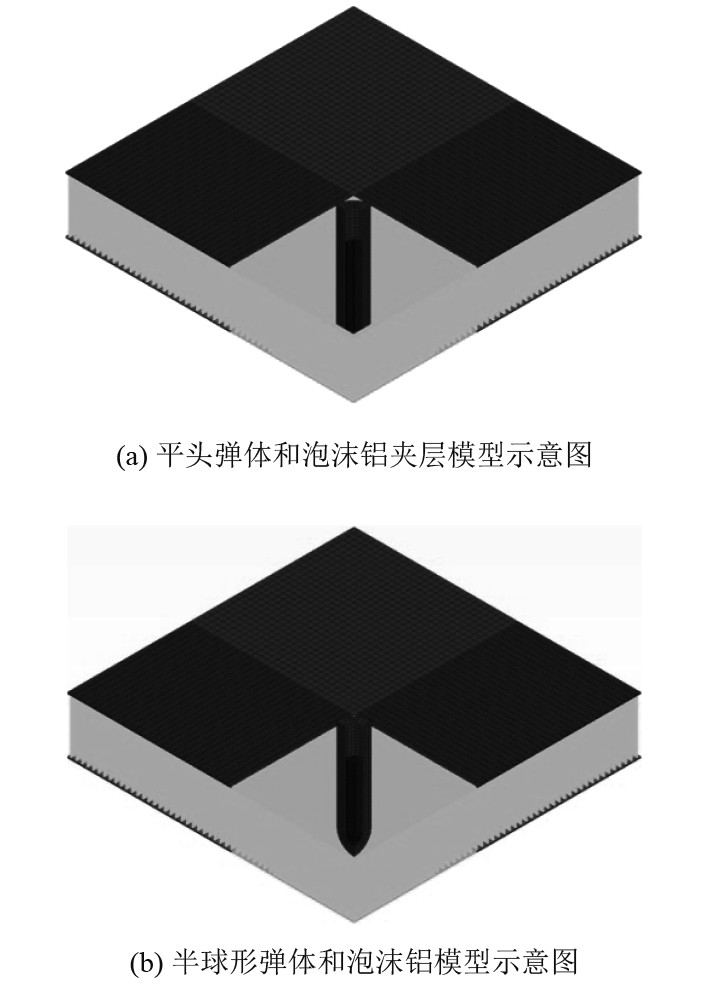
图3为泡沫铝夹层板和两种弹体数值计算模型,其形式主要为SPH-FEM耦合,中间受到撞击部分采用无网格粒子模式,周围不受撞击部分采用有限元网格形式。泡沫铝夹层结构为上下两层面板,材料为Q235钢,中间为泡沫铝,模型尺寸长和宽为210 mm、单层钢板厚度为0.4 mm,泡沫铝厚度为20 mm。其中,中间夹层泡沫铝材料受到撞击区域的粒子间距为0.6 mm,其余部分粒子间距为2 mm,上下面板受到撞击区域粒子间距为0.5 mm,其余部分为有限元网格且网格尺寸为2 mm,通过设置不同网格密度提高计算效率和节省计算时间。
|
图 3 不同弹体和泡沫铝夹层的模型示意图 Fig. 3 Model diagram of different projectile bodies and aluminum foam sandwich |
表1为Q235钢本构模型,即JOHNSON_COOK本构模型。而弹体的本构模型为MAT_RIGID,其材料密度为7 850 kg/m3,杨氏模量为200 GPa,泊松比为0.33,弹体总质量为34.5g[13]。表2为泡沫铝材料参数,采用的本构模型为MAT_CRUSHABLE_FOAM(63#),其中泡沫铝的屈服强度为2.01 MPa。图4为泡沫铝材料在静态压缩下得到的应力-应变曲线。
|
|
表 1 Q235钢材料参数[13] Tab.1 Material parameters of Q235 steel |
|
|
表 2 泡沫铝材料参数 Tab.2 Material parameters of aluminum foam |

|
图 4 应力-应变曲线 Fig. 4 Quasi-static compressive stress-strain curve of aluminum foam material with a density of 276 kg/m3 |
运用Ls-dyna软件进行仿真模拟,采用SPH-FEM耦合方法,其边界条件为CONTACT_TIED_NODES_TO_SURFACE_CONSTRAINED_OFFSET,这样可以实现粒子相互作用产生的力传递给有限元网格,从而实现数值计算。
3 实验结果与数值仿真对比 3.1 实验装置实验装置高压气室产生较高压强的气体,弹体置于弹托内,高压气体经过炮管对弹体作用使其获得一定的初始速度。经过弹托分离装置使得弹体与弹托分离后以一定的速度冲击靶板,靶板固定在靶架上,实验时采用高速相机获得连续视频或图片。
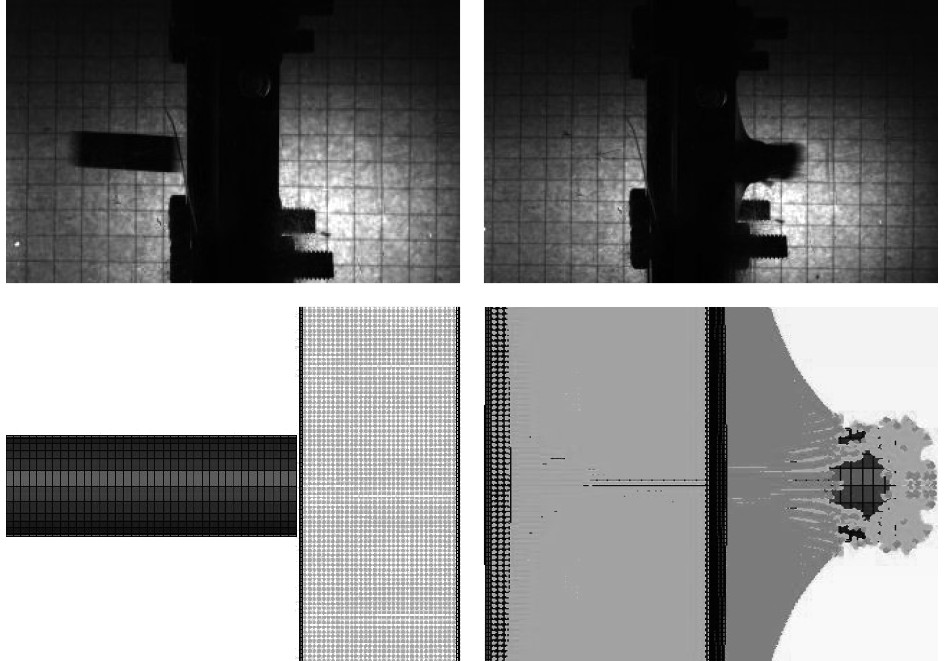
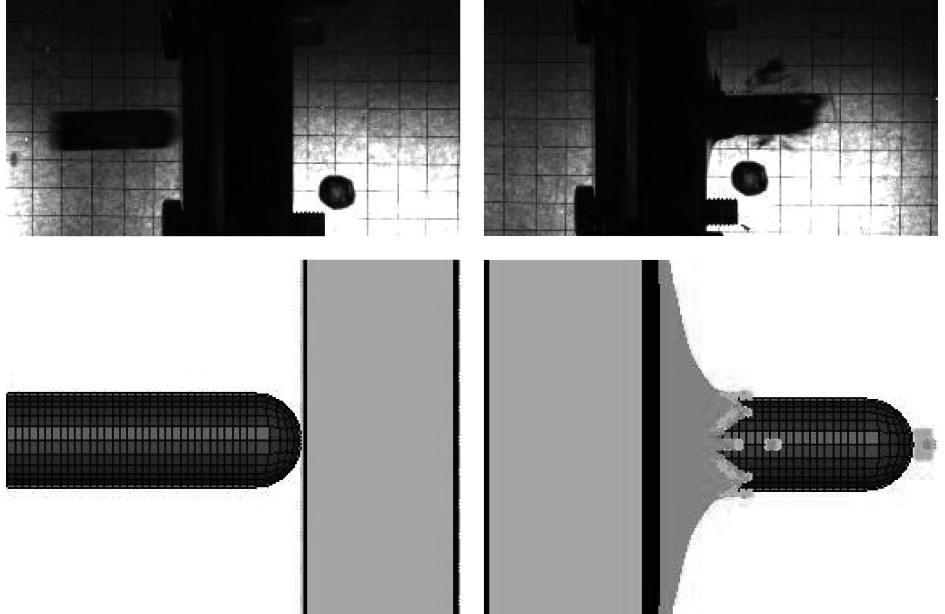
3.2 冲击过程的对比图5为平头弹体水平冲击泡沫铝夹层板的仿真与实验对比图。其中平头弹体初始速度为112.18 m/s,剩余速度为80.4979 m/s,而仿真的初始速度为113 m/s,剩余速度为77.2 m/s。图6为半球形弹体水平冲击泡沫铝夹层板仿真与实验对比图。其中实验的半球形弹体初始速度为124.53 m/s,剩余速度为104.26 m/s,仿真的初始速度为125 m/s,剩余速度为106.32 m/s。从实验与仿真对比看出,仿真的冲击过程与实验的冲击过程很接近,证明SPH-FEM耦合法对于模拟泡沫铝夹层板的模拟精确度较好。
|
图 5 平头弹体冲击泡沫铝夹层板过程(实验速度Vi=112.68 m/s,仿真速度Vi=113 m/s) Fig. 5 Process of flat head projectile impacting aluminum foam sandwich board (experimental velocity Vi=112.68 m/s, simulation velocity Vi=113 m/s) |
|
图 6 半球形弹体冲击泡沫铝夹层板过程(实验速度Vi=124.53 m/s,仿真速度Vi=125 m/s) Fig. 6 Process of hemispherical projectile impacting aluminum foam sandwich plate (experimental velocity Vi=124.53 m/s, simulation velocity Vi=125 m/s) |
图7(a)为平头弹体冲击泡沫铝夹层靶板的实验和仿真的速度曲线对比图。可看出,实验和仿真的计算结果非常相似。通过采用1stopt软件拟合得到仿真计算的弹道极限为83.08 m/s,而实验的弹道极限为86.53 m/s,误差为3.9%。图7(b)为半球形弹体冲击泡沫铝夹层靶板的实验和仿真速度曲线对比图。可看出虽然实验的数据较少,但是仿真和实验的结果也非常接近,且仿真的弹道极限为75.2 m/s,实验的弹道极限为74.2 m/s,误差为1.3%。在泡沫铝夹层靶板相同的情况下,讨论不同弹体对夹层板弹道极限的影响,通过对比得出,平头弹体冲击时,其弹道极限更大,原因是接触面积要更大,且发生剪切变形。而半球形弹体冲击时,接触面积更小,其弹道极限相比较小。

|
图 7 不同弹体冲击泡沫铝夹层板的剩余速度曲线实验和数值计算对比图 Fig. 7 Experimental and numerical comparison of residual velocity curves of different projectile impacting aluminum foam sandwich plate |
图8为平头弹对泡沫铝夹层板的冲击后,实验和仿真夹层靶板的变形状态的对比。仿真平头弹体的初始速度为139.3 m/s,剩余速度为113.02 m/s。而实验平头弹体初始速度为138.93 m/s,剩余速度为115.23 m/s。图9为半球形弹体对泡沫铝夹层板的冲击后,实验和仿真夹层靶板的变形形态对比结果。其中,实验半球形弹体初始速度为118.15 m/s。剩余速度为96.13 m/s,而仿真半球形弹体的初始速度为118.7 m/s,剩余速度为98.49 m/s。从2种不同形态的弹体对夹层靶板冲击结果对比可看出,平头弹体冲击过程中主要产生剪切力从而发生剪切变形,并且产生冲塞。而半球形弹体冲击过程主要产生撕裂变形,并且2种弹体冲击后都产生碟状变形。

|
图 8 平头弹体冲击后的泡沫铝夹层板的实验与仿真变形对比 Fig. 8 Experimental and simulation deformation comparison of aluminum foam sandwich plate after impact of flat head projectile body |

|
图 9 半球形弹体冲击后的泡沫铝夹层板的实验与仿真变形对比 Fig. 9 Experimental and simulation deformation comparison of aluminum foam sandwich plate after impact of hemispherical projectile |
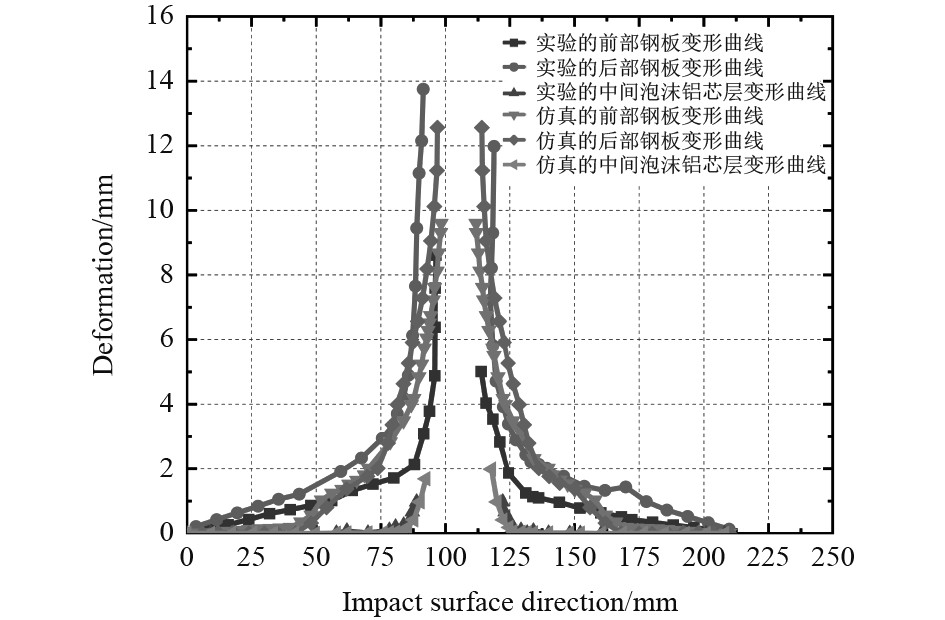
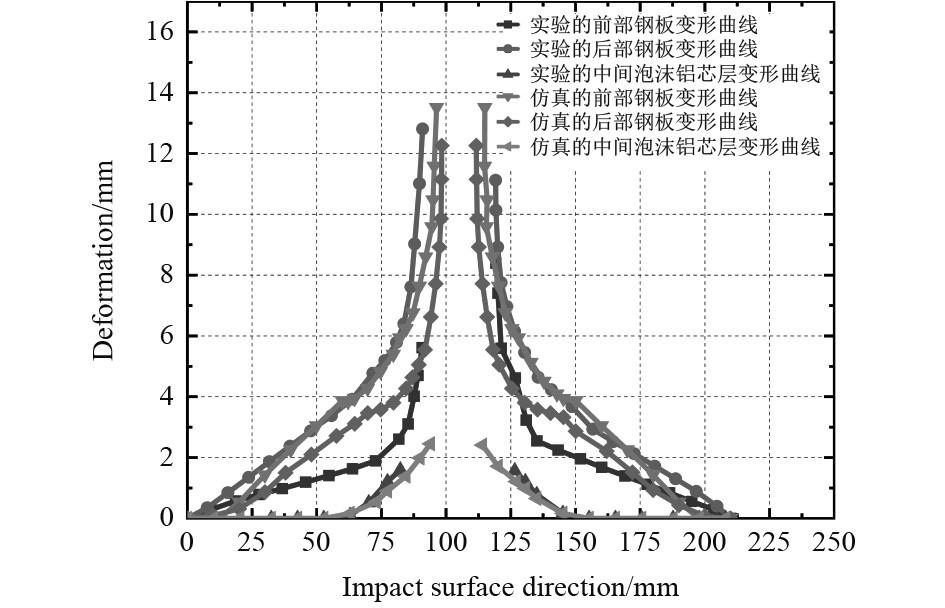
图10和图11分别为平头弹体和半球形弹体对泡沫铝夹层靶板冲击过后产生变形后,不同靶板的变形曲线。从仿真和实验的变形曲线对比来看,实验和仿真的结果很接近,并且最初受到弹体冲击的钢靶板变形要小于最后受到冲击的钢靶板,同时后部钢靶板的变形最大,中间泡沫铝的变形最小。对于平头弹体的冲击,由于最初接触的钢靶板更多地受到剪切力,而最后接触的钢靶板由于受到前部钢靶板和泡沫铝的冲塞挤压,产生撕裂变形,因此后部钢靶板的变形最大。
|
图 10 平头弹体冲击泡沫铝夹层板的变形曲线对比(实验初始速度为112.18 m/s,仿真初始速度为113 m/s) Fig. 10 Comparison of deformation curves of flat head projectile impacting aluminum foam sandwich plate (experimental initial velocity 112.18 m/s, simulation initial velocity 113 m/s) |
|
图 11 半球形弹体冲击泡沫铝夹层板的变形曲线对比(实验初始速度为124.53 m/s,仿真初始速度为125 m/s) Fig. 11 Comparison of deformation curves of hemispherical projectile impacting aluminum foam sandwich plate (experimental initial velocity 124.53 m/s, simulation initial velocity 125 m/s) |
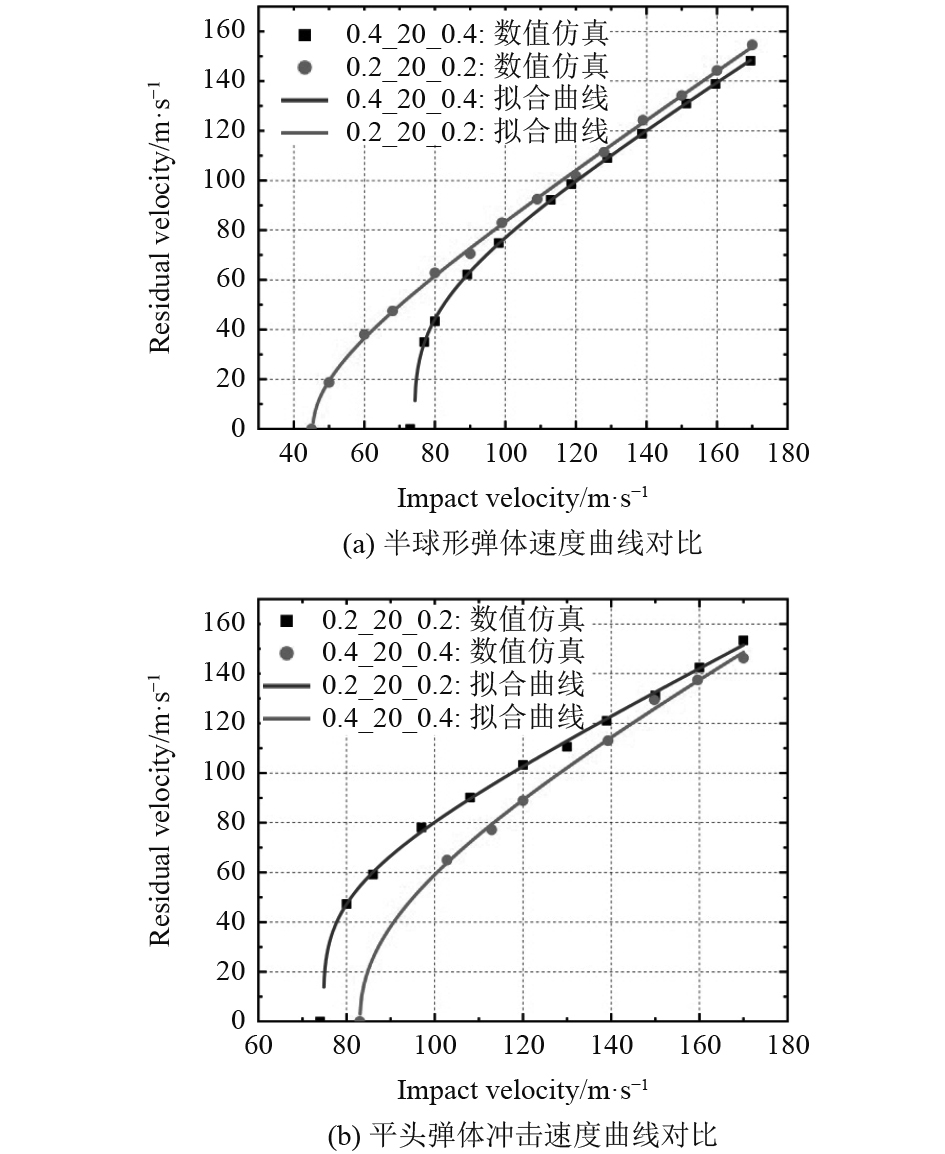
图12(a)为在相同的泡沫铝芯层厚度条件下,通过改变前后面板的厚度,讨论半球形弹体冲击泡沫铝夹层板的弹道极限。通过速度曲线对比可得,前后面板的厚度对弹道极限影响很大,且前后面板厚度越大,弹体冲击泡沫铝夹层板的弹道极限就越大,抗侵彻效果越好。对于图12(b)也存在相同结果,且通过对比两头的曲线变化和弹道极限,得出在改变面板厚度情况下,半球形弹体冲击夹层板的弹道极限变化程度没有平头弹体冲击夹层板的弹道极限变化程度大。半球形弹体冲击夹层板的弹道极限变化为10.72%,而平头弹体冲击夹层板的弹道极限变化为58.9%。
|
图 12 不同弹体在不同面板厚度条件下冲击泡沫铝夹层板的过程 Fig. 12 The impact process of different projectile bodies on aluminum foam sandwich plate under different panel thicknesses |
图13(a)和图13(b)分别为在前后面板厚度相同的条件下,通过改变泡沫铝芯层厚度,得到的平头弹体和半球形弹体冲击泡沫铝夹层板的速度曲线对比。根据曲线可分析得出,泡沫铝芯层厚度对弹体冲击泡沫铝夹层板的弹道极限影响较小,且对于半球形弹体来说影响更小,随着泡沫铝芯层厚度越大,其夹层弹道极限也越大。对于平头弹体冲击泡沫铝夹层板时,改变其泡沫铝芯层厚度对夹层弹道极限影响较大,主要由于平头弹体冲击夹层板时的接触面积更大,相比半球形弹体冲击夹层板时接触面更小。

|
图 13 不同弹体在不同芯层厚度条件下冲击泡沫铝夹层板的过程 Fig. 13 The impact process of different projectile bodies on aluminum foam sandwich plate under different core thickness conditions |
1)采用SPH-FEM耦合法可很好地模拟弹体冲击泡沫铝夹层板全过程,通过对比数值计算与实验测量的速度曲线、变形曲线和冲击过程,证明该方法的有效性且精度较高,并且研究泡沫铝夹层板的抗侵彻性能。
2) 通过数值计算发现,改变面板的厚度,增加前后面板厚度可提高泡沫铝夹层板的抗侵彻性能,且半球形弹体冲击夹层板的弹道极限变化程度比平头弹体冲击夹层板的弹道极限要小。
3)通过改变泡沫铝芯层厚度得出,增加泡沫铝芯层可提高泡沫铝夹层板的抗侵彻性能,但对于半球形弹体来说,抗侵彻性能的提高效果没有平头弹体明显。
| [1] |
张伟, 肖新科, 郭子涛, 等. 双层A3钢靶对平头杆弹的抗侵彻性能研究[J]. 高压物理学报, 2012, 26(2): 163-170. ZHANG Wei, XIAO Xin-ke, GUO Zi-Tao, et al. Study on anti-penetration performance of double layer A3 steel target against flat rod projectiles[J]. Chinese journal of high pressure physics, 2012, 26(2): 163-170. DOI:10.11858/gywlxb.2012.02.007 |
| [2] |
李金柱, 李明静, 李海生, 等. 玻璃钢-聚氨酯泡沫夹层板抗破片侵彻贯穿研究[J]. 北京理工大学学报, 2021, 9(2): 121-129. LI Jin-Zhu, LI Ming-Jing, LI Hai-sheng, et al. Glass fiber reinforced plastic - polyurethane foam sandwich panel perforation resistance fragment study[J]. Journal of Beijing institute of technology, 2021, 9(2): 121-129. DOI:10.15918/j.tbit1001-0645.2019.306 |
| [3] |
蔡玄龙. 钢/尼龙夹层板抗冲击性能研究[D]. 镇江: 江苏科技大学, 2017. CAI Xuan-long. Study on impact resistance of Steel/Nylon sandwich panel [D]. Zhenjiang: Jiangsu University of Science and Technology, 2017. |
| [4] |
焦凯. 冲击载荷下聚氨酯钢夹层板的力学性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. JIAO Kai. Study on mechanical properties of polyurethane steel sandwich panel under impact load [D]. Harbin: Harbin Engineering University, 2019. |
| [5] |
张伟, 管公顺, 哈跃, 等. 弹丸高速撞击压力容器损伤实验研究[J]. 实验力学, 2004(2): 229-235. ZHANG Wei, GUAN Gong-shun, HA Yue, et al. Experimental study on damage of projectile impacting pressure vessel at high speed[J]. Journal of Experimental Mechanics, 2004(2): 229-235. DOI:10.3969/j.issn.1001-4888.2004.02.017 |
| [6] |
XUE Bing, PENG Yu-xiang, REN Shao-fei, et al. Investigation of impact resistance performance of pyramid lattice sandwich structure based on SPH-FEM[J]. Composite Structures, 2021.
|
| [7] |
张志春, 强洪夫, 傅学金, 夏薇. 基于SPH-FEM转换算法的7.62mm步枪弹冲击30CrMnSiA钢板的数值计算[J]. 计算物理, 2012, 29(1): 73-81. ZHANG Zhi-chun, QIANG Hong-fu, FU Xue-jin, et al. Numerical calculation of 7.62mm stepping gun impacting 30crmnsia steel plate based on SPH-FEM conversion algorithm[J]. Computational physics, 2012, 29(1): 73-81. DOI:10.19596/j.cnki.1001-246x.2012.01.010 |
| [8] |
柳春, 余志祥, 郭立平, 等. 基于SPH-FEM耦合方法的落石冲击拱形钢筋混凝土棚洞数值模拟[J]. 振动与冲击, 2019, 38(13): 118-125. LIU Chun, YU Zhi-xiang, GUO Li-ping, et al. Numerical simulation of rockfall impact arch reinforced concrete shed based on SPH-FEM coupling method[J]. Vibration and shock, 2019, 38(13): 118-125. DOI:10.13465/j.cnki.jvs.2019.13.017 |
| [9] |
卞梁, 王肖钧, 章杰. SPH/FEM耦合算法在陶瓷复合靶抗侵彻数值模拟中的应用[J]. 高压物理学报, 2010, 24(3): 161-167. BIAN Liang, WANG Xiao-jun, ZHANG Jie. Application of SPH/FEM coupling algorithm in numerical simulation of ceramic composite target penetration resistance[J]. Chinese journal of high pressure physics, 2010, 24(3): 161-167. DOI:10.3969/j.issn.1000-5773.2010.03.001 |
| [10] |
张建伟, 主攀, 陈海舟, 等. 基于光滑粒子流体动力学方法的表中孔泄流模拟[J]. 水电能源科学, 2022, 40(3): 136–139+127. ZHANG Jian-wei, ZHU Pan, CHEN Hai-zhou, et al. Simulation of surface orifice discharge based on smooth particle hydrodynamics [J]. Journal of Hydropower and Energy Science, 202, 40(3): 136–139+127. |
| [11] |
韩俊辉, 姚昌荣, 余劲松, 等. 基于SPH-FEM耦合方法的泥石流冲击柱形结构物动力响应分析[J]. 四川建筑, 2020, 40(6): 146-149+152. HAN Jun-hui, YAO Chang-rong, YU Jin-song, et al. Dynamic response analysis of debris flow impact columnar structures based on SPH-FEM coupling method[J]. Sichuan architecture, 2020, 40(6): 146-149+152. DOI:10.3969/j.issn.1007-8983.2020.06.047 |
| [12] |
ZHANG Z, QIANG H, GAO W. Coupling of smoothed particle hydrodynamics and finite element method for impact dynamics simulation[J]. Engineering Structures, 2011, 33(1): 255-264. DOI:10.1016/j.engstruct.2010.10.020 |
| [13] |
王明辉. 泡沫铝夹层板抗侵彻性能研究[D]. 镇江: 江苏科技大学, 2016. WANG Ming-hui. Research on penetration resistance of aluminum foam sandwich panel [D]. Zhenjiang: Jiangsu University of Science and Technology, 2016. |
 2023, Vol. 45
2023, Vol. 45
