2. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
舰艇的抗冲击性能与其生命力息息相关,在设计研发阶段,如何提高舰艇的水下爆炸抗冲击性能尤为重要。Abaqus声固耦合法用声学单元模拟水域,在计算中远场水下爆炸时,可在保证计算精度的同时提高计算效率[1-4]。负泊松比内凹蜂窝结构具有优异的抗冲击性能和能量吸收特性,并且在减轻结构重量方面具有显著优势,是一种集轻量化和抗冲击吸能于一体的新型轻质结构,可在实现舰艇轻量化的同时提高其抗冲击性能[5-11]。
本文设计一种具有负泊松比内凹蜂窝肋板的双层圆柱壳结构,并基于Abaqus声固耦合法对双层圆柱壳在水下爆炸工况下的抗冲击响应进行数值模拟。主要分析双层圆柱壳外壳、内壳和肋板的最大变形、等效塑性应变、动能和内能结果,讨论了不同肋板间距工况对双层圆柱壳抗冲击响应的影响,为双层圆柱壳的设计提供参考。
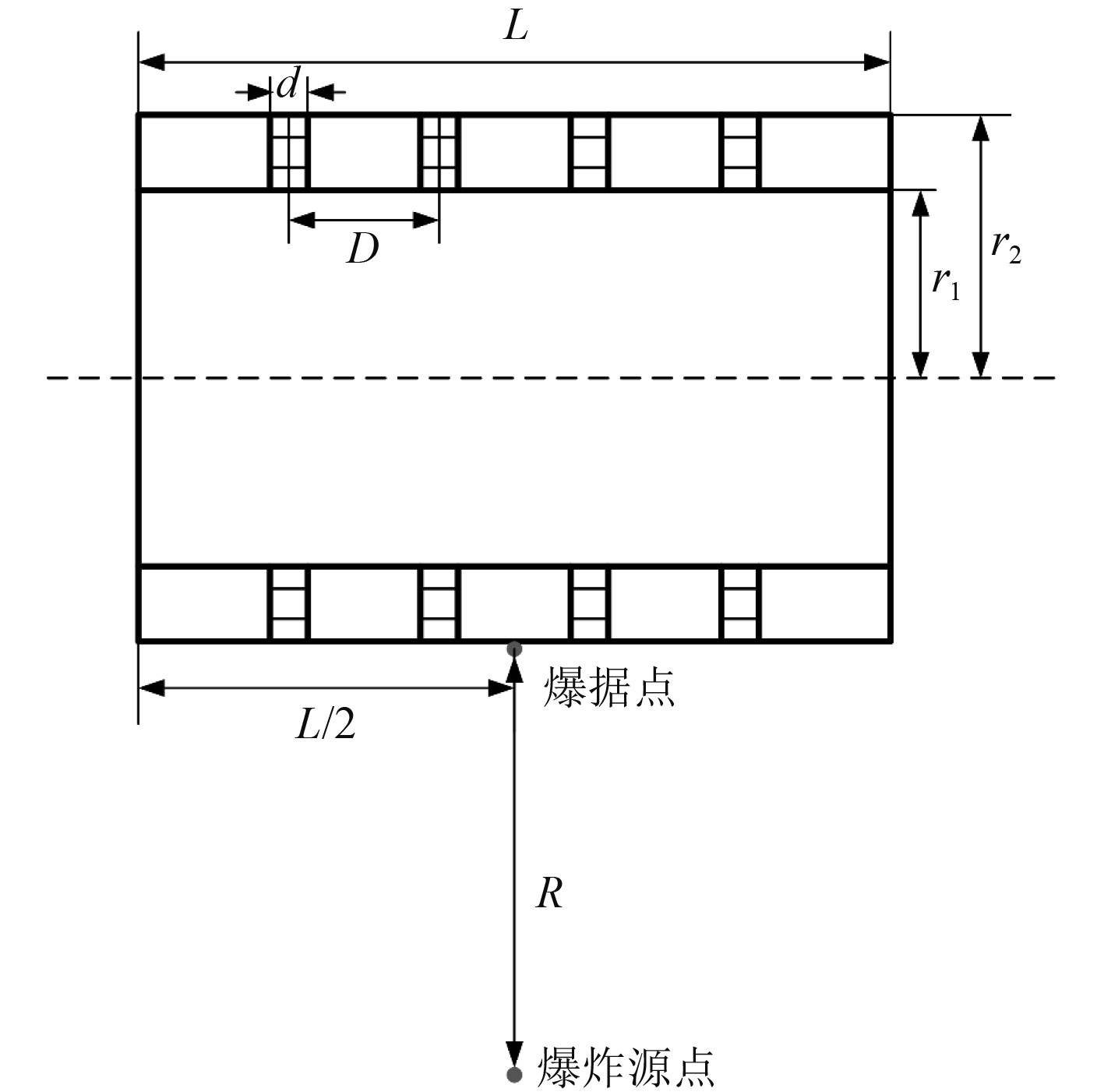
1 内凹蜂窝圆柱壳结构设计双层圆柱壳由内壳、外壳和肋板组成,如图1所示。图中圆柱壳长度L为5 m;内壳外径r1为3.52 m,内壳厚度为20 mm;外壳外径r2为4.3 m,外壳厚度为20 mm;d为肋板厚度,D为肋板间距。

|
图 1 双层圆柱壳 Fig. 1 Double-layer cylindrical shell |
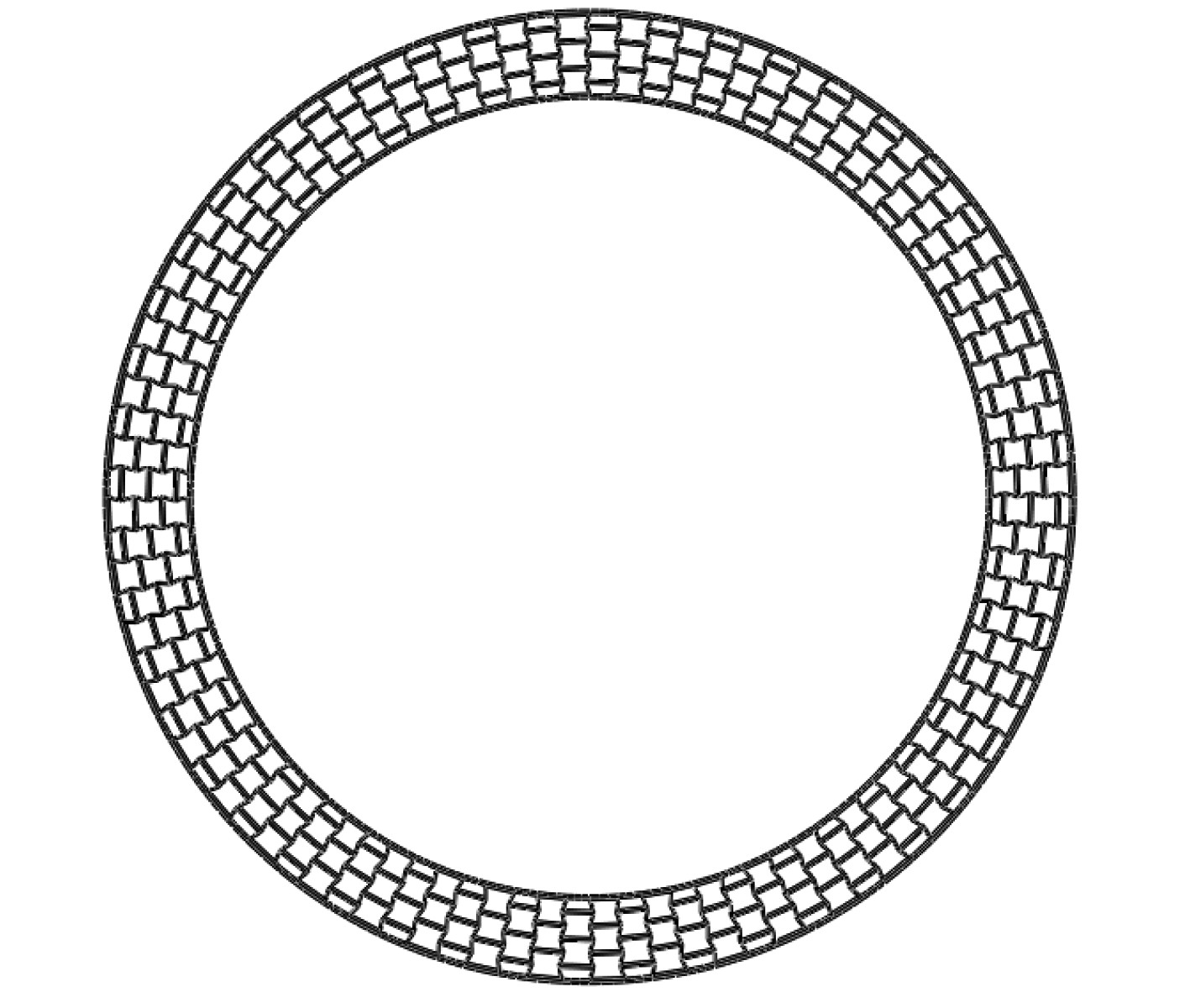
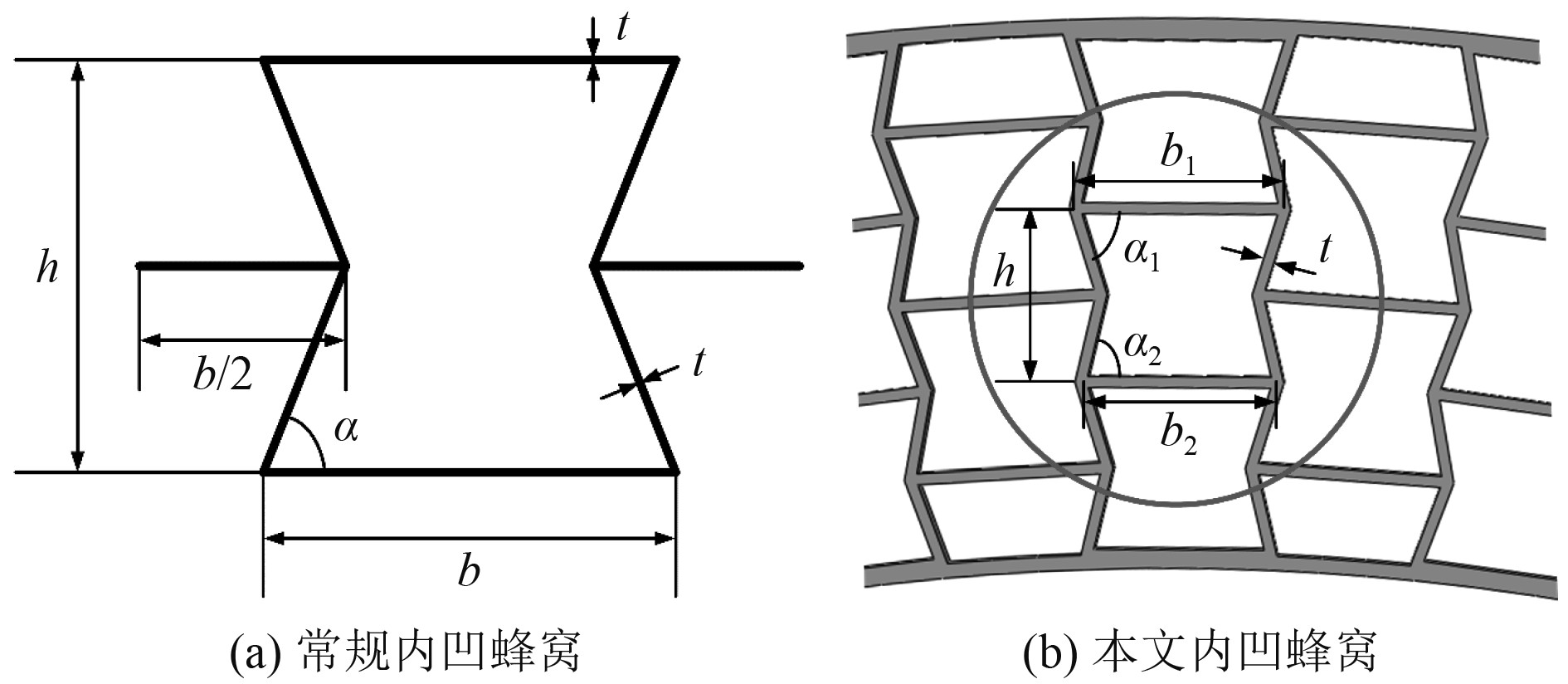
肋板为负泊松比内凹蜂窝结构,如图2所示。常规内凹蜂窝结构单胞截面如图3所示,图中t为胞元壁厚,b为胞元宽度,h为胞元高度,α为胞元夹角。由于内外壳半径不同,肋板内凹蜂窝不同单胞尺寸存在微小差异,以第2层单胞为例,t为16 mm,h为240 mm,α1为72.4°,α2为76.6°,b1为295 mm,b2为277 mm。
|
图 2 肋板示意图 Fig. 2 Diagrammatic sketch of ribs |
|
图 3 内凹蜂窝结构示意图 Fig. 3 Diagrammatic sketch of re-entrant honeycomb |
根据双层圆柱壳几何模型建立有限元模型,双层圆柱壳有限元模型中内壳、外壳的网格尺寸为50 mm,并且沿厚度方向划分3层网格,肋板的网格尺寸为50 mm,肋板每个胞元厚度方向至少划分3层网格。肋板与内外壳接触面使用Tie约束模拟肋板与内外壳之间的焊接。双层圆柱壳有限元模型如图4所示。

|
图 4 双层圆柱壳有限元模型 Fig. 4 Finite element model of double-layer cylindrical shell |
有限元模型包括水域和圆柱壳,水域由圆柱体和半球体组成,圆柱体半径为17.2 m、长为5 m,半球体半径为17.2 m。建立有限元模型时,水域采用声学单元,水域划分声学网格的相关材料参数见表1。圆柱壳材料为低碳钢,由于低碳钢是应变率敏感材料,采用Cowper-symbol应变率模型,低碳钢的材料参数见表2。
|
|
表 1 水材料参数 Tab.1 Material parameters of water |
|
|
表 2 低碳钢材料参数 Tab.2 Material parameters of Low-carbon steel |
水域内部靠近圆柱壳的部分网格尺寸为100 mm,外部尺寸为800 mm,采用渐变四面体网格。水域与圆柱壳的接触面设置Tie连接模拟流固耦合,流固耦合模型如图5所示。

|
图 5 水下爆炸流固耦合模型 Fig. 5 Fluid-structure coupling model of underwater explosion |
为了研究肋板间距对双层圆柱壳结构水下爆炸抗冲击性能的影响,设置不同肋板间距工况,见表3,为了保持肋板一定的总重量,不同肋板间距工况设置不同肋板宽度和肋板数量。
|
|
表 3 不同肋板间距工况 Tab.3 Different conditions of distance of ribs |
水下爆炸工况为:炸药当量为50 kg,爆距为10 m,爆距点位于圆柱壳轴向对称面,爆距点与爆炸源点相对位置如图6所示。在Abaqus中水下爆炸工况通过修改关键字施加。
|
图 6 水下爆炸工况示意图 Fig. 6 Diagrammatic sketch of underwater explosion |
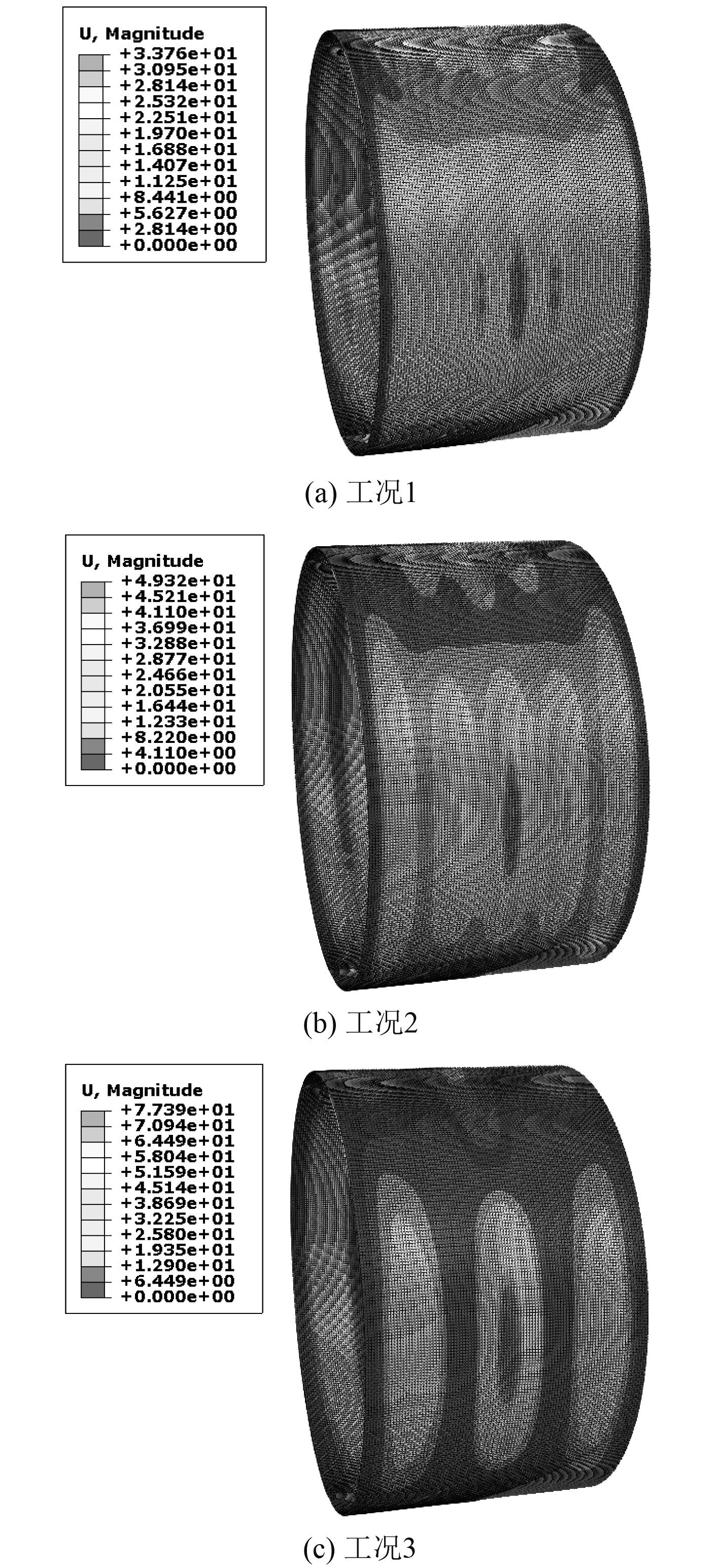
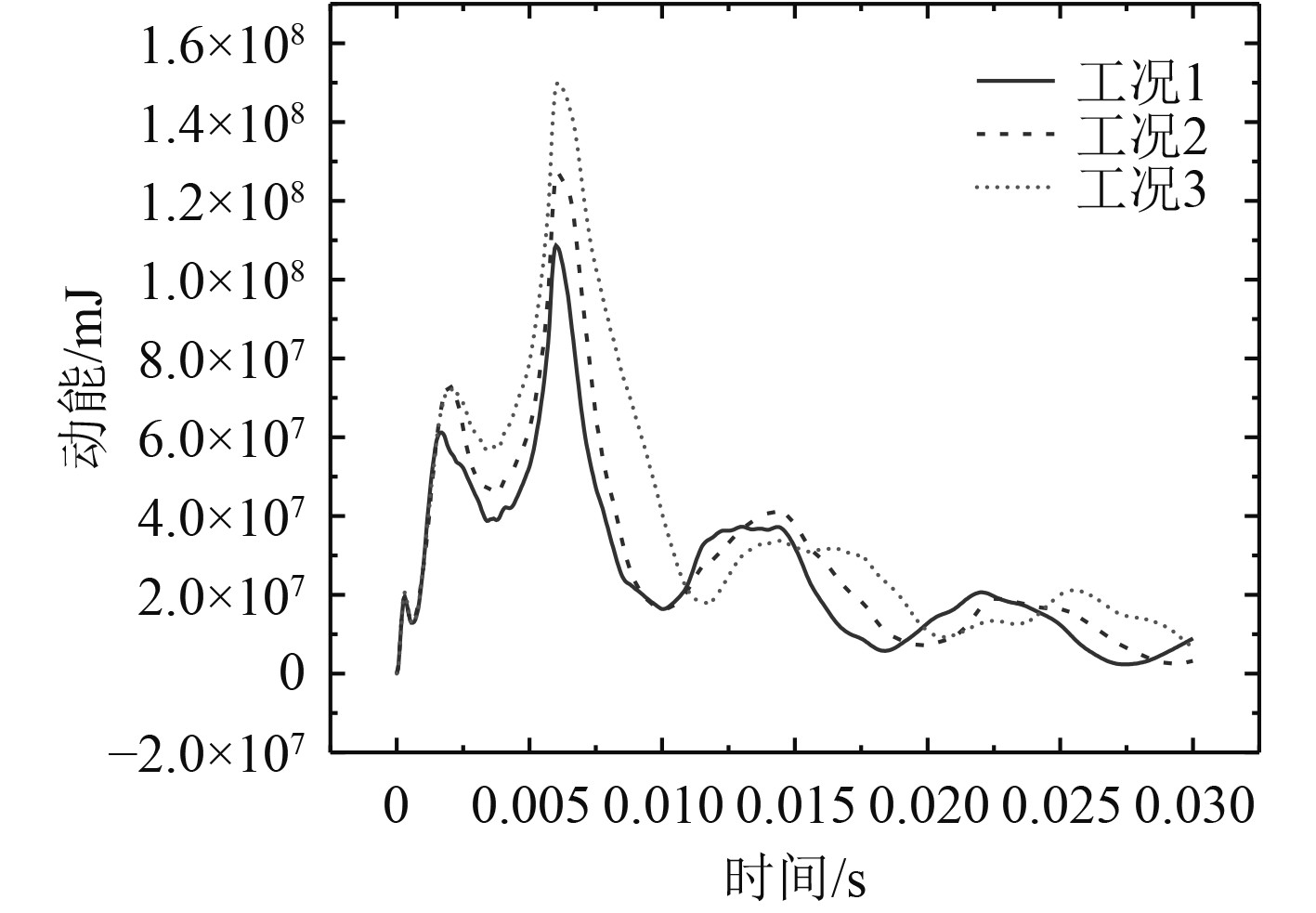
研究不同肋板间距对外壳水下爆炸抗冲击性能的影响。图7为不同肋板间距工况下外壳的最大位移云图对比,图8为不同肋板间距工况下,外壳动能曲线对比。
|
图 7 外壳最大变形云图 Fig. 7 Maximum deformation of outer shell |
|
图 8 外壳动能曲线 Fig. 8 Kinetic energy curve of outer shell |
图9为不同肋板间距工况下外壳的最大等效塑性应变云图对比,图10为不同肋板间距工况下,外壳内能曲线对比。

|
图 9 外壳最大等效塑性应变云图 Fig. 9 Maximum equivalent plastic strain of outer shell |

|
图 10 外壳内能曲线 Fig. 10 Internal energy curve of outer shell |
表4为不同肋板间距工况下外壳变形、动能、等效塑性应变和内能峰值计算结果汇总。
|
|
表 4 外壳计算结果汇总 Tab.4 Summary of results of outer shell |
从图7可看出,3种工况下外壳最大变形位置均发生在外壳迎爆面,且靠近爆距点。与工况3相比,工况1、工况2最大变形会发生“分区”现象,即工况1、工况2最大变形会发生在多组肋板之间的外壳区域,工况3只有2个肋板,最大变形只发生在这2个肋板之间的区域。从数值上看,工况1~工况3外壳最大变形有明显的增大,以工况1为基准,工况2、工况3最大变形涨幅分别达到45.9%、129%。从图8可看出,3种工况下,外壳动能在6 ms附近达到峰值,之后逐渐衰减到0。从数值上来看,工况1~工况3外壳的动能峰值逐渐增大,这与外壳的变形规律相吻合。从图9可看出,3种工况下,外壳最大等效塑性应变位置均发生在外壳迎爆面,工况1、工况2最大等效塑性应变发生在固支边界处和爆距点附近,工况3最大等效塑性应变则集中在爆距点附近。从数值上来看,工况1~工况3外壳最大等效塑性应变有明显增大,以工况1为基准,工况2、工况3最大等效塑性应变涨幅分别达到20.5%、53.6%。从图10可看出,3种工况下,外壳内能在10 ms附近达到峰值,之后趋于稳定。从数值上来看,工况1~工况3外壳的内能峰值逐渐增大,这与外壳的等效塑性应变变化规律相吻合。
综上所述,针对本文的双层圆柱壳结构,在保证肋板总重一定的情况下,增大肋板间距、增大肋板宽度、减少肋板数量,外壳最大变形、等效塑性应变会明显变大,同时最大变形、等效塑性应变发生的区域逐渐集中,有由多变少的趋势。从能量的角度来看,在保证肋板总重一定的情况下,增大肋板间距、增大肋板宽度、减少肋板数量,外壳动能、内能呈增大趋势,且涨幅较大。
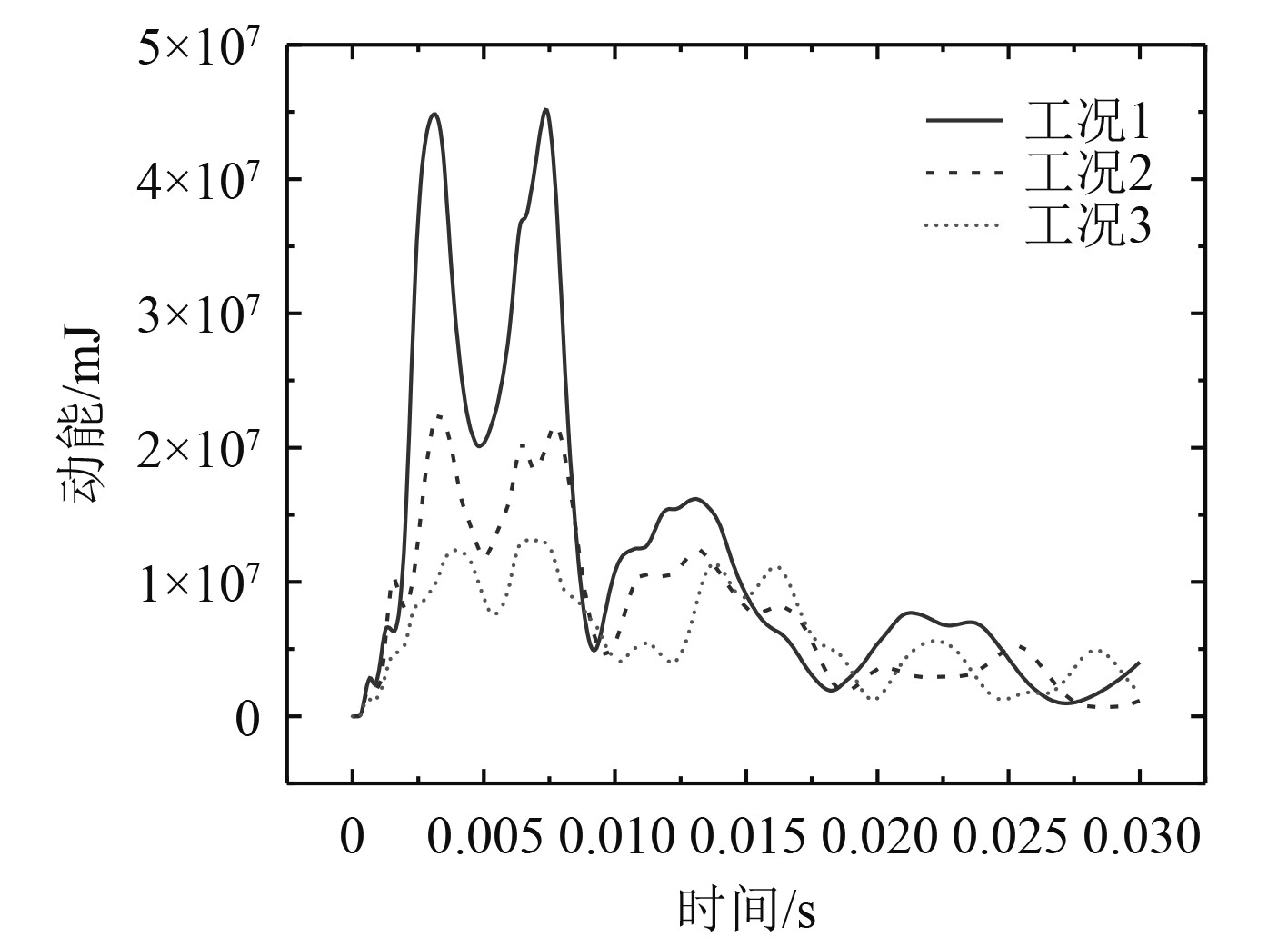
3.2 内壳水下爆炸抗冲击性能对比研究不同肋板间距对内壳水下爆炸抗冲击性能的影响。图11为不同肋板间距工况下内壳的最大位移云图对比,图12为不同肋板间距工况下内壳动能曲线对比。

|
图 11 内壳最大变形云图 Fig. 11 Maximum deformation of inner shell |
|
图 12 内壳动能曲线 Fig. 12 Kinetic energy curve of inner shell |
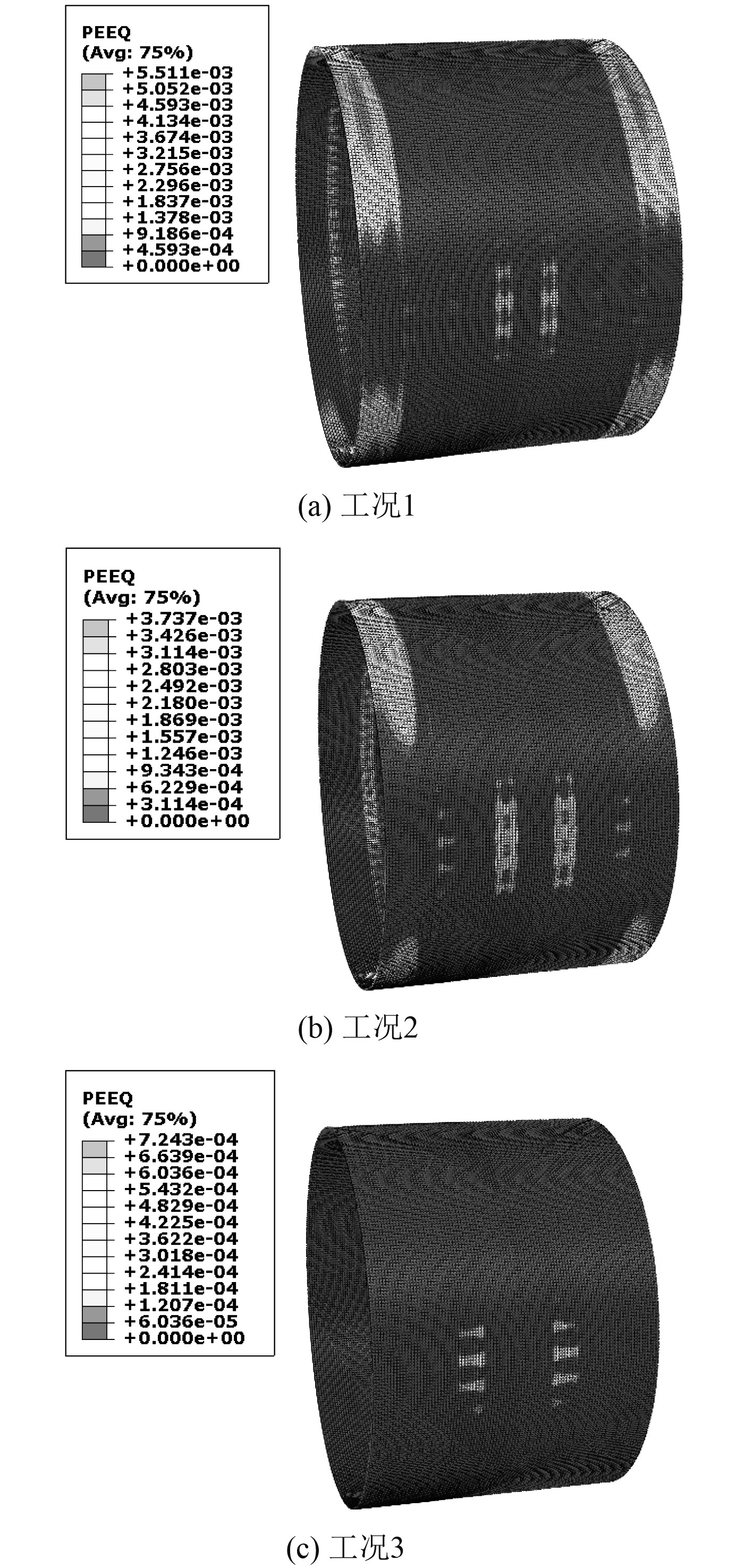
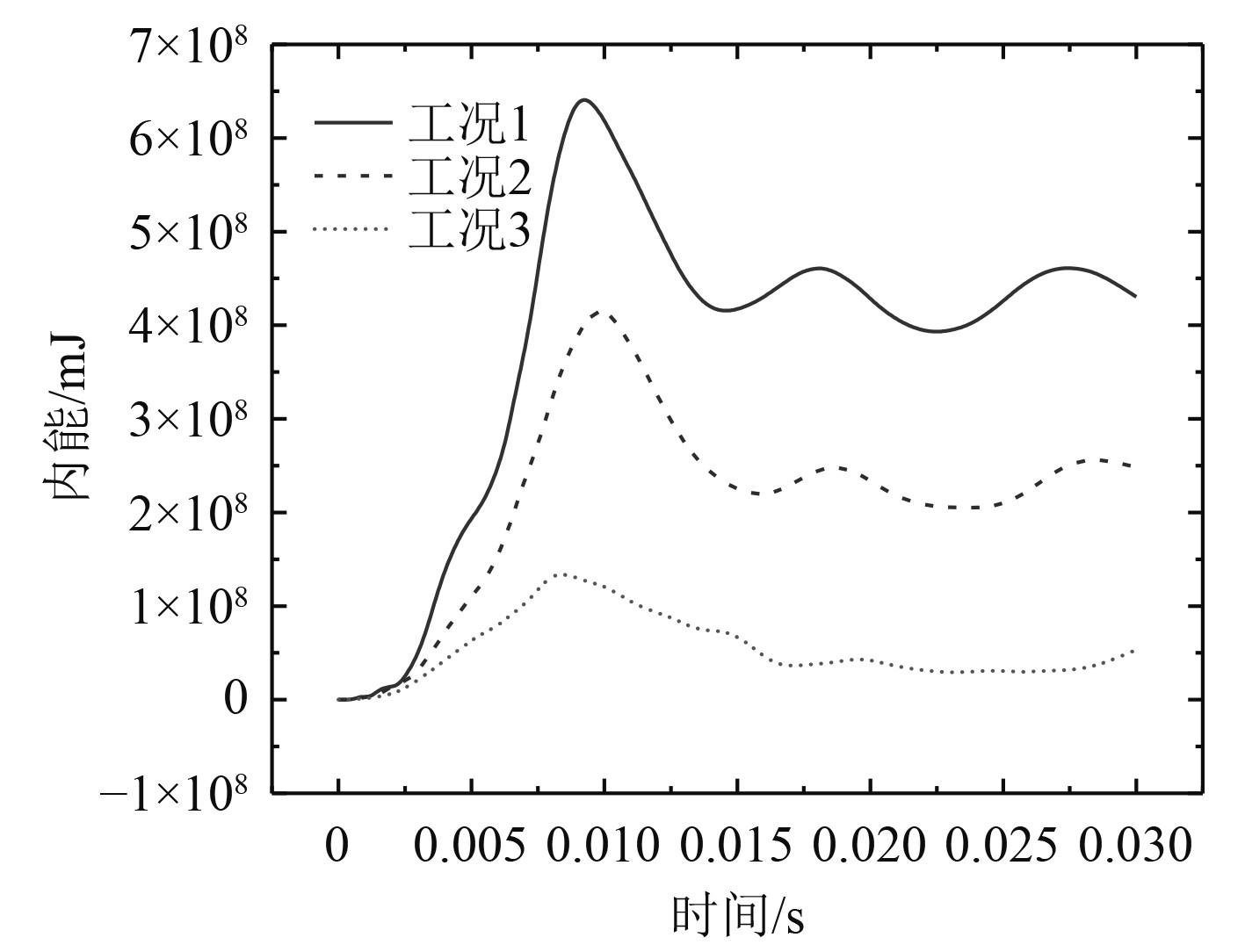
图13为不同肋板间距工况下内壳的最大等效塑性应变云图对比,图14为不同肋板间距工况下内壳内能曲线对比。
|
图 13 内壳最大等效塑性应变云图 Fig. 13 Maximum equivalent plastic strain of inner shell |
|
图 14 内壳内能曲线 Fig. 14 Internal energy curve of inner shell |
表5为不同肋板间距工况下,内壳变形、动能、等效塑性应变和内能峰值计算结果汇总。
|
|
表 5 内壳计算结果汇总 Tab.5 Summary of results of inner shell |
从图11可看出,3种工况下内壳最大变形位置均发生在内壳迎爆面,与外壳最大变形发生位置相比,外壳最大变形发生在肋板间,内壳最大变形发生在内壳与肋板连接处。由于工况1~工况3肋板间距逐渐增大,相应地内壳最大变形发生的区域逐渐外扩,但从数值上看,工况1~工况3内壳最大变形有明显减小,以工况1为基准,工况2、工况3最大变形减幅达到18.6%、61.3%。从图12可看出,3种工况下内壳动能在3 ms、7 ms出现2次峰值,且2次峰值数值相差不大,在第2次峰值后,逐渐衰减为0。从数值上看,工况1~工况3内壳动能峰值逐渐减小,这与内壳变形规律相吻合。从图13可看出,3种工况下内壳最大等效塑性应变位置均发生在内壳迎爆面,工况1、工况2最大等效塑性应变发生在固支边界处和内壳迎爆面中部,工况3最大等效塑性应变则集中在内壳迎爆面中部。从数值上来看,工况1~工况3内壳等效塑性应变有明显的减小趋势,以工况1为基准,工况2、工况3等效塑性应变减幅达到32.1%、86.9%。从图14可看出,3种工况下内壳内能在10 ms附近达到峰值,之后趋于稳定。从数值上看,工况1~工况3内壳的内能峰值逐渐减小,这与内壳等效塑性应变变化规律相吻合。
综上所述,针对本文的双层圆柱壳结构,在保证肋板总重一定的情况下,增大肋板间距、增大肋板宽度、减少肋板数量,内壳最大变形、等效塑性应变会明显减小,最大变形发生在内壳与肋板连接处,最大等效塑性应变发生在固支边界处和内壳迎爆面中部。从能量的角度来看,在保证肋板总重一定的情况下,增大肋板间距、增大肋板宽度、减少肋板数量,内壳动能、内能呈减小趋势,且减幅较大。
3.3 肋板水下爆炸抗冲击性能对比研究不同肋板间距对肋板水下爆炸抗冲击性能的影响。图15为不同肋板间距工况下肋板的最大位移云图对比,图16为不同肋板间距工况下肋板动能曲线对比。
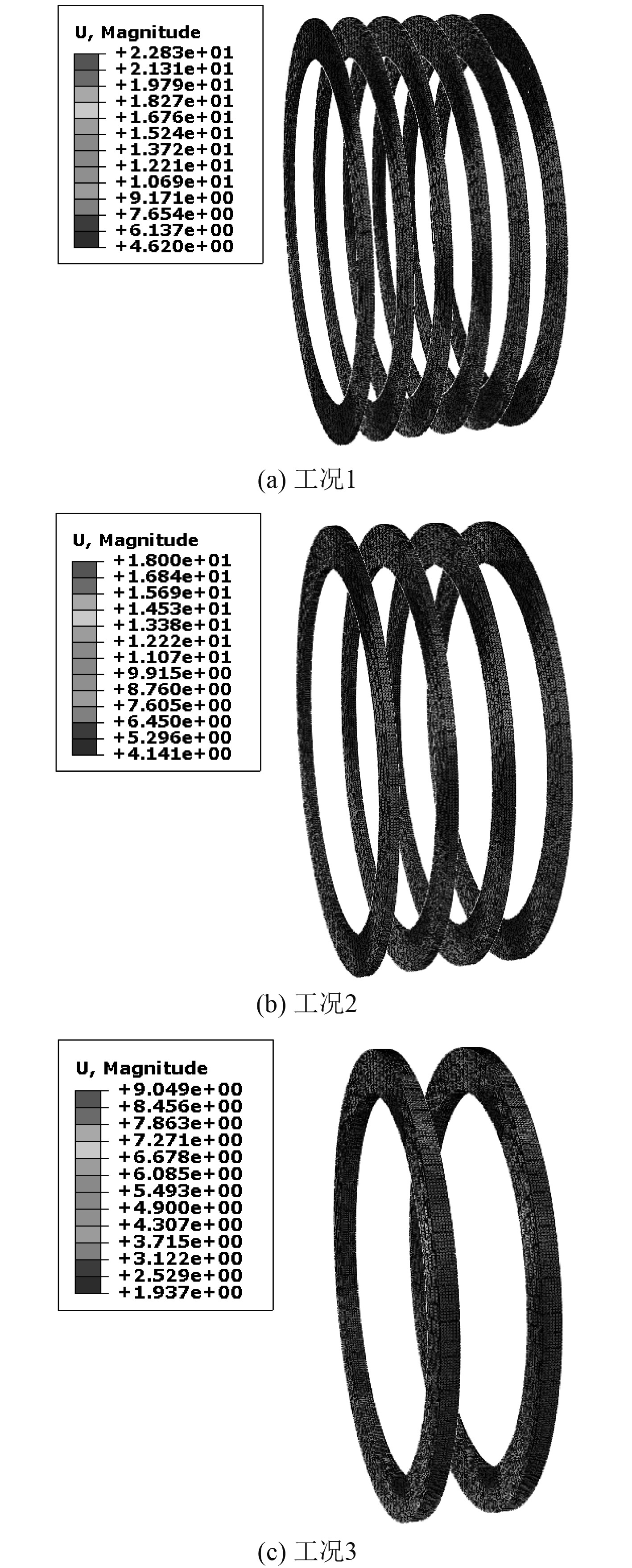
|
图 15 肋板最大变形云图 Fig. 15 Maximum deformation of ribs |

|
图 16 肋板动能曲线 Fig. 16 Kinetic energy curve of ribs |
图17为不同肋板间距工况下肋板的最大等效塑性应变云图对比,图18为不同肋板间距工况下肋板内能曲线对比。

|
图 17 肋板最大等效塑性应变云图 Fig. 17 Maximum equivalent plastic strain of ribs |

|
图 18 肋板内能曲线 Fig. 18 Internal energy curve of ribs |
表6为肋板间距不同时,肋板变形、动能、等效塑性应变和内能峰值结果汇总。
|
|
表 6 肋板计算结果汇总 Tab.6 Summary of results of ribs |
从图15可看出,3种工况下肋板最大变形均发生在肋板迎爆面,且靠近迎爆点的肋板变形更大。对比3种工况肋板的变形,工况1~工况3肋板最大变形逐渐减小。从图16可看出,3种工况下肋板动能在7 ms附近出现峰值,之后逐渐衰减为0。工况1~工况3肋板动能峰值逐渐减小。从图17可看出,工况1~工况3肋板等效塑性应变逐渐减小。从图18可看出,3种工况下肋板内能在10 ms附近达到峰值,之后趋于稳定,工况1~工况3肋板的内能峰值逐渐减小。
综上所述,针对本文的双层圆柱壳结构,在保证肋板总重一定的情况下,增大肋板间距、增大肋板宽度、减少肋板数量,肋板最大变形、等效塑性应变会明显减小。从能量的角度来看,在保证肋板总重一定的情况下,增大肋板间距、增大肋板宽度、减少肋板数量,肋板动能、内能呈减小趋势,且减幅较大。
4 结 语本文设计一种具有负泊松比内凹蜂窝肋板的双层圆柱壳结构,并基于ABaqus声固耦合法对双层圆柱壳在水下爆炸工况下的抗冲击性能进行数值模拟,主要分析双层圆柱壳外壳、内壳和肋板的最大变形、等效塑性应变、动能和内能等结果,讨论了不同肋板间距工况对双层圆柱壳抗冲击性能的影响。研究结果表明,针对本文的双层圆柱壳结构,在保证肋板总重一定的情况下,增大肋板间距、增大肋板宽度、减少肋板数量:外壳最大变形、等效塑性应变会明显变大,同时最大变形、等效塑性应变发生的区域逐渐集中,有由多变少的趋势;从能量的角度来看,外壳动能、内能呈增大趋势,且涨幅较大;内壳最大变形、等效塑性应变会明显减小,最大变形发生在内壳与肋板连接处,最大等效塑性应变发生在固支边界处和内壳迎爆面中部;从能量的角度来看,内壳动能、内能呈减小趋势,且减幅较大;肋板最大变形、等效塑性应变会明显减小;从能量的角度来看,肋板动能、内能呈减小趋势,且减幅较大。
| [1] |
姚熊亮, 张阿漫, 许维军. 声固耦合方法在舰船水下爆炸中的应用[J]. 哈尔滨工程大学学报, 2005(6): 707-712. YAO Xiongliang, ZHANG Aman, XU Weijun. Application of coupled acoustic-solid method in ship underwater explosion[J]. Journal of Harbin Engineering University, 2005(6): 707-712. |
| [2] |
贺平, 严勇. 圆筒水下爆炸冲击响应[J]. 数字海洋与水下攻防, 2021, 4(5): 405-411. HE Ping, YAN Yong. Shock response of cylinder underwater explosion[J]. Digital Ocean & Underwater Warfare, 2021, 4(5): 405-411. DOI:10.19838/j.issn.2096-5753.2021.05.011 |
| [3] |
朱云笛. 水下爆炸载荷作用下无人艇结构动态响应及防护结构研究[D]. 镇江: 江苏科技大学, 2021.
|
| [4] |
岳博闻. 近场水下爆炸对复合材料扫雷艇的损伤研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
|
| [5] |
姚永永. 内凹负泊松比蜂窝的静动态力学性能研究[D]. 太原: 太原理工大学, 2021.
|
| [6] |
邓锦郅. 分层功能梯度蜂窝结构冲击动力学响应的研究[D]. 西安: 长安大学, 2019.
|
| [7] |
杨康尧. 三维内凹蜂窝夹芯板抗爆性能仿真与优化[D]. 大连: 大连理工大学, 2019.
|
| [8] |
EBRAHIMI H, SOMEH L K, NORATO J, et al. Blast-resilience of honeycomb sandwich panels[J]. International Journal of Mechanical Sciences, 2018, 144: 1−9.
|
| [9] |
AHMED S, GALAL K. Effectiveness of FRP sandwich panels for blast resistance[J]. Composite Structures, 2017, 163: 454-464. DOI:10.1016/j.compstruct.2016.11.066 |
| [10] |
韩会龙, 张新春, 王鹏. 负泊松比蜂窝材料的动力学响应及能量吸收特性[J]. 爆炸与冲击, 2019, 39(1): 47-57. HAN Huilong, ZHANG Xinchun, WANG Peng. Dynamic response and energy absorption characteristics of honeycomb materials with negative Poisson's ratio[J]. Explosion and Shock Waves, 2019, 39(1): 47-57. |
| [11] |
王陶. 负泊松比结构力学特性研究及其在商用车耐撞性优化设计中的应用[D]. 南京: 南京理工大学, 2018.
|
 2023, Vol. 45
2023, Vol. 45
