2. 中国人民解放军92730部队,海南 三亚 572099
2. No. 92730 Unit of PLA, Sanya 572099, China
随着新型核装备及平台投入使用,涉核军事活动日益频繁,引起对核安全特别是舰艇核安全的关注度持续加大。同时,对辐射监测仪器性能要求越来越高。用于电离辐射探测的正比计数器按照外形结构不同可分为圆柱形、球形、鼓形、方形等[1]。不同的结构类型取决于它的使用需求,如多丝正比室[2]作为一种位置灵敏探测器,多设置一排平行的阳极丝,为了获得均匀的气体腔室空间和电场分布,往往选择2块平行板作为阴极,因此多采用方形结构。在某些正比谱仪当中,也有采用取鼓形结构的,这样的正比计数器阳极丝一般为环状。迄今为止,被应用最多的气体探测器结构为圆柱形和球形,这也是绝大多数基于正比计数器的商用便携式中子剂量当量率仪所采用的结构。
球形结构因其灵敏介质的中心对称性,具备了各向同性的方向响应这一最大优势,同时也更容易设计成紧凑型便携式仪器。对于中央丝状阳极,可通过设置合适的支撑子、绝缘子,或设置环绕阳极丝的金属螺旋线[3]等方式获得雪崩区域均匀电场。2006年,Giomataris等[4-5]设计的球形正比计数器放弃了传统的丝状阳极,选用中心阳极小球,结构如图1(a)所示。阳极球由金属杆连接并处在同样高压电位,为了避免金属杆上高压对电场的影响,设置了包裹金属杆的圆柱桶状“矫正器”,“矫正器”接地并与金属杆绝缘。这样的结构形成了如图1(b)所示围绕阳极中心对称的电场分布,但同时也带来了装配难度提高和机械噪声等问题。就应用于便携式仪器中的正比计数器而言,体积较小,使得金属杆和“矫正器”等部位变得十分精密且对震动敏感,加工难度和仪器可靠性在一定程度上制约了此类结构的发展。
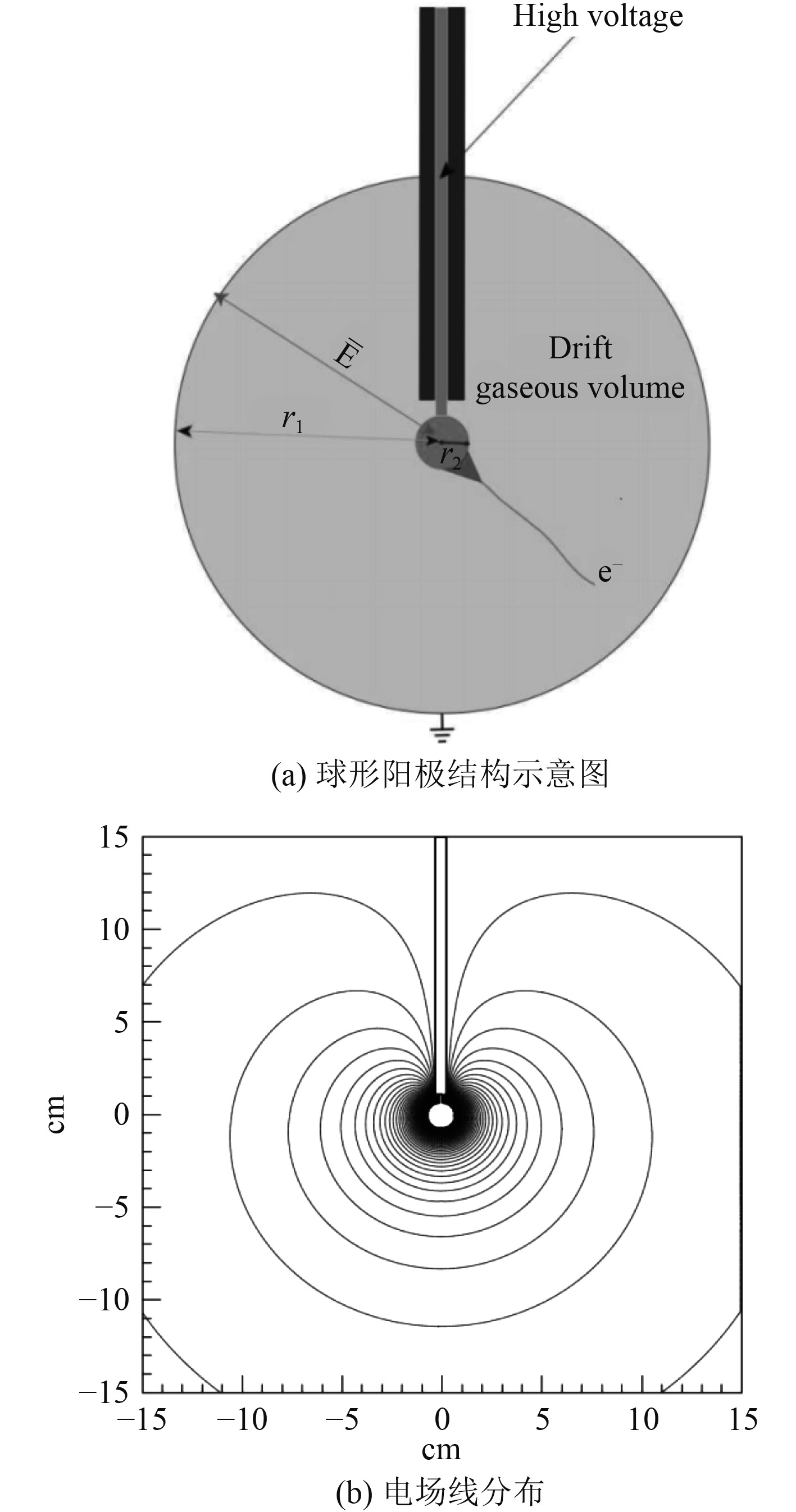
|
图 1 I.Giomataris等设计的球形阳极结构正比计数器 Fig. 1 The spherical anode proportional counter structure designed by I.Giomataris et al. |
在移动监测的运用背景下,仪器设计应尽可能做到紧凑与轻便,具有较强的稳定性及可靠性,同时对加工工艺要求和制造成本应尽可能低,“中心阳极丝+球形阴极外壳”的方案成为一种较好选择。
1 球形正比计数器电场均匀性研究无论球形还是圆柱体正比计数器,都不可避免地存在端效应问题,即电场沿阳极丝轴向方向至探头两端处会发生一定程度的畸变,对探测器放大倍数造成影响。多年来一直尝试抑制端效应,对圆柱体正比计数器可采用末端增加场管[6](处在特定电位下的金属管),牺牲一定的灵敏体积使阳极丝附近电场尽可能均匀。对球形正比计数器可设置一根环绕阳极丝的金属螺旋线,对其设置特定的电位,两端电场畸变的问题可得到有效解决。但这一做法同时带来了新的问题,金属螺旋线对机械震动较为敏感,伴随而来的是明显的噪声信号,且探测器结构变得精密复杂,在移动监测作业过程中可靠性降低。
1968年,Benjamin等[7]设计的球形正比计数器采用阴极球壳及阳极丝的结构,阳极丝两端由导体材料的支撑子固定,支撑子和阴极球壳之间由绝缘材料的绝缘子隔离。Benjamin通过在阴极球壳不同位置开孔射入粒子的方法进行了大量实验,通过电信号的不同来倒推电场均匀性,并不断地对阳极丝直径、支撑子直径、绝缘子直径、绝缘子距阳极丝端部距离、支撑子侵入球体距离共5个参数进行调整。最终得到一套最优的比例关系,即设球壳内直径为D,绝缘子直径为0.257D,阳极丝支撑子的直径为0.114D,阳极丝直径为5.5×10−4D,绝缘子距阳极丝端部距离为大于5.5×10−2D,支撑子侵入球体距离为0。这套设计方案和参数模板后来一直被沿用,这样的球形正比计数器结构被称之为Benjamin结构。

|
图 2 Benjamin型正比计数器结构 Fig. 2 Structure of Benjamin type proportional counter |
随着电子计算机的发展,可利用有限元分析软件Ansys进行复杂电磁场问题的数值分析,通过对由偏微分方程表征的连续数学模型所在场域,划分成有限多个离散单元,每个单元在有限的自由度下获得近似解,从而推导求解整个场域的问题。利用Ansys Workbench平台的电磁分析模块进行建模计算,构建直径为100 mm的球形正比计数器模型。按照Benjamin的模板,设置阳极丝直径为0.055 mm,支撑子直径11.4 mm,绝缘子直径25.7 mm,支撑子侵入球内0 mm,绝缘子距离阳极丝端部5.5 mm。考虑到阴极球壳和阳极丝在尺寸上差距近2 000倍,给建模过程中的网格划分带来了较大困难,借鉴林业在其文献[8-9]中推荐的做法,对阳极丝周围区域进行若干级的子区域划分,子区域为阳极丝的同心圆柱体,再对各个层级的子区域按适合的网格参数独立划分网格。通过这样的方法可提高阳极丝周围区域网格质量,从而提高计算精度。
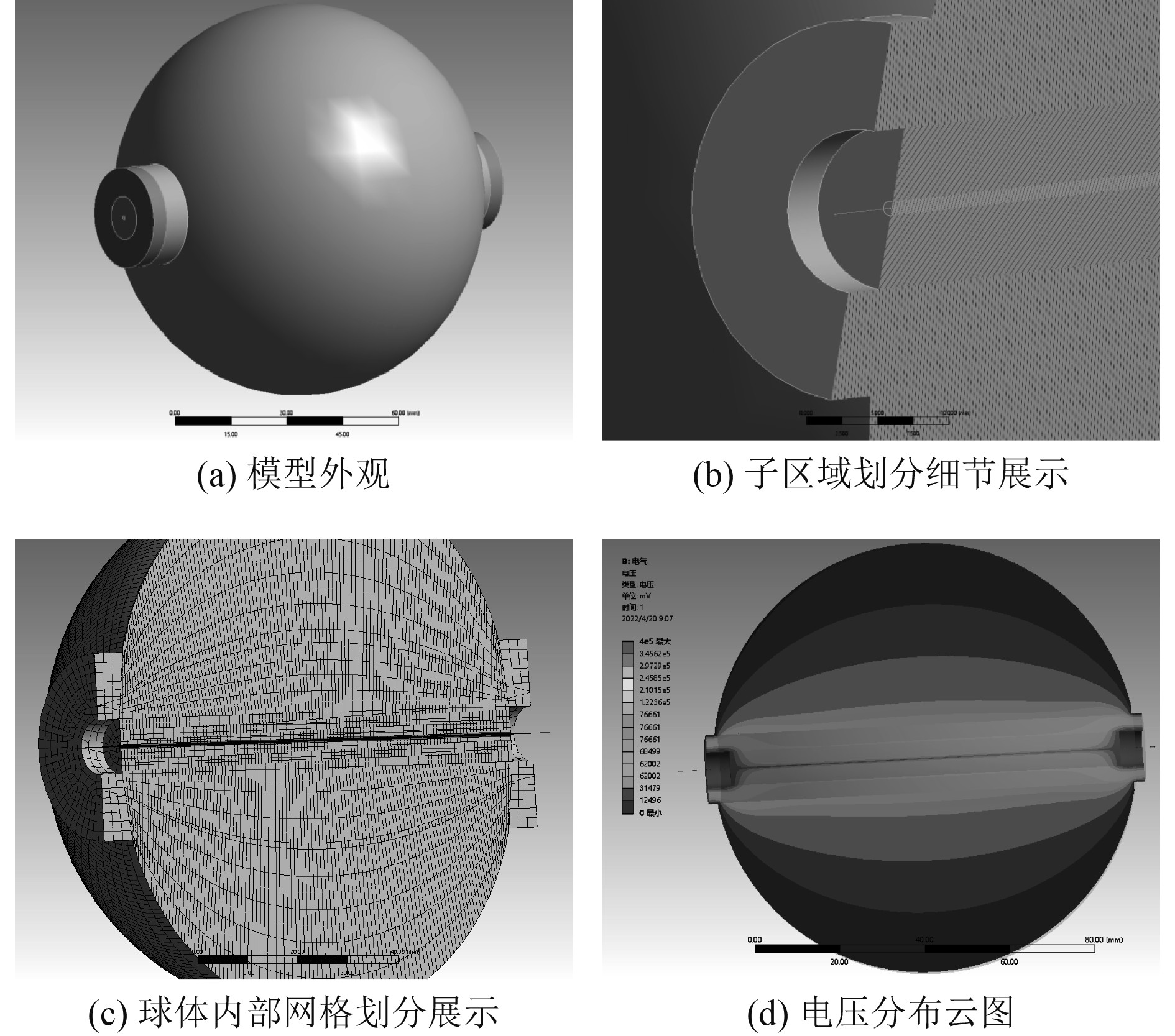
|
图 3 Ansys软件建模分析工作界面 Fig. 3 Interface of Ansys software in modeling and analysis |
取4倍于阳极丝直径的距离,平行于阳极丝构建路径,该路径处于电子雪崩区域,以此作为电场均匀性的考察路径,计算并分析该路径上的场强分布情况,如图4所示。可见,沿考察路径绝大部分区域电场较为均匀且基本与中心点场强相等,在向两端延申的过程中略微增强,最大增强0.94%。同时,可明显看到在靠近球体两端约10 mm区域出现电场强度的迅速衰减。该计算结果与Benjamin在实验中计算的结果基本吻合,说明有限元分析法可较好地模拟球形正比计数器内部电场真实的分布情况,同时也为Benjamin在1968年实验所得结论的精确性感到惊叹。对Benjamin推荐的参数进行适当调整,观察阳极丝周围场强的变化规律,寻找优化方案。
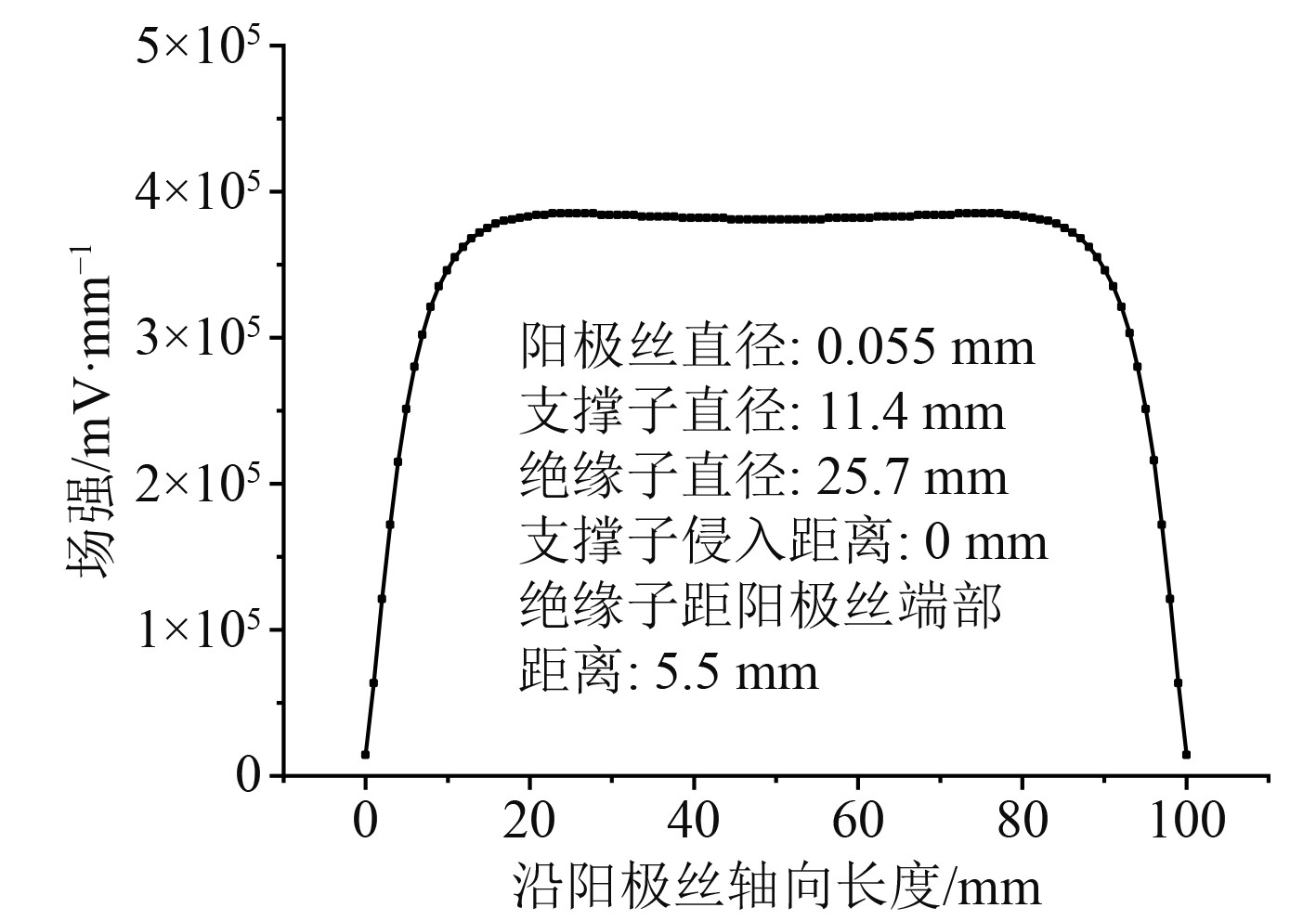
|
图 4 Benjamin型结构场强分布情况 Fig. 4 Electric field intensity distribution of Benjamin-type structures |
根据Benjamin模板的方案,对于100 mm直径的阴极球壳而言,支撑子直径为11.4 mm,在此基础上另取模板参数的50%、80%、120%、150%,即支撑子直径5.70 mm、9.12 mm、13.68 mm、17.10 mm进行模拟计算和分析,结果如图5所示。随着支撑子直径的减小,阳极丝两端的电场衰减区域出现明显压缩,但伴随而来的是电场在沿阳极丝向两端延申过程中出现更大程度的增强。当支撑子直径为5.7 mm时,可见阳极丝10 mm~20 mm、80 mm~90 mm位置场强出现明显“上拱”,相比中点处场强,最大增强比例为2.8%。而当支撑子直径扩大到17.1 mm时,增强比例减小到0.25%。对于这个数值,希望它越小越好,因为局部的场强增强意味着在这个区域发生雪崩的电子有着更高的放大系数,将给仪器带来更为严重的随机误差。在阳极丝两端,当场强下降至中心点的90%,即视为进入衰减区域。Benjamin模板的衰减区域占比为19.6%,当支撑子直径缩小到5.7 mm时,衰减区域占比13.73%;当支撑子直径扩大到17.1 mm时,衰减区域占比25.49%。
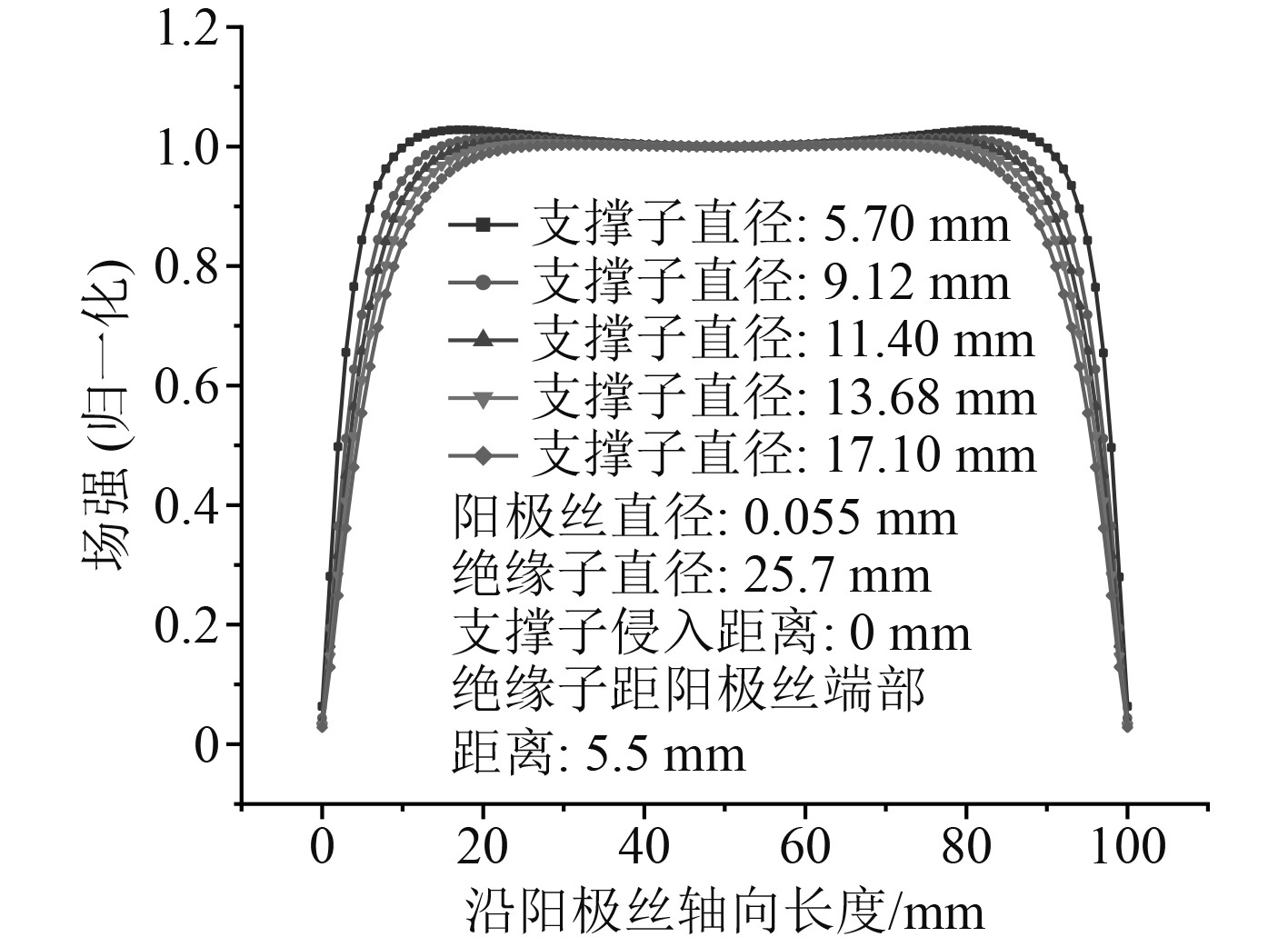
|
图 5 不同支撑子直径下的场强分布情况 Fig. 5 Distribution of electric field intensity under different supporter diameters |
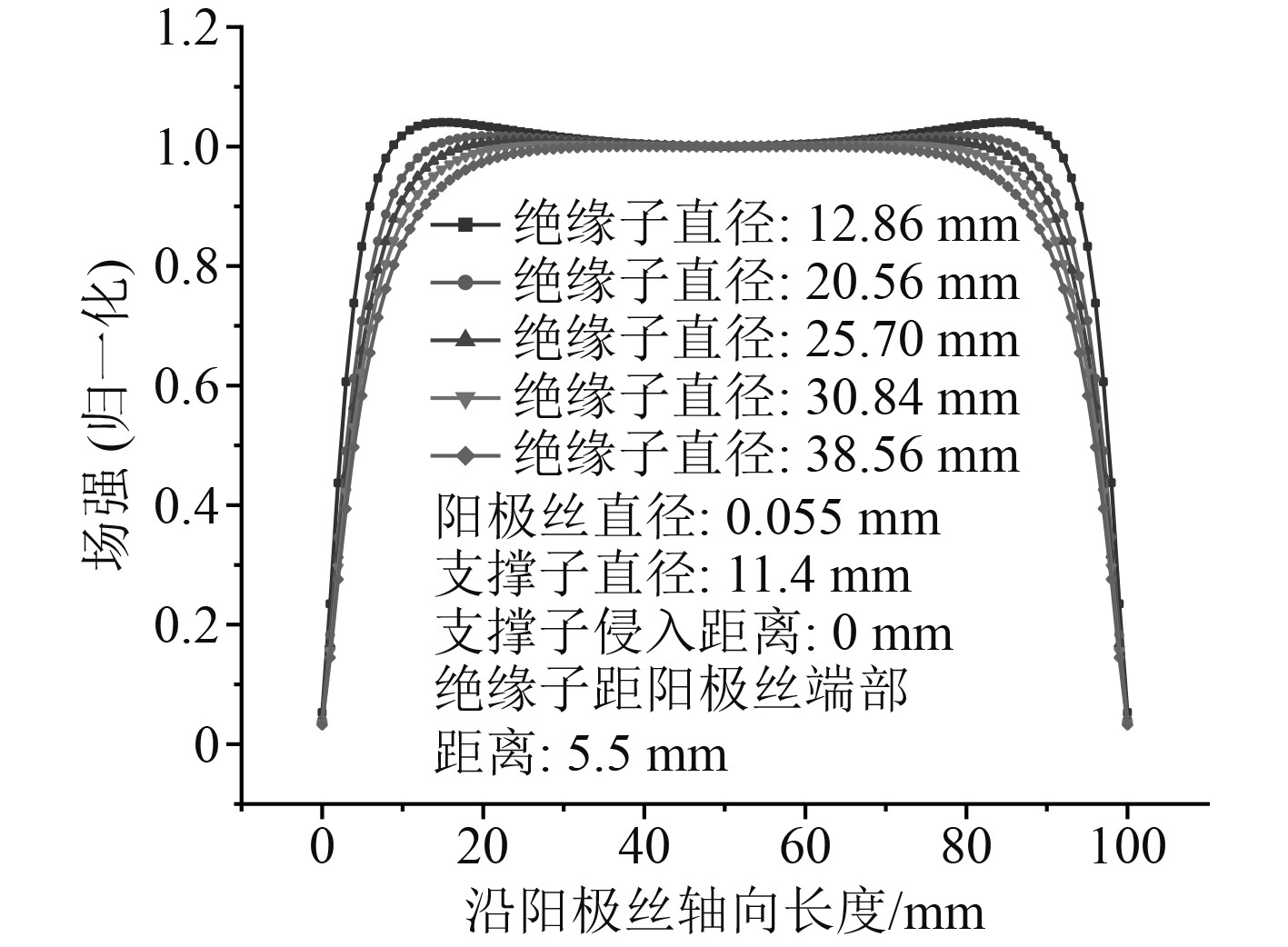
根据Benjamin模板,绝缘子直径为25.7 mm,取模板参数的50%、80%、120%、150%,得到绝缘子直径12.86 mm、20.56 mm、30.84 mm、38.56 mm,对这几组参数进行模拟计算得到场强曲线如图6所示。可发现,阳极丝周围场强随绝缘子直径的变化规律与支撑子直径的变化相似。当绝缘子直径减小为12.86 mm时,衰减区域占比减小至11.73%,但局部场强增强程度达4.05%;当绝缘子直径扩大到38.56 mm时,场强增强效应完全消失,但衰减区域占比扩大至19.61%。
|
图 6 不同绝缘子直径下的场强分布情况 Fig. 6 Distribution of electric field intensity under different insulator diameters |
按照Benjamin模板的设计,绝缘子距阳极丝末端为5.5 mm,在此基础上另取0 mm、2 mm、4 mm、7 mm进行对比,结果如图7所示。可见有限元分析计算结果十分接近,各场强曲线几乎重合,衰减区域长度变化不到0.3%,局部场强增强变化不到0.6%,以此说明绝缘子距阳极丝末端距离就计数器结构上的改变对场强的影响极小。文献[7]对此问题做了一定解释,通常绝缘子表面会堆积一定数量的正电荷,如果绝缘子距阳极丝过近,将会在一定程度上进一步削弱末端附近的电场强度。但根据绝缘子材料的不同情况将变得不同,且在本工作的有限元分析模型中难以被量化。可预见的是,在选用介电常数尽可能低的良好绝缘材料情况下,将允许绝缘子与阳极丝末端的距离缩小,以减小球体两端出现的多余的腔室空间。

|
图 7 绝缘子距阳极丝末端不同距离下的场强分布情况 Fig. 7 Distribution of electric field intensity under different distancebetween the insulator and the end of the anode wire |
Benjamin推荐的支撑子侵入距离为0 mm,同时对侵入距离为2 mm、4 mm、6 mm共4个方案进行分析计算,对比结果如图8所示。当侵入距离为0 mm时,局部场强增强0.94%,之后随着侵入距离的增加而减小;当侵入增加至4 mm时几乎完全消失,但随之而来的是有效灵敏体积的减小和衰减区域的扩宽;当侵入距离为6 mm时,衰减区域占比27.45%,算上支撑子占用的距离,将损失约35 mm长的有效区域,这个结果已经令人无法接受。

|
图 8 支撑子侵入不同距离下的场强分布情况 Fig. 8 Distribution of electric field intensity under different distance of supporter intrusion |
对于球形正比计数器而言,相比圆柱体正比计数器,最大的优势在于各向同性方向响应,但同时也存在更为复杂的端效应问题。Benjamin型球形正比计数器通过阳极丝两端设置支撑子和绝缘子的结构,使得沿阳极丝附近的雪崩区域具有较为均匀的电场强度。但考虑到2个端部加工区域的材料和结构均与阴极球壳有较大差异,这不可避免地会影响到从这个方向入射的粒子响应,特别对于表面覆盖慢化层的正比计数器而言更应引起重视。在Benjamin推荐的参数模板中,支撑子和绝缘子的直径分别达到了球体直径的11.4%和25.7%,这部分结构影响的探测角度为59.6°。对支撑子直径、绝缘子直径、支撑子侵入球体距离等参数对腔室内电场均匀性的影响进行计算和分析,发现当支撑子和绝缘子的直径减小时,阳极丝附近雪崩区域的电场都是朝着局部场强增强和衰减区域缩短的趋势发展,而这与支撑子侵入球体产生的影响相反。因此,这提供了一种思路,通过将支撑子侵入球体一定的距离,来作为缩小支撑子和绝缘子直径的补偿,在保持较好的电场均匀性同时,尽可能减小端部结构对角度响应的影响。
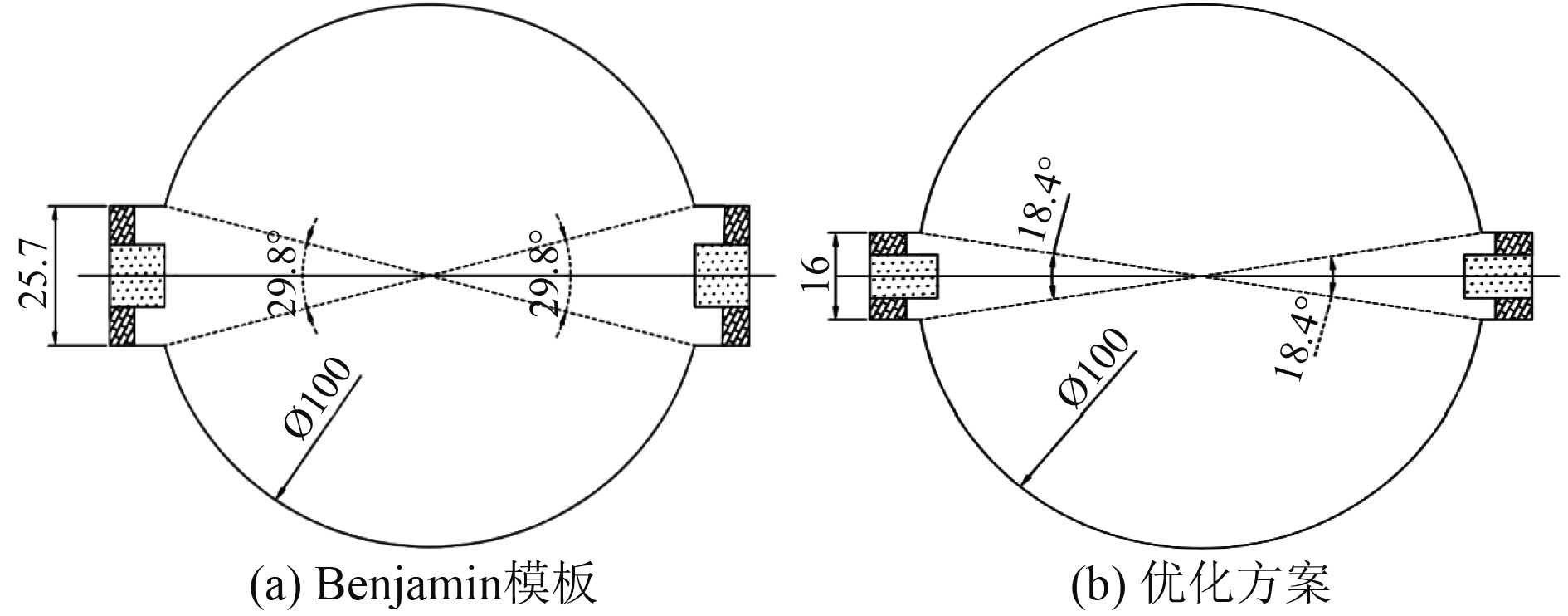
通过不断调整参数进行计算比较,发现当支撑子侵入球体3 mm时,可将支撑子直径缩小至8 mm;绝缘子直径缩小至16 mm,此时的局部场强增强比例为0.91%;衰减区域占比17.65%。这基本同Benjamin的模板参数计算结果相当,但端部结构带来的影响角度减小至36.8°,减少了38.3%,结构对比如图9所示。
|
图 9 优化方案与Benjamin模板的结构对比 Fig. 9 Structure comparison between optimization scheme and Benjamin template |
若想继续缩小端部结构尺寸,在保持阳极丝附近场强均匀性的前提下,势必会要求支撑子进一步侵入球体腔室,代价即牺牲更多的有效灵敏体积。优化方案与Benjamin模板的结构参数对比如表1所示。优化方案与Benjamin模板的指标对比如表2所示。
|
|
表 1 优化方案与Benjamin模板的结构参数对比 Tab.1 Comparison of structure parameters between optimization scheme and Benjamin template |
|
|
表 2 优化方案与Benjamin模板的指标对比 Tab.2 Performance comparison between optimization scheme and Benjamin template |
通过对比分析各类正比计数器结构优势特点,确定了“阳极丝+球形结构”的设计方案,选择Ansys有限元分析软件对Benjamin球形结构电场分布情况进行模拟计算,还原了Benjamin模板参数下阳极丝周围雪崩区域的场强数据。通过独立调整改变支撑子直径、绝缘子直径、绝缘子距阳极丝末端距离、支撑子侵入球体距离4个结构参数,计算并分析参数变化对场强分布的影响规律。考虑到端部结构改变了球体的均匀性,特别是对于覆盖有慢化层的球形探测器,对从两端入射到气体腔室的粒子可能表现出不同的响应。因此选择从局部场强增强的程度和场强衰减区域的占比2个指标入手,在对照Benjamin模板确保这2项指标不变差的基础上,通过将支撑子侵入球体3 mm距离,使球体端部结构由直径25.7 mm减小至16 mm,从而减小了对探测器方向响应性能的影响。
| [1] |
陈伯显, 张智. 核辐射物理及探测学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2011.
|
| [2] |
CHARPAK G, BOUCLIER R, BRESSANI T. The use of multiwire proportional counters to select and localize charged particles[J]. Nuclear Instruments and Methods, 1968, 62(3): 262-268. DOI:10.1016/0029-554X(68)90371-6 |
| [3] |
ROSSI H H, ROSENZWEIG W. A device for the measurement of dose as a function of specific ionization[J]. Radiology, 1955, 64(3): 404-411. DOI:10.1148/64.3.404 |
| [4] |
GIOMATARIS I, AUNE S, COLAS P, et al. NOSTOS experiment and new trends in rare event detection[J]. Nuclear Physics B - Proceedings Supplements, 2006, 150: 208-213. DOI:10.1016/j.nuclphysbps.2005.01.245 |
| [5] |
GIOMATARIS I, IRASTORZA I, SAVVIDIS I, et al. A novel large-volume spherical detector with proportional amplification read-out[J]. Journal of Instrumentation, 2008, 3(9): P09007-P09007. |
| [6] |
张伟华. 组织等效正比计数器结构优化设计[J]. 原子能科学技术, 2014, 48(5): 930-933. DOI:10.7538/yzk.2014.48.05.0930 |
| [7] |
BENJAMIN P W, KEMSHALL C D, REDFEARN J. A high resolution spherical proportional counter[J]. Nuclear Instruments and Methods, 1968, 59(1): 77-85. DOI:10.1016/0029-554X(68)90347-9 |
| [8] |
林业. 辐射生物效应评估中气体探测器关键技术研究[D]. 成都: 成都理工大学, 2018.
|
| [9] |
LIN Y, YUAN Y, FANG F, et al. A study of electric field distribution in Benjamin type proportional counter using finite element method[J]. Applied Radiation and Isotopes, 2018, 135: 142-146. DOI:10.1016/j.apradiso.2018.01.015 |
 2023, Vol. 45
2023, Vol. 45
