作为一种超视距雷达,高频地波雷达可以对海面上的环境以及移动的目标进行大面积全天候的超视距实时监控[1]。和其他雷达相比较,监测面积大、成本低是高频地波雷达的优点。同时高频地波雷达可以弥补常规微波雷达的低空盲区缺点,能够及时地探测到微波雷达无法探测到的目标,实现海面预警。高频地波雷达还可以弥补超视距雷达的近区盲点,无需依靠电离层[2]。随着高频地波雷达市场化技术的进一步发展,高频地波雷达的应用也经历了由目标探测到环境监控,再到目标探测的一个转变过程,并且经过近几年的研究,国外对高频地波雷达的研究已经有了长足的进步,其技术仍在飞快地发展[3]。由于我国在高频地波雷达研究方面起步比较晚,因此在高频地波雷达的技术上和国外相比存在一定的差距。
1 高频地波雷达技术 1.1 高频地波雷达探测机理和传统的微波雷达相比,高频地波雷达的工作机制决定了外部的噪声和干扰是其最主要的干扰源,并且会随着高频地波雷达探测的外部环境不同而变化[4]。高频地波雷达受到的外部噪声和干扰中既包含了海杂波、电离层等无源干扰,也包含了环境以及射频等有源干扰,此外还会受到流星余迹和雷电共同构成的冲击干扰。
海杂波是由高频地波雷达的发射信号和海浪发生谐振而产生的一种回波。在多普勒谱上,一阶连续谱和高阶谱共同构成了高频地波雷达的海杂波。其中一阶布拉格峰和雷达发射频率之间的关系,可以表示为:
| $ {f_B} = \pm \sqrt {g/{\text π} \lambda } \approx \pm 0.102\sqrt {{f_R}} \text{,} $ | (1) |
因为高频地波雷达的一般工作在长波段,这导致高频地波雷达的天线尺寸比较大,为了降低阵地面积,因此通常使用均匀线阵,但是这会导致部分能量会向上发送到天空中,然后经过电离层的反射,最终反馈给高频地波雷达的接收机,产生电离层干扰。高频地波雷达的电磁波发射到电离层上的折射指数可以表示为:
| $ {\mu ^2} = 1 - \frac{{f_p^2}}{{{f^2}}}\text{,} $ | (2) |
| $ {f_p} = \frac{1}{{2{\text π} }}\sqrt {\frac{{N_e^2}}{{m{\varepsilon _0}}}} 。$ | (3) |
式中,fp为入射频率。目标测量的最大距离是高频地波雷达最重要的性能,高频地波雷达方程则可以反映这个问题,公式为:
| $ {P_r} = {S_r}{A_r}\text{。} $ | (4) |
式中:Sr为功率密度;Ar为有效面积。
| $ {S_r} = \frac{{E_r^2\left( R \right)}}{\varOmega }\text{,} $ | (5) |
| $ {A_r} = \frac{{{G_r}{\lambda ^2}}}{{4{\text π} }}\text{。} $ | (6) |
结合高频地波雷达的系统损耗Ls、雷达信号的占空比γ以及发射功率Pt,则回波功率的计算公式为:
| $ P = \frac{{{E^2}\left( R \right){P_t}\gamma {G_t}{G_r}{\lambda ^2}\sigma }}{{a{\text π} {\varOmega ^2}P_0^2G_0^2{L_s}}}\text{。} $ | (7) |
垂直化的电磁波通常被高频地波雷达用来进行远程目标探测,地球表面上垂直极化的电偶极子所产生的空间磁场强度公式为:
| $ E=\frac{1}{k{n}^{2}R\mathrm{sin}\theta }·\frac{\partial }{\partial \theta }\left(\mathrm{sin}\theta \frac{\partial {U}_{r}}{\partial \theta }\right) \text{。} $ | (8) |
式中:k为空间波数,
| $ {U_r} = \frac{{\exp \left( { - jkD{m_0}} \right)}}{{{R_0}D\sin {{\left( {\dfrac{D}{{{R_0}}}} \right)}^{\frac{1}{2}}}}}\left( {{W_d} + {W_r} + {W_s}} \right)\text{。} $ | (9) |
通过式(8)可以实现光滑球体表面的高频地波雷达的距离计算,但是高频地波雷达的实际工作环境中,会存在海风以及海浪等因素的影响,因此如果直接使用式(8)进行解算,会带来很大的误差。引入海面粗糙度修正式(8),使其更符合实际情况。海面风浪高度可以使用二维傅里叶级数来表示,如下式:
| $ \zeta \left( {x,y} \right) = \sum\limits_{m,n = - \infty }^\infty {H\left( {m,n} \right)\exp \left( { - j\frac{{2{\text π} m}}{L}x - J\frac{{2{\text π} m}}{L}y} \right)} \text{。} $ | (10) |
式中:L为海浪区域的边长;H(m,n)为傅里叶系数。作为海浪的主要影响因素,风力可以将海浪分成饱和海浪以及涌浪2种,由于高频地波雷达在探测目标过程中需要一定时间的积累,因此海面粗糙程度在海风的作用下能够达到最大,通过解算,则可以获得不同海风下的海面平均高度,最终计算出地波雷达传播的电磁强度值。地波衰减随距离的变化曲线如图1所示,可以看出,随着距离的增大,衰减越严重。
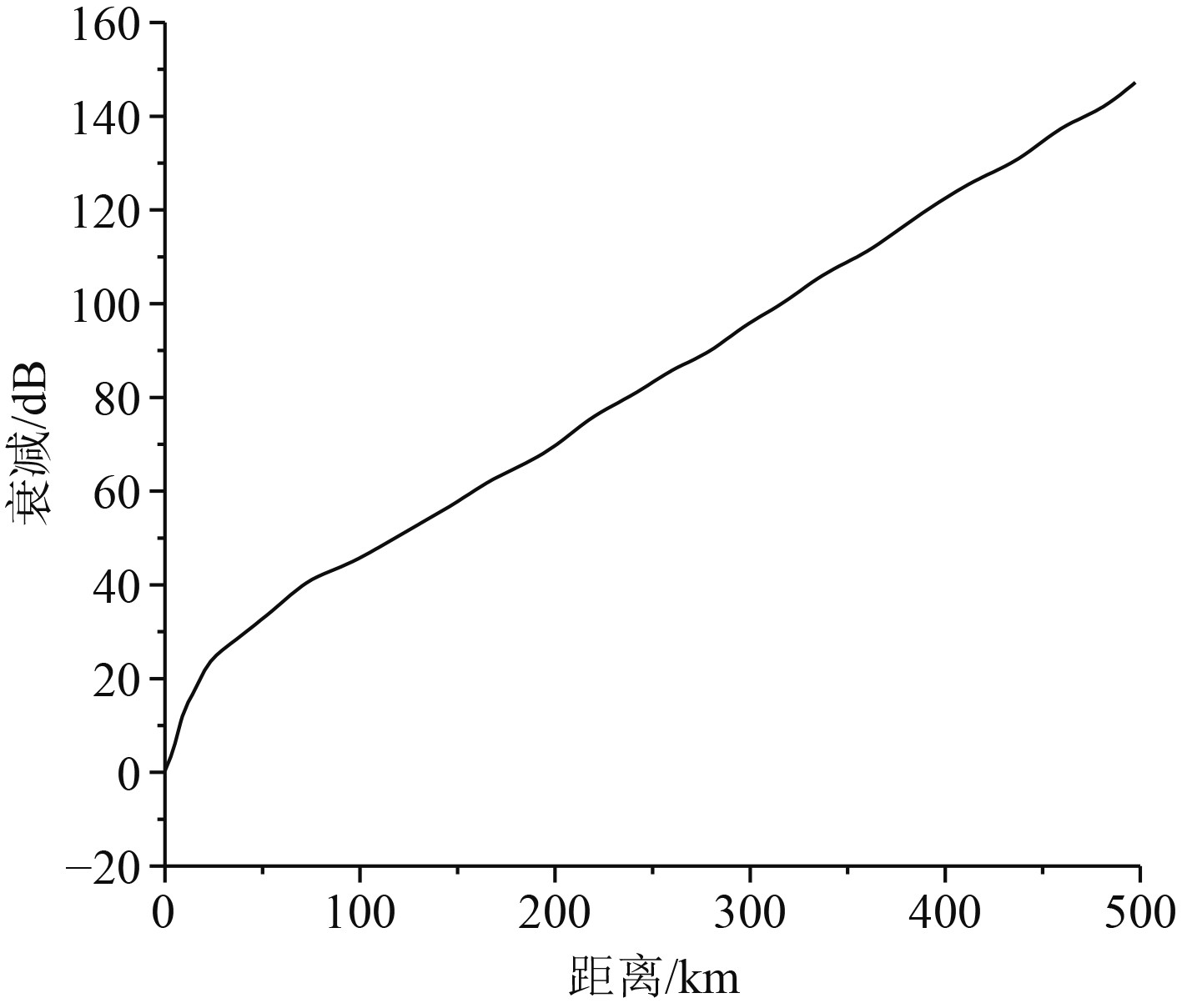
|
图 1 地波衰减随距离的变化曲线 Fig. 1 Curve of ground wave attenuation with distance |
高频地波雷达收到的回波信号中既包含了目标船舶的信息,也包含了海杂波、电离层杂波等干扰信号。由于海杂波在R-D谱图中沿着距离方向上延伸,因此采用基于距离向的曲线拟合算法可以极大地避开海杂波对船舶目标探测的影响[5]。随着距离的不断变大,高频地波雷达收到的回波信号的强度先强后弱,并且在电离层达到最大强度[6]。由于在距离向上的高频地波雷达信号的形式比较简单,因此使用二次曲线拟合即可,高频地波雷达信号在距离向上的拟合曲线函数为:
| $ g\left( x \right) = a{x^2} + bx + c \text{。} $ | (11) |
式中:系数a,b,c需要根据实际测量的数据得到。使用原始数值减去拟合数据获得处理结果,如下式:
| $ y\left( x \right) = g\left( x \right) - f\left( x \right)\text{。} $ | (12) |
式中:g(x)为多普勒单元数据;f(x)为拟合后的数据,相减的结果如果大于0则为目标,如果小于0则为杂波干扰信号。
在测试得到的高频地波雷达回波信号中,电离层的杂波是基于多普勒方向上分布的,并且电离层杂波在距离上存在一定的扩展[7]。在多普勒方向上绘制出某个距离单元格数据的幅值变化情况,则可以看出船舶目标信号位于海杂波和地杂波之间。考虑到高频地波雷达信号中存在大量的海杂波以及地杂波,这导致多普勒谱的结构相对比较复杂,因此功率谱的拟合曲线需要使用三次函数才行,公式为:
| $ f\left( x \right) = a{x^3} + b{x^2} + cx + d\text{。} $ | (13) |
根据不同的测试环境,式(13)中的系数a、b、c、d取值也会出现相应的变化。本文选取多普勒向中第1059个单元,并对这一单元数据进行拟合,最终获得拟合曲线,如图2所示。可以看出,距离向上的最大的幅值在60 km左右。多普勒向曲线拟合结果如图3所示,可以看出,多普勒向上拟合曲线近似于一条直线。
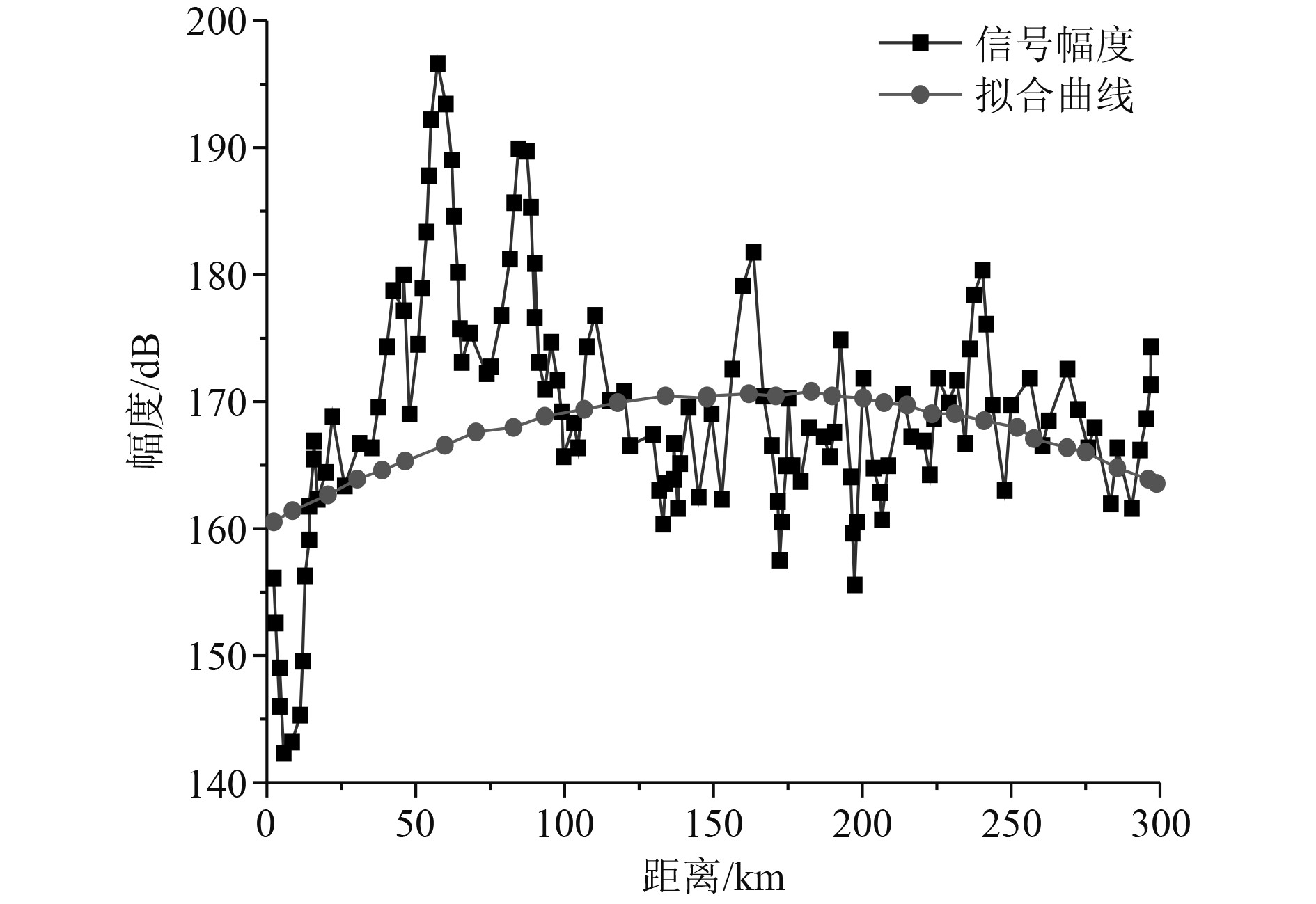
|
图 2 距离向曲线拟合 Fig. 2 Distance curve fitting |
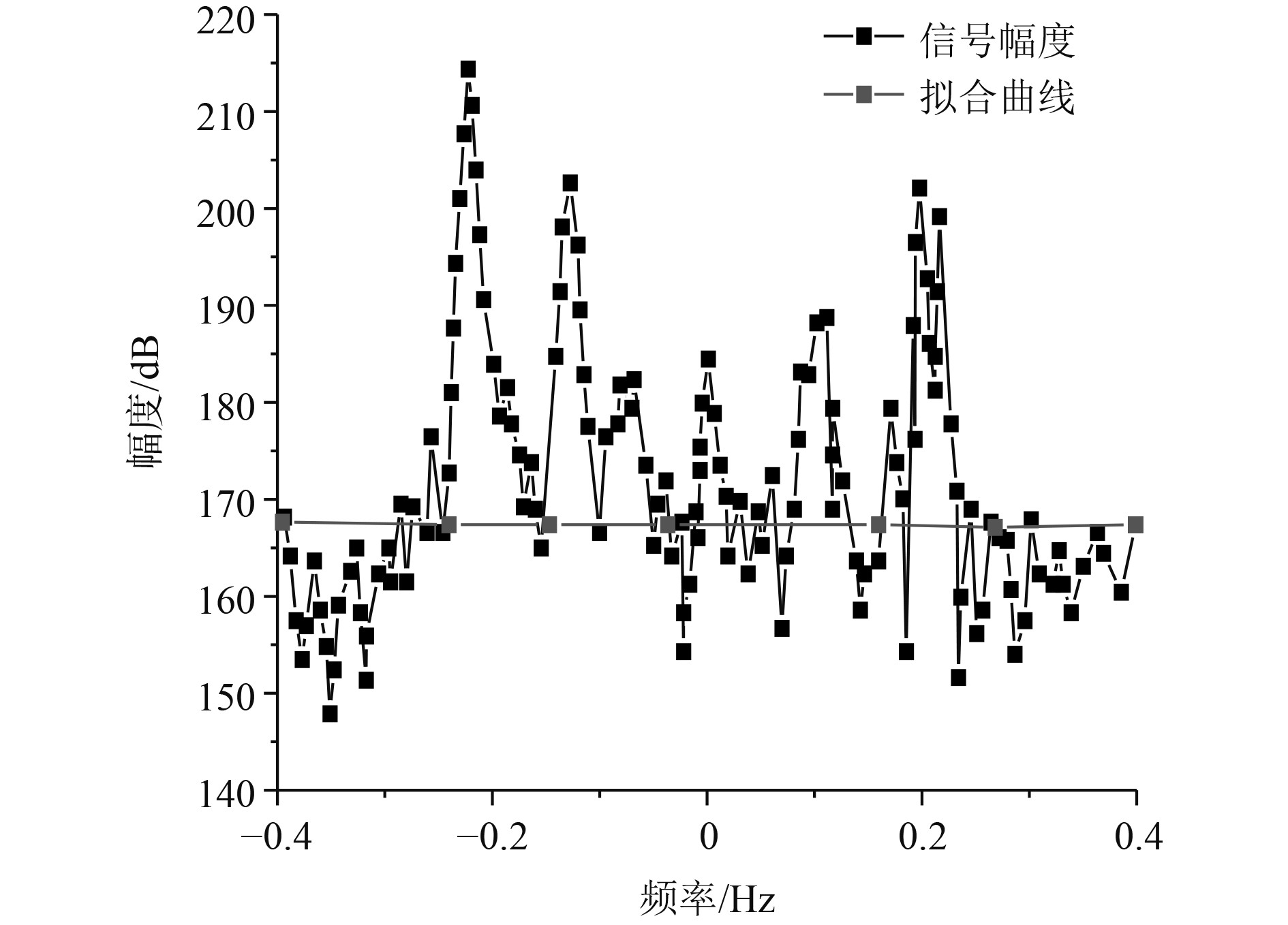
|
图 3 多普勒向曲线拟合 Fig. 3 Doppler curve fitting |
作为高频地波雷达信号的经典处理方法,恒虚警率技术可以为高频地波雷达的信号检测提供阈值。恒虚警算法以船舶目标探测为目的,将高频地波雷达的回波信号分割成噪声和目标两类,可以表示为:
| $ v\left( t \right) = s\left( t \right) + n\left( t \right)\text{。} $ | (14) |
式中:s(t)为船舶目标信号;n(t)为噪声信号。探测概率和虚警率的计算方法如下:
| $ {p_d} = \int_{}^\infty {{p_1}\left( x \right){\rm{d}}x} \text{,} $ | (15) |
| $ {p_{fa}} = 1 - \int_0^t {p\left( x \right){\rm{d}}x} \text{。} $ | (16) |
由于高频地波雷达需要进行杂波功率估算,因此需要构建杂波幅度的估算模型,高频地波雷达信号的多普勒向功率幅度的概率密度函数可以用式(17)来表示。多普勒向噪声功率曲线如图4所示,可以看出,最小幅度为150 dB。
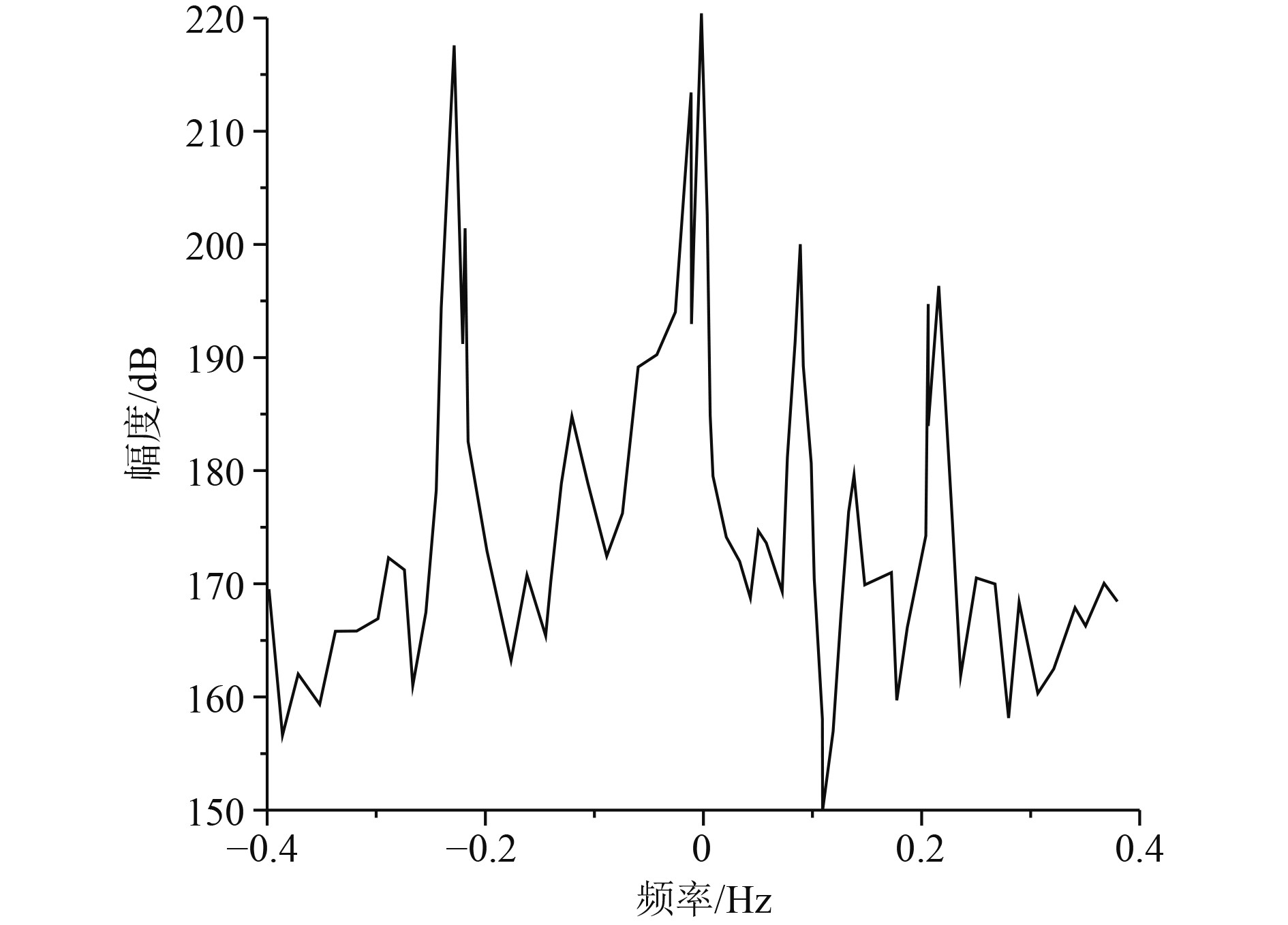
|
图 4 多普勒向噪声功率曲线 Fig. 4 Doppler noise power curve |
| $ P\left( x \right) = \left\{ {\begin{array}{*{20}{l}} \dfrac{x}{{\bar \sigma _s^2}}\exp \left( { - \dfrac{{{x^2}}}{{2\sigma _s^2}}} \right), & x \geqslant 0,\\ 0,&x < 0 。\end{array}} \right. $ | (17) |
高频地波雷达目标识别系统主要包含发射和接收2个独立的基站。发射机以及发射天线构成了高频地波雷达的发射站,接收机、中央主机以及信号处理机组成了高频地波雷达的接收站。高频地波雷达的系统结构如图5所示。
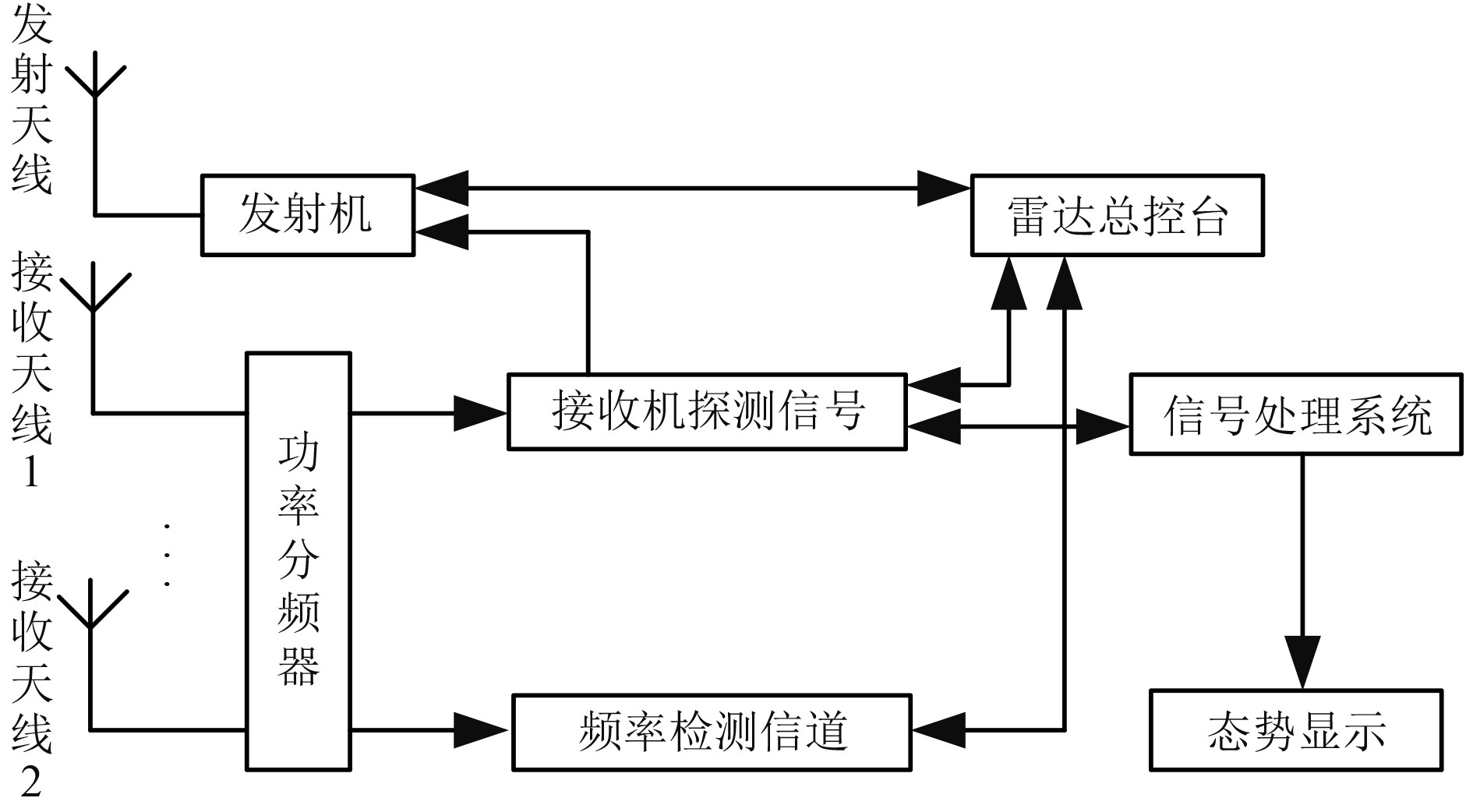
|
图 5 基于高频地波雷达的船舶目标识别系统 Fig. 5 Ship target recognition system based on high frequency ground wave radar |
以数字波束和脉冲压缩为基础,构建包括杂波抑制、恒虚警检测等功能的高频地波雷达船舶目标识别系统。高频地波雷达目标识别系统经过对雷达信号回波的解调、抽取以及FFT变换之后,可以得到每个通道中的距离谱信息,即高频地波雷达的基数据。为了降低解算难度,积累脉冲个数采用2的整数倍,高频地波雷达的船舶探测参数如表1所示。
|
|
表 1 高频地波雷达的船舶探测参数 Tab.1 Ship detection parameters of high-frequency ground wave radar |
通过脉冲压缩的方法可以获得距离维度信息,具体操作为:将通道维以及慢时间维固定住,然后对所有的通道维和慢时间维进行脉冲压缩处理,则可以得到距离谱,如图6所示。可以看出,幅值变化范围为−12~2 dB。以脉冲压缩为基础,进行数字波束处理,则可以得到方位维信息。具体操作为,将快时间和慢时间维固定住,然后对通道维执行数字波束处理,则可以获得方位谱信息,如图7所示。可以看出,幅值最低值为−13 dB。

|
图 6 距离谱 Fig. 6 distance spectrum |

|
图 7 方位谱 Fig. 7 Azimuth spectrum |
作为超视距雷达的一种,高频地波雷达被广泛的应用于民用和军事领域。在军事方面主要用在远距离目标监控以及预警,能够在强干扰环境下对高速运行的目标进行探测。由于高频地波雷达工作在高频段,因此对隐身目标也存在探测能力。在民用领域,高频地波雷达主要用于海面上的洋流、海风以及海浪等参数的监测,同时可以提供海洋的气象预警报告。高频地波雷达凭借其在海面上饶射衰减比较小的特点,可以用来对海面上的船舶目标进行大面积、远距离、全天候的监控,并且高频地波雷达的性价比高。因此只需要比较低的成本,即可实现对海面上船舶目标的宏观监测。
| [1] |
陈伯孝, 李锋林, 潘孟冠. 岸-舰双基地地波超视距雷达技术[J]. 雷达科学与技术, 2015(13): 333-339. |
| [2] |
张晖, 刘永信, 张杰等. 地波雷达与自动识别系统目标点迹最优关联算法[J]. 电子与信息学报, 2015(37): 619-624. |
| [3] |
毛涛, 夏卫民, 曲翠萍等. 高频地波超视距雷达特点及应用研究[J]. 现代雷达, 2009(31): 7-10. |
| [4] |
李娟. 高频地波激光雷达舰船目标识别跟踪系统的设计[J]. 激光杂志, 2017(38): 84-87. |
| [5] |
李庆忠, 韩怡. 高频地波雷达RD谱图海面目标检测算法[J]. 现代雷达, 2020(42): 6-12+18. |
| [6] |
孙伟峰, 周德明, 戴永寿等. 高频地波雷达海上目标航迹校正方法[J]. 中国海洋大学学报, 2017(47): 22-29. |
| [7] |
张悦旺. 高频地波雷达舰船目标识别系统的研究与设计[J]. 舰船科学技术, 2017(39): 106-108. |
 2023, Vol. 45
2023, Vol. 45
