2. 浙江省机器人与智能制造装备技术重点实验室, 浙江 宁波 315201;
3. 鸣志电器(太仓)有限公司, 江苏 苏州 215400
2. Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo 315201, China;
3. Mingzhi Electric Appliance (Taicang) Co., Ltd., Suzhou 215400, China
目前水下永磁推进电机成为各种船舶、潜艇、水下机器人的理想推进结构,但一直深受电机电磁噪声的困扰。随着各种仿真软件的快速发展,采用有限元进行电机电磁振动噪声的研究越来越多。文献[1-6]分别针对内转子、外转子、爪极和轴向磁通永磁同步电机的振动和噪声性能进行了有限元数值分析,文献[7]分析了极槽配合与绕组结构,对电磁振动的影响进行了分析。水下推进电机的振动噪声分析流程如图1所示。先利用电磁有限元软件计算电机的时间和空间磁场,同时通过磁场计算器计算并且处理后,得到电机定子上的电磁力。获得电磁力之后,通过傅里叶变换(FFT),将变换后的电磁力结果耦合到结构有限元中进行振动谐响应分析。最后将计算得到的电机外表面的振动导入到声域计算的有限元模型中作为声场模型激励源,从而计算电机的辐射噪声。另外,在谐响应分析之前,还可先进行模态分析中。文献[8-10]对各种电机的模态及固有频率均有详细的分析,为电机在谐响应分析中的声振特性情况做铺垫。

|
图 1 电磁振动噪声分析流程 Fig. 1 Analysis process of electromagnetic vibration noise |
本文主要从空气电机噪声再映衬到整个水下电机振动噪声分析,通过对800 r/min转速的水下推进电机振动噪声的研究,分析转速导致的振动噪声形成共振的特性。通过对壳体进行避免共振的研究,设计了一种抑制振动噪声的电机壳。
1 电机电磁特性及模态电磁噪声主要由电机气隙处不同阶次与频率的径向磁场相互作用产生的电磁力所引起,该电磁力主要作用在定子上引起振动,然后引发定子外声传播介质(空气/水)的振动从而产生辐射噪声。
1.1 电机的径向电磁力特性由径向电磁力密度产生机理可知,径向电磁力波是一个同时关于时间和空间变化的变量。
气隙磁密计算如下:
| $ b\left( {\theta ,t} \right) = f\left( {\theta ,t} \right) \cdot \lambda \left( {\theta ,t} \right) ,$ | (1) |
相应的气隙磁场所产生的径向电磁力波如下:
| $ {p_n}\left( {\theta ,t} \right) = \frac{{{b^2}\left( {\theta ,t} \right)}}{{2{\mu _0}}} 。$ | (2) |
式中:f(θ,t)为电机气隙磁动势总和;λ(θ,t)为气隙磁导率;μ0为气隙磁导率。
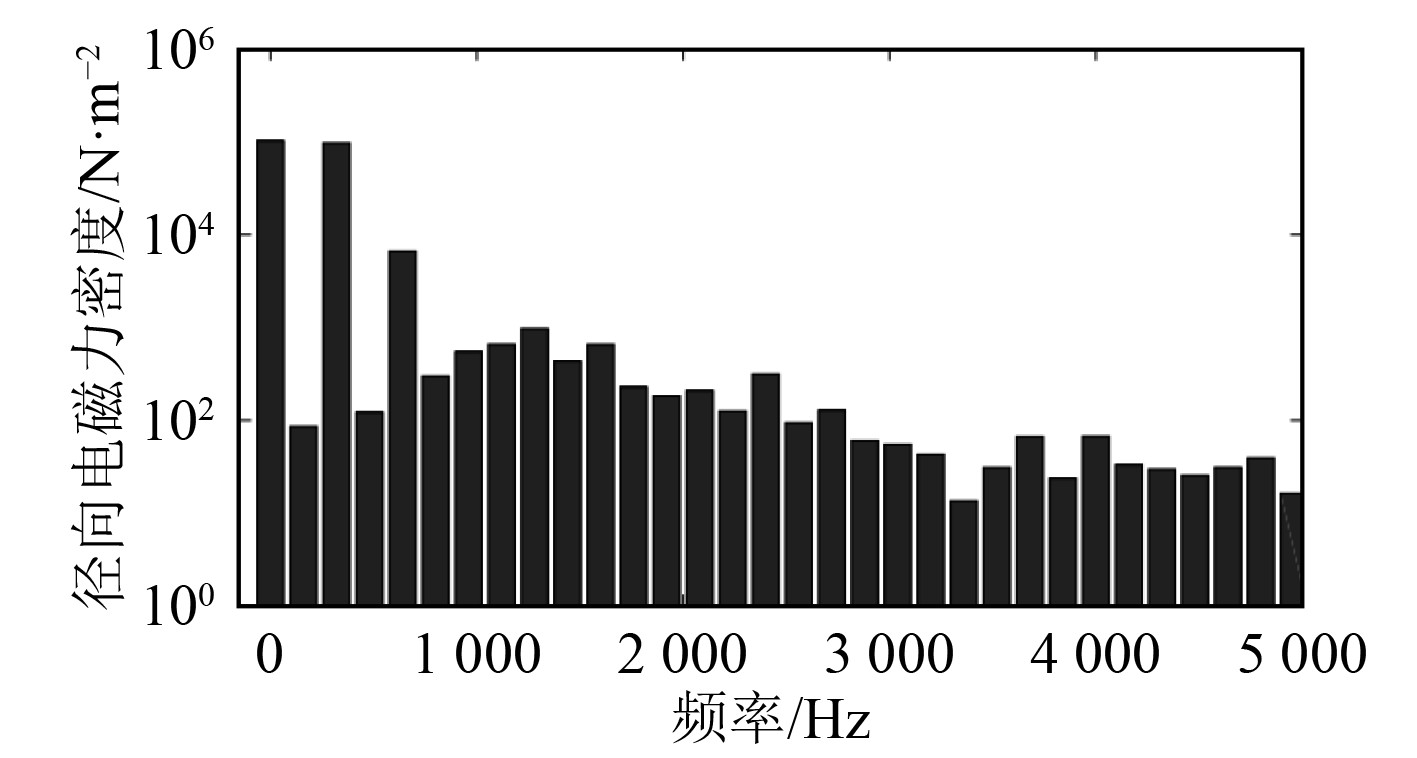
以某额定转速为800 r/min的水下推进电机为例有进行限元分析,当转速为800 r/min时,在一个电频率(160 Hz)周期对径向电磁力密度结果进行FFT变换,结果如图2所示。
|
图 2 推进电机径向电磁力密度频谱图 Fig. 2 Spectrum diagram of radial electromagnetic force density of propulsion motor |
结果表明,在该电机800 r/min转速时,气隙径向电磁力密度成分主要为电频率160 Hz的整数倍频。
1.2 定子结构模态由于定子结构的各阶模态都有其对应的固有频率,当径向电磁力波的频率和模态的固有频率接近或者重合时,会导致结构比较大的振动即共振,从而产生较大噪声。因此首先分析推进电机在不同转速下径向电磁力密度的频谱特性及电机定子的模态特性,判断二者关系推导产生共振的可能性。
| $ {f}_{m}=\frac{1}{2 \text{π} }\Bigg(\frac{{K}_{m}}{{M}_{m}}\Bigg)^{1/2} 。$ | (3) |
式中:fm为电机m阶振型定子固有频率;Km为定子刚度;Mm为定子质量[11]。
与电机径向电磁力振型对应的定子各阶模态如图3所示。

|
图 3 定子各阶模态 Fig. 3 Various modes of stator |
将定子各阶模态的固有频率分别和推进电机在转速为800 r/min时的径向电磁力密度较近频率点,对照分析如表1所示。由此可推测,在频率范围可能形成共振的频谱特性。
|
|
表 1 定子模态与激振力集中点 Tab.1 Stator mode and excitation force concentration point |
根据表1可知,推进电机在转速800 r/min时径向电磁力密度和定子固有频率接近的分别有0阶、1阶、2阶、3阶、4阶、5阶、7阶、10阶定子模态。结合图2该电机800 r/min时,电磁力大小进行对比分析。在频率160 Hz、3360 Hz、4960 Hz处的电磁力密度较小,2倍频(320 Hz)电磁力较大但320 Hz和3阶固有频率相差较远,因此不会形成明显的共振。
2 振动及噪声辐射将径向电磁力作为激振力耦合到谐响应模块分析定子结构振动,然后将定子外表面振动作为声学分析模块的激励源计算0~5 000 Hz频率范围的声学辐射噪声,求解推进电机1 m处水和空气噪声声压级频谱特性。
2.1 水下推进电机振动定子及机壳部分具有刚度和质量,进行结构分析时,将定子简化为一个圆筒型壳体。根据Hamilton 函数以及应力-应变的关系,结构场域的有限元求解计算满足下式:
| ${\boldsymbol{ M}}\frac{{{\partial ^2}u}}{{\partial {t^2}}} + {\boldsymbol{C}}\frac{{\partial u}}{{\partial t}} + {\boldsymbol{Ku }}= F 。$ | (4) |
式中:
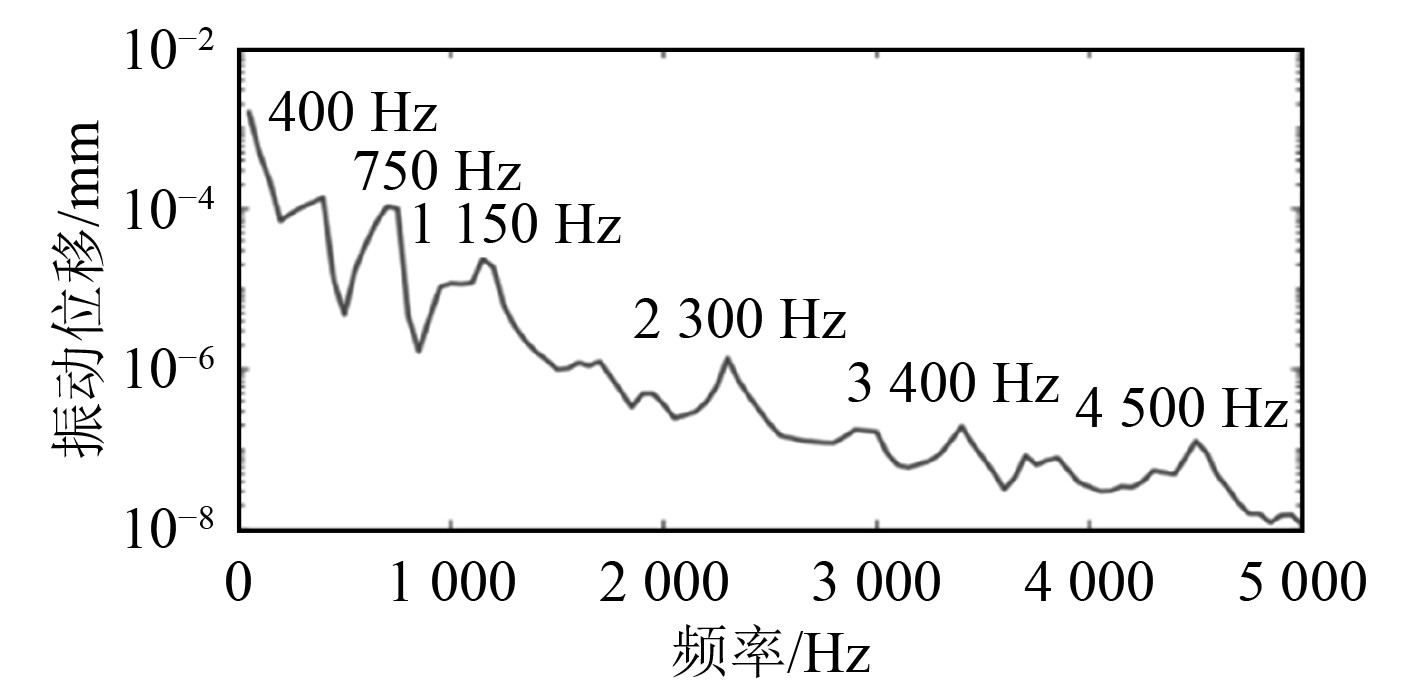
径向电磁力作用到定子得到的定子外表面振动位移如图4所示。
|
图 4 推进电机定子结构的振动位移 Fig. 4 Vibration displacement of stator structure of propulsion motor |
分析可知,在0 Hz处的变形最大,主要是由0阶0倍频电磁力引起的形变,不会产生噪声。其余较大的振动频率点为400 Hz、750 Hz、1 150 Hz和2 300 Hz处,主要由电频率倍频成分产生的电磁力所引起。
2.2 水下推进电机辐射噪声在得到定子表面振动位移的基础上,计算得到m阶振动辐射的声功率为:
| $ W=2\rho c{\text{π} }^{2}{f}_{m}^{2}{A}_{m}^{2}·2 \text{π} {R}_{0}{L}_{i}{I}_{rel} 。$ | (5) |
式中:ρc为水声阻抗;Am为振动位移;R0为定子外表面半径;Li为定子外表面长度;Irel为相对声强系数[13]。
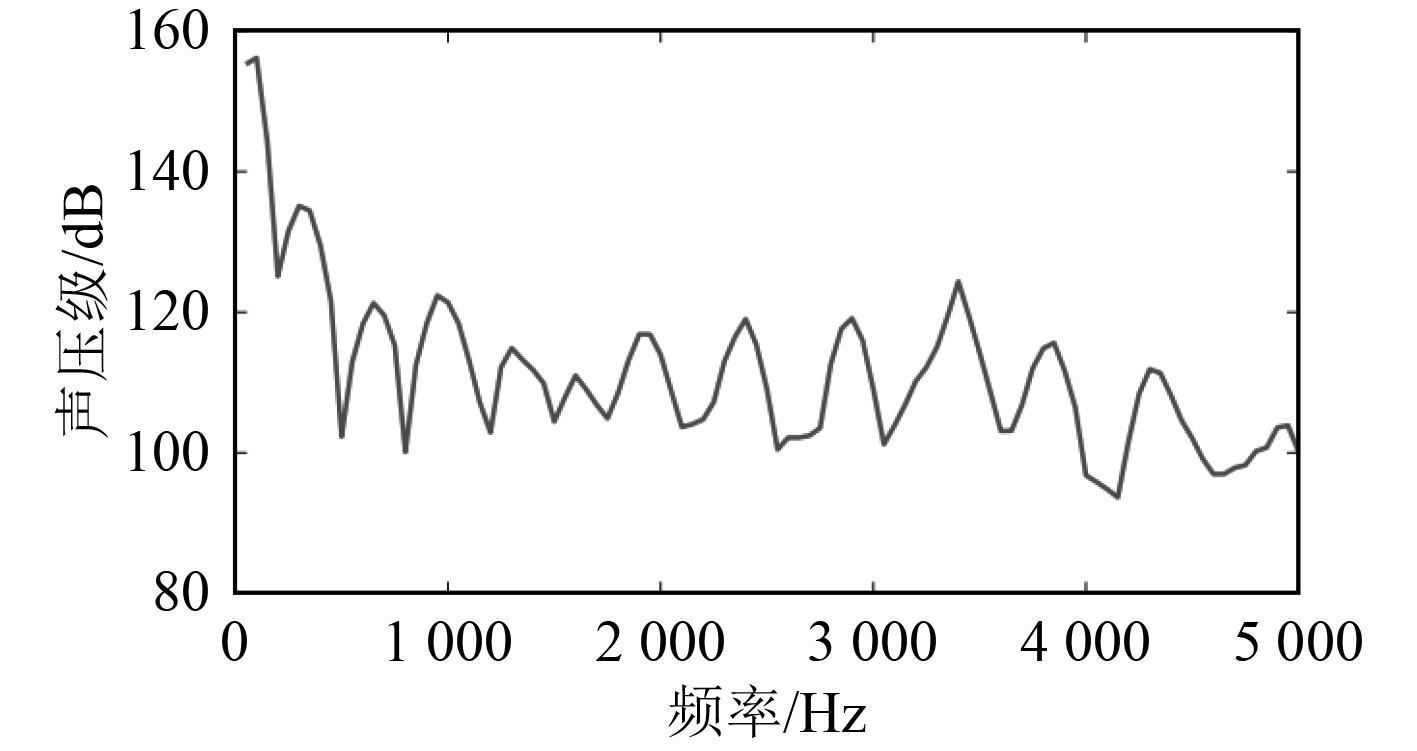
在水下永磁推进电机转速为 800 r/min 时距离定子结构1 m 处的声压级如图5所示。
|
图 5 水中推进电机声压级 Fig. 5 Sound pressure level of underwater propulsion motor |
根据推进电机水下声压级频谱图,结合图6声压级云图,推测水作为声音传播介质对定子结构0阶、2阶模态固有频率共振形成的声音传播方式的影响几乎没有。在图5中第1个峰值点在100 Hz附近,主要是因为水作为声音传播介质对于在定子模态的2阶模态共振,在声压云图上的传播特性没有抑制,因此结合推进电机在空气中此处的声压级,分析此处靠近定子结构的2阶模态固有频率处形成了整个频谱范围内的最大声压级值。

|
图 6 水中推进电机声压云图 Fig. 6 Sound pressure cloud diagram of underwater propulsion motor |
在图5中第2个峰值点在300~350 Hz处声压级值比较大,主要是因为800 r/min转速下的推进电机在电磁力2倍频320 Hz处的径向电磁力密度极大,且靠近3阶定子模态的固有频率,以及水作为声音传播介质对其传播影响较小。在频谱图5中唯一还存在共振影响下的声音传播点在3 400 Hz处,在该频率点的声压级云图如图6(b)所示,水作为声音传播介质对定子0阶模态共振形成的声音传播方式,以圆周各角度方向、声压级值近似等相均匀向外传播。
水下的声压级在750 Hz、1 150 Hz、2 300 Hz、4 500 Hz处分别形成以4阶、5阶、7阶、10阶模态共振时的声音传播规律,且在这几处的声压级均为明显较大的峰值。由图6(c)~图6(f)可知,在定子结构的噪声刚开始传播时,还是符合共振时的声音传播规律,但是随着在水中声音向远处传播由共振形成的声音传播振型被抑制,最终在声域1m处共振的声音传播指向性基本消除。而最终声压级峰值点均是由于推进电机800 r/min转速下的径向电磁力密度集中的电频率倍数的频率处。
2.3 推进电机振动噪声抑制通过对电机机壳的优化设计可以达到减振降噪的目的。电机电磁噪声源主要为径向电磁力,机壳的径向厚度对推进电机水下噪声的影响较大。
分别将机壳厚度控制在5 mm、10 mm、15 mm,20 mm、25 mm进行推进电机在0~5 000 Hz不同频率段内的水下噪声分析,结果如图7所示。距离电机机壳1 m处的声压级结果,0~5 000 Hz范围内的声压级最大值的抑制效果从定子到机壳厚度25 mm,依次为156.2 dB、146.4 dB、141.4 dB、139.4 dB、137.7 dB、136.4 dB。

|
图 7 不同机壳厚度对电机水下噪声影响 Fig. 7 Influence of different casing thickness on underwater noise of motor |
很明显在机壳厚度为15 mm之前每增加5 mm厚度对噪声抑制效果较为明显;其次最大声压级点明显机壳厚度为5 mm、10 mm的较大,而机壳厚度为15 mm处声压级值不但低于机壳厚度为20 mm时,且和机壳厚度为25 mm的声压级值大小差别很小。厚度为15 mm时噪声声压级曲线,波峰较少、曲线平缓,对辐射噪声抑制效果明显,故选择机壳厚度15 mm。经优化后的电机带机壳定子结构如图8所示。

|
图 8 推进电机定子结构 Fig. 8 Stator structure of propulsion motor |
通过对推进电机在转速800 r/min时裸定子和带机壳结构对水下噪声的影响,如图9所示。相比裸定子结构频谱范围声压级的最大值,加机壳后减少了29.7 dB。200~550 Hz频域内抑制效果相对较小,平均值降低了12 dB左右,主要由于电磁激振力相对较大。大于1000 Hz频域内抑制效果较为明显,平均差值在35 dB。高阶模态振型引起的噪声抑制效果较好。

|
图 9 机壳对电机在水中的声压级降低效果 Fig. 9 Effect of the casing on the reduction of the sound pressure level of the motor in water |
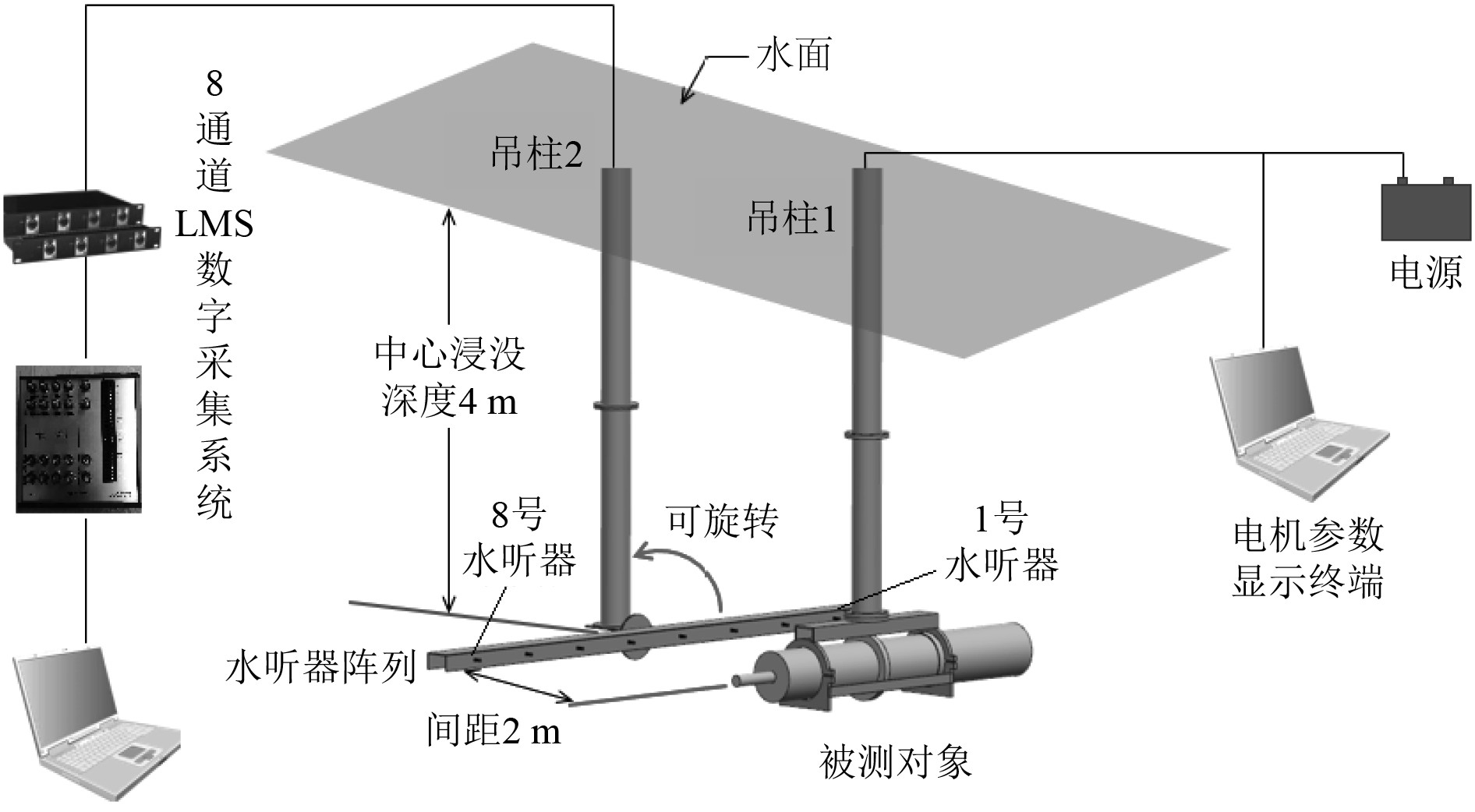
为验证推进电机水下辐射噪声等级,在消声水池搭建水下电机测试平台。测量系统主要由以下几个主要组件构成:测量换能装置(LST-SH01水听器),数据采集装置(LMS 数据采集系统),信号显示处理终端(笔记本电脑),如图10所示。
|
图 10 测量系统示意图 Fig. 10 Schematic diagram of measuring system |
电机由刚性吊环悬挂于测试平台的一根吊柱上。水听器采用线性阵列布置,整体悬挂于测试平台的另一根吊柱上。水听器阵列可以旋转,由水平阵列变换为竖直阵列,以采集更广范围的辐射噪声。
带优化后机壳结构水下推进电机在消声水池的1/3倍频程测试结果如图11所示。由测试数据可知,噪声最大处为80 Hz附近频带,声压级最大为125 dB。声压级与分析结果基本吻合,但频率段较分析频率略有下降,主要原因可能为分析模型中没有考虑附加质量所致。另外实测较大声压级处为20 Hz频带,主要由转子旋转的机械激振力所引起。在100~5000 Hz频带内测试结果显示最大噪声在200 Hz及2000 Hz附近,声压级115 dB左右。
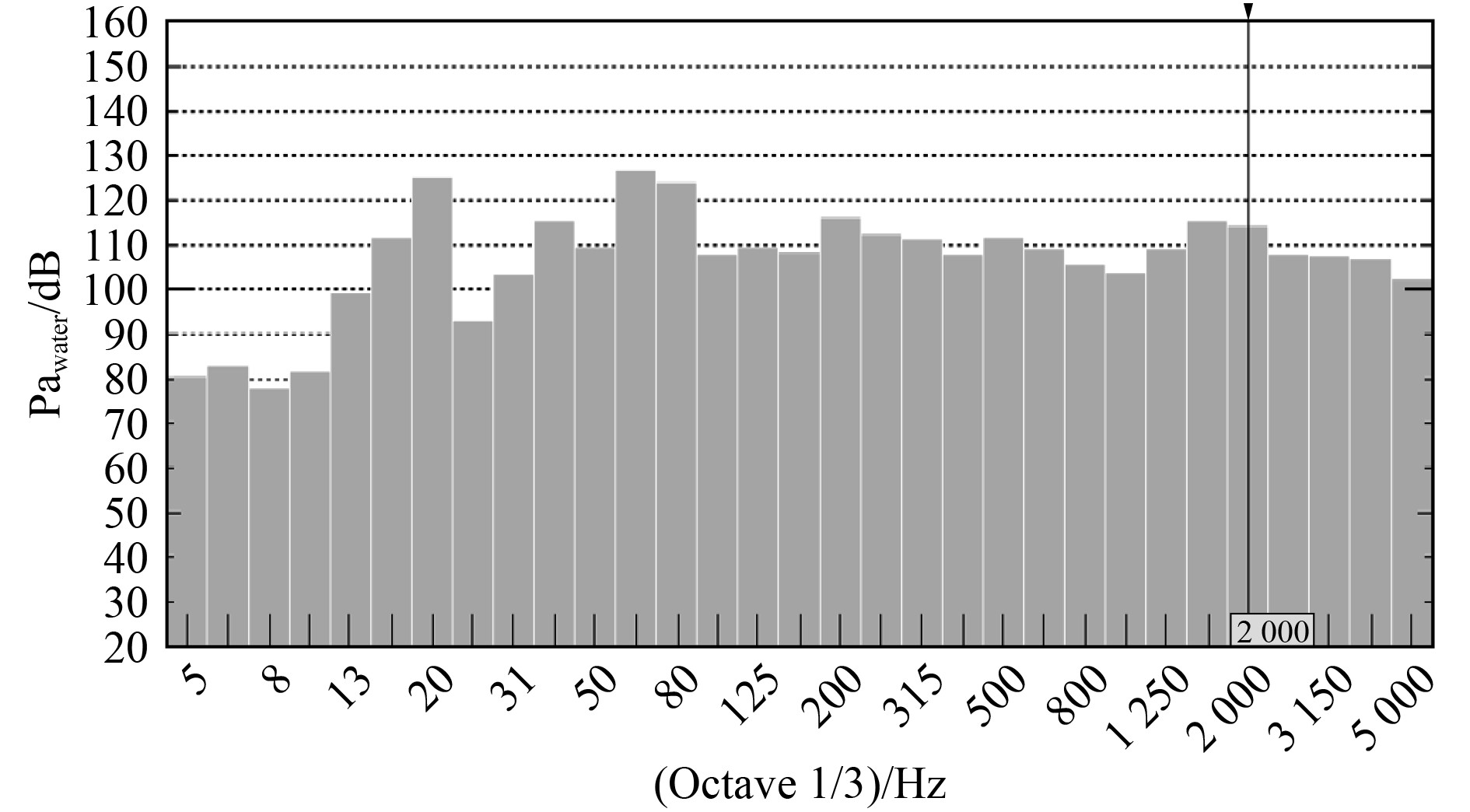
|
图 11 1/3倍频程声压级 Fig. 11 1/3 Octave sound pressure level |
本文分析推进电机径向电磁力、定子模态,采用谐响应联合仿真分析水下电机的振动和辐射噪声声压级特性。通过推进电机在消声水池的试验,1/3倍频程声压级测试结果表明,实测声压级幅值与分析结果基本吻合,所处频率点略有下降,验证了分析模型对水下推进电机噪声等级评估的准确性,对设计阶段的推进电机优化起到一定指导作用。
| [1] |
LIN F, ZUO S, DENG W, et al. Modeling and analysis of electromagnetic force, vibration, and noise in permanent-magnet synchronous motor considering current harmonics[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7455-7466. DOI:10.1109/TIE.2016.2593683 |
| [2] |
WU S. Vibroacoustic prediction and mechanism analysis of claw pole alternators[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 4463-4473. DOI:10.1109/TIE.2016.2645502 |
| [3] |
PARK S. A numerical prediction model for vibration and noise of axial flux motors[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5757-5762. DOI:10.1109/TIE.2014.2300034 |
| [4] |
RICK S, PUTRI A K, FRANCK D, et al. Hybrid acoustic model of electric vehicles: force excitation in permanent-magnet synchronous machines[J]. IEEE Transactions on Industry Applications, 2016, 52(4): 2979-2987. DOI:10.1109/TIA.2016.2547360 |
| [5] |
ZUO S, LIN F, WU X. Noise analysis, calculation, and reduction of external rotor permanent-magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6204-6212. DOI:10.1109/TIE.2015.2426135 |
| [6] |
LIN F, ZUO S, DENG W, et al. Modeling and Analysis of Acoustic Noise in External Rotor In-Wheel Motor Considering Doppler Effect[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4524-4533. DOI:10.1109/TIE.2017.2758742 |
| [7] |
兰华. 永磁同步电机的电磁力波与电磁振动研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
|
| [8] |
于慎波, 王辉. 电机定子圆柱壳体周向模态频率计算[J]. 电机与控制学报, 2014, 18(6): 102-107. |
| [9] |
张贤彪, 王东, 苏振中. 大型分体式磁轴承电动机系统定子模态分析[J]. 机械工程学报, 2016, 52(8): 1-7. |
| [10] |
谢颖, 王严, 吕森, 等. 小型异步电机模态计算与试验分析[J]. 电工技术学报, 2015, 30(16): 1-9. |
| [11] |
YANG, S. Low-noise electrical motors; Clarendon Press: Oxford, UK, 1981.
|
| [12] |
王倩营, 卢俊文, 舒涛. 非晶合金永磁电机的电磁振动噪声计算与分析[J]. 机电工程, 2019, 36(7): 695-700. |
| [13] |
陈永校, 诸自强, 应善成. 电机噪声的分析和控制[M]杭州: 浙江大学出版社, 1987.
|
 2023, Vol. 45
2023, Vol. 45
