2. 江苏科技大学 计算机学院,江苏 镇江 212100;
3. 舟山市江科船舶与海洋工程装备研发中心,浙江 舟山 212316
2. College of Computer Science, Jiangsu University of Science and Technology, Zhenjiang 212100, China;
3. Zhoushan Jiangke Ship and Marine Engineering Equipment Research and Development Center, Zhoushan 212316, China
随着智能船舶的推进,船舶自动化程度越来越高,船舶的推进方式由主机推进改成电力推进,在现代大型电力推进船舶中,推进系统的容量达到发电总容量的70%~80%,并且现代电力推进船舶上用电设备种类繁多,电力负荷系统十分复杂,负荷随机性强。因此船舶电力负荷预测成为了船舶电力系统能量优化管理和各动力源之间最佳负载功率分配的重要基础,准确的电力负荷预测能够帮助调控发电机组合理供电,应对推进负荷大幅波动对电网造成的冲击。根据预测结果还能够进一步优化能量管理策略,对船舶电网整体高效、经济、稳定运行起到至关重要的作用。
随着科学技术的进步和理论研究的深入,电力负荷预测的技术得到了很大的发展。目前在负荷预测领域中常用的预测方式有如下几种:时间序列法、回归分析法、灰色模型法、神经网络法、支持向量机。A.Farahat M 等[1]采用曲线拟合预测和时间序列模型对周日小时负荷进行预测,将曲线拟合预测(CFP)技术与遗传算法(GAs)相结合,获得高斯模型的最优参数。李钷等[2]用了主成分回归法对将影响负荷预测结果的几个主要因素进行提取,得出模型的解析形式。魏明奎等[3]利用BFGS-FA寻优算法对分数阶灰色预测模型的阶数进行寻优,得到最优阶数的分数阶灰色预测模型,提升了负荷预测的精度。但上述文献中所建立的预测模型在面对负荷数据出现损坏、缺失、异常值,负荷数据呈非指数性变化时,无法进行准确的负荷预测。支持向量机算法(Support Vector Machine,SVM)能够将预测问题转换为一个凸二次理论寻优问题,从而避免出现如神经网络算法中的局部极值收敛现象,能够解决小样本、非线性、高维数等实际预测问题,在船舶电力系统中的应用较为成熟。刘静[4]对电力推进船舶中的各电气设备进行分析,以试验的方式验证了支持向量机在船舶电力负荷预测中的准确性。侯文君等[5]通过粒子群算法对支持向量机中的参数进行优化,建立能够反映船舶短期电力负荷变化的预测模型。李东亮等[6]将最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)与模糊 c-均值聚类算法相结合,设计了一种行之有效的多模自适应船舶电力负荷预测算法。
但上述文献建立的负荷预测模型,在面对船舶电力系统工况复杂,负荷随机性强时,因其预测模型中的RBF核函数无法对训练样本特征向量分量的权重进行自动调节以及粒子群算法在搜素过程中的同质化倾向使模型中待优化参数准确度降低,最终导致所取得的负荷预测结果精度不高。因此,本文在传统的最小二乘支持向量机算法的基础上,将变种卡方核函数与RBF核函数相结合,并且针对蝴蝶优化算法(Butterfly Optimization Algorithm,BOA)以固定切换概率结合局部搜索与全局搜索、算法寻优速度较慢、算法后期因收敛于极值点而导致算力浪费这三方面缺陷,使用动态化切换概率、引入自适应惯性权重与佳点集策略对其进行改进。最后使用改进后全局搜索能力更强的蝴蝶优化算法进行参数寻优,通过新型的BOA-LSSVM预测模型对电力推进船舶的负载功率进行预测。
1 支持向量机算法Vapnik 和 Corinna Cortes 等在1995年首次提出了支持向量机算法,支持向量机算法在解决小样本、非线性、高维数问题时具有很强的优势,起初被广泛应用于模式识别等分类问题中。随着支持向量机算法理论的发展,Vapnik引入了不敏感损失参数ε,支持向量机算法被推广至函数拟合等其他机器学习问题中。其基本思想为在结构风险最小化的基础上,寻求一种在模型复杂度与算法学习能力之间的最佳折中[7],以求能够获得最好的泛化能力。
1.1 支持向量机的回归算法设支持向量机回归算法的训练样本为T,
| $ \begin{array}{c}T=\left\{\left({x}_{1},{y}_{1}\right),\dots ,\left({x}_{i},{y}_{i}\right),\dots ,\left({x}_{L},{y}_{L}\right)\right\} \end{array} 。$ | (1) |
其中,
| $ \begin{array}{c}y=f\left(x\right)=\left(\omega \cdot \phi \left(x\right)\right)+b\phi \left(x\right)\in S 。\end{array} $ | (2) |
由支持向量机算法的超平面思想与推广性界理论可知,回归预测的真实误差主要由在高维空间中平坦的
| $ R\left(\omega \right)=\frac{1}{2}{\parallel \omega \parallel }^{2}+\sum _{i=1}^{l}e\left(f\left({x}_{i}\right)-{y}_{i}\right) 。$ | (3) |
其中,
| $ \left(f\left({x}_{i}\right)-{y}_{i}\right)=\left\{\begin{split}&0,\left|f\left({x}_{i}\right)-{y}_{i}\right| < \varepsilon,\\ &\left|f\left({x}_{i}\right)-{y}_{i}\right|-\varepsilon ,{\rm{other}} 。\end{split}\right. $ | (4) |
根据结构风险最小化准则,最小化真实风险可表示为:
| $ {\rm{min}}\left[R\left(\omega \right)\right]={\rm{min}}[\frac{1}{2}{\parallel \omega \parallel }^{2}+\sum _{i=1}^{l}e\left(f\left({x}_{i}\right)-{y}_{i}\right)。$ | (5) |
由于该函数不可微,无法进行直接求解。而支持向量机回归算法因其核函数与对偶技巧可很好地避免该问题,通过引入松弛因子
| $ {\rm{min}}\left[R\left(\omega \right)\right]={\rm{min}}[\frac{1}{2}{\parallel \omega \parallel }^{2}+C\sum _{i=1}^{l}e\left(f\left({x}_{i}\right)-{y}_{i}\right)。$ | (6) |
约束条件为:
| $ {\rm{s.t.}}\left\{\begin{aligned} & {y}_{i}-\omega \cdot \phi \left(x\right)-b\geqslant e+{\xi }_{i},\\ & \omega \cdot \phi \left(x\right)+b-{y}_{i}\geqslant e+{{\xi }_{i}}^{*},\\ & {\xi }_{i},{{\xi }_{i}}^{*}\geqslant 0。\end{aligned}\right. $ | (7) |
在上述目标函数的基础上建立拉格朗日方程可得:
| $ \begin{split} L\left(\omega ,\xi ,{\xi }^{*}\right)=&\frac{1}{2}{\parallel \omega \parallel }^{2}+C\sum _{i=1}^{l}\left(\xi +{\xi }^{*}\right)-\\ & \sum _{i=1}^{l}{\alpha }_{i}\left(\left(e+{\mathrm{\xi }}_{i}\right)-{y}_{i}+\left(\left(\omega \cdot \varphi \left(x\right)\right)+b\right)\right)-\\ & \sum _{i=1}^{l}{{\alpha }_{i}}^{*}\left(\left(e+{{\xi }_{i}}^{*}\right)+{y}_{i}-\left(\left(\omega \cdot \varphi \left(x\right)\right)+b\right)\right)-\\ &\sum _{i=1}^{l}\left({\lambda }_{i}\cdot {\xi }_{i}+{{\lambda }_{i}}^{*}\cdot {{\xi }_{i}}^{*}\right) 。\end{split} $ | (8) |
若式(8)要取最小值,则L对
| $ \left\{\begin{aligned} & \frac{\partial L}{\partial \omega }=\omega -\sum _{i=1}^{l}\left({\alpha }_{i}-{{\alpha }_{i}}^{*}\right)\phi \left({x}_{i}\right)=0,\\ & \frac{\partial L}{\partial b}=\sum _{i=1}^{l}\left({\alpha }_{i}-{{\alpha }_{i}}^{*}\right)=0,\\ & {\frac{\partial L}{\partial {\xi }_{i}}=C-{\alpha }_{i}-{\lambda }_{i}=0},\\ &{\frac{\partial L}{\partial {{\xi }_{i}}^{*}}=C-{{\alpha }_{i}}^{*}-{{\lambda }_{i}}^{*}=0}。\end{aligned}\right. $ | (9) |
将式(9)代入式(8)后可得:
| $ \begin{split} & {\rm{min}}\frac{1}{2}\sum _{i,j=1}^{l}\left({\alpha }_{i}-{{\alpha }_{i}}^{\mathrm{*}}\right)\left({\alpha }_{j}-{{\alpha }_{j}}^{\mathrm{*}}\right)\left({\varphi }\left({x}_{i}\right),{\varphi }\left({x}_{j}\right)\right)+\\ & \sum _{i=1}^{l}{\alpha }_{i}\left(e-{y}_{j}\right)+{{\alpha }_{i}}^{*}\left(e+{y}_{j}\right) ,\end{split} $ | (10) |
| $ \omega =\sum _{i=1}^{l}\left({\alpha }_{i}-{{\alpha }_{i}}^{*}\right)\varphi \left({x}_{i}\right) 。$ | (11) |
其中,
| $ f\left(x\right)=\left(\sum _{i=1}^{l}\left({\alpha }_{i}-{{\alpha }_{i}}^{*}\right)\varphi \left({x}_{i}\right)\cdot \varphi \left(x\right)\right)+b 。$ | (12) |
最小二乘支持向量机算法为支持向量机算法的扩展,LSSVM算法将SVM算法中的不等式约束转化为等式约束[8],将SVM算法中的求二次规划问题转化为对一个线性模型进行求解。
LSSVM的优化问题为:
| $ \begin{split} & {\rm{min}}\left[J\left(\omega ,b,e\right)\right]={\rm{min}}\left[\frac{1}{2}{\parallel \omega \parallel }^{2}+\frac{1}{2}C\sum _{i=1}^{l}{{e}_{i}}^{2}\right],\\ & {\rm{s.t.}}{\mathrm{\omega }}^{{\rm{T}}}\varphi \left({x}_{i}\right)+b+{e}_{i}={y}_{i},i=1,\dots ,l 。\end{split} $ | (13) |
其中,
| $ \begin{split} L\left(\mathrm{\omega },{b},{e},\lambda \right)=& \frac{1}{2}{\parallel \omega \parallel }^{2}+\frac{1}{2}C\sum _{i=1}^{l}{{e}_{i}}^{2}-\\ & \sum _{i=1}^{l}{\lambda }_{i}\left({\omega }^{{\rm{T}}}\varphi \left({x}_{i}\right)+b+{e}_{i}-{y}_{i}\right) 。\end{split} $ | (14) |
同样的,为求L的最小值,求L对
| $\left[ \begin{array}{cccccccccccccc} {0}&{E}\\ {{{\boldsymbol{E}}}^{{\rm{T}}}}&{{\boldsymbol{K}}+{{\boldsymbol{C}}}^{-1}{\boldsymbol{I}}} \end{array}\right]\left[\begin{array}{llllllll} {b}\\ {{\boldsymbol{A}}}\end{array}\right]=\left[\begin{array}{lllllllll} {0}\\ {{\boldsymbol{Y}}} \end{array}\right]。$ | (15) |
其中,
由Mercer条件可得核函数:
| $ \begin{array}{c}{\rm{K}}\left({x}_{i},{x}_{j}\right)={\varphi \left({x}_{i}\right)}^{{\rm{T}}}\cdot \varphi \left({x}_{j}\right) \end{array}。$ | (16) |
因此,LSSVM的回归算法的函数最终为:
| $ f\left(x\right)=\sum _{i,j=1}^{l}{\lambda }_{i}{\rm{K}}\left({x}_{i},{x}_{j}\right)+b 。$ | (17) |
RBF核函数因其表达形式简单、径向对称、解析性好等优点在短期电力负荷预测方面所取得的效果十分显著。虽然RBF核函数通过计算输入特征向量与训练样本特征向量间的欧式距离,使得与输入特征向量相似程度最高的样本特征向量所对应的
| $ K\left({x}_{i},{x}_{j}\right)=\delta \left[\frac{{{x}_{i}}^{{\rm{T}}}{x}_{j}}{{\left|\left|{x}_{i}+{x}_{j}\right|\right|}_{L1}}\right]+\left(1-\delta \right)\mathrm{exp}\left[-\frac{{\left|\left|{x}_{i}-{x}_{j}\right|\right|}^{2}}{2{\sigma }^{2}}\right]。$ | (18) |
式中:
由文献[5]可知,PSO为解决船舶负荷预测支持向量机模型参数优化的常用方法。但因其迭代方式的特性,除在迭代过程开始前各粒子的初始随机飞行速度外,后续各粒子的飞行姿态皆受个体历史最优解和全局历史最优解的影响,导致各粒子集中地向全局历史最优解方向靠拢。即粒子群在优化过程中具有同质化倾向,所以该算法有着“易早熟”的缺陷。因此本文使用全局搜素能力更强的蝴蝶优化算法对LSSVM模型中的惩罚因子C,标准化参数
蝴蝶优化算法受大自然界中蝴蝶的觅食与求偶行为的启发[9],蝴蝶通过感知空气中的气味浓度确定食物源与配偶的潜在位置,蝴蝶群中每只蝴蝶的适应度值决定了蝴蝶所散发的香味强度,BOA算法将蝴蝶种群搜索模式分为全局搜索与局部搜素两种模式。全局搜索为蝶群向散发香味的个体目标飞行,局部搜素为蝴蝶无法感知周围个体目标所散发的香味时,将进行随机移动。BOA算法将全局搜索与局部搜索相结合,提高了算法中种群的多样性,使算法的全局寻优与局部寻优能力得到了提升。
BOA算法的具体流程如下:
1)算法参数进行初始化。蝴蝶个数设置为N,蝴蝶维数dim,算法迭代次数Niter,蝴蝶初始位置
2)计算蝶群中每只蝴蝶的当前适应度值,并记录蝶群中的全局最优解,通过适应度值计算各蝴蝶散发的香味浓度,香味浓度计算公式如下式:
| $ \begin{array}{c}f=c\cdot{I}^{a} \end{array} 。$ | (19) |
式中:
3)在[0,1]之间生成一个均匀分布的随机数rand,用于对蝶群的搜索方式进行决策。
4)当rand<p时,蝶群进行全局搜索,各蝴蝶飞向蝶群中的全局最优解,全局搜索方式如下式:
| $ \begin{array}{c}{X}_{i}^{t+1}={X}_{i}^{t}+\left({r}^{2}\cdot{g}^{*}-{X}_{i}^{t}\right)\cdot f \end{array}。$ | (20) |
式中:
5)当rand≥p时,蝶群进行局部搜索,各蝴蝶在自身周围进行随机游走,局部搜索方式如下式:
| $ \begin{array}{c}{X}_{i}^{t+1}={X}_{i}^{t}+\left({r}^{2}\cdot{X}_{j}^{t}-{X}_{k}^{t}\right)\cdot f \end{array} 。$ | (21) |
式中:
基础的蝴蝶优化算法虽然已经用了混合飞行方式将算法的局部寻优与全局寻优相结合,但其是在固定的切换概率p之下将2种寻优模式结合,切换概率p一般取值为0.8。由此可见,在大概率进行全局寻优的条件下,算法会有很高的可能性过早收敛于局部极值点,并且算法后期局部寻优模式出现的概率过小,无法对极值点周围进行较为有效寻优,使算法浪费了大量寻优迭代过程的算力。针对此缺点,对基础蝴蝶优化算法做出如下改进:
1)使切换概率进行动态变化
在BOA算法中,切换概率p取值越大种群进行全局寻优的概率就越大,反之进行局部寻优的概率就越大。将切换概率动态化后,p值将随迭代次数的增加产生由大到小的改变,可使各蝴蝶在算法前期进行强烈的全局搜索,迅速飞向全局最优解周围,在搜索过程后期对全局最优解周围展开局部寻优。切换概率动态化方式如下式:
| $ {p}_{d}={p}_{\rm max}-({p}_{\rm max}-{p}_{\rm min})*\frac{Curcount}{ Loopcount}。$ | (22) |
式中:
2)自适应惯性权重系数
在群智能算法中,惯性权重用于调节与平衡算法的全局寻优与局部寻优能力。当惯性权重越大时,算法全局搜索能力强,能够跳出局部最优。当惯性权重越小时,算法局部搜索能力越强,搜索精度得到提升。本文在BOA算法的全局搜索模式中引入自适应惯性权重,使惯性权重随算法迭代次数的增加呈现下降的趋势,设置方法如下式:
| $ \omega ={\omega }_{\rm min}+\left({\omega }_{\rm max}-{\omega }_{\rm min}\right)\cdot{\left(\frac{ Loopcount-Curcount}{ Loopcount}\right)}^{2} 。$ | (23) |
式中:
| $ \begin{array}{c}{X}_{i}^{t+1}={\omega \cdot X}_{i}^{t}+\left({r}^{2}\cdot{g}^{*}-{X}_{i}^{t}\right)\cdot f \end{array} 。$ | (24) |
3)佳点集策略
使用平均粒距与适应度方差作为评判算法是否收敛于极值点的指标,平均粒距的基本定义如下式:
| $ D\left(k\right)=\frac{1}{\left|n\right|\left|L\right|}\sum _{i=1}^{n}\sqrt{\sum _{j=1}^{Q}{\left({x}_{ij}-\stackrel-{{x}_{j}}\right)}^{2}}。$ | (25) |
式中:设算法当前迭代次数为k;n为种群的蝴蝶个数;L为粒子的搜索过程中,搜索的空间对角线值,
| $ {\sigma }^{2}=\sum _{i=1}^{n}{\left(\frac{{{f}^{k}}_{i}-\bar{\bar f}}{f}\right)}^{2} ,\\ \begin{array}{c}f=\left\{\begin{array}{l}{\max}\left|{f}_{i}-\bar{\bar f}\right|,{\max}\left|{f}_{i}-\bar{\bar f}\right| > 1,\\ 1,{\rm{other}}。\end{array}\right. \end{array} $ | (26) |
式中:
步骤1 种群中蝴蝶个数为n,含n个点的佳点集
步骤2 佳点集中的
| $ {{x}_{ij}}'=i*{\rm cos}\frac{2{\text{π}} j}{z} 。$ | (27) |
步骤3 令
| $ {{x}_{ij}}'={Lb}_{j}+{\rm mod}\left({{x}_{ij}}',1\right){*(Ub}_{j}-{Lb}_{j}) 。$ | (28) |
式中:
在种群经佳点集策略重新初始化后,蝴蝶均匀分布于解空间中,此时强制令
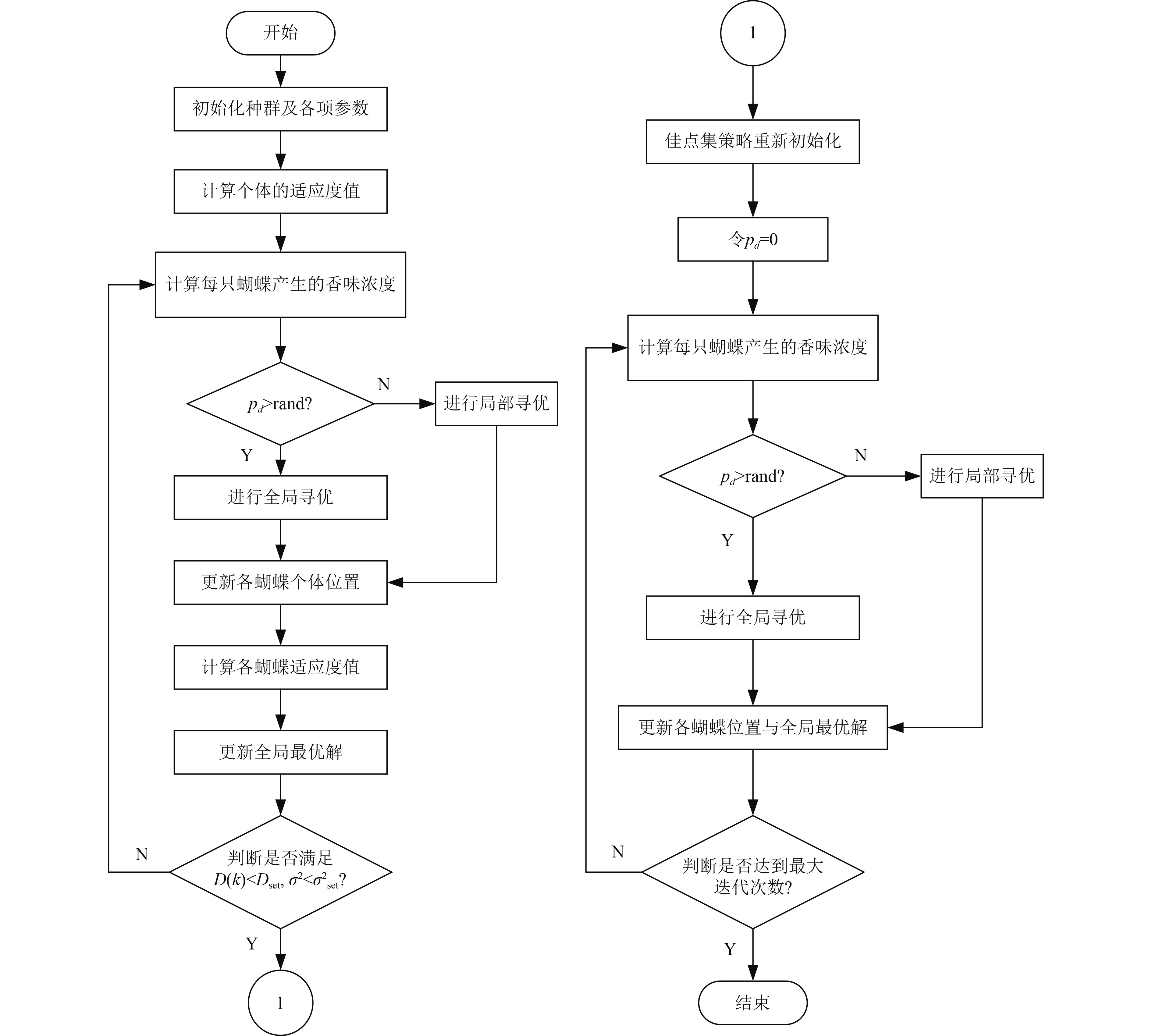
|
图 1 改进后的蝴蝶优化算法流程图 Fig. 1 Flow chart of improved butterfly optimization algorithm |
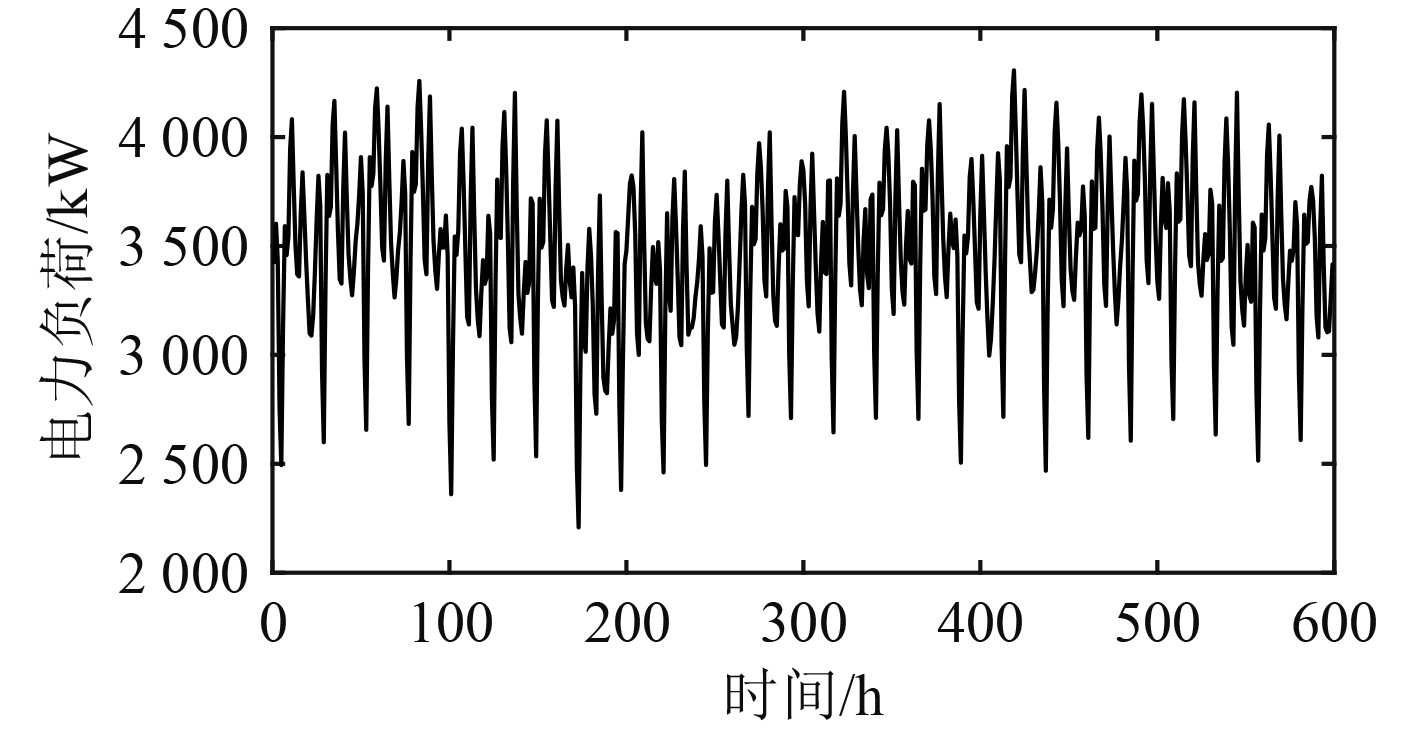
选择某全电力推进远洋运输船的每小时历史负荷数据作为测试对象,负荷数据来源于文献[10],负荷曲线如图2 所示。在船舶负荷数据进行常规的平滑化及归一化数据处理后,使用百分比法对负荷数据进行拆分,将前80%即前480 h的船舶每小时平均负荷功率作为训练集,后20%即后12 h时的船舶负荷数据作为测试集。
|
图 2 实际负荷曲线图 Fig. 2 Actual load curve |
选择平均相对误差函数作为蝴蝶优化算法的适应度函数,具体公式如下式:
| $ MRE=\frac{1}{u}\sum _{i=1}^{l}\left(\frac{{|w}_{i}-{v}_{i}|}{{v}_{i}}\right) 。$ | (29) |
式中:u为输出预测个数,取120;
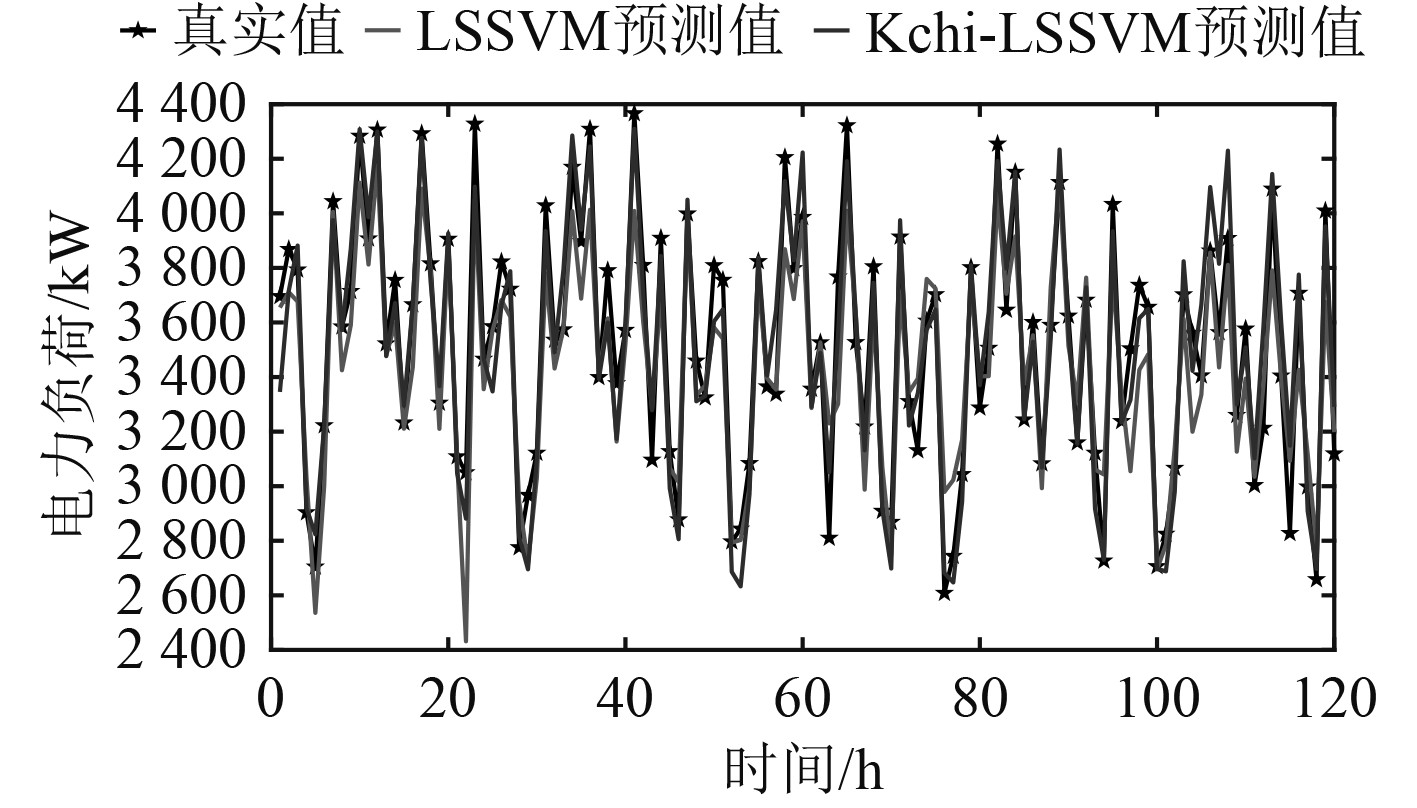
|
图 3 2种预测模型预测效果 Fig. 3 Prediction effect of two prediction models |

|
图 4 2种预测模型预测相对误差 Fig. 4 Relative error of two prediction models |
由图4可知,虽有个别点融合变种卡方核函数的LSSVM预测模型预测精度不如基础的LSSVM模型,但在整体预测效果上,由于变种卡方核函数通过对特征向量间L1范数的计算,降低了对预测结果影响程度较低的特征向量分量权重,提高了对预测结果影响程度较高的特征向量分量权重,从而使得Kchi-LSSVM的相对误差曲线相较于LSSVM的相对误差曲线波动更为平缓。在计算平均相对误差后,如表1所示,Kchi-LSSVM模型预测结果的平均相对误差为3.0036%,LSSVM模型预测结果的平均相对误差为4.2420%。在变种卡方核函数与RBF核函数结合后,模型的预测精度由95.7580%提升至96.9964%。
|
|
表 1 预测结果各评价指标数据对比 Tab.1 Data comparison of each evaluation index of the prediction results |
在使用BOA算法与改进后的BOA算法,即IBOA算法对LSSVM模型中的惩罚因子C,标准化参数

|
图 5 各预测模型预测效果对比图 Fig. 5 Comparison chart of prediction effect of each prediction model |

|
图 6 各预测模型预测相对误差对比图 Fig. 6 Comparison chart of prediction relative error of each prediction model |
可知,采用IBOA算法对Kchi-LSSVM的3个参数进行寻优化后,得到的回归模型更为准确。IBOA算法相较于基础BOA算法,通过了动态化切换概率使BOA算法的全局寻优与局部寻优相结合。在算法迭代的初始阶段,由于切换概率设置值过高,蝴蝶群大概率处于全局寻优模式下,并且在自适应惯性权重
BP、RBF、Elman神经网络具有较强的学习能力与泛化能力,因此这3种预测方法为短期电力负荷预测中的常用方法。将BP、RBF、Elman神经网络与本文提出的IBOA-Kchi-LSSVM模型的预测效果进行对比,结果如图7和图8所示。

|
图 7 改进后预测模型与3种神经网络预测效果对比图 Fig. 7 Comparison chart of prediction effect between improved prediction model and three neural networks |
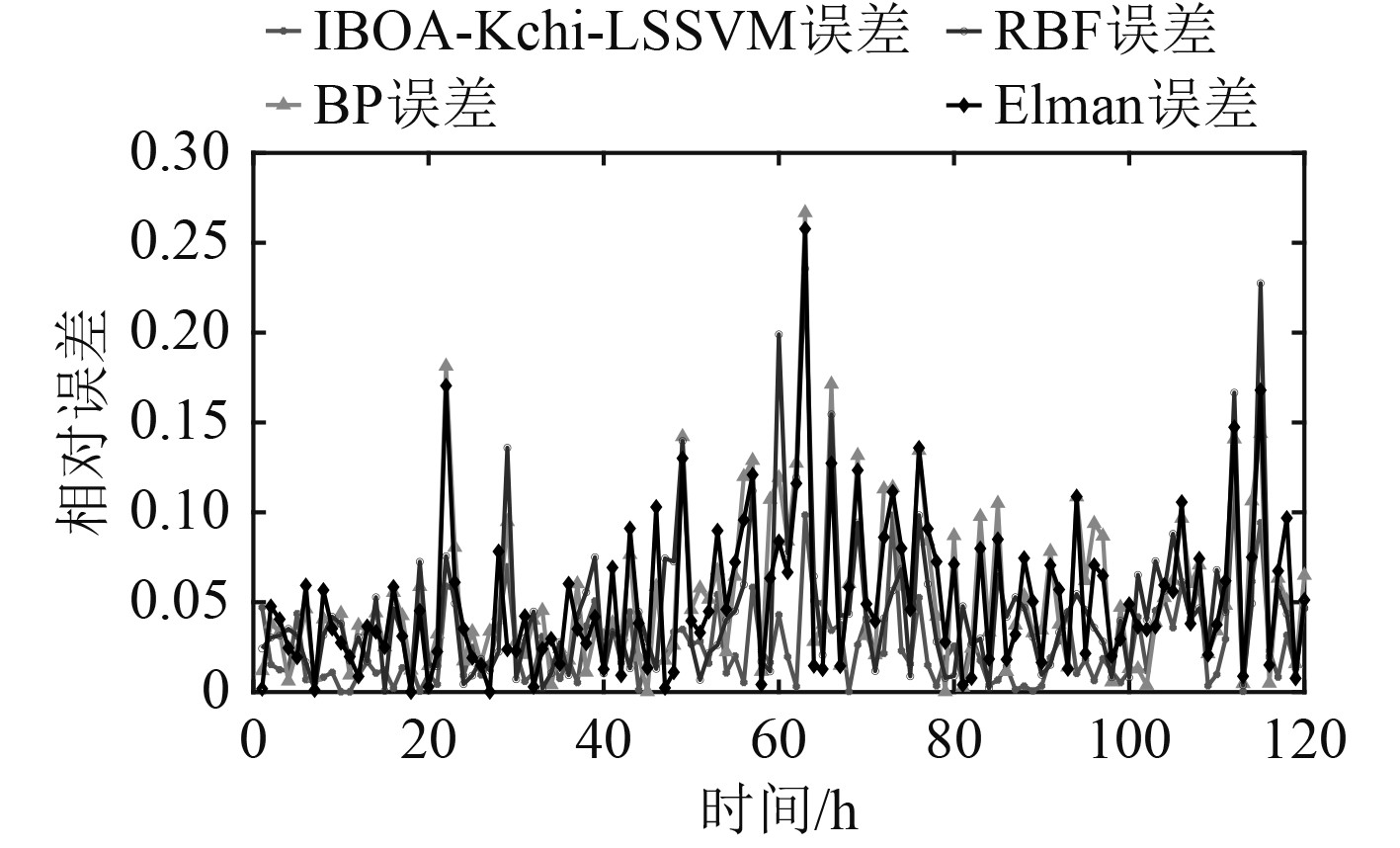
|
图 8 改进后预测模型与3种神经网络预测相对误差对比图 Fig. 8 Comparison chart of relative error between improved prediction model and three neural networks |
同时,平均绝对误差(Mean Absolute Error,MAE)、平均相对误差(Mean Relative Error,MRE)与均方根误差(Root Mean Square Error,RMSE)也是回归算法准确性的重要评价标准。本文所述的各预测模型所取得的预测结果各项评价指标如表1所示。
4 结 语本文针对电力推进船舶负荷非线性变化,随机性较强,难以预测的问题,在传统的LSSVM算法作为预测模型的基础上,将变种卡方核函数与RBF核函数进行融合,同时考虑样本间绝对距离与相对距离这2种距离度量方式对预测结果产生的影响,以提升模型的预测性能,并对BOA算法进行改进,引入自适应惯性权重、动态化切换概率与佳点集策略,平衡算法的全局搜索与局部搜索。最后,使用改进后的BOA算法对变种卡方核函数的权重系数以及模型中的其他参数进行寻优,构建了一种IBOA-Kchi-LSSVM的船舶负荷预测模型。仿真实验结果表明,改进后的BOA算法全局搜素能力更强并且能够在全局极值点周围展开精细化局部搜索,所求的回归模型更为准确,相较于基础的LSSVM预测模型。本文提出的预测模型将负荷预测精度提升至97.5119%,并且该模型所取得的负荷预测结果明显优于BP、RBF、Elman神经网络,其预测结果在各项评价指标中均为最优。
| [1] |
FARAHAT M A, TALAAT M. Short-term load forecasting using curve fitting prediction optimized by genetic algorithms[J]. International Journal of Energy Engineering, 2012, 2(2): 6. |
| [2] |
李钷, 李敏, 刘涤尘. 基于改进回归法的电力负荷预测[J]. 电网技术, 2006, 30(1): 99-104. LI P, LI M, LIU D C. Power load forecasting based on improved regression[J]. Power System Technology, 2006, 30(1): 99-104. DOI:10.13335/j.1000-3673.pst.2006.01.020 |
| [3] |
魏明奎, 周全, 蔡绍荣, 等. 基于BFGS-FA优化的分数阶灰色模型的中长期负荷预测[J]. 广西大学学报(自然科学版), 2020, 45(2): 270-276. WEI M K, ZHOU Q, CAI S R, et al. Mid-long term load forecasting based on fractional grey model optimized by BFGS-FA[J]. Journal of Guangxi University (Natural Science Edtiton), 2020, 45(2): 270-276. |
| [4] |
刘静. 最小二乘SVM在电力推进船舶电力负荷短期预测的应用[J]. 舰船科学技术, 2021, 43(24): 61-63. LIU J. Application of least square SVM in short-term forecasting of electric load of electric propulsion ship[J]. Ship Science and Technology, 2021, 43(24): 61-63. DOI:10.3404/j.issn.16727649.2021.12A.021 |
| [5] |
侯文君, 汪英英, 姚艺新, 等. 支持向量机的船舶短期电力负荷预测方法[J]. 舰船科学技术, 2018(18): 79-81. HOU W j, WANG Y Y, YAO Y X, et al. Short-term load forecasting method based on support vector machine[J]. Ship Science and Technology, 2018(18): 79-81. |
| [6] |
李东亮, 张晓锋, 程刚, 等. 多模自适应舰船电力负荷预测算法[J]. 舰船科学技术, 2012, 34(12): 51-54,87. LI D L, ZHANG X F, CHENG G, et al. A multi-mode adaptive load forecasting algorithms of warship[J]. Ship Science and Technology, 2012, 34(12): 51-54,87. DOI:10.3404/j.issn.1672-7649.2012.12.010 |
| [7] |
蒋妍. 基于最小二乘支持向量机的聚氯乙烯汽提过程预测模型[J]. 塑料科技, 2020, 48(2): 84-88. JIANG Y. Prediction model of PVC stripping process based on least square support vector machine[J]. Plastics Technology, 2020, 48(2): 84-88. |
| [8] |
李腾, 朱希安, 王占刚. 矿井突水水源判别的FOA-LSSVM模型[J]. 北京信息科技大学学报(自然科学版), 2020, 35(3): 41–45. LI T, ZHU X A, WANG Z G. FOA-LSSVM model for source identification of mine water inrush [ J ]. Journal of Beijing Information Science & Technology University (Natural Science Edition), 2020, 35(3): 41–45. |
| [9] |
王依柔, 张达敏, 徐航, 等. 基于自适应扰动的疯狂蝴蝶算法[J]. 计算机应用研究, 2020, 37(11): 3276-3280. WANG Y R, ZHANG D M, XU H, et al. Crazy butterfly algorithm based on adaptive perturbation[J]. Application Research of Computers, 2020, 37(11): 3276-3280. |
| [10] |
姚池. 全电驱船舶电网能量优化管理策略研究[D]. 重庆: 重庆大学, 2017.
|
 2023, Vol. 45
2023, Vol. 45
