2. 中国船级社武汉分社, 湖北 武汉 430000;
3. 国家水运安全工程技术研究中心可靠性工程研究所, 湖北 武汉 430063
2. China Classification Society Wuhan Branch, Wuhan 430000, China;
3. Reliability Engineering Institute, National Engineering Research Center for Water Transportation Safety, Wuhan 430063, China
船舶舵机可以控制航向和调整操纵性,是保障航行安全的关键甲板设备[1]。转叶式舵机具有占地面积小、质量轻、机械效率高等优点,是船舶舵机的主要类别之一[2]。它是一种回转式转舵机构,转叶固定在转子外壁,定叶固定在缸体内壁,两者与缸盖、缸底之间都设有密封装置,将转舵油缸分为几个密闭腔室。当液压油进入腔室后,对叶片施压,驱动转子转动,进而控制舵的转向。工作中,转叶外端的密封件与缸体内壁长期处于高压紧密贴合状态,两者之间不可避免地产生摩擦磨损,时间越长,磨损越严重。为了保证船舵快速响应、不跑舵、不滞舵,保持油缸内油压稳定是关键,而油压稳定性受液压系统的密封性制约。感知转叶式舵机的工作状态和对其进行故障诊断极其重要。传统机电液系统的故障诊断是对温度、油、水等常规性能参数进行采样化验,并结合轮机员的工作经验来判断,这已经不能满足智能化发展进程对转叶式舵机故障诊断精度和维修决策快速响应的要求[3]。
国内外学者对舵机故障展开了大量研究。胡良谋等[4]利用回归型支持向量机设计了一个液压舵机的故障诊断系统。章家宝等[5]采用模糊聚类方法对电动舵机致命性故障进行实时诊断。Xu等[6]提出基于长短时记忆神经网络识别算法来识别舵机的不同故障类型。Marcelo等[7]利用转换故障树创建的贝叶斯信念网络确定舵机系统中最可能产生的故障原因。然而,这些方法只是从单一层面进行故障诊断,没有从宏观和微观角度进行系统分析,不能精准地反映转叶式舵机的工作状态。因此,基于上述2个角度,采用C#和Matlab混合编程的方法对转叶式舵机进行故障分析与诊断。
C#是专门用于.NET的编程语言,开发的系统界面友好、执行速度快,具有高效的设备操作能力。与C#相比,Matlab开发程序界面和对外围设备的控制能力差,但其编程简单、对信号的分析与数据处理能力强[8]。因此,吸取两者所长,基于C#与Matlab混合编程,利用C#完成界面开发任务,Matlab完成数据分析和图形生成任务,开发界面友好和执行能力高效的转叶式舵机故障诊断系统。
1 转叶式舵机故障诊断算法与软件设计转叶式舵机密封件的磨损加剧,产生的磨粒增多,使得密封件产生异常磨损,诱发振动,引起密封失效。摩擦系数信号能够从微观层面反映转叶式舵机密封件的摩擦磨损状态,而振动信号能够从宏观层面反映其运行状态,2种信号相互印证,能精准反映舵机的工作状态。因此,基于这2种信号,采用C#和Matlab混合编程的方法实现转叶式舵机密封件的故障诊断。首先用Matlab提取转叶式舵机密封件的摩擦系数信号和振动信号时域特征,然后采用BP神经网络进行故障诊断,最后在C#环境下构建转叶式舵机故障诊断系统。
1.1 时域特征提取密封件与缸体内壁之间的摩擦磨损过程往往具有随机性,致使振动信号与摩擦系数信号呈现非平稳、非线性等特点,且实时采集数据量大,需要对这2种信号进行特征提取,以便故障诊断。常用的特征提取方法包括时域分析法和频域分析法等,时域分析法直接对原始信号进行分析,具有准确和逼近原始信息的特点。因此,采用Matlab对振动信号与摩擦系数信号进行时域分析。由于不同的无量纲指标表征能力不一样,为了减小诊断误差,需要多个指标对故障进行多维度的表征。本文选取的主要时域特征指标如下:
最大值
| $ X_{\max }=\max \left\{x_{i}\right\},$ | (1) |
平均值
| $ \bar{X}=\frac{1}{N} \sum_{i=1}^{N} x_{i},$ | (2) |
峰峰值
| $ X_{\text {ypp }}=\max \left(x_{i}\right)-\min \left(x_{i}\right),$ | (3) |
方差
| $ \sigma_{x}^{2}=\frac{1}{N-1} \sum_{i=1}^{N}\left(x_{i}-\bar{X}\right)^{2} ,$ | (4) |
峭度
| $ K=\frac{\dfrac{1}{N} \displaystyle\sum_{i=1}^{N} x_{i}^{4}}{X_{r m s}^{4}},$ | (5) |
均方根值
| $ X_{\pi m w}=\sqrt{\frac{1}{N} \sum_{i=1}^{N} x_{i}^{2}},$ | (6) |
波形因子
| $ S=\frac{X_{\text {TMw }}}{\dfrac{1}{N} \displaystyle\sum_{f=1}^{N}\left|x_{i}\right|} ,$ | (7) |
峰值因子
| $ C=\frac{\max \left|\left(x_{i}\right)\right|}{X_{\mathrm{rma}}},$ | (8) |
脉冲因子:
| $ I=\frac{\max \left|\left(x_{i}\right)\right|}{\dfrac{1}{N} \displaystyle\sum_{f=1}^{N}\left|x_{i}\right|} ,$ | (9) |
裕度因子
| $ L=\frac{\max \left|\left(x_{i}\right)\right|}{\left[\dfrac{1}{N} \displaystyle\sum_{i=1}^{N} \sqrt{\left|x_{i}\right|}\right]^{2}} 。$ | (10) |
式中:
BP神经网络具有很好的非线性逼近特性和自适应学习能力,能够很好地表现转叶式舵机密封件振动信号与摩擦系数信号非平稳、非线性等特点。采用3层BP神经网络,即输入层、隐含层和输出层。BP神经网络的学习过程包括信号的正向传播和误差的反向传播,各层的权值和阈值不断自学习训练[9]。基于BP神经网络的转叶式舵机故障诊断模型构造如下:
1)输入层和输出层节点数
提取振动信号与摩擦系数信号的10个特征值,则输入层节点数为10。通常,转叶式舵机密封件在正常运行过程中,磨粒粒径一般在20 μm内[10];当粒径在20~70 μm范围内时,会出现异常磨损;若粒径超过100 μm,则会出现严重磨损[11]。因此,选择纯液压油和磨粒粒径分别为50 μm、120 μm和160 μm这4种类型,模拟正常磨损、轻微磨损、严重磨损和剧烈磨损4种状态,编码分别为(1 0 0 0)、(0 1 0 0)、(0 0 1 0)和(0 0 0 1),则输出层节点数为4。
2)隐含层节点数
隐含层节点数的选择可以根据下述经验公式确定其范围:
| $ k=\sqrt{n+m}+a 。$ | (11) |
式中:
根据式(11),隐含层节点数
3)其他BP神经网络结构参数
选择tansig和logsig函数作为输入层到隐含层、隐含层到输出层的传递函数,设定的期望误差为0.0001,学习率为0.3 s,训练次数为2000。
4)信号的正向传播过程
BP神经网络的输入层变量通过加权求和以及隐含层神经元的阈值,在激活函数的作用下,得到隐含层神经元的输出:
| $ h_{k}=f\left(\sum_{i} w_{i k} x_{i}+\theta_{k}\right) 。$ | (12) |
式中:
隐含层各输出变量通过加权求和以及输出层神经元的阈值,在激活函数的作用下,得到输出层神经元的输出:
| $ y_{j}=f\left(\sum_{k} \omega_{k j} h_{k}+\theta_{j}\right) 。$ | (13) |
式中:
5)误差的反向传播过程
通过网络的实际输出和期望输出来计算误差,则输出节点的误差为:
| $ E=\frac{1}{2} \sum_{j}\left(Y_{j}-y_{j}\right)^{2}。$ | (14) |
式中,
若误差不满足要求,首先从输出层逐层求取各层神经元的实际输出与期望输出的误差函数,然后根据误差梯度下降法来修正各层的权值和阈值,使修改后的神经网络的误差在可接受范围内[12]。
1.3 C#.NET与Matlab接口Matlab与C#通过接口实现混合编程,将Matlab编写的程序编译为COM组件或者.NET程序集供C#调用[13-14]。采用.NET程序集的方式进行混合编程。主要分为2个步骤:1)把Matlab程序编译为.NET程序集;2)C#调用Matlab生成的.NET程序集。具体流程如下:
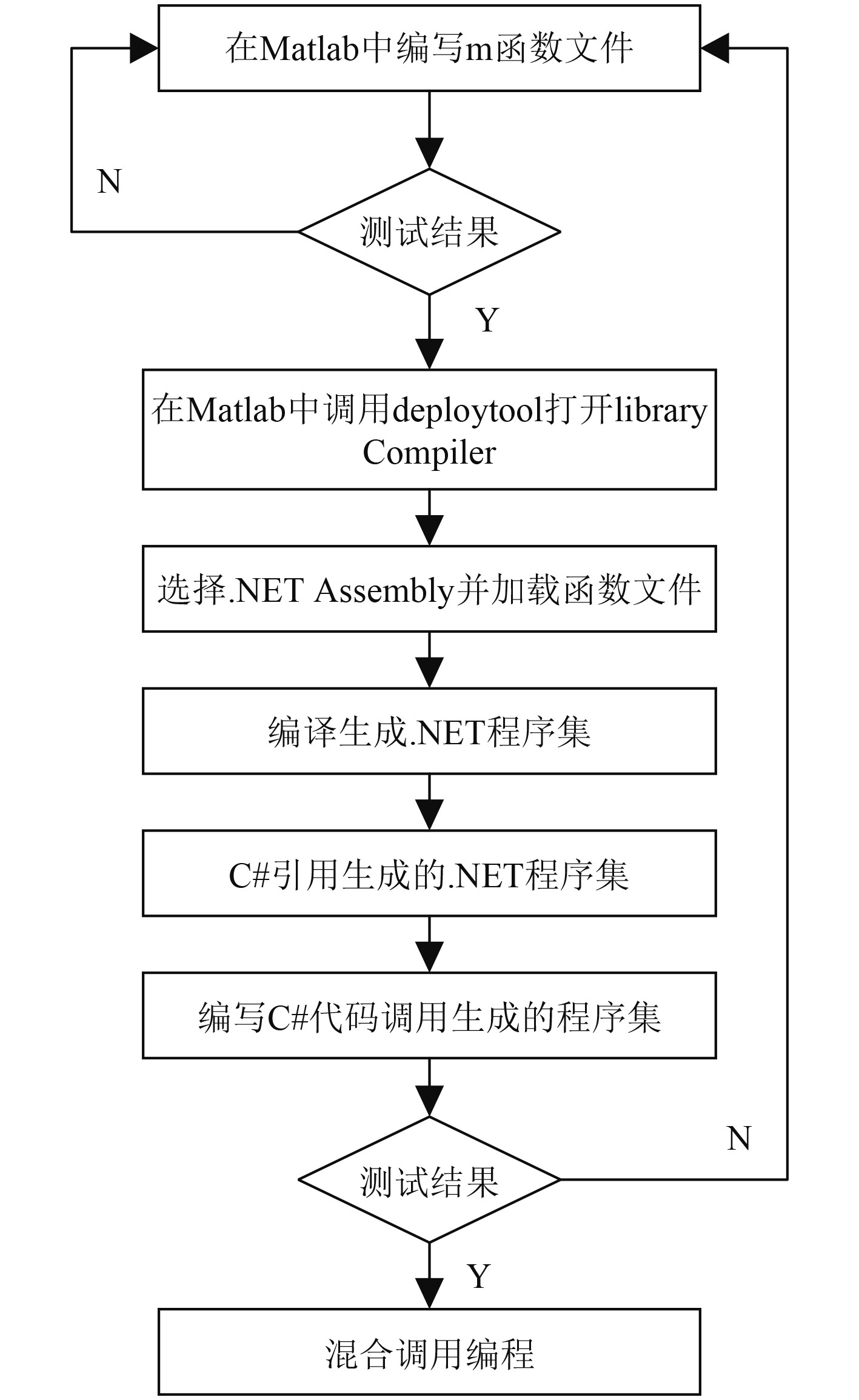
|
图 1 混合编程流程图 Fig. 1 Flowchart of hybrid programming |
通过.NET组件技术生成2个dll文件,分别用于实现摩擦系数信号和振动信号的时域特征提取及BP神经网络的故障诊断。
1.4 转叶式舵机故障诊断系统功能设计船舶转叶式舵机故障诊断系统主要有四大功能模块,分别是信号分析模块、故障诊断模块、故障数据库和管理模块,如图2所示。
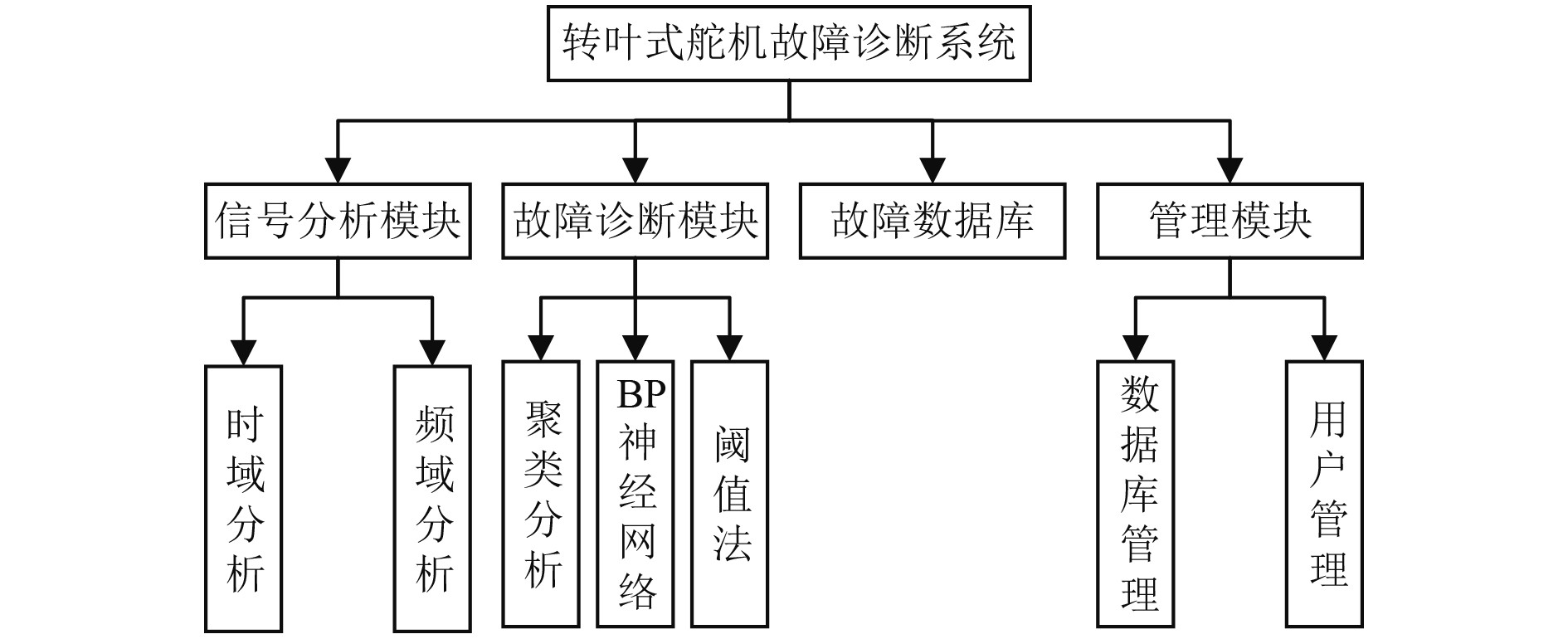
|
图 2 转叶式舵机故障诊断系统图 Fig. 2 Fault diagnosis system diagram of rotary vane steering gear |
信号分析模块通过计算信号的统计特征分析设备的故障情况,主要包括时域分析和频域分析;故障诊断模块负责识别转叶式舵机密封件的故障类型,系统设计了聚类分析、BP神经网络和阈值法3种故障诊断方法,本文通过BP神经网络进行故障诊断;故障数据库模块设计了故障实体表、故障原因表和故障位置表,用于查询故障发生的原因和位置;管理模块分为数据库管理和用户管理,数据库管理实现对SQL Server数据库中数据的增、删、改、查等操作,用户管理主要包括权限管理和密码修改。
2 实例分析 2.1 实验数据选用粘度等级为ISO VG68(美孚)的纯液压油、分别混合有50 μm、120 μm和160 μm这3种不同粒径大小铁粉液压油模拟转叶式舵机密封件在正常磨损、轻微磨损、严重磨损和剧烈磨损4种状态,并提取转叶式舵机密封件在这4种状态下的振动信号和摩擦系数信号的特征值,为后续的故障诊断提供知识库。其中,转叶式舵机密封件在轻微磨损条件下的振动信号如图3(a)所示,振幅较大,表明摩擦副之间磨损较为剧烈。轻微磨损条件下的摩擦系数如图3(b)所示,摩擦系数先减小,然后逐渐趋于稳定,原因可能是开始阶段摩擦副之间处于磨合磨损阶段。
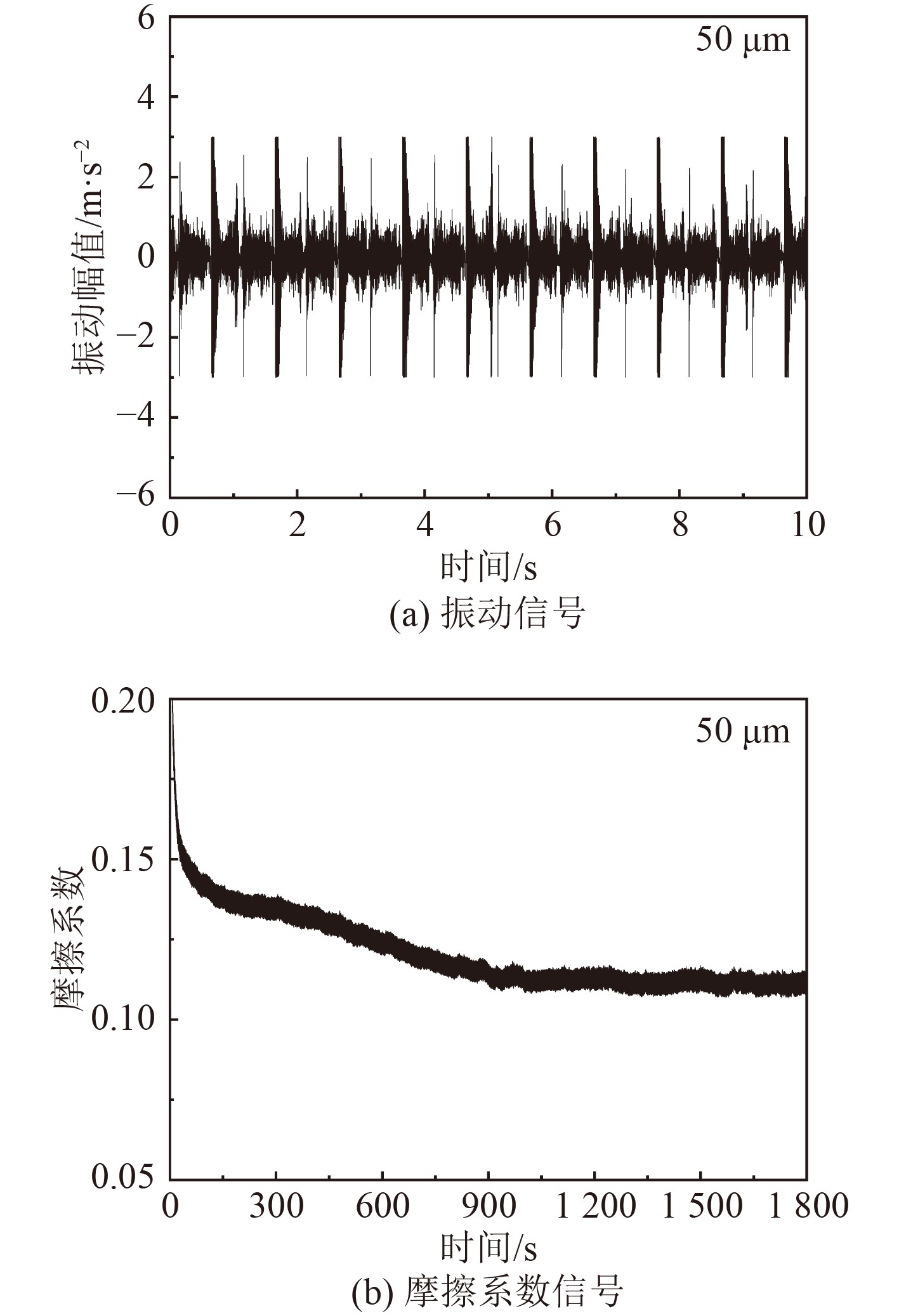
|
图 3 原始信号图 Fig. 3 Original signal diagram |
获取转叶式舵机密封件与缸体内壁之间在不同磨损程度情况下的振动信号及摩擦系数信号特征值是进行故障诊断的关键,表1和表2yl 采用式(1)~式(10)求振动信号及摩擦系数信号的特征值。从表1可知,添加磨粒后的振动信号比纯液压油工况更显著,随着磨粒尺寸的增大,振动幅值从1 m/s2增加到5 m/s2,峰峰值也随之增大,表明磨损程度加剧。方差与均方根值均随着磨损程度的增大而增大,纯液压油下,方差与均方根值分别为0.04 m/s2和0.2 m/s2。在剧烈磨损(160 μm)工况下,方差和均方根值分别为0.8 m/s2和0.9 m/s2。振动信号围绕零点上下波动,故在表征故障时,平均值并不显著。综上,最大值、峰峰值、方差与均方根值能较好地映射出振动信号在不同磨损程度的变化程度,具有较好的故障识别精度。
|
|
表 1 振动信号特征值 Tab.1 Characteristic values of vibration signal |
|
|
表 2 摩擦系数信号特征值 Tab.2 Characteristic value of friction coefficient signal |
从表2可知,添加磨粒后的摩擦系数大于纯液压油下的摩擦系数。纯液压油下的摩擦系数稳定在0.07左右,随着磨粒尺寸的增加,摩擦系数的最大值和平均值增至0.17左右,表明摩擦副之间的磨损加剧。峰峰值和均方根值均随着磨粒粒径的增加而增大,这表明摩擦副之间的波动幅度增大、磨损程度加剧。综上,最大值、平均值、峰峰值和均方根值能够较好地映射出摩擦系数信号在不同磨损程度的变化情况。
2.2 BP神经网络仿真测试将上述时域特征参数作为标准知识库作为网络的输入,网络的输出对应正常磨损、轻微磨损、严重磨损和剧烈磨损4种状态。把时域特征参数分为训练集与测试集,训练集用于模型的训练,测试集用于检验模型的准确性。为了防止输入的样本数据存在奇异值,导致网络训练时间延长甚至不能收敛,首先对导入的样本数据进行归一化处理,然后把处理后的数据作为网络的训练数据,最后保存训练后的网络模型。归一化公式如下:
| $ \bar{x}_{i}=\frac{x_{i}-x_{\min }}{x_{\max }-x_{\min }}。$ | (15) |
式中:
通过磨损实验数据验证该系统的可行性,一组是纯液压油下的振动信号,另一组是磨粒尺寸为50 μm的摩擦系数信号。在时域分析界面上设置了SQL Server数据库和Excel两个样本数据入口,通过时域分析按钮进行时域分析,特征值显示在系统界面,点击数据入库按钮把特征值存储在SQL Server数据库中。图4(a)为纯液压油时的振动信号图,图4(b)为磨粒尺寸为50 μm时的摩擦系数信号图。
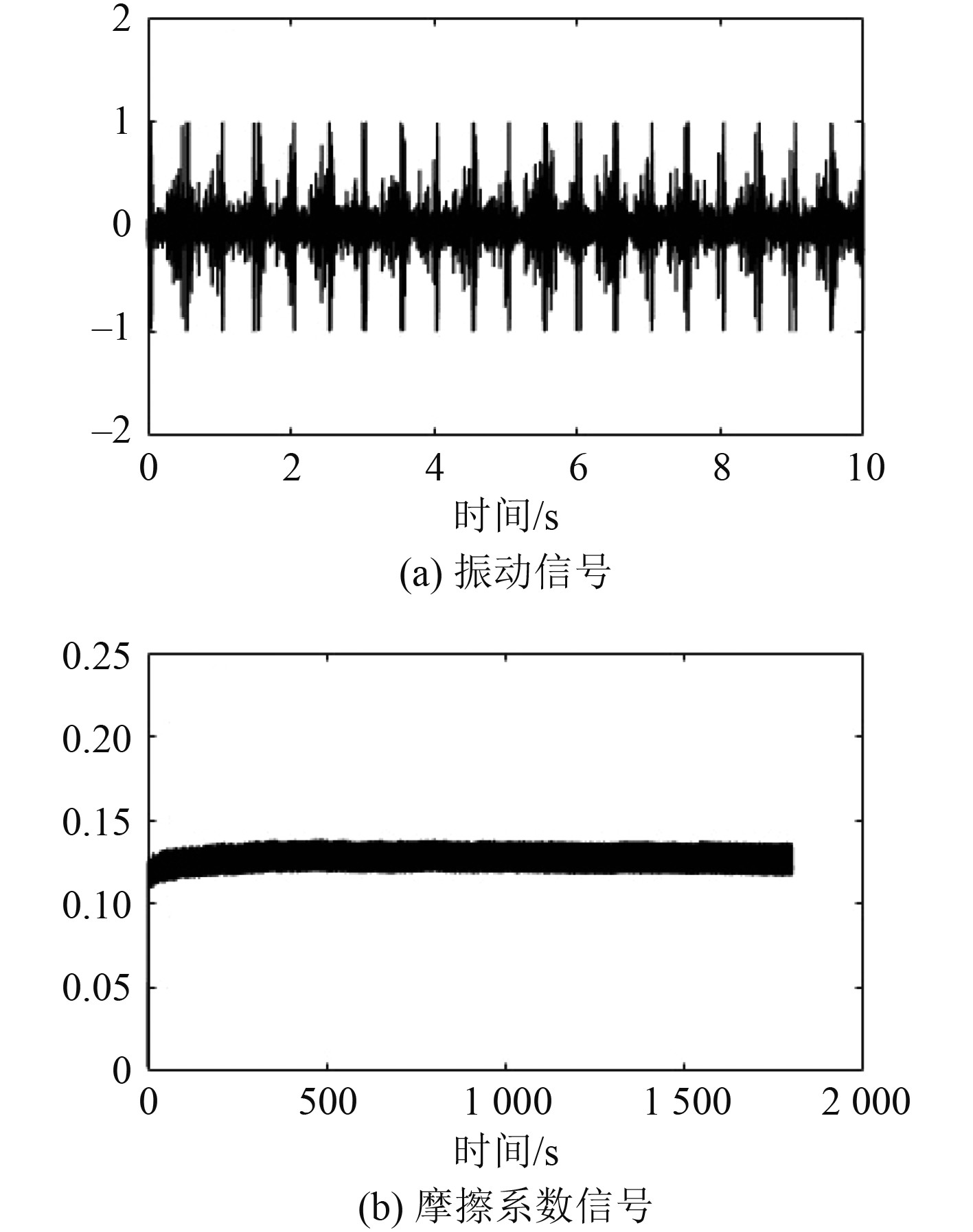
|
图 4 振动信号与摩擦系数信号图 Fig. 4 Vibration signal and friction coefficient signal diagram |
采用式(1)~式(10)求振动信号和摩擦系数信号的特征值,结果如表3所示。
|
|
表 3 待测特征值 Tab.3 Eigenvalues to be measured |
在故障诊断模块中,首先导入特征数据,然后点击开始训练按钮,程序会进行故障诊断,并将诊断结果显示在文本框里。BP神经网络在经过32次训练后,误差精度就达到了要求。诊断结果与测试样本真实故障一致,证明C#与Matlab混合编程是可行的。
3 结 语本文以.NET为开发平台,采用C#和Matlab混合编程技术构建了船舶转叶式舵机故障诊断系统。该系统实现了对不同工况下的振动信号和摩擦系数信号的时域特征提取,并根据提取到的特征值进行故障诊断。故障诊断结果表明随着磨粒粒径的增大,振动信号的幅值和摩擦系数显著增加,转叶式舵机密封件的磨损加剧,说明该系统能够快速、准确的识别转叶式舵机密封件的磨损状态。因此,C#和Matlab混合编程在船舶机械故障诊断方面有着潜在的应用前景,为船舶转叶式舵机可靠性运行提供了技术保障。
| [1] |
王必改. 船舶舵机故障的原因分析与探讨[J]. 天津航海, 2020(4): 16-19. |
| [2] |
张李伟, 庄才亮, 夏明宽, 等. 性能卓越的转叶式舵机设计[J]. 船舶与海洋工程, 2014(2): 35-39. |
| [3] |
徐恒达. 船舶柴油机故障分析诊断系统[D]. 大连: 大连理工大学, 2015.
|
| [4] |
胡良谋, 曹克强, 徐浩军. 基于回归型支持向量机的液压舵机故障诊断[J]. 系统仿真学报, 2007(23): 5509-5512. |
| [5] |
章家保, 徐伟. 模糊聚类方法在电动舵机致命故障检测中的应用[J]. 红外与激光工程, 2014, 43(S1): 123-129. |
| [6] |
XU Y X, YANG C N. Fault recognition of electric servo steering gear based on long and short-term memory neural network[C]//International Conference on Unmanned Aircraft Systems (ICUAS). Athens, Greece: IEEE, 2020: 1605–1613.
|
| [7] |
MARTINS M R, da Silva D F, MARUYAMA F M, et al. The bayesian networks applied to a steering gear system fault diagnostics[C]//International Conference on Offshore Mechanics and Arctic Engineering. Shanghai, China: ASME, 2010: 639–645.
|
| [8] |
ZHANG Y, AN J P, CHEN P. Research of hybrid programming with c#. net and matlab[J]. Physics Procedia, 2012, 24: 1677-1681. DOI:10.1016/j.phpro.2012.02.247 |
| [9] |
刘鑫, 贾云献, 孙磊, 等. 基于BP神经网络的变速箱故障诊断方法研究[J]. 计算机测量与控制, 2017, 25(1): 12-15. |
| [10] |
MA L, SHI H, ZHANG H, et al. High-sensitivity distinguishing and detection method for wear debris in oil of marine machinery[J]. Ocean Engineering, 2020, 215: 107452. DOI:10.1016/j.oceaneng.2020.107452 |
| [11] |
向晶晶, 董从林, 白秀琴, 等. 转叶式舵机密封件在不同磨粒尺寸下的摩擦学特征研究[J]. 中国机械工程, 2022, 33(4): 397-405. |
| [12] |
张祥罗. 风力机中发电机在线故障特征提取与故障诊断系统研究[D]. 广州: 华南理工大学, 2013.
|
| [13] |
侯伟真, 李正强, 张玉环, 等. 基于C#和Matlab的HJ-1-CCD气溶胶光学厚度反演系统的开发[J]. 遥感信息, 2013, 28(5): 28-31+36. |
| [14] |
刘亚, 王静, 田新诚. 基于C#和Matlab混合编程的轴承故障诊断系统[J]. 计算机应用, 2018, 38(S2): 236-238+242. |
 2023, Vol. 45
2023, Vol. 45
