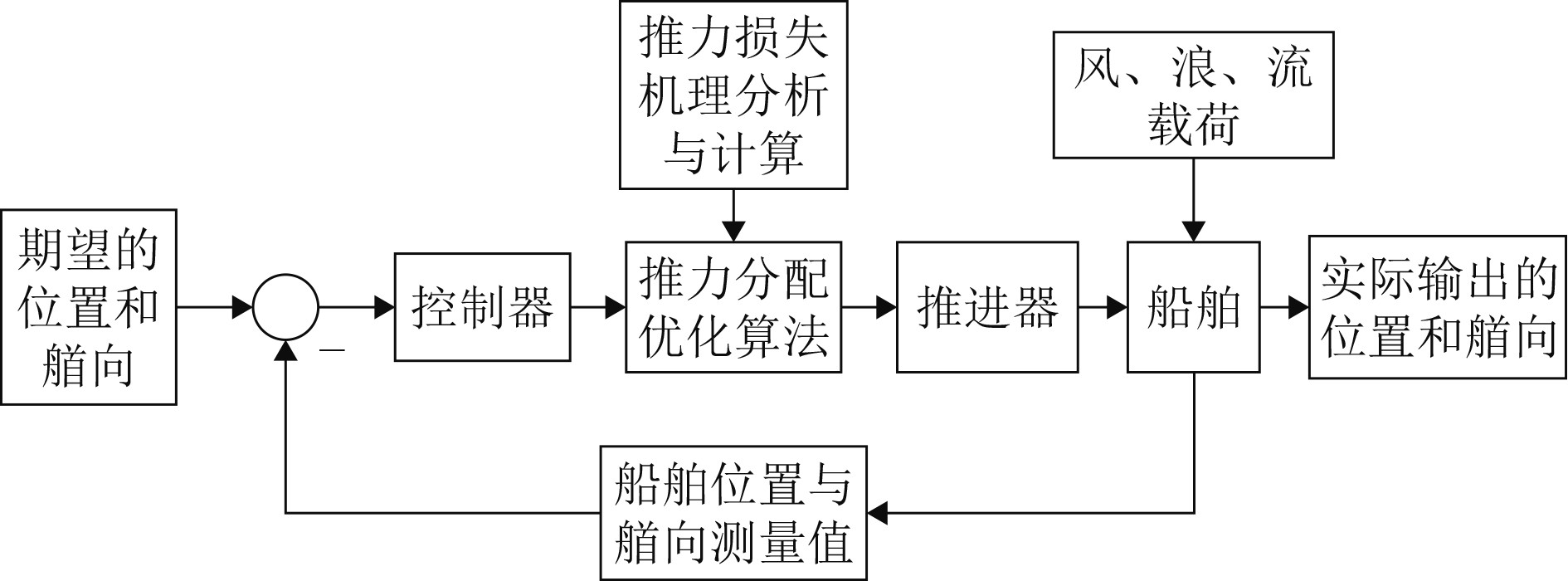
动力定位系统是利用船舶自身搭载的推进器产生推力来抵御环境外力[1],从而可以到达指定位置或实现定点定位。动力定位系统主要由三部分系统组成,分别为测量系统、控制系统和推进系统,各系统在控制流程中的简要作用如图1所示。其中,推进系统根据控制器发出的控制指令,同时考虑了推力分配目标的力和力矩、推力限制、偏转角限制等约束条件,从而得到各个推进器的推力及方位角,进而能够将所需要的期望推力指令合理分配给各个推进装置,从而使船舶能够保持在固定位置或者设定航线上。
|
图 1 动力定位系统控制流程总框图 Fig. 1 General block diagram of dynamic positioning system |
推力分配优化是一个多约束的优化求解过程,目标是在多个推进器共同作用下得到一个控制力和力矩来满足控制器所需要的期望控制力和力矩。在20世纪90年代,Sordalen[2]研究了矩阵奇异值在动力定位技术中的应用,采用矩阵分解的方法避免发生奇异性,这有利于降低推进装置的磨损程度,从而有效保护了推进器。Johansen等[3-4]将序列二次规划方法应用到推力优化分配问题上,该方法不会在分配过程中出现奇异值的情况,并通过实验证明方法的可靠性。在传统的序列二次规划中增加了多启动的计算机制,具有更好的全局搜索能力。尚留宾等[5]提出了一种改进的粒子群算法,讨论了不同粒子决策变量对优化结果的影响,最终找到最优的决策变量来达到快速收敛和高实时性的目的。虽然提出的改进算法有一定效果,但未考虑约束条件所带来的影响,而约束条件会降低算法的全局搜索能力。
推力分配优化方法的好坏决定了船舶动力定位系统种推力分配模块性能的高低,近些年来许多学者采用了大量的优化方法来解决推力分配问题。这些方法主要是针对以下几点进行优化:一是算法能够具有较强的收敛性;二是算法能够在全局范围找到最优解。针对推力分配优化算法中存在常陷入局部最优且计算时限太长等问题,本文将粒子群算法和细菌觅食算法结合起来,提出一种粒子群-细菌觅食混合优化算法来解决推力分配优化问题,该算法具有寻优精确、容易实现和收敛快等优点。
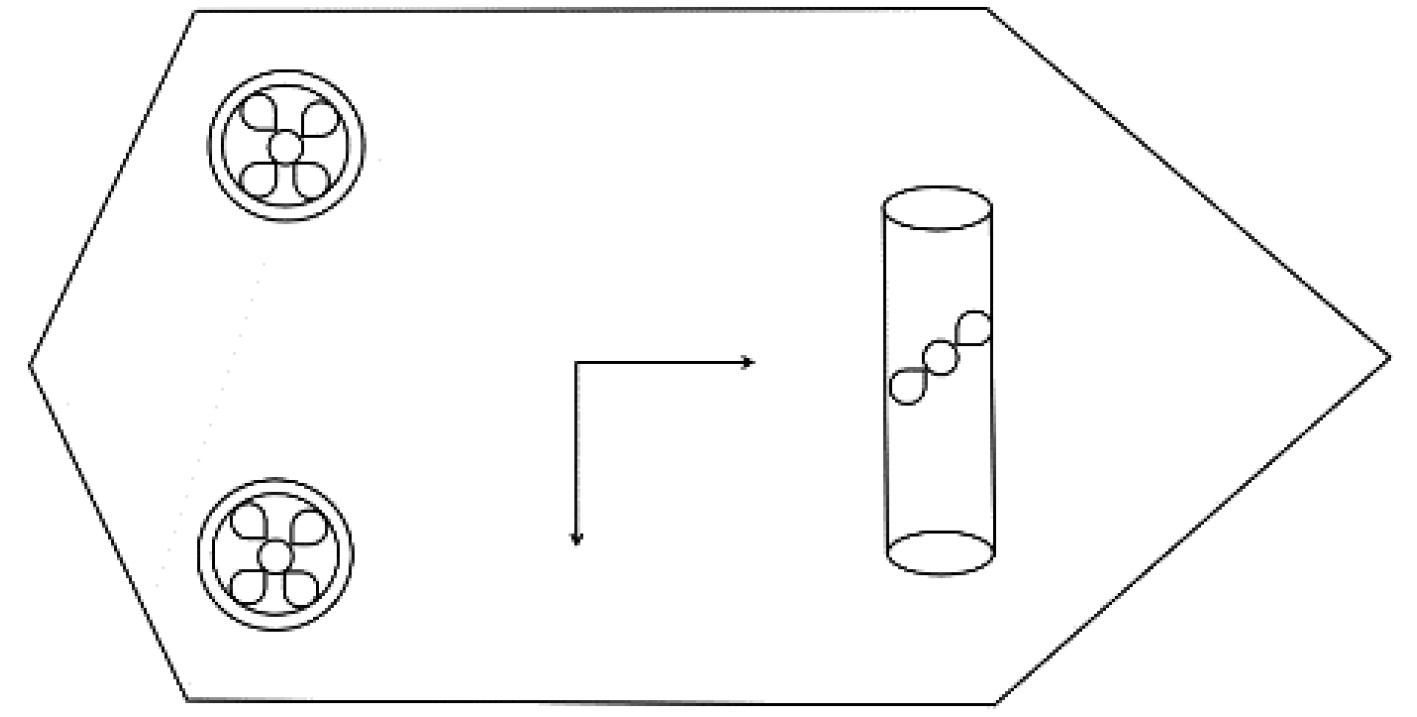
1 船舶推进器数学模型选用一艘挪威科技大学实验室的缩尺模型船(CS3)并对其进行仿真,此模型船在船尾装有2台全回转推进器,船首装有1台槽道式推进器,模型船的配置参数见表1,各推进器的布置如图2所示。
|
|
表 1 模型船的配置参数 Tab.1 Configuration parameters of the model ship |
|
图 2 模型船的推进器位置示意图 Fig. 2 Schematic diagram of propeller position of model ship |
该船的惯性矩阵
| $ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {75}&0&0 \\ 0&{77}&{ - 1.07} \\ 0&{ - 1.07}&{14.7} \end{array}} \right]\text{,}{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {6.9}&0&0 \\ 0&{19.3}&{0.59} \\ 0&{0.59}&{6.8} \end{array}} \right] 。$ |
为了简化计算过程并能够准确描述船舶运动时的状态,只在纵荡、横荡和首摇三自由度运动上建立船舶的数学模型。针对只有这3个自由度运动的船舶,其运动学方程如下式[6]:
| $ {\dot {\boldsymbol{\eta}} = {\boldsymbol{R}}\left( {\boldsymbol{\psi}} \right){\boldsymbol{v}}} 。$ | (1) |
也可改写为:
| $ \begin{array}{c}\dot{{\boldsymbol{\eta}} }=\left[{\begin{array}{c} \dot x\\ \dot y \\ {\dot{\psi }}\end{array}}\right]=\left[\begin{array}{ccc}\cos\psi & -\sin\psi & 0\\ \sin\psi & \cos\psi & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\mu \\ v\\ \gamma \end{array}\right]\end{array}。$ | (2) |
其中:
在研究船舶的三自由度运动规律时,一般不考虑船舶的高频运动部分。建立动力学模型时,可把目标船舶当成是一个质量均匀的刚体,那么船舶的运动就可认定是在船舶重心处的质点运动情况,且设船舶所处的海域中水域的水流速度为0。因此船舶动力学的三自由度数学模型如下式[7]:
| $ {{\boldsymbol{M}}\dot {\boldsymbol{v}} + {\boldsymbol{Dv}} = {{\boldsymbol{\tau}} _T} + {\boldsymbol{d}}} 。$ | (3) |
其中:
| $ {\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} {{X_w}} \\ {{Y_w}} \\ {{N_w}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_{\rm wave}} + {X_{\rm wind}} + {X_{\rm current}}} \\ {{Y_{\rm wave}} + {Y_{\rm wind}} + {Y_{\rm current}}} \\ {{N_{\rm wave}} + {N_{\rm wind}} + {N_{\rm current}}} \end{array}} \right] 。$ | (4) |
推力分配问题是一个非线性数学优化问题,如何正确建立一个目标函数并且设置约束条件对问题的求解起着至关重要的作用。
2.1 推力分配的目标函数推力分配优化是一个多约束的优化求解过程,通过建立合理的目标函数,从而在多个推进器共同作用下得到一个控制力和力矩来满足控制器所需要的目标控制力和力矩。考虑到各推进器实际输出的推力指令和目标指令之间的误差、船舶推进装置的能量消耗、推力约束、偏转角度的约束和函数解的奇异性,构建的目标函数如下式:
| $ \begin{split} {\rm{Min}}\left( {a,T,s} \right) =& W{P_{\rm total}} + {s^{\rm{T}}}Qs + {(\alpha - {\alpha _0})^{\rm{T}}}{{\varOmega }}\left( {\alpha - {\alpha _0}} \right)+ \\ & \frac{\rho }{{\varepsilon + \det \left( {B\left( \alpha \right){B^{\rm{T}}}\left( \alpha \right)} \right)}}。\end{split} $ | (5) |
式中:
| $ \begin{array}{*{20}{c}} {{P_{\rm total}} = \displaystyle\sum\limits_{i = 1}^{i = n} {P_i} = \displaystyle\sum \limits_{i = 1}^{i = n} 2\pi \sqrt {\frac{1}{{\rho {K_{{T_i}}}}}} \frac{{{K_{{Q_i}}}}}{{{K_{{T_i}}}{D_i}}}T_i^{\frac{3}{2}} = \displaystyle\sum \limits_{i = 1}^{i = n} {k_i}T_i^{\frac{3}{2}}}。\end{array} $ | (6) |
| $ \begin{split} &B\left( \alpha \right) = \\ &\left[ {\begin{array}{*{20}{c}} {\cos({\alpha _1})} & \ldots & {\cos({\alpha _n})} \\ {\sin({\alpha _1})} & \ldots & {\sin({\alpha _n})} \\ { - {l_{y1}}\cos\left( {{\alpha _1}} \right) + {l_{x1}}\sin\left( {{\alpha _1}} \right)} & \ldots & { - {l_{yn}}\cos\left( {{\alpha _n}} \right) + {l_{xn}}sin\left( {{\alpha _n}} \right)} \end{array}} \right] \end{split}。$ | (7) |
通常来说,约束条件分为不等式和等式两种,在建立推力分配目标函数时,本文考虑了以下几种约束:即推进器推力是否符合期望值、推力和偏转角限制及推力和偏转角变化率限制,则得到如下约束表达式:
| $ \begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{l}} {s = \tau - B\left( \alpha \right)f},\\ {{T_{\rm min}} \leqslant x \leqslant {T_{\rm max}}},\\ {\Delta {T_{\rm min}} \leqslant {x_i} - {x_{i,0}} \leqslant \Delta {T_{\rm max}}},\\ {{\alpha _{\rm min}} \leqslant \alpha \leqslant {\alpha _{\rm max}}} ,\\ {\Delta {\alpha _{\rm min}} \leqslant {\alpha _i} - {\alpha _{i,0}} \leqslant \Delta {\alpha _{\rm max}}} 。\end{array}} \right.} \end{array} $ | (8) |
式中:
推力分配优化算法的好坏决定了船舶动力定位系统中推力分配模块性能的高低。将粒子群算法和细菌觅食算法结合,提出一种改进的粒子群-细菌觅食混合优化算法来解决推力分配优化问题。
3.1 细菌觅食、粒子群算法及其改进策略细菌觅食优化算法(BFO)主要研究了大肠杆菌觅食行为中的4个主要过程,分别是趋化行为、复制行为、迁徙行为和聚集行为[8]。BFO算法在模拟细菌运动时为了便于描述觅食行为设置了以下参数:趋化操作记为
细菌在趋向性操作过程中,其位置更新公式如下式:
| $ \begin{array}{*{20}{c}} {{x^i}\left( {j + 1,k,l} \right) = {x^i}\left( {j,k,l} \right) + C\left( i \right){\boldsymbol{\varPhi }}\left( j \right)} 。\end{array} $ | (9) |
式中:
细菌经历过次数为
在大肠杆菌的迁徙过程中会设定一个迁徙概率
细菌的聚集操作是个体之间相互作用和影响的行为,细菌个体通过释放信号来引诱或是排斥其他个体,其聚集操作的具体行为如下式:
| $ \begin{split} {J_{cc}} &({x^i},P(j,k,l))= \\ & \sum\limits_{r = 1}^S {J_{cc}^r} ({x^i},{x^r}) =\\ & \sum\limits_{r = 1}^S {\left[ { - {d_{\rm attract}}\exp \left( { - {w_{\rm attract}}\sum\limits_{m = 1}^p {{{\left( {x_m^i - x_m^r} \right)}^2}} } \right)} \right]}+ \\ & \sum\limits_{r = 1}^S {\left[ { - {h_{\rm repellant}}\exp \left( { - {w_{\rm repellant}}\sum\limits_{m = 1}^p {{{\left( {x_m^i - x_m^r} \right)}^2}} } \right)} \right]} 。\end{split} $ | (10) |
式中:
细菌觅食算法存在一些缺陷,较大的步长虽然能够加快算法的收敛速度,但会导致无法找到最优解或是陷入早熟的情况,而步长较小会影响算法的计算效率和收敛速度。随着时间的推移,细菌的游动范围会缩小,固定的步长会影响算法的收敛速度,因此本文提出一种自适应游动步长的方法来解决这些问题。该方法在保证算法求解精度的同时也加快了收敛速度,其游动步长更新公式如下式:
| $ \begin{array}{*{20}{c}} {C'\left( i \right) = C\left( i \right) \times {e^{ - n}}} \end{array} 。$ | (11) |
式中,
粒子群优化算法(PSO)的基本单位是粒子。假定粒子是处在一个d维空间,粒子的数量为N个,则第
| $ \begin{array}{*{20}{c}} {v_{id}^{k + 1} = v_{id}^k + {c_1}ran{d_1}\left( {pbest_{id}^k - x_{id}^k} \right) + {c_2}ran{d_2}\left( {gbest_{id}^k - x_{id}^k} \right)} \end{array} ,$ | (12) |
| $ \begin{array}{*{20}{c}} {x_{id}^{k + 1} = x_{id}^k + v_{id}^{k + 1}} \end{array}。$ | (13) |
式中:
将PSO算法中的记忆步骤加入到BFO算法中的聚集操作中,使得细菌也具备较强的全局搜索能力,其基本思想为:首先PSO算法在搜索空间内进行全局寻优,在搜索的过程中记录下个体的最优信息,然后将每个粒子假设为细菌,并用BFO算法进行局部搜索,即把式(10)中的社会认知部分加入到BFO算法的位置更新公式(9)中,那么式(10)中社会认知部分用式(14)表示,并使用自适应游动步长来替代原固定步长游动,最终得到细菌的位置更新方程,如下式:
| $ \begin{array}{*{20}{c}} {v_{id}^{k + 1} = wv_{id}^k + {c_2}rand_2^k\left( {gbest_{id}^k - x_{id}^k} \right)} \end{array},$ | (14) |
| $ \begin{array}{*{20}{c}} {{x^i}\left( {j + 1,k,l} \right) = {x^i}\left( {j,k,l} \right) + v_{id}^{k + 1} + C'\left( i \right)} \end{array} 。$ | (15) |
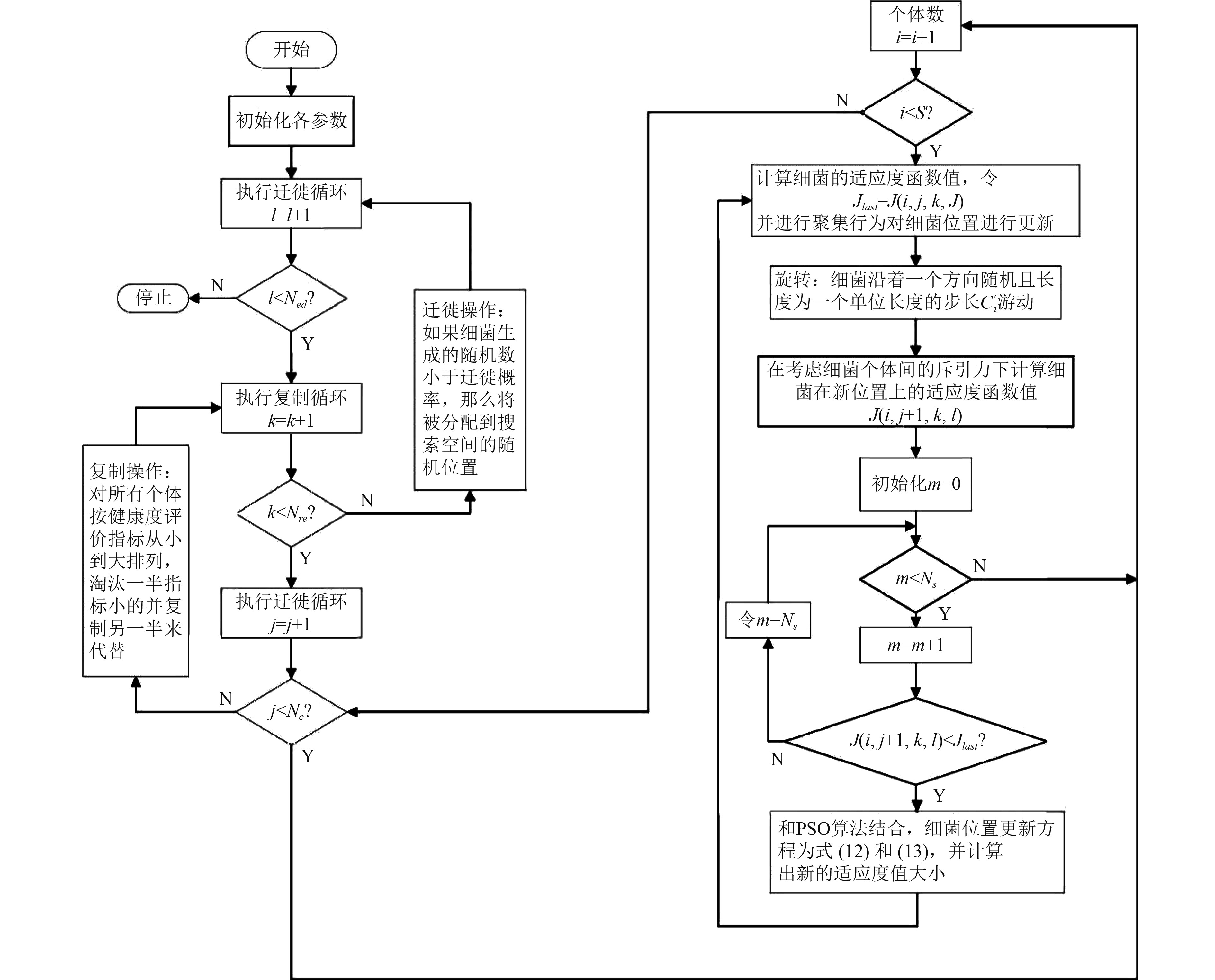
针对提出的改进策略,混合算法的主要实施步骤如流程图3所示。
|
图 3 改进优化算法的流程图 Fig. 3 Flow chart of improved optimization algorithm |
为了对比优化算法的优劣,将提出的改进算法与常规的粒子群和细菌觅食算法进行对比研究分析,分别开展推进器实际输出的合力及力矩与期望合力及力矩变化,以及各推进器的推力幅值、方位角变化、期望合力及力矩和实际输出之间的误差变化研究。
仿真中,推力参数设置如下:
设置的仿真条件为:船舶的初始位置为
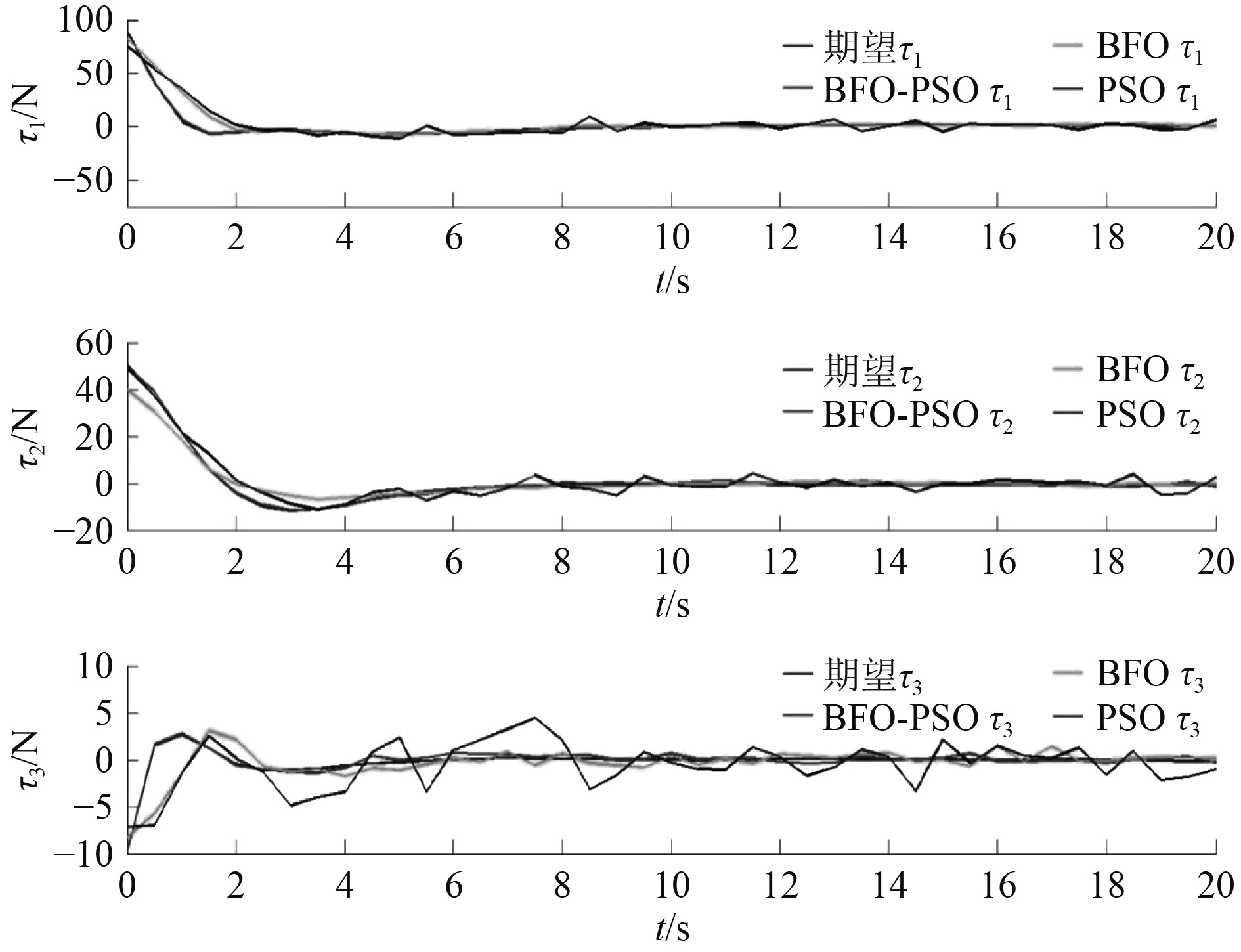
从图4~图7仿真结果来看,由于对推力幅值和方位角设置了约束条件,3种算法对应的推力幅值和方位角都能够在约束范围内。但是,采用PSO-BFO混合算法进行推力分配时,推力幅值和方位角的变化更平缓,没有明显的突变,能更有效地减少推进设备的磨损,同时还能降低不必要的功率消耗。在降低船舶能量消耗方面,PSO-BFO混合算法具有较明显的优势。
|
图 4 不同算法优化下期望合力及力矩和实际输出的合力及力矩变化曲线 Fig. 4 Variation curve of expected resultant force and torque and actual output resultant force and torque under different algorithm optimization |
|
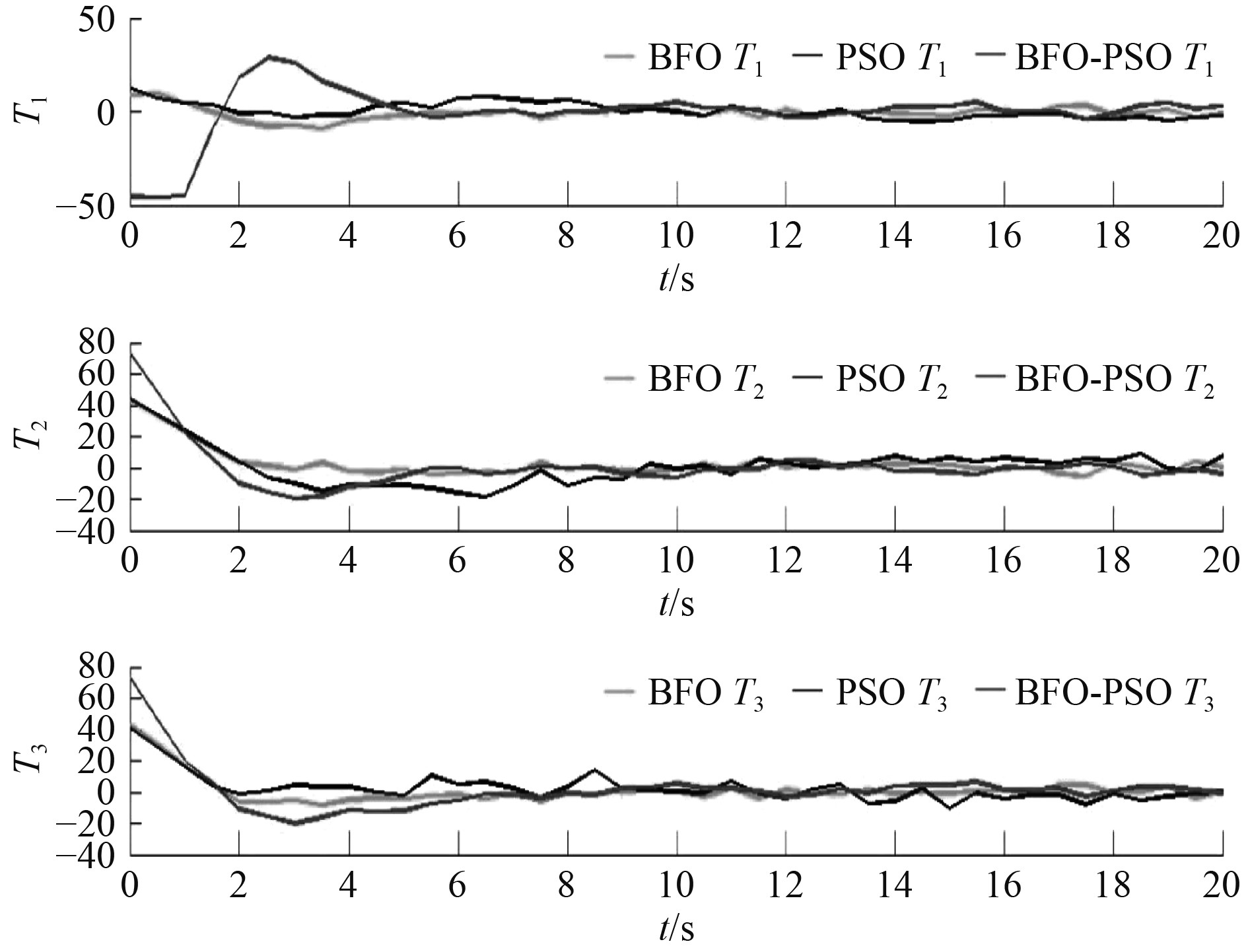
图 5 不同算法优化下各推进器的推力幅值变化曲线 Fig. 5 Thrust amplitude variation curve of each propeller under different algorithm optimization |
|
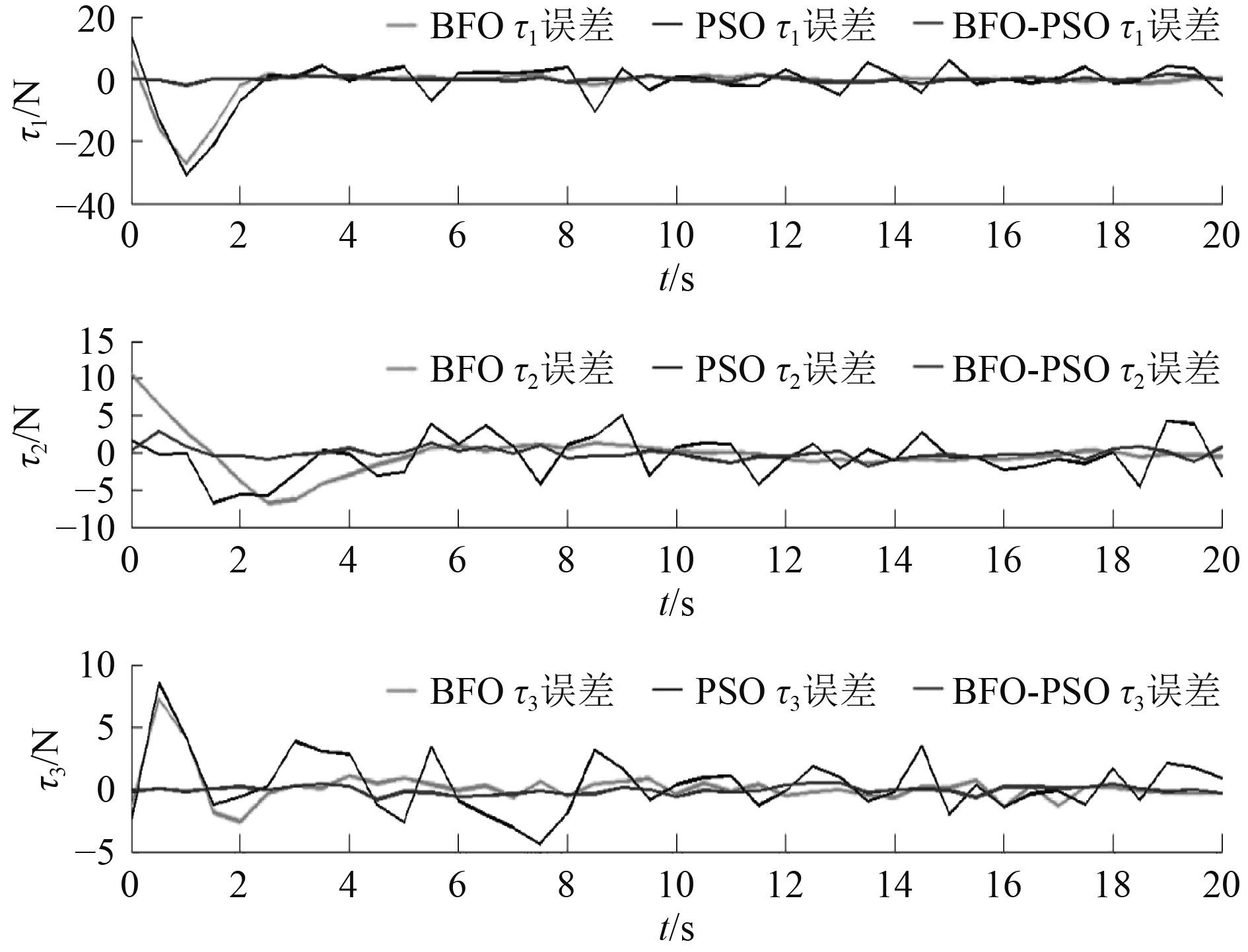
图 7 不同算法优化下期望合力及力矩和实际输出之间的误差变化曲线 Fig. 7 Error curve between expected resultant force and torque and actual output under different algorithm optimization |
从图6可看出,槽道推进器的角度一直保持在90°,符合船舶推进器的实际工作情况。利用混合算法优化的推力分配优化中全回转推进器角度变化更为缓慢,不会出现急剧变化加深推进器的磨损程度。
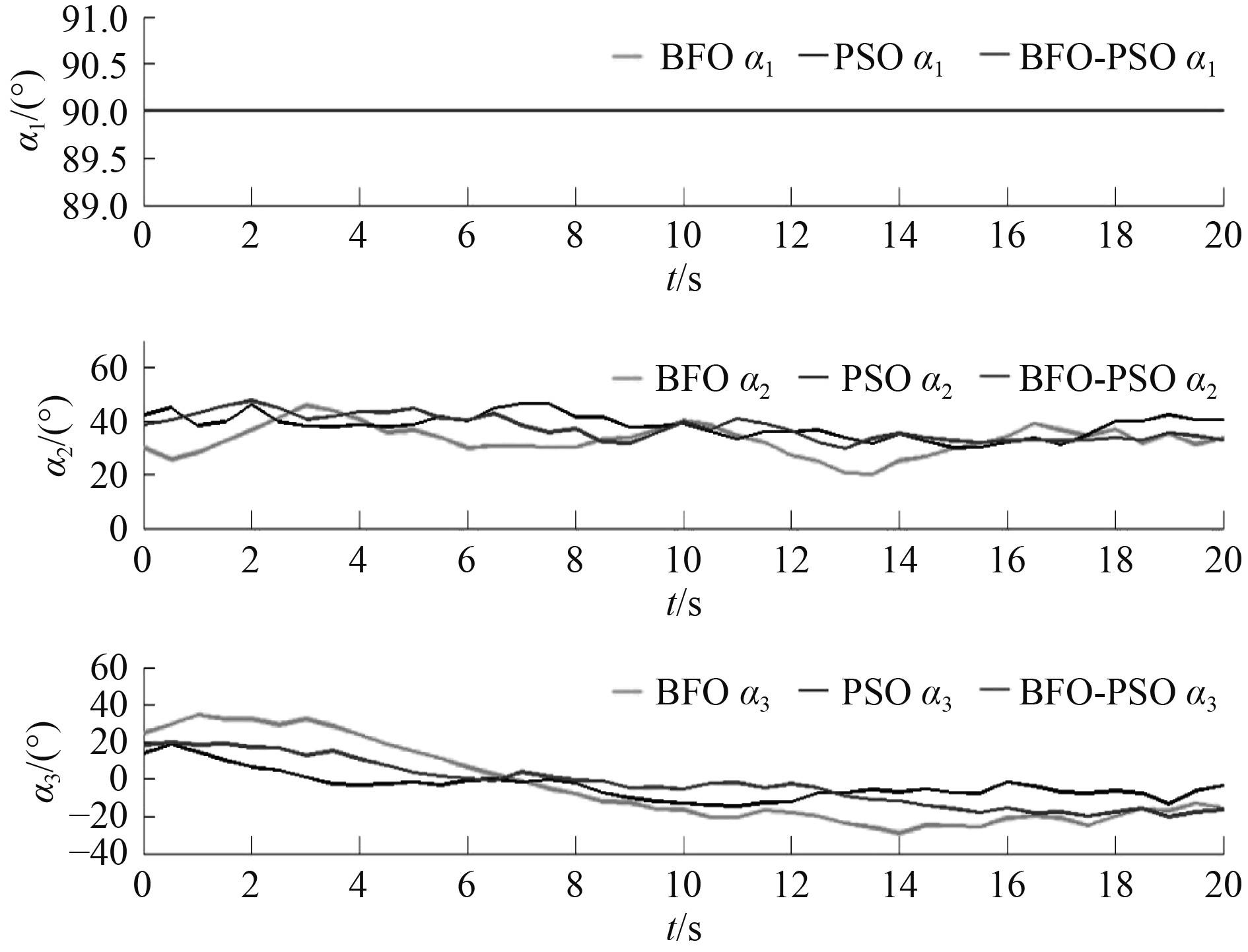
|
图 6 不同算法优化下各推进器的方位角变化曲线 Fig. 6 Azimuth curve of each propeller optimized by different algorithms |
根据图4和图7可知,在3种算法下推力器产生的实际推力及力矩基本和期望推力及力矩保持一致,但改进算法相比于另两种基本算法推力分配优化效果更好,实际产生的推力及力矩和期望推力及力矩的误差更小。误差变化最大下降20%左右,输出稳定后平均误差变化下降6%~10%,改进算法能够减少推进器功率的消耗,同时能够更加准确地输出船舶动力定位推力分配所需要的期望推力及力矩。
5 结 语针对粒子群优化算法易出现早熟和细菌觅食算法全局优化能力差的问题,提出了一种粒子群-细菌觅食混合优化算法,混合算法中在BFO算法的位置更新公式加入PSO的社会认知部分,从而改变了细菌位置更新方程,同时提出了自适应步长的思想来改变BFO算法中细菌的游动步长,从而提高了算法的求解精度;利用改进的混合算法对目标函数进行优化,并利用Matlab软件对3种优化算法进行仿真,通过分析和比较3种算法下推力分配的效果,结果显示改进的算法在求解精度和收敛速度上都比未改进的算法更优秀,表明混合算法具有更好的优化效果,验证了所提出算法的有效性。
| [1] |
蓝雪. 船舶动力定位系统推力分配与控制方法研究[D]. 上海: 上海交通大学, 2018.
|
| [2] |
SORDALEN O J. Optimal thrust allocation for marine vessels[J]. Control Engineering Practice, 1997, 5(9): 1223-1231. DOI:10.1016/S0967-0661(97)84361-4 |
| [3] |
JOHANSEN T A, FOSSEN T I, BERGE S P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J]. IEEE Transactions on Control Systems Technology, 2004, 12(1): 211-216. DOI:10.1109/TCST.2003.821952 |
| [4] |
FOSSEN T I, JOHANSEN T A. A survey of control allocation methods for ships and underwater vehicles[C]. Control and Automatic, 2006.14th Mediterranean Confeerence on. IEEE, 2006: 1-6.
|
| [5] |
尚留宾, 王威, 刘志华. 基于粒子群算法的动力定位推力分配决策变量优选[J]. 船舶工程, 2019, 41(10): 81-84+97. DOI:10.13788/j.cnki.cbgc.2019.10.17 |
| [6] |
FOSEEN T I. Handbook of marine graft hydrodynamics and motion control[M]. Chichester: John Wiley&Sons, 2011.
|
| [7] |
FOSEEN T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles[M]. Trondheim: Marine Cybernetics, 2002.
|
| [8] |
李亚品, 邹德旋, 段纳. 基于遗传-细菌觅食组合算法的非线性模型优化[J]. 电子科技, 2019, 32(5): 16-20. |
| [9] |
谷旭平, 唐大全. 基于细菌觅食算法的多异构无人机任务规划[J]. 系统工程与电子技术, 2021, 43(11): 3312-3320. DOI:10.12305/j.issn.1001-506X.2021.11.32 |
 2023, Vol. 45
2023, Vol. 45

