水下无人航行器(Underwater Unmanned Vehicle, UUV)依托其无人、经济、可大规模部署等优点,受到各国广泛关注。在军事领域,凭借UUV分布式、自主化的优势,可执行传统载人平台无法完成的多种复杂作战任务,如近海全方位、长周期、体系化的无人防御警戒,目标海域清扫侦察,对敌高价值水下目标进行集群联合打击[1-3]等。受制于水声通信高延迟、低带宽问题,充分考虑载人指挥控制平台隐蔽性安全性,在UUV执行任务前,需对UUV所执行作战任务进行预分配,保证所执行任务满足战略战术需求。因此,对多UUV进行任务分配是UUV高效执行作战任务的必要流程,也是当前水下无人系统研究热点。
21世纪以来,各国纷纷开展无人系统任务分配专项研究工作,将任务分配问题与控制科学、人工智能、决策理论以及建模优化技术相融合,形成多种解决方法,如合同网法、线性规划法、群体智能法[4]。李娟等[5]提出了一种基于改进合同网算法的异构多UUV任务分配策略,将任务负载率指标和令牌环网概念结合起来, 有效解决选择招标者及其任务不合理的问题。范学满等[6]假设了每个任务由单个UUV完成,将NSGA-II与动态规划算法相结合,以最短路径为基准,优化得到个固定数量UUV各自任务序列。李建军等[7]改进量子行为粒子群优化(Quantum-behaved Particle Swarm Optimizer,QPSO)算法,设计混沌QPSO算法,以总时间、总收益、总代价为目标,对多个UUV分别分配任务序列。卢骞等[8]采用MODSPO算法引入改进SA算法,增强对UUV协同任务的搜索能力。上述文献通过不同方法实现UUV任务序列的生成,解决在UUV任务分配过程中的部分问题,促进UUV集群任务分配领域的发展。但实际应用场景中,UUV与保障船需保持信息交互,以确保指挥员对态势信息的掌握。对各UUV进行任务分配,不仅考虑UUV续航、功能,还需考虑与保障船交互关系。
本文在已有研究基础上,充分考虑执行水下任务的多种约束条件,建立任务分配模型,通过改进集合粒子群优化算法(S-PSO)的惯性系数,引入遗传算法变异操作,提高算法的局部搜索和全局探索能力。
1 问题描述与建模 1.1 基本描述我方保障船于某海域释放多艘UUV。该海域中存在多个任务点,每个任务点的任务对UUV能力需求存差异。由于不涉及路径规划和跟踪,本文不考虑UUV动力学模型异构。我方保障船根据各UUV状态信息、任务基本信息等,在确保总任务时间最优情况下,降低多UUV执行任务的总能耗、总路程,实现多UUV任务分配,生成UUV任务序列。其中,部分任务需多艘UUV联合执行,且规定多艘UUV执行同一任务。以最后到达任务点UUV时间为任务开始时间,最后完成该任务UUV结束时间为任务结束时间。
每艘UUV任务序列采用有向图表示,设
| $ x_{ij}^n = \left\{ {\begin{array}{*{20}{c}} 1,{j \in {M^n}},\\ 0,{j \notin {M^n}} 。\end{array}} \right. $ | (1) |
式中:
设任务信息为:任务区域中心坐标点、预估任务耗时、预估任务能耗、预估任务所需UUV数量、所需UUV的能力;UUV信息格式为:初始位置坐标点、航行速度、单位距离能耗、总能量、能力、充电时间。对各UUV任务的预分配和任务序列的生成,为多目标多约束规划问题。任务分配目标为任务的总时间
| $ \begin{array}{*{20}{c}} {\min }&{\alpha T + \beta C + \gamma E} 。\end{array} $ | (2) |
式中:
| $ T = \sum\limits_{i,j \in {\rm X}} {{t_{i \to j}}} ,$ | (3) |
| $ C = \sum\limits_{n \in {N_{uuv}}} {\sum\limits_{i,j \in M} {{d_{ij}}x_{ij}^n} } ,$ | (4) |
| $ E = \sum\limits_{n \in {N_{uuv}}} {\sum\limits_{i,j \in M} {(E_d^n{d_{ij}}x_{ij}^n + {E_j})} } 。$ | (5) |
式中:
进行任务分配时,需要满足的约束条件分别为:
1)每个任务对于每艘UUV最多执行1次。
| $ \sum\limits_{i \in M} {\sum\limits_{j \in M,j \ne 1} {{x_{ij}}} } = 1。$ | (6) |
2)每艘UUV均由起始位置出发,执行完成全部预分配任务时返回指定充电位置。
| $ \sum\limits_{j \in M} {{x_{1j}}} \geqslant 1 ,$ | (7) |
| $ \sum\limits_{i \in M} {{x_{i1}}} \geqslant 1 。$ | (8) |
3)每艘UUV预装订任务序列执行完成返回指定位置的总能耗不能超过自身总能量。
| $ \sum\limits_{i \in M} {\sum\limits_{j \in M} {{E_j}{x_{ij}} + {E_d}{d_{ij}}{x_{ij}}} } < {E_{uuv}}。$ | (9) |
4)每艘UUV在执行每个任务后,剩余能量
| $ {E_{remain}} - {E_j}{x_{ij}} - {E_d}{d_{ij}}{x_{ij}} > {E_d}{d_{j1}}{x_{j1}}。$ | (10) |
5)参与执行任务的UUV需满足任务对UUV能力约束,设
| $ {{ {\boldsymbol{A}}}_j} \subseteq \bigcup\limits_{n \in {N_{{\rm{uuv}}}}} {{ A}_{{\rm{uuv}}}^nx_{ij}^n}。$ | (11) |
6)考虑水下弱通信环境,为保障UUV与保障船之间的稳定通信,设由水声通信设备确定的有效通信距离为
| $ \left| {{p_i} - {p_0}} \right|{x_{ij}} < {d_{{\rm{sonar}}}} 。$ | (12) |
在满足约束条件下,求解使目标取得极小值的任务序列。采用改进的S-PSO进行迭代求解。传统S-PSO规则简单,收敛速度快,减少任务分配环节的时间消耗,适合多UUV协同作战等具有一定时效性需求的任务分配[9]。S-PSO在每次迭代求解过程中,均可获得多个任务序列可行解。
在对UUV集群进行任务分配时,设一个粒子的位置为:
| $ {{\boldsymbol{X}}_i} = \bigcup\limits_{n \in {N_{uuv}}} {X_i^n} ,$ | (13) |
即一个粒子的位置代表一组UUV可行任务分配序列的集合,
粒子移动速度用可行性概率集合表示:
| $ {{\boldsymbol{V}}_i} = \bigcup\limits_{n \in {N_{uuv}}} {V_i^n} ,$ | (14) |
| $ {\boldsymbol{V}}_i^n{\text{ = }}\left\{ {{p_{ij}} \in \left[ {0,1} \right]|i \in M,j \in M} \right\} 。$ | (15) |
各个粒子速度更新公式为:
| $ {{\boldsymbol{V}}_i}^\prime = \omega {{\boldsymbol{V}}_i} + {c_1}{r_1}({X_{{\rm{best}}}} - {{\boldsymbol{X}}_i}) + {c_2}{r_2}({P_{best}} - {{\boldsymbol{X}}_i}) 。$ | (16) |
式中:
区别于传统S-PSO,在迭代求解过程中,为提高迭代初期的全局搜索能力,迭代后期的局部搜索精度,惯性系数采用动态值。其表达式为:
| $ \omega = {\omega _{{\rm{High}}}} - ({\omega _{{\rm{High}}}} - {\omega _{{\rm{Low}}}}) \times \frac{k}{K} 。$ | (17) |
式中:
此外,在传统S-PSO基础上,结合遗传算法的变异操作,设各粒子的位置矩阵中的每个元素在遍历开始时均有
| $ x_{ij}^n = \left\{ {\begin{array}{*{20}{c}} 1,{{r_m} < {p_m}},\\ 0,{{r_m} \geqslant {p_m}} 。\end{array}} \right. $ | (18) |
不同于遗传算法的随机变异,本文算法产生的变异需要满足基本约束条件,若不满足约束条件,则变异不成立。为避免因变异概率过大导致迭代算法退化为随机选择,
速度更新公式中,矩阵之间的运算不再遵循数值计算规则,采用如下运算规则:
| $ \begin{gathered} {\boldsymbol{A}} - {\boldsymbol{B}} = \left\{ {{a_{ij}}|{b_{ij}} = 0,i \in M,j \in M} \right\} \cup \\ \left\{ {{a_{ij}} = 0|{b_{ij}} \ne 0,i \in M,j \in M} \right\} ,\\ \end{gathered} $ | (19) |
| $ {\boldsymbol{A}} + {\boldsymbol{B}} = \left\{ {{p_{ij}} = \max \left\{ {{a_{ij}},{b_{ij}}} \right\}|i \in M,j \in M} \right\} ,$ | (20) |
| $ c{\boldsymbol{A}} = \left\{ {{p_{ij}}|i \in M,j \in M} \right\} ,$ | (21) |
| $ {p_{ij}} = \min \left\{ {\max \left\{ {c \times {a_{ij}},0} \right\},\min \left\{ {c \times {a_{ij}},1} \right\}} \right\}。$ | (22) |
式中:
综上所述,粒子位置更新流程如图1所示。

|
图 1 粒子位置更新流程 Fig. 1 Particle position update process |
通过图1流程更新获得的粒子位置
为验证方案的可行性和算法的有效性,对4艘UUV分配10个任务的场景进行仿真实验。为便于分析,使图像更直观,假定在执行任务前,各UUV均需前往给定任务区域某坐标点位置,从该坐标点开始执行任务;全部UUV初始位置相同,完成自身任务序列后返回位置相同且与初始位置一致;在分配任务前,已对执行任务完成最长时间和UUV最大耗能进行预估。
3.2 仿真结果及分析设置求解算法的参数
|
|
表 1 待分配任务信息 Tab.1 Task information to be assigned |
|
|
表 2 UUV信息 Tab.2 UUV information |
采用改进S-PSO算法和传统S-PSO算法,分别经迭代求解获得4艘UUV任务序列。采用改进的S-PSO算法求解获得的任务序列如表3所示,形成如图2所示航迹图,横坐标为区域坐标。图中每个任务点对应的3个数字分别表示任务编号、在该UUV任务序列中的排序、UUV编号。可知,UUV1与UUV3从保障船出发,共同执行完成任务2后再分别执行其他任务。UUV2完成任务7、任务10后,与UUV4汇合,联合执行任务9。由于UUV能力限制,出现返航补充能量再执行任务的情况。
|
|
表 3 仿真生成的UUV任务序列 Tab.3 UUV task sequence generated by simulation |
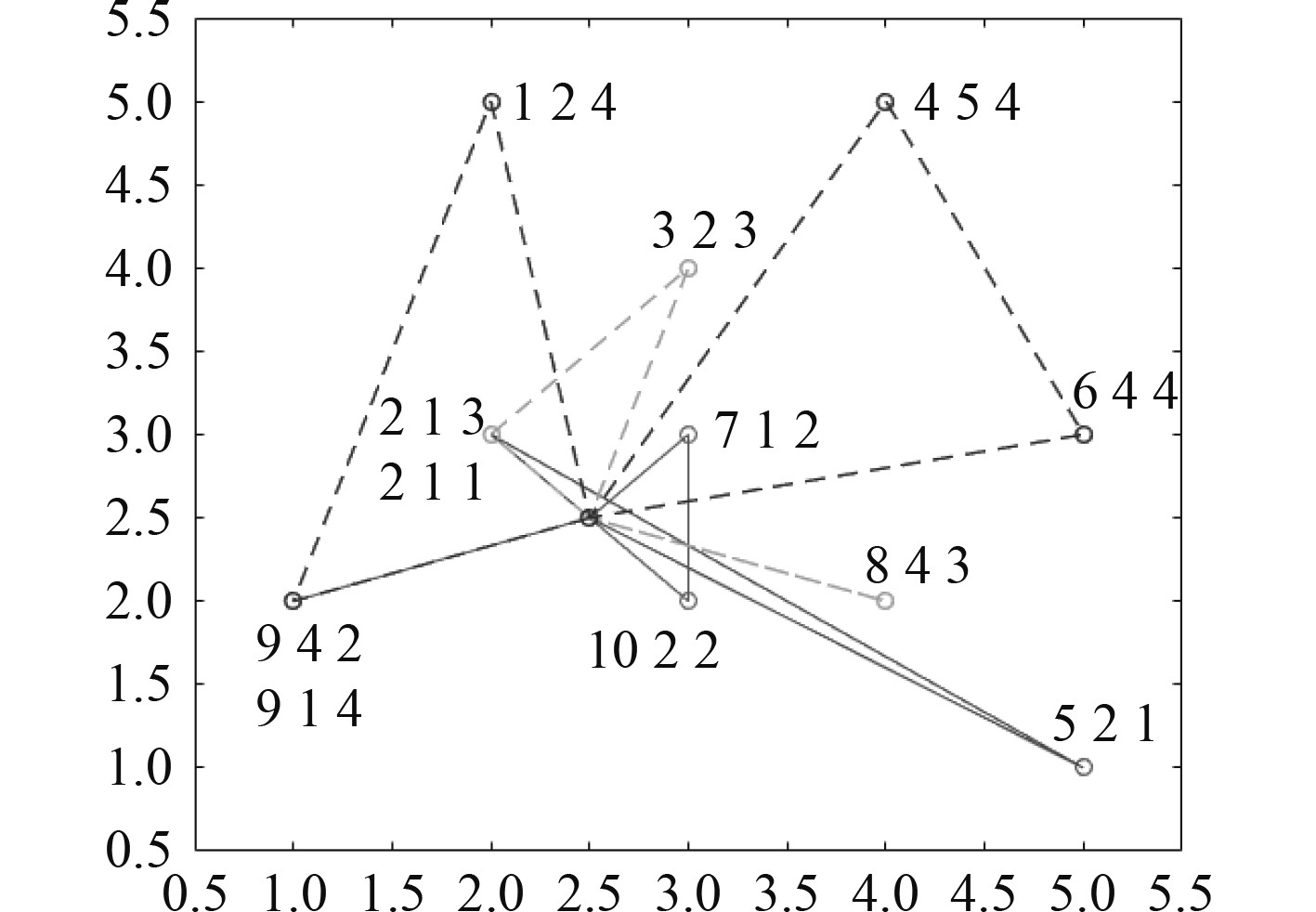
|
图 2 采用改进S-PSO生成的UUV任务序列图 Fig. 2 UUVs task sequence with modified S-PSO |
传统S-PSO求解的任务序列如图3所示,UUV1的任务序列明显长于采用改进S-PSO生成的任务序列。由于任务完成的总体时间受到完成任务用时最长的UUV影响,对其他UUV约束不强,使得在迭代求解过程中,陷入局部最优解,这促使能力较差的UUV1而不是能力较强的UUV3执行过多任务。尽管改变粒子群的初始值和粒子数量可能会出现图2基于改进S-PSO算法获取的解,但改变初始值和增多粒子数量的方式存在偶然性,其效率相对于改进S-PSO算法较低。
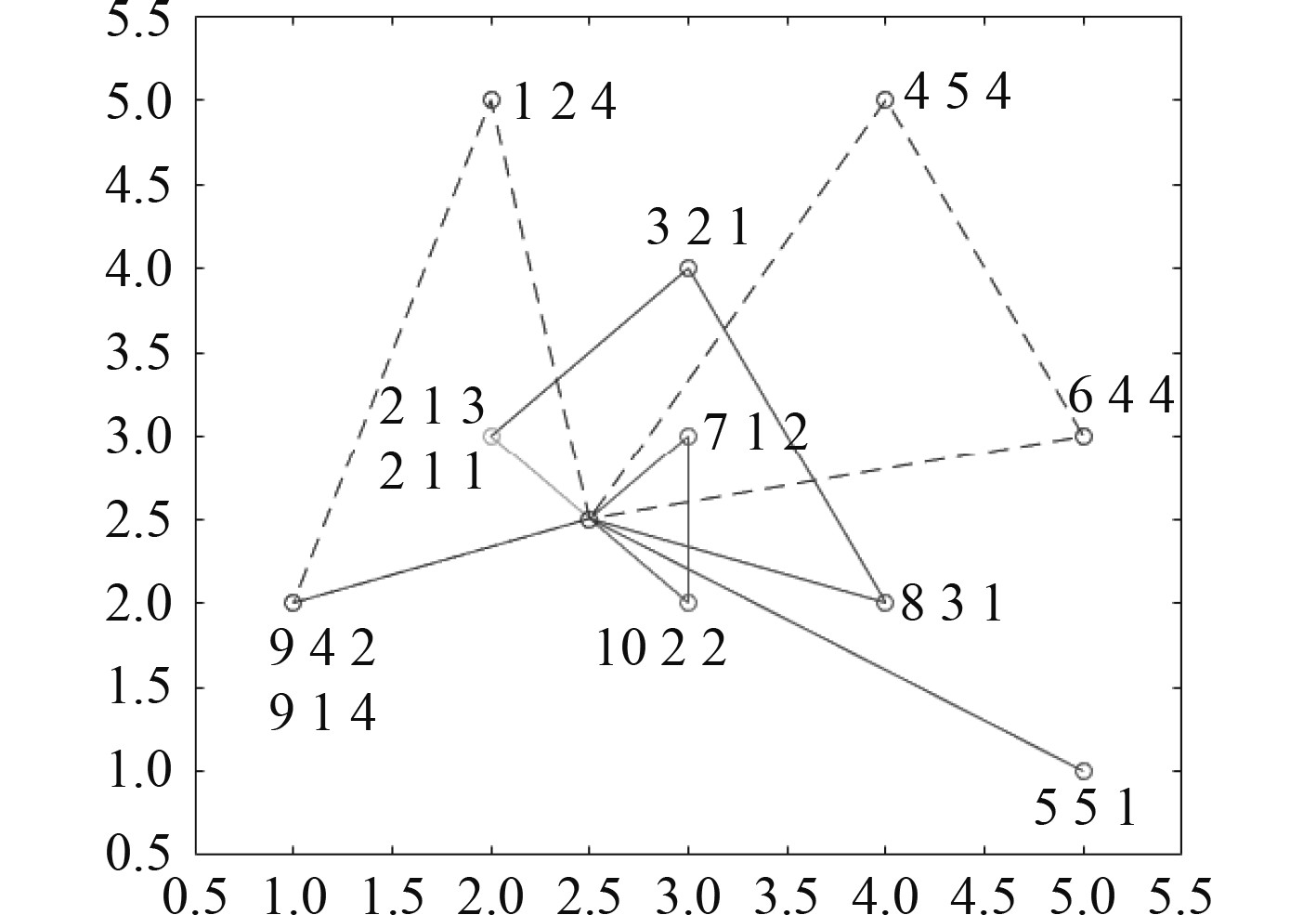
|
图 3 传统S-PSO生成的UUV任务序列图 Fig. 3 UUVs task sequence with S-PSO |
为进一步比较本文算法与传统S-PSO的搜索性能和收敛性,选取在迭代过程中获得的目标评估值进行分析,评估值越小,表明越逼近最优解。由评估值可知,传统S-PSO尽管在迭代早期收敛速度较快,但过早陷入局部最优解;改进S-PSO降低部分收敛速度情况下,提高全局搜索与局部搜索能力,使结果更趋近全局最优解。

|
图 4 评估值随迭代次数收敛情况 Fig. 4 Convergence of evaluation value with the number of iterations |
本文针对多UUV任务分配问题,建立包含任务所需UUV数量、能力、UUV自身功能、UUV续航、保障船与UUV通信距离限制等多约束条件的任务分配模型。结合遗传算法变异操作,采用动态惯性系数,形成改进S-PSO算法。实验结果表明,所提出的多约束多目标任务分配方法,能获取多UUV的最优任务分配,算法实现简单,搜索能力较好,满足UUV实际工程应用的要求。
| [1] |
赵留平, 李环, 王鹏. 水下无人系统智能化关键技术发展现状[J]. 无人系统技术, 2020, 3(6): 12-24. |
| [2] |
王雅琳, 刘都群, 杨依然. 2019年水下无人系统发展综述[J]. 无人系统技术, 2020, 3(1): 55-59. |
| [3] |
邓鹏, 李伟, 王新华. 水下无人平台“蜂群”作战体系研究[J]. 兵器装备工程学报, 2018, 39(8): 8-10+47. |
| [4] |
张鑫明, 韩明磊, 余益锐, 黄田力, 陈谦, 吴铭. 潜艇与UUV协同作战发展现状及关键技术[J]. 水下无人系统学报, 2021, 29(5): 497-508. DOI:10.11993/j.issn.2096-3920.2021.05.001 |
| [5] |
李娟, 张昆玉. 基于改进合同网算法的异构多AUV协同任务分配[J]. 水下无人系统学报, 2017, 25(6): 418-423. |
| [6] |
范学满, 王新鹏, 薛昌友. 基于混合优化算法的多UUV协同侦查任务分配方法研究[J]. 指挥控制与仿真, 2021, 43(6): 94-99. DOI:10.3969/j.issn.1673-3819.2021.06.017 |
| [7] |
李建军, 张汝波, 杨玉. 基于混沌QPSO算法的多AUVs任务分配[J]. 华中科技大学学报(自然科学版), 2015, 43(S1): 424-427. |
| [8] |
卢骞, 潘成胜, 丁元明. 基于MODPSO-SA算法的多AUV任务分配[J]. 电光与控制, 2021, 28(1): 31-36+46. |
| [9] |
CHEN W, ZHANG J, CHUANG H S H, et al. A novel set-based particle swarm optimization method for discrete optimization problems[J]. IEEE transactions on evolutionary computation, 2010, 14(2): 278-300. DOI:10.1109/TEVC.2009.2030331 |
| [10] |
马云红, 刘云昊, 杨誉乔. 基于一致性群组算法的多无人机自主协同任务分配[J]. 无人系统技术, 2021, 4(4): 51-58. |
| [11] |
朱大奇, 孙兵, 李利. 基于生物启发模型的AUV三维自主路径规划与安全避障算法[J]. 控制与决策, 2015(5): 798-806. DOI:10.13195/j.kzyjc.2014.0339 |
| [12] |
魏得路, 张雪松, 胡明. 基于多信息素蚁群算法的联合任务分配方法[J]. 中国电子科学研究院学报, 2019, 14(8): 798-807+812. DOI:10.3969/j.issn.1673-5692.2019.08.004 |
 2023, Vol. 45
2023, Vol. 45
