0 引　言

如今，人们在海洋、河流和其他水下环境中的活动越来越广泛^[1]，水下探索的需求也日益增高，伴随着这一现象，水下通信成为了这一目标的难题之一。目前，大多数水下设备采用声音通信，尽管声学通信已被很好地应用，但仍存在一些固有缺陷，如带宽窄，高延迟等^[2-3]。因此，近年来，水下天线实验（也称射频（RF）通信技术实验）成为海洋研究中必不可少的部分之一^[4]。基于这种需求，本文提出一种应用于水下探索的新型四旋翼自主水下航行器。

本文实验的关键部分是用于携带水下天线的弱磁型四旋翼水下自主航行器（Low-Magnetic Autonomous Underwater Vehicle , LM-AUV）。在此实验中，该AUV的可控性起着关键作用，因为必须将水下天线的深度和姿态限制在一个很小的范围内，这需要保持对AUV的动态控制。Li^[5]设计了一种AUV平台用于克服强电流的同时使姿态稳定。Santhakumar^[6]提出一种应用于长形AUV的高效动态控制方法。Koh^[7]采用了一种特殊的推进器配置，并使用了PD控制器来解决水下机器人（ROV）的姿态稳定问题。Serrani^[8]在测量速度偏移量下，提出一种强鲁棒性的姿态稳定控制器。文献[9]集中讨论在未知的扰动或波动电流下，如何使AUV姿态保持稳定。但是，LM-AUV仅允许弱电流通过推进器，以避免对天线的电磁干扰。在这种情况下，上述文献中的推进器以及控制器布置都不是很可靠。

为解决上述问题，参考某些潜水式无人飞行器^[10]和异型水下航行器^[11-12]，本文提出一种新型LM-AUV设计方法，通过调整出最优的PID参数对该LM-AUV进行深度以及姿态的稳定控制，并验证该控制系统的稳定性和鲁棒性。

1 LM-AUV外形设计

本文的LM-AUV采用欠驱动结构，同时令其4个推进器垂直对称地安装在XY平面上，并且每个推进器在向前和向后方向上都具有相同的推力动力学特性。这种推力机构可以用来分离控制力，从而方便地保持深度和防侧倾。推进器的选型上采用低电流型电机，因为低电流推进器所能提供的推力有限，因此对该AUV的控制系统精度要求较高。这4个推进器的几何布置相对分散，全部置于外拓展架上，并令其尽可能地远离搭载实验装置的水密舱，同时采用并联连接电路，从而减少内部电流对射频实验的干扰，达到弱磁性系统的目的。

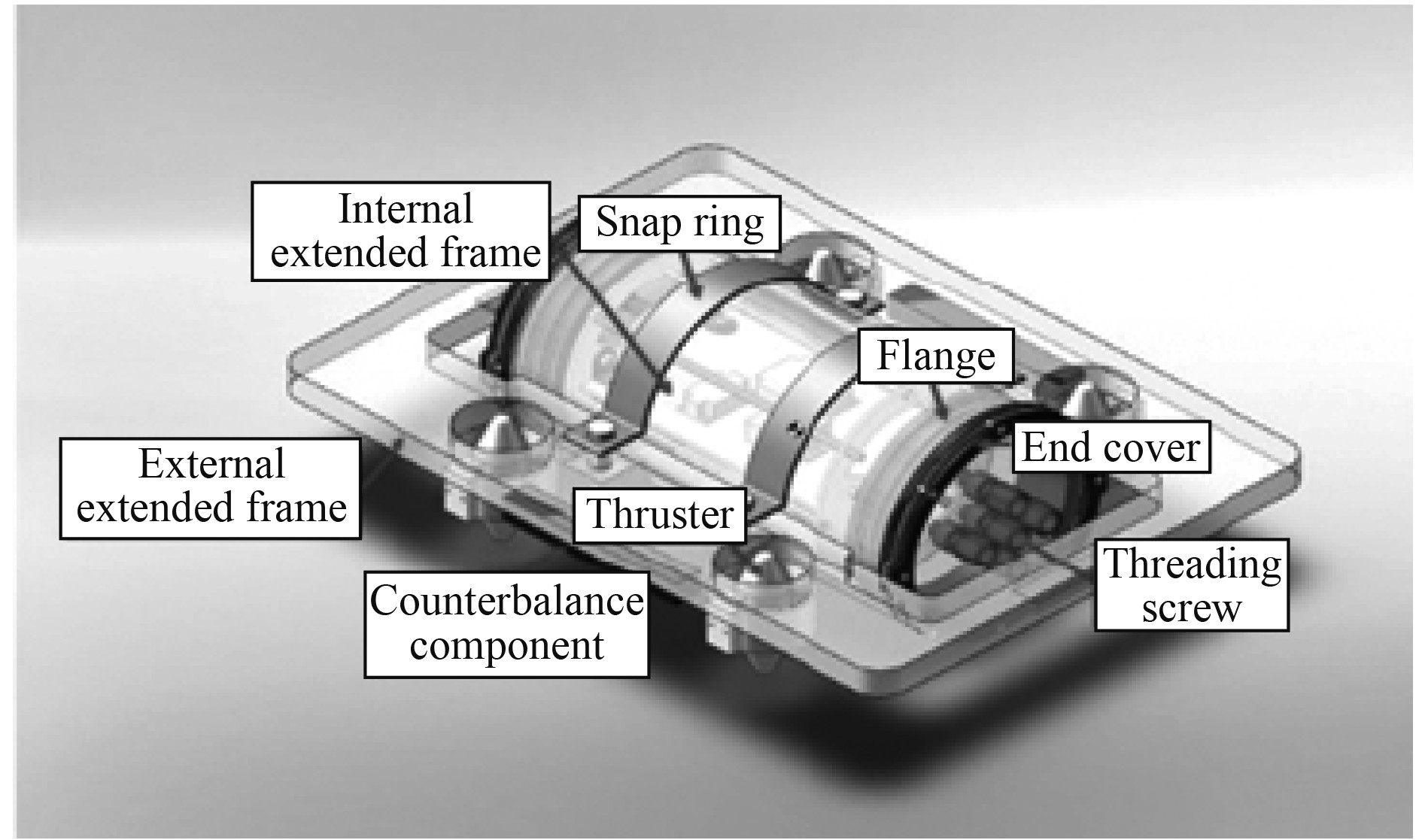
从图1可以看出，到LM-AUV原型机的机械系统组成包括1个防水外壳、2个端盖、2个法兰、1组螺丝、1组卡环、2个框架和一些平衡组件。水密外壳和外部框架通过4个半圆形卡环固定在一起。推进器和平衡组件固定在外部框架的底部，以降低重心并增强自稳定性，而电路板和其他电子组件则固定在内部框架上。法兰上的密封槽用于放置O形密封圈，以实现轴向/径向多次密封。螺纹螺钉也通过O形圈密封件与端盖密封，并使用环氧树脂密封进行一定程度的自密封。

表1为总体设计参数。该实验中所有流体动力学参数都是通过CFD仿真获得的，其余参数也是基于LM-AUV原型机的实际测量所得。

2 LM-AUV数学模型

水下机器人的通用数学模型包括运动学模型和动力学模型^[13]。运动模型描述了以地球为参照的惯性固定坐标系（I-FRAME）和以LM-AUV自身为参照的坐标系（B-FRAME）运动之间的几何关系，可以写为：

$ \dot{{{\boldsymbol{\xi}}}{}}={}{J(}{\Theta}{)}\cdot{\nu}。$

动力学模型主要描述AUV的速度矢量与力和力矩之间的关系，可以通过以下公式给出：

$ {{\boldsymbol{M}}}\dot{{\nu}{}}+{}{{\boldsymbol{C}}}\left({\nu}\right){\nu}{}+{}{{\boldsymbol{D}}(}{\nu)\nu}{}+{}{g}\left({\Theta}\right){}={}{\tau}+{w}。$

上面提到的物理符号遵循SNAME^[14]指定的标准。其中 ${{\boldsymbol{\xi}} }={[X,Y,Z]}^{{\rm{T}}}\in {R}^{3}$ 是I-FRAME中LM-AUV的位置矢量， $J\left(\mathbf{\varTheta }\right)$ 为将B-FRAME与基于I-FRAME的转换矩阵相关联的变换矩阵。根据SNAME符号定义可得出以下2组向量：欧拉角 $\mathbf{\varTheta }={\left[\varphi ,\vartheta ,\psi \right]}^{{\rm{T}}}$ ，速度向量 $\boldsymbol{\nu }=[{u,v,w,p,q,r]}^{{\rm{T}}}\in {R}^{6}$ 。其中，速度向量 $ \mathit{\nu } $ 中的6个变量代表该AUV运动的6个自由度，分别是横荡、纵荡、垂荡、横摇、纵摇、首摇。 ${\boldsymbol{M}}={M}_{RB}+ {M}_{A}\in {R}^{6\times 6}$ 为该AUV的惯性矩阵， ${\boldsymbol{C}}\left(\mathit{\nu }\right)\in {R}^{6\times 6}$ 和 ${\boldsymbol{D}}\left(\mathit{\nu }\right)= D+{D}_{2}\left(\mathit{\nu }\right)\in {R}^{6\times 6}$ 分别表示科里奥利向心矩阵和阻尼矩阵，其中 $ D $ 是线性阻尼， $ {D}_{2}\left(\mathit{\nu }\right) $ 是二阶阻尼。 $\boldsymbol{\tau }={B}_{c}\mathit{u}$ 是一个六维向量，包括B-FRAME中的控制力和力矩，其中 $ {B}_{c}\in {R}^{6\times 4} $ 是一个控制矩阵， $\boldsymbol{u}\in {R}^{4}$ 是一个分量与向量相关的向量，与该AUV推进器的角速度相关联， $\boldsymbol{w}\in {R}^{6}$ 表示作用在该AUV上的干扰矢量。

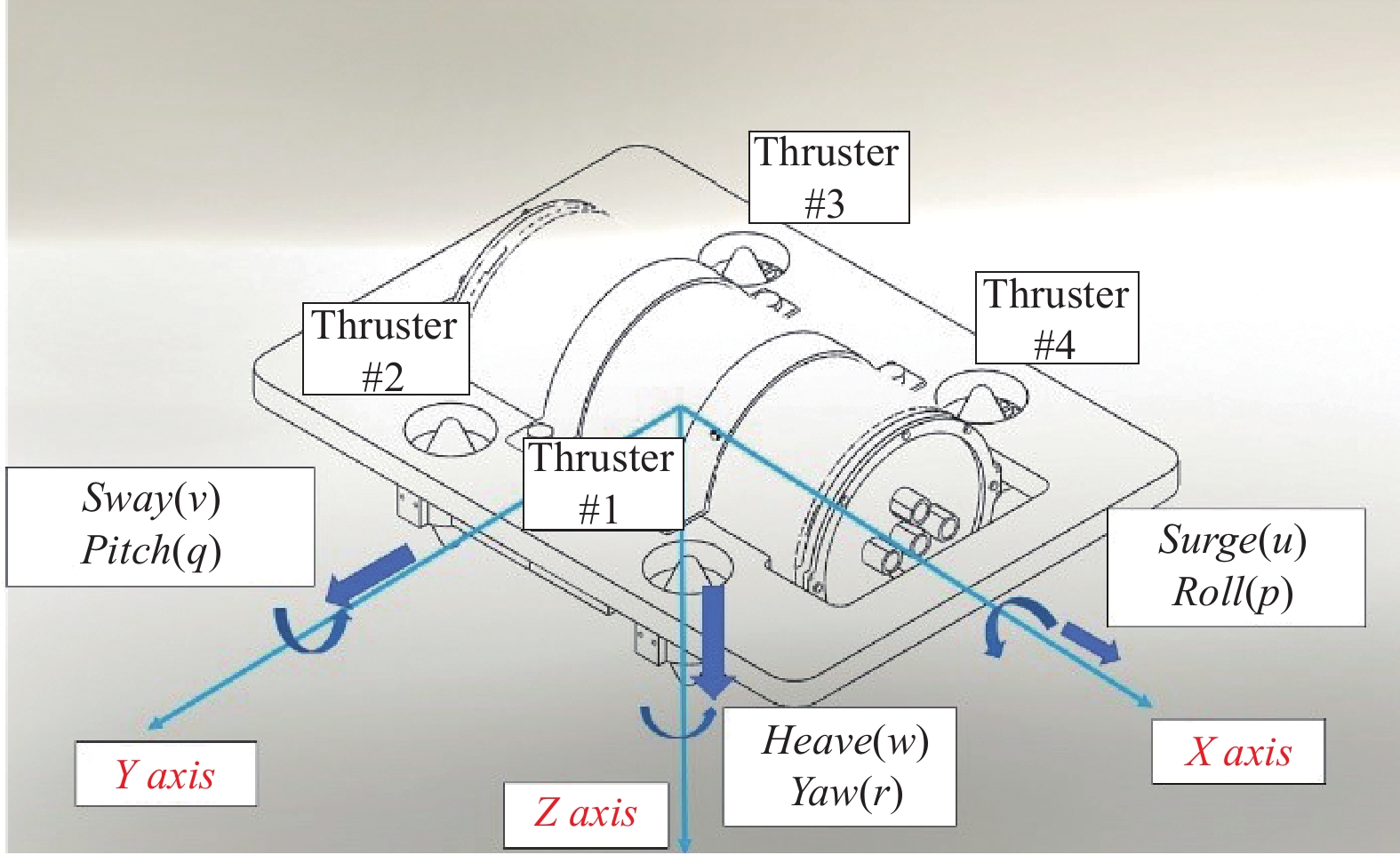
其中，笛卡尔坐标系和运动的定义如图2所示。

$ \begin{split} \left[\begin{aligned}{{f}}_{{z}}\\ {{\tau}}_{{x}}\\ {{\tau}}_{{y}}\\ {{τ}}_{{z}}\end{aligned}\right]=& \left[\begin{aligned}{\omega }_{{1}}\left|{\omega }_{{1}}\right|\\ {\omega }_{{2}}\left|{\omega }_{{2}}\right|\\ {\omega }_{{3}}\left|{\omega }_{{3}}\right|\\ {\omega }_{{4}}\left|{\omega }_{{4}}\right|\end{aligned}\right] \times\\ & \left[\begin{array}{ccccccccccccccccc} {{C}}_{{t}}& {{C}}_{{t}}&{{C}}_{{t}}&{{C}}_{{t}}\\ \dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}&-\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}&-\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}&\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}\\ \dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}&\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}& -\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}&-\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}\\ {0}&0 & 0& 0\end{array}\right]。\end{split} $

上述左等式中向量的4个项分别表示沿Z轴的力和围绕X轴、Y轴和Z轴的转矩。 $ {\omega }_{i}(i=\mathrm{1,2},\mathrm{3,4}) $ 为每个推进器的转速，其定义为：若 $ {\omega }_{i} > 0 $ 则推进器沿顺时针方向致动，反之亦然。 $ d $ 为LM-AUV的形心与推进器之间的距离。 $ {C}_{t} $ 是积分推力系数，其满足等式 $ {C}_{t}=T/{\omega }^{2} $ ，其中 $ T $ 该AUV推进系统的总推力。

通过上面的表达式，可以获得下式：

$ {}{{\boldsymbol{u}}}={\left[{{u}}_{{1}}{,}{{u}}_{{2}}{,}{{u}}_{{3}}{,}{{u}}_{{4}}\right]}^{\rm{T}}={\left[{\omega }_{{1}}\left|{\omega }_{{1}}\right|{,}{\omega }_{{2}}\left|{\omega }_{{2}}\right|{,}{\omega }_{{3}}\left|{\omega }_{{3}}\right|{,}{\omega }_{{4}}\left|{\omega }_{{4}}\right|\right]}^{\rm{T}} ，$

$ {\boldsymbol{B}}_{{c}}=\left[\begin{array}{ccccccccccc} {0}& {0}& {0}& {0}\\ {0}& {0}& {0}& {0} \\ {{C}}_{{t}} & {{C}}_{{t}}& {{C}}_{{t}}&{{C}}_{{t}} \\ \dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}} & -\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}& -\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}} & \dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}\\ \dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}& \dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}& -\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}& -\dfrac{\sqrt{{2}}}{{2}}{d}{{C}}_{{t}}\\ {0}& 0& 0& 0 \end{array}\right] $

3 LM-AUV电气及控制系统设计 3.1 电气系统设计

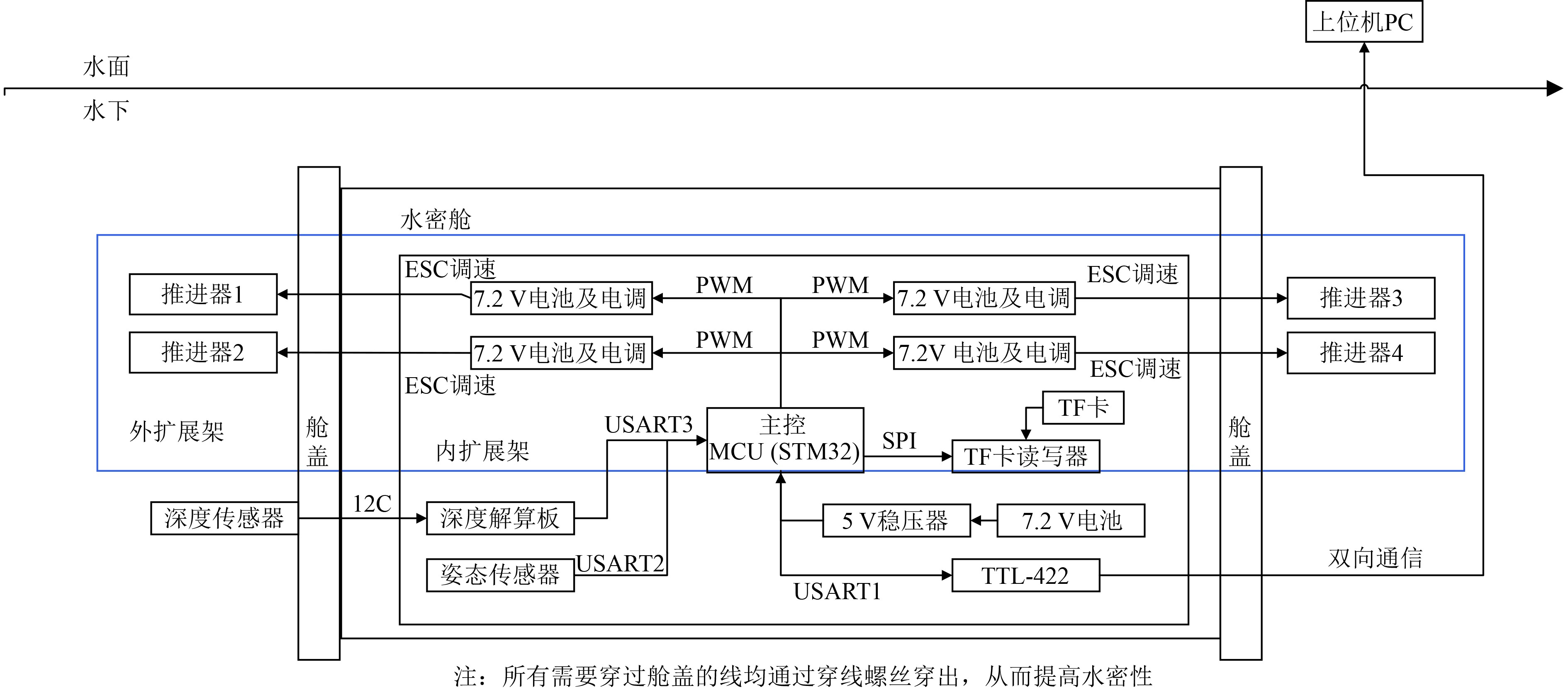
电气系统的示意图如图3所示，包括一个控制子系统，一个通信子系统和电源，控制电路采用STM32F1系列微控制器（MCU）作为中央处理单元。由深度传感器和姿态航向参考系统（AHRS）收集的深度和姿态信息，用作控制系统的数字输入。控制器产生的PWM波是双向无刷电子调谐器的数字输出，其通过电调连接到无刷直流（BLDC）推进器，从而改变推力，调整姿态和深度并实现动态定位平衡。LM-AUV原型机通过无浮力电缆与主机进行实时通信与数据反馈，并通过上位机自带的通信软件对LM-AUV的运行参数、控制参数等进行实时调控。当LM-AUV运行时，深度、姿态和PWM值可实时显示在上位机的通信软件中，同时该原型机带有TF卡模块，可以将工作运行时的数据以及日志存储在TF卡中备份，以便后续分析数据时使用。最后，LM-AUV原型机使用集成在其机舱内的5块DC7.2V模型电池进行供电。其中4块电池分别对应4个推进器独立供电，剩余1块电池则负责MCU等电气系统的供电.通信协议采用TTL-422，该协议降低了远距离传输难度，从而实现上位机对LM-AUV的实时监控以及控制。

3.2 控制系统设计

LM-AUV的运动控制仅包含升沉运动、横摇运动和纵摇运动这3个自由度的控制，所涉及的参数有深度、横倾角、纵倾角以及电机PWM值等。其中，位移、角位移控制回路主要实现的是对该无人水下试验平台进行自动定位控制，即输入一个预定深度或角度值。通过控制系统的调整后输出每个推进器所需分配的PWM波，从而实现这3个自由度的定位控制。其控制回路图如图4所示。

图中定深减摇控制器控制系统采用比例—积分—微分（Proportional-integral-differential, PID）控制。其是一种基于线性模型设计的控制算法，其结构简单、参数性质明确、便于现场调试^[15]。PID控制器是线性的，即误差量输入与控制量输出是线性相关的。将误差量输入到控制器后，通过控制STM32单片机（主控MCU）向LM-AUV的4个无刷直流推进器输出PWM波，以达到控制LM-AUV的运动状态，从而实现定深减摇的目的。

在弱磁型无人水下航行器的控制系统设计中，PID控制器拥有结构简单、控制性优、鲁棒性强等特点被广泛应用^[16]。将PID控制器中的比例、微分、积分环节进行拉普拉斯变换后可得出该控制器的控制算法为：

$ {u=e\cdot}\frac{{U(s)}}{{E(s)}}={{e\cdot(K}}_{{p}}+{{K}}_{{i}}\frac{{1}}{{s}}+{{K}}_{{d}}\cdot{s)} 。$

式中：K_p为比例系数；K_i为积分系数；K_d为微分系数；u为输出控制量。

PID控制器中的比例、积分、微分部分都起着不同作用^[17-18]：

1）比例部分可成比例反映出控制系统的偏差值，当输出值与输入值有误差时，可以快速将控制其偏差，以减小输出值的波动。但是，如果K_p过大，会增加输出值的超调，使系统的整体稳定性降低。

2）积分部分可利用误差值的积分量进行控制，消除该控制系统的稳态误差，提高该控制系统的无差度。但是K_i过大会导致该控制系统稳定性下降，导致其动态响应变慢，故K_i值一般取适当大小即可。

3）微分部分可利用误差值的微分量进行控制，提高该控制系统的响应速度，同时提高其稳定性，加快输出值达到预定值（即输入值）的时间。与前2项不同的是，微分部分不可以单独存在，它经常与比例部分并存。若K_d过大，会导致该控制系统波动时间变长，不能稳定在理想值之间。故K_d值和K_p值的调试需要同时进行，以达到对该系统的最优控制效果。

4 实验及数据处理

对LM-AUV进行一系列实验，该AUV通过深度传感器、姿态传感器对深度信息和姿态角信息进行捕获、并交由集成与AUV控制系统中的MCU进行处理，以PWM波形式传递给4个推进器，实现其在水下的定深、减摇等功能。本文所搭建的四旋翼式小型LM-AUV在华中科技大学船舶水池实验室完成了水下3 m的定深减摇实验，深度误差控制在0.06 m（深度传感器精度误差0.01 m）、姿态角误差控制在5°，并进一步完成了水下3 m的基础上进行一系列的姿态角稳态控制、所达成的误差控制在10°以内。特别地，为了增强该LM-AUV的稳定性，需要在下水前使用铅块进行重量配平，使该LM-AUV在水中处于正浮力状态，并采用无浮力电缆，避免在该LM-AUV工作过程中因为线缆的因素而降低控制系统的稳定性。

由于四旋翼式水下机器人正常工作与调试均需要与串口进行大量交互，在保留通用串口助手基本功能的基础上，开发了DEBUG模式、IMU控制命令模式、深度解算板配置模式、电调配置模式，以及四旋翼式水下机器人系统状态输出界面等，用于实现该LM-AUV的各种功能并实时监测该LM-AUV的工作状态。

双向电调器的有效PWM占空比在0.05～0.1之间（即本实验中相应的PWM值为1 000～2 000），中间值为0.75（PWM值为1 500）。为了进一步增强该LM-AUV的续航性，MCU对这4个推进器所输出的PWM占空比被限制在0.065～0.085（即PWM值在1300～1700）。

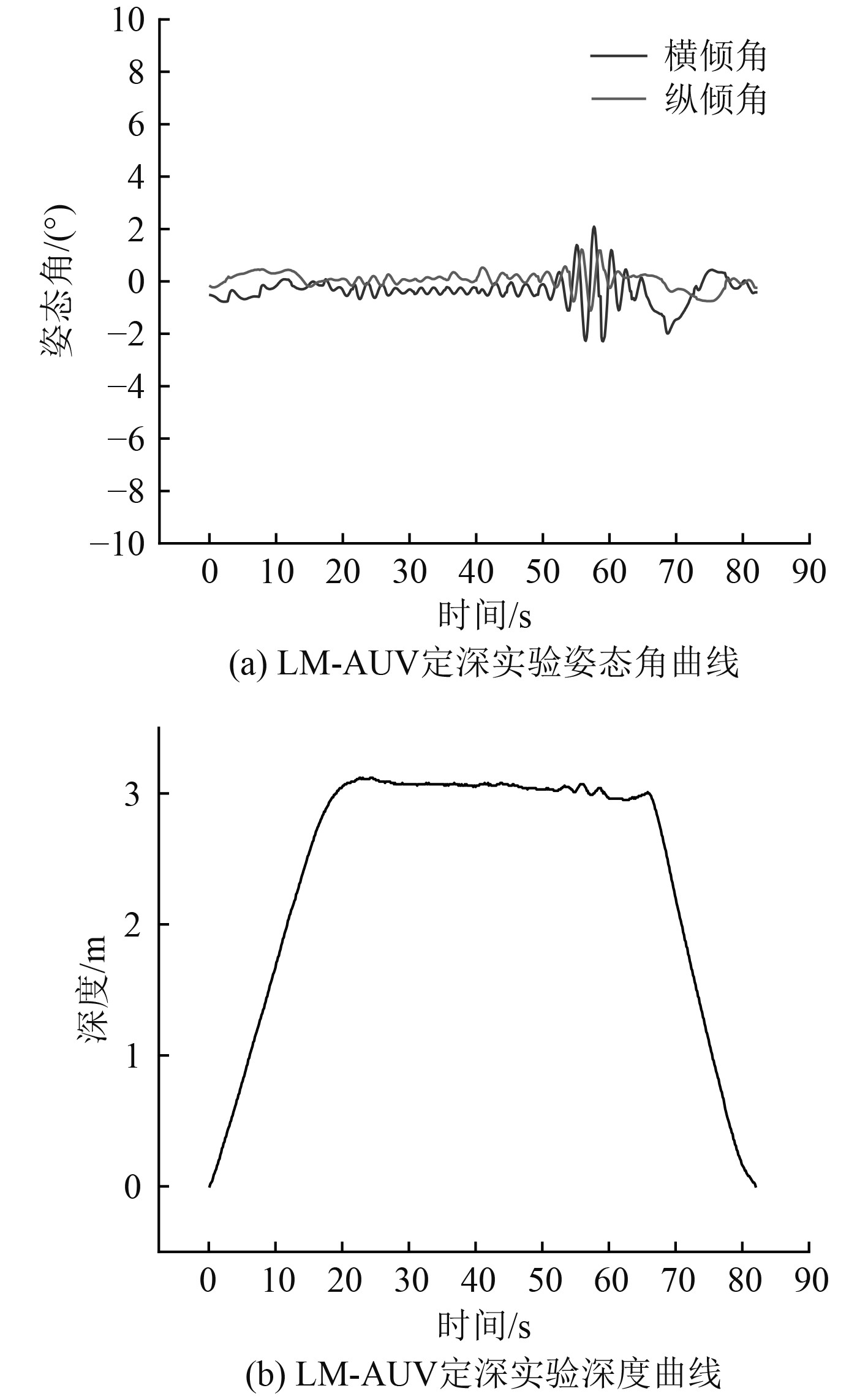
图5为期望深度3 m，俯仰角以及横摇角均设为0°的定深实验数据。

在定深实验完成的基础上，进行将横摇角和俯仰角分别定为25°和15°的定姿态角实验。相关实验结果如图6所示。

根据2次实验整理关键性能参数，如表2所示。

LM-AUV在接收到定深3 m的信号后，由MCU输出的PWM波驱动4个推进器达到下潜的效果。由于该LM-AUV在下潜的过程中受到水中暗流扰动，会导致其姿态角产生变化，由AHRS模块收集姿态角误差传入MCU中，对4个推进器分别进行PWM波的调整，以达到在运动中姿态稳定的效果。从图表可知，该LM-AUV在定深的过程中俯仰角和横倾角都得到了稳定控制，均在0°上下波动，深度超调量控制在0.2 m以内，并在30 s内稳定在指定深度。因此可得出结论：该控制系统对深度控制具有鲁棒性，并且控制过程相对稳定，结果可靠。

同样分析可知，该LM-AUV在3 m定深的前提下，由上位机向其发送将横摇角和俯仰角分别稳定在25°和15°的指令后，在20 s内完成对横倾角以及俯仰角的控制，使其进入相对应的稳定区间。由于水池中存在水流干扰以及使用了低成本的AHRS，导致数据噪声较多。当LM-AUV进入稳态状态后，横摇角以及俯仰角分别存在10°以及7°的动态误差，同时由于PID控制器调整得当，横摇角以及俯仰角分别存在1°以及−1°的稳态误差，超调量均控制在10°～15°以内。由此得出结论，该LM-AUV控制系统对横摇角与俯仰角的z姿态控制具有稳定性，系统的鲁棒性较强，且结果可靠。

5 结　语

本文提出一种将PID用于LM-AUV深度控制和姿态控制的稳态系统，首先使用数值分析的方法对其有效性进行证明，并设计实验以验证所提出的控制系统稳定性。同时将该PID控制器应用于LM-AUV实体模型中，并完成了相对应的深度控制实验以及姿态控制实验，得出结果均为可靠。未来将继续改良该LM-AUV原型机的控制系统，进一步运用模糊PID控制、滑模控制等现代控制算法进行优化，使其控制效果更优，响应速度加快同时压低超调量，减少稳态误差并降低其波动性。将对该LM-AUV硬件进一步升级，如使用高性能的传感器增强其数据回传的精确度，减少各状态量回传的噪点，并增加数据传输频率等。