无人船的智能控制十分关键,其核心是避障路线规划设计,避障路线规划效果是判断无人船智能航行水平的重要依据[1 − 2]。无人船避障路线规划是以航行环境建模为前提,通过智能优化算法实现无人船最佳避障路线的设计[3 − 4]。随着技术手段的不断革新及智能化水平的提高,各种智能算法被引入到避障路线规划中,实现无人船航行效率与避障能力的大幅提升。
李清亮等[5]为使无人船能够安全航行于含有障碍物的水域环境,在障碍物区域标记的基础上,采用最优时间控制目标函数描述无人船避障问题,通过控制参数优化和时间尺度变换对优化问题求解,再基于精确罚函数实现各状态约束的处理,从而实现无人船航迹规划和自动避障。但是该算法求解难度较高,优化参数的选取对无人船避障路线规划效果影响较大。吕进锋等[6]通过在海图上进行节点设置与扩充,完成路径网络图的建立后,采用改进和声算法实现无人船避障路线优化,该算法会因障碍物节点位置改变而使规划的避障路线不可行,且规划路线无法满足最短要求。蚁群算法是可实现全局路径规划的智能优化算法,通过正反馈机制指引路径规划问题逐步向最优解逼近,具备强大的鲁棒性能。因此,本文设计复杂开放水域的无人船避障路线蚁群规划算法,保证全局收敛效率,同时规划出具有较少拐点、路径最短的避障路线。
1 无人船避障路线蚁群规划算法 1.1 复杂开放水域障碍物栅格化处理依据无人船半径对复杂开放水域环境中的障碍物作膨胀处理后,将障碍物所在栅格填充完整,保证无人船在复杂开放水域航行过程不发生碰撞。障碍物栅格化处理如图1所示。

|
图 1 障碍物的栅格化处理 Fig. 1 Grid processing of obstacles |
改进蚁群算法通过对各栅格中心点进行查询,实现无人船避障路线规划。
1.2 蚁群算法蚁群算法是一种智能优化算法,其设计灵感源于蚂蚁觅食行为[8],蚂蚁在寻找食物时,会将一种特殊物质分泌在其食物搜索路径中,完成一段时间搜索后,距离相对较小的搜索路径上含有的信息素含量较高,其他蚂蚁将按照信息素高的路径继续搜索。
蚂蚁在觅食时,将搜索节点的信息素含量以及启发信息作为依据,完成后续搜索节点的确定。对于第
| $ P_{ij}^k = \frac{{{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^\alpha } \times {{\left[ {{\rho _{ij}}\left( t \right)} \right]}^\beta }}}{{{k_{allow}}}} \text{。} $ | (1) |
式中:
蚂蚁觅食过程中分泌的信息素具有挥发性,蚁群中各蚂蚁均执行完搜索任务后,将对各搜索路径上的信息素浓度进行调整,公式为:
| $ \tau = \left( {1 - \lambda } \right){\tau _{ij}} + \Delta {\tau _{ij}} \times P_{ij}^k。$ | (2) |
其中:
| $ \Delta {\tau }_{ij}^{k}=\left\{\begin{array}{l}\dfrac{Q}{{L}_{k}}\times \tau ,第k只蚂蚁由i节点移动到j节点,\\ 0\text{,}{\rm{other}}。\end{array}\right. $ | (3) |
式中:
将无人船受到的势场信息融入到启发信息中,实现启发信息的改进处理,确保蚂蚁沿着合力方向执行搜索任务。势场合力启发信息通过下式进行描述:
| $ {\rho _s}\left( t \right) = {C^{{F_{tol}} \times \cos \theta }} \times \Delta \tau _{ij}^k 。$ | (4) |
其中:
将
| $ {\rho '_{ij}}\left( t \right) = {\rho _s}\left( t \right) \times {\rho _{ij}}\left( t \right)。$ | (5) |
在人工势场法中,当目标节点引力与障碍物斥力相同时,势场合力将等于0,将获得一个局部最小值,为避免无人船避障路线规划陷入局部最小问题,将势场力融入到蚁群算法自身启发信息中,可确保无人船在势场合力等于0时,也能实现最优避障路线规划。
1.3.2 信息素浓度增量优化对各搜索路径上的信息素浓度进行优化处理,提高无人船避障路线规划效果,其计算公式为:
| $ \Delta \tau _{ij}^k\left( t \right) = \frac{{{Q^*} \times {{\rho '}_{ij}}\left( t \right)}}{{{L_{n,k}} \times f\left( {{\theta _{ij}}} \right)}}\text{。} $ | (6) |
其中,信息素浓度的高低通过
通过设计的信息素浓度增量优化,可对蚂蚁搜索路径上的信息素浓度高低进行自主更新,以提高无人船全局最佳避障路线收敛效率。
应用蚁群算法对无人船避障路线进行规划时,容易陷入局部最优困局,这是由于蚂蚁在后续移动节点选取时,一旦其处于凹型障碍环境或无新节点可选,就会停在原处不动。本文对状态转移概率进行优化处理,通过引入稳定因子
| $ P_{ij}^k\left(t\right)=\Delta\tau_{ij}^k\left(t\right)\times\left(\frac{T_j-O_j}{S_j}\right)^{\gamma}。$ | (7) |
式中:对于节点
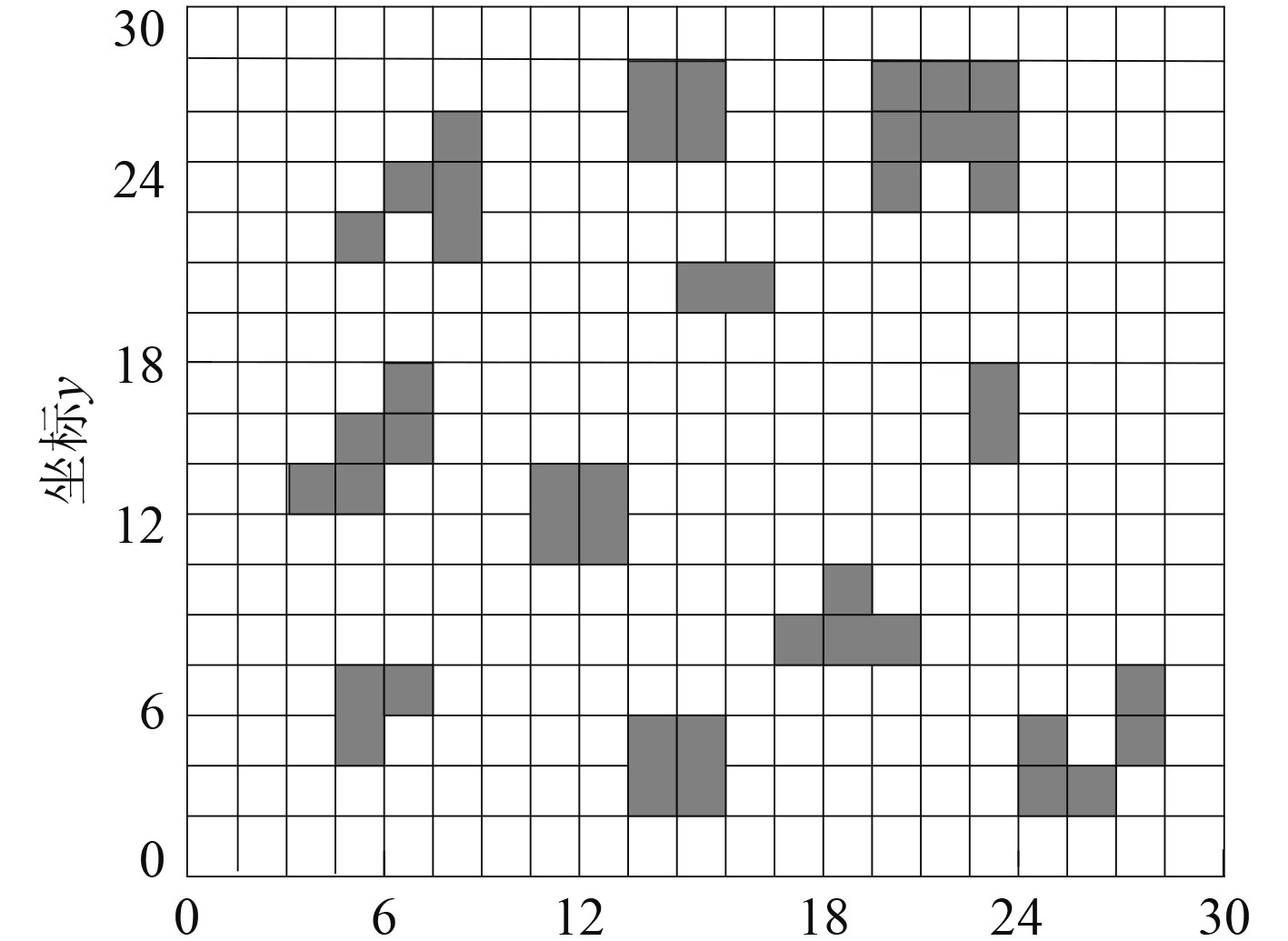
以航行于复杂开放水域的某无人船为实验对象,对无人船航行环境进行建模,获得30×30栅格地图,航行环境中的障碍物用灰色栅格标记。在上述环境采用本文算法对无人船避障路线进行规划,分析本文算法的避障性能。无人船航行环境建模结果如图2所示。
|
图 2 复杂开放水域航行环境建模结果 Fig. 2 Modeling results of complex open water navigation environment |
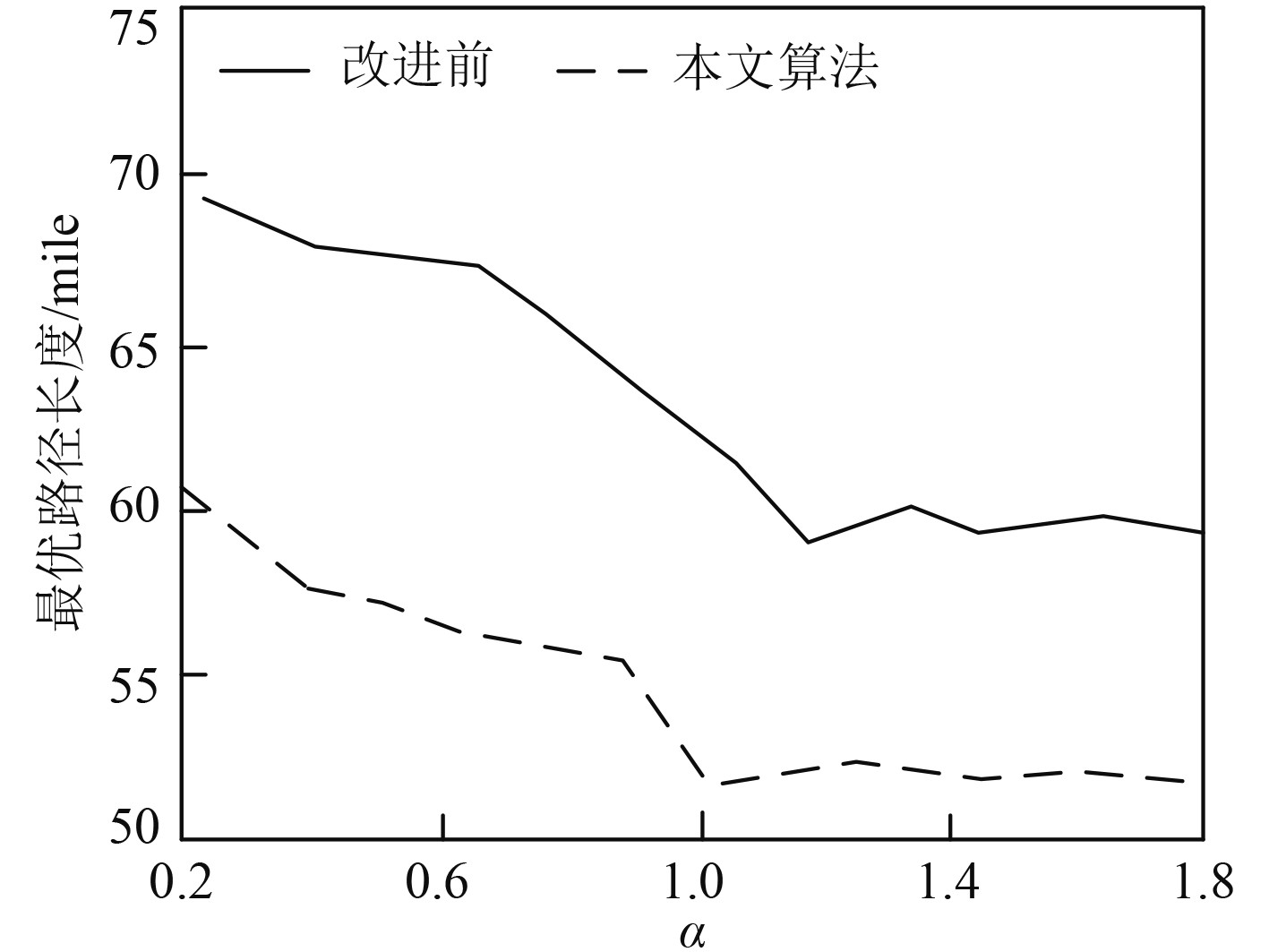
蚁群算法性能的优劣直接影响无人船避障路线规划效果,启发参数
|
图 3
启发参数
|
|
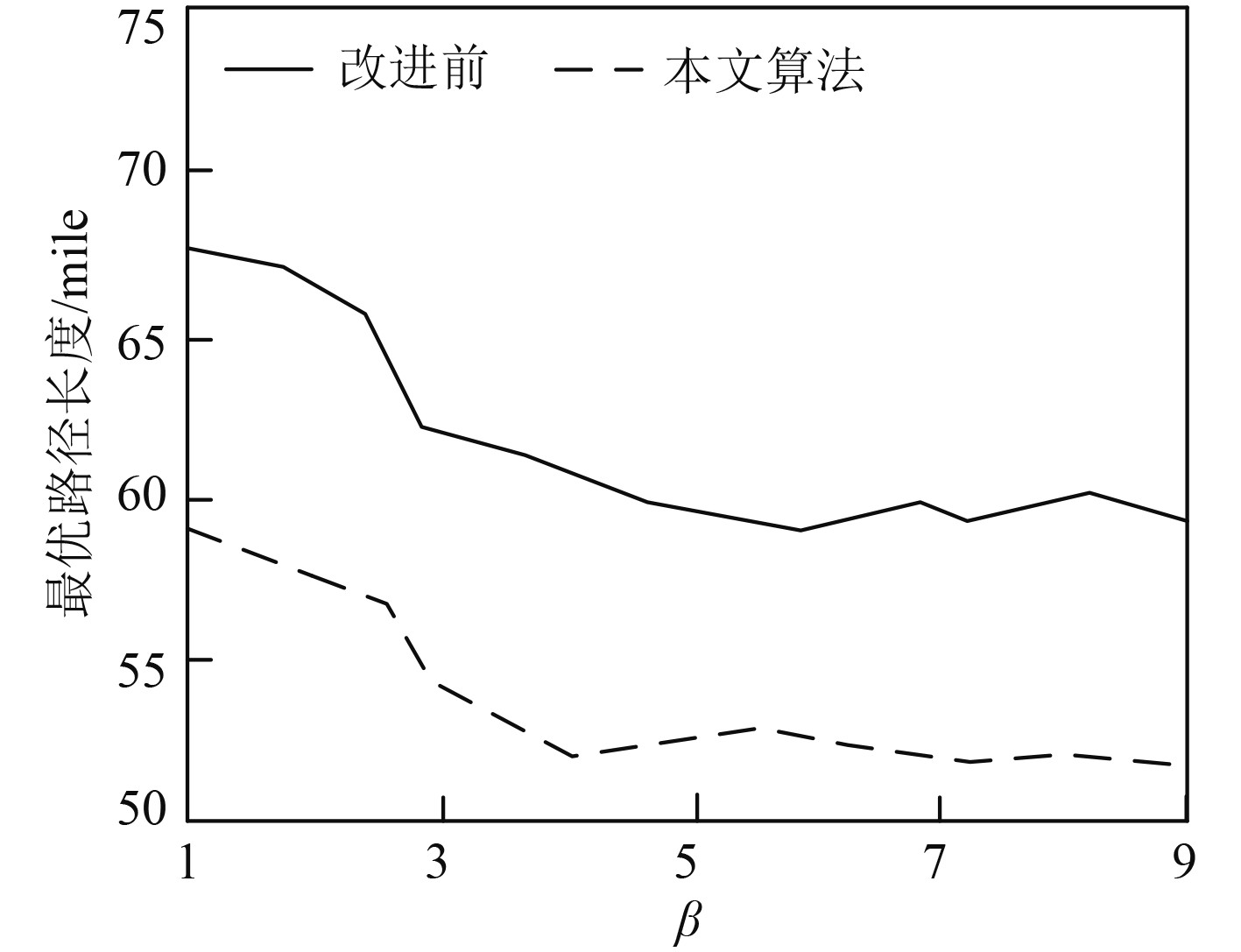
图 4
启发参数
|
可知,启发参数
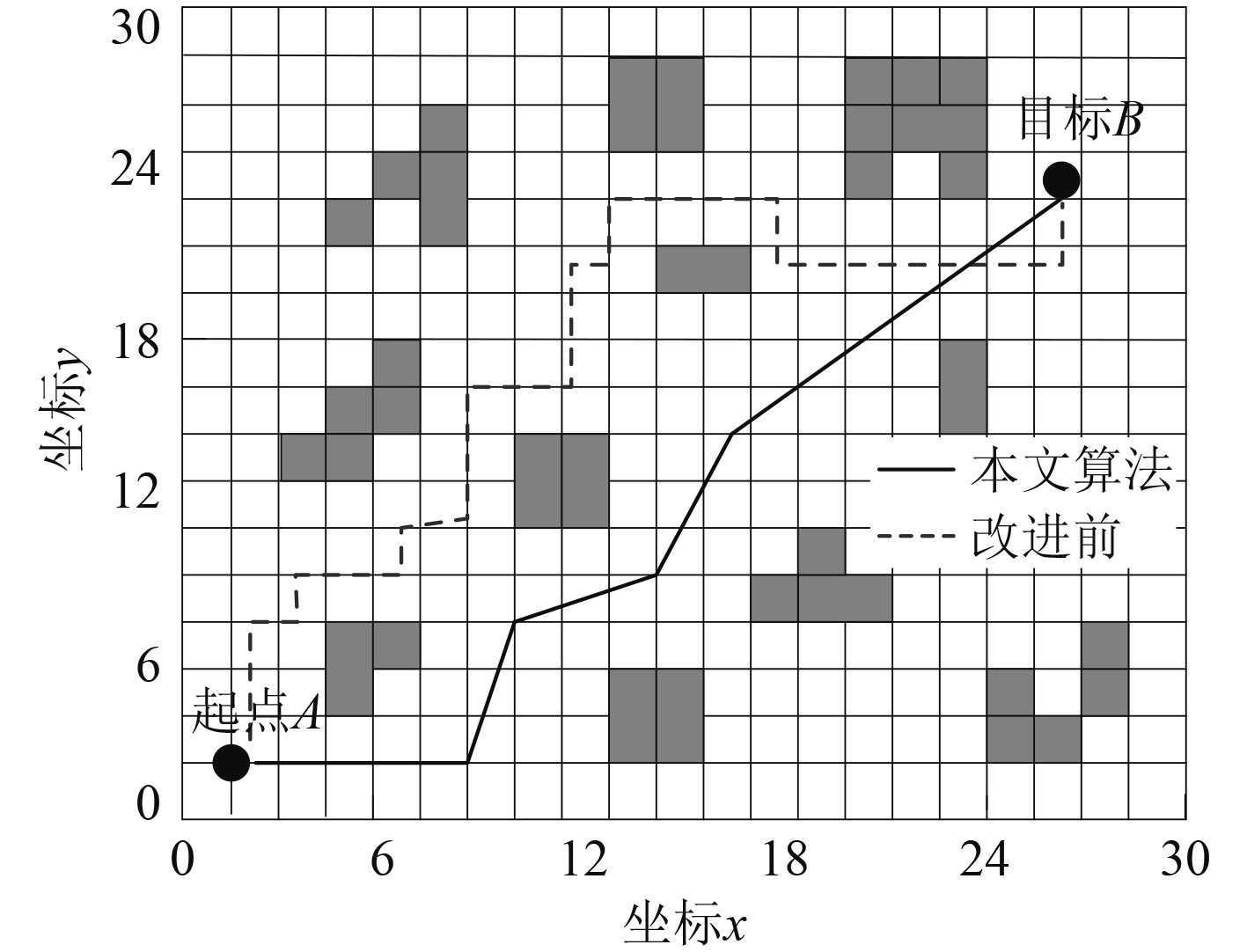
在图2航行环境下,无人船航行初始点为A,航行目标点为B,将本文算法应用到无人船避障路线规划中,通过对算法改进前后的避障路线规划结果以及收敛曲线进行对比分析,验证本文算法的应用性,实验结果如图5和图6所示。
|
图 5 算法改进前后避障路线规划结果对比分析 Fig. 5 Comparative analysis of obstacle avoidance route planning results before and after algorithm improvement |
|
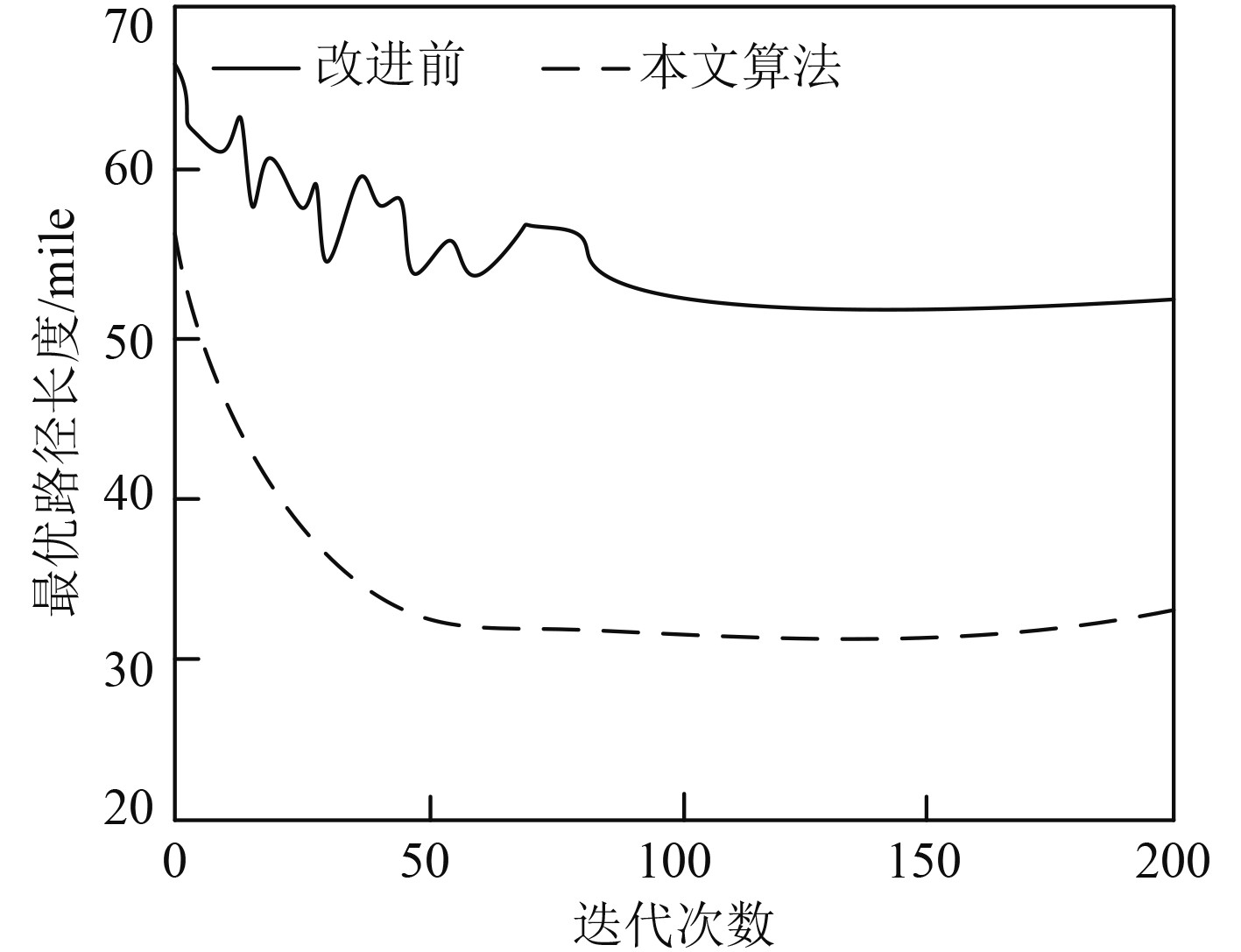
图 6 改进前后算法性能对比分析 Fig. 6 Comparative analysis of algorithm performance before and after improvement |
可知,随着迭代次数的不断增加,算法改进前后的收敛曲线均呈现出不断降低的发展趋势,本文算法经过50次迭代即可实现最佳路径长度曲线的快速收敛,改进前算法需要100次迭代方能达到稳定状态,且迭代前期曲线波动起伏较大,曲线平滑性差。改进前算法的避障路线规划结果中存在更多的拐点,路线曲折、避障路线更长。采用本文算法规划设计的无人船避障路线平整度高、避障路线长度降低了40.39%,拐点数降低了60%。
3 结 语以航行于复杂开放水域的无人船为实验对象,在分析蚁群算法性能影响因素的基础上,通过对比分析改进前后无人船避障路线规划结果研究本文算法的优越性。实验结果表明:
1)蚁群规模为80,启发参数
2)本文算法可实现无人船避障路线规划,设计的避障路线长度比改进前降低了40.39%、拐点数减少60%。
| [1] |
杨琪森, 王慎执, 桑金楠, 等. 复杂开放水域下智能船舶路径规划与避障方法[J]. 计算机集成制造系统, 2022, 28(7): 2030-2040. Yang Qi-sen, Wang Shen-zhi, Sang Jin-nan, et al. Path planning and real-time obstacle avoidance methods of intelligent ships in complex open water environment[J]. Computer Integrated Manufacturing Systems, 2022, 28(7): 2030-2040. DOI:10.13196/j.cims.2022.07.009 |
| [2] |
白响恩, 江明哲, 徐笑锋, 等. 基于双向搜索的改进蚁群算法的船舶路径规划[J]. 中国航海, 2022, 45(3): 13-20. Bai Xiang’en, Jiang Ming-zhe, Xu Xiao-feng, et al. Ship route planning using improved ant colony algorithm with bi-directional search strategy[J]. Navigation of China, 2022, 45(3): 13-20. DOI:10.3969/j.issn.1000-4653.2022.03.003 |
| [3] |
殷绍伟, 彭力, 戴菲菲. 融合改进A~*蚁群和滚动窗口法的平滑路径规划[J]. 计算机科学与探索, 2021, 15(10): 1969-1979. Yin Shao-wei, Peng Li, Dai Fei-fei. Smooth path planning by integrating improved A~* ant colony and rolling window method[J]. Computer Science and Exploration, 2021, 15(10): 1969-1979. DOI:10.3778/j.issn.1673-9418.2011061 |
| [4] |
张子然, 黄卫华, 陈阳, 等. 基于双向搜索的改进蚁群路径规划算法[J]. 计算机工程与应用, 2021, 57(21): 270-277. Zhang Zi-ran, Huang Wei-hua, Chen Yang, et al. Improved ant colony path planning algorithm based on bidirectional search[J]. Computer Engineering and Applications, 2021, 57(21): 270-277. DOI:10.3778/j.issn.1002-8331.2106-0061 |
| [5] |
李清亮, 李彬, 孙国皓, 等. 基于精确罚函数的无人艇航迹规划和自动避障算法[J]. 中国舰船研究, 2021, 16(1): 89-95. Li Qing-liang, Li Bin, Sun Guo-hao, et al. Trajectory planning and automatic obstacle avoidance algorithm for unmanned surface vehicle based on exact penalty function[J]. Chinese Journal of Ship Research, 2021, 16(1): 89-95. DOI:10.19693/j.issn.1673-3185.02209 |
| [6] |
吕进锋, 马建伟, 李晓静. 基于改进的随机路径图及和声算法的舰船航线规划[J]. 控制理论与应用, 2020, 37(12): 2551-2559. Lv Jin-feng, Ma Jian-wei, Li Xiao-jing. Route planning based on improved probabilistic roadmap and harmony search[J]. Control Theory & Applications, 2020, 37(12): 2551-2559. |
| [7] |
童帮裕, 胡坚堃. 基于改进蚁群算法的船舶冰区航行路径规划[J]. 中国航海, 2020, 43(1): 24-28. Tong Bang-yu, Hu Jian-kun. Improved ant colony optimization for navigation path planning in ice zone[J]. Navigation of China, 2020, 43(1): 24-28. DOI:10.3969/j.issn.1000-4653.2020.01.005 |
| [8] |
马庆禄, 黄光浩. 基于改进人工势场法的自动驾驶路径规划方法[J]. 计算机仿真, 2022, 39(8): 160-165. Ma Qing-lu, Huang Guang-hao. Automatic driving path planning based on improved artificial potential field method[J]. Computer Simulation, 2022, 39(8): 160-165. DOI:10.3969/j.issn.1006-9348.2022.08.030 |
 2023, Vol. 45
2023, Vol. 45
