2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
水空跨域航行器(也称跨介质飞行器)[1-3]是一种同时具备空中飞行与水下潜航能力的新概念航行器,因其兼具快速性与隐蔽性的优势在科考与军事领域具有广阔应用前景而受到关注。当前的跨域航行器按照结构的不同可为3类[4-5]:固定翼式、旋翼式和仿生式。固定翼跨域航行器[6-10]飞行原理与固定翼飞机相同,大都采用螺旋桨作为推进器,续航时间长,但机动性较差。旋翼跨域航行器[11-13]受多旋翼无人机启发,由旋翼提供拉力进行垂直水面起降,机动灵活,但续航时间短。这一类跨域航行器主要依靠空气螺旋桨进行水空跨域过程,水面垂直起飞过程中旋翼桨盘处于近水面垂直状态,受水空2种介质密度变化影响较大。相关研究对于航行器的螺旋桨在2种介质中的推力情况进行了测试,没有对螺旋桨近水面垂直状态下的推力情况进行分析。仿生跨域航行器[14-15]受不同生物运动模式启发,使用扑翼、喷流、波动鳍等方式进行空中和水下航行,目前尚未实现持续航行的能力。
目前对于具有持续航行能力的跨域航行器,无论是固定翼式还是旋翼式航行器,桨叶式推进器均为其动力构型的主要选择。对于旋翼式跨域航行器,推进器近水面工作是其不可回避的任务场景,而推进器在近水面垂推工况下的推力特性与航行器能否实现水面垂直起飞直接相关。本文研究对象是“海鲲”水空跨域航行器涵道推进器近水面垂推工况下的推力损失机理。“海鲲”是一种倾转四旋翼构型的跨域航行器,水面起飞模式与旋翼式跨域航行器相同,采用改进的水空两用涵道推进器[16]提供推力进行水面垂直起飞。目前对于涵道推进器的下洗尾流与壁面的相互干扰研究主要集中在单一介质工况下与地面的交互作用[17-19],对于推进器近水面垂直状态下的推力特性研究开展较少。本文使用实验测试与CFD仿真分析相结合的方式对“海鲲”所用的涵道推进器近水面垂推工况下推力损失机理展开初步研究,为旋翼式跨域航行器的研制。及其水面垂直起飞/降落功能的实现提供参考。
1 实验方案 1.1 涵道推进器模型“海鲲”跨域航行器采用倾转四旋翼构型,由4个涵道推进器提供动力,具备水面垂直起降能力。每个推进器与机翼翼梢处的舵机相连,可独立转动实现矢量推力。水面起飞时,推进器旋转轴与机翼垂直,使桨叶与水面相平,桨叶上表面距离水面高度为0.1 m。
实验用涵道推进器的涵道由唇口、过渡段(喉部)和扩张段3部分组成,涵道直径150 mm,长度750 mm,扩张角

|
图 1 涵道推进器 Fig. 1 Ducted propeller |
推进器由1台安装在涵道内的无刷直流电机驱动,电机与推进器一起水平固定安装在测力传感器的上部,由测力传感器测量整个涵道推进器系统的推力。螺旋桨旋转轴与地面平行,桨叶内外两侧区域保持空旷,保证推进器尾流自由发展,避免产生地面效应影响实验结果。推进器与测力传感器垂直固定在实验台架上,推进器下方放置尺寸为3 m×2 m×0.75 m的泳池,实验测试时泳池水深0.7 m。推进器距水面高度可以在0.1~0.5 m之间手动调节,可以测试离水面高度对于推进器推力的影响。
实验使用ATI六维力传感器测量涵道螺推进器整体推力,采集时传感器的 Z 轴方向与涵道推进器轴向平行,Z方向最大量程为500 N,最大误差 1.25%。使用直流稳压电源为电机供电,使用信号发生器控制电机转速,使用数据采集板卡对于推进器电机转速、电压和电流数据进行采集,汇总数据由计算机进行整理。
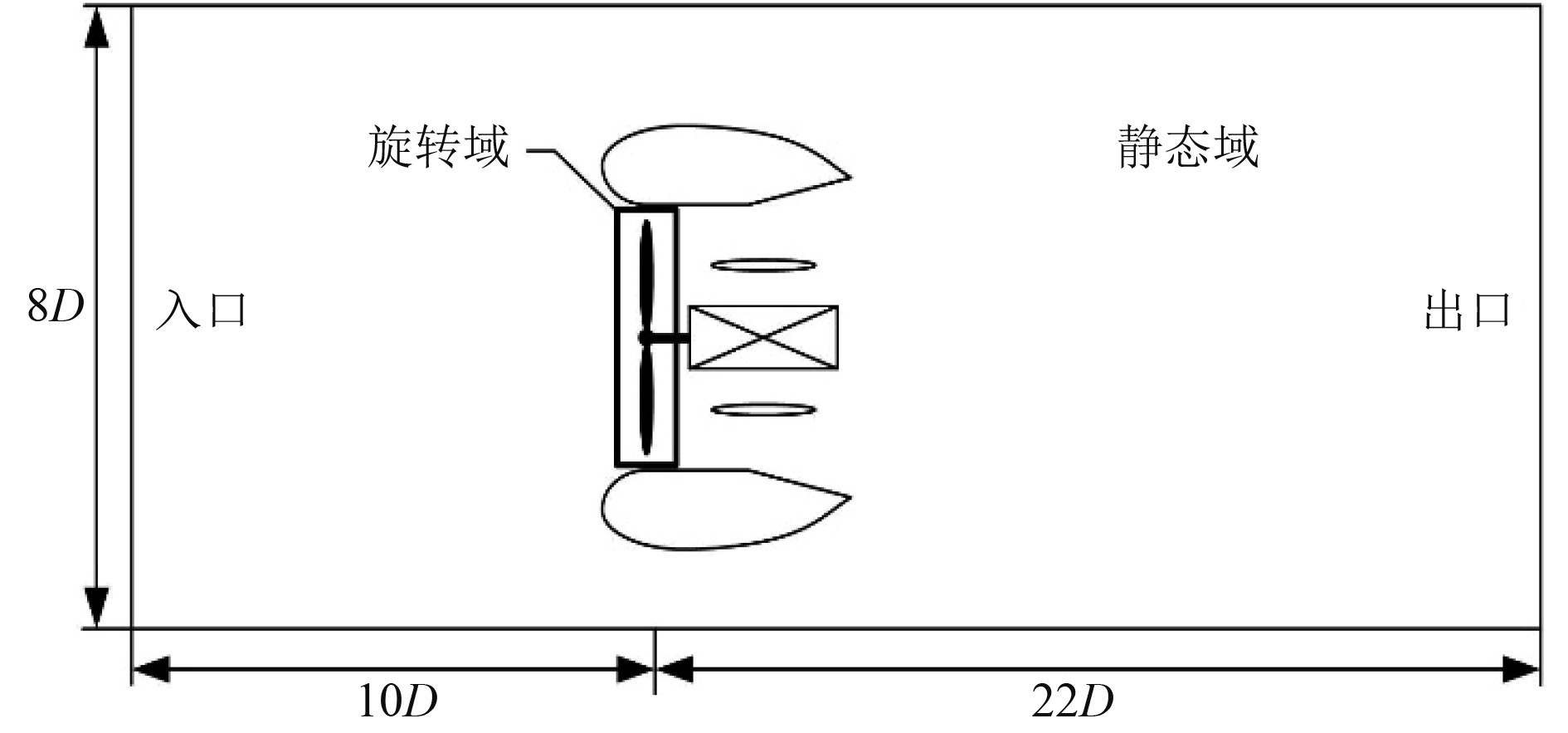
2 仿真方法采用非结构滑移网格技术,将整个计算域分为包含涵道的静态域和包含桨叶的旋转域。桨叶做旋转运动,涵道及远场处于静止状态,2个区域间通过交界面互换流场求解的信息。计算域为半径为8 D的圆柱,入口距桨叶中心距离为10 D,出口距桨叶中心为22 D,其中D为螺旋桨直径,如图2所示。
|
图 2 计算域划分示意图 Fig. 2 Schematic diagram of computing domain division |
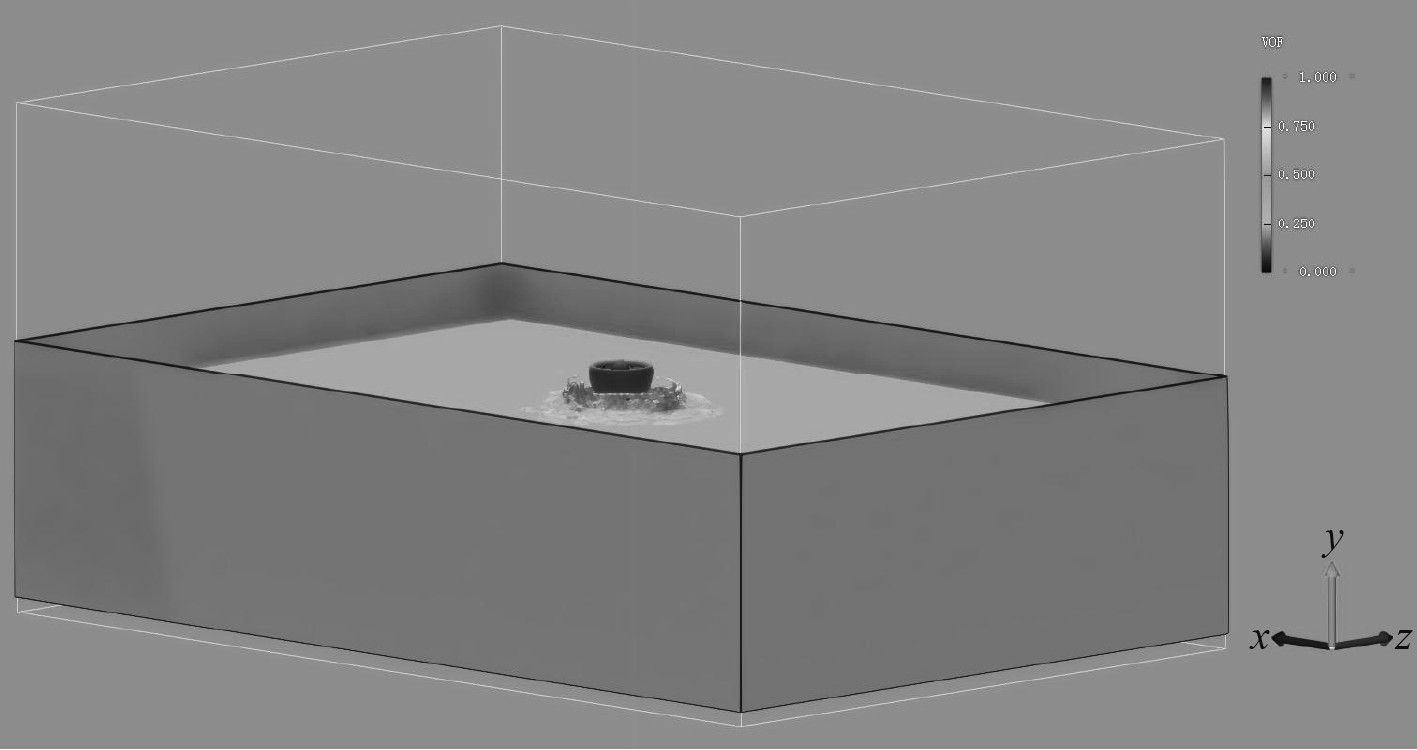
对涵道推进器壁面附近网格进行加密,远场网格稀疏化。桨叶、涵道壁面采用棱柱网格构成壁面边界层,边界层层数为10,网格沿壁面法向增长率为1.3。边界条件设为压力入口、压力出口,推进器桨叶和涵道表面设置为无滑移壁面。图3为整个计算域的网格与推进器表面网格的分布,最终得到的涵道推进器网格总数为500万。引入多相流模型对推进器在近水面处运行情况进行仿真,推进器下方构建与实验测试所用泳池尺寸相同的无滑移壁面,水深设定为0.7 m,与水面推力实验情景相同,如图4所示。

|
图 3 网格分布 Fig. 3 Distribution of grid |
|
图 4 近水面推力仿真 Fig. 4 Thrust simulation near water |
采用雷诺时均方程进行数值模拟,湍流模型选用为剪切应力输运k-ω模型(SST k-ω)[20]。SSTk-ω模型结合了k-ω模型在近壁面处对于逆压梯度的敏感性,与k-ε模型在远场区域对自由来流不敏感的特点,适合应用于压力场变化的物理现象,能准确模拟推进器的流场和尾迹。
3 结果分析首先使用本文的数值计算方法对涵道推进器在空气中不同转速运转进行数值仿真,并与实验值进行对比。计算得到的涵道推进器的推力以及相应的功率变化分别见表1和表2。可以看出在各个转速下,数值计算得到的推力和功率值与实验结果吻合良好,说明该数值计算方法能够较好地模拟实验所用涵道推进器空气中的推力特性。
|
|
表 1 推进器推力计算结果与实验值对比 Tab.1 Thrust comparison of propeller between simulation and experiment |
|
|
表 2 推进器功率计算结果与实验值对比 Tab.2 Power comparison of propeller between simulation and experiment |
在推进器近水面推力实验中,首先保持推进器上表面距离水面高度为0.1 m(“海鲲”水面漂浮时推进器距水面高度),改变转速测试推进器推力,记录整个过程的推力和转速信息。
图5(a)为推进器距离水面0.1 m,转速1.1×104 r/min时的推力仿真结果,仿真推力均值为21.3 N,实验数据为21.8 N,误差为2.2%。推进器保持1.1×104 r/min转速不变,距离水面不同高度下推力的仿真结果与实验数据的对比如图5(b)所示,各高度下推力误差均小于6%。可知,推进器近水面推力损失随推进器距离水面高度提高而减小,减小速率随高度提高而降低。推进器距离水面高度在0.1~0.3 m之间时,推力损失迅速减小;距离水面高度在0.3~0.5 m时,推力损失缓慢趋近于0,此时推进器推力与空中工况基本相同。

|
图 5 近水面推力仿真 Fig. 5 Thrust simulation near water |
仿真结果较好复现了实验得到的推力随距离水面高度的增加逐渐恢复至空气中同转速下推力这一过程,本文建立的数值模拟方法能较好反映出推进器近水面推力情况。
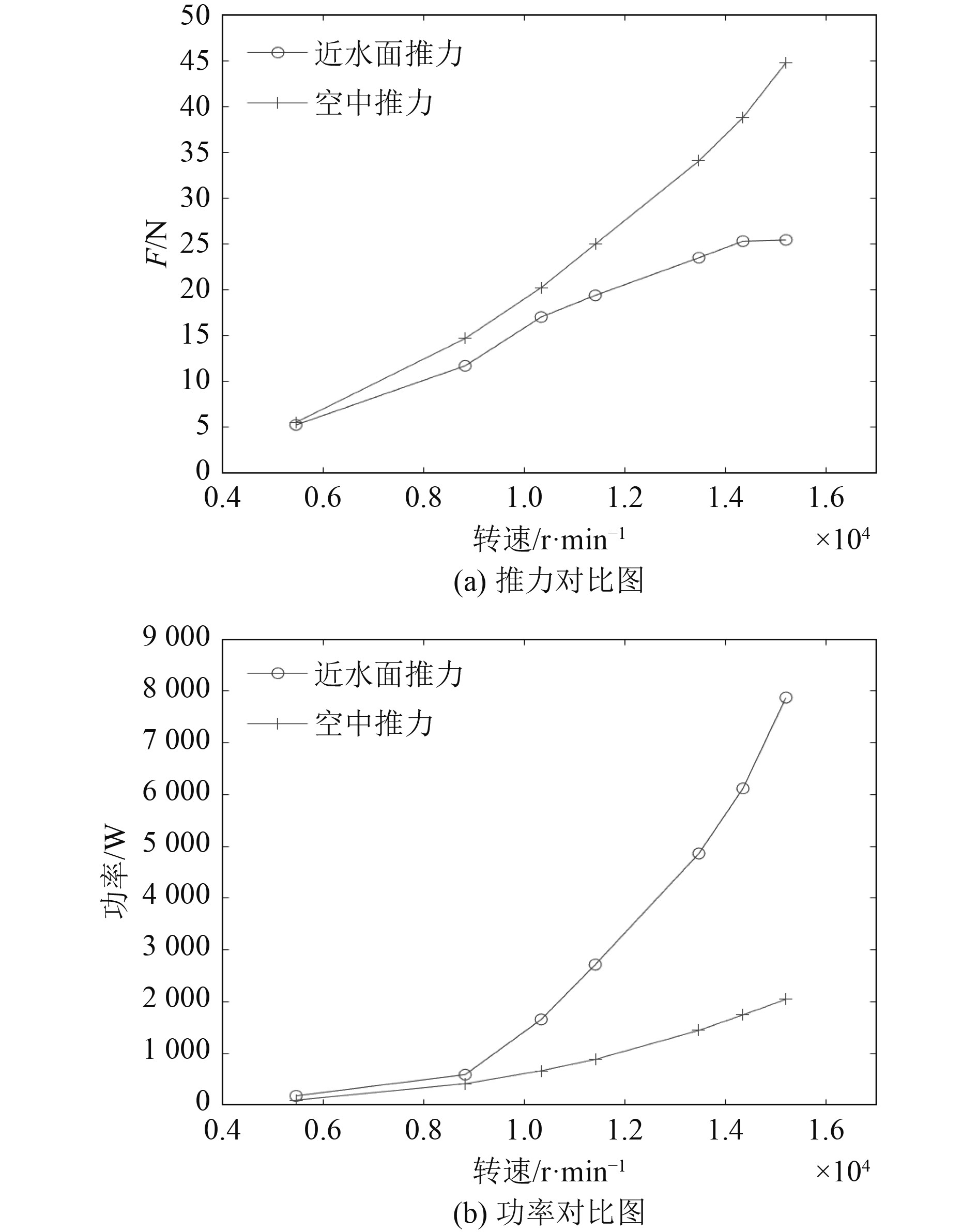
结合空气中实验数据,绘制推进器空中与距离水面0.1 m 2种工况下的推力与功率对比图如图6所示。可以看出,涵道推进器在水面上方垂直运转时,由于水面的影响使得推进器整体拉力减小,并且所需要的功率增大。涵道螺旋桨系统推进器在距离水面高度0.1 m的工况下运转,消耗的功率大于同转速下推进器在空中消耗的功率。随着转速增加其消耗的电机功率非线性地迅速增大至电机最大输出值,过早达到了电机工作上限,与空中工况相比推进器转速无法继续提高由此产生了推进器近水面推力损失。推进器近水面运转时产生的推力较同转速下推进器空中推力小,并且随着转速增加推力的增长速度较空中缓慢,两者的差值迅速放大,产生了同转速下推进器近水面推力损失。随转速升高近水面悬停时,涵道螺旋桨的额外消耗功率由83 W增加到5 825 W,推力损失由0.3 N增加到19.3 N。
|
图 6 近水面实验结果对比图 Fig. 6 Diagram of experiment results comparison |
根据空中与近水面推力实验结果的对比初步推断造成推进器近水面推力损失的因素为,推进器尾流冲击水面形成的飞溅液滴撞击推进器桨叶,造成电机负载增大,较空气中同转速下消耗更多电机功率,使推进器峰值转速与推力降低。对于相同转速下推进器近水面推力小于空气中产生的推力,可以从涵道推进器推力构成进行分析。涵道推进器产生的推力由螺旋桨和涵道2部分组成,其中螺旋桨由于叶盘前后压差产生推力,而涵道唇口段前缘形成了较大的负压区,产生了附加拉力。推进器垂直于近水面处时,尾流受到阻塞,从而影响了推进器的推力。
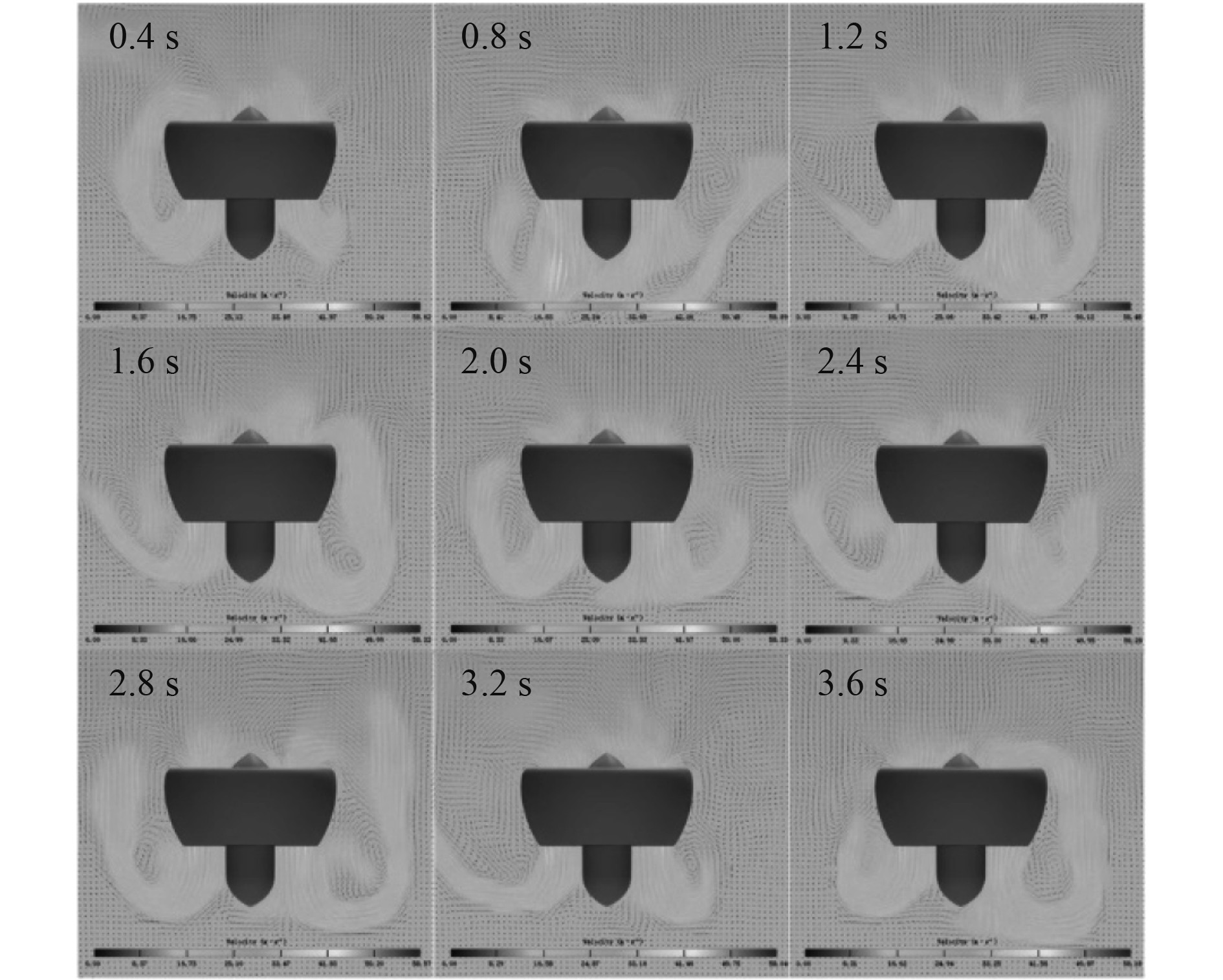
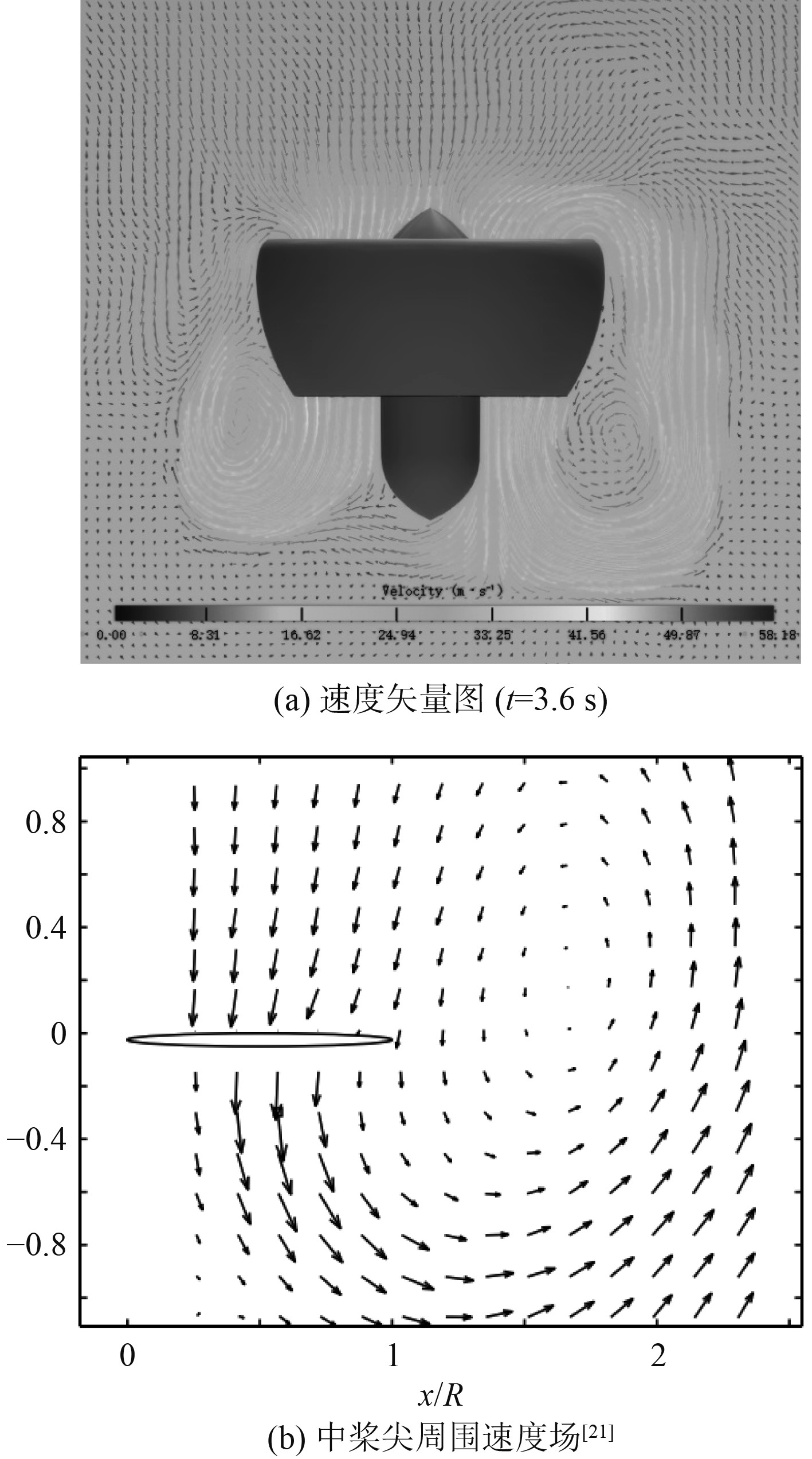
图7为y-z平面上不同时刻下的推进器周围速度矢量分布。可以看出,推进器尾流冲击水面后反弹至推进器两侧,间歇性地被推进器吸入从而形成封闭环状气流例如3.6 s时刻。图8为水空体积分数云图。图9(a)与图9(b)文献[21]采用粒子图像测速实验得到的典型涡环状态下桨尖周围速度矢量分布明显相似,可知图9(a)中t=3.6 s时推进器已处于涡环状态。涡环状态是指直升机垂直下降时,旋翼的诱导速度与相对气流方向相反。此时如果下降率较大超过了一定数值,沿旋翼周围形成环状旋涡流动状态。直升机的旋翼涡环状态使直升机周围气流不均匀、不稳定,旋翼消耗发动机功率但不能有效产生拉力,出现所谓“带功率沉陷”现象[22]。本文涵道推进器于水面上方垂直悬停,尾流冲击水面反弹形成的气水混合物,受到唇口低压区域的吸引,经唇口段吸入涵道内,形成位于涵道外部的“涡环”,致使推进器进入涡环状态。
|
图 7 速度矢量图 Fig. 7 Diagram of velocity vector |
|
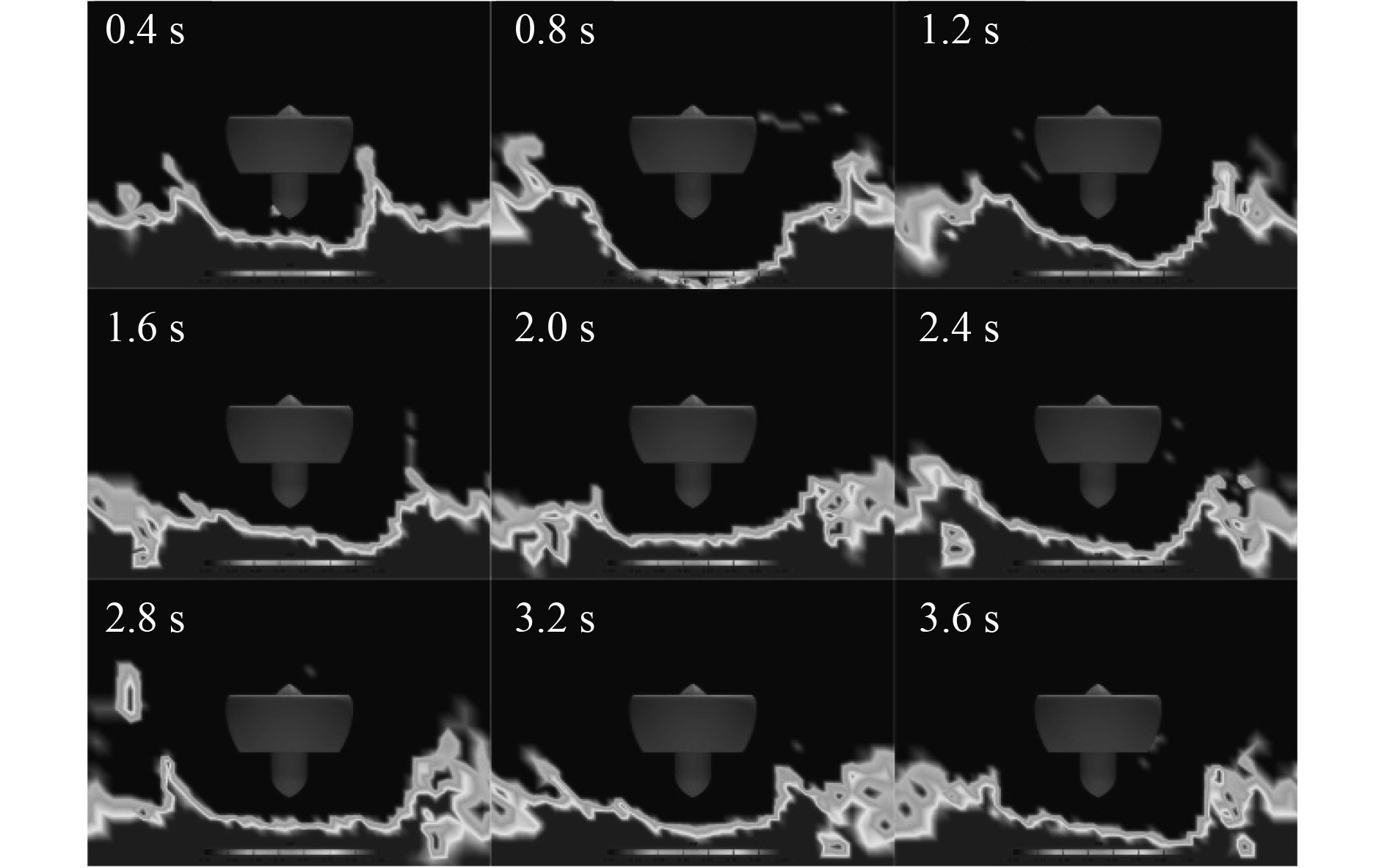
图 8 水空体积分数云图 Fig. 8 Cloud map of water-air volume fraction |
根据图8和图9进一步分析可知,推进器在近水面处能否进入涡环状态与其下方水面形状、高度相关。当推进器下方水面距离涵道扩张段较远时如图9中0.8、2.4、3.2 s时刻,对比图9对应时刻的速度矢量图可得经水面反弹的尾流呈现远离涵道两侧的趋势;当水面距离扩张段较近时如0.4、1.6、3.6 s时刻,反弹气流会绕过唇口段被吸入推进器中,围绕涵道外部形成涡环。推进器下方水面总体上呈U字型凹陷,当水面U字型底部较为平缓、两侧竖直部分垂直度较好时,推进器容易吸入反弹气流从而形成涡环;当U字型底部出现倾斜时,经其较低一端反弹气流更容易形成涡环,见图8和图9中1.6 s和3.6 s时刻。
|
图 9 速度矢量图 Fig. 9 Diagram of velocity vector |
为探寻涵道推进器在不同高度不同转速下运转的推力特性,对推力按式(1)无因次化处理为推力系数:
| $ {C_T} = \frac{T}{{\rho {n^2}{D^4}}} $ | (1) |
式中:T为推力,单位N;ρ为 空气密度,ρ = 1.225 kg/m3;n为转速,单位rad/s;D为涵道,内径D=0.15 m。近水面距离分别取为 H/D=0.67、1.33、2.00、2.67、3.33,H为涵道出口与水面之间的实际距离。
图10 为不同近水面距离涵道推进器推力系数与转速的关系。当推进器转速处于5000 r/min以下,近水面距离小于 H/D = 2时,推力系数随着近水面距离的增加呈现减小至一稳定值的趋势。当近水面距离大于 H/D = 2时,推进器拉力与空气中已经基本上接近。其原因是推进器处于低转速运行时推力较小,尾流对于水面的冲击较弱,推进器下方水面较平坦近似于地面,由于地面效应造成推进器推力较空气中运转时增大。随着近水面距离增大后,推进器尾流受到水面的阻塞作用衰减较快,地面效应迅速减弱。推进器转速增加至7000 r/min以上时,下方水面受推进器尾流冲击增大,水面发生剧烈形变,进而改变了反弹气流的方向,使推进器进入涡环状态产生推力损失。推进器转速由7000 r/min逐渐提高,随着近水面距离的依次增加,反弹气流对涵道推进器拉力的影响在减小,推力系数逐渐增加接近推进器空气中运行时的对应值,如图10(b)所示。值得注意的是,当推进器近水面距离等于 H/D = 0.67时,推力系数随转速增加而迅速减小,说明推进器的效率在大幅降低,与近水面推力实验时出现额外功率损耗的现象相符。该涵道推进器在跨域航行器水面起飞实际应用中,应考虑采用提高推进器距水面高度的起飞策略以保证高效地产生足量推力完成航行器水面起飞任务。

|
图 10 涵道推进器近水面推力系数 Fig. 10 Trust fractor of ducted propeller near water surface |
本文从水空跨域航行器水面垂直起飞需求出发,通过推力实验与CFD仿真相结合的方法对其涵道推进器近水面垂直状态出现的推力损失机理进行了初步研究,结论总结如下:
1)推进器在近水面以较高转速垂直运转时,与同转速下空中工况相比产生推力损失,且所需功率增加。转速由5700 r/min升高至15000 r/min额外功率消耗由83 W增加到5 825 W,推力损失由0.3 N增加到19.3 N。
2)推进器近水面推力损失随推进器距离水面高度提高而减小。推进器转速1.1×104 r/min,距离水面高度由0.1 m升高至0.3 m时,推力损失迅速减小;距离水面高度在0.3 m到0.5 m时,推力损失缓慢趋近于0,此时推进器推力接近空中工况。
3)推力损失的原因为推进器尾流冲击其下方水面形成的反弹气水混合物被推进器吸入,使推进器周围空气流动进入不稳定的涡环状态。这中涡环状态与推进器距离水面的高度以及水面的凹陷形状相关。当水面距离推进器越近、水面凹陷形状越近似U字型时,反弹的气水混合物越容易被推进器吸入,使推进器进入涡环状态。
4)推进器近水面低速运转时,由于地面效应推力与空气中工况相比有所增加。随着近水面高度增加,地面效应迅速衰减,推进器推力恢复至空中工况。
| [1] |
胡志强, 杨翊, 周振溪, 等. 一种可垂直起降的折叠翼潜空跨域航行器: 中国, 112549885A [P]. 2021-03-26. HU Z Q, YANG Y, ZHOU Z X, et al. A kind of VTOL water-air cross-domain marine robot with folding wings: China, 112549885A [P]. 2021-03-26. |
| [2] |
胡志强, 杨翊, 耿令波, 等. 多旋翼水空两栖跨域航行器: 中国, 108128450A[P]. 2018-06-08. HU Z Q, YANG Y, GENG L B, et al. A kind of many rotor water-air amphibious cross-domain marine robot: China, 108128450A[P]. 2018-06-08. |
| [3] |
杨兴帮, 梁建宏, 文力, 等. 水空两栖跨介质无人飞行器研究现状[J]. 航行器, 2018, 40(1): 102-114. YANG X B, LIANG J H, WEN L, et al. Research status of water-air amphibious trans-media unmanned vehicle[J]. Robot, 2018, 40(1): 102-114. |
| [4] |
唐胜景, 张宝超, 岳彩红, 等. 跨介质飞行器关键技术及飞行动力学研究趋势分析[J]. 飞航导弹, 2021(6): 7-13. TANG S J, ZHANG B C, YUE C H, et al. Analysis of key technologies and flight dynamics research trends of cross-media aircraft[J]. Aerodynamic Missile Journal, 2021(6): 7-13. DOI:10.16338/j.issn.1009-1319.20210843 |
| [5] |
刘相知, 崔维成. 潜空两栖航行器的综述与分析[J]. 中国舰船研究, 2019, 14(S2): 1–14. LIU X Z, CUI W C. An overview and analysis of the water-air amphibious vehicles[J]. Chinese Journal of Ship Research, 2019, 14(S2): 1–14. |
| [6] |
ZUFFEREY R, A. O A, FARINHA A, et al. Consecutive aquatic jump-gliding with water-reactive fuel[J]. Science Robotics, 2019, 4(34).
|
| [7] |
WEISLER W, STEWART W, ANDERSON M, et al, Testing and characterization of a fixed wing cross-domain unmanned vehicle operating in aerial and underwater environments[J]. IEEE Journal of Oceanic Engineering, 2018, 43(4): 969–982.
|
| [8] |
WEISLER W, STEWART W, ANDERSON M, et al. Dynamic modeling of passively draining structures for aerial–aquatic unmanned vehicles[J]. IEEE Journal of Oceanic Engineering, 2019: 1–11.
|
| [9] |
FABIAN A, FENG Y F, SWARTZ E, et al. Hybrid aerial underwater vehicle[R]. Lexington, USA: MIT Lincoln Lab, 2012.
|
| [10] |
YAO G C, LIANG J H, WANG T M, et al. Submersible un-manned flying boat: Design and experiment[C]//IEEE International Conference on Robotics and Biomimetics. Piscataway, USA: IEEE, 2014: 1308–1313.
|
| [11] |
DREWS P L J, NETO A A, CAMPOS M F M. Hybrid unmanned aerial underwater vehicle: modeling and simulation[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2014: 4637–4642.
|
| [12] |
MERCADO RAVELL D, MAIA M, DIEZ F. Modeling and control of unmanned aerial/underwater vehicles using hybrid control[J]. Control Engineering Practice, 2018, 76(7): 112-122. |
| [13] |
ALZU'BI H, MANSOUR L, RAWASHDEH O. Loon Copter: Implementation of a hybrid unmanned aquatic-aerial quadcopter with active buoyancy control[J]. Journal of Field Robotics, 2018, 35(5): 764-778. DOI:10.1002/rob.21777 |
| [14] |
HOU T G, YANG X B, SU H H, et al. Design and experiments of a squid-like aquatic-aerial vehicle with soft morphing fins and arms[C]//IEEE Proceedings of 2019 International Conference on Robotics and Auto mation(ICRA), 2019.
|
| [15] |
CHEN Y F, WANG H Q, HELBLING E F, et al. A biologically inspired, flapping-wing, hybrid aerial-aquatic microrobot[J]. Science Robotics, 2017, 2(11): eaao5619. DOI:10.1126/scirobotics.aao5619 |
| [16] |
郜天柱, 胡志强, 杨翊, 等. 水空两栖涵道风扇推进器推力理论分析及实验验证[J]. 航行器, 2019, 41(2): 222-231. GAO T Z, HU Z Q, YANG Y, et al. Theoretical analysis and experimental verification on thrust of aquatic-aerial amphibious ducted fan propeller[J]. Robot, 2019, 41(2): 222-231. |
| [17] |
LEE T E, LEISHMAN J G, RAMASAMY M. Fluid dynamics of interacting blade tip vortices with a ground plane[J]. Journal of the American Helicopter Society, 2010, 55(2): 022005. DOI:10.4050/JAHS.55.022005 |
| [18] |
JARDIN T, PROTHIN S, MAGAÑA C G. Aerodynamic performance of a hovering microrotor in confined environment[J]. Journal of the American Helicopter Society, 2017, 62(2): 1-7. |
| [19] |
GOURDAIN N, SINGH D, JARDIN T, et al. Analysis of the turbulent wake generated by a micro air vehicle hovering near the ground with a lattice boltzmann method[J]. Journal of the American Helicopter Society, 2017.
|
| [20] |
张德良. 计算流体力学教程[M]. 2 版. 北京: 高等教育出版社, 2011.
|
| [21] |
GREEN R B, GILLIES E A, BROWN R E. The flow field around a rotor in axial descent[J]. Journal of Fluid Mechanics, 2005(354): 237-261. |
| [22] |
王适存. 直升机空气动力学[M]. 南京: 南京航空航天大学出版社, 1991.
|
 2023, Vol. 45
2023, Vol. 45
