轴频、工频等低频电磁场因频率低,线谱特征明显,通常被广泛应用于水下远距离探测[1-5]。为了评价不同场源的可探测性,一种合适的方法是将不同场源模型等价为时谐电偶极子与时谐磁偶极子,并根据空气-海水-海床3层介质对其进行建模[6-7]。由于船壳为磁性良导体材料,对电磁信号具有一定的屏蔽作用,在对电磁场源建模时,应当首先明确壳体的屏蔽系数[8-10]。
文献[1]给出屏蔽系数的理论计算公式,但其场源主要分布在轴上,而实际的场源分布位置相对随机,为此需要一种新的屏蔽系数计算公式。文献[2]给出了时谐偶极子在3层介质下产生的低频电磁场计算模型,但没有考虑艇壳对于低频电磁场的屏蔽作用,而实际的船壳,由于不同频率的电磁场信号波长不同,屏蔽效果也不同。因此,屏蔽系数公式应当与频率相关。
本文基于定义的屏蔽系数计算公式,首先构建基于有限元法的计算模型,对1~20 Hz频段的屏蔽系数进行仿真计算,其次完成了壳体屏蔽系数实测,获得了一致的铁磁性壳体屏蔽系数变化规律。
1 舰船低频电磁场屏蔽以实际舰船分析,舱内有丰富的时变电磁辐射源,其中电力推进、辅机设备、配电设备等观测导航设备均会产生数十至数百赫兹的信号,同时推力轴、艉轴、轴承等磁性材料旋转也会产生与桨转动频率一致的低频磁场信号。这些场源产生的低频电磁场在建模时均需考虑到铁磁性舰船壳体的屏蔽作用。
以磁性轴旋转为例分析,假定长度为
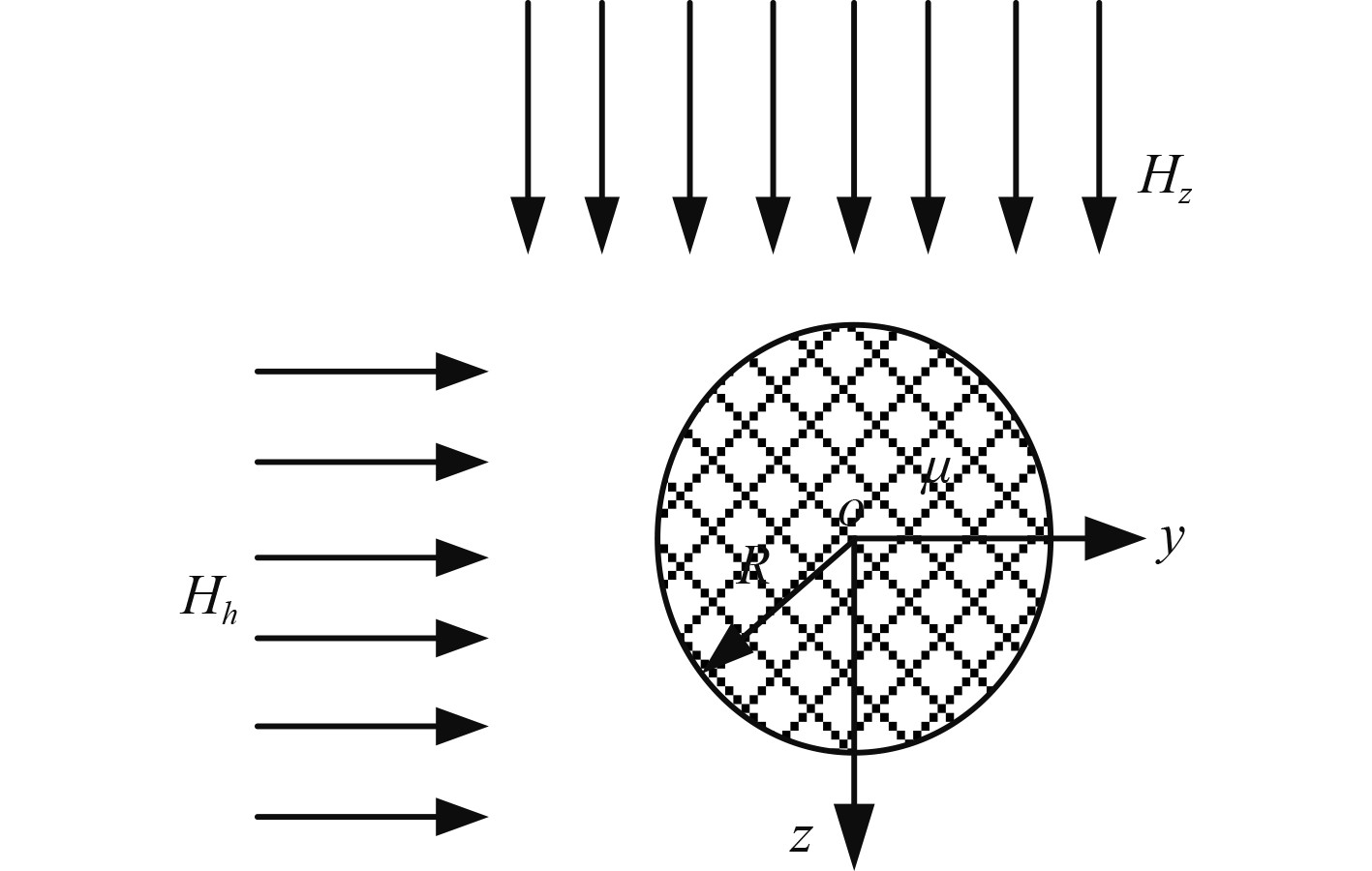
|
图 1 轴截面示意图 Fig. 1 Schematic diagram of shaft section |
将轴近似为旋转椭球体模型,根据旋转椭球体模型可知,轴的纵向、横向、垂向的等效磁矩
| $ \begin{gathered} {M_x} = {J_x}V = \frac{{\left( {\mu - 1} \right)}}{{1 + \left( {\mu - 1} \right){N_x}}}\frac{{{H_x}}}{{{L_l}}}\pi {R^2}L ,\\ {M_y} = {J_y}V = \frac{{\left( {\mu - 1} \right)}}{{1 + \left( {\mu - 1} \right){N_y}}}\frac{{{H_y}}}{{{L_s}}}\pi {R^2}L ,\\ {M_z} = {J_z}V = \frac{{\left( {\mu - 1} \right)}}{{1 + \left( {\mu - 1} \right){N_z}}}\frac{{{H_z}}}{{{L_s}}}\pi {R^2}L 。\\ \end{gathered} $ | (1) |
式中:
定义磁场屏蔽系数
| $ S = \frac{{{B_e}}}{{{B_i}}},0 < S < 1。$ | (2) |
其中:
将式(2)所计算的磁场屏蔽系数引入式(1),可得到
| $ \begin{gathered} {M_x}(f) = \frac{{\left( {\mu - 1} \right)}}{{1 + \left( {\mu - 1} \right){N_x}}}\frac{{{H_x}}}{{{L_l}}}{\text{π}} {R^2}LS(f),\\ {M_y}(f) = \frac{{\left( {\mu - 1} \right)}}{{1 + \left( {\mu - 1} \right){N_y}}}\frac{{{H_y}}}{{{L_s}}}{\text{π}} {R^2}LS(f),\\ {M_z}(f) = \frac{{\left( {\mu - 1} \right)}}{{1 + \left( {\mu - 1} \right){N_z}}}\frac{{{H_z}}}{{{L_s}}}{\text{π}} {R^2}LS(f) 。\\ \end{gathered} $ | (3) |
式中:
COMSOL软件基于边界元法(Boundary Element Method,BEM)方法计算,BEM方法以边界积分方程为数学基础,同时采用与有限元法(Finite Element Method,FEM)方法相似的划分单元离散技术。通过将边界离散为边界元,将边界积分方程离散为代数方程组,再用数值方法求解代数方程组,得到原问题边界积分方程的解。BEM的最大特点就是降低了求解问题的维数,将三维问题化为其边界面上的二维问题,只以边界变量为基本变量,域内未知量可在需要时根据边界变量求出。该方法具有较高的精度,而且在很多情况下比有限元法更有效。目前,COMSOL软件已被广泛应用于舰船腐蚀相关静态电场和磁场的建模以及ICCP系统保护电流优化和舰船电场隐身领域。
为了研究舰船壳体磁场屏蔽系数的变化规律,采用COMSOL有限元软件“AC/DC-磁场”接口的频域分析模块进行仿真计算。将模型简化为均匀椭球壳体,并利用交流线圈产生交变磁场以模拟轴频磁场,仿真模型如图2所示。
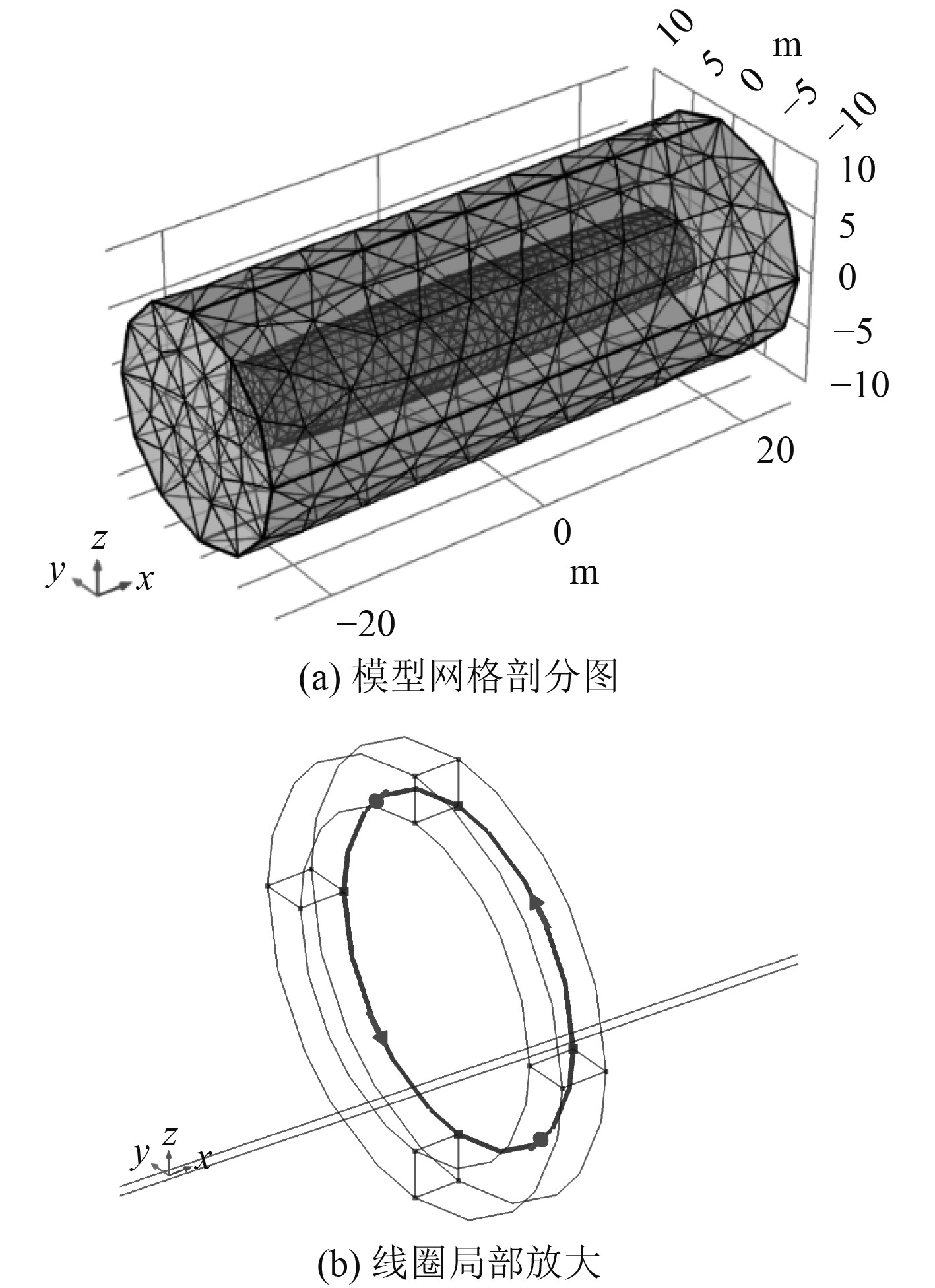
|
图 2 仿真几何体 Fig. 2 Geometry of simulation software |
图2(a)为模型网格剖分图,外部为一圆柱体无限元域,内层为切去两端的椭球壳,最内部为一圆环线圈。线圈方向可调整(线圈如图2(b)),从而产生不同方向的磁矩,x为纵向,y为横向,z为垂向。
仿真参数设置如表1所示。
|
|
表 1 仿真参数设置表 Tab.1 Parameter setting of simulation software |
设置计算带宽1~20 Hz步长1 Hz的频域参数,对有无屏蔽壳下的外界磁场进行仿真计算,取线圈正下方2.6 m的深度平面,横向距离5.1 m、6.1 m、7.1 m、8.1 m的4个测点设置虚拟传感器采集磁场数据进行计算(为了保证结果的正确性,该测点设置与后文实际测量试验保持一致)求得不同频率与不同方向的磁场屏蔽系数结果绘制如图3所示。
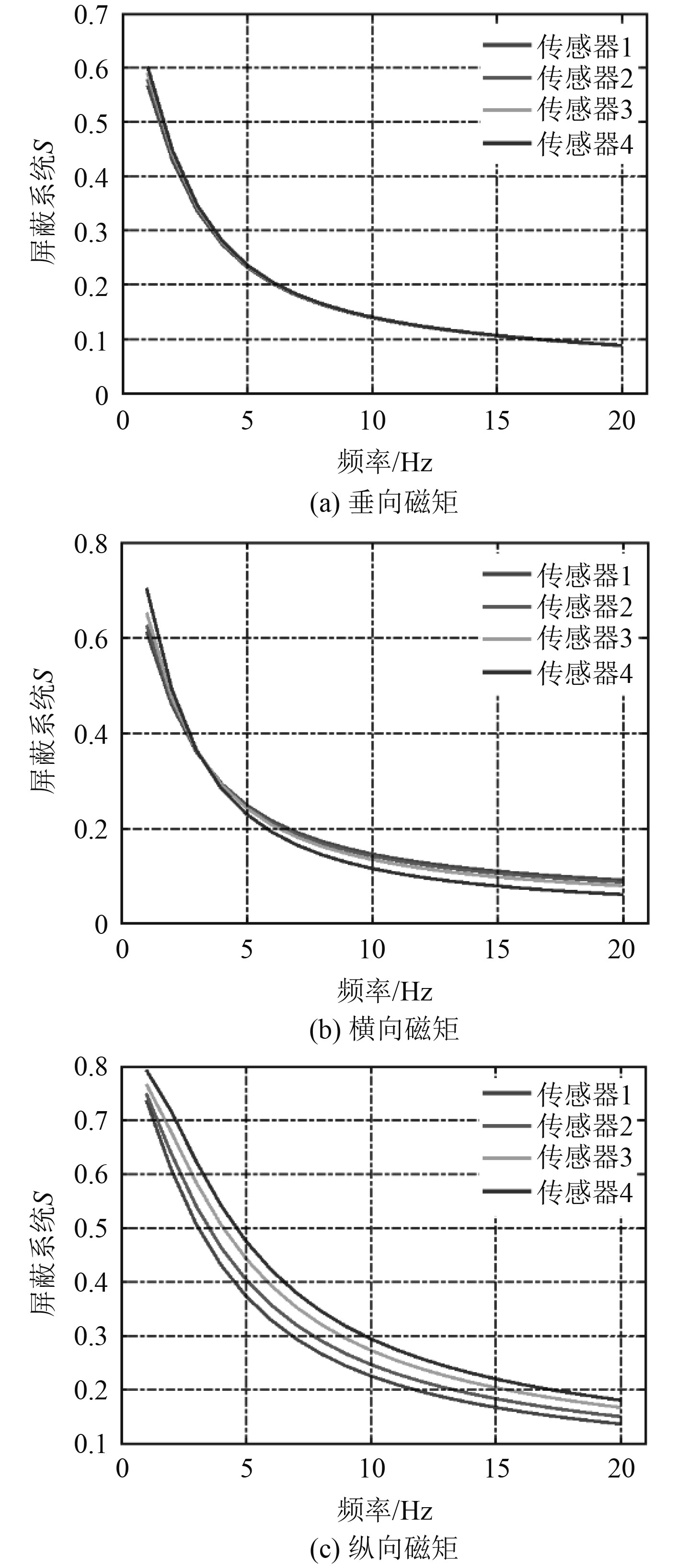
|
图 3 仿真计算的磁场屏蔽系数 Fig. 3 Magnetic field shielding coefficient calculated by simulation |
由图3可知,仿真计算中,对于所设计参数的单层壳体,计算不同方向磁矩的磁场屏蔽系数相差不大,且磁场屏蔽系数随着频率的上升而下降,即频率越高磁场屏蔽越严重;线圈产生垂向与横向磁矩时,随着距离的增加磁场屏蔽系数无明显改变,而线圈产生纵向磁矩时,磁场屏蔽系数随着距离的增大而增大,且纵向磁矩时的磁场屏蔽系数略大于垂向与横向;1 Hz对应的屏蔽系数在0.6~0.8之间,5 Hz对应的屏蔽系数在0.2~0.5之间,10 Hz对应的屏蔽系数为0.2左右。
3 实际测量方法为了验证仿真计算结果,得到舰船壳体磁场屏蔽系数的分布规律。基于仿真模型,在实船的双层壳体中进行磁屏蔽系数的测量试验,试验布置示意图如图4所示。
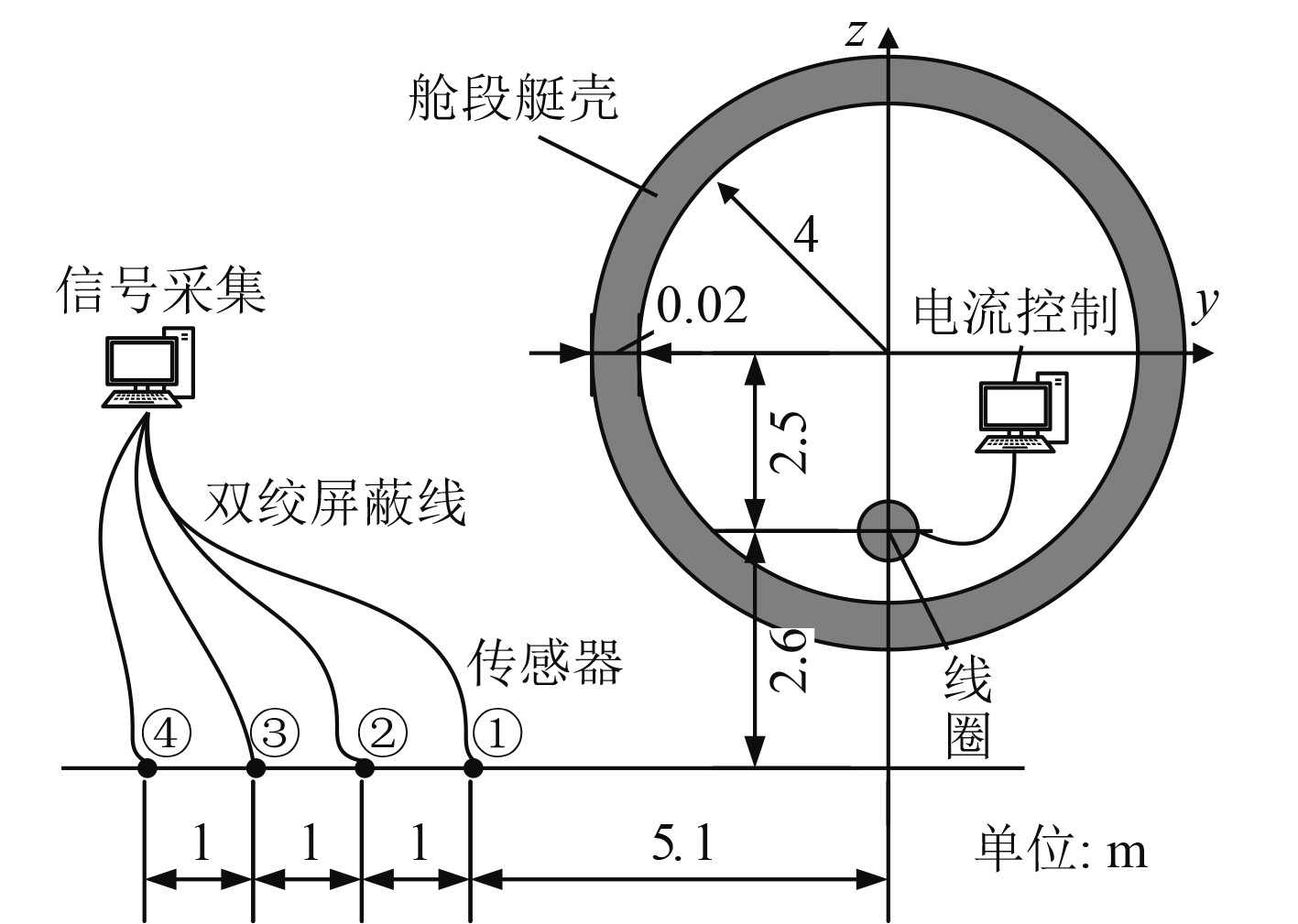
|
图 4 试验布置示意图 Fig. 4 Schematic diagram of test arrangement |
图4中,壳体为实际耐压壳体,其材料为921A,相对磁导率为110。模拟磁源由匝数
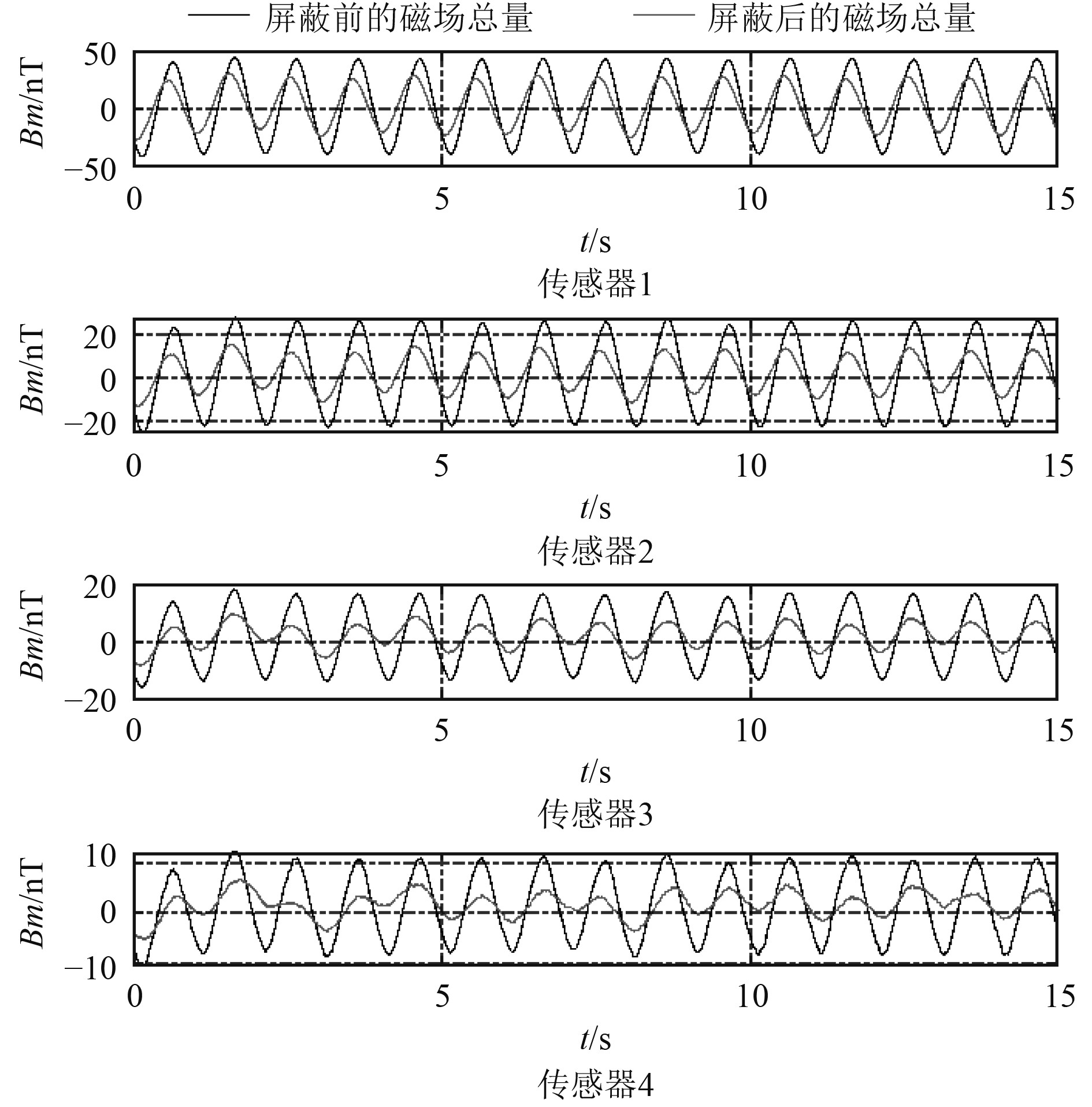
|
图 5 磁场屏蔽前后的磁场总量测量结果 Fig. 5 Total magnetic field measurement results before and after magnetic field shielding |
由于传感器室外摆放不可避免存在旋转偏移,所测各磁场分量存在误差。因此对磁场总量波动峰值进行分析,低频磁场波动的峰值为各分量的磁场幅值再平方求和开根,将所求得磁场屏蔽前后的峰值数据按照磁场屏蔽系数计算公式计算,并绘制各方向磁矩的屏蔽系数随频率变化规律如图6所示。
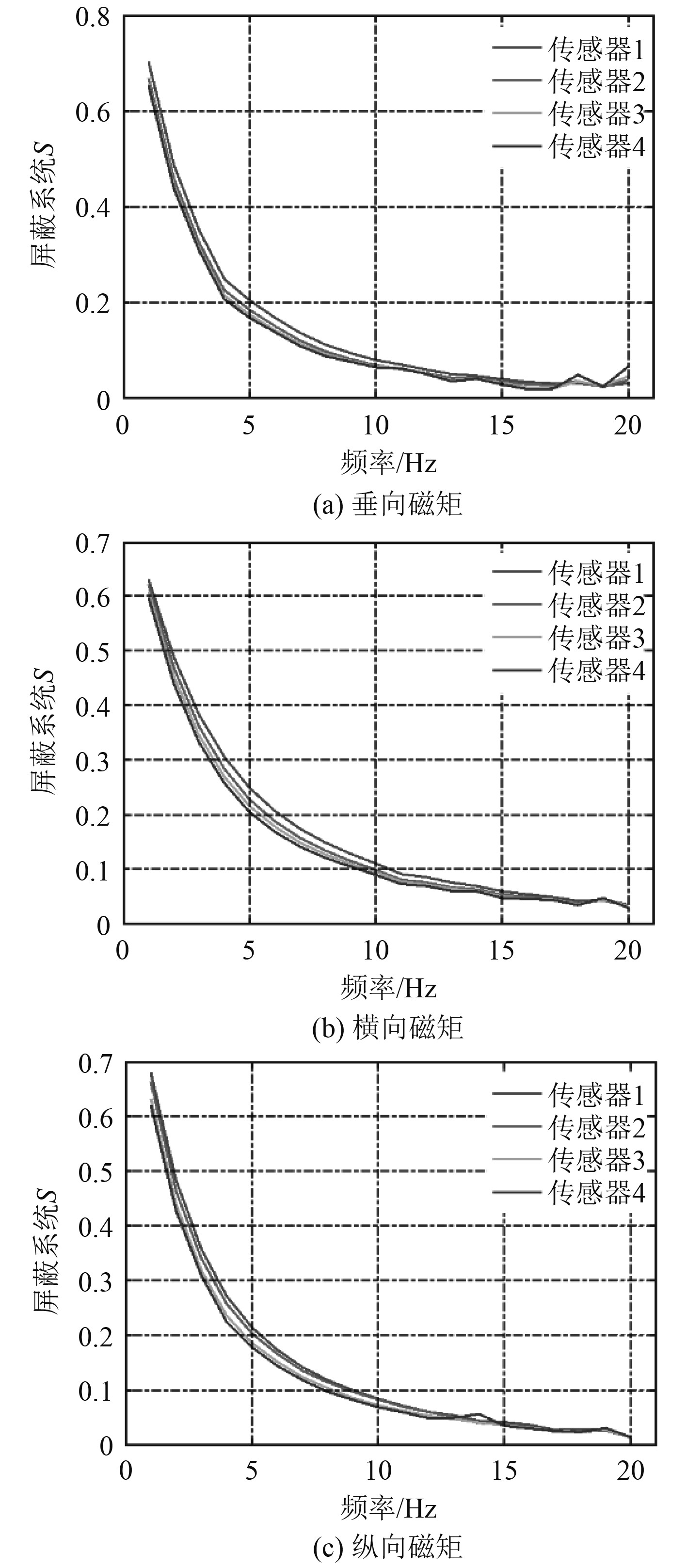
|
图 6 实测的磁场屏蔽系数 Fig. 6 The measured magnetic shielding coefficient |
由图6可知,实际舱段的磁场屏蔽系数测量中,不同方向磁矩的磁场屏蔽系数相差不大,且磁场屏蔽系数随着频率的上升而下降。即频率越高磁场屏蔽越严重,磁场屏蔽系数随着距离的增加略有减小,至15 Hz以上时,由于所测得的磁场量级较小,有局部的波动,但变化趋势不变。1 Hz对应的屏蔽系数在0.6~0.7之间,5 Hz对应的屏蔽系数在0.2~0.3之间,10 Hz对应的屏蔽系数为0.1左右。
4 结 语为实现对磁性源产生的轴频电磁场进行准确建模,本文基于舰船壳体模型对壳体的磁屏蔽系数进行研究,通过理论推导、仿真分析以及试验验证可得到以下结论:
1)根据理论模型仿真计算的磁屏蔽系数随着频率变化的变化规律与试验验证相近,证明了本文所用理论模型以及仿真计算的正确性。对于已知船型的磁场屏蔽系数,可用仿真计算代替测量,降低工程难度。
2)对于同一舰船壳体,磁屏蔽系数随着频率的增加而逐渐减小。
3)1 Hz对应的屏蔽系数在0.6~0.7之间,5 Hz对应的屏蔽系数在0.2~0.3之间,10 Hz对应的屏蔽系数为0.1左右。
下一步将,根据本文得出的磁屏蔽系数变化规律,对磁性源产生的轴频电磁场进行建模。
| [1] |
耿攀, 王向军, 王建勋, 等. 船舶磁防护与电场防护耦合性分析[J]. 数字海洋与水下攻防, 2019, 2(1): 77-80. GENG Pan, WANG Xiang-jun, WANG Jian-xun, et al. Coupling analysis of ship magnetic protection and electric field protection[J]. Digital Ocean and Underwater Attack and Defense, 2019, 2(1): 77-80. |
| [2] |
毛伟, 张宁, 林春生. 在三层介质中运动的时谐水平偶极子产生的电磁场[J]. 电子学报, 2009, 37(9): 2077-2081. MAO Wei, ZHANG Ning, LIN Chun-sheng. Electromagnetic field generated by a time-harmonic horizontal dipole moving in a three-layer medium[J]. Acta Electronica Sinica, 2009, 37(9): 2077-2081. |
| [3] |
张岳, 胡祥云, 韩波. 我国轴频电场研究现状[J]. 地球物理学进展, 2022, 37(3): 1342-1351. ZHANG Yue, HU Xiang-yun, HAN Bo. Research status of axial frequency electric field in China [J]. Progress in Geophysics, 222, 37(3): 1342-1351. |
| [4] |
田永民, 李忠猛. 运动多桨舰船在浅海中的轴频电磁场计算及仿真[J]. 舰船电子工程, 2018, 38(4): 118-121. TIAN Yong-min, LI Zhong-meng. Axial frequency electromagnetic field calculation and simulation of moving multi-propeller ship in shallow sea[J]. Ship Electronic Engineering, 2018, 38(4): 118-121. DOI:10.3969/j.issn.1672-9730.2018.04.030 |
| [5] |
徐震寰, 李予国, 罗鸣. 船舶轴频电磁场信号的海底测量及其特性分析[J]. 哈尔滨工程大学学报, 2018, 39(4): 652-657. XU Zhen-huan, LI Yu-guo, LUO Ming. Seabed measurement and characteristic analysis of ship shaft frequency electromagnetic field signal[J]. Journal of Harbin Engineering University, 2018, 39(4): 652-657. DOI:10.11990/jheu.201612066 |
| [6] |
张立琛, 王英民, 陶林伟. 舰船腐蚀相关轴频电磁场场源建模[J]. 哈尔滨工程大学学报, 2017, 38(10): 1525-1530. ZHANG Li-chen, WANG Ying-min, TAO Lin-wei. Modeling the electromagnetic field source of ship corrosion-related axial frequency[J]. Journal of Harbin Engineering University, 2017, 38(10): 1525-1530. |
| [7] |
张立琛, 王英民, 郭拓. 基于磁偶极子的舰船轴频电磁场场源建模与试验验证[J]. 西北工业大学学报, 2016, 34(5): 829-836. ZHANG Li-chen, WANG Ying-min, GUO Tuo. Modeling and experimental verification of ship axial frequency electromagnetic field source based on magnetic dipole[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 829-836. |
| [8] |
张晚英, 施乐, 张杰峰, 等. 多层圆柱形磁屏体磁屏蔽特性研究[J]. 湖南大学学报(自然科学版), 2017, 44(8): 84-90. ZHANG Wan-ying, SHI Shi, ZHANG Jie-feng, et al. Research on magnetic shielding characteristics of multilayer cylindrical magnetic plate[J]. Journal of Hunan University (Natural Science Edition), 2017, 44(8): 84-90. |
| [9] |
吴逸汀, 盛卫星, 韩玉兵, 等. 金属材料低频磁场屏蔽效能研究[J]. 电波科学学报, 2015, 30(4): 673-678. WU Yi-ting, SHENG Wei-xing, HAN Yu-bing, et al. Research on shielding efficiency of metal materials in low frequency magnetic field[J]. Chinese Journal of Radio Science, 2015, 30(4): 673-678. |
| [10] |
李安金, 赵仁涛. 低频磁场屏蔽问题简述[J]. 科技信息, 2013(3): 211-212+242. LI An-jin, ZHAO Ren-tao. Brief introduction of low frequency magnetic field shielding[J]. Science and Technology Information, 2013(3): 211-212+242. |
 2023, Vol. 45
2023, Vol. 45
