0 引　言

大型船舶在狭水道中的航行问题，成为航行安全领域急需解决的重要问题。狭水道条件指航道较窄、水域较浅的航道环境。大型船舶在开阔的深水域航行时，航行性能良好^[1]。由广阔的水域进入狭水道条件的水域时，大型船舶的航行性能受到影响，研究狭水道条件下的大型船舶操纵安全优化方法极为必要。大型船舶在狭水道条件下航行时，船舶周围流场存在变化，船舶航速与吃水，影响船舶的附加质量与附加惯性矩^[2]。船舶航速过快时，增加船舶的吃水影响操纵性能^[3]；航速过慢时，容易导致舵效降低的情况。对狭水道条件下的大型船舶操纵安全进行优化，是保障大型船舶可靠航行的重要方式。

目前，已经有众多学者针对船舶操纵进行研究。马琳等^[4]利用改进证据推理方法，评价船舶的操纵性能。该方法定义了性能匹配度，利用性能匹配度匹配船舶航行需求与船舶操纵性能，引入证据可靠性，提升船舶操纵性能的评价精度。将操纵性能评价结果，作为提升船舶操纵水平的依据。张艳云等^[5]将支持向量机方法应用于船舶在波浪中的操纵水平提升中，该方法构建了船舶的三自由度操纵运动模型，利用所构建的模型预报船舶运动状态，辨识船舶的航行运动参数，应用于船舶操纵运动控制中。

上述方法虽然可以实现船舶航行时的有效操控，但是并未考虑船舶航行时，狭水道条件等航行环境的影响。针对以上方法在船舶操纵研究中存在的问题，提出狭水道条件下的大型船舶操纵安全优化方法，为船舶和船员的安全提供有效保障。

1 大型船舶操纵安全优化方法 1.1 大型船舶运动结构构建

船舶在海上航行时，用一个六自由度运动模型表示，包括跟随大型船舶的3个移动与3个转动的附体坐标轴。大型船舶的六自由度运动参数分别为前进速度 $ u $ 、横漂速度 $ v $ 、起伏速度 $ w $ 、转首角速度 $ r $ 、横摇角速度 $ p $ 、纵摇角速度 $ q $ 。

构建大型船舶的平面运动结构表达式如下：

$ \left\{ {\begin{array}{*{20}{l}} {X = m\left( {u - v \times r} \right)} ，\\ {Y = m\left( {v - u \times r} \right)} ，\\ {N = I \times r + M \times \left( {v + u \times r} \right)} 。\end{array}} \right. $

(1)

式中： $ X $ 与 $ Y $ 分别表示横向坐标轴与纵向坐标轴， $ N $ 表示重力坐标轴， $ I $ 表示转动惯量， $ M $ 与 $ m $ 分别表示船舶的广义质量矩阵与附加质量矩阵。

大型船舶在实际航行时，受到风浪、航道等外力与环境影响，无法长时间进行理想化的平面运动^[6]。受天气、风浪等环境因素影响时，容易出现航向摆偏情况，甚至可能出现搁浅等危险。

1.2 大型船舶的黑箱模型评价指标构建

船舶航行时，仅考虑其横向运动、纵向运动以及转首运动。构建大型船舶的黑箱模型，所构建的黑箱模型仅需考虑输入与输出，无需考虑大型船舶的内部结构状态。设置大型船舶黑箱模型作为操纵安全优化的动态系统，选取非线性状态空间方程作为黑箱模型结构。狭水条件下的大型船舶的黑箱模型，即大型船舶在狭水道条件下，依据当前时间的状态变量和输入的控制变量，进行期望输出变量的非线性映射^[7]。利用大型船舶运动结构的输出变量，明确在下个时间步长时的状态变量。

大型船舶的黑箱模型状态变量的非线性映射过程表达式为：

$ {X_s} = \frac{{{x_s}\left( t \right) \times u\left( t \right) \times {x_s}\left( {t + 1} \right) \times \lambda }}{{\left( {X,Y,N} \right)}}。$

(2)

式中： $ u\left( t \right) $ 与 $ {x_s}\left( t \right) $ 分别表示大型船舶的输入控制变量与当前状态变量， $ \lambda $ 表示时间步长， $ {x_s}\left( {t + 1} \right) $ 表示大型船舶在下一个时间步长时的状态变量。

选取径向基函数作为非线性映射的核函数，将大型船舶操纵安全优化的黑箱模型输入空间映射至高维特征空间内，求解大型船舶操纵安全优化的非线性问题。径向基核函数的表达式为：

$ K = \gamma \times \left( {{x_i} - {x_j}} \right) \times {X_s}。$

(3)

式中： $ {x_i} $ 与 $ {x_j} $ 分别表示输出、输入的大型船舶操纵状态样本； $ \gamma $ 表示核函数宽度。

构建黑箱模型的目标是无需输入大型船舶的真实运动状态时，即可获取船舶运动与轨迹预测结果。狭水条件下，大型船舶的当前运动状态，由前一个步长的输出变量决定。通过输入控制变量，以及大型船舶状态变量初值，确定狭水道条件下大型船舶的操纵状态。选取决定系数作为黑箱模型的评价指标，该指标的表达式为：

$ R = K \times \frac{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} }} 。$

(4)

式中： $ {\hat y_i} $ 与 $ {y_i} $ 分别表示大型船舶状态样本的预测值以及真值， $ \bar y $ 表示全部状态样本真值的平均值。黑箱模型评价指标的构建考虑船舶在狭水道中的状态变量，只有通过准确捕捉和描述船舶在狭水道中的状态变化，才能建立有效的黑箱模型以评估船舶的性能和操纵安全性。

1.3 大型船舶在狭水道条件下状态变量

大型船舶在狭水道条件下的状态变量是用来描述船舶在狭水道中的动态和状态变化的指标，船舶在静水中运动时，设置舵角信号作为操纵安全优化模型的输入控制变量，将船舶在各自由度上的加速度，设置为模型期望输出变量。狭水道条件下，需要将波浪力、环境信息等参数加入操纵安全优化模型中。不考虑外部影响，仅考虑外力作用下，大型船舶在狭水道条件下，船舶的推进和操纵装置控制力，在黑箱模型内部，自动拟合大型船舶对狭水道条件的动态响应。

船舶由螺旋桨驱动，航行时的环境变化，影响船舶的推进效率，螺旋桨的推力和扭矩容易存在波动。将船舶的螺旋桨推力与螺旋桨扭矩，与船舶舵角同时作为黑箱模型的控制变量，令所构建模型展示船舶在狭水道条件下的内部动力学特性。

设置船舶在狭水道条件下的运动参数，作为黑箱模型的状态变量：

$ x\left( t \right) = R \times \left[ {\alpha \left( t \right),\beta \left( t \right),\chi \left( t \right)} \right] 。$

(5)

式中： $ \alpha \left( t \right) $ 与 $ \beta \left( t \right) $ 分别表示船舶航行时的纵向速度和横向速度， $\ \chi \left( t \right) $ 表示船舶的转首角速度。各自由度运动参数的加速度作为黑箱模型的响应，由此完成狭水道条件下的大型船舶操纵安全优化方法研究。

2 实验分析

为了验证本文方法对狭水道条件下，大型船舶操纵安全的优化性能，选取某型号为A09351的船舶作为测试对象，利用Matlab软件模拟该船的运行状态。该船的水下排水量为7000 t，全长96 m，宽度为10.5 m，吃水9.5 m。测试该船的操纵安全性能时，选取Stokes二阶波作为航行的入射波模型，设置波高为2.2 m，波浪入射角度为145°，20 s为一个波浪周期。风速为8 m/s，均匀风的入射角为85°。

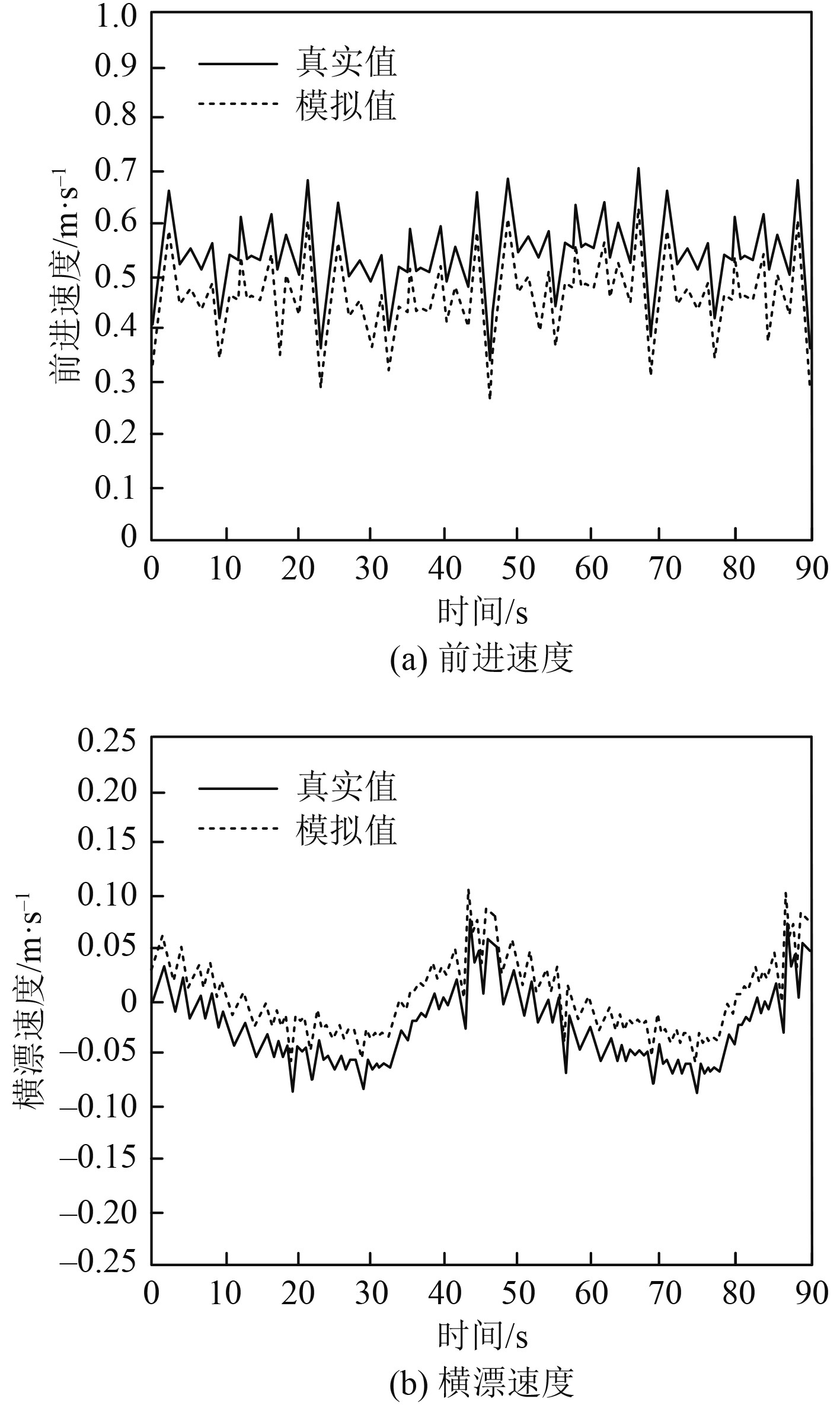
统计采用本文方法构建的运动模型模拟该船舶航行时，前进速度、横漂速度的模拟结果，统计结果如图1所示。

可以看出，采用本文方法对该船的运动状态进行模拟，不同自由度的速度分量，与真实速度值极为接近。结果表明，运动轨迹模拟结果与实际结果十分吻合，所构建的运动模型满足大型船舶的运动特性。

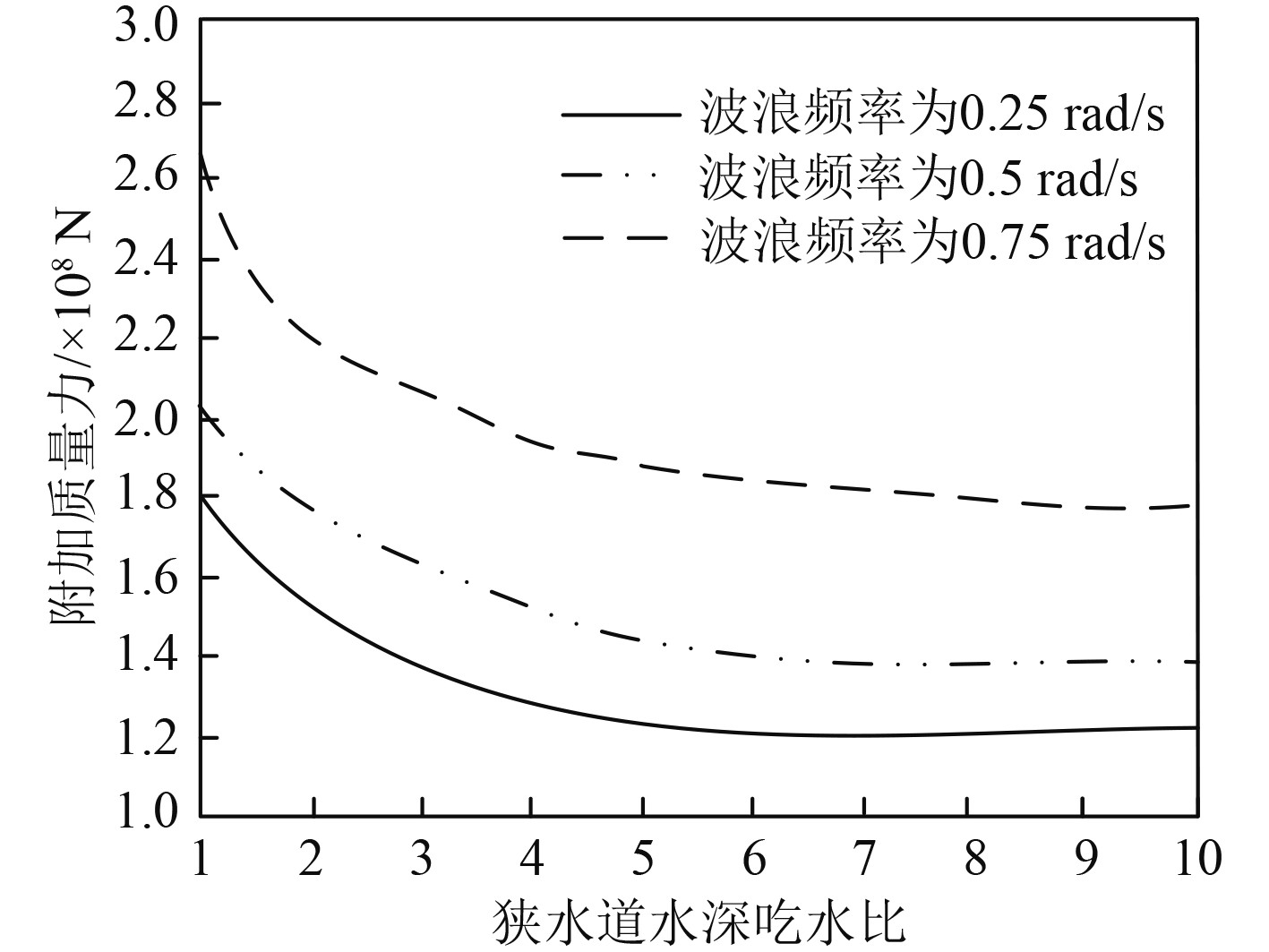
统计不同波浪频率时，狭水道水深吃水比对船舶附加质量力的影响，统计结果如图2所示。

可以看出，大型船舶的附加质量力受波浪频率影响明显。当狭水道的水深吃水比小于5时，船舶的附加质量力即力矩曲线变化幅度较大。狭水道的水深吃水比继续增加时，附加质量力逐渐平缓，此时狭水道水深对附加质量力影响极小。

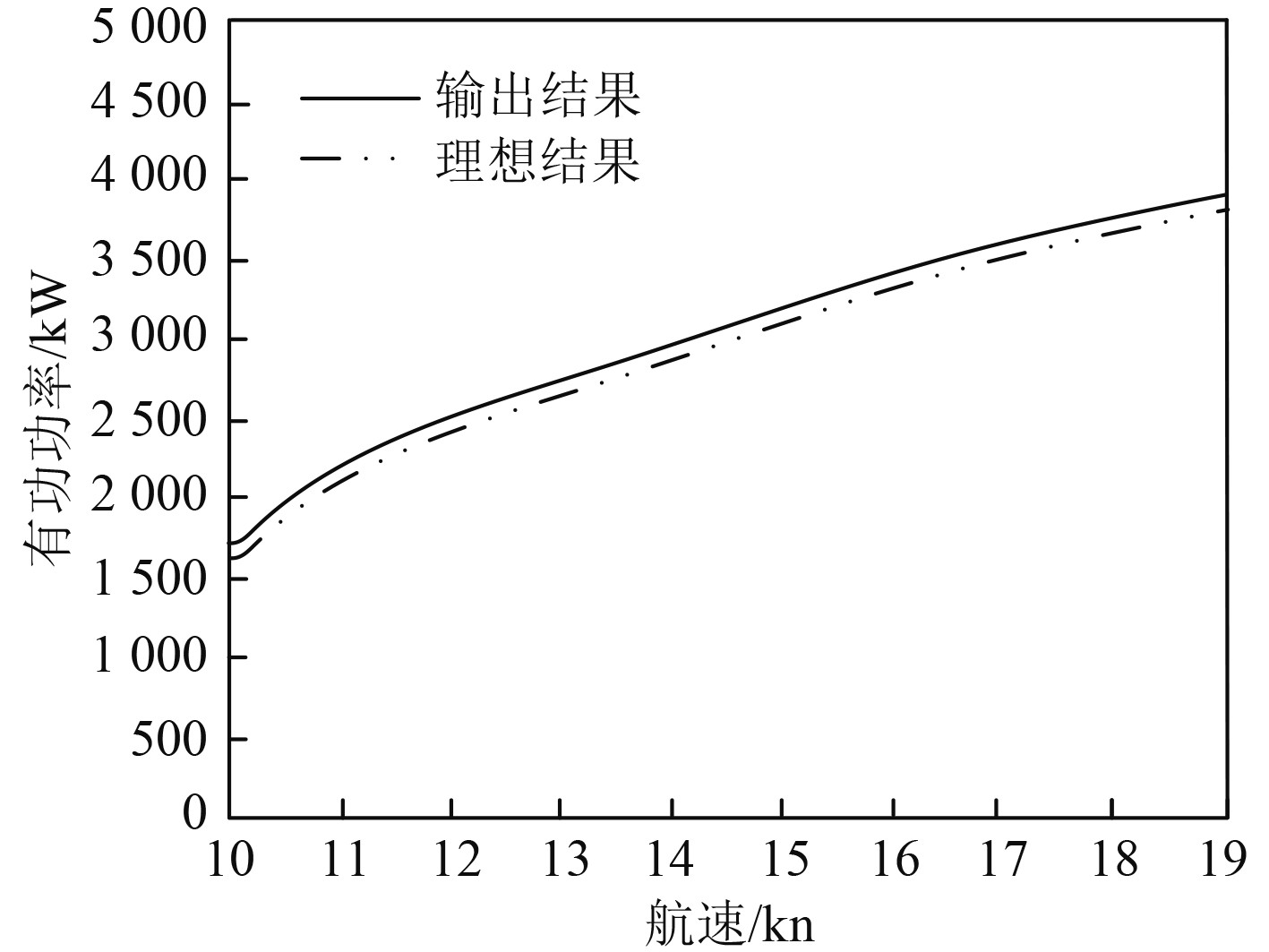
统计狭水道条件下，采用本文方法对大型船舶操纵安全进行优化，船舶主机的输出有功功率与理想有功功率的对比结果，统计结果如图3所示。大型船舶螺旋桨转速与理想转速对比结果如图4所示。

可以看出，采用本文方法对大型船舶操纵安全进行优化，在狭水道条件下，主机输出的有功功率与螺旋桨转速，均与理想数值十分接近，螺旋桨转速低于最大允许转速。实验结果验证采用本文方法后，大型船舶可以保持理想的航行状态，提升了大型船舶在狭水道条件下的航行安全性。本文方法的大型船舶操纵安全优化性能理想，适用于实际应用。

3 结　语

大型船舶引航员和驾驶员在狭水道区域航行时，通过操纵安全优化，避免航行期间出现事故风险。加强对大型船舶操纵安全优化的研究，对于提升船舶航行安全具有重要意义。狭水道条件是复杂的船舶航行条件，研究狭水道条件下的大型船舶操纵安全优化方法，具有较高的必要性。本文方法可以实现大型船舶操纵安全的有效优化，提升船舶航行可靠性。通过运用该方法，可以提高船舶在狭水道环境中的操纵能力和安全性，保证船舶的顺利通行，并减少事故的发生。