燃气轮机与相关噪声处理技术已经引起了学者们越来越多的关注[1]。声衬作为航空涡扇发动机降噪不可或缺部件,是抑制风扇噪声最有效的方法之一[2-3]。声衬作为一种流行被动阻尼装置,在控制燃气轮机热声不稳定性方面起到至关重要的作用[4-5]。因此,声衬设计必须能够在较宽频率范围内,抑制风扇噪声和热声产生的多余噪声。
在过去几十年里,为深入了解声衬吸声机理并改善其性能,学者们进行了大量数值模拟、理论计算和实验研究[6-9]。
本文使用声传输损失表征声衬吸声性能,描述入射声波被吸收部分,对由多个狭缝谐振器组成的声衬在切向流作用下的噪声衰减性能进行数值模拟,模拟包括单层和双层结构中的10种狭缝声衬。利用COMSOL软件求解频域线性Navier-Stokes方程,用传输损失等具体分析不同孔隙率声衬吸声特性。
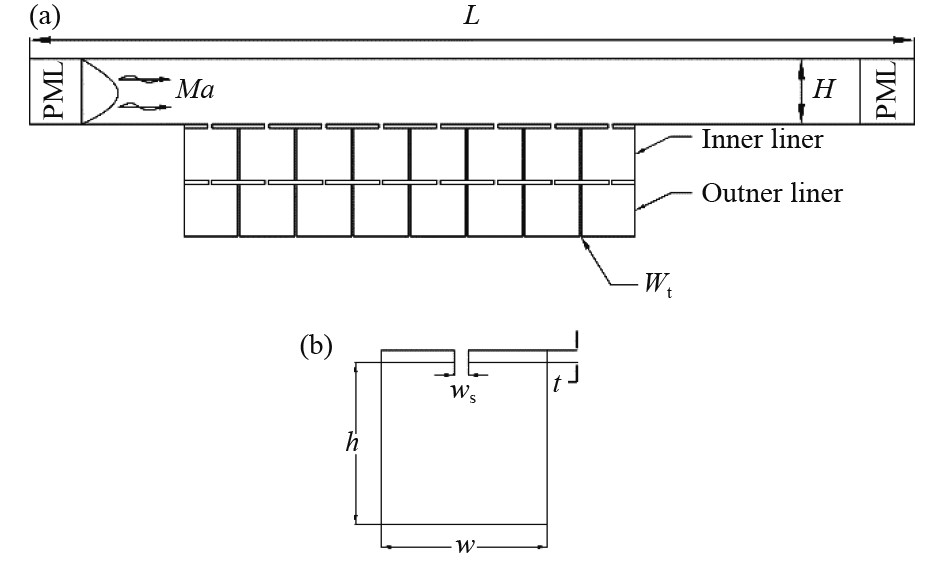
1 数值模型描述 1.1 双层声衬几何模型数值模型的整个计算域如图1所示。双层声衬安装在矩形管道下壁,其内衬和外衬均由8个几何参数相同的狭缝赫姆霍兹谐振器组成,相邻2个谐振器之间的厚度为Wt= 1.3 mm。图1(b)为1个狭缝赫姆霍兹谐振器的结构示意图,其中,h为共振腔高度,w为共振腔宽度,
|
图 1 双层声衬的几何模型 Fig. 1 Geometric model of double-layer acoustic liner |
|
|
表 1 双层声衬的结构参数 Tab.1 Structural parameters of the double-layer of acoustic liner |
本文建立的是二维模型,使用雷诺平均Navier-Stokes方程作为系统控制方程。
质量守恒控制方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {\boldsymbol{u}}} \right) = 0。$ | (1) |
动量守恒控制方程:
| $ \rho \frac{{\partial {\boldsymbol{u}}}}{{\partial t}} + \rho \left( {{\boldsymbol{u}} \cdot \nabla } \right){\boldsymbol{u}} = \nabla \cdot \sum + \rho {\boldsymbol{f}} 。$ | (2) |
| $ \sum = - p\delta - \frac{2}{3}\mu \delta {{s}} + 2\mu {{s}}。$ | (3) |
式中:µ表示速度,m/s;
能量守恒控制方程:
| $ \rho \frac{{\partial e}}{{\partial t}} + \rho \left( {{\boldsymbol{u}} \cdot \nabla } \right)e = - p\nabla \cdot {\boldsymbol{u}} + \nabla \cdot \left( {k\nabla T} \right) + \varPhi,$ | (4) |
| $ \mathop \varPhi \nolimits_{} \mathop { = - \frac{2}{3}\mu }\nolimits_{} \mathop {\left( {\frac{{\partial \mathop u\nolimits_k }}{{\partial \mathop x\nolimits_k }}} \right)}\nolimits^2 \mathop { + \frac{\mu }{2}}\nolimits_{} \mathop {\left( {\frac{{\partial \mathop u\nolimits_i }}{{\partial \mathop x\nolimits_j }} + \frac{{\partial \mathop u\nolimits_j }}{{\partial \mathop x\nolimits_i }}} \right)}\nolimits^2。$ | (5) |
式中:
为了封闭方程组还需要给出压强和内能的热力学方程:
| $ p = p(\rho ,T),e = e(\rho ,T) 。$ | (6) |
为了简化模型,计算流体力学选择COMSOL软件中的SST湍流模型,之后使用线性Navier-Stokes频域声场(LNS)模型确定本模型的声学特性。频域计算范围设为
|
|
表 2 测试工况 Tab.2 Test conditions |
| $ \mathop {TL = 10\lg }\nolimits_{} \left( {{{\mathop w\nolimits_{\text{i}} } \mathord{\left/ {\vphantom {{\mathop w\nolimits_{\text{i}} } {\mathop w\nolimits_t }}} \right. } {\mathop w\nolimits_t }}} \right)\mathop { = 20\lg }\nolimits_{} \left| {{{\mathop p\nolimits_i } \mathord{\left/ {\vphantom {{\mathop p\nolimits_i } {\mathop p\nolimits_t }}} \right. } {\mathop p\nolimits_t }}} \right|。$ | (7) |
式中:
为证明双层声衬模型的可行性,数值研究当Ma=0.3、

|
图 2 数值结果与文献实验结果的比较 Fig. 2 Comparison of numerical results and experimental results in literature |
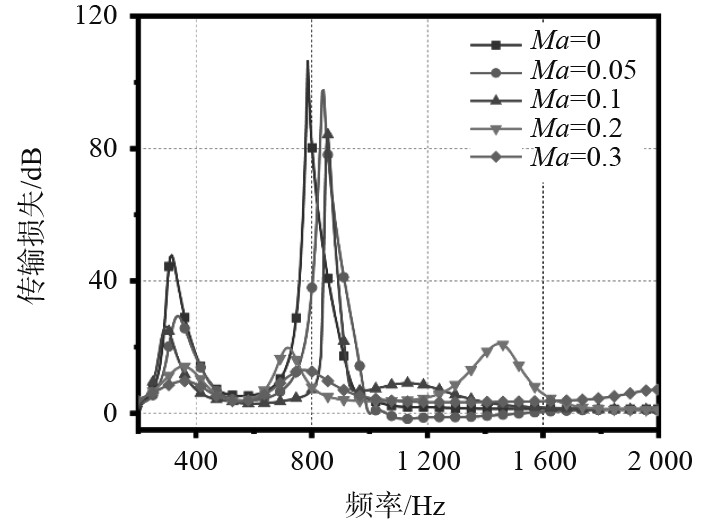
图3为双层声衬f-A在切向流作用下,产生的传输损失随频率的变化。可知,当马赫数
|
图 3 声衬f-A在各流速下产生的传输损失随频率的变化 Fig. 3 Variation of transmission loss of acoustic liner f-A with frequency at various flow rates |
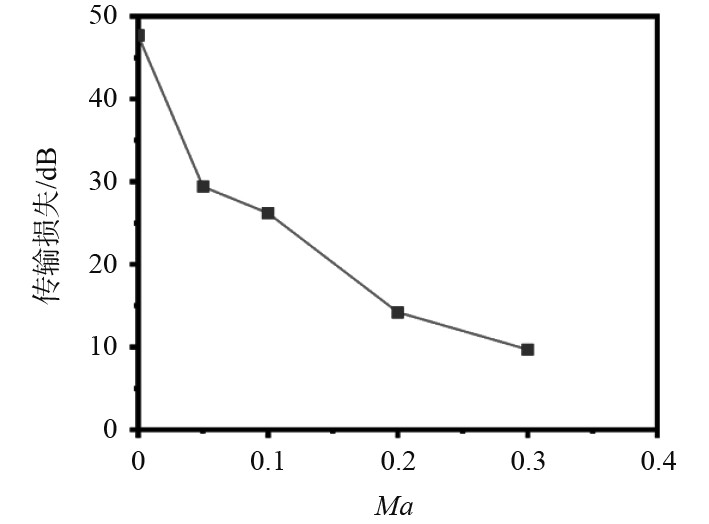
|
图 4
当
|
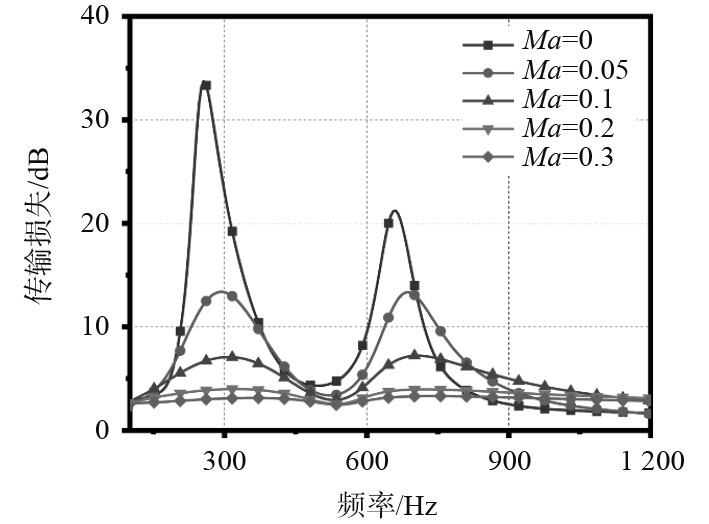
首先选择孔隙率较小的声衬a-A作为研究对象,选择5种切向流速对a-A的噪声衰减行为进行模拟研究。图5为声衬a-A产生的传输损失在整个测试频带上的变化。可知,在各流速下,a-A均产生了2个传输损失峰值,且随着流速的增加,峰值略向高频漂移,但吸声性能逐渐降低,这也与上述声衬f-A的变化基本相同。但与f-A相比产生的局部最大传输损失较小,这可能是因较小孔隙率造成的。
|
图 5 声衬a-A在各流速下产生的传输损失随频率的变化 Fig. 5 Variation of transmission loss with frequency generated by acoustic lining a-A at each flow rate |
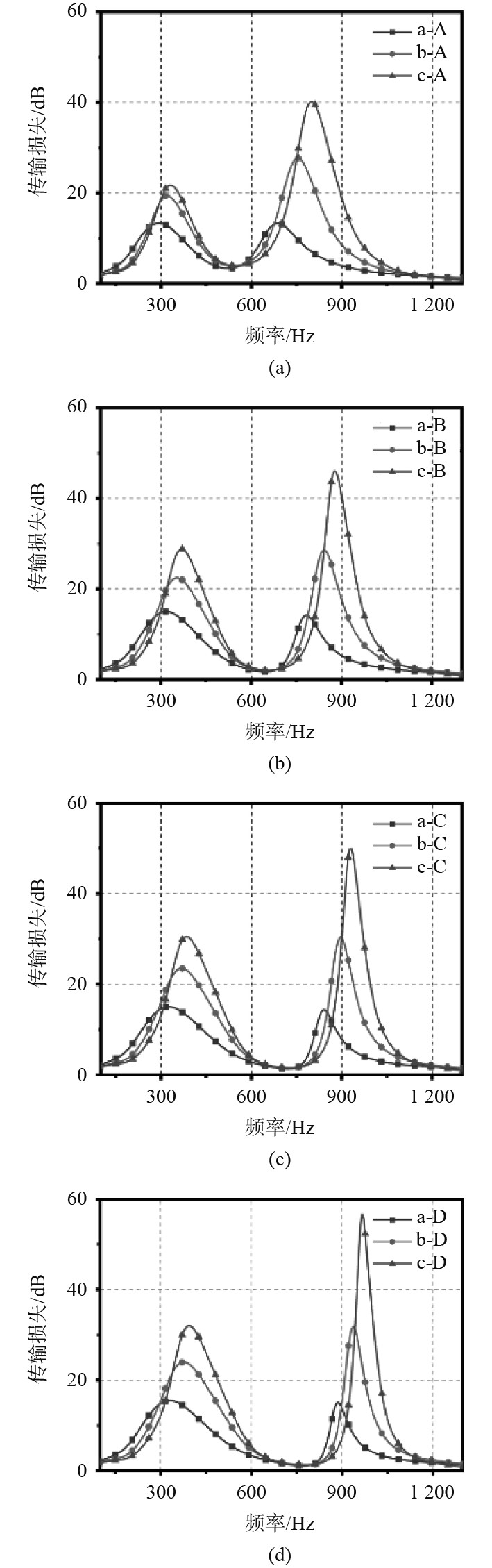
为了更深入研究孔隙率的影响,进一步增大声衬孔隙率。图6总结比较了当马赫数Ma=0.05时,3种内衬与4种外衬组合的声衬吸声性能。如图6(a)所示,当外衬孔隙率
|
图 6 当Ma=0.05时,声衬吸声性能的比较 Fig. 6 Comparison of sound absorption performance of acoustic liner when Ma=0.05 |
当内衬孔隙率

|
图 7 当Ma=0.1时,声衬吸能性能的比较 Fig. 7 Comparison of sound absorption performance of acoustic liner when Ma=0.1 |
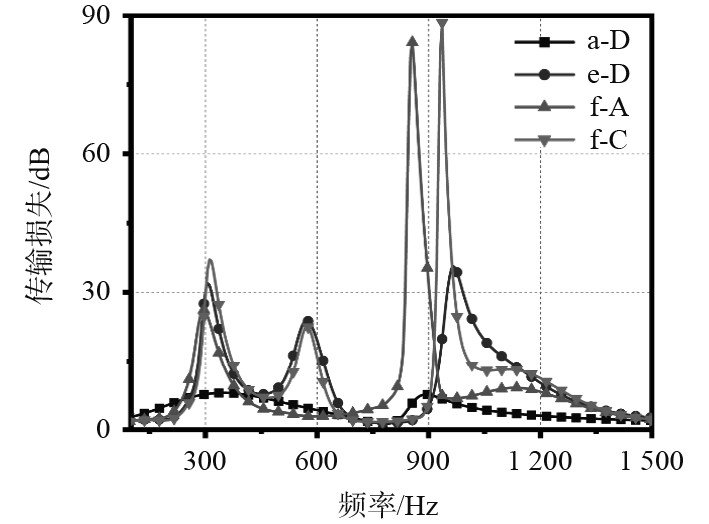
了解2个孔隙率哪个对双层声衬吸声性能的影响较大是很有必要的。因此,比较当Ma=0.1时,4种双层声衬的吸声性能,如图8所示。可知,当内衬孔隙率
|
图 8 当Ma=0.1时,4种声衬吸声性能的比较 Fig. 8 Comparison of sound absorption performance of four acoustic liners when Ma=0.1 |
赵鹏瑜等[12]研究分析了切向流作用下,孔隙率对单层声衬吸声性能的影响,发现孔隙率较大的单层声衬具有更好的吸声效果,因此这里选取孔隙率为3.85%的单层声衬,即声衬c,与双层声衬c-C吸声性能进行比较。当Ma=0、Ma=0.05和Ma=0.1时,单、双层声衬产生的传输损失如图9所示。结果表明,双层声衬在3个切向流速下均产生了2个传输损失峰,但是2个尖峰之间存在吸声低谷,传输损失很小,如图9(a)中的550~800 Hz。这是由于双层声衬的反共振现象[11]引起的。单层声衬在3个切向流速下仅产生了一个传输损失峰,但正好对应双层声衬的吸声低谷,如图9(b)中的550~850 Hz,在此频段中,单层声衬的吸声性能更佳。

|
图 9 单层和双层声衬在切向流作用下吸声性能的比较 Fig. 9 Comparison of the sound absorption performance of the single and double-layer of acoustic liner under the effect of grazing flow |
图10为当Ma=0.2以及Ma=0.3时,单、双层声衬吸声性能的比较。由图可知,单层声衬在2个高流速情况下产生了2个传输损失峰,双层声衬产生了3个传输损失峰。然而,值得关注的是,在300~1 000 Hz之间,虽然双层声衬产生了2个吸声尖峰,但存在一个吸声低谷,反观单层声衬在此频率范围内虽然只有一个传输损失峰,但产生的最大传输损失与双层差别不大,甚至在此频率范围内吸声效果更好。综合图9~图10来看,双层声衬在较宽的频率范围内吸声性能要好得多。因此,根据频率范围的不同,它比单层声衬具有更大消声潜力。

|
图 10 当Ma=0.2以及Ma=0.3时,单层和双层声衬在切向流作用下吸声性能的比较 Fig. 10 Comparison of the sound absorption performance of the single and double-layer of acoustic liner under the effect of grazing flow,as Ma=0.2 and Ma=0.3 |
对内衬和外衬分布在管道两侧的对称声衬进行数值模拟研究。
对称声衬的几何结构如图11所示,结构参数和上文相同。主管道两侧谐振器的孔隙率相同,研究一种较小孔隙率

|
图 11 对称声衬几何结构 Fig. 11 Geometry of the symmetrical acoustic liner |
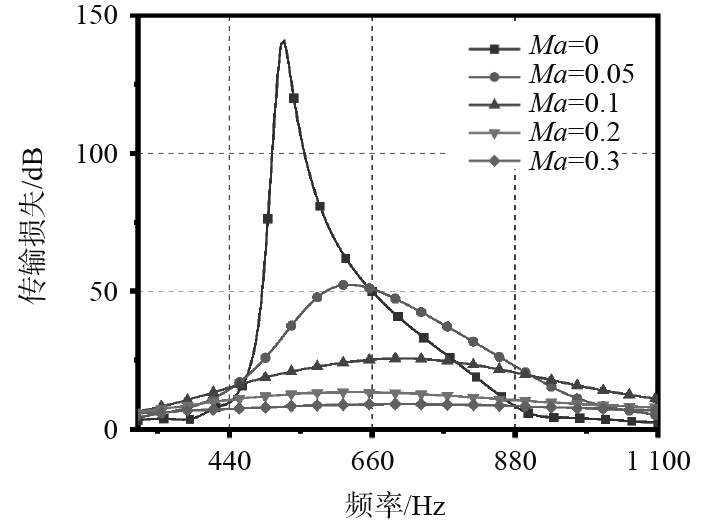
图12给出了主管道两侧孔隙率
|
图 12
当
|
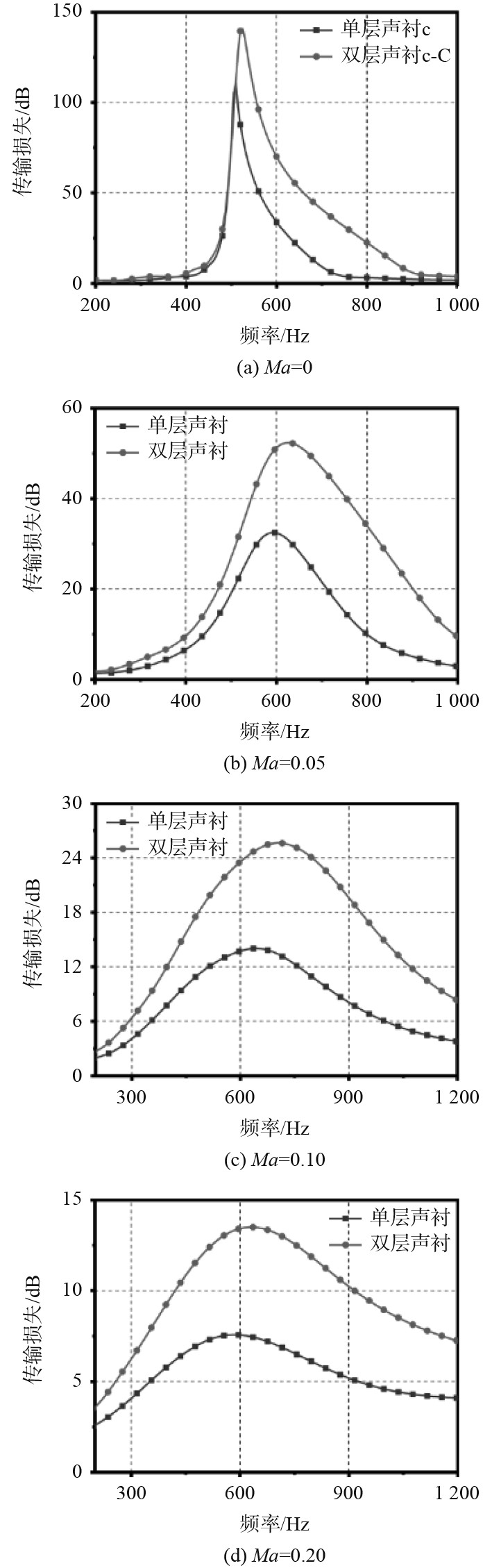
图13给出了管道两侧孔隙率均为2.57%的对称声衬与相同孔隙率单层声衬,在各切向流速下产生的传输损失的比较。结果表明,在无流情况下,即Ma=0时,对称声衬产生的局部最大传输损失最高达到140 dB,比相同孔隙率的单层声衬高了28 dB,且对应的共振频率也比单层声衬高另一方面,对称声衬的有效吸声频带更宽,如图13(a)所示,在400~900 Hz之间,对称声衬吸声能力几乎均比单层声衬要高。随着切向流速的增加,对称声衬表现的吸声能力比单层声衬更强的特点越来越明显,如图13(b)~图13(d)所示。
|
图 13 对称声衬与单层声衬在各切向流速下产生的传输损失的比较 Fig. 13 Comparison of transmission losses generated by symmetric and single-layer of acoustic liner at various grazing flow rates |
综合来看,对称声衬所表现的吸声能力是比单层声衬更强。
3 结 语本文主要对比分析了单层和双层结构的10种声衬模型在不同切向流作用下的吸声性能,以传输损失评估了不同孔隙率对声衬吸声特性的影响。从数值模拟结果发现的结论如下:
1)切向流对声衬噪声衰减行为起到举足轻重的作用。切向流速的增加会大幅降低声衬吸声性能,但会使声衬产生的共振频率向高频漂移,其表现为声衬在高频具有更佳的吸声能力。
2)当内衬孔隙率较小,外衬孔隙率较大时,声衬在低切向流速Ma=0.05时,均会产生2个传输损失尖峰;相反,当内衬孔隙率较大,外衬孔隙率较小时,且在高切向流速Ma=0.2的情况下,声衬会产生多个尖峰;但对于两种孔隙率均较大的声衬,在低切向流速Ma=0.1时,声衬就会产生多个尖峰。总之,在切向流的作用下,2种孔隙率对声衬性能的影响不相上下,随着两种孔隙率的增加,声衬的吸声性能也显著增强。
3)对于孔隙率较大的单双声衬,双层声衬在较宽的频率范围内吸声性能要好得多,它比单层声衬具有更大的消声潜力。
4) 对于孔隙率较小的对称声衬,其吸声性能类似于单层声衬。与孔隙率相同的单层声衬相比,发现在各切向流速下,对称声衬均表现出更高的吸声性能,且有效吸声频带更宽,共振频率更高。
综合来看,在切向流作用下,双层声衬和对称声衬所表现的吸声能力是比单层声衬更强。但是,对于双层声衬和对称声衬,需要更多的安装空间,因此,需进行不断的优化设计,以满足实际工业需要。
| [1] |
MA X Q, SU Z T. Development of acoustic liner in aero engine: A review[J]. Science China Technological Sciences, 2020, 63(12): 2491-2504. |
| [2] |
CHEN C, LI X D, YIN L. Numerical and experimental investigations on the flow drag of a multi-slit acoustic liner[C]//25th AIAA/CEAS Aeroacoustics Conference, Delft, Netherlands, 2019−2660.
|
| [3] |
ZHAO D, LI X Y. A review of acoustic dampers applied to combustion chambers in aerospace industry[J]. Progress in Aerospace Sciences, 2015, 74: 114-130. DOI:10.1016/j.paerosci.2014.12.003 |
| [4] |
LIANG L X, ZHANG G Y, WANG G Q. Effects of acoustic liner on thermoacoustic instabilities in a premixed swirl combustor[J]. Aerospace Science and Technology, 2021, 118.
|
| [5] |
ASHUTOSH T, JHA N K, HOTA R N. A generalized compliance model for study of acoustic damping behavior of mixed porosity segmented perforated liner[J]. Applied Acoustics, 2021, 183.
|
| [6] |
KOOIJMAN G, HIRSCHBERG A, GOLLIARD J. Acoustical response of orifices under grazing flow: effect of boundary layer profile and edge geometry[J]. Journal of Sound and Vibration, 2008, 315(4): 849-874. |
| [7] |
LAWN C. The acoustic impedance of perforated plates under various flow conditions relating to combustion chamber liners[J]. Applied Acoustics, 2016, 106(1): 144-154. |
| [8] |
DAI X, JING X, SUN X. Acoustic-excited vortex shedding and acoustic nonlinearity at a rectangular slit with bias flow[J]. Journal of Sound and Vibration, 2014, 333(13): 2713-2727. DOI:10.1016/j.jsv.2014.02.029 |
| [9] |
ZHAO D, JI C, LI J W, et al. Experimental comparison of noise dissipation effects of single-and double-layer acoustic liners[J]. Applied Acoustics, 2018, 141: 281-292. DOI:10.1016/j.apacoust.2018.07.024 |
| [10] |
TAM C K, PASTOUCHENKO N N, JONES M G, et al. Experimental validation of numerical simulations for an acoustic liner in grazing flow: Self-noise and added drag[J]. Journal of Sound and Vibration, 2014, 333(13): 2831-2854. DOI:10.1016/j.jsv.2014.02.019 |
| [11] |
杨嘉丰, 薛东文, 李卓瀚, 等. 切向流条件下短舱单/双自由度声衬实验研究[J]. 航空学报, 2020, 41(11): 337-347. DOI:10.7527/S1000-6893.2020.23860 |
| [12] |
赵鹏瑜, 杨兴林, 马恒, 等. 切向流作用下单层声衬噪声阻尼性能的数值研究[J]. 噪声与振动控制, 2022, 42(3): 229-236. DOI:10.3969/j.issn.1006-1355.2022.03.041 |
 2023, Vol. 45
2023, Vol. 45
