2. 亚普汽车部件股份有限公司, 江苏 扬州 225009
2. Yapu Auto Parts Co., Ltd., Yangzhou 225009, China
对船首构型研究发现,不同首部构型对船舶在平整冰下的破冰能力有着重要影响[1]。相关人员并没有对船舶在冰区运行的过程之中首部结构的碎冰阻力所造成的影响进行细致研究,而对于不同类型参数的改变对整体船身所遭受到的碎冰阻力的改变规律也没有细致探究。船舶的首部构型对于破冰能力以及效率有着较为重要的作用,所以可合理对船舶的首部结构进行调整来使船舶的破冰能力得以提升。
Luo等[2]结合CFD-DEM对某一冰区散货船在冰槽中和碎冰的相互影响进行研究,冰粒的实际形状用各向同性的四面体以及不太规则的多面体表示,为碎冰中的船舶行驶提供一定参考。童波等[3]利用数值方法建立碎冰模型,并结合遗传算法对浮冰MCD、密集度以及冰厚和速度对实际浮冰阻力所造成影响的规律进行了细致探究。Sun等[4]经过对船与浮冰的撞击所形成的冲击载荷的改变进行模拟,最终得到了科学的校准办法及触觉数控处理技术。
本文研究对象为“雪龙”号破冰船,利用Voronoi原理对不同规则分布的三维碎冰进行建立模型。同时利用Ls-dyna船舶在冰区航行中的船首参数对碎冰能力的影响规律进行分析,对船体的首柱倾角、外倾角和水线进角这3个参数进行改变来实现模拟工作。从而更好地对碎冰条件下,不同类型的参数对船体所受到的冰阻力影响进行详细探究。
1 ALE算法目前,众多学者运用Ansys/Ls-dyna对结构物与海冰的碰撞进行数值计算。基于Ls-dyna进行分析时,通常采用ALE算法。在ALE描述下,引入拉格朗日和欧拉坐标,任意物理量f可表示为:
| $ \frac{{\partial f\left( {{X_i},t} \right)}}{{\partial t}} = \frac{{\partial f\left( {{x_i},t} \right)}}{{\partial t}} + {{\Delta }}{v_{\text{i}}}\frac{{\partial f\left( {{x_i},t} \right)}}{{\partial t}},\quad {{\Delta }}{v_i} = {u_i} - {w_i} 。$ | (1) |
式中:
| $ \left( {\frac{{\partial \rho }}{{\partial t}} + \Delta {v_i}\frac{{\partial \rho }}{{\partial {x_i}}}} \right) + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0 。$ | (2) |
参照牛顿第二定律详细探究流体微元的实际运动状况,从而得到实际的流体单元方程:
| $ {\tau _{ij}} = - p{\delta _{ij}} + \mu \left(\frac{{\partial {u_i}}}{{{x_j}}} + \frac{{\partial {u_j}}}{{{x_i}}}\right) 。$ | (3) |
式中:
结合流体单元的惯性力、质量力、压力以及粘性力相平衡能够得到:
| $ {g_i} - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_j}}} + \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}} = \frac{{\partial {u_i}}}{{\partial t}} + \Delta {v_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} 。$ | (4) |
把式(3)中的应力张量
| $ {g_i} - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_j}}} + \mu \frac{{{\partial ^2}{\sigma _i}}}{{\partial {x_i}\partial {x_j}}} = \frac{{\partial {u_i}}}{{\partial t}} + \Delta {v_j}\frac{{\partial {u_i}}}{{\partial {x_j}}}。$ | (5) |
为了让船-水-冰流固耦合及对于碰撞现象所导致的严重变形问题得以妥善解决,利用ALE算法来科学约束结构域以及实际的流体域。将船及冰定义成拉格朗日实体,而海水和空气为欧拉实体。结合罚函数来对流固耦合效应进行科学约束[5]。
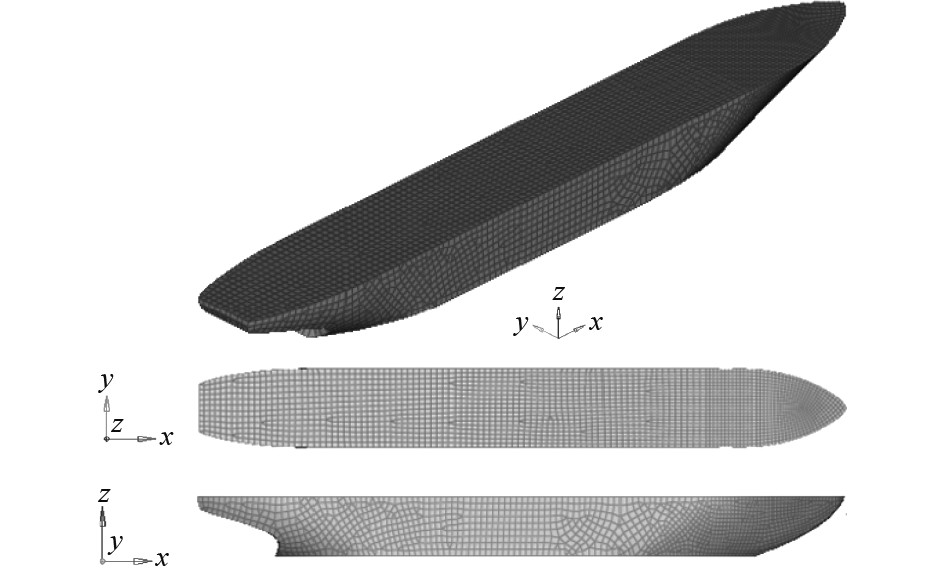
2 计算模型及参数设置 2.1 破冰船有限元模型的建立本文主要研究“雪龙”号破冰船,对其在碎冰环境条件下船体所遭受到的冰阻力进行细致探究。表1为破冰船的尺度参数。船的首部位置网格为0.5 m,有8782个网格。而船的尾部位置以及中间位置的网格为1 m,有10298个网格。图1为船体实际的有限元模型。
|
|
表 1 船舶主尺度 Tab.1 Ship's main scale |
|
图 1 破冰船壳有限元模型 Fig. 1 Finite element model of ice breaker hull |
冰体材料本构模型采用各向同性弹性断裂失效模型[6]。冰体材料模型参数如表2所示。
|
|
表 2 冰体材料参数 Tab.2 The material parameters of ice |
利用GRUNISEN状态方程来对海水材料相关性质进行细致描述,可得到实际的状态方程:
| $ \begin{split} p = & {\rho _0}c\mu \frac{{\left[ {1 + \left( {1 - \dfrac{{{\gamma _0}}}{2}} \right)\mu - \dfrac{h}{2}{\mu ^2}} \right]}}{{{{\left[ {1 - \left( {{S_1} - 1} \right)\mu - {S_2}\dfrac{{{\mu ^2}}}{{\mu + 1}} - {S_3}\dfrac{{{\mu ^3}}}{{{{(\mu + 1)}^2}}}} \right]}^2}}} +\\ & ({\gamma _0} + b\mu )E。\end{split} $ | (6) |
式中:
Voronoi图定义如下:
设定平面P之中包含n个不一样的离散点,此时将p称之为生成元。
| $ \begin{split} & P=\left\{{p}_{1},{p}_{2},\mathrm{...}{p}_{n}\right\},(2\leqslant n < \infty )\text{,}{p}_{i}\ne {p}_{j}\text{,}\\ & i\ne j(i\text{,}j\in {I}_{n}=\left\{1\text{,}\mathrm{...}\text{,}n\right\}) 。\end{split} $ | (7) |
假设凸多边形
| $ V({p_i}) = \left\{ {p\left| {d(p - {p_i}) \leqslant d(p - {p_j}),i \ne j,i,j \in {I_n}} \right.} \right\} 。$ | (8) |
式中:
| $ V(P) = { \cup _{{p_i} \in P}}V(pi) 。$ | (9) |
依据航拍状况,对相关数据进行分析,结合MCD原理来建立碎冰的实际等效直径、具体厚度以及密集度模型[7-8]。生成二维碎冰模型浮冰区域的实际长度以及宽度分别为345 m×112 m。Voronoi结构的缩放因子在1.3的情况下,所得模型的浮冰数量是323,密集度为50%。流程图包含碎冰区域的长度与宽度、实际的碎冰数量、厚度的初始值、厚度的最终值以及缩放因子这6个因素共同组成。第一步,先得到二维碎冰域。
在对碎冰的特性进行综合考虑之后,利用二维模型得到三维模型,并对碎冰的厚度分布区域进行设置,同时将区域之中的随机厚度作用到碎冰域的每块海冰上。结合平均值求解器和可视化的程序来进一步优化厚度。
图2为利用该流程图所建立的三维碎冰模型。

|
图 2 三维碎冰模型及局部放大图 Fig. 2 Three-dimensional broken ice model and partial enlarged view |
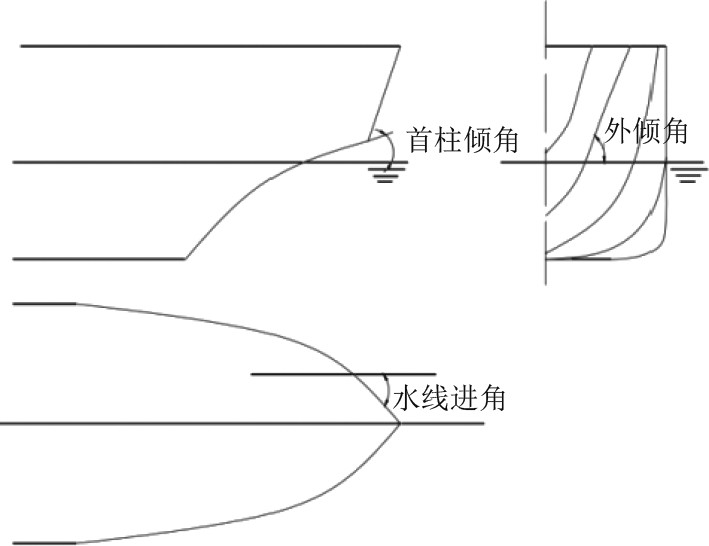
正常情况下的破冰船首部结构都是倾斜的,从而在运行过程之中能够爬上冰层,同时在破冰阶段对冰层形成垂直向下的压力,进一步使冰块出现弯曲断裂现象。图3为首部整体的角度图[9]。在所有的参数之中,首柱倾角对海冰的破坏模式产生重要影响。外倾角以及水线角会对船体以及冰的碰撞之中,船肩位置的排冰以及下浸效能造成重要作用[10]。
|
图 3 极地破冰船首部形状 Fig. 3 The shape of the polar icebreaker head |
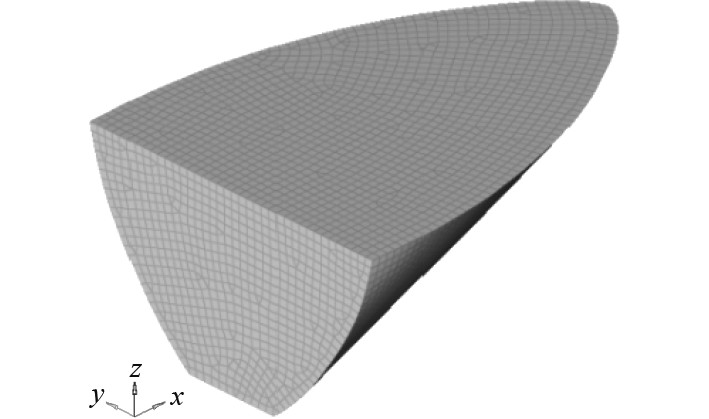
在整体的数值模拟之中,只对船首以及船肩位置进行计算。船首整体长度为30 m,利用壳单元来对网格进行划分,网格为0.3 m,约为6415个。图4为船首的数值有限元模型。
|
图 4 “雪龙”号破冰船首部有限元模型 Fig. 4 Finite element model of the first part of Xuelong icebreaker |
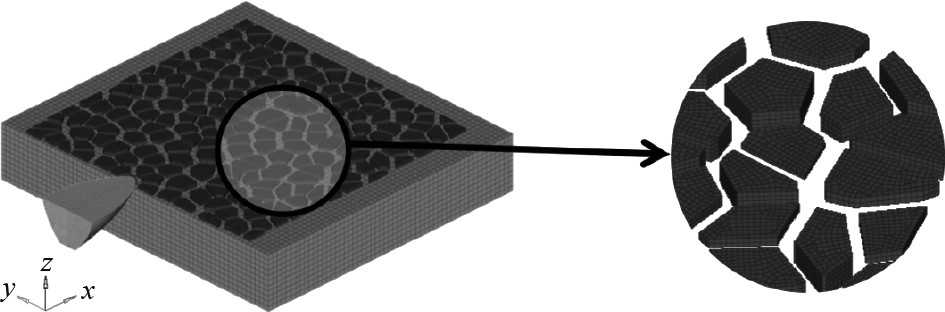
为了让整体计算量得以减轻,模拟的碎冰域是100 m×100 m,密集程度约60%。不同类型厚度的范围则是在1~1.5 m之间,冰的平均厚度则是1.25 m。碎冰区域网格则是0.5 m×0.5 m×0.5 m,约有62247个网格。图5为建立的船首的有限元模型。
|
图 5 碎冰区破冰船船首有限元模型(已隐去空气域) Fig. 5 Finite element model of the bow of the icebreaker in the ice breaking area (the air domain has been hidden) |
使用的破冰船首柱倾角为24°。依据文献[11]取值标准,所有角度划分为5个水平,水平公差是2°,在每一个首部位置的角度利用2°改变幅度依次进行增加或是降低。首柱倾角对于海冰的下压能力有着十分重要的影响。不改变目前水线的型线,在较小范围的去缩放水线上部1 m位置纵向的首部型值点,从而让坐标在规定的范围内改变,这样就可改变首柱倾角。表3为结合实际的水平公差改变之后的幅度和首柱倾角匹配关系,图6为不同首柱倾角的具体度数。
|
|
表 3 首柱倾角对应值 Tab.3 Corresponding values of bow inclination |
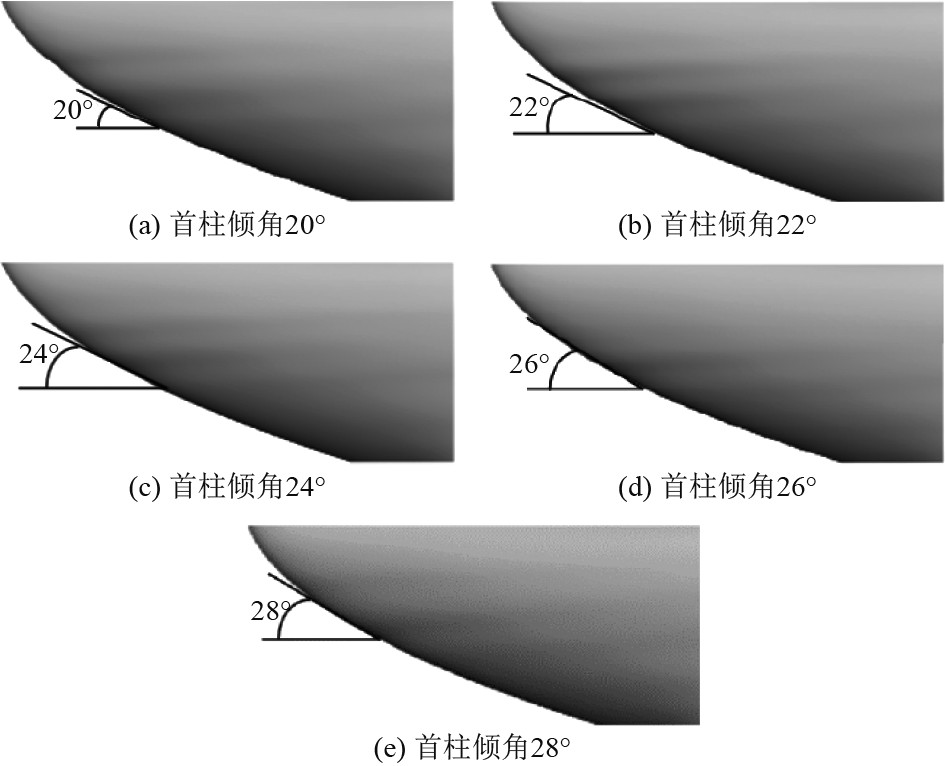
|
图 6 不同首柱倾角度数 Fig. 6 Different bow angle degrees |
在t=0.704 s的时候,破冰船驶入碎冰区,最开始首柱先和区域相接触,而首部位置对碎冰进行挤压,此时碎冰出现破坏现象,之后船首位置就会将碎冰向两侧排开来。在t=5.63 s时,船的首部位置会完全到达碎冰区内。图7为不同类型的首柱倾角的船舶船首位置在碎冰区域具体的运行状况。由于所有工况下的船体首柱倾角都不会超过90°。所以弯曲破坏为海冰关键破坏模式。观察模拟结果可得,如果首柱倾角不一样,船首位置的冰堆积状况也不一样。倾角越小,碎冰不容易出现堆积现象,首柱面所碰触的碎冰会挤压到船底位置,从而出现破碎现象。由于角度的不断增加,会让较多的碎冰堆积到首部前面的位置。

|
图 7 不同首柱倾角下船舶在碎冰区航行状态 Fig. 7 Navigation status of ship in broken ice area with different bow angles |
为了更好地对船体在碎冰区域中,不同类型的首柱倾角下的碎冰载荷和由于时间推移而出现的变化规律进行详细分析,首先绘制在船的首部位置到达碎冰区域的x方向上冰载荷-时间历程曲线,如图8所示。可以发现,首柱倾角不一样时,冰在不同时域上的波动性都较强,同时拥有较为明显的周期性。角度较小时,碎冰不易出现堆积现象,所以此时载荷的峰值很小。而由于角度的不断增加,也让更多的碎冰出现了堆积,进一步增加了实际的冰载荷。
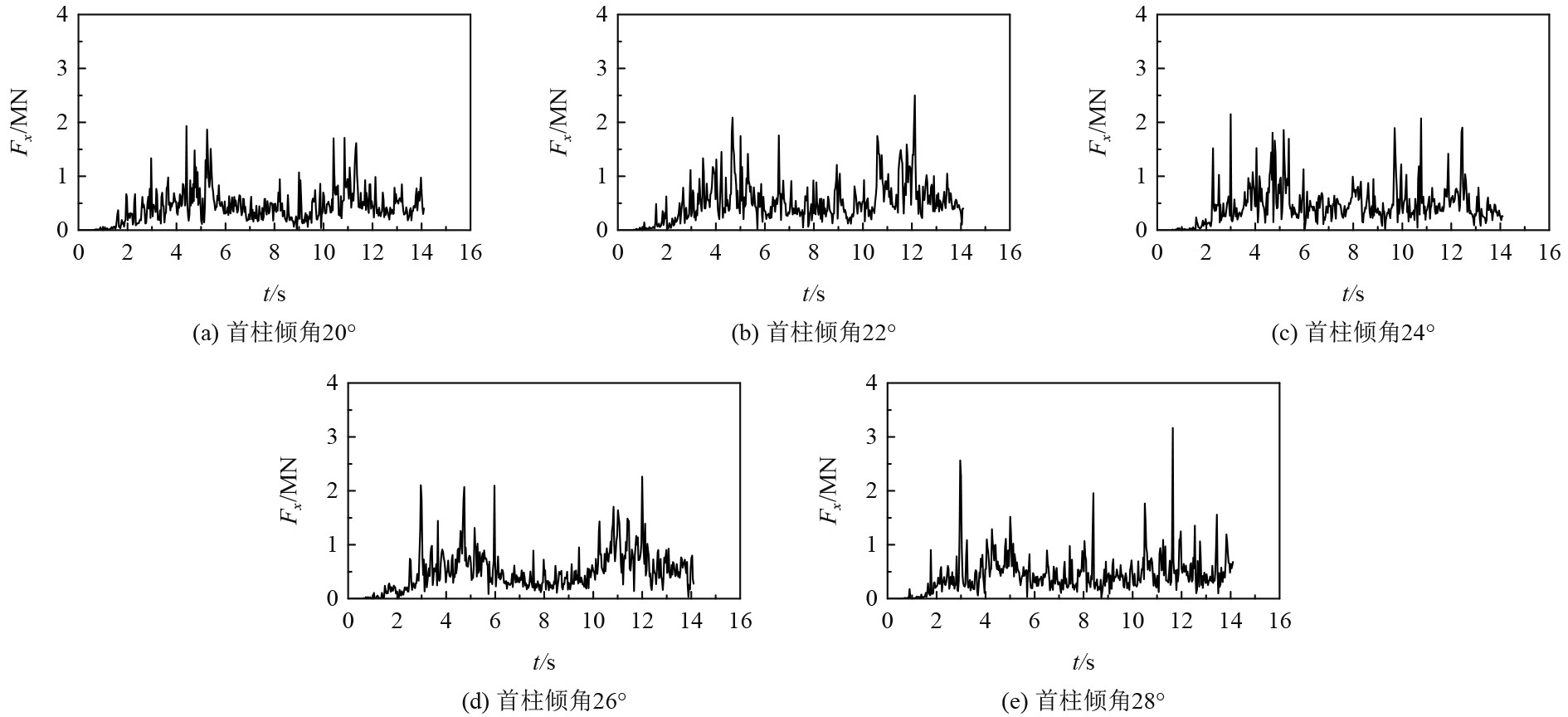
|
图 8 不同首柱倾角下冰载荷时间历程曲线 Fig. 8 Time history curve of ice load under different stem inclination angles |
如图9所示,对x方向上的载荷取平均值,由于倾角的不断增加,实际的碎冰阻力也会一直提升。首柱倾角从20°增加到28°时,此时的阻力也提升了18.5%,主要是由于船和冰在碰撞时,船体最开始和冰出现相互影响的范围是在首部位置的首柱面。由于船体不断运行,挤压现象也在一直产生,首柱倾角增加,从而冰和船体的接触区域也会增加,而挤压力的垂直分量就会减小,冰不容易形成弯曲断裂现象。
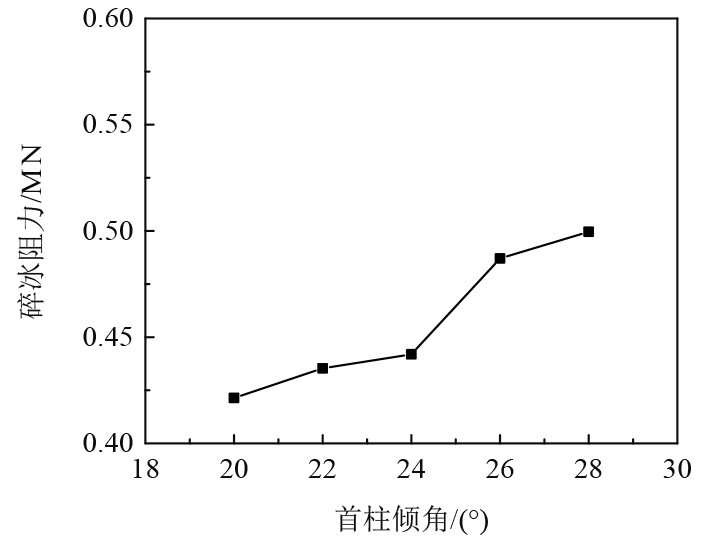
|
图 9 碎冰阻力随首柱倾角变化曲线 Fig. 9 Relationship between ice breaking resistance and stoop inclination |
较小的首柱倾角会提升海冰的下压能力,从而形成较小的纵向冰阻力,可进一步让船的破冰性能得以提升。
3.3 水线进角对船舶碎冰阻力影响研究 3.3.1 计算工况设置“雪龙”号破冰船的水线进角是22°。而水线进角对整体破冰性能所造成的影响,可以让船体水线之下的船首旁边以及肩部位置所出现的堆积现象得以清除。表4。为改变幅度和水线进角的匹配关系,图10为不同类型水线进角的实际度数。
|
|
表 4 水线进角对应值 Tab.4 Corresponding value of waterline advance angle |
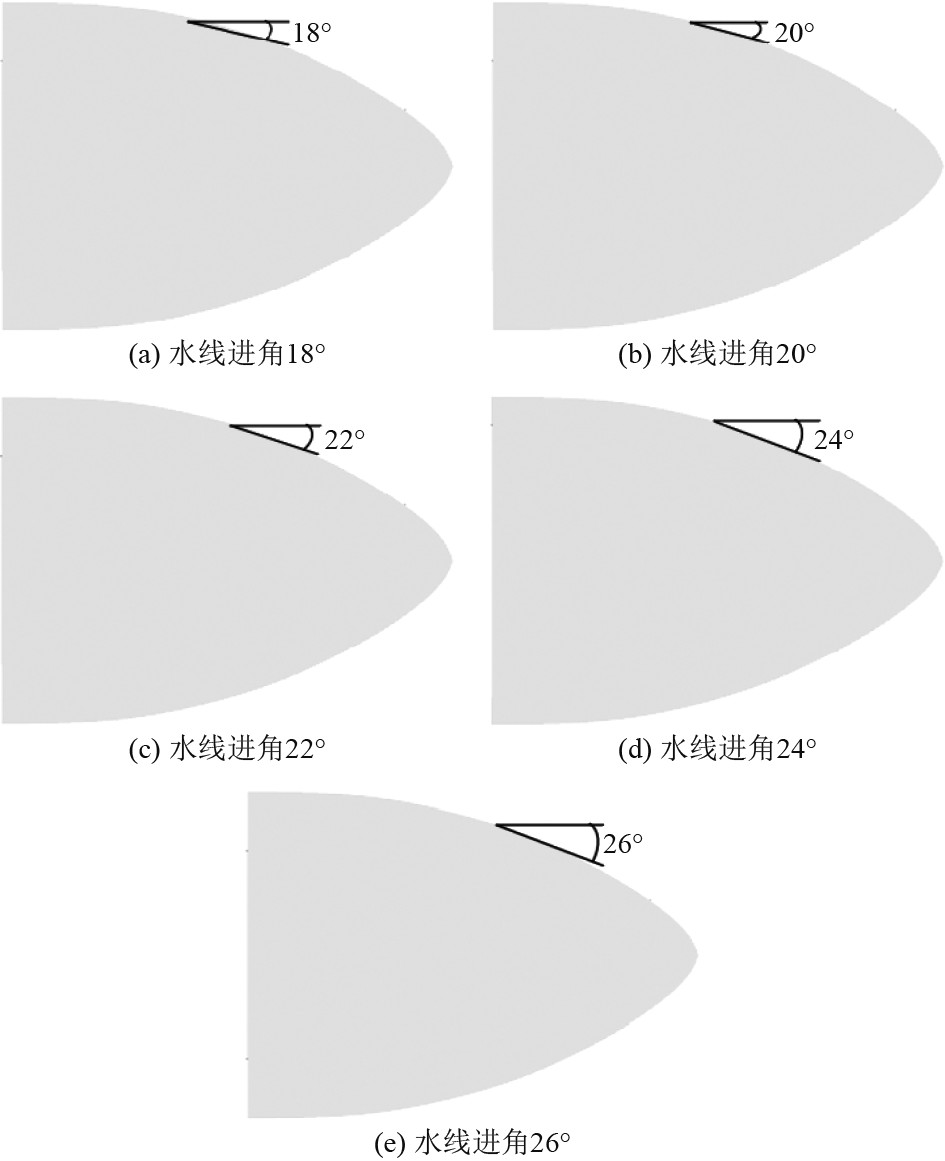
|
图 10 不同水线进角度数 Fig. 10 Different waterline approach angles |
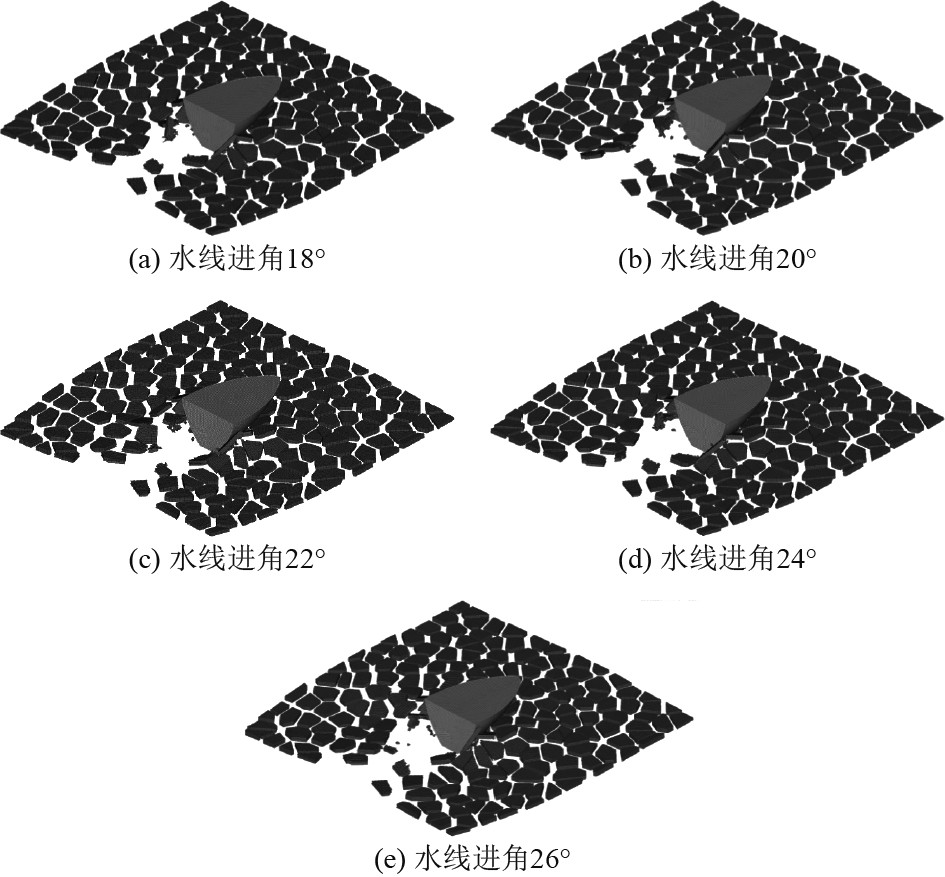
结合上述调整的船首部位置的水线进角仿真碎冰区域的冰阻力以及不同类型水线进角的船体在碎冰中的运行状况,如图11所示。船体在碎冰区域运行的过程中会形成堆积冰,主要可划分为2种状况:首先是碎冰不能绕过船体在水线下船身的局部以及肩部位置出现堆积现象,而另一种则是碎冰被挤压到冰层上所形成的堆积现象。
|
图 11 不同水线进角下破冰船碎冰区航行状态 Fig. 11 Navigation status of icebreaker in ice breaking area at different water line approach angles |
通过分析可得,由于首部位置的水线进角在不断地提升,实际的水线构型也不断扩张,而肩部位置的实际碎冰状况变得十分严重,出现碎冰的状况也变得频繁。此时更容易出现较小的碎冰,从而没有较为明显的堆积现象。
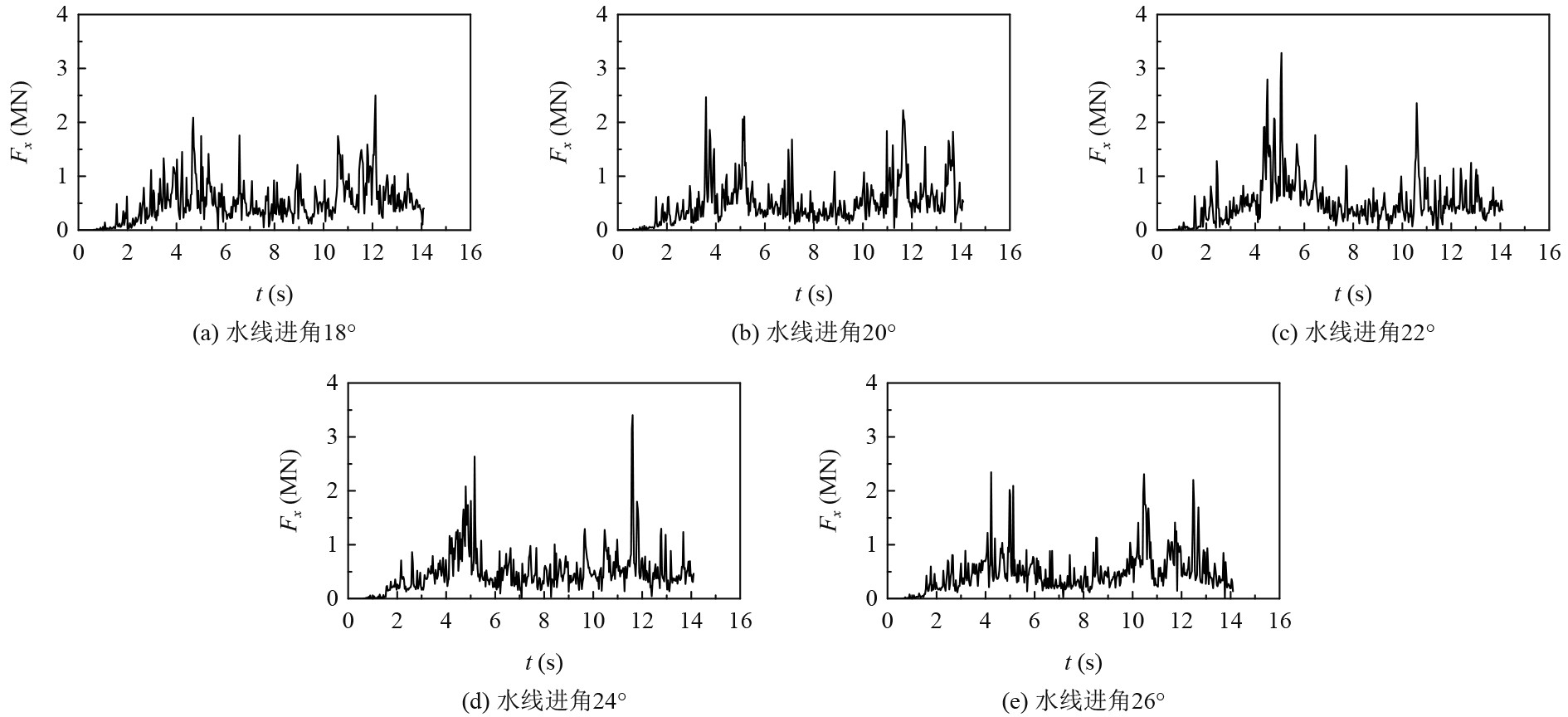
为了对船体在碎冰区域不同水线进角状况下,冰载荷随着时间所改变的规律进行细致探究,绘制不同水线进角下,冰载荷时间历程曲线具体如图12所示。能够得到由于船体水线进角的持续增加,此时载荷到达了极大的峰值,这是由于将船体肩部位置的碎冰堆积现象清除掉所形成的。
|
图 12 不同水线进角下冰载荷时间历程曲线 Fig. 12 Time history curve of ice load under different water line angles |
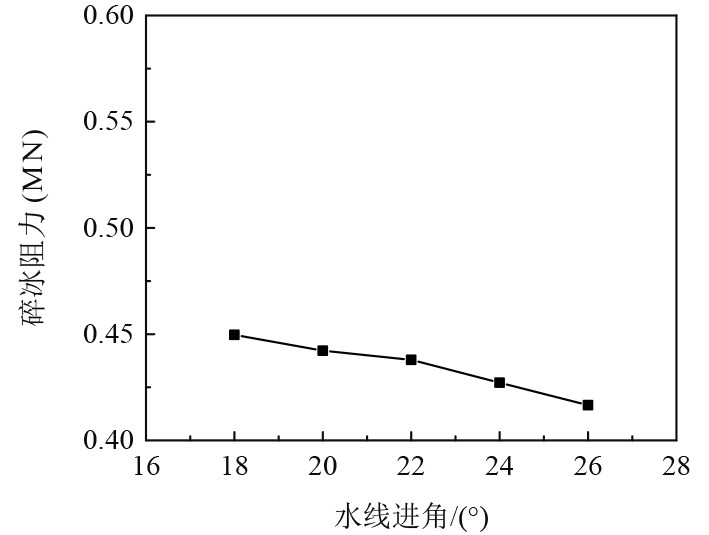
统计数值模拟碎冰载荷,得到如图13所示的碎冰阻力和水线进角的改变关系图。如果船体的首部位置水线进角在规定的范围之内,此时船体所受的阻力就会随着进角的增加而不断减小。角度从18°改变到26°时,整体的碎冰阻力降低了7.9%。主要是因为水线进角的增加,船体的首部结构在不断扩张,从而可以让碎冰在出现弯曲破坏的基础之上产生二次破坏现象,进一步减小冰块的尺寸,为清除工作提供帮助。而二次破坏的实际载荷要比第一次低,这样就可以让船首所受到的载荷减少。
|
图 13 碎冰阻力与水线进角关系 Fig. 13 Relationship between ice breaking resistance and waterline approach angle |
另一方面,如果水线进角较小,能够让船体的首部位置向两侧方向进行延伸。而对于此区域的冰体堆积清除工作会产生不利影响,所以提升水线进角能够让碎冰清理能力得以提升,对于船体的破冰能力提升是十分有利的。本次的研究对象水线进角是22°,整体水线结构比较狭窄,出现碰撞现象之后,冰块会堆积在船体的首部以及肩部位置,会形成大量堆积的现象。对其水线进角进行适当增大,船首水线构型可以相对外扩,有利于提高其排冰和破冰能力。
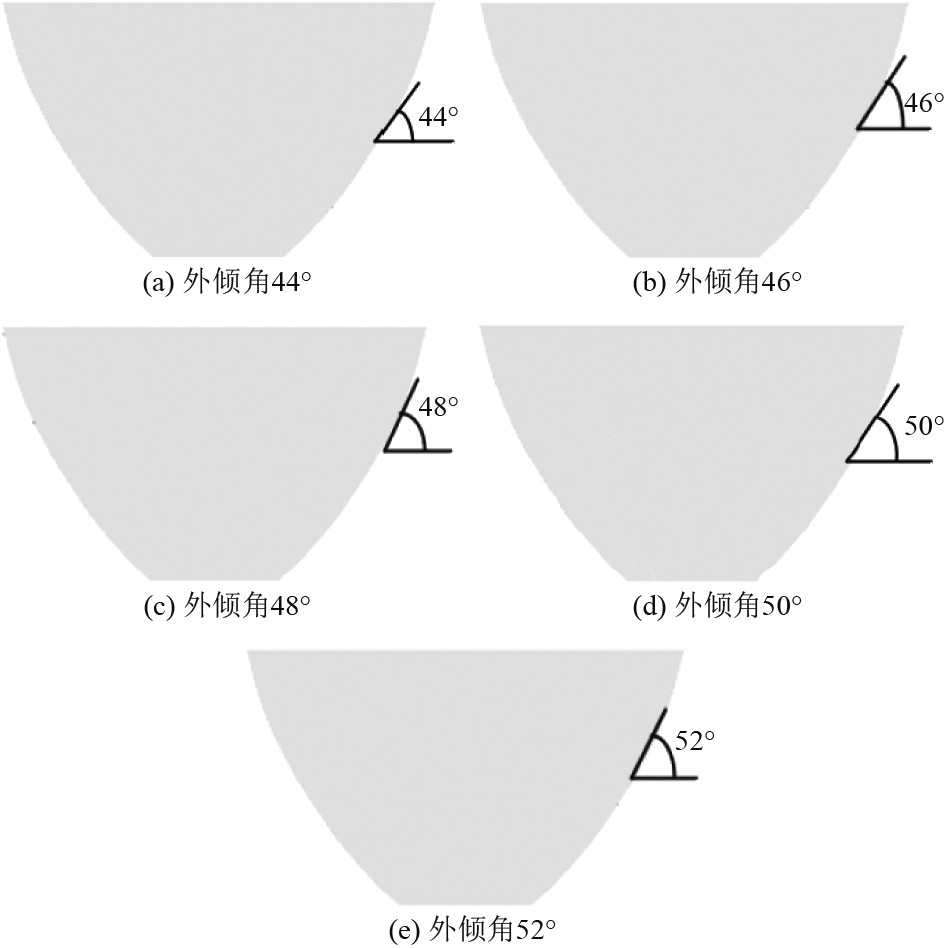
3.4 外倾角对船舶碎冰阻力影响研究 3.4.1 计算工况设置破冰船的外倾角是48°。增加外倾角对于破冰效果以及清理堆积冰都有着十分重要的影响。不改变目前的水线型线,合理的去缩放水线上部1m位置辅助水线的型值点,从而让其和水平改变幅度相匹配,这样就可改变外倾角。由于度数的不断增加,而船的首部位置在不断扩张。表5为变化幅度以及外倾角的匹配关系,图14为不同类型外倾角的度数。
|
|
表 5 外倾角对应值 Tab.5 Corresponding values of camber angle |
|
图 14 不同外倾角度数 Fig. 14 Different extroversion angles |
在对辅助水线首部型值点的横向坐标进行合理调整后,依次的数值模拟分析外倾角改变之后的航行情况及船舶在碎冰区域运行的首部位置冰阻力。图15为不同类型的外倾角作用下,船体实际的碎冰区域运行状况。发现如果角度越大,此时首部位置的两舷外飘增加,从而会加重船身两侧的碎冰堆积现象。

|
图 15 不同外倾角下碎冰区破冰船航行状态 Fig. 15 Navigation status of icebreaker in ice breaking area with different camber angles |
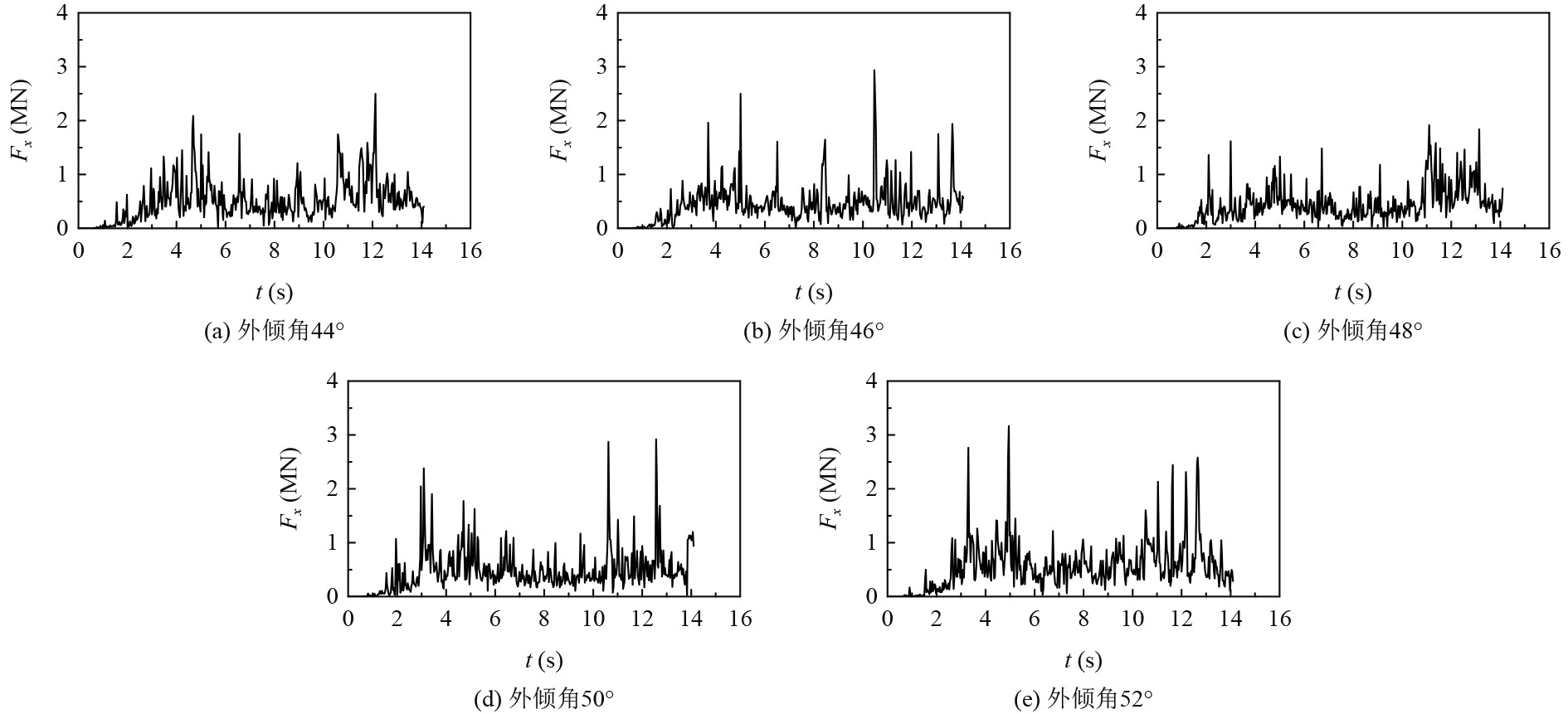
为了对船体在不同类型外倾角的状况下,冰载荷由于时间所改变的规律进行细致研究,绘制船首到达碎冰范围的x方向冰载荷-时间历程的曲线图。如图16所示。可以看出,外倾角为48°时,此时冰载荷的时历曲线峰值较小。
|
图 16 不同外倾角下冰载荷时间历程曲线 Fig. 16 Time history curve of ice load under different camber angles |
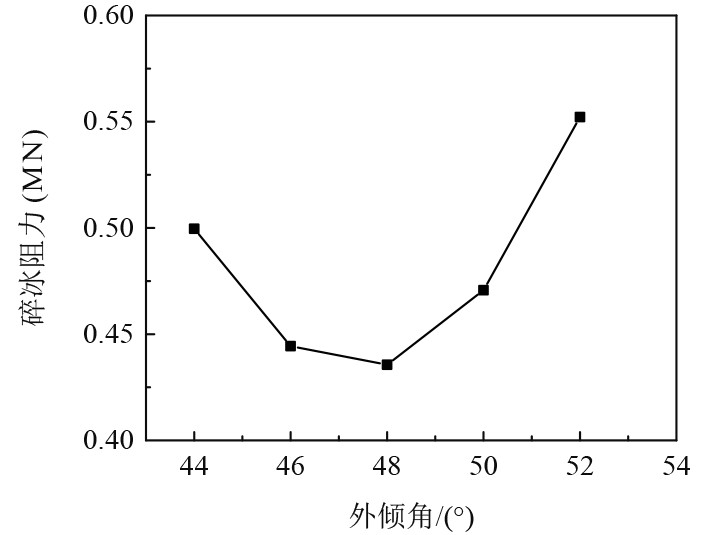
统计所得到的模拟数据,得到如图17所示的碎冰阻力随水线进角改变的关系图。在对首柱倾角以及水线进角的改变,对船体遭受阻力产生的影响的规律进行比较,得到改变外倾角对船体所受到的冰阻力产生不同的影响并不单纯只是由于角度的提升而阻力在不断减小,是一种明显的波动改变。如果首部外倾角的改变幅度是0°时,此时船体受到的碎冰阻力最小。如果改变幅度是正数,冰阻力由于角度的增加而不断加大,如果是负数时,阻力则由于角度增加而降低。
|
图 17 碎冰阻力与外倾角关系 Fig. 17 Relationship between ice breaking resistance and camber angle |
观察外倾角与碎冰阻力的关系图可知,在初始状态下的首部结构外倾角的度数,对船体所受到的冰阻力影响是最小的。而初始状况船首结构的外倾角拥有良好的破冰性能,阻力由于角度的增加呈现出一定的波动性改变。这是由于角度的提升,船首在不断进行扩张,而船和冰的相互影响也就进一步提升了接触面的倾角,从而也就让两者出现碰撞现象时,需更大的压力才可破坏掉碎冰。碎冰的阻力由于外倾角的增加而增大,首部位置周边的冰阻力纵方向分量不只是由于角度的增加或减少而体现出一种单调的改变,是较为明显的波动改变。
4 结 语本文采用Voronoi图完成了不规则碎冰域的建模。对碎冰区影响船舶破冰能力的首部参数进行了细致研究。同时利用Ls-dyna对不同关键参数下碎冰阻力的相关数据进行详细计算,使用定量的方法对每一个参数的改变对船体所受到碎冰阻力影响进行分析,得到下面几点结论:
1)不同首柱倾角的情况下,冰载荷在时域上拥有较强的周期性以及波动性。首柱倾角较小时,碎冰不容易出现堆积现象,而实际的载荷峰值也很小。首柱倾角从20°增加到28°,实际的碎冰阻力也就提升了18.5%。同时也表明,首柱倾角较小能让船首位置的海冰下压能力得以提升,并且破坏海冰,拥有较好的破冰效果。
2)随着船首部水线进角的增加,破冰船首部位置的水线构型在不断地扩展,此时的碎冰破碎状况十分剧烈,容易出现特别小的碎冰,没有特别明显的海冰堆积现象。当角度从18°提升到26°时,实际的阻力则降低了7.9%,表明较大水线进角使船体有良好清除海冰的能力。
3)碎冰阻力由于外倾角的提升出现了较为明显的波动改变。若外倾角没有改变,此时船体所受到的阻力最小。如果实际的变化幅度是正数,碎冰阻力会由于角度的提升而不断增加。相反,变化幅度为负数,实际的阻力则由于角度的提升而不断降低。相对而言,原船首结构的外倾角之下,船体的破冰性能更加良好。
| [1] |
CLEARY P W, SAWLEY M L. DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge[J]. Applied Mathematical Modelling, 2002, 26(2): 89-111. DOI:10.1016/S0307-904X(01)00050-6 |
| [2] |
LUO W, JIANG D, Wu T, et al. Numerical simulation of an ice-strengthened bulk carrier in brash ice channel[J]. Ocean Engineering, 2020, 196: 237-245. |
| [3] |
童波, 涂勋程, 谷家扬, 等. 基于参数化设计的浮冰区船舶冰阻力研究[J]. 船舶力学, 2019, 023(7): 755-762. TONG Bo, TU Xun-cheng, GU Jia-yang, et al. Study on ship ice resistance in floating ice area based on parametric design[J]. Ship Mechanics, 2019, 023(7): 755-762. DOI:10.3969/j.issn.1007-7294.2019.07.001 |
| [4] |
SUN J, HUANG Y. Investigations on the ship-ice impact: Part 1. Experimental methodologies[J]. Marine Structures, 2020, 72: 174-181. |
| [5] |
HALLQUIST J . LS-DYNA keyword user's manual[S]. Version: 970. 2003: 217-219.
|
| [6] |
刚旭皓. 冰区船首部连续破冰模式下破冰阻力研究[D]. 北京: 中国舰船研究院, 2020.
|
| [7] |
郭华洛. 基于参数化技术的建筑表皮生成研究[D]. 广州: 广州大学, 2019.
|
| [8] |
YULMETOV R, LUBBAD R, LØSET S. Planar multi-body model of iceberg free drift and towing in broken ice[J]. Cold Regions Science and Technology, 2016, 121: 154-166. DOI:10.1016/j.coldregions.2015.08.011 |
| [9] |
刘禹. 内河破冰船首部型式研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [10] |
中国船级社. 极地船舶指南[S]. 人民交通出版社, 2016.
|
| [11] |
毛方云. 基于破冰能力的极地航行船舶首部构型研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
 2023, Vol. 45
2023, Vol. 45
