0 引　言

鱼水雷等水中兵器水下爆炸产生的冲击波和气泡载荷对舰船会造成局部或整体毁伤，致使其丧失作战能力^[1-3]。气泡脉动过程是一个非常复杂的能量传递与释放过程，整个运动过程包括了气泡的膨胀、收缩、变形及向自由表面漂移等一系列复杂的运动形式。气泡内部的高压驱使周围的水介质以小于声速的速度向外扩散（滞后流），气泡运动过程中还产生脉动压力及射流载荷，这些载荷都会对水中结构造成严重破坏^[4-6]。目前对炸药水下爆炸产生的气泡载荷及其对结构的毁伤效应研究比较多^[7-9]，但对水下高压气泡运动引起的流场载荷特性研究较少。

本文基于Fluent的VOF模型开展气泡动态特性数值模拟，得到了气泡脉动周期、流场中测点处压力及质点速度，并分析了气泡初始内压和初始半径对气泡动态特性的影响。结果表明，气泡初始内压和初始半径越大，气泡最大膨胀半径越大，脉动周期越长，流场中测点处压力峰值及质点速度峰值越大。

1 数学模型 1.1 控制方程

考虑表面张力的动量方程：

$ \frac{\partial }{{\partial t}}\left( {\rho \overrightarrow v } \right) + \nabla (\rho \overrightarrow v \overrightarrow v ) = - \nabla p + \nabla \cdot [\mu (\nabla \overrightarrow v + \nabla {\overrightarrow v ^{\rm{T}}})] + \rho g + \overrightarrow F 。$

(1)

式中： $ \overrightarrow v $ 为速度矢量； $\ \rho $ 为流体密度； $\ \mu $ 为粘性系数； $ p $ 为压强； $ \overrightarrow F $ 为表面张力源项。

可压缩流体连续性方程：

$ \nabla \cdot (\rho \overrightarrow v ) = 0 。$

(2)

采用VOF法追踪界面的相函数输运方程：

$ \frac{{\partial {a_q}}}{{\partial t}} + \overline v \cdot \nabla {a_q} = 0。$

(3)

式中， $ {a_q} $ 为第 $ q $ 相体积分数。对于式（1）中的 $\ \rho $ 和 $\ \mu $ 由体积分数决定：

$ \rho = {\rho _1}{a_q} + (1 - {a_q}){\rho _2}，$

(4)

$ \mu = {\mu _1}{a_q} + (1 - {a_q}){\mu _2}。$

(5)

式中， $ {\ \rho _1} $ 、 $ {\ \rho _2} $ 、 $ {\ \mu _1} $ 、 $ {\ \mu _2} $ 分别为2种不同流体的密度和粘度。

1.2 表面张力计算

采用Brack Bill等提出的连续表面张力模型（Continuum Surface Force, CSF）^[10]。VOF模型中附加的表面张力，通过散度原理表示为体积力，添加到动量方程中的源项，体积力表示表面张力的影响作用：

$ {\overrightarrow F _{vol}} = \sum\limits_{i < j} {{\sigma _{ij}}} \frac{{{a_i}{\rho _i}{k_j}\nabla {a_j} + {a_j}{\rho _j}{k_i}\nabla {a_i}}}{{\dfrac{1}{2}({\rho _i} + {\rho _j})}}。$

(6)

式中： $k = \nabla \cdot \mathop {\boldsymbol{n}}\limits^ \wedge$ 为表面曲率，其中， $\mathop {\boldsymbol{n}}\limits^ \wedge = \dfrac{{\overrightarrow {{n}} }}{{\left| {\overrightarrow n } \right|}}$ 为单位法向矢量， $\overrightarrow {\boldsymbol{n}} = \nabla {a_q}$ 为界面法向矢量。

若一个单元中只有两相，则 $ {k_i} = - {k_j} $ ， $ \nabla {a_i} = - \nabla {a_j} $ ，上式可简化为：

$ {\overrightarrow F _{vol}} = \sum\limits_{i < j} {{\sigma _{ij}}} \frac{{\rho {k_j}\nabla {a_i}}}{{\dfrac{1}{2}({\rho _i} + {\rho _j})}} 。$

(7)

2 数值计算模型

为了避免固壁对气泡运动产生影响，本文计算水域设为5 m×5 m，气泡初始半径为r₀，初始内压为p₀，选取计算域的中心为坐标原点，设置测点为N(0 m, 1 m)，气泡和水的密度分别为ρ₁=1.02×l0⁻³ kg/m³及ρ₂=1.0×l0³ kg/m³，表面张力系数为σ=0.72 N/m，计算模型如图1所示。水域边界为压力出口边界条件，水域初始压力与压力出口边界压力值相等。采用VOF多相流模型和标准k-ε两方程湍流模型，利用一阶隐式格式对时间项离散，压力与速度耦合采用PISO算法，压力项的离散采用PRESTO!方法，扩散项和对流项的离散采用一阶迎风格式，体积分数的离散采用QUICK格式。

3 结果及分析 3.1 气泡动态特性

对气泡初始内压p₀=10 MPa、气泡初始半径r₀=0.01 m的情况进行数值模拟。图2为不同时刻气泡的形状。气泡膨胀运动并压缩周围水介质，气泡半径逐渐增大。气泡内部压强逐渐减小，当气泡内部压强与周围水介质压强相当时，气泡在惯性作用下继续膨胀；t=37 ms时，气泡半径达到最大，内部压强小于周围水介质的压强，气泡又开始缩小，气泡内部压强逐渐增大，当气泡内部压强与周围水介质压强相当时，气泡在惯性作用下继续缩小；t=73 ms时，气泡半径收缩到最小，气泡内部压强大于周围水介质，又开始压缩周围水介质而膨胀运动，开始新的脉动周期。在后期气泡的收缩过程中，气泡下表面运动速度比上表面运动速度快，形成射流。气泡膨胀阶段，重力对气泡形状和上升速度的影响不是很大，表现为气泡在膨胀阶段基本保持为球形，以及气泡中心位置基本保持不变；气泡收缩且上浮阶段，气泡形状从原来的球形变成了上突下凹的蘑菇形，而且上升速度明显加快。

图3为前3次脉动周期内气泡的体积分数随时间的变化，体积分数可以反映脉动过程中气泡半径的变化。可以看出，气泡运动周期逐渐增大，最大半径逐渐减小。这是因为，随着气泡的周期性脉动，与周围水介质不断相互作用，发生动量和能量交换，使得气泡的能量逐渐减小。

图4(a)为N点压力时程曲线。可以看出，随着气泡脉动次数的增加，测点压力峰值迅速减小。图4(b)为N点质点速度时程曲线，当气泡开始膨胀时，质点速度迅速增大，随后缓慢减小直至为0，气泡膨胀到最大。此时，气泡开始缩小，质点速度缓慢增大，随后迅速减小直至为0，开始下一个周期运动。

3.2 气泡初始内压对气泡特性的影响

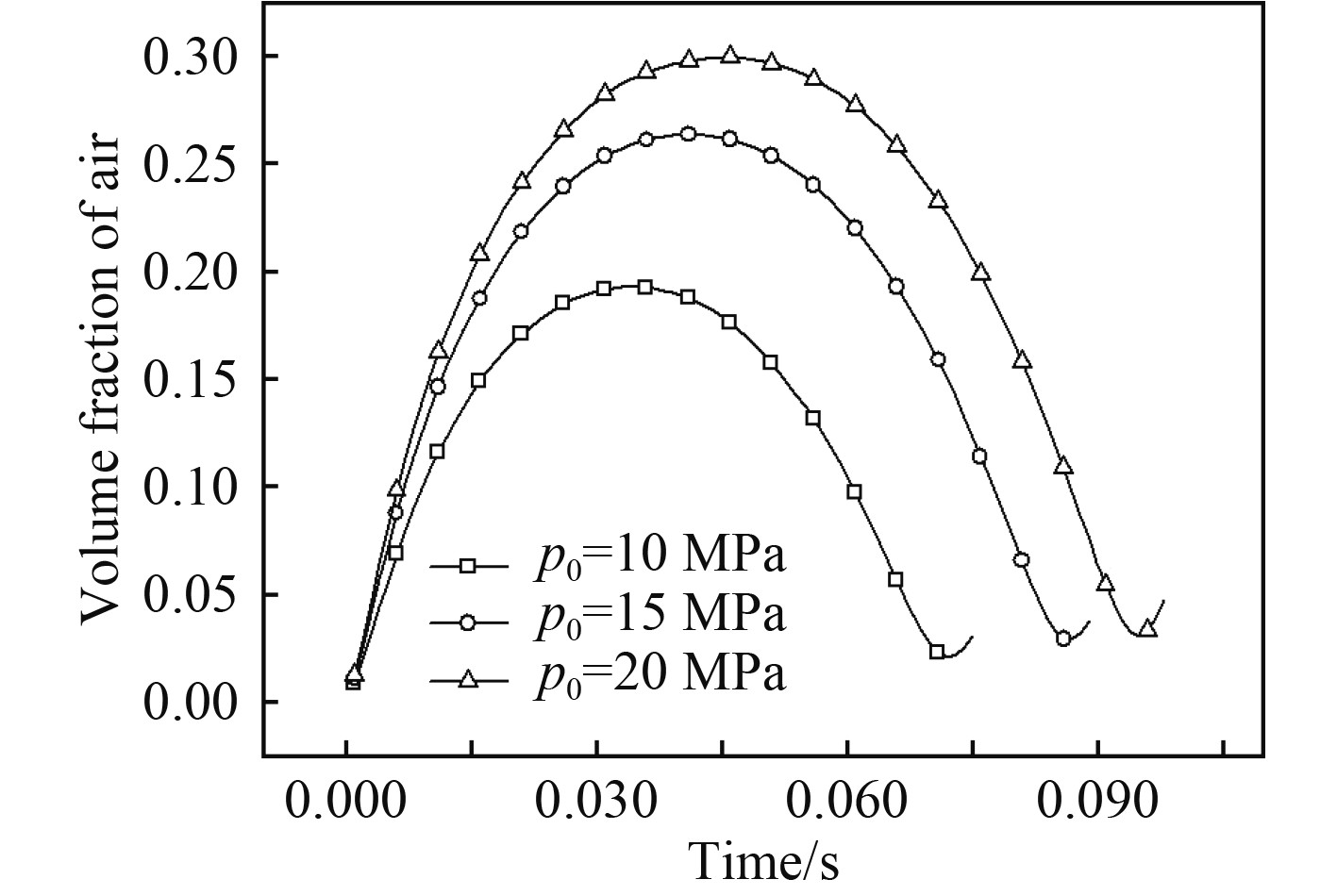
为了分析气泡初始内压对气泡特性的影响，对初始内压分别为p₀=10 MPa、p₀=15 MPa、p₀=20 MPa，气泡初始半径均为r₀=0.01 m的3种工况进行了数值模拟。图5为初始内压不同时，第1次脉动周期内气泡体积分数随时间的变化。初始内压越大，气泡最大膨胀半径越大，脉动周期越长。这是因为，气泡初始内压越大，初始能量也越大，气泡与周围水介质相互作用达到内外压力平衡需要的时间越长，膨胀运动能达到的最大半径也越大。

图6为初始内压不同时，N点压力和质点速度的时程曲线。可以看出，初始内压越大，测点处的压力峰值越大，质点达到的速度峰值越大，脉动周期越长。

3.3 气泡初始半径的影响

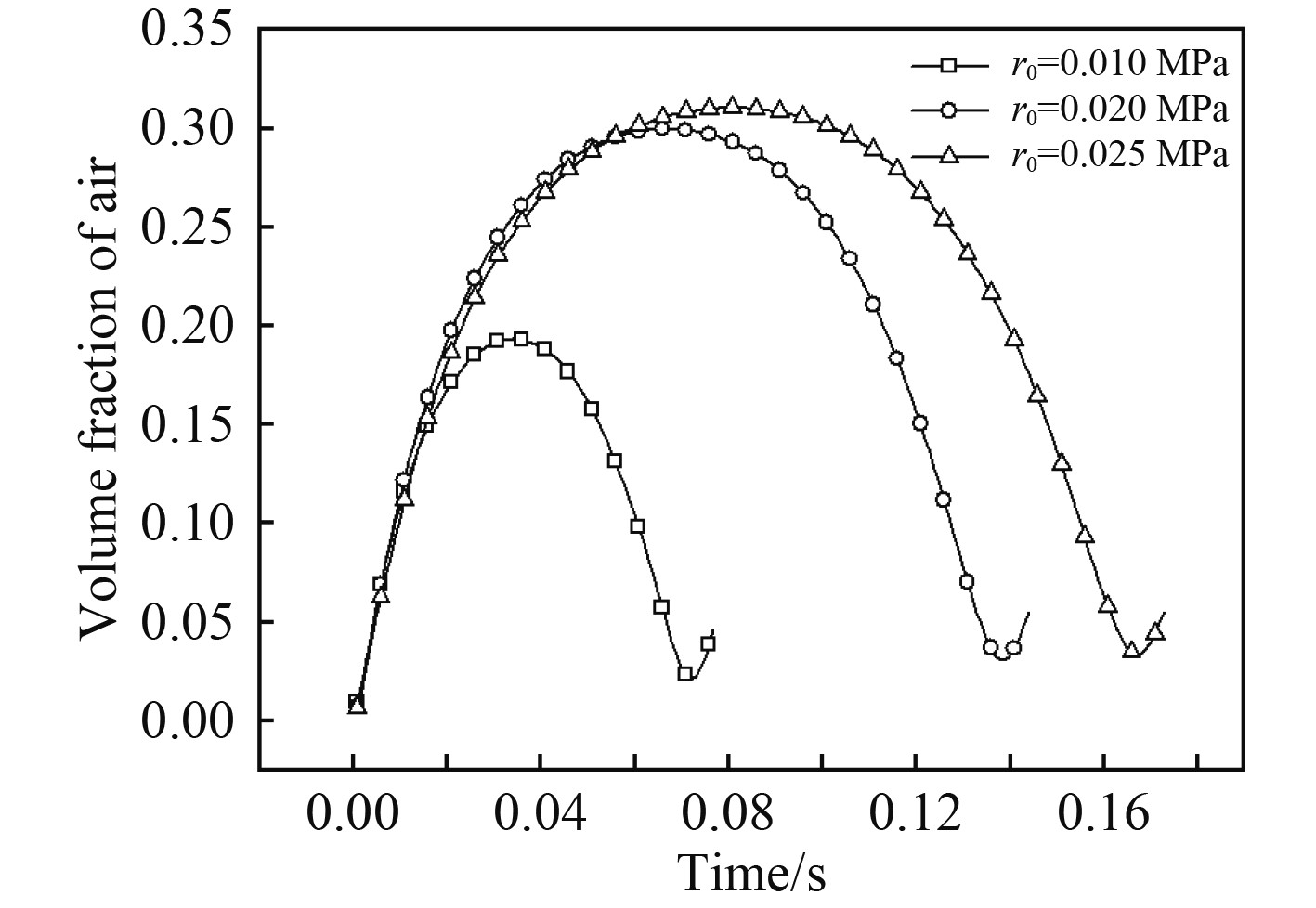
为了分析气泡初始半径对气泡特性的影响，对初始内压均为p₀=10 MPa，气泡初始半径分别为r₀=0.01 m、r₀=0.02 m、r₀=0.025 m的3种工况进行了数值模拟。图7为气泡初始半径不同时，第1次脉动周期内气泡体积分数随时间的变化。初始半径越大，气泡最大膨胀半径越大，脉动周期越长。这是因为，初始内压相同，初始半径越大，气泡的初始能量越大，与水介质相互作用时间越长，气泡膨胀运动能达到的最大半径也越大。

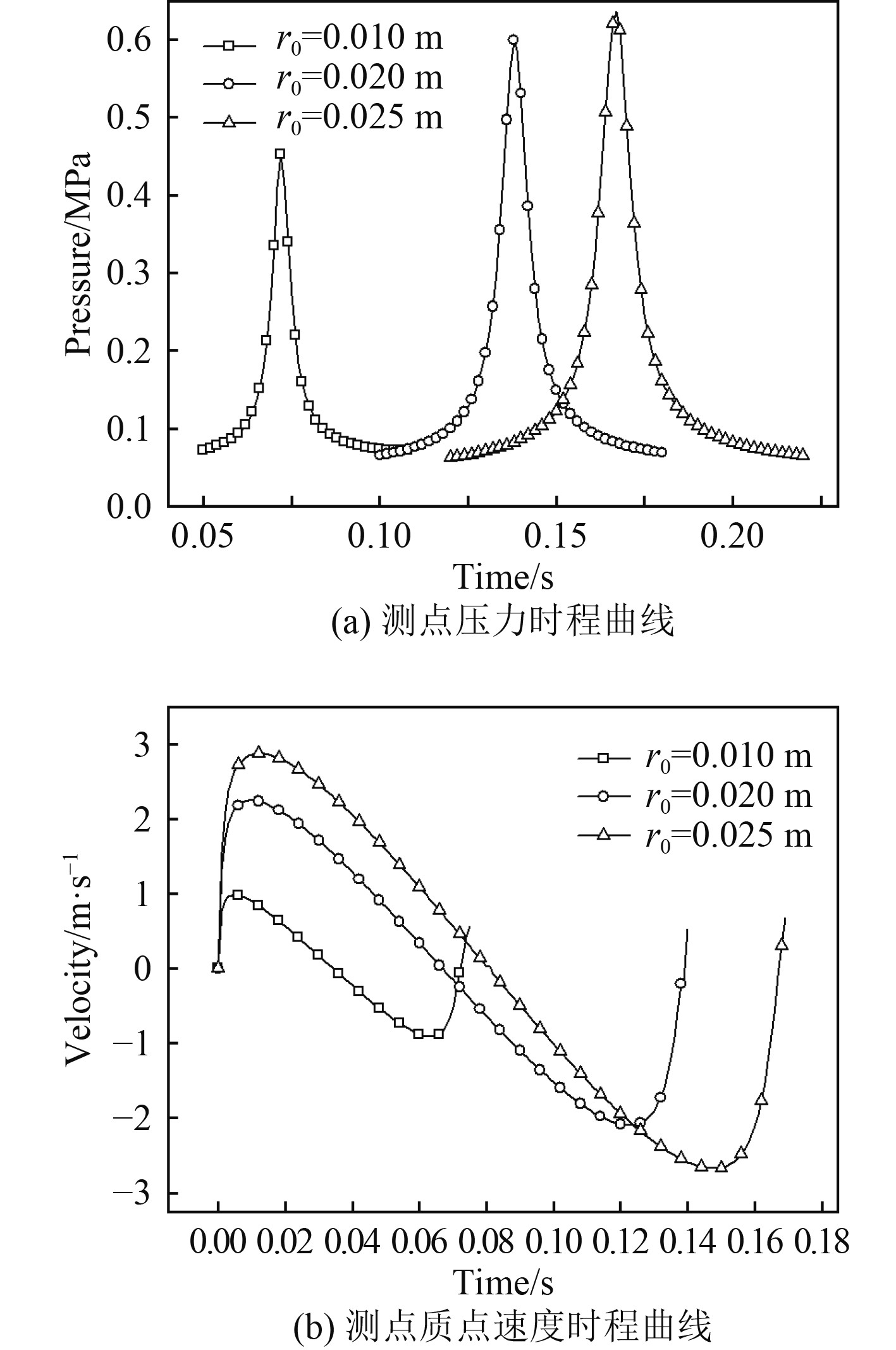
图8为气泡初始半径不同时，N点压力和质点速度的时程曲线。可以看出，初始半径越大，测点处的压力峰值越大，质点达到的速度峰值越大，脉动周期越长。

4 结　语

本文基于Fluent的VOF模型对气泡动态特性进行数值模拟，得到了气泡脉动周期、流场中测点处压力及质点速度。分析气泡初始内压和气泡初始半径对气泡动态特性的影响，结果表明，气泡初始内压和初始半径越大，气泡最大膨胀半径越大，脉动周期越长，流场中测点处压力峰值及质点速度峰值越大。水下爆炸气泡的初始状态直接影响其动态特性，数值模拟结果对水下爆炸气泡动态特性研究具有参考意义。