0 引　言

加肋圆柱壳是潜艇等水下航行器的基本结构，研究加肋圆柱壳的振动特性对于降低水下航行器的振动，提高水下潜器的隐蔽性在现代战争中显得极为重要。

传统的加肋圆柱壳结构的肋骨是等间距布置的，把相邻2个肋骨间环形壳板看作一个结构单元，那么，整个圆柱壳是由多个结构单元沿轴向依次连接构成的，这样的结构可以称为周期结构。在工程实际和理论研究中，周期性结构广泛存在，如耦合振子链系统、耦合多跨梁、耦合质量摆模型、肋骨周期布置的加筋板等，学者们对周期结构的振动特性进行了大量的研究^[1-2]，结果表明：周期结构整体振动幅值在某些频带较大，这些频带被称为“通频带”，在通频带内，整体振动能量大；通频带之间为“止频带”。结构整体振动能量小，结构的通频带与止频带交替出现^[3-4]。从振动控制的角度分析，振动能量在止频带不能远距离传播，被限制于激振源附近^[5-6]。因此，为控制周期结构的振动，应尽可能使振动频率处于止频带^[7-8]。

对周期结构的结构单元进行不规则扰动，就形成非周期结构。由于非周期结构的结构单元是随机、不规则分布，因此，结构波在传播过程中会发生不规则反射^[9]。当结构单元分布的不规则程度达到一定水平^[10]，并且相邻结构单元的耦合度等参数满足一定条件，那么，无论是在通频带还是止频带，不规则反射会很明显，能量会因反射作用而被限制于激振源附近。

对于非周期结构的一维振动，如耦合振子链系统、耦合多跨梁等的振动，从波动的角度看，这些模型都是一维波传播模型，动力学表达比较简单，主要采用解析法确定振动衰减程度^[1,9]。对于非周期结构的二维振动以及其他复杂振动，如肋骨非周期布置的加筋板和加肋圆柱壳、封闭的不规则结构等的振动，主要采用数值模拟、模型试验等方法进行研究。对圆柱壳，主要研究肋骨间距非周期布置对圆柱壳振动的控制作用。结果表明，肋骨位置的改变主要影响和控制结构在高频的振动，对低频振动的影响很小，其原因主要是肋骨间的结构波是短波，结构短波主要影响圆柱壳高频振动^[10-11]。然而，对实际的水下大型潜器，如潜艇等，需要降低结构的低频振动^[12]。

舱段间的结构波是长波，结构长波主要影响圆柱壳在低频段的振动。因此，本文以前述肋骨非周期布置圆柱壳振动特性研究为基础，用大肋骨将圆柱壳分成多个小段，并且各个小段轴向长度的布置是非周期的。研究大肋骨非周期布置圆柱壳的振动特性，以及通过将圆柱壳沿轴向分成多个轴向长度非周期分布的小段对长圆柱壳低频振动的控制作用，为工程实际提供参考。

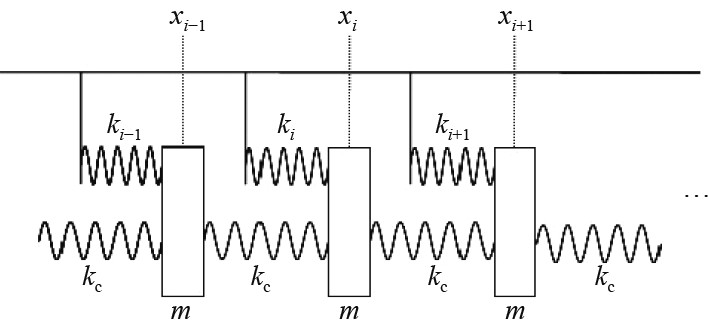
1 基本理论 1.1 非周期耦合振子链系统振动衰减计算方法

耦合振子链系统如图1所示，当耦合弹簧刚度 $ {k_{\text{c}}} = 0 $ 时，各弹簧振子之间没有耦合作用。各振子的质量均为 $ m $ ，第 $ i $ 个振子的对地弹簧刚度为 $ {k_i} = {k_{\text{m}}} + {\alpha _i} $ ， $ {\alpha _i} $ 是小量，表示各对地弹簧刚度在平均刚度 $ {k_{\text{m}}} $ 基础上的变化量。当耦合弹簧刚度 $ {k_{\text{c}}} \ne 0 $ 时，用传递关系表示耦合振子链系统的动力关系^[13]为：

$ \left( {\begin{array}{*{20}{c}} {{x_i}} \\ {{x_{i + 1}}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&{\dfrac{{ - m{\omega ^2} + {k_i}}}{{{k_c}}} + 2} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{x_{i - 1}}} \\ {{x_i}} \end{array}} \right)，$

或

$ {X_{i + 1}} = {T_i}{X_i}。$

(1)

式中： $ {x_i} $ 为第 $ i $ 个振子质量的位移复数幅值； $ \omega $ 为圆频率； $ i $ 为振子编号， $ i \in ( - \infty , + \infty ) $ ， $ {X_i} = {({x_{i - 1}},{x_i})^{\text{T}}} $ 为第 $ i $ 个单元的状态，它由第 $ i - 1 $ 个振子和第 $ i $ 个振子的位移复数幅值共同表示，第 $ i $ 个单元的状态通过状态传递矩阵 $ {T_i} $ 变换为第 $ i + 1 $ 个单元的状态 $ {X_{i + 1}} $ 。

Kissel等^[13-15]对非周期耦合振子链系统的研究表明，当各对地弹簧刚度 $ {k_i} $ 相同，即 $ {\alpha _i} = 0 $ ， $ {k_i} = {k_{\text{m}}} $ 时，系统是周期系统。此时，当圆频率 $ \omega $ 处于通频带内时，系统对输入的能量能以不衰减的波的形式沿系统传播，其中波数 $ k $ 和圆频率 $ \omega $ 满足如下关系式：

$ 1 + \frac{{\omega _0^2 - {\omega ^2}}}{{2V}} = \cos k。$

(2)

式中： $ {\omega _0} $ 为解耦振子的固有频率， $ V $ 被称为耦合系数，计算公式为，

$ \left\{ \begin{gathered} \omega _0^2 = \frac{{{k_{\text{m}}}}}{m} ，\\ V = \frac{{{k_{\text{c}}}}}{m} 。\\ \end{gathered} \right. $

(3)

其中，通频带频率满足

$ \left| {1 + \frac{{\omega _0^2 - {\omega ^2}}}{{2V}}} \right| \leqslant 1 。$

(4)

如果对地弹簧刚度受到不规则扰动，即 $ {\alpha _i} \ne 0 $ ，那么系统成为非周期系统。此时，系统对输入系统的能量以指数衰减形式沿系统传播。将第1个振子的能量用 $ {e_1} $ 表示，能量传递到第 $ N $ 个振子时变为 $ {e_N} $ ，那么振动能量衰减率 $ {\gamma _N} $ 可表示为：

$ {\gamma _N} = - \frac{1}{{2N}}\ln \left| {\frac{{{e_N}}}{{{e_1}}}} \right|。$

(5)

式中， $ {\gamma _N} $ 称为振动能量衰减率，表示非周期系统中相邻单元对输入能量的的平均指数衰减率。当 $ N \to \infty $ 时，振动能量衰减率为^[13-15]：

$ \gamma = \mathop {\lim }\limits_{N \to \infty } {\gamma _N} \approx \frac{1}{2}\frac{{{\sigma ^2}\left( {\omega _i^2} \right)}}{{4{V^2} - {{\left( {{\omega ^2} - \omega _0^2 - 2V} \right)}^2}}}。$

(6)

式中， $ {\omega _i} = \sqrt {{{{k_i}} \mathord{\left/ {\vphantom {{{k_i}} m}} \right. } m}} $ 为各独立解耦弹簧振子的固有频率。对于非周期系统， $ \omega _i^2 $ 服从均匀概率分布，概率密度函数为：

$ \eta ({\omega }_{i}^{2})=\left\{\begin{array}{cc}\dfrac{1}{\beta },& {\omega }_{i}^{2}\in \left[{\omega }_{0}^{2}-\dfrac{\beta }{2},{\omega }_{0}^{2}+\dfrac{\beta }{2}\right]。\\ 0,& {\rm{others}}。\end{array} \right.$

(7)

式中： $ \beta $ 为 $ \omega _i^2 $ 的散布范围， $ {\sigma ^2}\left( {\omega _i^2} \right){\text{ = }}{{{\beta ^2}} \mathord{\left/ {\vphantom {{{\beta ^2}} {12}}} \right. } {12}} $ 是 $ \omega _i^2 $ 的标准方差。根据式（6）和式（7）可知，当耦合振子链系统一定时，参数 $ V $ 、 $ \omega _0^2 $ 、 $ {\sigma ^2}\left( {\omega _i^2} \right) $ 一定。

1.2 圆柱壳模型的振动等效参数

将加肋圆柱壳的径向振动等效为耦合振子链的振动，获得振动等效参数 $ V $ 、 $ \omega _0^2 $ 、 $ {\sigma ^2}\left( {\omega _i^2} \right) $ 以及圆柱壳的振动能量衰减率计算公式。

首先，构造周期和非周期圆柱壳模型。

加肋圆柱壳模型如图2所示。用大肋骨将图2所示的模型沿轴向等分成尽量多的小段，本文取24段，如图3所示。每个大肋骨的截面形状和尺寸相同，如图4所示。圆柱壳的主尺度、板厚、环向肋骨及材料参数如表1所示。

如图3所示，圆柱壳模型的相邻大肋骨的间距 $ l $ 为常数，记作 $ \Delta l $ ， $ \Delta l{\text{ = 3}}{\text{.8}} $ m。保持大肋骨数量不变，改变每个大肋骨的轴向位置，改变量是小量并使相邻大肋骨之间的轴向距离分布是不规则的、随机的。

改变量服从均匀概率分布，其中第 $ g $ 号大肋骨的轴向位置 $ {x_g} $ 满足概率密度函数：

$ P({x}_{g})=\left\{\begin{array}{cc}\dfrac{1}{\Delta x}\text{，}& \left|{x}_{g}-g\cdot \Delta l\right| < \Delta x/2，\\ 0\text{，}& {\rm{others}}。\end{array}\right. $

(8)

式中： $ P({x_g}) $ 为随机变量 $ {x_g} $ 的概率密度函数； $ \Delta x{\text{/2}} $ 为大肋骨轴向位置的最大改变量，其具体取值是根据相邻大肋骨之间的平均距离以及研究问题的需要等因素确定。相邻大肋骨之间的轴向距离 $ l = {x_{g + 1}} - {x_g} $ 是随机变量，其平均值等于上述的 $ \Delta l $ ，标准方差 ${\sigma ^2}\left( l \right){\text{ = }} {{{{(\Delta x)}^2}} \mathord{\left/ {\vphantom {{{{(\Delta x)}^2}} 6}} \right. } 6}$ ^[11]。

为了研究振动沿圆柱壳轴向的衰减规律，在圆柱壳端部的一根环形肋骨上施加简谐激振力，激振力沿着圆柱壳截面的径向作用在肋骨上的一点，激振力的频率范围是1～1000 Hz。

将周期圆柱壳的振动进行分解并获得振动等效参数。用有限元法分析圆柱壳在激振力作用下的响应，得到圆柱。

壳的径向振动速度场 $ v(\theta ,x,f) $ 。其中， $ x $ 表示圆柱壳轴向位置； $ \theta $ 表示周向位置； $ f $ 表示激振力频率。用波数分析法对径向振动速度场进行分解。文献[16]对波数分析法进行了详细地阐述。将 $ v(\theta ,x,f) $ 分解为系列行进波叠加，即

$ \begin{split} v(\theta ,x,f) =& \sum\limits_{n = 0}^\infty \left\{ \int_{ - \infty }^{ + \infty } \frac{1}{{2{\text{π}} }}\left[ {V^{\text{c}}}(n,{k_x},f)\cos n\theta\right.\right. +\\ & \left. {V^{\text{s}}}(n,{k_x},f)\sin n\theta \right]{e^{{\text{j}}{k_x}x}}{\rm{d}}{k_x} \}。\end{split} $

(9)

式中： $ {V^{\text{c}}} $ 和 $ {V^{\text{s}}} $ 表示各行进波分量的复数幅值；每一分量的频率、轴向波数、周向振动模式和对称模式分别用 $ f $ ， $ {k_x} $ ， $ n $ 和上标c，s表示。 $ {V^{\text{c}}} $ 和 $ {V^{\text{s}}} $ 的具体表达式为：

$ \begin{split} & {V^{{c}}}(n,{k_x},f) = \frac{\alpha }{{\text{π }}}\int_{ - {\text{π }}}^{\text{π }} {A(\theta ,{k_x},f)\cos n\theta {\text{d}}\theta }，\\ & {V^{{s}}}(n,{k_x},f) = \frac{\alpha }{{\text{π }}}\int_{ - {\text{π }}}^{\text{π }} {A(\theta ,{k_x},f)\sin n\theta {\text{d}}\theta } 。\end{split} $

(10)

式中： $A(\theta ,{k_x},f) = \displaystyle\int_{ - \frac{L}{2}}^{\frac{L}{2}} {v(\theta ,x,f)} {e^{ - {{j}}{k_x}x}}{\rm{d}}x$ ， $\alpha = \left\{\begin{array}{l}1/2，n=0，\\ 1，n=1,\ 2,\ \cdots \end{array}\right.$ 其中， $ L $ 表示圆柱壳地轴向长度。

当激振力频率为 $ f $ 、圆柱壳截面周向振动模式为 $ n $ 时，轴向波数是 $ {k_x} $ 的行进波具有的振动能量计算如下：

$ W(n,{k_x},f) = {\left| {{V^{\text{c}}}} \right|^2} + {\left| {{V^{\text{s}}}} \right|^2}。$

(11)

将 $ W(n,{k_x},f) $ 对 $ {k_x} $ 积分，得到频率为 $ f $ 时圆柱壳截面以周向振动模式 $ n $ 振动的总能量：

$ {E_n}(f) = \int_{ - \infty }^{ + \infty } {W(n,{k_x},f)} {\text{d}}{k_x}。$

(12)

截面周向振动模式 $ n $ 一定时，截面振动能量沿轴向的分布用 $ E_x^n(x,f) $ ，计算式为：

$ \begin{split} E_x^n(x,f) = & \frac{1}{{2{\text{π }}}}\left[ {{\left| {\int_0^L {{V^{\text{c}}}(n,{k_x},f){e^{{{j}}{k_x}x}}{\text{d}}x} } \right|}^2}\right. +\\ & \left. {{\left| {\int_0^L {{V^{\text{s}}}(n,{k_x},f){e^{{{j}}{k_x}x}}{\text{d}}x} } \right|}^2} \right]。\end{split} $

(13)

做出一定周向振动模式下的 $ {E_n} \sim f $ 曲线， $ n $ =2时的 $ {E_n} \sim f $ 曲线如图5所示。将每个通频带的振动等效为耦合振子链的振动^[11]，根据式（2）～式（4）可知，通频带的下限频率相当于解耦弹簧振子的固有频率，等效耦合系数由通频带的带宽、中心频率确定。对一个具体的通频带，如果其上、下限频率分别是 ${\omega _ + } = 2{\text{π}} {f_ + }$ 、 ${\omega _ - } = 2{\text{π}} {f_ - }$ ，那么相应的振动等效参数分别为：

$ \left\{ \begin{gathered} {\omega _0} = {\omega _ - } ，\\ V = \frac{{\omega _ + ^2 - \omega _ - ^2}}{4} = \frac{{\left( {{\omega _ + } - {\omega _ - }} \right)\left( {{\omega _ + } + {\omega _ - }} \right)}}{4} = \frac{{{\omega _{\text{c}}}\Delta \omega }}{2} 。\\ \end{gathered} \right. $

将圆频率 $ \omega $ 用频率 $ f $ 表示，则有：

$ \left\{ \begin{gathered} {f_0} = {f_ - } ，\\ V = \left( {f_ + ^2 - f_ - ^2} \right){{\text{π }}^2} = 2{{\text{π }}^2}{f_{\text{c}}}\Delta f。\\ \end{gathered} \right. $

(14)

式中： $ {\omega _{\text{c}}} $ ， $ {f_{\text{c}}} $ 为通频带中心频率； $ \Delta \omega = {\omega _ + } - {\omega _ - } $ 或 $ \Delta f = $ $ {f_ + } - {f_ - } $ 为通频带的带宽。

除了 $ V $ 和 $ \omega _0^2 $ ，用式（6）计算振动能量衰减率，还要确定 $ {\sigma ^2}\left( {\omega _i^2} \right) $ ， $ {\sigma ^2}\left( {\omega _i^2} \right) $ 需要根据大肋骨非周期布置参数确定。对大肋骨的轴向位置进行不规则扰动，使圆柱壳成为非周期结构。文献[17]详细阐述了 $ {\sigma ^2}\left( {\omega _i^2} \right) $ 计算式的推导过程，直接应用，于是得到振动能量衰减率的计算公式，即

$ \gamma \left( \omega \right) \approx \frac{4}{3}\frac{{\omega _0^4}}{{\omega _{\text{c}}^2{{\left( {\Delta \omega } \right)}^2} - {{\left( {{\omega ^2} - \omega _0^2 - {\omega _{\text{c}}}\Delta \omega } \right)}^2}}}{\left( {\frac{{\Delta x}}{{\Delta l}}} \right)^2}{\cos ^4}\theta。$

将圆频率 $ \omega $ 用频率 $ f $ 表示，则有，

$ \gamma \left( f \right) \approx \frac{4}{3}\frac{{f_0^4}}{{f_{\text{c}}^2\Delta {f^2} - {{\left( {{f^2} - f_0^2 - {f_{\text{c}}}\Delta f} \right)}^2}}}{\left( {\frac{{\Delta x}}{{\Delta l}}} \right)^2}{\cos ^4}\theta。$

(15)

式中： $\cos \theta = \dfrac{{{k_x}}}{{{k_h}}} = {\left[ {1 - {{\left( {\dfrac{n}{{{k_h}R}}} \right)}^2}} \right]^{\frac{1}{2}}}$ ， ${k_h} = {\left( {\dfrac{{\rho h\omega _0^2}}{{{{E{h^3}} \mathord{\left/ {\vphantom {{E{h^3}} {\left[ {12\left( {1 - {\nu ^2}} \right)} \right]}}} \right. } {\left[ {12\left( {1 - {\nu ^2}} \right)} \right]}}}}} \right)^{\frac{1}{4}}}$ ， $ n $ 为周向振动模式； $ R $ 为圆柱壳半径； $ \rho $ 为圆柱壳材料密度； $ E $ 为弹性模量； $ \nu $ 为泊松比， $ h $ 为圆柱壳板厚度。

由式（15）可知，要计算 $ \gamma \left( f \right) $ ，先要确定周期圆柱壳某一周向振动模式 $ n $ 下的通频带的带宽 $ \Delta f $ 、中心频率 $ {f_{\text{c}}} $ 、下限频率 $ {f_ - } $ （即 $ {f_0} $ ），以及非周期圆柱壳大肋骨布置的不规则程度 $ \Delta x/\Delta l $ 等参数，然后就可计算通频带内不同频率时的 $ \gamma \left( f \right) $ 。

2 圆柱壳振动能量衰减率的理论计算

本文主要研究大肋骨非周期布置对圆柱壳在低频段的振动控制作用，因此，要确定对低频振动贡献大的周向振动模式，分析圆柱壳振动衰减率与大肋骨间距布置不规则程度之间的关系等。

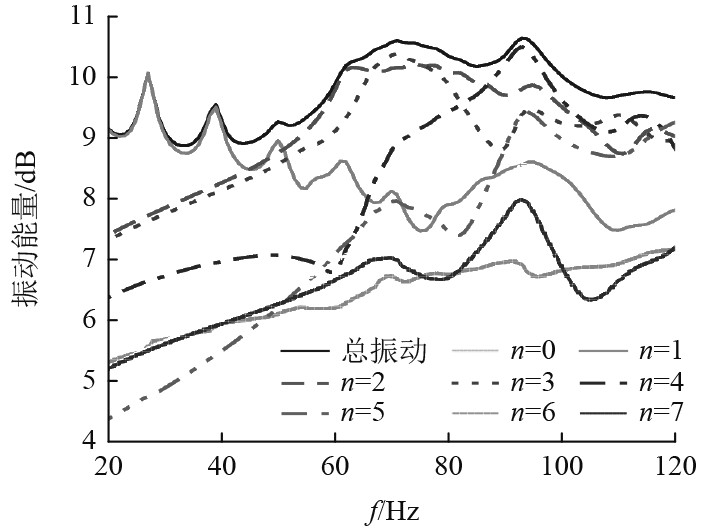
首先要获得图3所示的周期圆柱壳振动等效参数。采用有限元法，以1Hz为步长，计算频率 $ f $ 在1～1 000 Hz范围内变化时周期圆柱壳的振动响应，以此为基础，采用波数分析法，分别获得周向振动模式 $ n $ =0，1，……，15时的 $ {E_n} \sim f $ 曲线，确定对低频振动贡献大的周向振动模式。然后根据式（14）获得低频段范围内各通频带等效参数 $ {f_0} $ 和 $ V $ 。图6为周期圆柱壳各周向振动模式的能量以及圆柱壳总的振动能量随频率的变化规律。可知，在低频段，如120 Hz以下，对总振动贡献大的是 $ n $ =2，3，4阶周向振动模式，并且在低频段， $ n $ =2，3，4的 $ {E_n} \sim f $ 曲线只有一个通频带。在获得通频带等效参数 $ {f_0} $ 和 $ V $ 后，对大肋骨布置不规则程度参数 $ \Delta x/\Delta l $ 取一系列的值，也就获得了一系列非周期圆柱壳模型。用式（15）分别计算各个非周期圆柱壳的振动能量衰减率。如图7所示， $ \Delta x/\Delta l $ =40%时，周向振动模式 $ n $ ，分别取2，3，4的振动能量衰减率在通频带内随频率变化的规律。

由图7可知，在与各周向振动模式相应的通频带内，振动能量衰减率 $ \gamma $ 随频率的增大而减小，并且随着频率的增大，振动衰减变慢，振动衰减程度变小。因此，大肋骨不规则布置控制的是圆柱壳的低频振动。

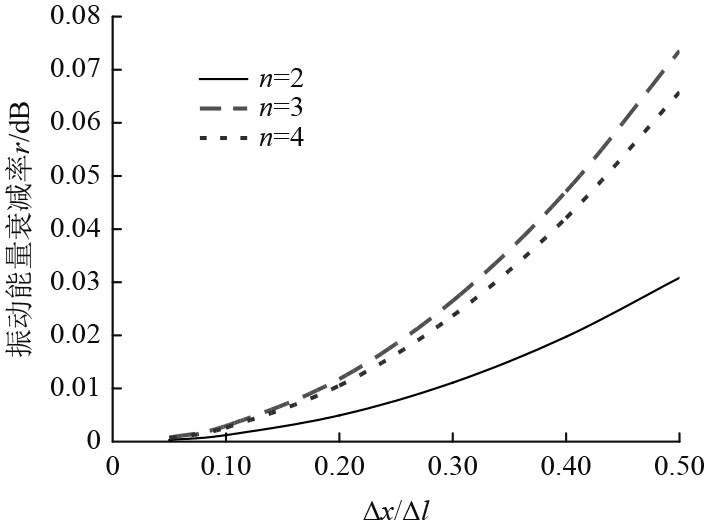
根据式（15），当激振力频率 $ f $ 一定时，振动能量衰减率与 $ \Delta x/\Delta l $ 的平方成正比，为了直观地显示 $ \Delta x/\Delta l $ 对振动能量衰减率的影响规律，做出通频带中心频率处振动能量衰减率随 $ \Delta x/\Delta l $ 变化的曲线，如图8所示。可以看出，无论在哪个周向振动模式下， $ \Delta x/\Delta l $ 的增大将导致振动能量衰减率迅速增大。因此，为了增强振动控制，应适当增大 $ \Delta x/\Delta l $ 。

3 振动衰减的数值模拟

通过数值模拟的方法验证大肋骨间距非周期布置对圆柱壳振动传递的控制效果。

$ \Delta x/\Delta l $ 由小到大取一系列的值，对于每一个 $ \Delta x/\Delta l $ 值，按照式（8）用随机函数确定大肋骨在圆柱壳轴向的位置，建立非周期圆柱壳有限元模型，如图9所示。

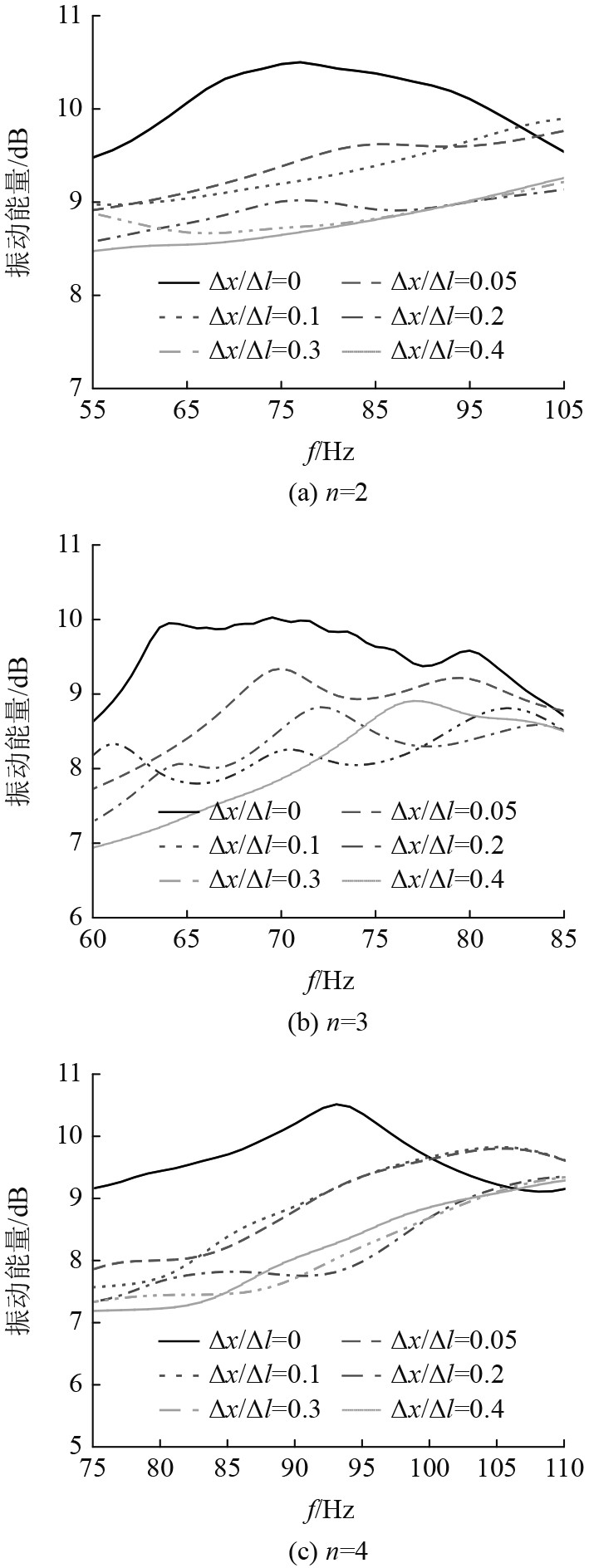
采用有限元法、波数分析法分析非周期圆柱壳的振动特性，并与周期圆柱壳进行比较。图10（a）、10（b）、10（c）分别为 $ n $ =2，3，4阶时，周期与非周期圆柱壳的 $ {E_n} \sim f $ 曲线的对比图。可以看出，在通频带，尤其是频带中部，大肋骨非周期布置使圆柱壳振动衰减，而且衰减程度随着 $ \Delta x/\Delta l $ 值的增大而增强。

为了直观显示振动从振源开始沿圆柱壳轴向向远离振源方向的传递特性，根据式（13）计算圆柱壳截面的振动能量，从而得到截面振动能量沿轴向的变化规律。以周向振动模式 $ n $ =3、激振力频率 $ f $ 等于通频带下限频率60Hz为例，分别做出 $ \Delta x/\Delta l $ =30%、35%、40%、45%、50%时，截面振动能量随截面轴向位置变化的曲线，如图11所示。振动能量呈震荡特征，但是，从轴向看，随着距离振源的距离的增大，振动能量呈衰减分布。式（15）是采用理论推导的方法得到 $ \gamma $ 的解析式， $ \gamma $ 表示振动能量在空间的衰减率。因此，可以做出与 $ \gamma $ 相对应的振动能量衰减线，衰减线是倾斜直线，斜率等于 $ \gamma $ 。由震荡曲线和倾斜直线的对比可知，通过理论方法能够较准确地确定圆柱壳振动能量沿着轴向的衰减规律。

4 结　语

通过大肋骨将圆柱壳分成多个轴向长度随机分布的小段舱段，研究大肋骨的不规则布置对圆柱壳振动传递的控制作用，得出如下结论：

1）可以用耦合振子链系统振动能量衰减率理论公式计算圆柱壳的振动能量衰减率。将圆柱壳的径向振动等效为不同周向振动模式的一维振动的叠加，将一维振动等效为耦合振子链的振动，从而就可以用耦合振子链系统振动能量衰减率理论公式计算圆柱壳的振动能量衰减率。通过与数值模拟的结果比较可知，可以采用上述方法研究圆柱壳振动能量衰减特性。

2）在低频段，圆柱壳振动能量衰减率随频率增大而减小，随 $ \Delta x/\Delta l $ 的增大而增大。在低频段的通频带，在频率下限振动能量衰减率最大，随着频率的增大，振动能量衰减率迅速减小，然后缓慢减小，在频率上限处振动能量衰减率最小。当其他参数不变，圆柱壳的振动能量衰减率与 $ \Delta x/\Delta l $ 的平方成正比，并且当 $ n $ 较大时，振动能量衰减率随 $ \Delta x/\Delta l $ 的增大程度比 $ n $ 较小时更明显。

3）用大肋骨将圆柱壳分成多个轴向长度随机分布的小段，可以构造非周期圆柱壳结构。这种结构能够控制振动沿着圆柱壳轴向向远离振源方向的传递，从而达到减弱圆柱壳整体振动水平的目的。