0 引　言

船舶航行图像采集时容易受到雾霾天气、船舶航行状态等因素影响^[1]，导致获取的图像存在模糊不清甚至变形等问题，造成船舶航行图像质量大幅降低，这将使得图像中蕴含的大量有价值信息掩藏在模糊背景之中^[2]，难以实现船舶航行图像的后续应用。采取有效措施对模糊船舶图像进行视觉优化，以实现有价值信息的利用^[3]。

魏冬等^[4]针对水下图像模糊的问题，提出在对模糊图像进行颜色校正的基础上，利用基于融合暗通道先验的去模糊方法恢复清晰图像，但该方法存在图像对比度拉伸过大等问题，导致去模糊后的图像视觉效果不理想。李博^[5]针对图像边缘模糊等问题，提出基于视觉传达的图像复原方法，利用深度学习网络对边缘模糊图像特征进行提取，以其作为稀疏正则化模型ScSR的输入，完成图像复原，但该方法不适用高模糊度图像的处理，存在严重失真问题。鉴于上述方法存在的问题，本文研究基于视觉传达的模糊不清船舶航行图像优化方法，以改善图像质量，提高图像信息辨识度。

1 模糊不清船舶航行图像优化 1.1 建立模糊船舶航行图像模型

建立模糊船舶航行图像模型是实现图像去模糊的前提，模糊船舶航行图像模型可通过在高清晰度船舶航行图像与模糊核卷积处理的基础上，添加一定噪声得到，公式为：

$ B = k \otimes L + \eta 。$

(1)

式中： $ B $ 为模糊不清船舶航行图像； $ L $ 为高清晰度船舶航行图像； $ k $ 为模糊核通过，即点扩展函数（PSF）； $ \eta $ 为图像噪声； $ \otimes $ 为卷积计算符号。

模糊船舶航行图像复原的关键是模糊核的精准估计，这是反卷积处理实现的前提。

1.2 模糊船舶航行图像预处理

模糊不清船舶航行图像一般都有较清晰的强边缘，但往往弱边缘区域更大，且其中含有大量噪声，这将直接影响模糊核估计的准确度^[6]。因此，本文采用双边滤波器与冲击滤波器相结合方式对模糊不清船舶航行图像进行处理，以达到图像边缘增强目的。利用双边滤波器对模糊不清船舶航行图像进行处理，在不改变图像边缘特征的基础上，实现图像去噪、纹理平滑目标，通过对其邻域像素的加权计算，可完成双边滤波器输出像素值的确定，计算公式为：

$ g\left( {i,j} \right) = \frac{{\sum\limits_{k,l} {f\left( {k,l} \right)\omega \left( {i,j,k,l} \right)} }}{{\sum\limits_{k,l} {\omega \left( {i,j,k,l} \right)} }}。$

(2)

式中：g(i,j)为双边滤波器输出结果；(i,j)为像素点，其邻域像素值表示为f(k,l)，其权重系数表示为ω(i,j,k,l)。

$ \omega \left( {i,j,k,l} \right) = d\left( {i,j,k,l} \right) \times r\left( {i,j,k,l} \right)。$

(3)

式中：d(i,j,k,l)为定义域核，r(i,j,k,l)为值域核。

冲击滤波器具有突出的图像特征增强性能，本文用其实现船舶航行图像强边缘的增强处理，通过下式描述冲击滤波过程：

$ D_{t+1}=D_t-\mathrm{sgn}\left(\Delta D_t\right) \left\| \nabla D_t \right\| \mathrm{d}t。$

(4)

式中：D_t为 $ t $ 时间点下的模糊船舶航行图像， $ \Delta {D_t} $ 为拉普拉斯算子； $ \nabla {D_t} $ 为图像梯度。

1.3 模糊核的正则化估计

模糊不清船舶航行图像的模糊核具有稀疏性特点，为使模糊核的稀疏性不变，在模糊核估计过程中，用下式定义其能量函数：

$ \mathop {\min }\limits_{k,\nabla I} \frac{{\left\| {\nabla L \otimes k - \nabla B} \right\|_2^2}}{2} + \gamma \left\| k \right\|_2^2 + \lambda \left\| {\nabla L} \right\|_0^{} + \beta \left\| {\nabla k} \right\|_2^{}。$

(5)

式中： $ \nabla $ 为梯度计算符号， $ \gamma $ 、 $ \lambda $ 、 $ \beta $ 为正则项权值分别。通过上式可确定0范数的近似值，同时沿横向、纵向将其展开。通过交替迭代确定模糊核 $ k $ 、高清晰度船舶航行图像的梯度 $ \nabla L $ 。

首先对模糊核进行调整。令 $ \nabla L $ 不变， $ k $ 计算公式为：

$ \begin{split} \min k = &\frac{{\left\| {{\partial _x}L \otimes k - {\partial _x}B} \right\|_2^2 + \left\| {{\partial _y}L \otimes k - {\partial _y}B} \right\|_2^2}}{2} + \\ & \gamma \left\| k \right\|_2^2 + \beta {\phi _0}\left( {{\partial _x}k} \right) + \beta {\phi _0}\left( {{\partial _x}k} \right) 。\\ \end{split} $

(6)

为计算出 $ {\phi _0}\left( {{\partial _*}k} \right) = \sum\limits_i \phi \left( {{\partial _*}{k_i}} \right) $ ，本文引入补充变量 $ {l_1} $ 并使其满足下式条件：

$ \left\{\begin{gathered}l_{1x_i}=\left\{\begin{gathered}0,\left|\partial_xk_i\right|\leqslant\rm{\varepsilon\;}1，\\ \partial_xk_i,\mathrm{otherwise}，\\ \end{gathered}\right. \\ l_{1y_i}=\left\{\begin{gathered}0,\left|\partial_yk_i\right|\leqslant\rm{\varepsilon\;1}，\\ \partial_yk_i,\mathrm{otherwise}，\\ \end{gathered}\right. \\ \end{gathered}\right. $

(7)

由此可将式（6）转换为：

$ \begin{split} \min k = &\frac{{\left\| {{\partial _x}L \otimes k - {\partial _x}B} \right\|_2^2 + \left\| {{\partial _y}L \otimes k - {\partial _y}B} \right\|_2^2}}{2}+ \\ &\gamma \left\| k \right\|_2^2 + \beta \sum\limits_i {\left\{ {{{\left| {{l_1}_{{x_i}}} \right|}_0} + \varepsilon _1^{ - 2}{{\left( {{\partial _x}{k_i} - {l_1}_{{x_i}}} \right)}^2}} \right\}} + \\ &\beta \sum\limits_i {\left\{ {{{\left| {{l_1}_{{y_i}}} \right|}_0} + \varepsilon _1^{ - 2}{{\left( {{\partial _y}{k_i} - {l_1}_{{y_i}}} \right)}^2}} \right\}} 。\end{split} $

(8)

式（8）是对二次凸优化问题的描述，利用FFT算法即可完成高清晰度船舶航行图像梯度与模糊核之间的卷积计算，获得 $ k $ 的最佳估计结果，其公式为：

$\begin{split} &{k = \frac{1}{F}\times}\\ &{\left[ {\frac{{\overline {F\left( {{\partial _x}L} \right)} \cdot F\left( {{\partial _x}B} \right) + \overline {F\left( {{\partial _y}L} \right)} \cdot F\left( {{\partial _y}B} \right) + \varepsilon _1^{ - 2}\beta \left( {\overline {F\left( {{\partial _x}} \right)} \cdot F\left( {{l_1}_x} \right) + \overline {F\left( {{\partial _y}} \right)} \cdot F\left( {{l_1}_y} \right)} \right)}}{{\overline {F\left( {{\partial _x}L} \right)} \cdot F\left( {{\partial _x}B} \right) + \overline {F\left( {{\partial _y}L} \right)} \cdot F\left( {{\partial _y}B} \right) + 2\gamma + \varepsilon _1^{ - 2}\beta \left( {\overline {F\left( {{\partial _x}} \right)} \cdot F\left( {{l_1}_x} \right) + \overline {F\left( {{\partial _y}} \right)} \cdot F\left( {{l_1}_y} \right)} \right)}}} \right] 。}\end{split}$

(9)

式中： $ F $ 为傅里叶变换，1/F为其逆过程， $ \overline {F\left( * \right)} $ 为 $ F\left( * \right) $ 的共轭结果； $ \cdot $ 为点乘运算符。

再令 $ k $ 不变，对 $ \nabla L $ 进行计算，公式描述为：

$ \begin{split} & \mathop {\min }\limits_{\nabla L} \frac{{\left\| {{\partial _x}L \otimes k - {\partial _x}B} \right\|_2^2 + \left\| {{\partial _y}L \otimes k - {\partial _y}B} \right\|_2^2}}{2} + \\ & \lambda {\phi _0}\left[ {\left( {{\partial _x}L} \right) + \left( {{\partial _y}k} \right)} \right]，\end{split} $

(10)

同时加入补充变量 $ l $ ：

$ \left\{\begin{gathered}l_{x_i}=\left\{\begin{gathered}0,\left|\partial_xL_i\right|\leqslant\varepsilon，\\ \partial_xL_i,\mathrm{otherwise}，\\ \end{gathered}\right. \\ l_{y_i}=\left\{\begin{gathered}0,\left|\partial_yL_i\right|\leqslant\varepsilon，\\ \partial_yL_i,\mathrm{otherwise}。\\ \end{gathered}\right. \\ \end{gathered}\right. $

(11)

通过计算 $ {\phi _0}\left( {\partial *L} \right) = \displaystyle\sum\limits_i {\phi \left( {{\partial _*}{L_i}} \right)} $ ，即可完成 $ \nabla L $ 最佳结果的确定，通过不断对 $ k $ 、 $ \nabla L $ 进行交替计算，即可实现模糊不清船舶航行图像模糊核的估计。

1.4 基于梯度稀疏约束的反卷积

在确定模糊不清船舶航行图像模糊核的最优估计结果后，通过基于梯度稀疏约束的反卷积方法实现模糊船舶航行图像的复原。正则项为：

$ {\rho _L}\left( L \right) = {\left\| {\nabla L} \right\|^{0.8}}，$

(12)

高清晰度船舶航行图像 $ L $ 的迭代方程为：

$ L' = \mathop {\min }\limits_L \left\{ {{{\left\| {B - L*k} \right\|}_2} + \beta \cdot {{\left\| {\nabla L} \right\|}^{0.8}}} \right\}。$

(13)

其中，β为正则化约束系数，其值决定了模糊船舶航行图像梯度的平滑强度，二者之间具有正比例关系。

经过反卷积处理，即可获得去模糊后的船舶航行图像。

1.5 基于视觉传达的船舶航行图像优化

实现模糊不清船舶航行图像的复原后，基于人眼视觉特性，运用HSV色彩模型对复原后的船舶航行图像作优化处理，以满足视觉传达要求。基于视觉传达的船舶航行图像优化即是获得反映图像颜色特征的空间模型，从而实现船舶航行图像视觉效果的改善。

2 性能测试与分析

图1为采集的2幅模糊不清船舶航行图像，图1（a）晴朗天气下采集，船舶快速运动是导致图像模糊的主要因素；图1（b）雾霾天气下采集。采用本文方法对图像进行去模糊处理，结果如图2所示。分析可知，经本文方法进行去模糊处理后，图像清晰度获得显著提升，图像目标信息得到充分还原，细节纹理信息丰富，边缘特征突出，这充分说明本文方法可实现模糊船舶航行图像的处理，去模糊性能较好，但去模糊后的船舶航行图像存在视觉传达效果较差的问题，主要表现为图像颜色暗淡、图像明亮度不够、色彩饱和度不高等，因此，需对其进一步处理，以满足人眼视觉要求。

采用本文方法对图2船舶航行图像进行视觉传达优化，通过对比优化前后图像视觉差异，分析本文方法的视觉传达优化性能，实验结果如图3所示。分析可知，图2船舶航行图像经过视觉传达优化后，图像质量获得显著提升，图像清晰度更高、色彩饱和度更好、图像亮度、对比度等指标均达到视觉传达要求。实验结果表明，本文方法具有船舶航行图像视觉传达优化性能，优化效果显著。

结构相似度（SSIM）、信息熵是评价图像视觉效果的重要指标，前者反映视觉传达优化后图像与清晰图像的一致程度，后者度量视觉传达优化后图像所含信息量的多少，两指标值越大，船舶航行图像的视觉传达优化效果越突出。从数据集中随机选取7幅模糊不清船舶航行图像，采用本文方法对其进行视觉优化处理，通过对比分析去模糊后、视觉优化后图像与清晰船舶航行图像的结构相似度、信息熵指标值差异，验证本文方法的视觉优化性能，实验结果如表1所示。分析可知，视觉优化后的船舶航行图像与清晰船舶航行图像的结构相似度指标值介于[0.911,0.967]之间，信息熵指标最小值为9.24、最大值为9.49；去模糊后的船舶航行图像与清晰图像之间的结构相似度指标最大值为0.947、最小值为0.900，信息熵指标最大、最小值分别为9.37、9.11。通过对比发现，视觉传达优化可有效提升船舶航行图像质量，两指标值均有一定程度提升。实验结果表明，本文方法具有船舶航行图像视觉传达优化性能，图像视觉效果显著提升。

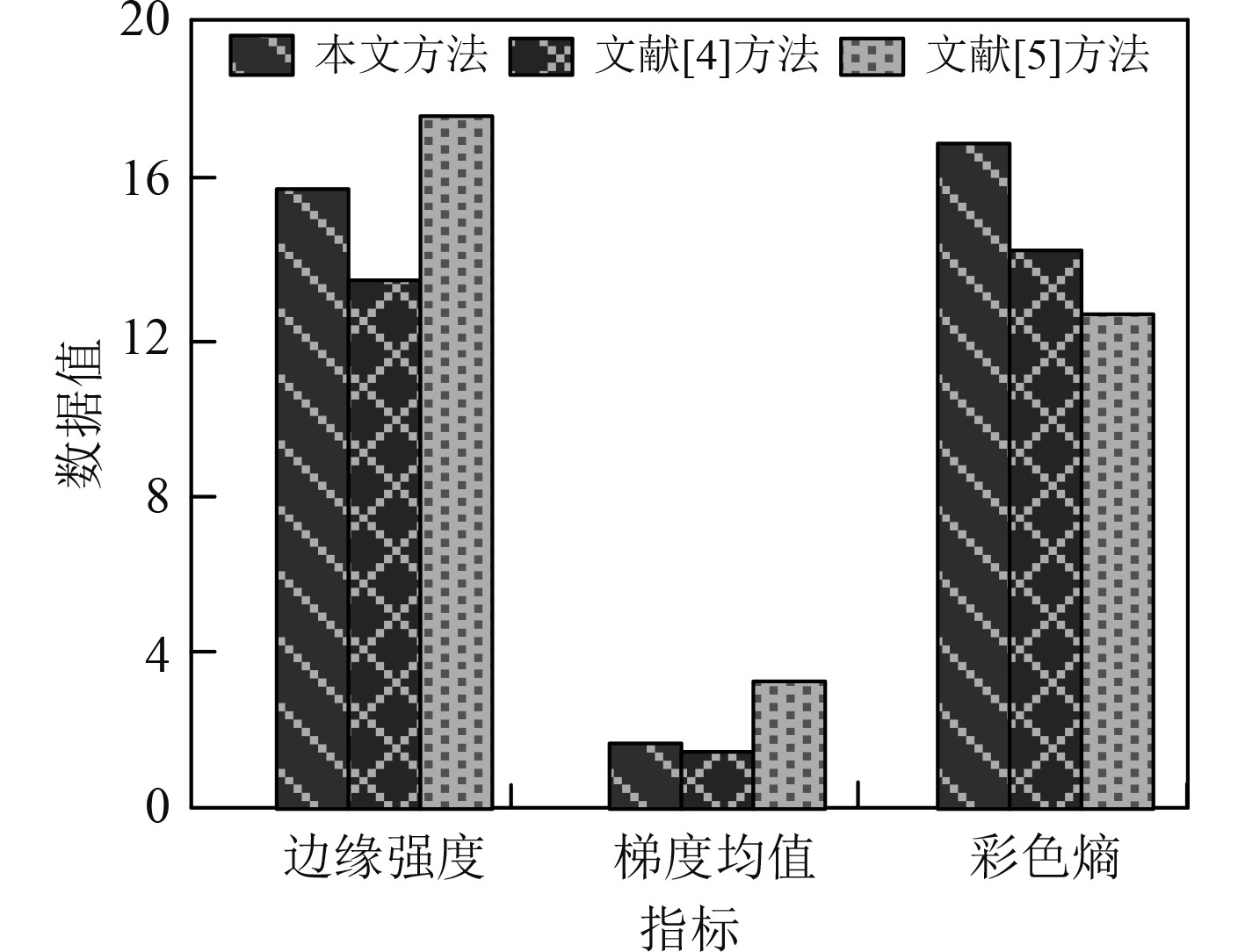
设定清晰船舶航行图像的边缘强度、梯度均值、彩色熵分别为15.16、1.60、17.00，前者衡量船舶航行图像的清晰度、中间指标度量图像细节的对比度，后者反映图像颜色的饱和度。将本文方法、文献[4]的颜色校正和去模糊方法、文献[5]的图像重建方法的各指标评价结果与清晰图像的各指标值进行对比，通过分析各指标差异，验证本文方法的优越性，实验结果如图4所示。分析可知，利用文献[5]方法对模糊船舶航行图像进行视觉优化处理，图像的边缘强度指标、梯度均值指标均高于清晰船舶航行图像对应参数值，其彩色熵远低于参数设定值，这说明该方法处理后的船舶航行图像存在严重失真问题；文献[4]方法处理后的图像仅在图像细节对比度上具有良好表现；应用本文方法对模糊船舶航行图像进行优化处理，可达到清晰图像参数设定要求。实验结果表明，本文方法的图像视觉传达优化性能优于文献[5]方法。

3 结　语

本文通过对模糊船舶航行图像进行预处理，提高图像模糊核的估计效果，以此获得高质量去模糊船舶航行图像，基于人眼视觉特性，通过对去模糊后的图像进行视觉优化，以获得最优视觉效果的船舶航行图像。实验结果表明，本文方法可实现模糊船舶航行图像的视觉传达优化，优化后的图像SSIM、信息熵指标最大值可达到0.967、9.49；边缘强度、梯度均值、彩色熵指标达到设定要求，图像视觉优化效果突出。