0 引　言

舰船机电设备的复杂性与多样性等特点^[1]，加大了其控制难度。在舰船航行过程中，当机电设备控制错误时，则会直接影响舰船航行的安全性^[2]。传统的人工控制方式，机电设备控制效率低，且控制误差较高，不利于舰船安全航行^[3]。为此，需要研究舰船机电设备自动控制系统，以解决上述问题。白洪芬等^[4]依据舰船机电设备运行数据，构建舰船机电设备数学模型，并添加动态适应机电设备的新型趋近律，实现自动控制系统的快速响应，通过扩展状态观测器，对机电设备运行参数展开观测补偿，抑制机电设备自动控制时的抖动问题。该系统可有效自动控制舰船机电设备，且自动控制的稳定性较优。孙志豪等^[5]通过整流模块，在舰船机电设备运行数据内，提取功率和频率响应特征，利用逆变模块，依据响应特征，矢量控制机电设备。该系统具备机电设备自动控制的可行性。但上述系统均不具备异常数据剔除功能，影响舰船机电设备自动控制精度。贝叶斯统计模型具备较优的参数估计效果，可解决过拟合问题^[6]，提升数据分类检测精度。为此，研究贝叶斯统计模型在舰船机电自动控制系统中的应用，提升机电自动控制精度，确保舰船安全航行。

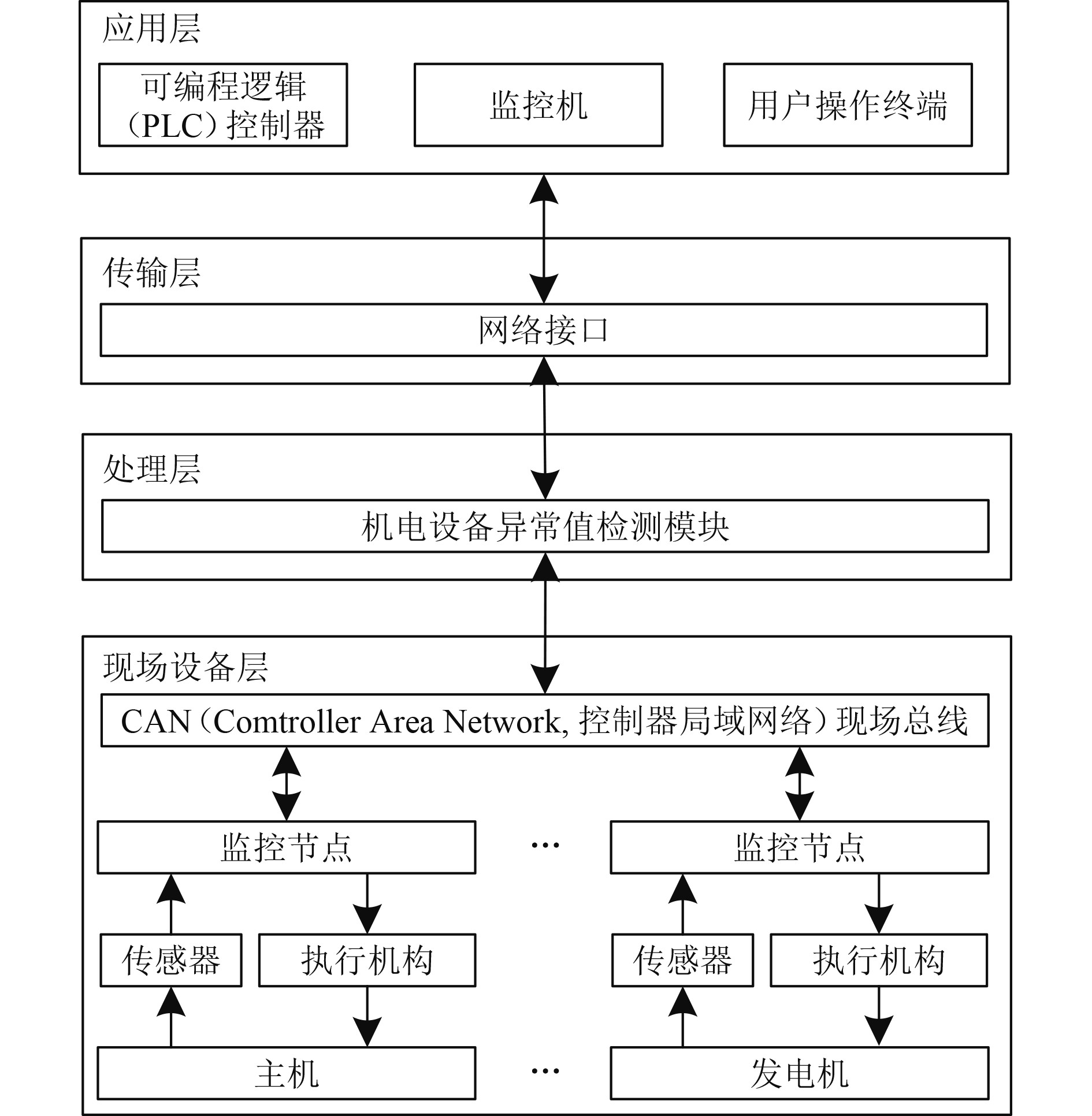
1 舰船机电自动控制系统

为实现舰船机电设备的自动控制，设计舰船机电设备自动控制系统。该系统包含现场设备层、处理层、传输层与应用层4层，舰船机电设备自动控制系统的总体结构如图1所示。

1）现场设备层利用监控节点采集舰船机电设备的运行数据，并经由CAN总线传输至处理层。同时该层在接收舰船机电设备控制指令后，利用执行机构依据控制指令，自动控制机电设备。

2）处理层中机电设备异常值检测模块，利用贝叶斯统计模型，检测舰船机电设备运行数据采集结果内的异常值，并剔除异常值，避免因输入异常值，而影响机电设备自动控制精度。

3）传输层通过网络接口，将异常值剔除后的舰船机电设备运行数据，传输至应用层，同时还负责将控制指令，传输至现场设备层。

4）应用层中PLC控制器依据舰船机电设备运行数据，确定舰船机电设备控制向量；用户操作终端依据控制向量，生成舰船机电设备控制指令；通过监控机实时监测舰船机电设备自动控制过程。

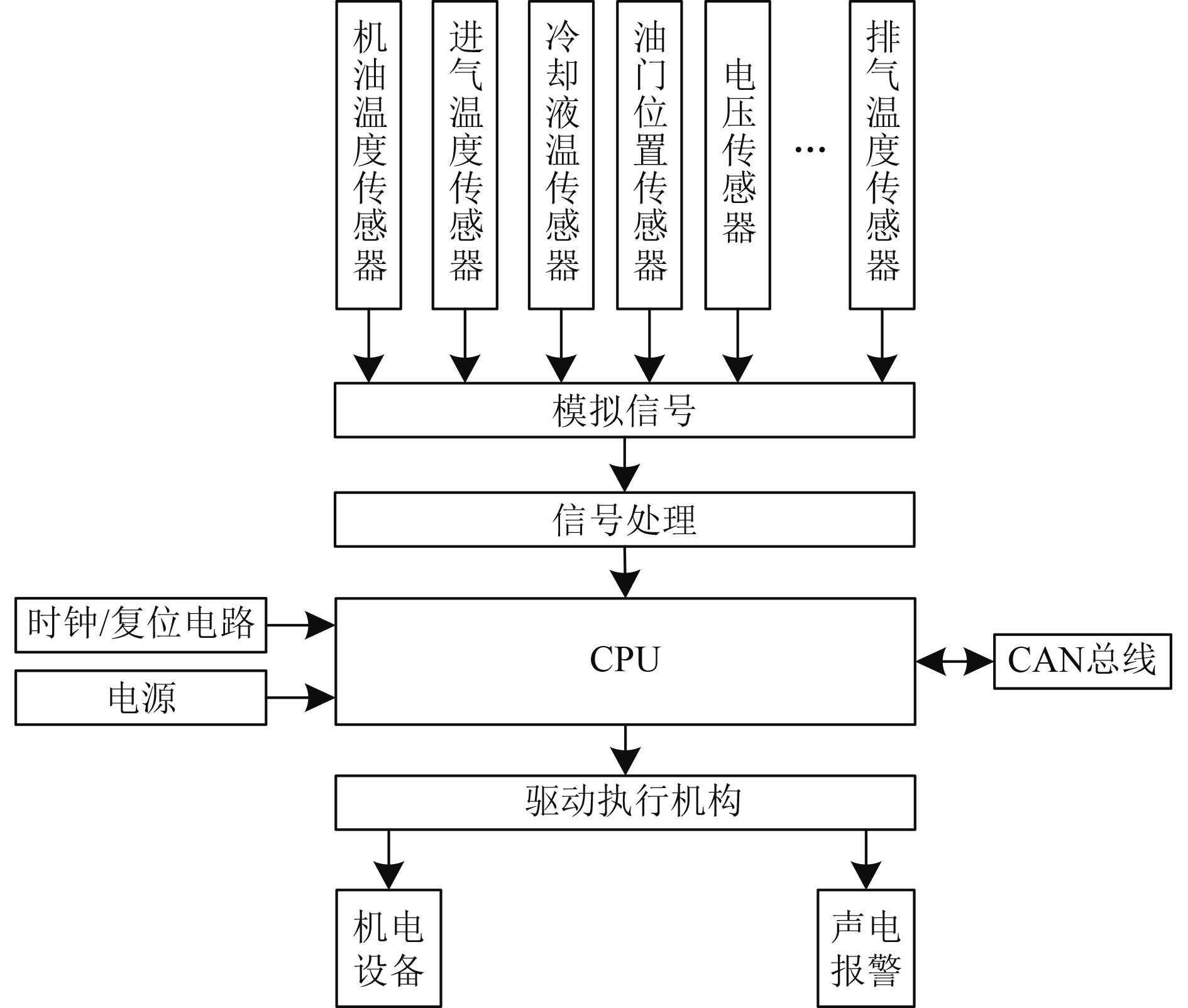
1.1 舰船机电设备运行数据采集的监控节点

现场设备层利用监控节点采集舰船机电设备运行数据，监控节点的硬件框图如图2所示。

监控节点通过控制不同类型的传感器，采集机电设备运行数据，并通过信号处理单元，对采集的运行数据进行预处理，滤除噪声数据，由CPU整合处理，经由CAN总线传输至处理层。利用电源单元，为监控节点提供电力支持。利用时钟/复位电路，控制CPU的复位状态，避免CPU发出错误指令。当CPU接收舰船机电设备控制指令时，通过分析控制指令，驱动执行机构，自动控制机电设备；通过声电报警单元，呈现机电设备运行状态。

1.2 舰船机电设备运行数据异常值检测

处理层中机电设备异常值检测模块，利用贝叶斯统计模型，检测舰船机电设备运行数据内的异常值，并将其剔除。构建考虑平差的舰船机电设备运行数据模型，公式如下：

$ \left\{ \begin{gathered} Z = {\boldsymbol{A}}X + {\boldsymbol{\varDelta}} ，\\ {\boldsymbol{\varDelta}} \sim {N_n}\left( {0,\frac{{\sigma _0^2}}{{\boldsymbol{W}}}} \right) 。\\ \end{gathered} \right. $

(1)

其中： $ {\text{Z}} = \left( {Z_1},{Z_2}, \cdots ,{Z_n} \right) $ 为采集的舰船机电设备运行数据样本； $ X $ 为模型参数； $ n $ 为机电设备运行数据样本数量；设计阵 $ {\boldsymbol{A}} = \left( {{a_1},{a_2}, \cdots ,{a_n}} \right) $ ，权矩阵为 $ {\boldsymbol{W}} = ( {w_1}, $ $ {w_2}, \cdots ,{w_n} )$ ； $ \sigma _0^{} $ 为未知单位权方差； ${\boldsymbol{ \varDelta}} = ( {\Delta _1},{\Delta _2}, \cdots , $ $ {\Delta _n}) $ 为 $ Z $ 的误差向量； $ {N_n}\left( {0, \displaystyle\frac{{\sigma _0^2}}{Z}} \right) $ 为正太分布。

令后验概率阵为 $ {\boldsymbol{Q}} = \dfrac{1}{{\boldsymbol{W}}} $ ， $ {\boldsymbol{Q}} $ 内的元素是后验概率 $ {q_i} $ ，当 $ {q_i} = W\left( {{\theta _i} = 1\left| {{Z_i}} \right.} \right) > \dfrac{1}{2} $ 时，那么判定第 $ i $ 个舰船机电设备运行数据样本 $ {Z_i} $ 内存在异常值；反之， $ {Z_i} $ 内无异常值。其中， $ {Z_i} $ 内引入的随机变量是 $ {\theta _i} $ 。利用吉布斯抽样，求解 $ {q_i} $ ，具体步骤如下：

步骤1　令舰船机电设备运行数据的初始向量为 $ {{\boldsymbol{Y}}_0} = \left( {\sigma _0^{},{\theta _0},{X_0}} \right) $ 。

步骤2　第 $ t \geqslant 1 $ 次抽样时，舰船机电设备运行数据样本向量是 $ {{\boldsymbol{Y}}_{t - 1}} = \left( {\sigma _{t - 1}^{},{\theta _{t - 1}},{X_{t - 1}}} \right) $ ，因此，第 $ t $ 次抽样时，舰船机电设备运行数据样本向量为 $ {{\boldsymbol{Y}}_t} = \left( {\sigma _t^{}, {\theta _t}, {X_t}} \right) $ 。 $ \sigma _t^{} $ 在条件分布 $ W\left( {\sigma _t^{}\left| {Z,{\theta _{t - 1}},{X_{t - 1}}} \right.} \right) $ 内抽取， $ {\theta _t} $ 在条件分布 $ W\left( {\sigma _t^{}\left| {Z,{\theta _{t - 1}},{X_{t - 1}}} \right.} \right) $ 内抽取， $ X_t^{} $ 在条件分布 $ W( X| Z,\theta_{t - 1}, $ $ X_{t - 1} )$ 内抽取。

步骤3　当马尔科夫链稳定时，结束抽样，获取吉布斯样本 $ \hat Y $ ，依据 $ \hat Y $ 便可计算获取 $ {q_i} = W\left( {{\theta _i} = 1\left| {{Z_i}} \right.} \right) $ 。通过贝叶斯统计模型，估计 $ X $ 的值，公式如下：

$ \hat X = {\left( {{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{WA}}} \right)^{ - 1}} {{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{W}}\left( {Z - \lambda } \right)。$

(2)

式中： $ \hat X $ 为 $ X $ 的估计结果； $ \lambda $ 为异常值参数向量。

代入后验概率计算过程中，得到最终的后验概率计算结果，进行舰船机电设备运行数据异常值检测，并剔除检测到的异常值。

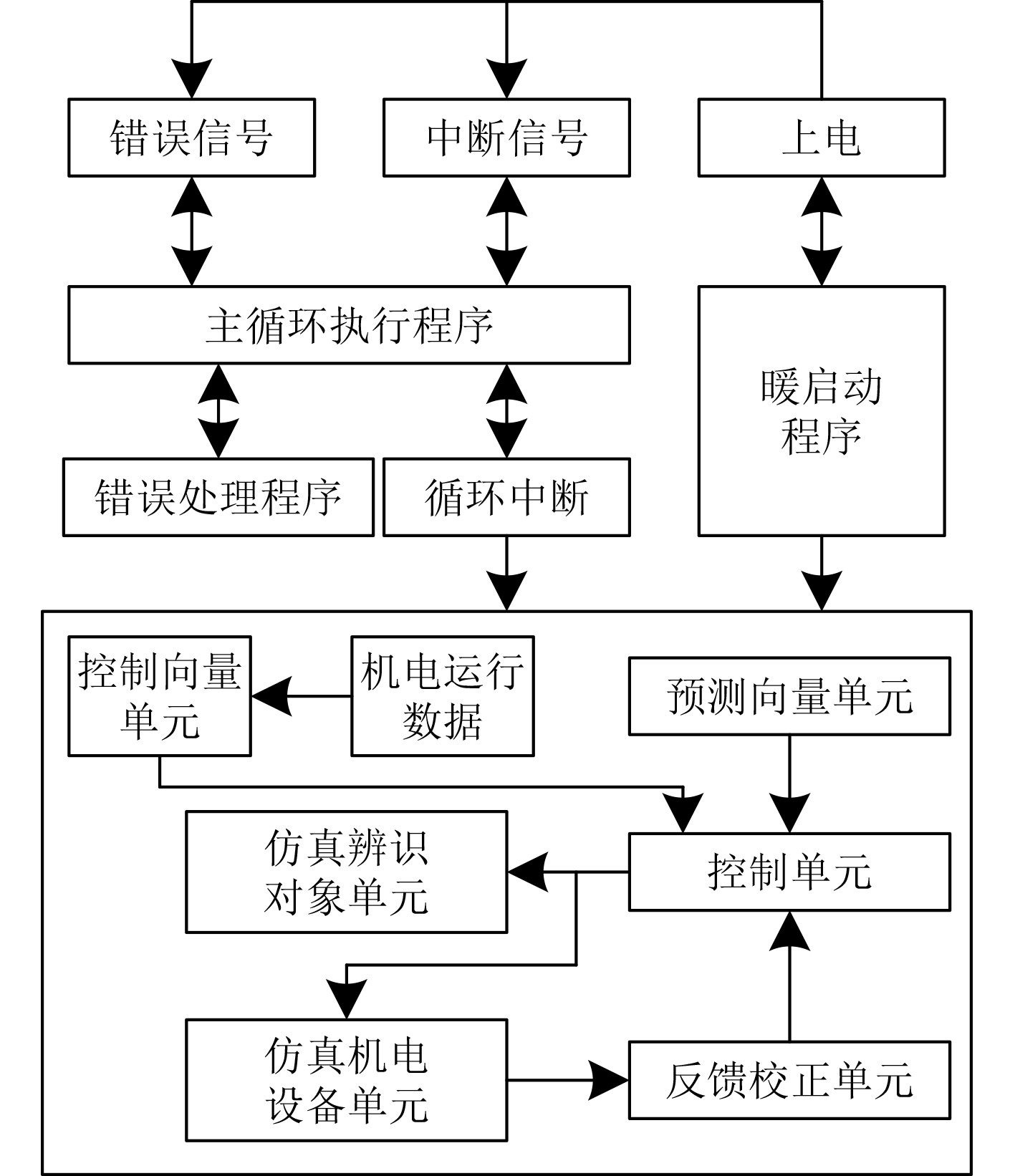
1.3 舰船机电的PLC控制器

应用层利用PLC控制器，结合异常值剔除后的机电设备运行数据，完成舰船机电的自动控制，PLC控制器的舰船机电自动控制过程如图3所示。

利用PLC控制器自动控制舰船机电的具体步骤如下：

步骤1　通过暖启动程序，初始化用户操作终端的上电过程。

步骤2　通过预测向量单元，初始化舰船机电自动控制的预测向量。

步骤3　将异常值剔除后的舰船机电运行数据输入，控制向量单元，通过该单元输出舰船机电自动控制向量。

步骤4　将预测向量、运行数据与自动控制向量，输入控制单元与反馈校正单元，再次输出舰船机电自动控制向量，并传输至仿真机电设备单元与仿真辨识对象单元，得到二者的输出值后，通过反馈校正单元，校正舰船机电自动控制向量误差，调用控制单元，结合自动控制向量误差，得到最终的舰船机电自动控制向量。

2 结果与分析

以某舰船机电设备为实验对象，该舰船机电设备主要包含动力装置、辅助装置、推进装置与中央冷却水系统等。

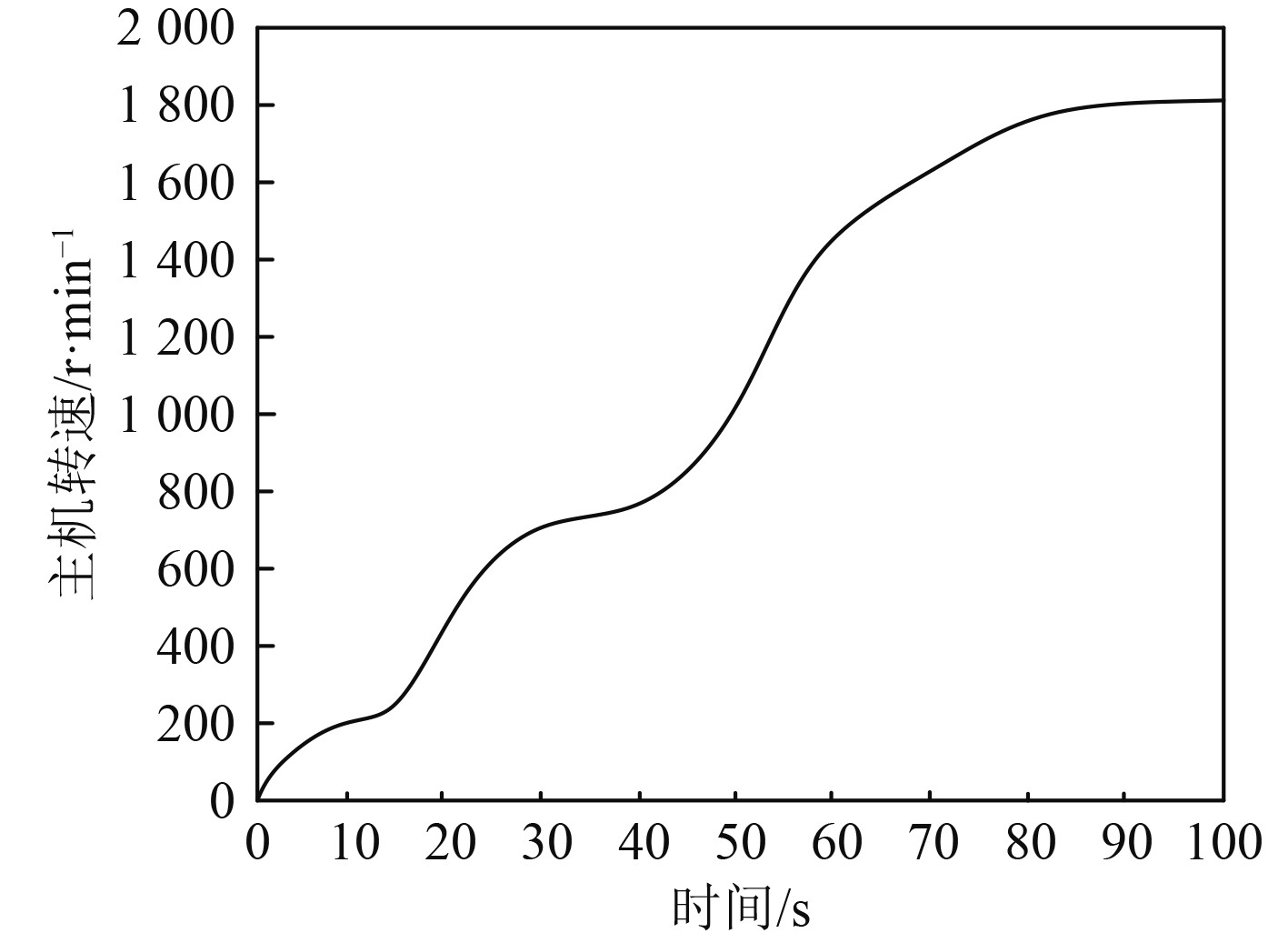
利用本文系统采集该舰船机电设备运行数据，以动力装置内的主机转速为例，采集结果如图4所示。可知，本文系统可有效采集舰船主机转速，由采集结果可知，该舰船启动过程中，主机转速缓慢上升，当运行时间到达90 s左右时，主机转速稳定在1 800 r/min左右。实验证明，本文系统可有效采集舰船机电设备运行数据。

利用本文系统对采集的机电设备运行数据，进行异常值检测，以主机转速、发电机电压与发电机电流为例，在3种类型的运行数据样本内，共选择15个样本，利用本文系统对这3种类型的15个样本进行异常值检测，异常值检测结果如表1所示。可知，本文系统可有效计算舰船机电设备运行数据样本的后验概率。其中，主机转速数据样本编号为5与15的后验概率大于0.5，说明这2个样本内包含异常值，需剔除这2个样本；发电机电压数据样本编号为10、12与13的后验概率大于0.5，说明这3个样本内包含异常值，需剔除这3个样本；发电机电流数据样本编号为2与11的后验概率大于0.5，说明这2个样本内包含异常值，需剔除这2个样本。实验证明，本文系统可有效检测舰船机电设备运行数据异常值。

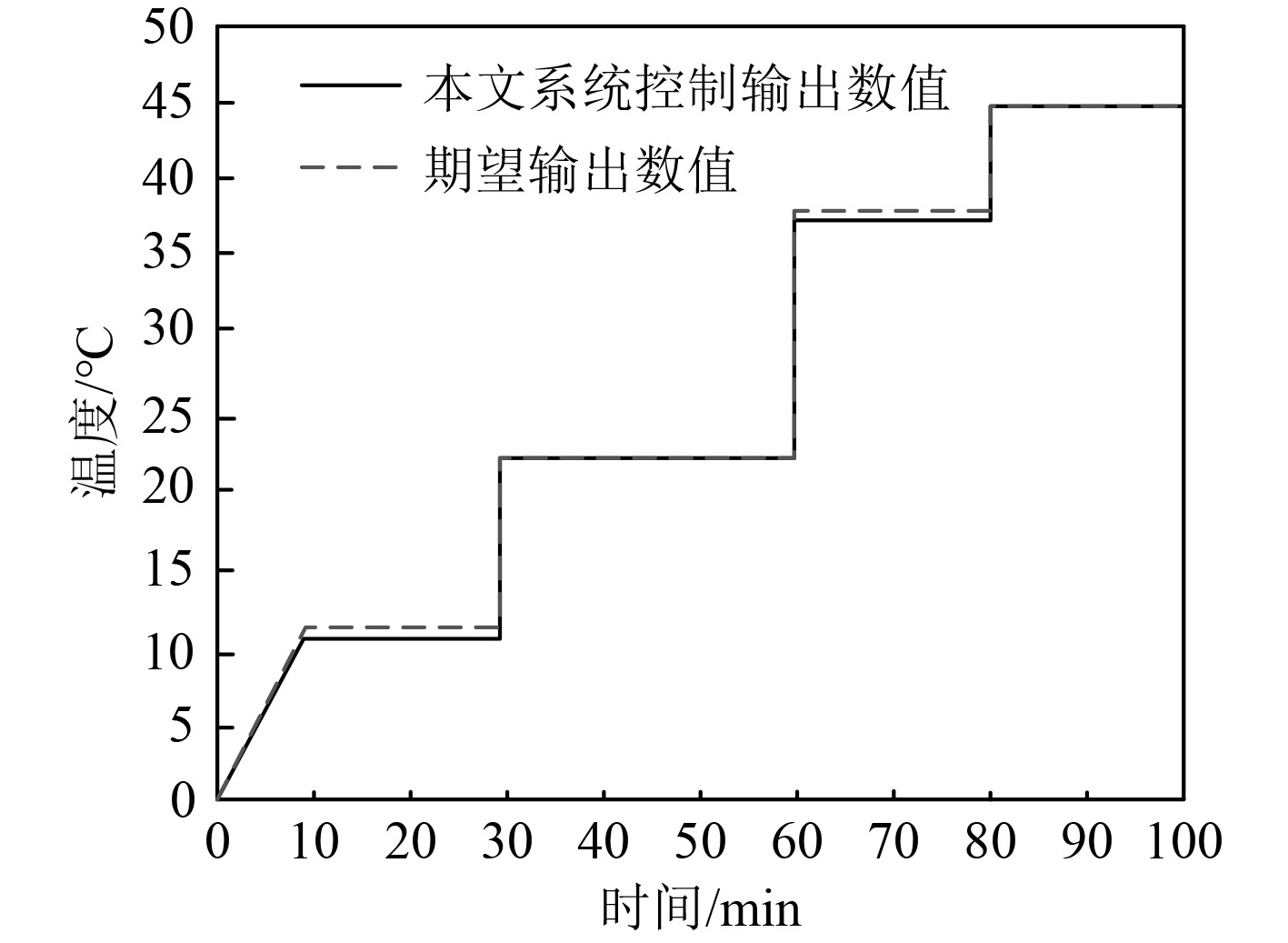
利用本文系统对该舰船机电进行自动控制，以中央冷却水系统的低温水进机温度为例，本文系统的自动控制结果如图5所示。可知，本文系统可有效自动控制中央冷却水系统的低温水进机温度，且本文系统自动控制的输出数值，与期望数值相差甚小，具备较优的温度跟踪效果，说明本文系统的舰船机电自动控制精度较高。

3 结　语

舰船机电设备的控制效果，直接影响舰船航行的安全性。为此，研究贝叶斯统计模型在舰船机电自动控制系统中的应用。利用贝叶斯统计模型，精准分类异常数据，提升舰船机电自动控制精度，为舰船安全航行提供保障。