自20世纪80年代以来,舰船电力推进技术得到了长足的发展[1],由此而出现并兴起的吊舱推进装置、轮缘推进器等水下推进装置越来越受到各国造船领域的关注。这一类的水下推进装置将电机和螺旋桨结合在一起,具有噪声低、功率密度高、效率高、可靠性高、易于模块化等优点[2-4]。在此基础上而发展出的液体泵也同样比传统液体泵更具优势。
机泵一体化装置正是由此而研发出的一种舰船用排水装置,它由轴流泵和Halbach结构的永磁同步电机集成,省去了传统泵体的传动轴系,使泵和管道融合在一起,电机转子内侧有螺旋桨结构作为轴流泵的泵叶,泵叶外缘与电机转子内缘相接,电机转子外缘通过滑动轴承与泵体机座内缘相接,其实物结构如图1所示。

|
图 1 机泵一体化装置 Fig. 1 Physical drawing of machine pump integrated device |
振动噪声性能是水面舰船以及水下航行器的一个重要指标,机泵一体化装置的噪声主要由Halbach结构的永磁同步电机所产生的噪声以及螺旋桨产生的噪声组成,本文主要研究装置在水中运行时电机所产生的噪声。对于电机振动噪声而言,Jordan[5]早在1950年撰写了第一部关于电机振动噪声的书籍;20世纪60年代末,Elison等[6]学者把电机放入有限长圆柱进行电磁噪声辐射功率计算。诸自强[7-10]通过解析推导,并采用有限元方法进行验证,发现解析解与有限元解之间吻合良好,建立了计算永磁电机电磁噪声的计算方法。时至今日,对水中工作的电机振动噪声鲜有研究。因此本文利用有限元的方法,分析Halbach结构的永磁同步电机在水中工作时的噪声传播规律,并运用热负荷理论提出电机优化方法。
1 流体中电机噪声特性 1.1 电机噪声理论分析电机因振动而产生噪声,噪声可在介质中以声波的形式传播[11]。在研究电机电磁噪声辐射时,一般把电机看作圆柱形或球形辐射器,此时定子表面的振动为:
| $ y = \sum\limits_{n = 0}^\infty {{y_{{n}}}} = \sum\limits_{n = 0}^\infty {{A_{{n}}}} \cos \left( {{\omega _{\text{n}}}t - n\varphi } \right)。$ | (1) |
式中:ωn为电机旋转角频率;φ为相位角。同时电机表面振动声强可表示为:
| $ I = 2\rho c{ {\text{π}} ^2}f_n^2A_n^2{I_{cn}}。$ | (2) |
式中:ρ为介质的密度;c为在介质中的声波传递速度;fn为电机振动的n阶固有频率;Icn为相对声强系数。
其中相对声强系数计算公式可表示为:
| $ {I_{{{cn}}}} = \frac{I}{{{I_{{p}}}}} = \frac{2}{{ {\text{π}} \left( {k{R_0}} \right)\left[ {J_{{n}}^{\prime 2}\left( {k{R_0}} \right) + Y_{{n}}^{\prime 2}\left( {k{R_0}} \right)} \right]}} 。$ | (3) |
式中:Ip为电机在无穷大噪声辐射平面时产生的振动声强;kR0为电机外表面半径,k=ωn/c,R0为电机整体的外半径;Jn(kR0)为以kR0为参数的第一类贝塞尔函数;Yn(kR0)为以kR0为参数的第二类贝塞尔函数[12]。
则声功率可表示为:
| $ W = 2\rho c{ {\text{π}} ^2}f_{{n}}^2A_{{n}}^2\left( {2 {\text{π}} {R_0}L} \right){I_{{{cn}}}}。$ | (4) |
式中,L为电机轴向长度。当声波以正弦波的形式传播时,振动声强可表示为:
| $ I = \frac{{{P^2}}}{{{Z_0}}} 。$ | (5) |
式中,Z0为介质的特性阻抗,Z0=ρc。因声压、声强以及声功率数值范围变化较大,需引入声压级、声强级和声功率级的基准量。
其中声压级表示为:
| $ {L_P} = 20\log \frac{P}{{{P_0}}} 。$ | (6) |
声强级表示为:
| $ {L_I} = 10\log \frac{I}{{{I_0}}}。$ | (7) |
声功率级表示为:
| $ {L_w} = 10\log \frac{W}{{{W_0}}} 。$ | (8) |
式中:P0、I0、W0分别为基准声压、基准声强、基准声功率。
总声压级表示为:
| $ {L_P} = 10\lg \sum\limits_{i = 1}^n 1 {0^{{L_{P{{i}}}}/10}} 。$ | (9) |
通常在研究电机噪声时主要是测量电机在空气中的噪声,而本文所研究的机泵一体化装置运行在水中,需测量水中的噪声。水和空气是2种不同的声传播介质,噪声在2种介质中传播特性也不尽相同。
假设空间中一点P为声压较高的点,其幅值可以近似为[41]:
| $ \left| P \right| = \frac{{\omega {u_0}\rho }}{{ {\text{π}} kR}}\frac{{2L}}{{H_n^\prime (f)}}。$ | (10) |
式中:
对于海水与空气2种不同的噪声传播介质,点P的声压幅值比为:
| $ \gamma = \frac{{{P_{{\text{air}}}}}}{{{P_{{\text{water}}}}}} = \frac{{{\rho _{{\text{air}}}}{c_{{\text{air}}}}}}{{{\rho _{{\text{water}}}}{c_{{\text{water}}}}}}\frac{{H_n^\prime \left( {{f_{{\text{air}}}}} \right)}}{{H_n^\prime ({f_{{\text{water}}}})}} = {\gamma _Z}{\gamma _H} 。$ | (11) |
式中:Pair为空气中的噪声;Pwater为海水中的噪声;
可知,即使是力波阶数n、电机表面振动加速度u0都相同时,2种介质的声压除了与特性阻抗ρ有关外,还与介质声辐射效率系数密切相关。
将式(11)两边取对数可得:
| $ \Delta \gamma = 20\lg {P_{{\text{air}}}} - 20\lg {P_{{\text{water}}}} = 20\lg \left( {\gamma /{p_{ref}}} \right) 。$ | (12) |
这里pref取海水中的基准声压值1×10−6,图2给出了不同力波阶数作用下的Δγ值,图中的横坐标为海水介质中的噪声频率值。

|
图 2 不同力波作用下的Δγ值 Fig. 2 Under the action of different force waves Δγ value |
可以看出,当噪声频率f值比较小时,尤其对于高阶力波,声压幅值比Δγ的上升趋势较快但初始值较小。但是当f值较大时,可以认为在空气中测量的噪声值加上式(12)中的Δγ声压差,基本上可换算为在水中的噪声。在0阶力波作用下,Δγ的变化比较平缓;在2阶及4阶力波作用下,在f值比较小时,Δγ很小,这可以说明在小噪声频率值时,高阶力波在空气和海水2种介质中的声辐射特性差别比较小,且随着力波阶数的增加,2种介质的差别越小。当 f值超过4时,3种力波引起的声压幅值比Δγ皆趋于平缓,且均接近于65 dB附近。因此在不同力波作用下,在空气和水中的声压相差大约65 dB。
2 海水与空气中噪声仿真对比 2.1 噪声体声网格的建立使用 Ansys Workbench中的Maxwell 仿真软件机泵一体化装置,24槽20级Halbach永磁同步电机转子系统理想状态下的额定负载进行仿真分析,电机具体参数如表1所示,仿真模型如图3所示。
|
|
表 1 电机的基本参数 Tab.1 Basic parameters of motor |

|
图 3 电机二维仿真模型 Fig. 3 Two dimensional simulation model of motor |
将仿真结果代入Harmonic Response模块,计算电机的振动形变,然后运用Harmonic Acoustic模块对电机的噪声进行仿真计算。具体流程如图4所示。

|
图 4 Halbach电机振动噪声仿真流程图 Fig. 4 Flow chart of Halbach motor vibration and noise simulation |
由于不同介质的噪声域不同位置所测量的噪声声压差别较大。因此选取距离电机定子外表面0.01 m处为噪声声压的测量点,并对不同噪声频率下的噪声声压进行仿真测量。图5为空气介质中和海水介质中Halbach结构的永磁同步电机噪声声压级频谱对比图。
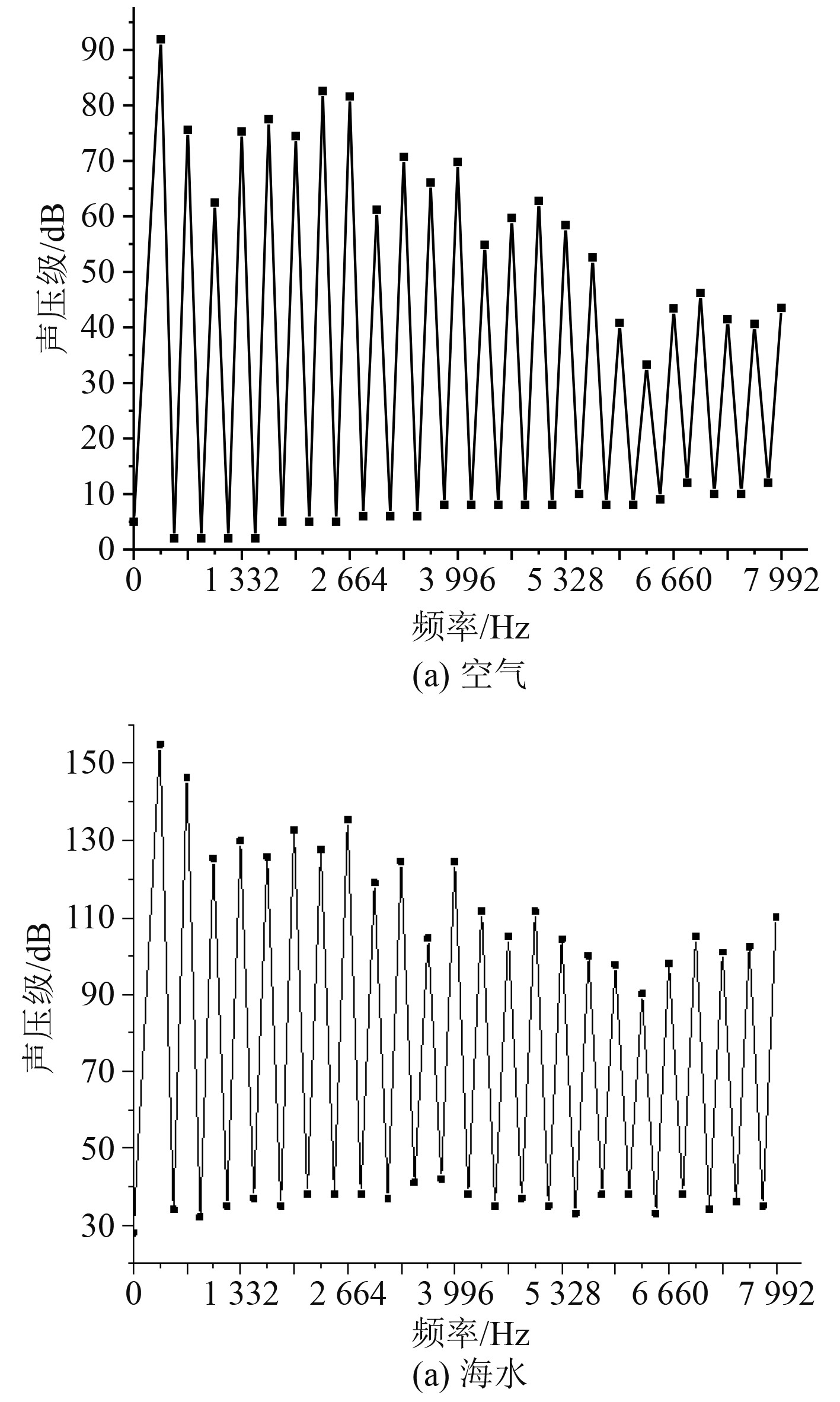
|
图 5 空气和海水中电机噪声声压级频谱对比图 Fig. 5 Spectrum comparison of sound pressure level of motor noise in air and sea water |
可知:1)Halbach结构的永磁同步电机在海水中的噪声声压级明显高于电机在空气中的噪声声压级;2)低频段的噪声对2种介质中的电机噪声总声压级贡献明显大于高频段,说明Halbach结构的永磁同步电机在2种介质产生的噪声频率主要集中在低频段。
将电机噪声域设置为空气和海水2种不同介质,并设置噪声域圆环半径为1 m。图6为Halbach结构的永磁同步电机在空气和海水2种不同介质中噪声峰值时的噪声声压分布。

|
图 6 2种介质在噪声峰值时的声压分布 Fig. 6 Sound pressure distribution of two media at noise peak |
从空气和海水2种不同介质中Halbach结构的永磁同步电机噪声分布可看出:1)在噪声峰值频率下电机在海水中的噪声声压最大值比其在空气中的噪声声压最大值高出大约65 dB,与理论分析结果相符;2)从电机定子外表面到仿真外围边界,噪声在海水和空气中均会随着传播距离的增加出现衰减现象,但在空气中的噪声衰减速度要明显高于在海水中的衰减速度。因此同一时间范围同一频率下,电机噪声在海水中的传播范围要比在空气中更远。
3 Halbach结构电机噪声抑制由于机泵一体化装置中电机工作时的外部环境是海水,机壳浸入海水之中,比同样工作在空气中的电机拥有更好的冷却条件。同时为了平衡装置水下运行时承受的压强,电机内部一般都会涂抹绝缘油。这些有利的条件都为电机提供了良好的冷却环境,因此,与普通电机相比,工作在水下的电机可拥有较高的热负荷。通过提高电机热负荷,增加电机定子轭厚,进一步研究定子轭厚对电机径向电磁力谐波的影响,从而对电机的振动噪声性能进行优化。
3.1 基于电机热负荷理论优化分析根据热负荷表达式:
| $ Q{\text{ = }}AJ 。$ | (13) |
式中:A为电机的线负荷;J为电流密度。电机线负荷表达式为:
| $ A=\frac{{2mN{I_{{N}}}}}{{{\text{π}} {D_i}}}。$ | (14) |
式中:m为电机相数;N为电机每相串联匝数;IN为电机额定电流;Di为电机定子内径。
电流密度J可表示为:
| $ J = \frac{{{I_1}}}{{a{\text{π}} \left[ {{N_{{\text{t}}1}}{{\left( {\dfrac{{{d_1}}}{2}} \right)}^2} + {N_{{\text{t}}2}}{{\left( {\dfrac{{{d_2}}}{2}} \right)}^2}} \right]}} 。$ | (15) |
式中:I1为电机定子电流的有效值;a为并联支路数;Nt1、Nt2均为电机定子线圈的导线根数;d1和d2均为导线的直径。
永磁同步电机在外部工作环境为海水时,线负荷可取到90~110 A/mm。根据式(14)、式(15),可通过减小定子内径提高线负荷,改变电机定子线圈的导线根数、改变导线的直径来提高电流密度从而提高热负荷,从而达到可以增加定子轭厚的目的,并对电机的径向电磁力谐波产生影响。本文提出的改进方案为:改变定子内径,同时改变电机定子线圈的导线根数和导线的直径来降低槽长,进而增大热负荷。具体方案参数如表2所示,电机定子槽模型如图7所示。
|
|
表 2 电机优化参数表 Tab.2 Motor optimization parameter table |

|
图 7 电机定子槽模型 Fig. 7 Motor stator slot model |
在实际应用中,机泵一体化装置中的驱动电机工作在带载状态,因此对电机优化方案进行负载仿真。求径向气隙磁密,求出的气隙磁密波形如图8所示。

|
图 8 电机负载气隙磁密波形 Fig. 8 Air gap flux density waveform of motor under load |
求出优化后电机负载气隙磁密波形并与原电机负载气隙磁密波形对比,进行傅里叶分解,分解后对比如图9所示。

|
图 9 电机优化前后气隙磁密对比 Fig. 9 Comparison of air gap magnetic density before and after motor optimization |
可以看出,电机优化前后的基波气隙磁密幅值相近,电机优化后基本上对各个频率下的谐波含量都起到了抑制作用。其中对3、5、7次谐波的抑制作用比较明显,优化后气隙磁密波形的正弦性得到了提升。
根据谐波畸变率公式:
| $ THD = \sqrt {\sum\limits_{n = 2}^H {{{\left(\frac{{{G_n}}}{{{G_1}}}\right)}^2}} } 。$ | (16) |
式中:G为谐波电流的有效值;H为谐波阶数的上限值。计算优化前后电机的谐波畸变率,计算结果如表3所示。
|
|
表 3 电机优化前后谐波畸变率 Tab.3 Harmonic distortion rate before and after motor optimization |
可以看出,电机优化后谐波畸变率降低,但幅度并不明显。结合前文电机优化前后气隙磁密对比分析,可认为电机优化后性能得到了提升。
3.3 优化电机噪声仿真分析运用电机噪声分析模块,选取距离电机定子外表面0.01 m处为噪声声压的测量点对优化前后电机进行噪声仿真。优化前后电机的噪声声压级曲线对比如图10所示。
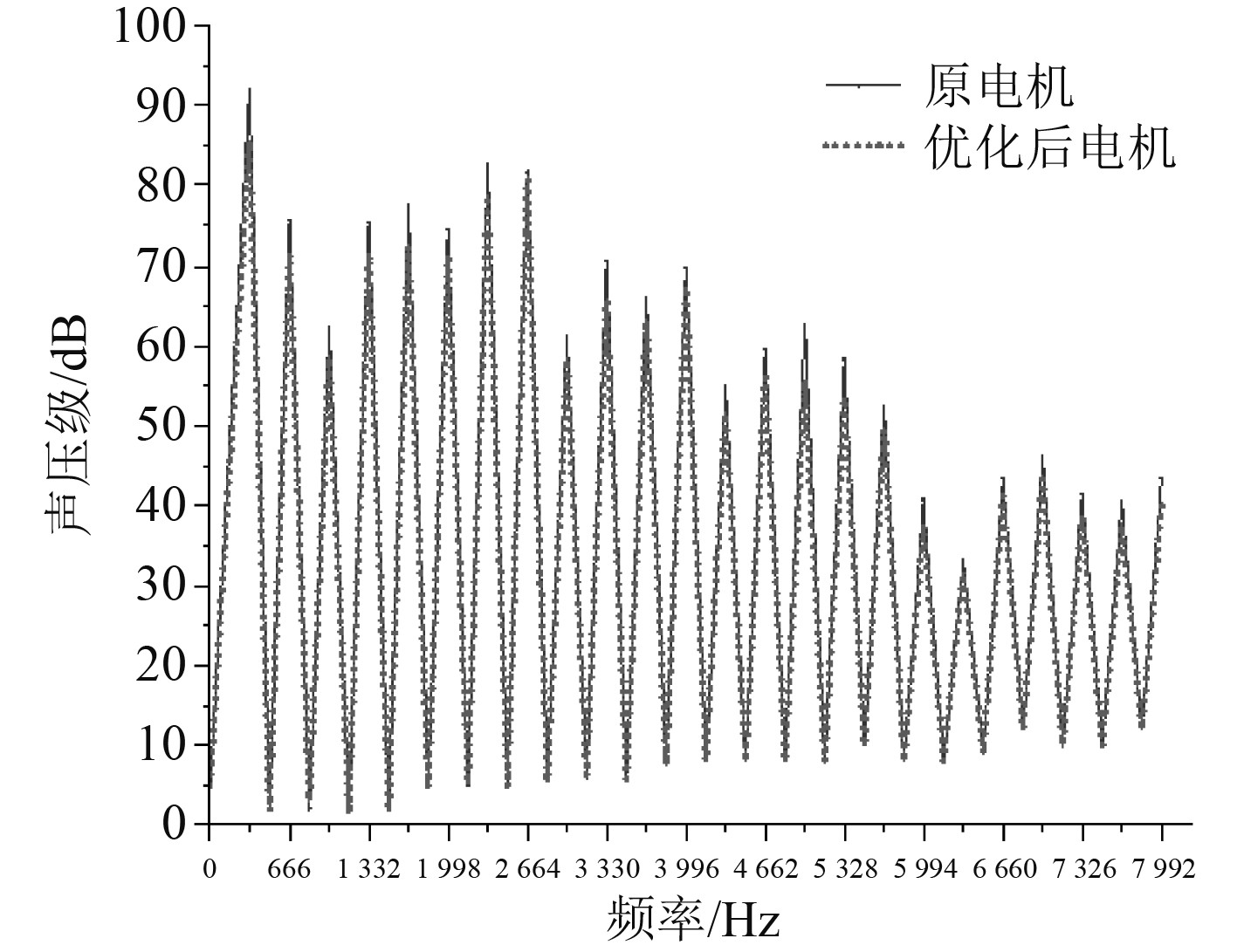
|
图 10 电机噪声频谱曲线对比图 Fig. 10 Comparison diagram of motor noise spectrum curve |
可以看出,增加电机定子轭厚的电机优化方案可在一定程度上降低电机的噪声总声压级。
1)在电机噪声声压级最大的频率段附近时,电机噪声由优化前的91.98 Hz降低到优化后的85.68 Hz;
2)优化前后电机均在333.3 Hz的整数倍附近产生较大的噪声,且优化后的电机在不同频率段的噪声声压级均有不同程度的降低;
3)电机的主要噪声点产生在低频段较多,4 000 Hz后的噪声声压级有明显的下降。
4 结 语本文介绍了电机的噪声及其传播原理,通过理论分析求得电机在2种介质中的噪声声压级差异,并利用有限元Ansys软件对Halbach结构的永磁同步电机水下以及空气中的噪声进行仿真对比分析。分析结果验证了理论分析的正确性,运用电机热负荷理论提出可以通过增加定子轭厚来改善电机的振动噪声性能,并提出具体优化方案,最后通过仿真验证了方案的可行性。
| [1] |
马伟明. 舰船综合电力系统中的机电能量转换技术[J] . 电气工程学报, 2015, 10(4): 3-10. MA Weiming Electromechanical energy conversion technology in ship integrated power system [J]. Journal of electrical Engineering, 2015, 10 (4): 3-10. |
| [2] |
高海波. 吊舱式电力推进装置的发展及应用[J] . 武汉理工大学学报(交通科学及工程版), 2006(2): 77–80. GAO Haibo Development and application of pod type electric propulsion device [J]. Journal of Wuhan University of Technology (Traffic Science and Engineering Edition), 2006(2): 77–80. |
| [3] |
LENA Bergh. Electrical systems in pod propulsion[D]. Chalmers University of Technogy, 2007.
|
| [4] |
陈亚听, 黄友朋. 电力推进的好处[J] . 船电技术, 2001, (5): 48–50. CHEN Ya-Ting, HUANG You-Peng. Advantages of electric propulsion [J]. Marine electric technology, 2001, (5): 48–50. |
| [5] |
JORDAN H. Gerauscharme Elektromotoren [M] . Verlag W. Girardet. Essen, 1950.
|
| [6] |
ELLISON A J, YANG S J. Calculation of acoustic power radiated by electric machine[J]. Acoustics, 1971(25): 28-34. |
| [7] |
ZHU Z Q. Instantaneous magnetic field distributíon in brushless permanent magnet DC motors, Part 1: open-circuít field[J]. IEEE Transactions on Magnetics, 1993, 29(1): 124-135. DOI:10.1109/20.195557 |
| [8] |
ZHU Z Q, HOWE D. Instantaneous magnetic field distríbution in brushless permanent magnet DC motors, Part II: armature-reaction field[J]. IEEE Transactions on Magnetics, 1993, 29(1): 136-142. DOI:10.1109/20.195558 |
| [9] |
ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors, Part III: effect of stator slotting[J]. IEEE Transactions on Magnetics, 1993, 29(1): 143-151. DOI:10.1109/20.195559 |
| [10] |
ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors, Part IV: magnetic field on load[J]. IEEE Transactions on Magnetics, 1993, 29(1): 152-158. DOI:10.1109/20.195560 |
| [11] |
YU H, TIAN L, ZHANG G. Transfer path analysis of structural vibration on propulsion motor[C]// IEEE Magnetics Conference, 2015.
|
| [12] |
赵旭. 水下航行器推进电机设计及减振降噪研究[D] . 沈阳: 沈阳工业大学, 2016.
|
 2023, Vol. 45
2023, Vol. 45
