海上风机支撑结构长期处于各种交变载荷的作用下,在经过足够多的循环之后支撑结构会形成裂纹,随着交变载荷循环次数的增加,裂纹不断发展扩大,最终结构将无法正常运行并产生断裂破坏[1]。因此,对于海上风机支撑结构在服役期正常运行情况下,受到外部海洋环境载荷作疲劳损伤分析,具有重要意义。
Stieng等[2]对于不同外部海洋环境条件下的海上风机疲劳热点位置以及分布概率进行研究,得出海上风机结构在波浪载荷单独作用下的疲劳损伤值大于单独风载荷作用。而且风浪载荷耦合作用下,海上风机的基础结构相较于塔架结构对疲劳更加敏感。Nispel等[3]在对海上风机疲劳热点位置分布概率的分析基础上,对海上风机疲劳热点出现的位置提出了新见解。孟繁鑫[4]在建立海上风机导管架式的基础上,忽略海流载荷的作用,仅对风浪联合作用下导管架式海上风机支撑结构的时域疲劳进行分析,并提出一种管节点的优化方法。王德如[5]建立了海上风机三桩式支撑结构,对风浪联合作用下的海上风机支撑结构疲劳进行分析,得出风机支撑结构在极限载荷下的疲劳寿命。
本文以美国能源国家实验室NREL开发的5 MW海上风机单桩式支撑结构为研究对象,对海上风机支撑结构在风浪流共同作用下的疲劳损伤进行时域分析和理论验证计算,探讨了海上风机结构物时域疲劳随风、浪、流的变化规律情况,为后续海上风机的设计与建造提供参考依据。
1 时域疲劳分析理论MLife是由NREL开发的风机疲劳计算软件,能够在考虑湍流风场变化、风机运行状态变化下,完成风机在运营期内结构的疲劳损伤计算[6]。
MLife通过内嵌雨流计数法统计得到对应应力时程的幅值和循环作用次数,并确定对应应力幅值下结构所能承受的最大循环作用次数:
| $ {N}_{i}={\left(\frac{{L}^{ult}-\left|{L}^{MF}\right|}{\frac{1}{2}{L}_{i}^{RF}}\right)}^{m} 。$ | (1) |
式中:
| $ {L}_{i}^{RF}={L}_{i}^{R}\left(\frac{{L}^{ult}-\left|{L}^{MF}\right|}{{L}^{ult}-\left|{L}_{i}^{M}\right|}\right)。$ | (2) |
式中:
基于Miner疲劳线性累积损伤理论,MLife计算海上风机支撑结构的疲劳损伤累积,公式为
| $ {D}_{i}={\sum }_{i}\frac{{n}_{i}}{{N}_{i}\left({L}_{i}^{RF}\right)}。$ | (3) |
式中:
| $ {D}_{\text{total}}={\sum }_{j}{\sum }_{i}\frac{{n}_{ji}^{\text{Life}}}{{N}_{ji}}。$ | (4) |
式中:
基于FAST建立整体模型,输出VTK文件。通过ParaView软件,对模型进行可视化处理[7]。计算模型如图1所示,风机具体参数如表1所示。

|
图 1 5 MW单桩式风机整体模型 Fig. 1 Overall model of 5 MW single pile wind turbine |
|
|
表 1 NREL 5 MW风机参数 Tab.1 NREL 5 MW wind turbine parameters |
海上风机分为正常运行状态、停机状态、紧急停机状态3种不同的工作状态[8]。本文忽略极端载荷的影响,仅考虑风机在正常运行下,外部风浪流等海洋环境载荷对风机疲劳寿命的影响,具体工况设置如表2所示。
|
|
表 2 工况设计 Tab.2 Design of working conditions |
其中,工况DCL1~DCL4为正常4个风浪流耦合工况,工况DCL5~DCL8为风机在额定风速11.4m/s运行情况下,通过改变波浪入射角度、海流入射角度以达到考虑风浪夹角、海流夹角对风机整体响应的影响,而设置的对照工况。
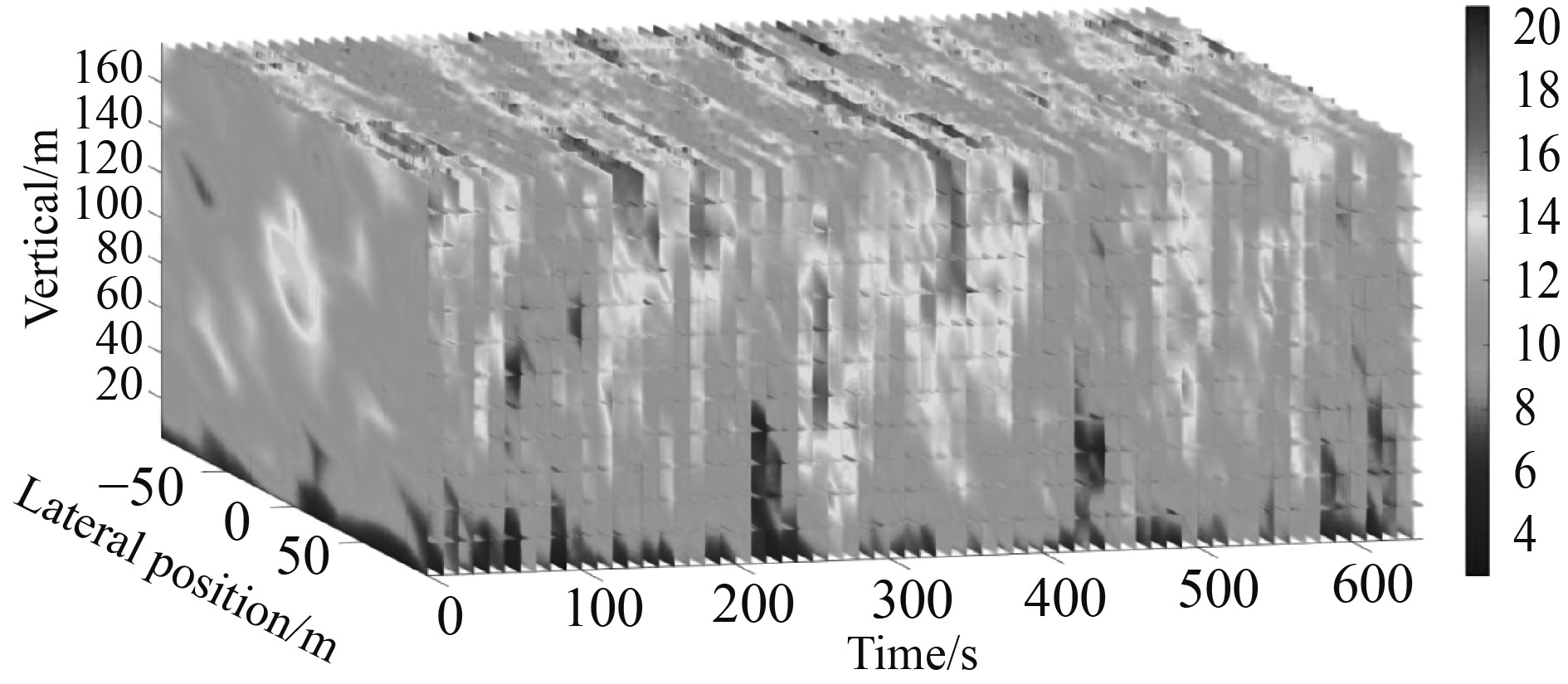
|
图 2 Von Karman风谱11.4 m/s风轮平面风速时程分布图 Fig. 2 Von Karman wind spectrum 11.4 m/s wind rotor plane wind speed time-history distribution |
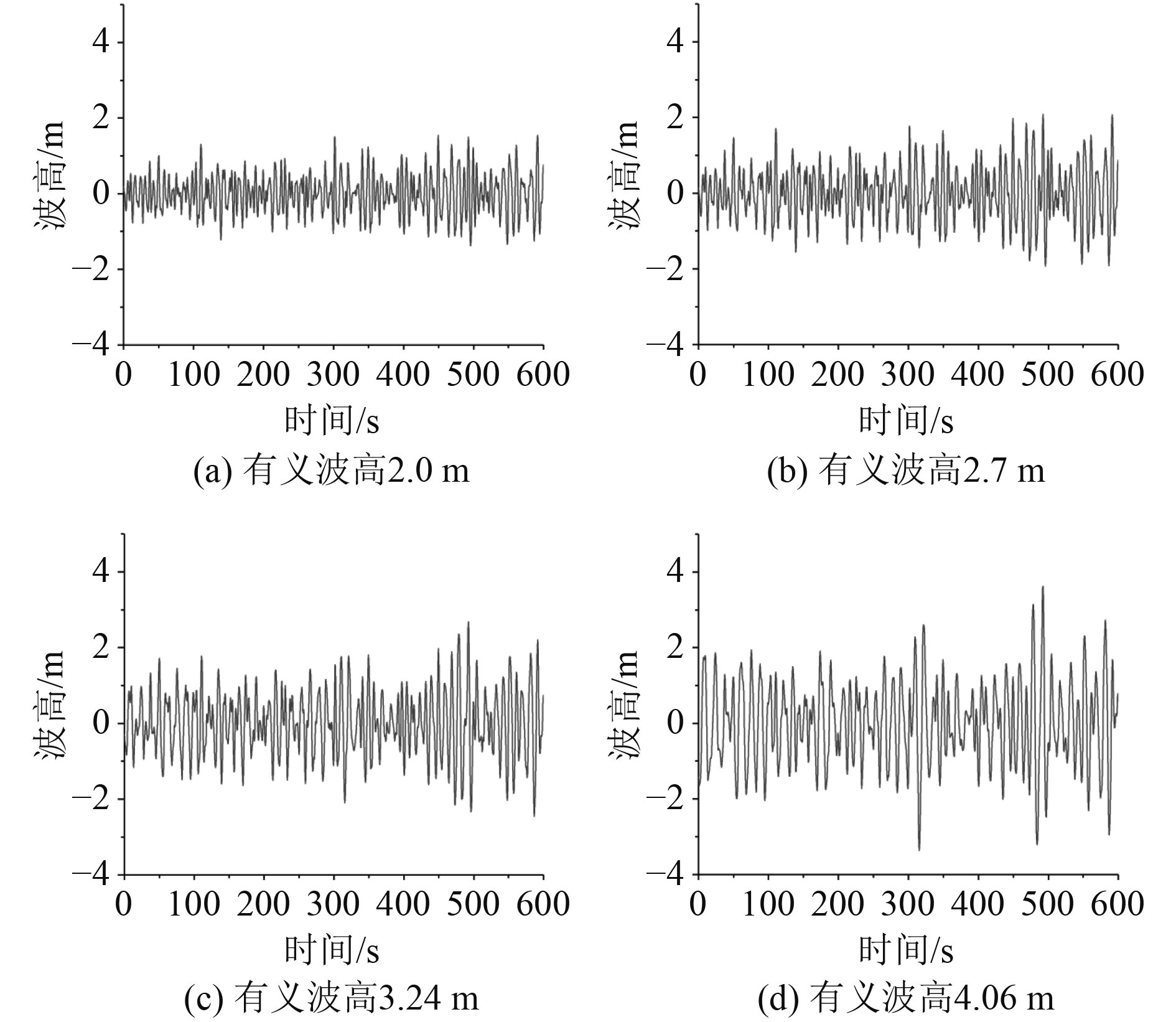
|
图 3 不规则波波高时程图 Fig. 3 Irregular wave height time history |
计算流程图如图4所示。
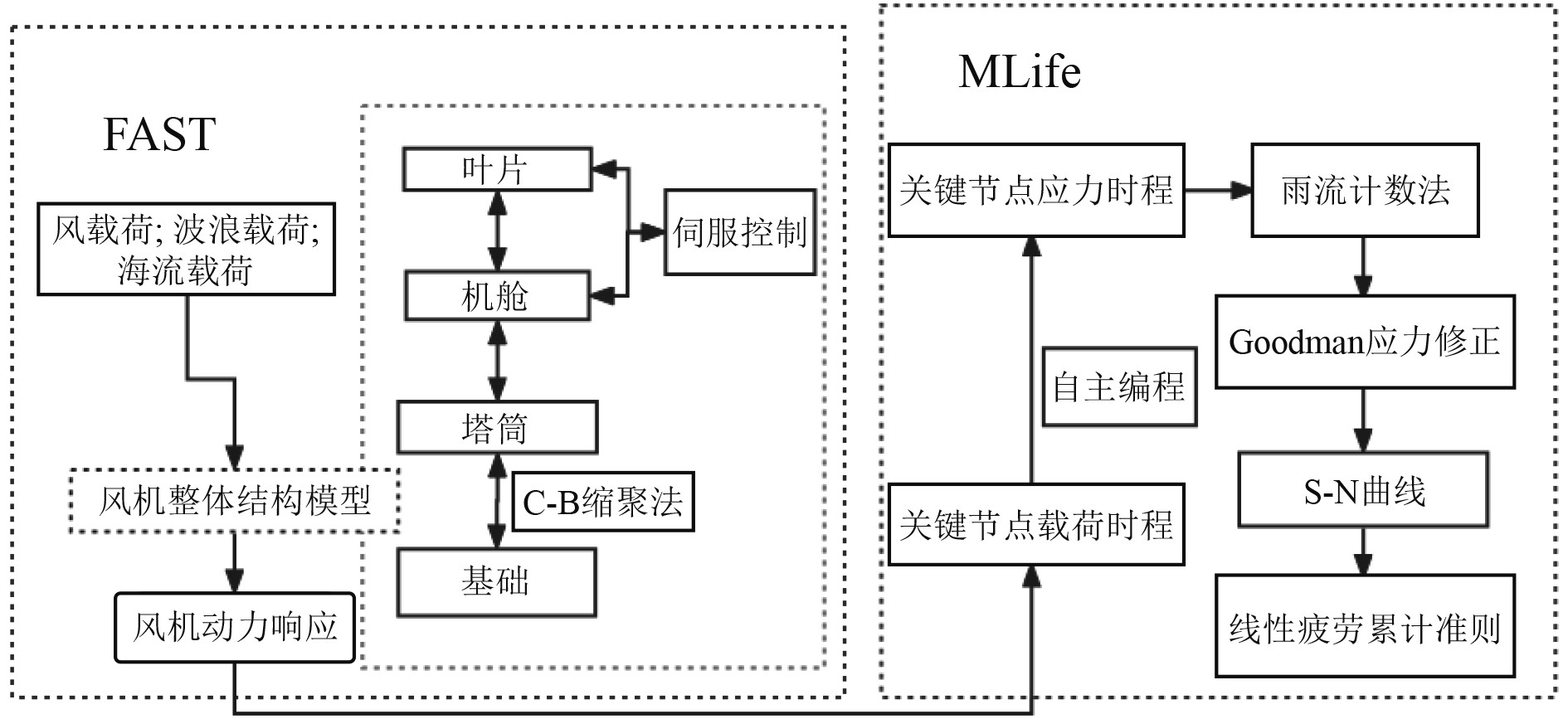
|
图 4 FAST联合MLife联合疲劳分析流程 Fig. 4 FAST combined with MLife combined fatigue analysis process |
1)风浪流耦合工况DCL1~DCL4,疲劳计算结果4组风浪流耦合工况DCL1~DCL4对选定的3个节点进行载荷内力时程转换,以与风浪流入射角度一致的0°方向的热点应力时程为例,4个工况下0°方向节点的应力时程如图5所示。
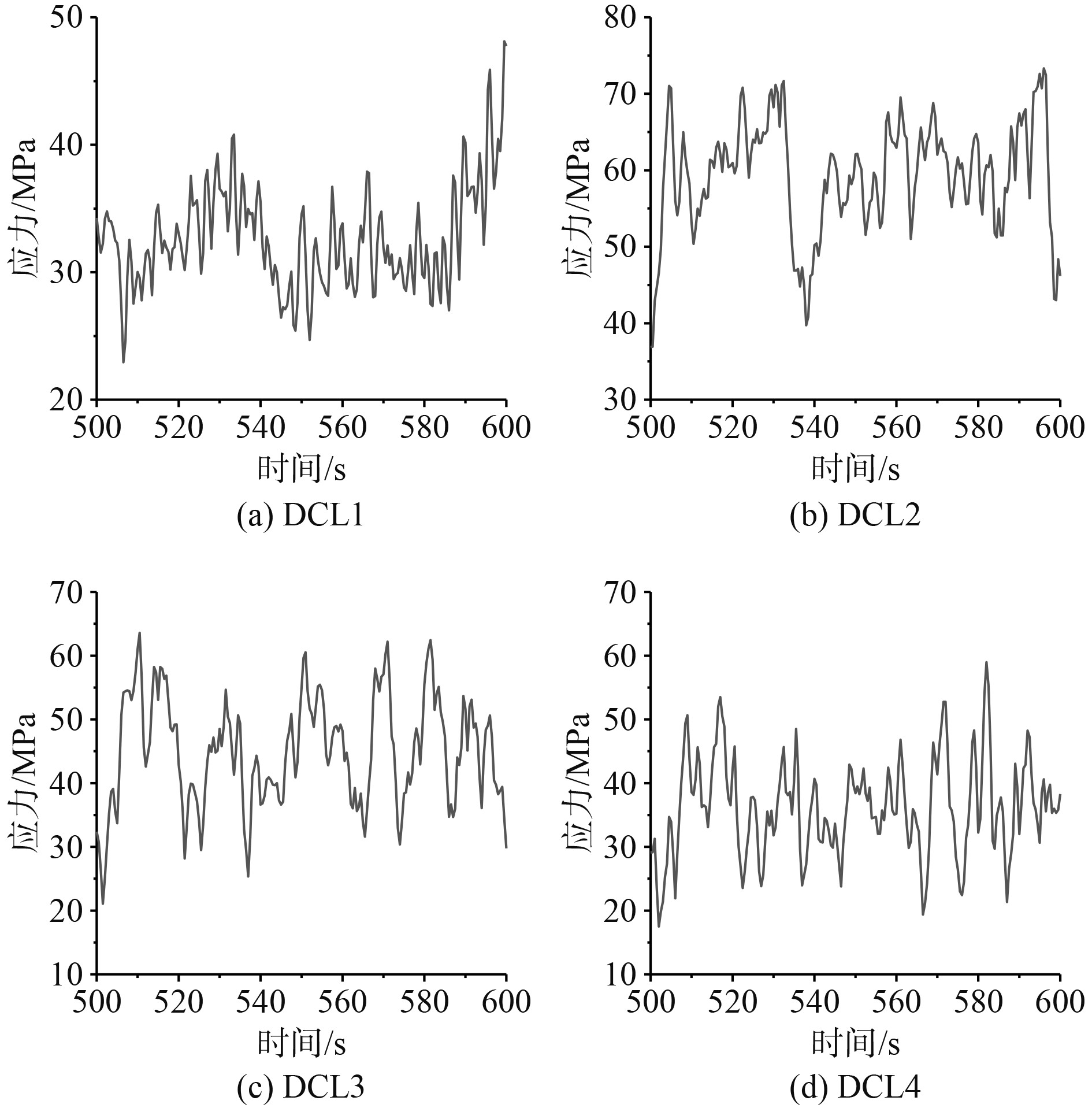
|
图 5 风浪流耦合工况DCL1~DCL4应力时程 Fig. 5 Wind-wave-current coupling condition DCL1-4 stress time history |
MLife通过得到的节点应力时程,输出了选定节点短期1 s内疲劳损伤的次数,输出结果为
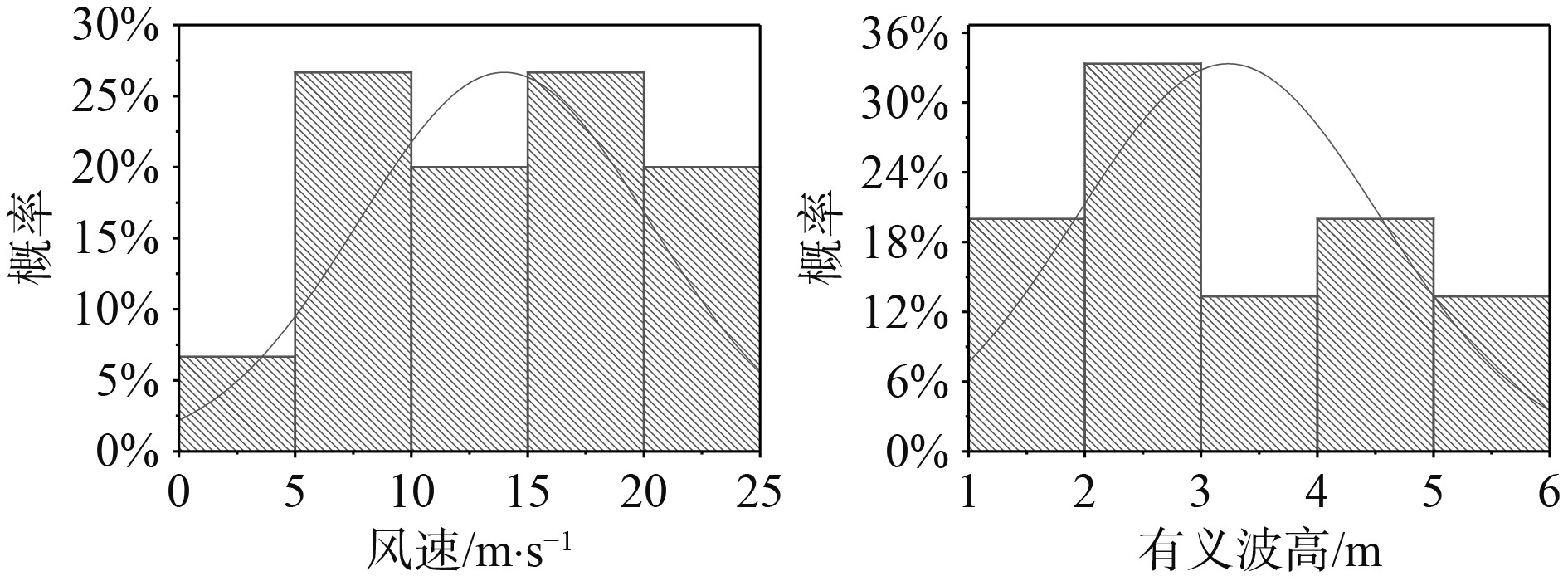
海上风机支撑结构在其使用寿命服役期内会受到不同荷载工况的组合,为了能够精确地预测支撑结构的疲劳损伤,在进行疲劳损伤计算时,应当尽可能多地涵盖各种运行工况。通过各工况疲劳损伤值与其在服役期间发生的概率,进行叠加计算可得到海上风机支撑结构总的疲劳损伤值。各工况出现概率,基于海洋环境数据进行概率分析,各风速和波浪出现的概率如图6所示。拟合得到各工况出现的概率为:DCL1为37.6%,DCL2为28.6%,DCL3为11.4%,DCL4为22.4%。各节点疲劳损伤状况如表3所示。
|
图 6 风和波浪出现概率 Fig. 6 Probability of wind and waves |
|
|
表 3 风浪流耦合工况下25年内疲劳损伤结果 Tab.3 Fatigue damage results in 25 years under wind-wave-current coupling conditions |
计算结果表明,单工况下各节点的疲劳损伤随着气动载荷和水动力载荷的增大而增大,而对于同一工况下,不同角度下节点的疲劳损伤值差异变化幅度较小,节点1(0°方向)与节点2(45°方向)损伤值相等,略大于节点3(90°方向)。考虑安全系数
2)风浪夹角工况DCL5~DCL6,疲劳计算结果
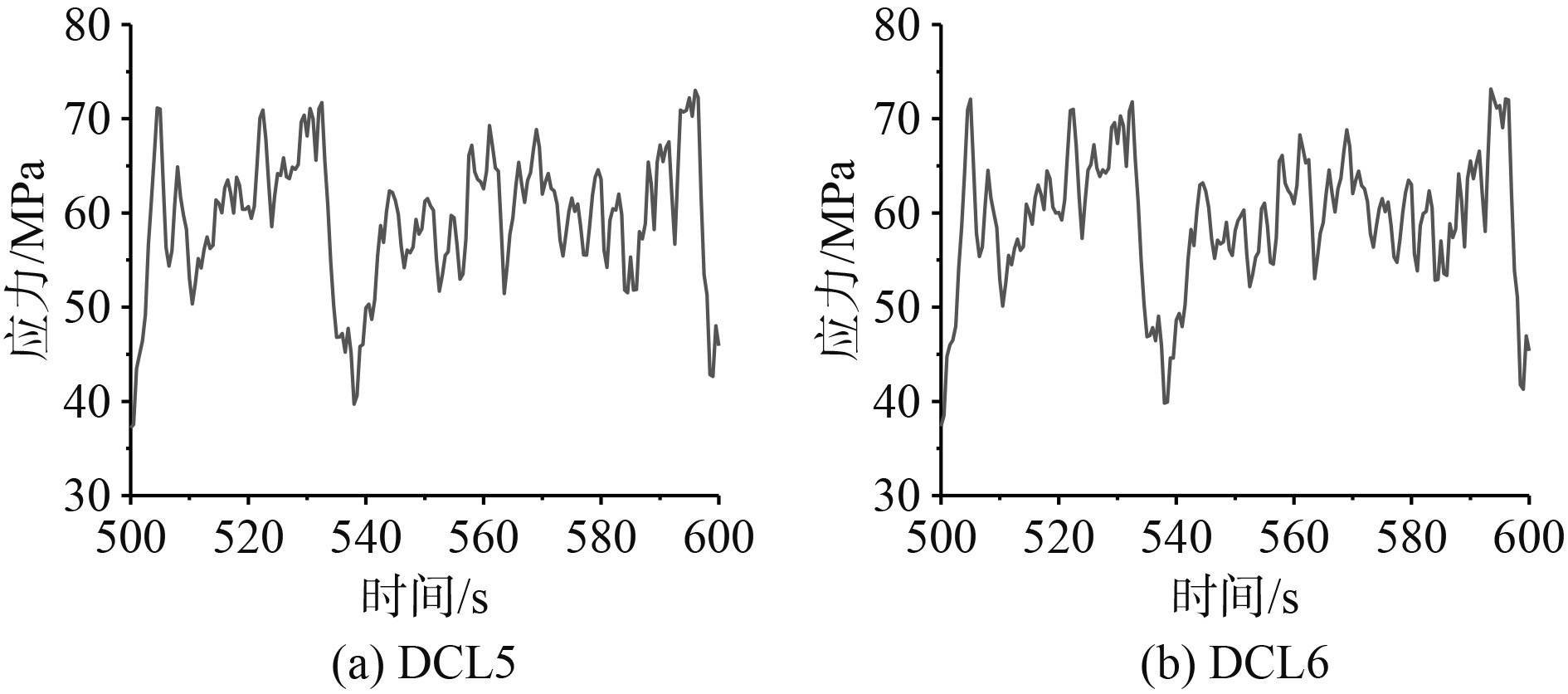
DCL4工况下风浪夹角为45°,海流载荷与波浪载荷的角度一致,DCL5工况下风浪夹角为90°,海流载荷与波浪载荷角度一致,以节点1(0°方向)为例,其500~600 s热点应力时程如图7所示。
|
图 7 风浪夹角工况DCL5~DCL6热点应力时程图 Fig. 7 Time-history diagram of hot spot stress in DCL5-6 wind-wave angle condition |
DCL5与DCL6均为对比工况,均不考虑在服役期间出现概率。各节点MLife计算疲劳损伤结果如表4所示。
|
|
表 4 风浪夹角工况下25年内疲劳损伤结果 Tab.4 Fatigue damage results in 25 years under wind and wave angle conditions |
可知,在工况DCL5和DCL6条件下,各个节点的疲劳损伤值均大于工况DCL2,这说明风浪之间角度的改变对风机支撑结构疲劳损伤有较大的影响。工况DCL5最大疲劳损伤发生在节点2(45°方向),疲劳损伤结果为0.02537。工况DCL6最大疲劳损伤发生在节点3(90°方向),疲劳损伤结果为0.02533,这说明风浪角度的改变对海上风机支撑结构,在其相应角度下节点位置造成的疲劳损伤大于其他位置。
2)浪流夹角工况DCL7-DCL8,疲劳计算结果
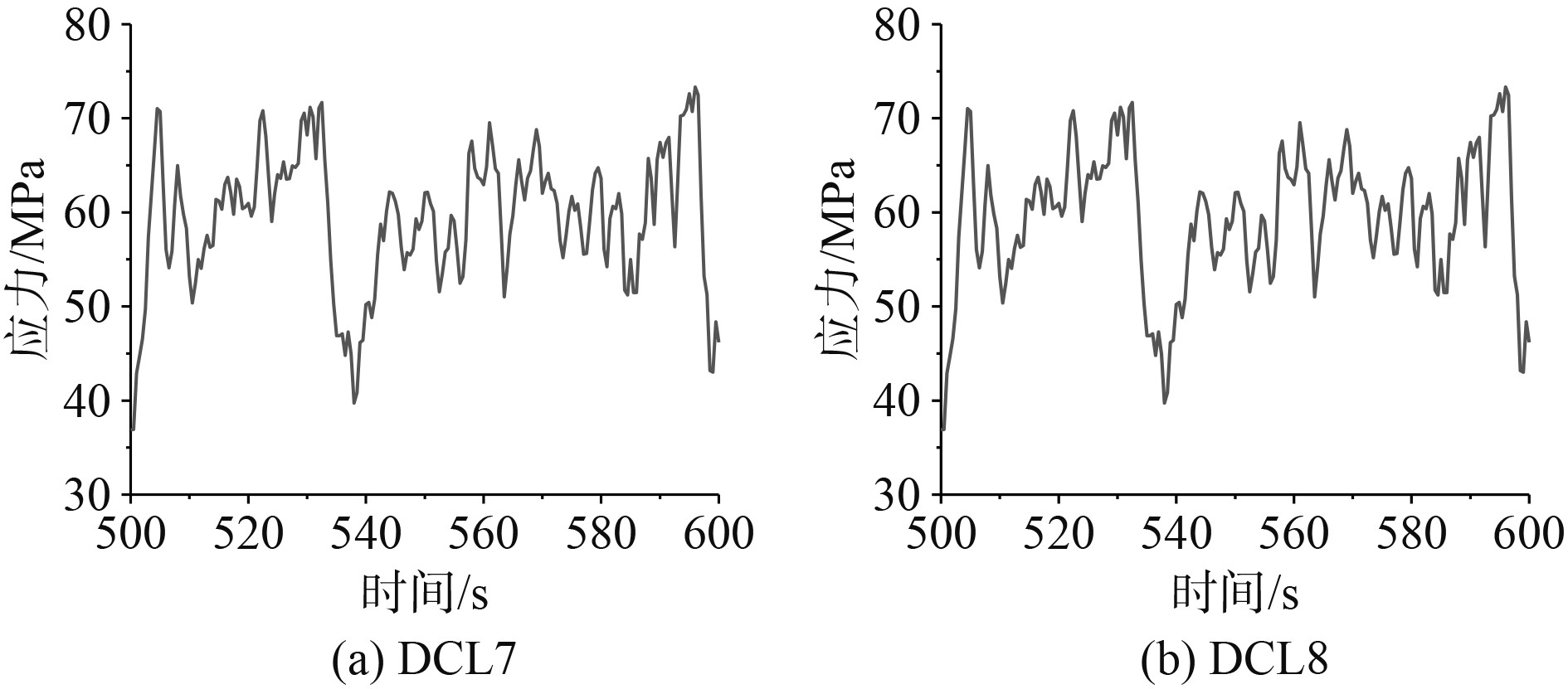
DCL7工况下,海流角度为45°,风载荷与波浪载荷入射角度一致,DCL8工况下海流角度为90°,风载荷与波浪载荷入射角度一致,以节点1(0°方向)为例,其500~600 s热点应力时程如图8所示。
|
图 8 浪流夹角工况DCL7~DCL8热点应力时程图 Fig. 8 Time history diagram of hot spot stress for DCL7-8 under wave-current angle condition |
DCL7与DCL8均为对比工况,均不考虑在服役期间出现概率。各关键节点MLife计算疲劳损伤结果如表5所示。
|
|
表 5 浪流夹角工况下25年内疲劳损伤结果 Tab.5 Fatigue damage results in 25 years under wave-current angle conditions |
可知,在工况DCL7和DCL8条件下,各个节点的疲劳损伤值均大于工况DCL2,这说明浪流之间角度的改变对风机支撑结构疲劳损伤有较大影响。工况DCL7最大疲劳损伤发生在节点2(45°方向),疲劳损伤结果为0.02387,工况DCL8最大疲劳损伤发生在节点3(90°方向),疲劳损伤结果为0.02331。这说明浪流角度的改变对海上风机支撑结构,在其相应角度下节点位置造成的疲劳损伤大于其他位置。
3.2 理论计算验证为了验证MLife疲劳计算结果,通过编写雨流计数法代码,对500~600 s内热点应力时程进行雨流计数,并基于所述时域疲劳计算理论,计算各工况下疲劳损伤数值。
1)风浪流耦合工况下疲劳损伤计算结果
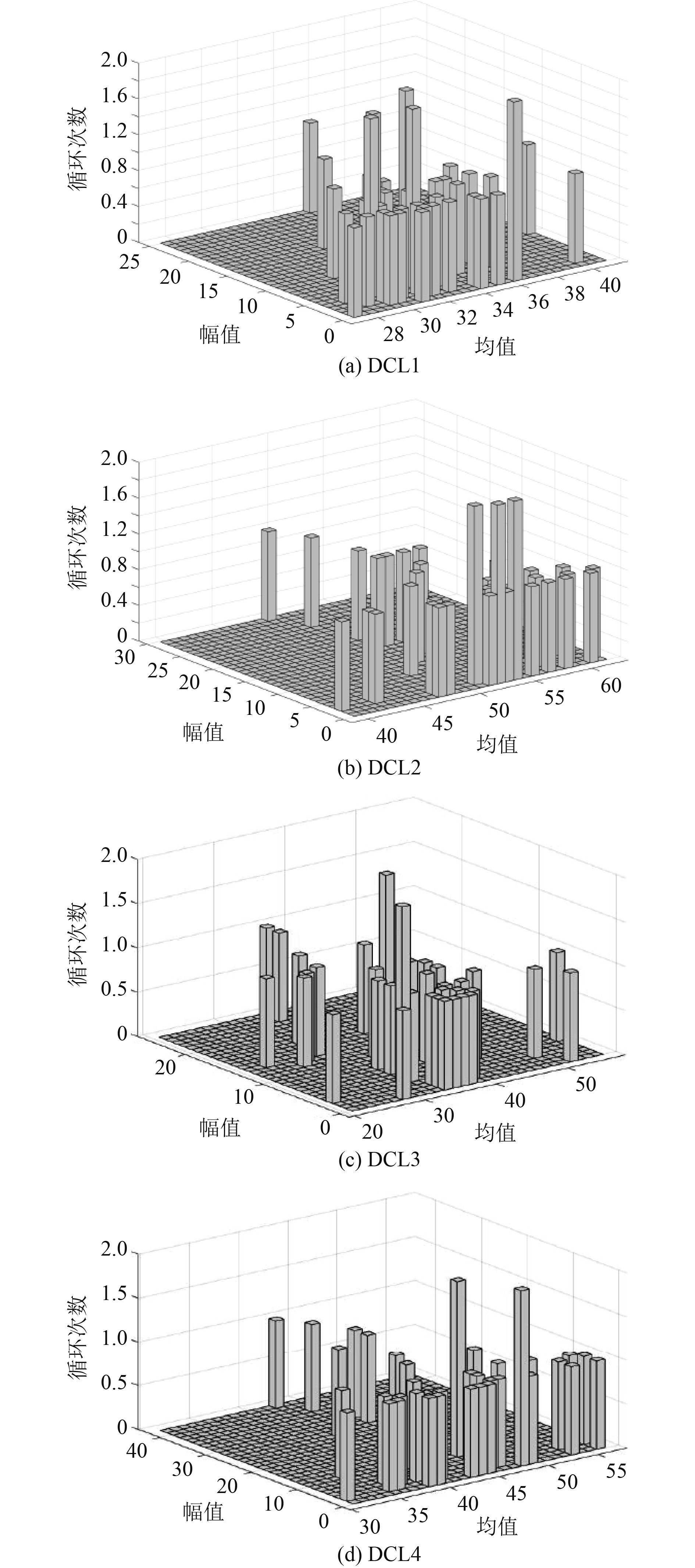
以与风浪流入射角度一致的节点1(0°方向)的热点应力时程为例,进行雨流计数,4个工况DCL1~DCL4雨流计数如图9所示。
|
图 9 风浪流耦合工况DCL1~DCL4雨流计数图 Fig. 9 Wind-wave-current coupling condition DCL1~DCL4 rain flow count diagram |
风浪流耦合工况DCL1~DCL4疲劳理论计算结果如表6所示。
|
|
表 6 风浪流耦合工况下25年内疲劳损伤结果 Tab.6 Fatigue damage results in 25 years under wind-wave-current coupling conditions |
2)考虑风浪夹角工况下疲劳计算结果
工况DCL5~DCL6雨流计数如图10所示。
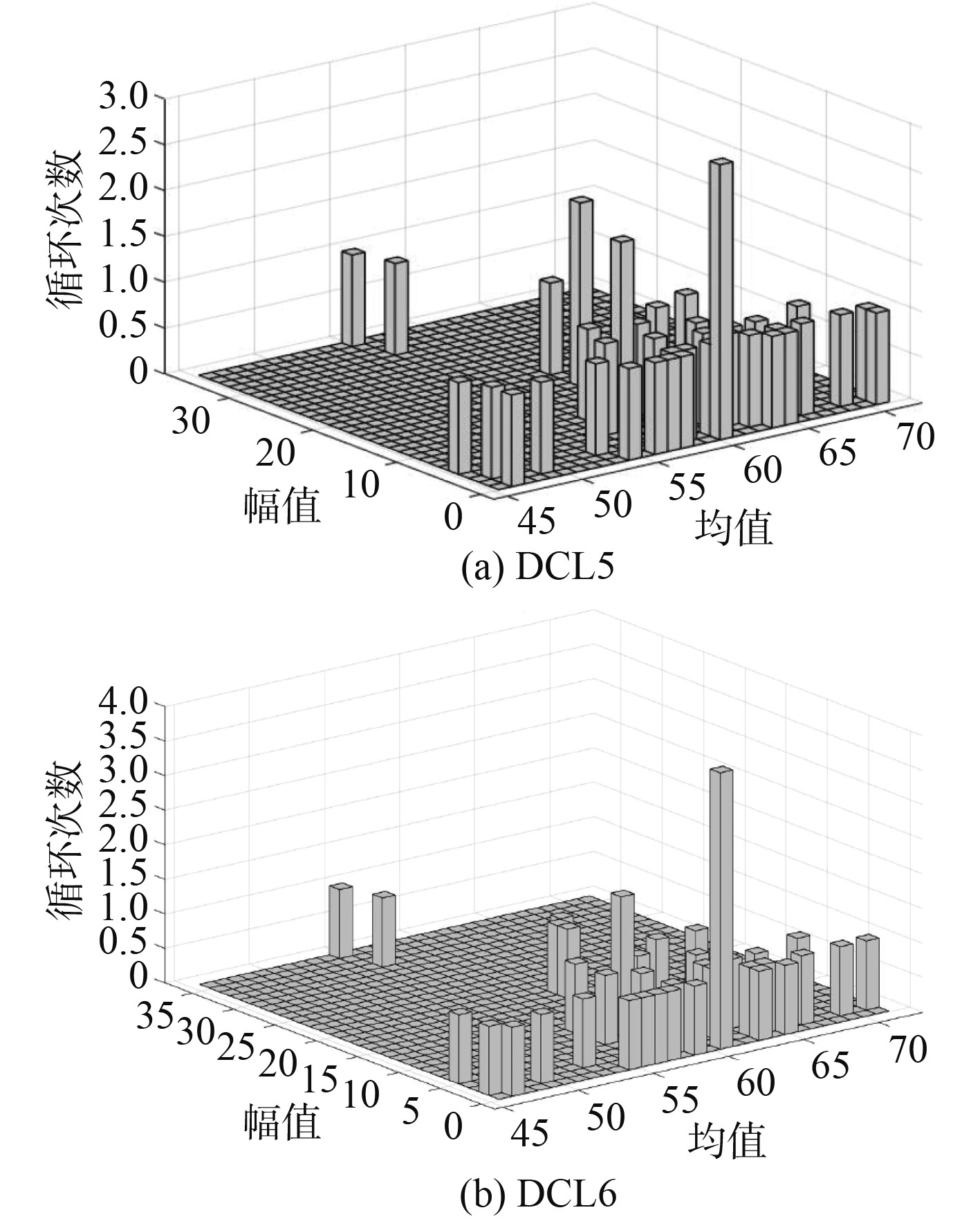
|
图 10 风浪夹角工况DCL5~DCL6雨流计数图 Fig. 10 DCL5~DCL6 rain flow count diagram for wind and wave angle conditions |
风浪夹角工况DCL5~DCL6疲劳理论计算结果如表7所示。
|
|
表 7 风浪夹角工况下25年内疲劳损伤结果 Tab.7 Fatigue damage results in 25 years under wind and wave angle conditions |
3)考虑浪流夹角工况下疲劳计算结果
工况DCL7~DCL8雨流计数如图11所示。
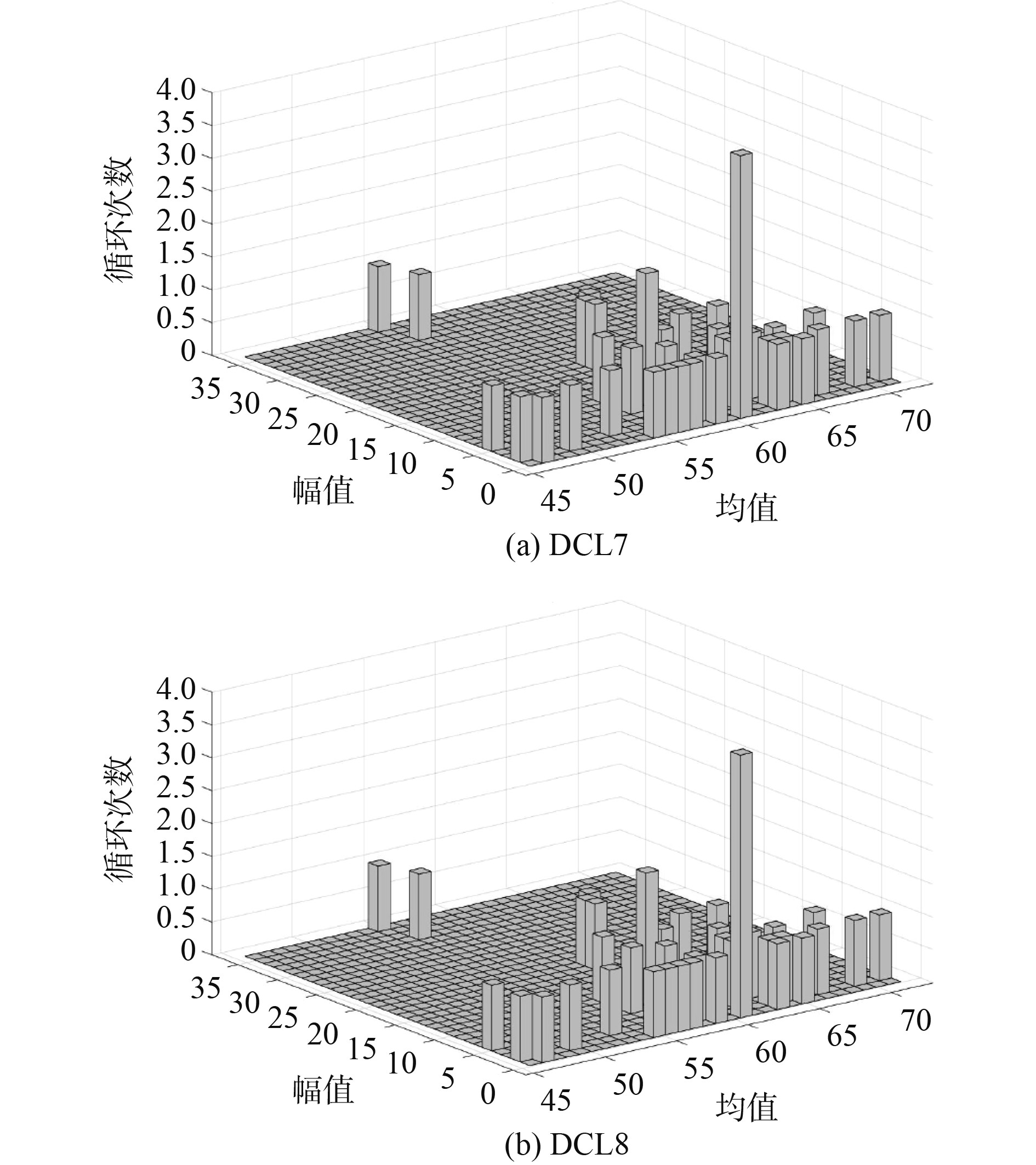
|
图 11 浪流夹角工况DCL7~DCL8雨流计数图 Fig. 11 DCL7~DCL8 rainflow counting diagram for wave and current angle condition |
浪流夹角工况DCL7~DCL8疲劳理论计算结果,表8所示。
|
|
表 8 浪流夹角工况下25年内疲劳损伤结果 Tab.8 Fatigue damage results in 25 years under wave-current angle condition |
对各工况下2种疲劳计算方法下,节点的结果进行整理,如表9所示。疲劳损伤结果由图12和图13所示。
|
|
表 9 计算结果对比 Tab.9 Comparison of calculation results |
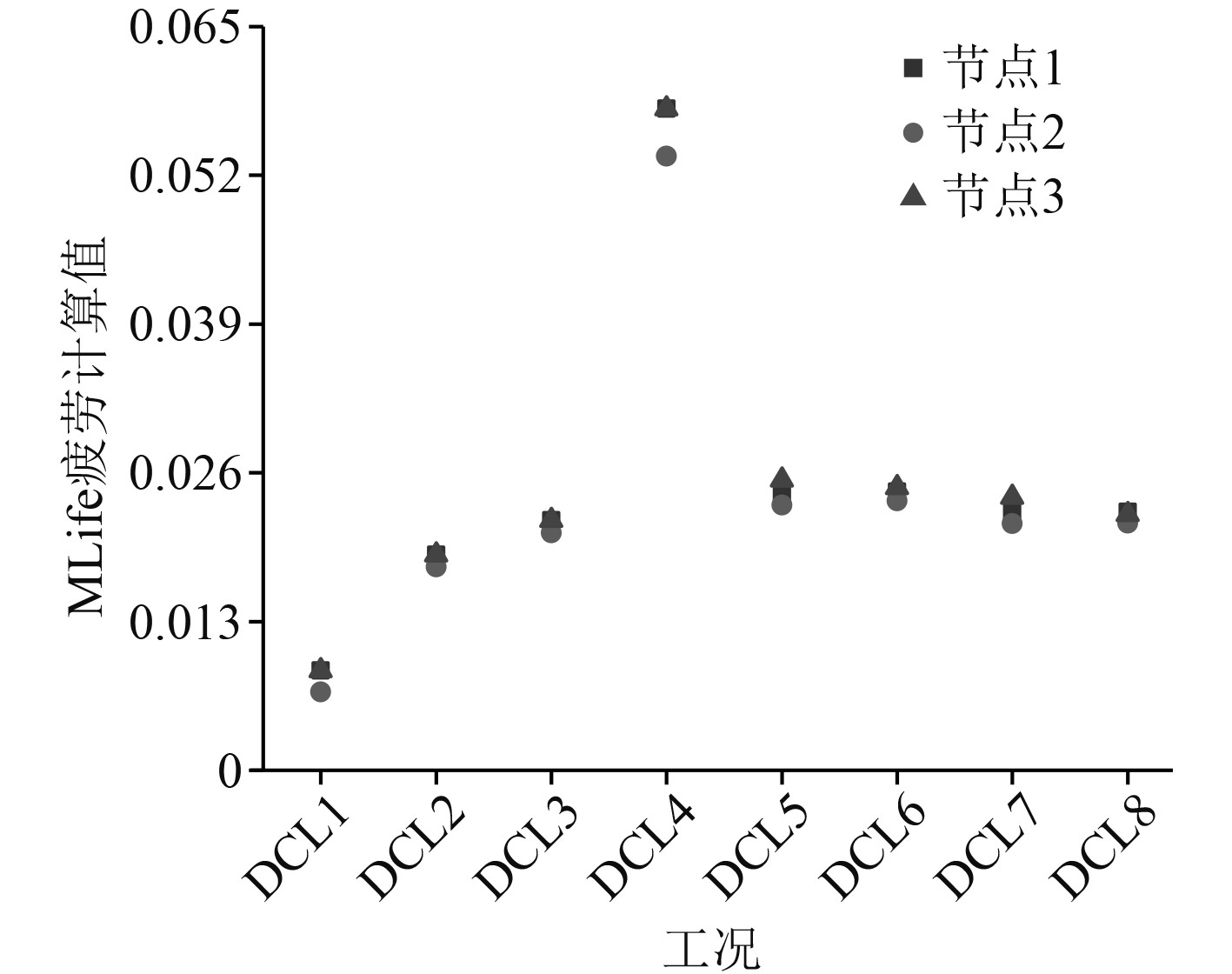
|
图 12 MLife疲劳损伤结果 Fig. 12 MLife fatigue damage results |
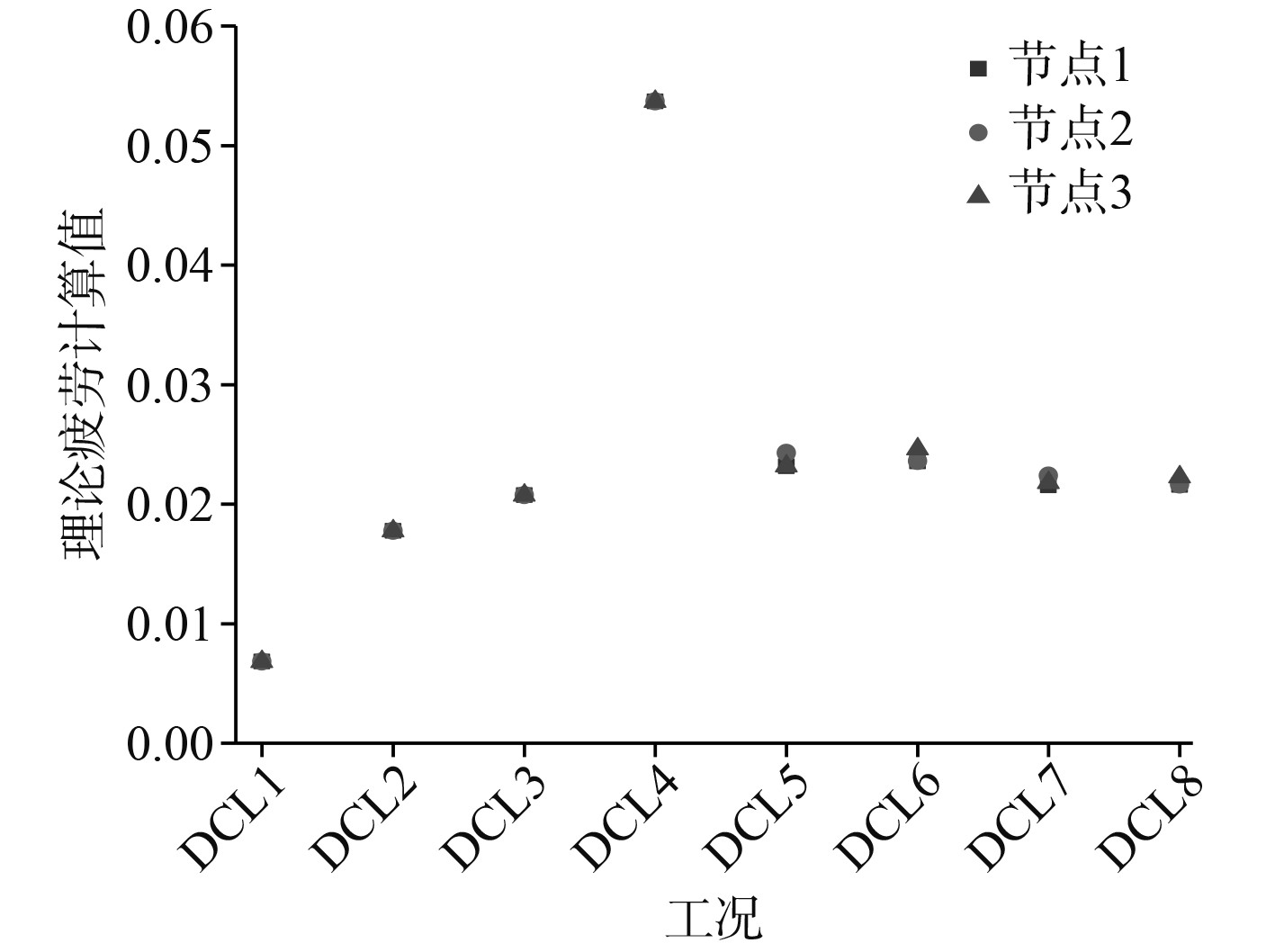
|
图 13 理论计算疲劳损伤结果 Fig. 13 Theoretical calculation of fatigue damage results |
各关键节点的疲劳损伤如表10所示。通过对比分析可发现,MLife计算结果比理论计算结果偏大,平均误差为6.15%小于10%,FAST联合MLife时域疲劳分析,计算结果可靠。
|
|
表 10 计算误差分析 Tab.10 Computational error analysis |
综合考虑本文各工况下的疲劳损伤计算结果,可发现随着风浪流载荷的增大(DCL1~DCL4工况下),海上支撑结构疲劳损伤逐渐增大,DCL4为疲劳损伤最大工况。此外,通过对比工况DCL2和DCL5~DCL8,可发现无论是MLife时域疲劳损伤计算结果还是理论计算结果,海上风机支撑结构在不同的工况下,最大疲劳损伤发生的工况为DCL5~DCL8,也就是风浪角度变化与浪流角度变化的工况。结果表明风浪角度变化工况与浪流角度变化工况,对海上风机支撑结构造成的疲劳损伤均大于风浪流角度一致工况下的疲劳损伤,而且风浪角度变化工况所造成的疲劳损伤比浪流角度变化工况要大。因此,在后续的研究中应重点考虑风浪角度、海流角度变化对海上风机支撑结构造成的疲劳损伤。
4 结 语本文以5 MW海上风机单桩式支撑结构为研究对象,介绍了海上风机时域疲劳分析理论和计算方法。通过FAST与MLife联合时域仿真疲劳分析得出主要结论如下:
1)计算结果表明,海上支撑结构疲劳损伤值随着风浪流载荷的增大而增大;风浪角变化、海流角变化工况下的疲劳损伤均大于对照的风浪流耦合角度一致工况。风浪角变化工况下的疲劳损伤相对于浪流角变化工况而言,损伤值要大。因此,对海上风机支撑结构的疲劳损伤研究应关重点考虑风浪角变化、海流角变化对其产生的影响。
2)基于雨流计数法,设置不同的工况,对关键节点疲劳损伤进行理论计算,最后通过分析2种计算方式得到的结果。结果表明MLife计算对比理论计算,其节点疲劳损伤结果偏大,但总的平均误差为6.15%,小于10%,计算结果可靠。
| [1] |
李境伟, 窦培林, 张兴刚. 超深水半潜式平台典型节点强度分析[J]. 舰船科学技术, 2021, 43(19): 72-78. LI Jingwei, DOU Peilin, ZHANG Xinggang. Analysis of the typical node strength of the ultra-deepwater semi-submersible platform[J]. Ship Science and Technology, 2021, 43(19): 72-78. |
| [2] |
STIENG L E S, HETLAND R, SCHAFHIRT S, et al. Relative assessment of fatigue loads for offshore wind turbine support structures[J]. Energy Procedia, 2015, 80: 229-236. DOI:10.1016/j.egypro.2015.11.426 |
| [3] |
NISPEL A, EKWARO-OSIRE S, DIAS J P. Probabilistic analysis of the fatigue life of offshore wind turbine structures[C]//Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers, 2020, 84249: V012T42A004.
|
| [4] |
孟繁星. 风浪联合作用下的海上风机支撑结构时域疲劳分析[D]. 哈尔滨: 哈尔滨工程大学, 2017
|
| [5] |
王德如. 海上风机固定式三桩支撑结构的疲劳分析[D]. 上海: 上海交通大学, 2017
|
| [6] |
HAYMAN G J, BUHL M. MLife user’s guide Version 1.00[R]. National Renewable Energy Laboratory, USA, 2012.
|
| [7] |
王瑞良. 5 MW风力发电机动态特性仿真[D]. 秦皇岛: 燕山大学, 2015.
|
| [8] |
孙寅博, 窦培林. Truss Spar结构浮式风机基础总体强度分析[J]. 舰船科学技术, 2021, 43(7): 107-110. SUN Yin-bo, DOU Pei-lin. Analysis of the overall foundation strength of Truss Spar structure floating fan[J]. Ship Science and Technology, 2021, 43(7): 107-110. DOI:10.3404/j.issn.1672-7649.2021.04.022 |
 2023, Vol. 45
2023, Vol. 45
